Prediction of the Ultra-Low-Cycle Fatigue Damage of Q345qC Steel and its Weld Joint
Abstract
1. Introduction
2. Theoretical Model for ULCF of Structural Steel
2.1. Continuum Damage Mechanics Model for Monotonic Tension
2.2. Continuum Damage Mechanics Model for ULCF
3. Calibration of Material Parameters for CDM
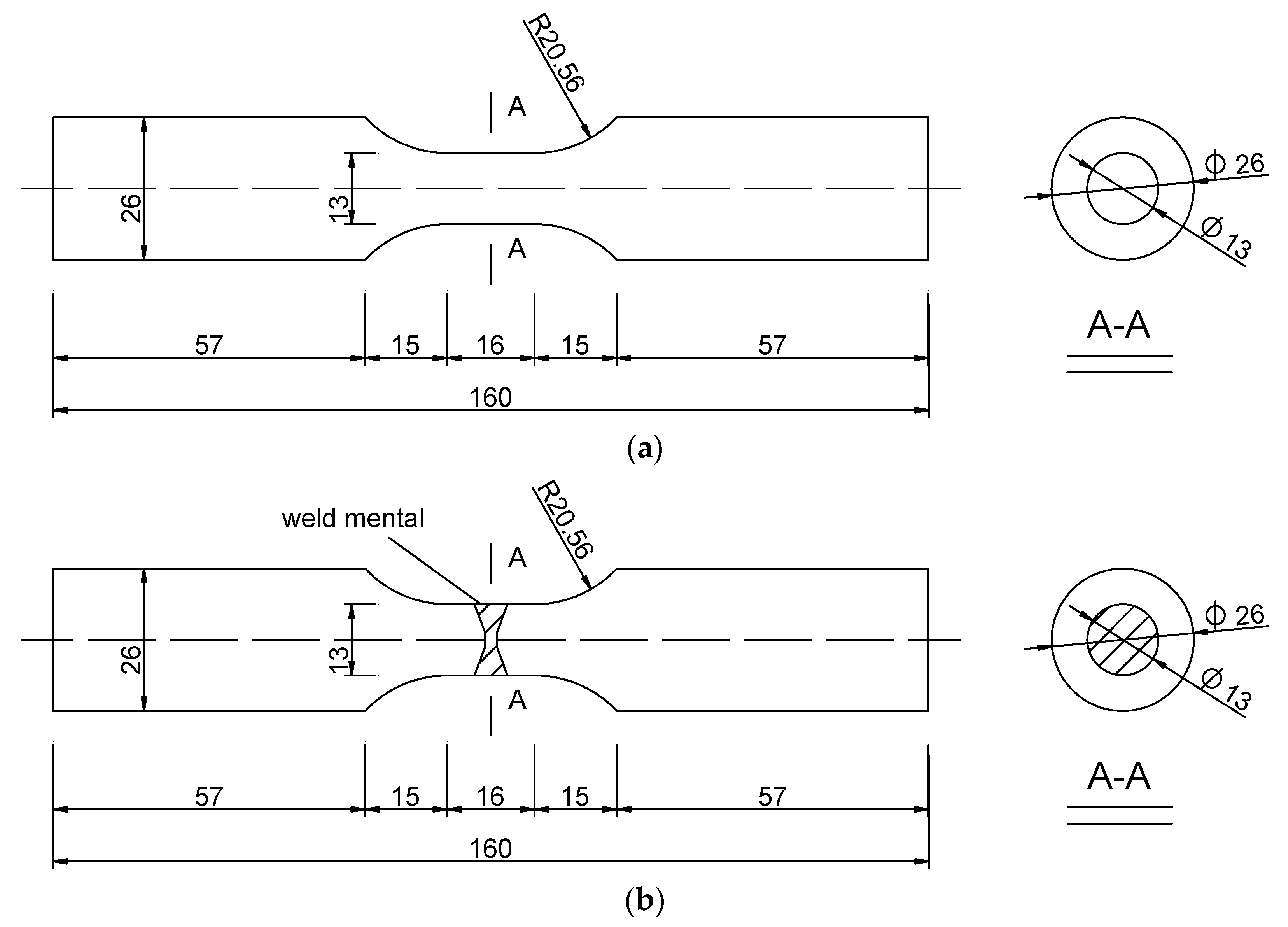
3.1. Uniaxial Tensile Test for Notched Round Bar Specimen
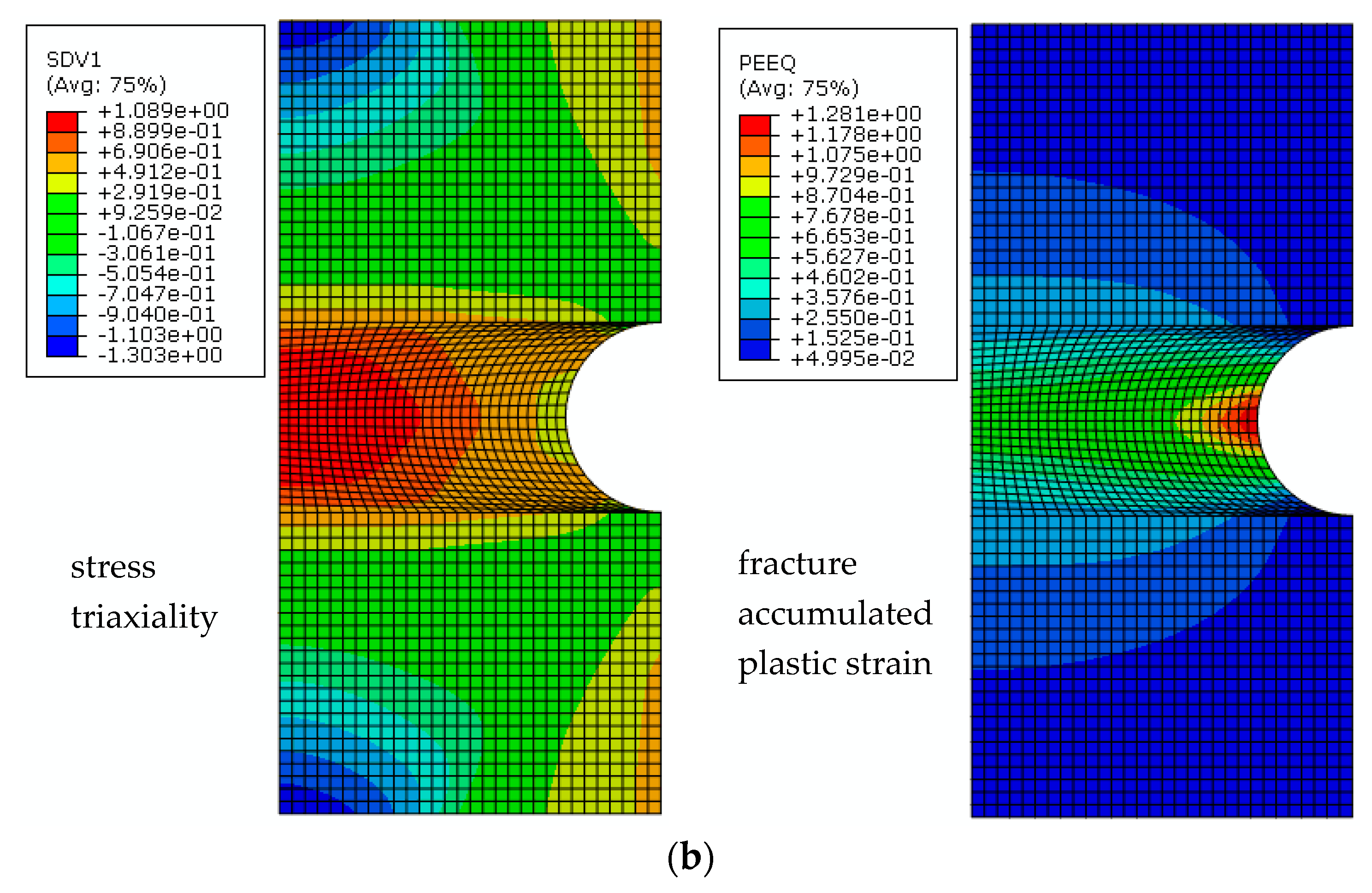
3.2. Calibration of Material Parameters for CDM by Finite Element Analysis
4. ULCF Life Prediction for the Q345qC Base Material and Welded Joints
4.1. ULCF Test for Base Material and Welded Joints
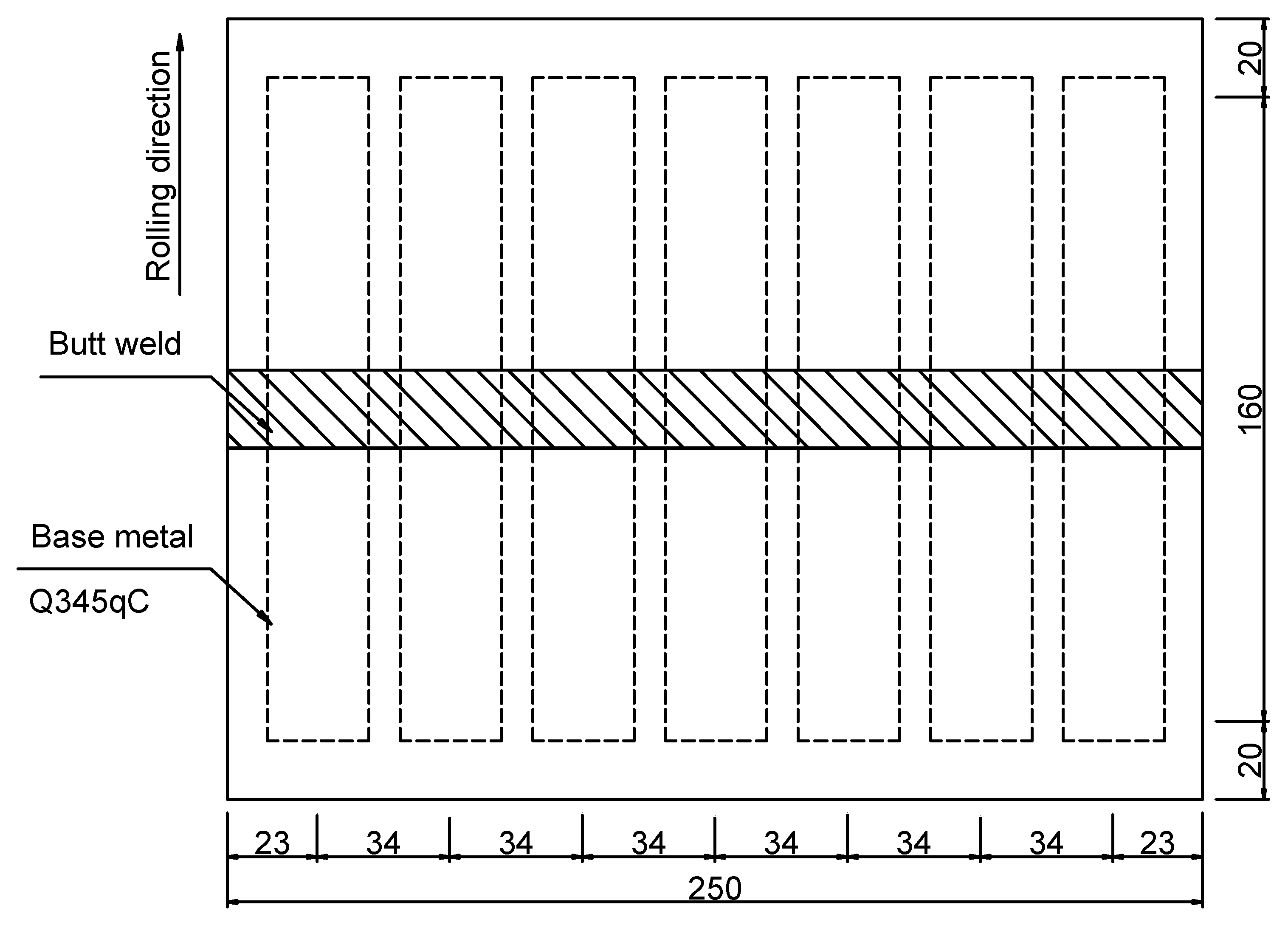
4.1.1. Material and Size of Test Specimen
4.1.2. Test Device and Loading System
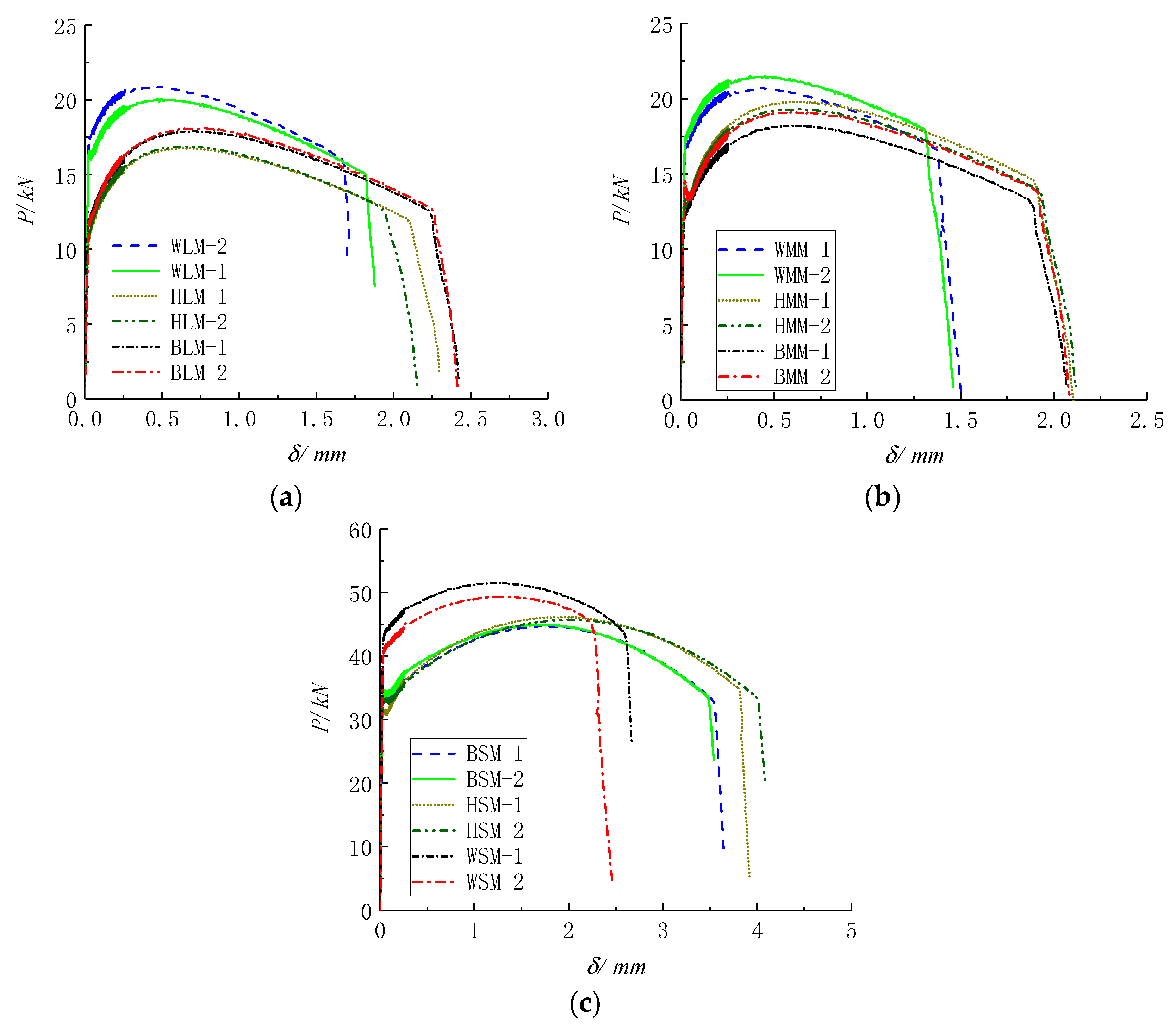
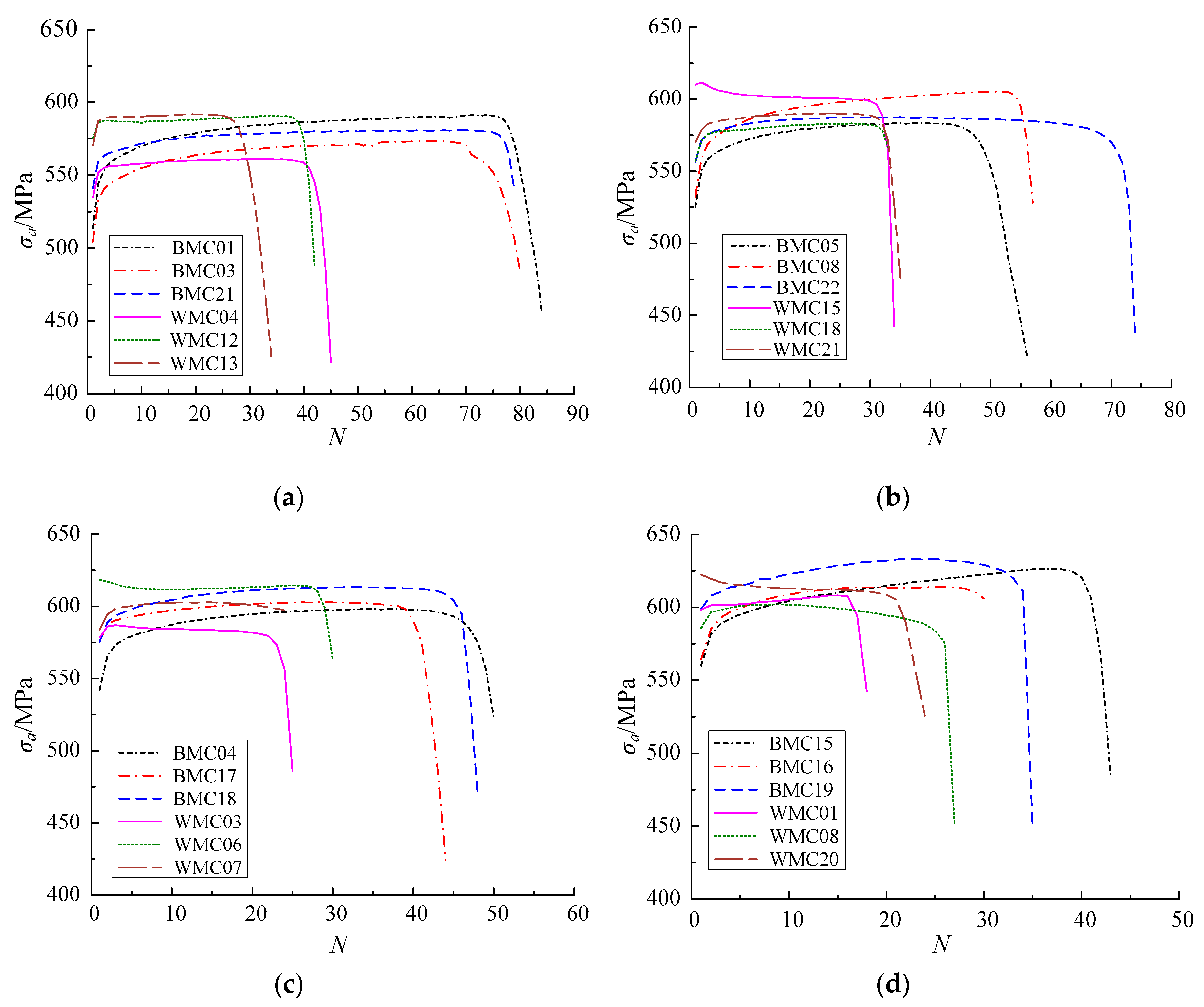
4.1.3. Test Results
4.2. ULCF Predictions for Base Material and Welded Joints
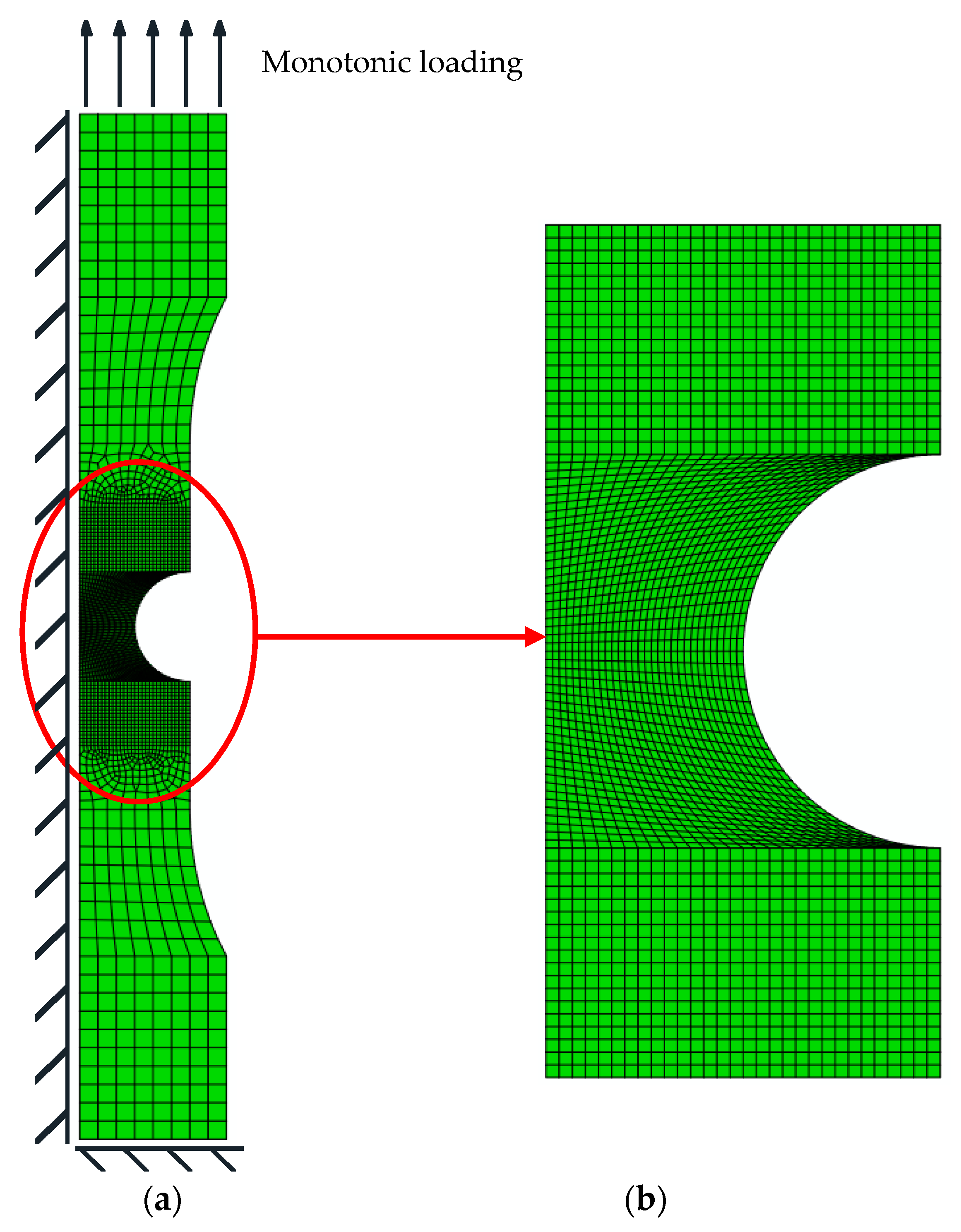
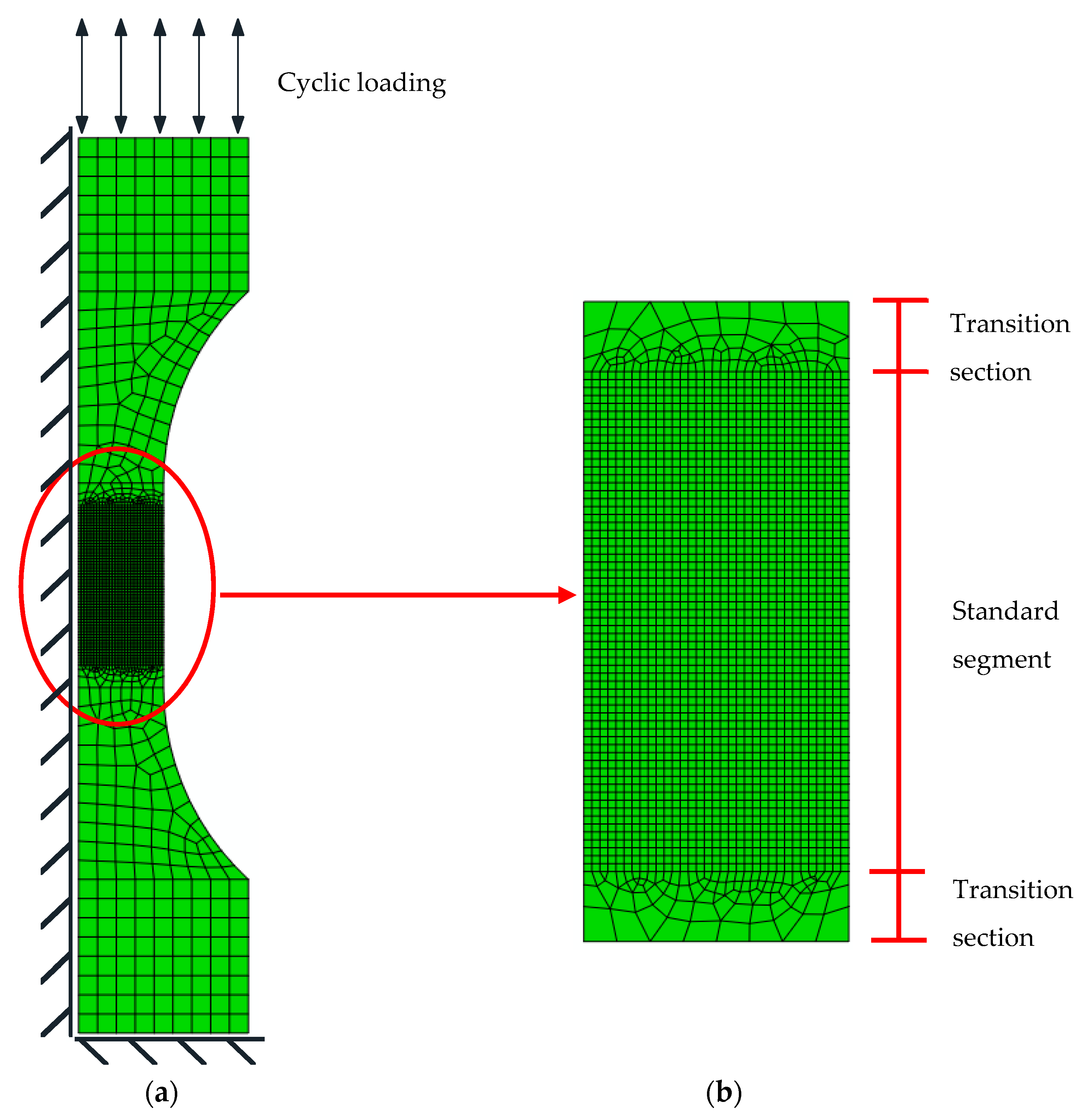
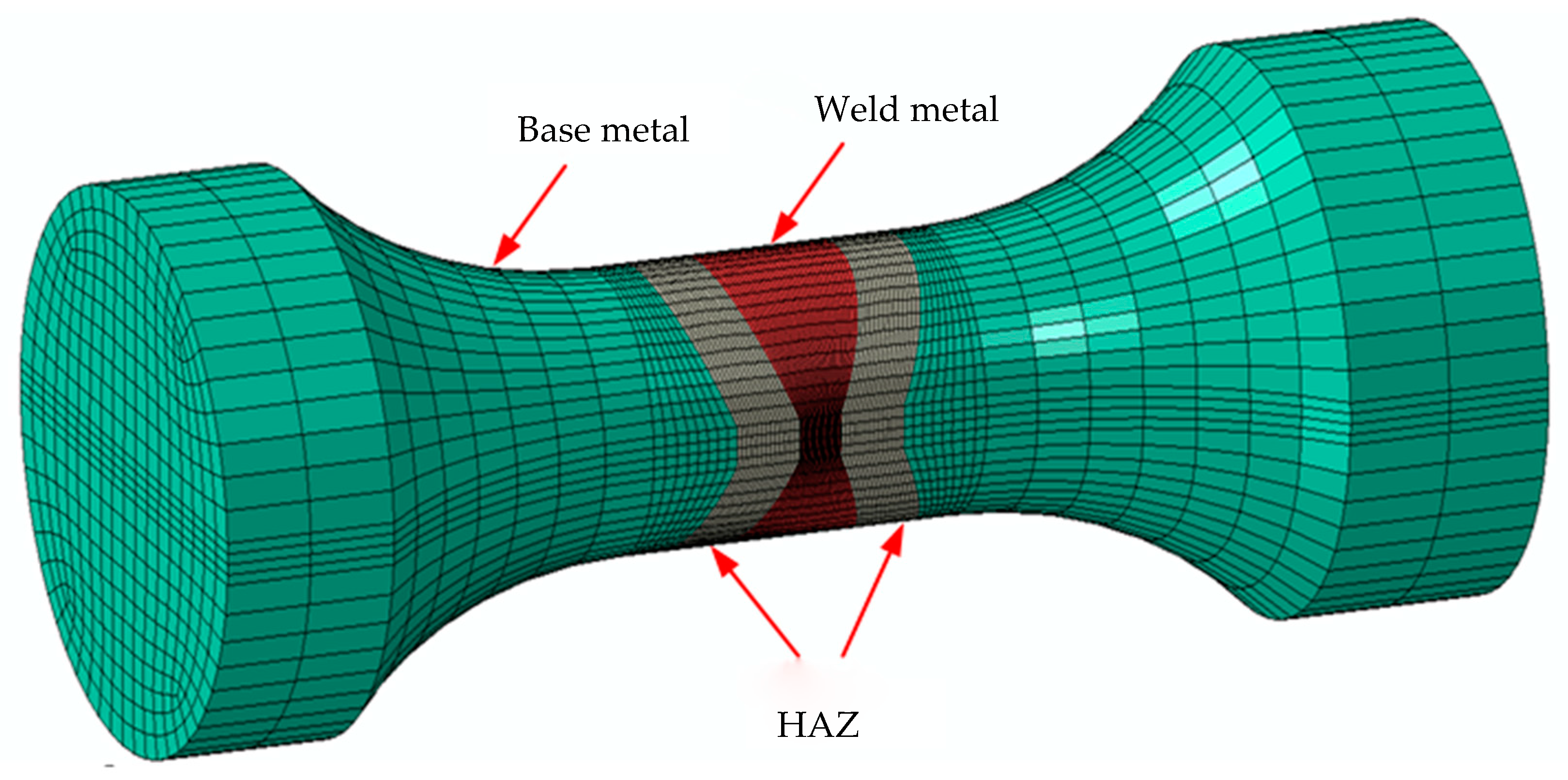
4.2.1. Establishment of a Finite Element Model
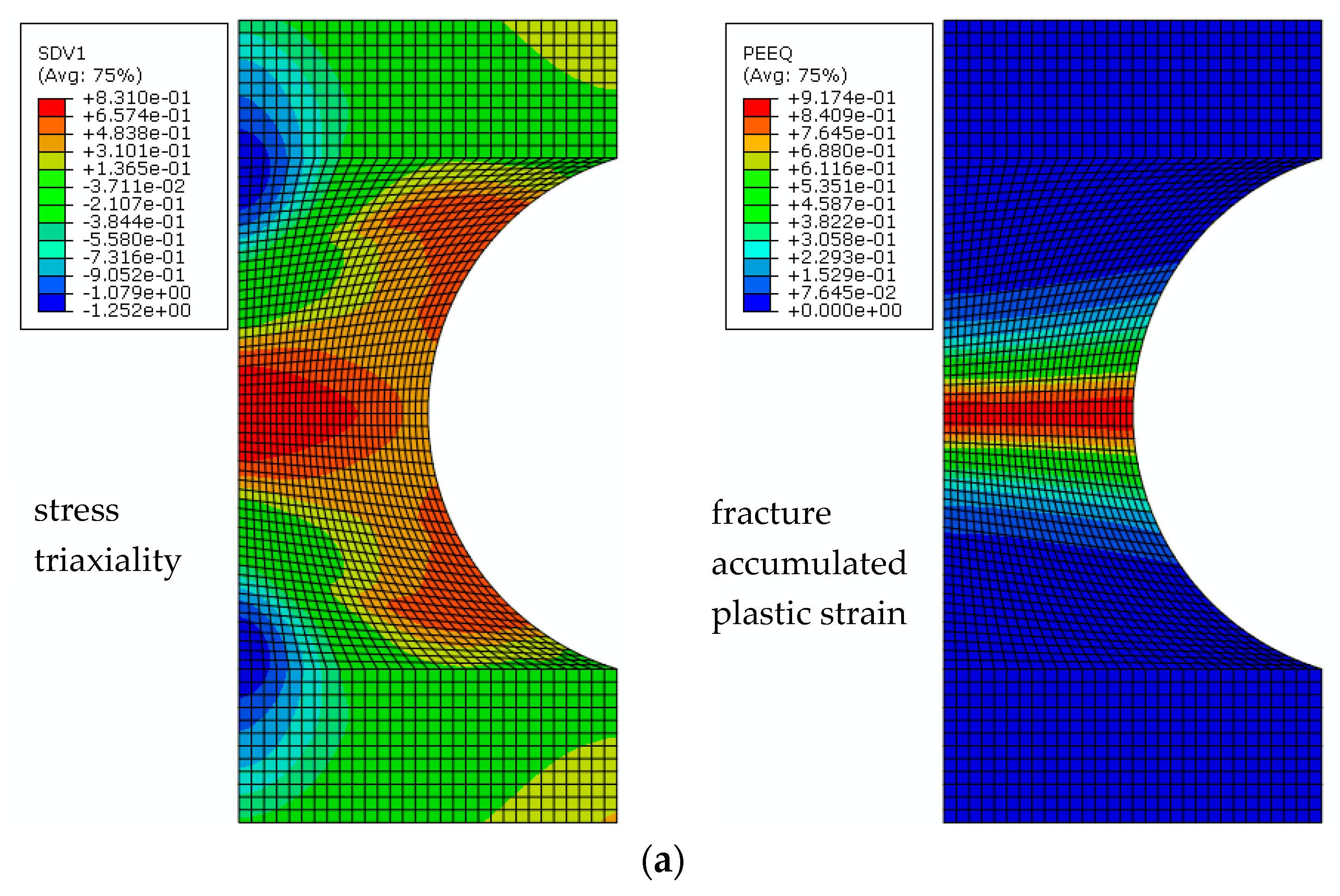
4.2.2. Fatigue Life Prediction Based on the CDM Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kawashima, K.; Unjoh, S. The damage of highway bridges in the 1995 Hyogo-Ken Nanbu earthquake and its impact on Japanese seismic design. J. Earthq. Eng. 1997, 3, 505–541. [Google Scholar] [CrossRef]
- Subcommittee on Investigation of Seismic Damage of Steel Structure. Investigation of causes of damage to steel structure on Hanshin-Awaji earthquake disaster. Proc. JSCE 2000, 64, 17–30. (In Japanese) [Google Scholar]
- Miller, D.K. Lessons learned from the Northridge earthquake. Eng. Struct. 1998, 20, 249–260. [Google Scholar] [CrossRef]
- Goto, Y.; Ebisawa, T.; Lu, X.L. Local buckling restraining behavior of thin-walled circular CFT columns under seismic loads. J. Struct. Eng. 2014, 140, 1–14. [Google Scholar] [CrossRef]
- Wang, Z.F.; Toshitaka, Y. Ultimate strength and ductility of stiffened steel tubular bridge piers. Int. J. Steel Struct. 2011, 11, 81–90. [Google Scholar] [CrossRef]
- Usami, T.; Ge, H.B.; Saizuka, K. Behavior of partially concrete-filled steel bridge piers under cyclic and dynamic loading. J. Constr. Steel Res. 1997, 41, 121–136. [Google Scholar] [CrossRef]
- Tong, L.; Huang, X.; Zhou, F.; Chen, Y. Experimental and numerical investigations on extremely-low-cycle fatigue fracture behavior of steel welded joints. J. Constr. Steel Res. 2016, 119, 98–112. [Google Scholar] [CrossRef]
- Pereira, J.; De Jesus, A.M.; Fernandes, A. A new ultra-low cycle fatigue model applied to the X60 piping steel. Int. J. Fatigue 2016, 93, 201–213. [Google Scholar] [CrossRef]
- Kuwamura, H.; Takagi, N. Similitude law of prefracture hysteresis of steel members. J. Struct. Eng. 2004, 130, 752–761. [Google Scholar] [CrossRef]
- Bleck, W.; Dahl, W.; Nonn, A.; Amlung, L.; Feldmann, M.; Schafer, D.; Eichler, B. Numerical and experimental analyses of damage behavior of steel moment connection. Eng. Fract. Mech. 2009, 76, 1531–1547. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Y.Q.; Shi, Y.J.; Xiong, J.; Yang, L. Extremely low cycle fatigue prediction of steel beam-to-column connection by using a micro-mechanics based fracture model. Int. J. Fatigue 2013, 48, 90–100. [Google Scholar] [CrossRef]
- Mendes, L.A.; Castro, L.M. A simplified reinforcing steel model suitable for cyclic loading including ultra-low-cycle fatigue effects. Eng. Struct. 2014, 68, 155–164. [Google Scholar] [CrossRef]
- Nip, K.H.; Gardner, L.; Davies, C.M. Extremely low cycle fatigue tests on structural carbon steel and stainless steel. J. Constr. Steel Res. 2010, 66, 96–110. [Google Scholar] [CrossRef]
- Huang, X.W.; Tong, L.W.; Zhou, F. Prediction of fracture behavior of beam-to-column welded joints using micromechanics damage model. J. Constr. Steel Res. 2013, 85, 60–72. [Google Scholar] [CrossRef]
- Kuwamura, H. Transition between fatigue and ductile fracture in steel. J. Struct. Eng. 1997, 123, 864–870. [Google Scholar] [CrossRef]
- Kermajani, M.; Malek Ghaini, F.; Miresmaeili, R.; Aghakouchak, A.A.; Shadmand, M. Effect of weld metal toughness on fracture behavior under ultra-low cycle fatigue loading (earthquake). Mater. Sci. Eng. A 2016, 668, 30–37. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhang, J.X.; Zhao, P.F.; Huang, Y.; Yu, Z.H.; Fang, X.Y. Low-cycle fatigue behaviors of a new type of 10% Cr martensitic steel and welded joint with Ni-based weld metal. Int. J. Fatigue 2016, 88, 78–87. [Google Scholar] [CrossRef]
- Song, F.Y.; Xie, X. Effect analysis of corrosion on low cycle fatigue behavior of structural steel. J. Zhejiang Univ. 2018, 52, 1–10. [Google Scholar]
- Ge, H.B.; Ohashi, M.; Tajima, R. Experimental study on ductile crack initiation and its propagation in steel bridge piers of thick-walled box sections. J. Struct. Eng. JSCE 2007, 53, 493–502. (In Japanese) [Google Scholar]
- Xue, L. A unified expression for low cycle fatigue and extremely low cycle fatigue and its implication for monotonic loading. Int. J. Fatigue 2008, 30, 1691–1698. [Google Scholar] [CrossRef]
- Kuwamura, H.; Akiyama, H. Brittle fracture under repeated high stresses. J. Constr. Steel Res. 1994, 29, 5–19. [Google Scholar] [CrossRef]
- Tateishi, K.; Hanji, T.; Minami, K. A prediction model for extremely low cycle fatigue strength of structural steel. Int. J. Fatigue 2007, 29, 887–896. [Google Scholar] [CrossRef]
- Coffin, L.F.J. A study of the effects of cyclic thermal stresses on a ductile metal. Trans. ASME 1954, 76, 931–950. [Google Scholar]
- Manson, S.S. Behavior of Materials under Conditions of Thermal Stress; University of Michigan: Ann Arbor, MI, USA, 1953; pp. 1–37. [Google Scholar]
- Kuroda, M. Extremely low cycle fatigue life prediction based on a new cumulative fatigue damage model. Int. J. Fatigue 2002, 24, 699–703. [Google Scholar] [CrossRef]
- Kanvinde, A.M.; Deierlein, G.G. Cyclic void growth model to assess ductile fracture initiation in structural steels due to ultra low cycle fatigue. J. Eng. Mech. 2007, 133, 701–712. [Google Scholar] [CrossRef]
- Liao, Y.H.; Xie, X.; Tang, Z.Z. Low cycle fatigue properties and fracture mechanism of Q345qC steel and its welded joint. J. Zhejiang Univ. 2018, 52, 73–81. [Google Scholar]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Hancock, J.W.; Mackenzie, A.C. On the mechanics of ductile failure in high-strength steel subjected to multi-axial stress-states. J. Mech. Phys. Solids 1976, 24, 147–169. [Google Scholar] [CrossRef]
- Adasooriya, N.D.; Siriwardane, S.C.; Ohga, M. A simplified approach to predict the failure of steel members under interaction effect of fracture and fatigue. Int. J. Fatigue 2013, 47, 161–173. [Google Scholar] [CrossRef]
- Xing, J.H.; Guo, C.L.; Li, Y.Y.; Chen, A.G. Damage coefficient identification of micromechanical fracture prediction models for steel Q235B. J. Harbin Inst. Technol. 2017, 49, 184–188. (In Chinese) [Google Scholar]
- Li, S.L.; Xie, X.; Liao, Y.H. Improvement of cyclic void growth model for ultra-low cycle fatigue prediction of steel bridge piers. Materials 2019, 12, 1615. [Google Scholar] [CrossRef] [PubMed]
- Bonora, N. A nonlinear CDM model for ductile failure. Eng. Fract. Mech. 1997, 58, 11–28. [Google Scholar] [CrossRef]
- Girão Coelho, A.M. Rotation capacity of partial strength steel joints with three-dimensional finite element approach. Comput. Struct. 2013, 116, 88–97. [Google Scholar] [CrossRef]
- Cheng, G.; Zuo, J.; Lou, Z. Continuum damage model of low-cycle fatigue and fatigue damage analysis of welded joint. Eng. Fract. Mech. 1996, 55, 155–161. [Google Scholar] [CrossRef]
- Liao, F.F.; Wang, W.; Chen, Y.Y. Extremely low cycle fatigue fracture prediction of steel connections under cyclic loading. J. Tongji Univ. Nat. Sci. Ed. 2014, 42, 539–546. [Google Scholar]
- Bataille, J.; Kestin, J. Irreversible process and physical interpretation of rational thermodynamics. J. Non-Equilib. Thermodyn. 1979, 4, 229–258. [Google Scholar] [CrossRef]
- Wang, B.; Hu, N.; Kurobane, Y.; Makino, Y.; Lie, S.T. Damage criterion and safety assessment approach to tubular joints. Eng. Struct. 1998, 22, 424–434. [Google Scholar] [CrossRef]
- Dhar, S.; Dixit, P.M.; Sethuraman, R. A continuum damage mechanics model for ductile fracture. Int. J. Press. Vessel. Pip. 2000, 77, 335–344. [Google Scholar] [CrossRef]
- Wang, T.J. A continuum damage model for ductile fracture of weld heat affected zone. Eng. Fract. Mech. 1991, 40, 1075–1082. [Google Scholar] [CrossRef]
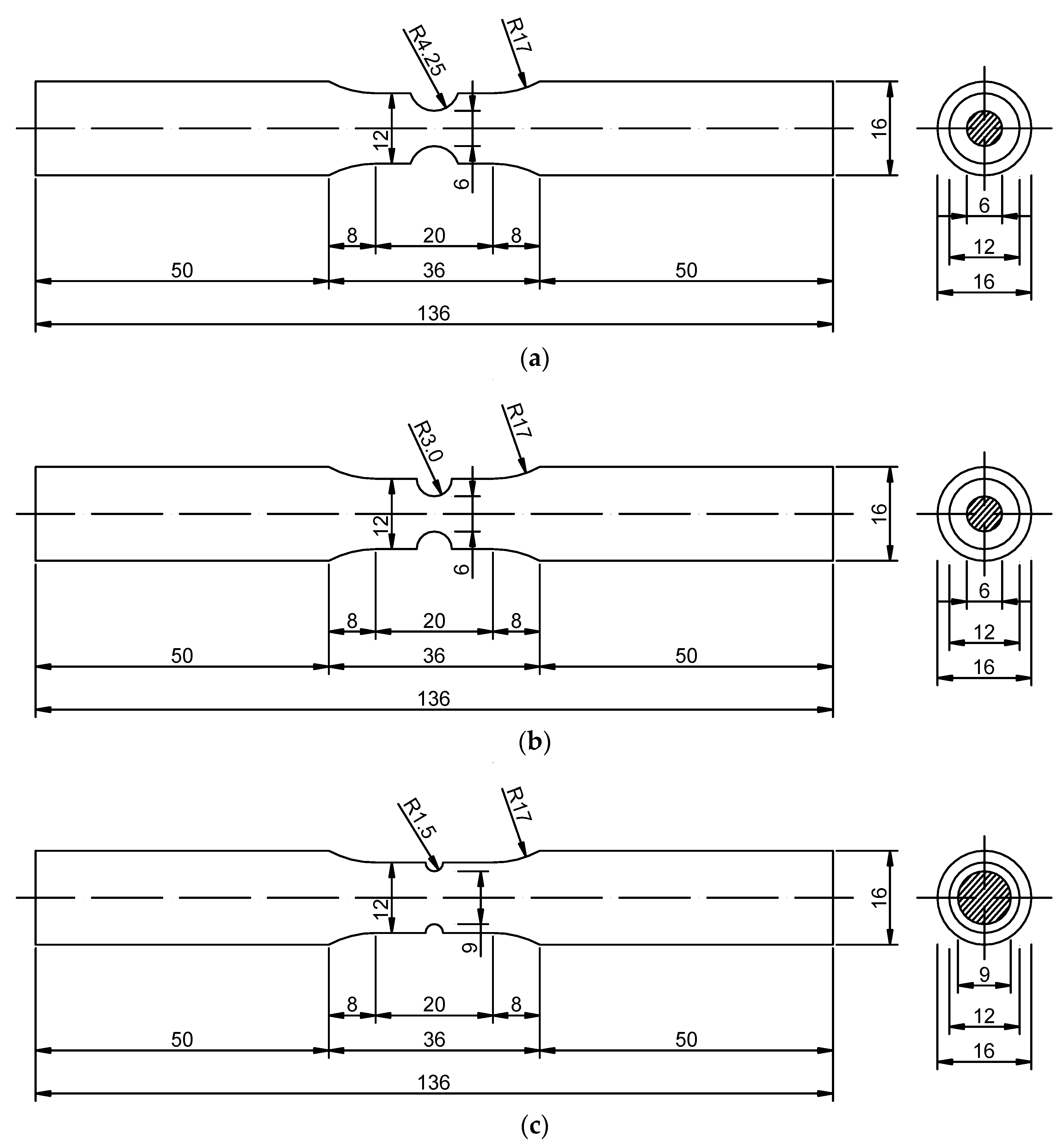


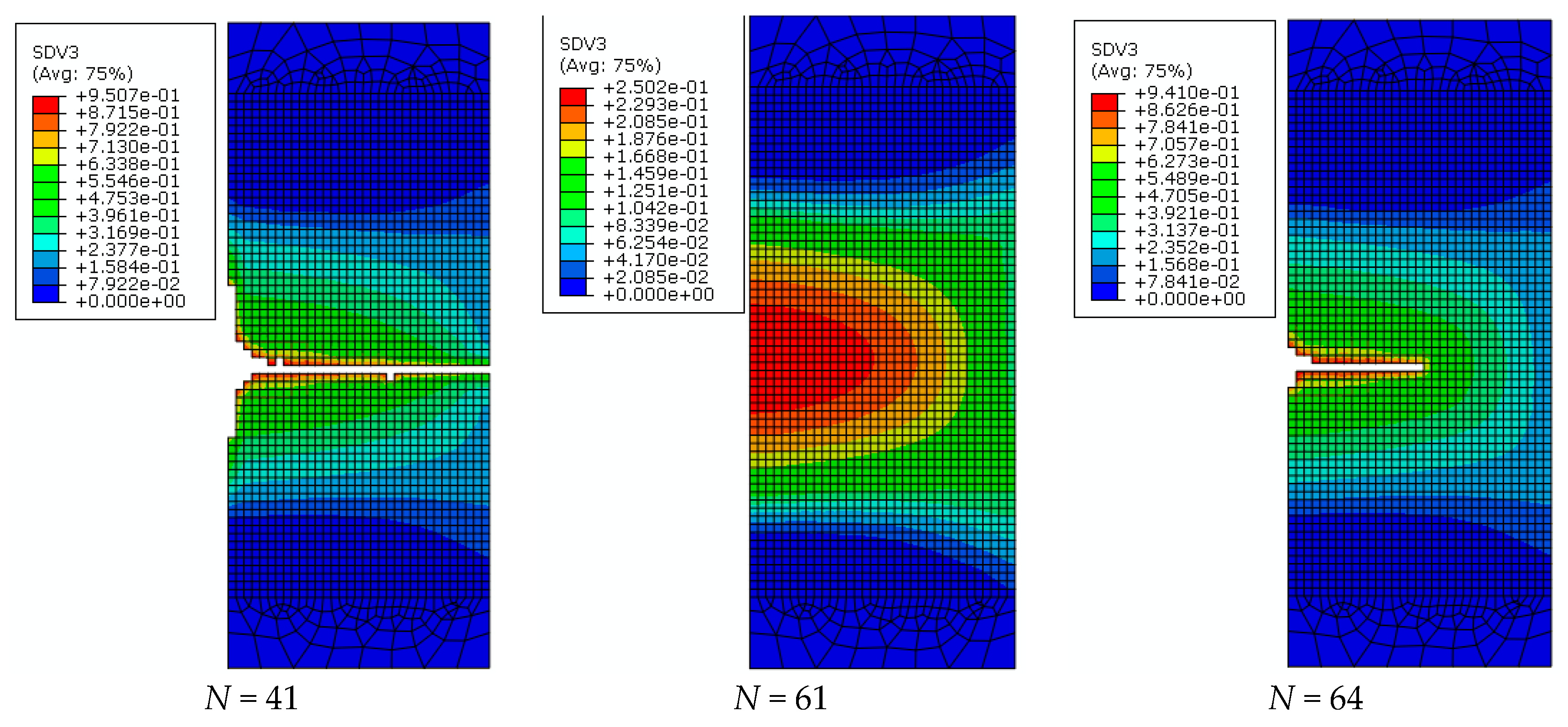
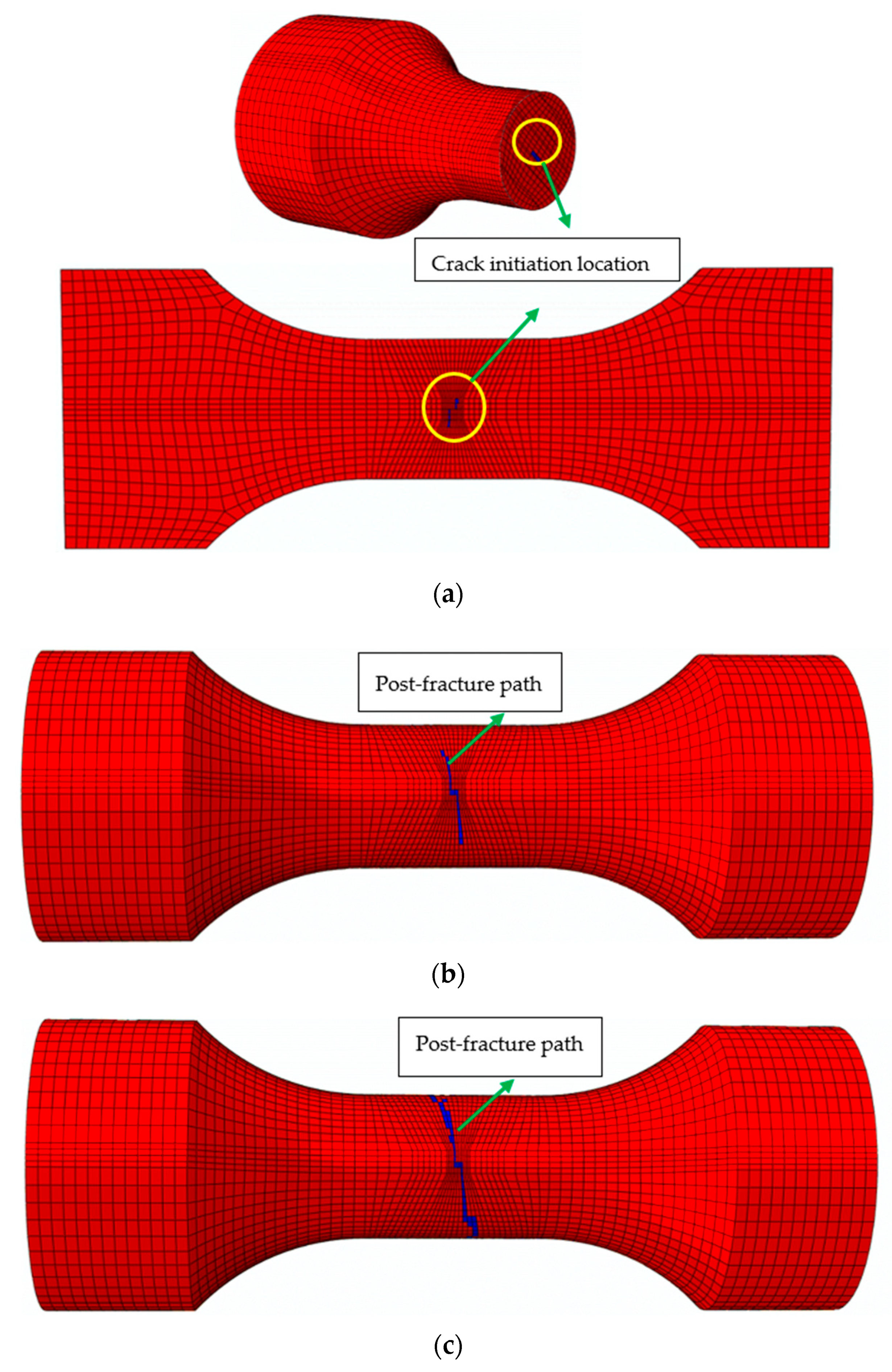
| Material | Notch Radius (mm) | Number | Clamping Segment Diameter (mm) | Gauge Segment Diameter (mm) | Intermediate Segment Length (mm) | Notch Root Diameter (mm) |
|---|---|---|---|---|---|---|
| Base metal | 4.25 | BLM-1 | 15.95 | 11.96 | 35.98 | 6.04 |
| BLM-2 | 15.95 | 11.92 | 36.09 | 6.04 | ||
| 3.0 | BMM-1 | 15.99 | 11.94 | 35.73 | 5.97 | |
| BMM-2 | 16.02 | 11.95 | 35.79 | 6.04 | ||
| 1.5 | BSM-1 | 15.94 | 11.9 | 36.02 | 9.08 | |
| BSM-2 | 15.97 | 11.89 | 35.90 | 9.04 | ||
| Heat affected zone | 4.25 | HLM-1 | 15.99 | 12.01 | 36.16 | 5.85 |
| HLM-2 | 15.97 | 11.97 | 36.18 | 5.79 | ||
| 3.0 | HMM-1 | 15.99 | 12.00 | 35.94 | 6.40 | |
| HMM-2 | 15.95 | 11.93 | 35.89 | 6.24 | ||
| 1.5 | HSM-1 | 15.99 | 12.01 | 36.37 | 9.35 | |
| HSM-2 | 16.04 | 11.96 | 35.99 | 9.35 | ||
| Weld metal | 4.25 | WLM-1 | 15.96 | 12.02 | 36.02 | 6.33 |
| WLM-2 | 16.00 | 11.91 | 36.53 | 6.25 | ||
| 3.0 | WMM-1 | 15.97 | 11.92 | 36.03 | 6.24 | |
| WMM-2 | 15.94 | 11.91 | 36.37 | 6.29 | ||
| 1.5 | WSM-1 | 15.99 | 12.04 | 36.40 | 9.43 | |
| WSM-2 | 16.05 | 11.96 | 36.27 | 9.36 |
| Material | R (mm) | Number | δf (mm) | ||||
|---|---|---|---|---|---|---|---|
| Base metal | 4.25 | BLM-1 | 2.240 | 1.3186 | 0.8310 | 0.8893 | 0.5047 |
| BLM-2 | 2.262 | 1.3186 | 0.8337 | 0.9119 | 0.5387 | ||
| 3.0 | BMM-1 | 1.876 | 1.3186 | 0.8916 | 0.7882 | 0.4210 | |
| BMM-2 | 1.917 | 1.3186 | 0.8920 | 0.8153 | 0.4541 | ||
| 1.5 | BSM-1 | 3.543 | 1.3186 | 1.089 | 0.6634 | 0.3895 | |
| BSM-2 | 3.477 | 1.3186 | 1.096 | 0.6366 | 0.3648 | ||
| Average | 0.4455 | ||||||
| Standard deviation | 0.0613 | ||||||
| Dispersion coefficient (Standard deviation / Average) | 13.75% | ||||||
| Heat affected zone | 4.25 | HLM-1 | 2.098 | 1.3084 | 0.8205 | 0.8262 | 0.4179 |
| HLM-2 | 1.934 | 1.3084 | 0.8145 | 0.7380 | 0.3111 | ||
| 3.0 | HMM-1 | 1.895 | 1.3084 | 0.8862 | 0.7963 | 0.4310 | |
| HMM-2 | 1.922 | 1.3084 | 0.8865 | 0.8087 | 0.4464 | ||
| 1.5 | HSM-1 | 3.808 | 1.3084 | 1.0572 | 0.7760 | 0.5035 | |
| HSM-2 | 4.009 | 1.3084 | 1.0570 | 0.7768 | 0.5044 | ||
| Average | 0.4357 | ||||||
| Standard deviation | 0.0649 | ||||||
| Dispersion coefficient (Standard deviation / Average) | 14.91% | ||||||
| Weld metal | 4.25 | WLM-1 | 1.821 | 0.9882 | 0.8629 | 0.7813 | 0.5736 |
| WLM-2 | 1.672 | 0.9882 | 0.8595 | 0.7109 | 0.4591 | ||
| 3.0 | WMM-1 | 1.371 | 0.9882 | 0.9430 | 0.6221 | 0.3790 | |
| WMM-2 | 1.306 | 0.9882 | 0.9470 | 0.5904 | 0.3419 | ||
| 1.5 | WSM-1 | 2.593 | 0.9882 | 1.2070 | 0.4540 | 0.2805 | |
| WSM-2 | 2.264 | 0.9882 | 1.2082 | 0.3329 | 0.1700 | ||
| Average | 0.3673 | ||||||
| Standard deviation | 0.1280 | ||||||
| Dispersion coefficient (Standard deviation / Average) | 34.84% | ||||||
| Δεt/% | Number | Nf | Nr | Nf/Nr |
|---|---|---|---|---|
| 7 | BMC01 | 78 | 84 | 92.9% |
| BMC03 | 76 | 81 | 93.8% | |
| BMC21 | 78 | 80 | 97.5% | |
| WMC04 | 43 | 46 | 93.5% | |
| WMC12 | 40 | 42 | 95.2% | |
| WMC13 | 29 | 34 | 85.3% | |
| 8 | BMC05 | 51 | 57 | 89.5% |
| BMC08 | 55 | 57 | 96.5% | |
| BMC22 | 72 | 75 | 96.0% | |
| WMC15 | 32 | 35 | 91.4% | |
| WMC18 | 32 | 33 | 97.0% | |
| WMC21 | 33 | 36 | 91.7% | |
| 9 | BMC04 | 47 | 51 | 92.2% |
| BMC17 | 41 | 45 | 91.1% | |
| BMC18 | 45 | 48 | 93.8% | |
| WMC03 | 24 | 26 | 92.3% | |
| WMC06 | 29 | 31 | 93.5% | |
| WMC07 | 24 | 25 | 96.0% | |
| 10 | BMC15 | 41 | 44 | 93.2% |
| BMC16 | 30 | 31 | 96.8% | |
| BMC19 | 33 | 35 | 94.3% | |
| WMC01 | 17 | 19 | 89.5% | |
| WMC08 | 25 | 27 | 92.6% | |
| WMC20 | 21 | 25 | 84.0% |
| Δεt/% | Number | Crack initial location | Fatigue life Nf | Average Nf’ | Standard deviation | Dispersion coefficient |
|---|---|---|---|---|---|---|
| 7.0 | BMC01 | Section edge | 78 | 77 | 0.94 | 0.01 |
| BMC03 | Section edge | 76 | ||||
| BMC21 | Section edge | 78 | ||||
| WMC04 | HAZ edge | 43 | 37 | 6.02 | 0.16 | |
| WMC12 | HAZ edge | 40 | ||||
| WMC13 | HAZ edge | 29 | ||||
| 8.0 | BMC05 | Section edge | 51 | 59 | 9.10 | 0.15 |
| BMC08 | Section edge | 55 | ||||
| BMC22 | Section edge | 72 | ||||
| WMC15 | HAZ edge | 32 | 32 | 0.47 | 0.01 | |
| WMC18 | HAZ edge | 32 | ||||
| WMC21 | HAZ edge | 33 | ||||
| 9.0 | BMC04 | Section edge | 47 | 44 | 2.49 | 0.06 |
| BMC17 | Section edge | 41 | ||||
| BMC18 | Section edge | 45 | ||||
| WMC03 | HAZ edge | 24 | 25 | 2.36 | 0.09 | |
| WMC06 | HAZ edge | 29 | ||||
| WMC07 | HAZ edge | 24 | ||||
| 10.0 | BMC15 | Section edge | 41 | 34 | 4.64 | 0.13 |
| BMC16 | Section edge | 30 | ||||
| BMC19 | Section edge | 33 | ||||
| WMC01 | Weld edge | 17 | 21 | 3.27 | 0.16 | |
| WMC08 | Weld edge | 25 | ||||
| WMC20 | HAZ edge | 21 |
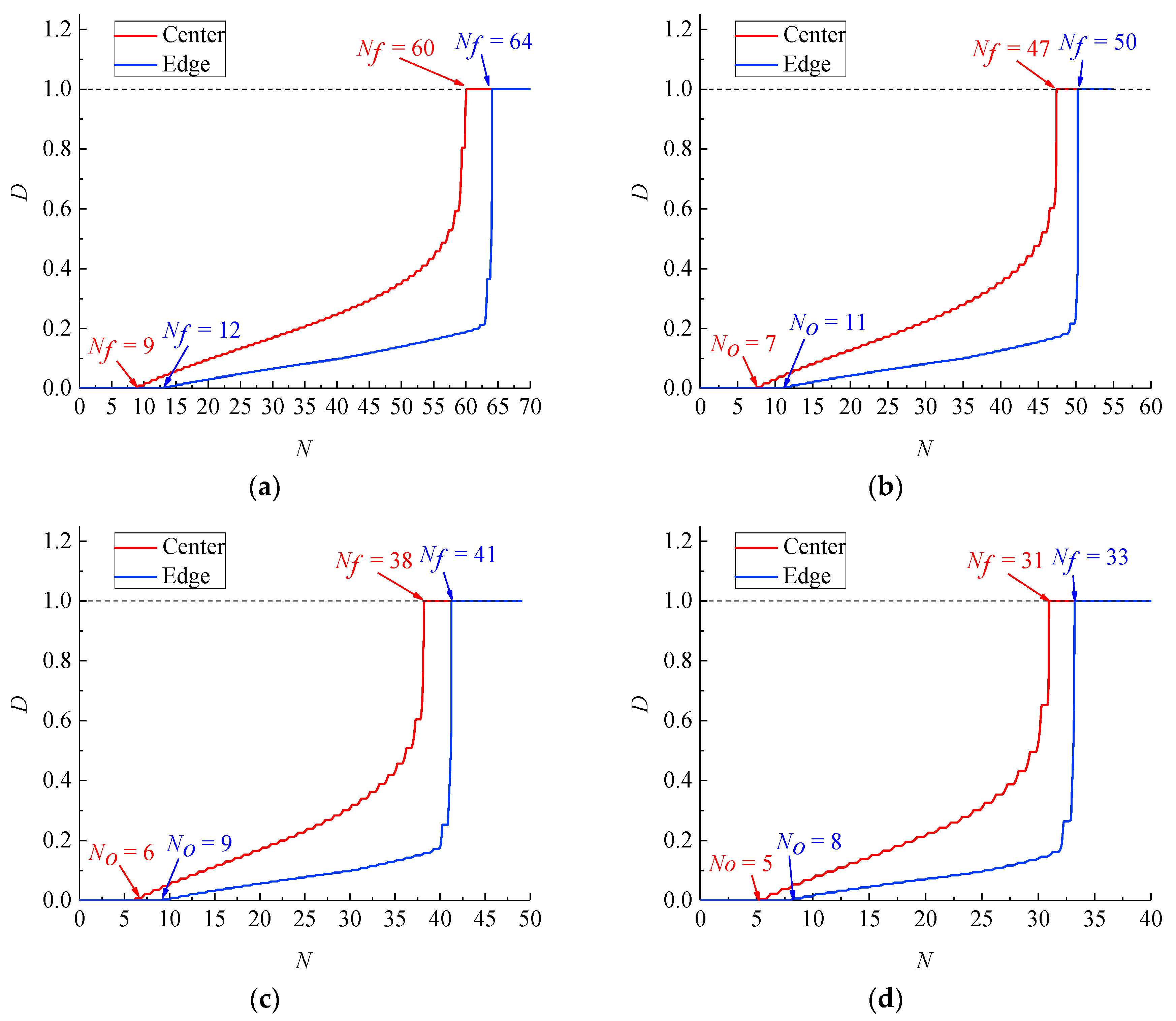
| Δεt % | Nf (Test) | Relative Error (%) | Nr (Test) | Relative Error (%) | ||
|---|---|---|---|---|---|---|
| 7.0 | 60 | 77 | −22.1 | 64 | 82 | −21.9 |
| 8.0 | 47 | 59 | −20.3 | 50 | 63 | −20.6 |
| 9.0 | 38 | 44 | −13.6 | 41 | 48 | −14.6 |
| 10.0 | 31 | 35 | −11.4 | 33 | 37 | −10.8 |
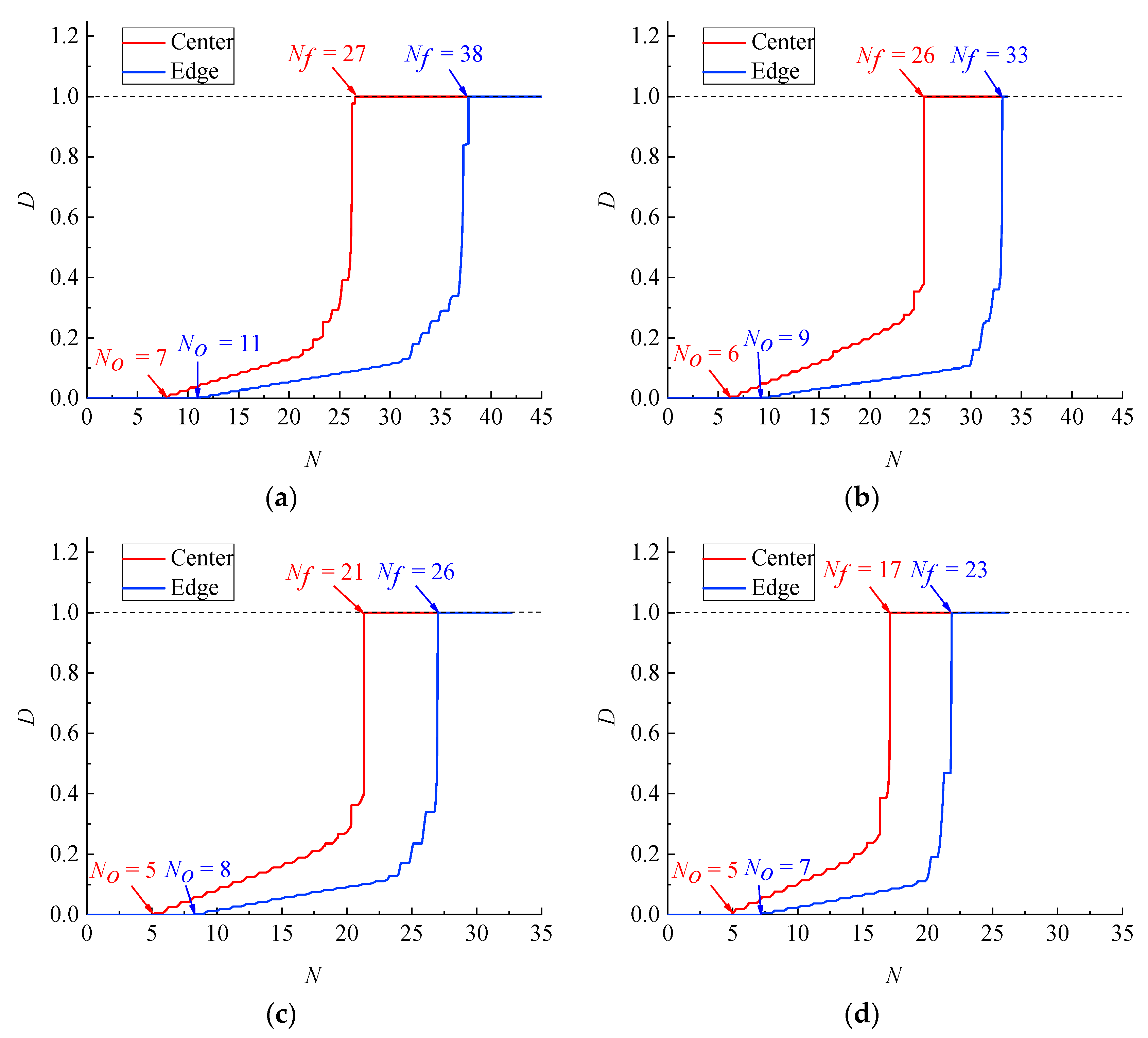
| Δεt % | Nf (Test) | Relative error (%) | Nr (Test) | Relative error (%) | ||
|---|---|---|---|---|---|---|
| 7.0 | 27 | 37 | −27.0 | 38 | 41 | −7.3 |
| 8.0 | 26 | 32 | −18.8 | 33 | 35 | −5.7 |
| 9.0 | 21 | 26 | −19.2 | 26 | 27 | −3.7 |
| 10.0 | 17 | 21 | −19.0 | 23 | 24 | −4.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Zhuge, H.; Xie, X. Prediction of the Ultra-Low-Cycle Fatigue Damage of Q345qC Steel and its Weld Joint. Materials 2019, 12, 4014. https://doi.org/10.3390/ma12234014
Tian Q, Zhuge H, Xie X. Prediction of the Ultra-Low-Cycle Fatigue Damage of Q345qC Steel and its Weld Joint. Materials. 2019; 12(23):4014. https://doi.org/10.3390/ma12234014
Chicago/Turabian StyleTian, Qin, Hanqing Zhuge, and Xu Xie. 2019. "Prediction of the Ultra-Low-Cycle Fatigue Damage of Q345qC Steel and its Weld Joint" Materials 12, no. 23: 4014. https://doi.org/10.3390/ma12234014
APA StyleTian, Q., Zhuge, H., & Xie, X. (2019). Prediction of the Ultra-Low-Cycle Fatigue Damage of Q345qC Steel and its Weld Joint. Materials, 12(23), 4014. https://doi.org/10.3390/ma12234014





