Numerical Modelling of the Mechanical Behaviour of Biaxial Weft-Knitted Fabrics on Different Length Scales
Abstract
1. Introduction
2. Materials and Physical Testing
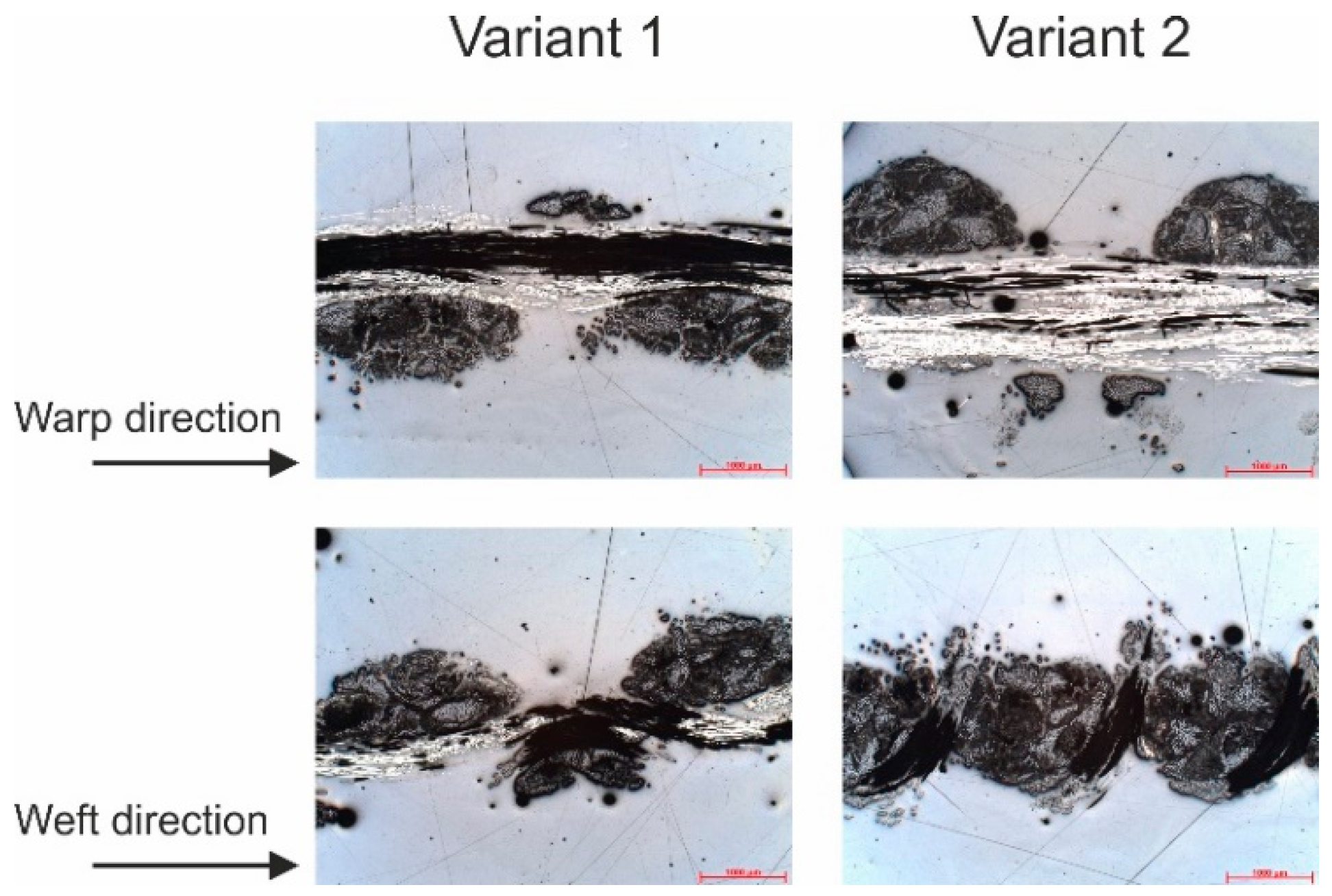
2.1. Yarn Manufacturing and Testing
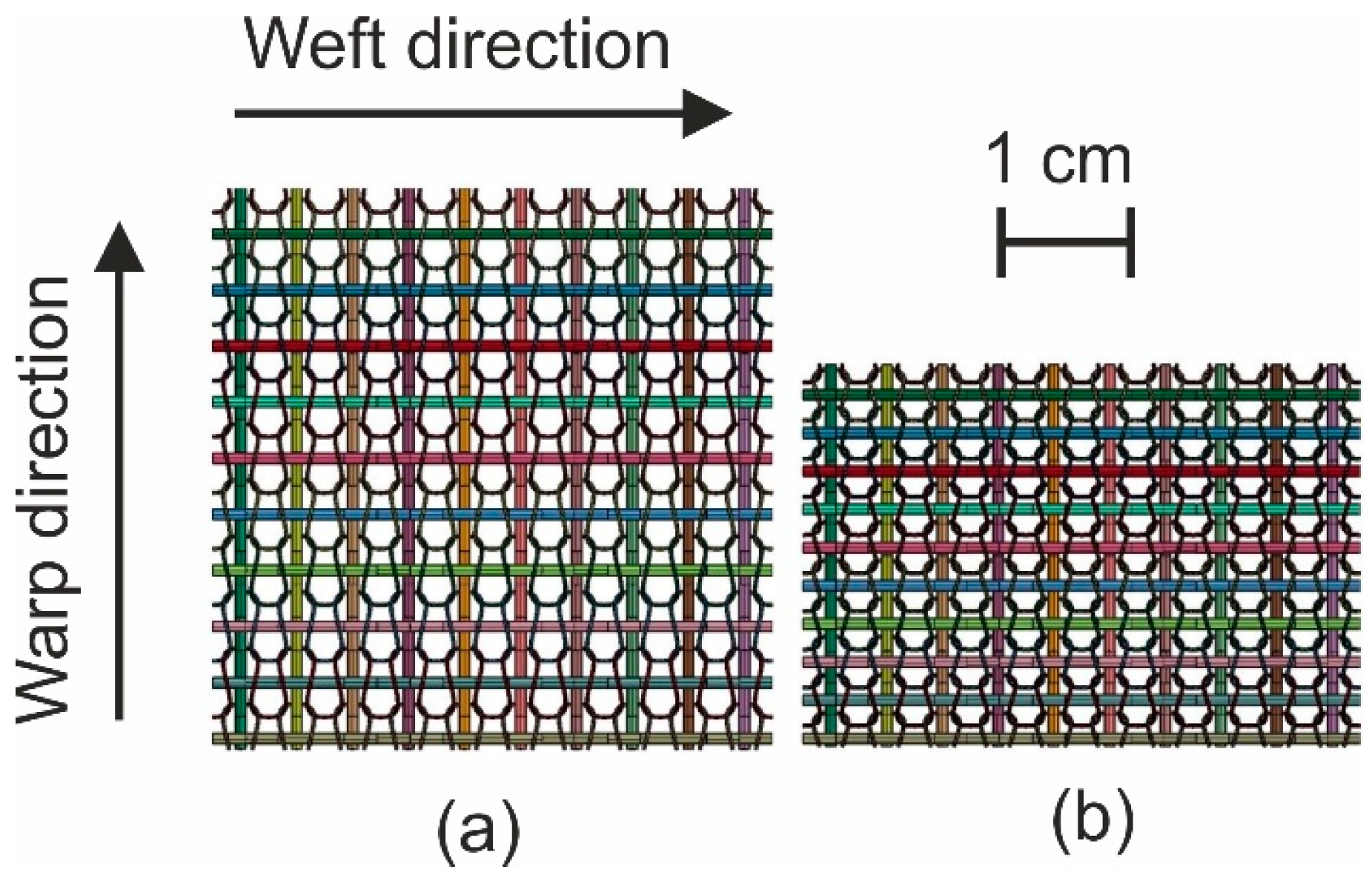
2.2. Fabric Manufacturing
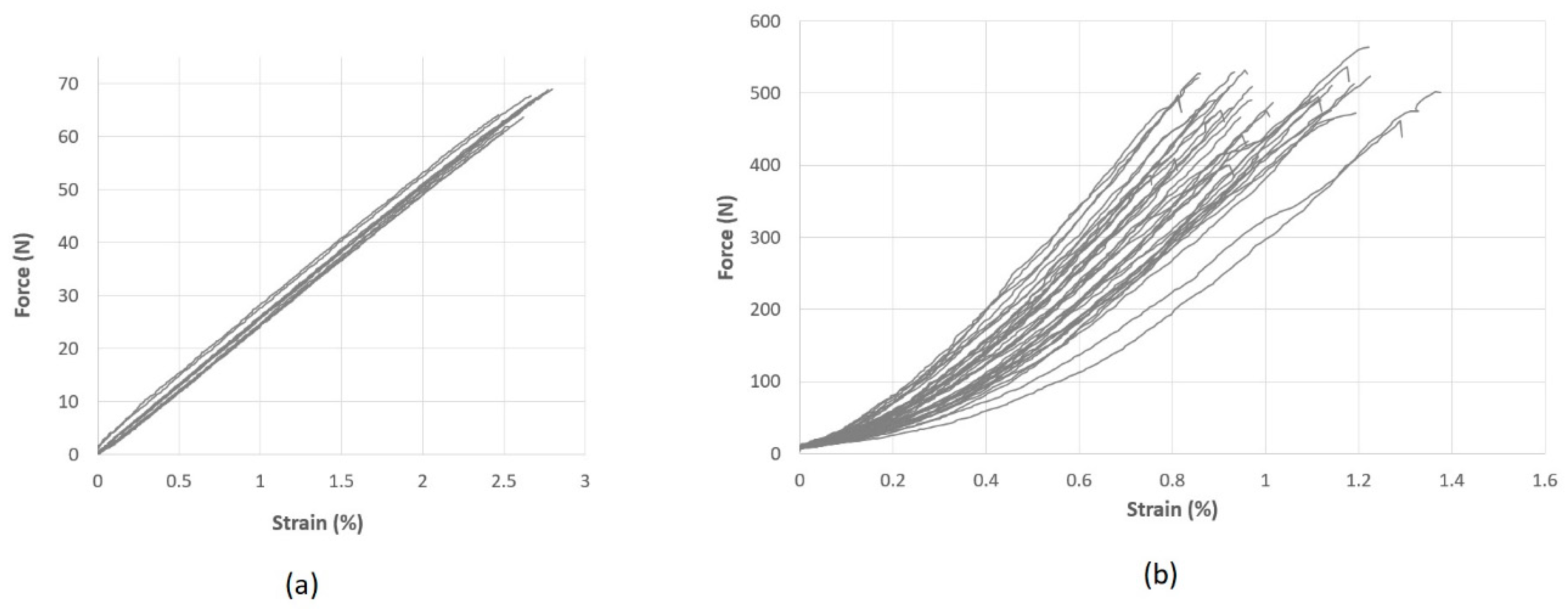
2.3. Fabric Testing
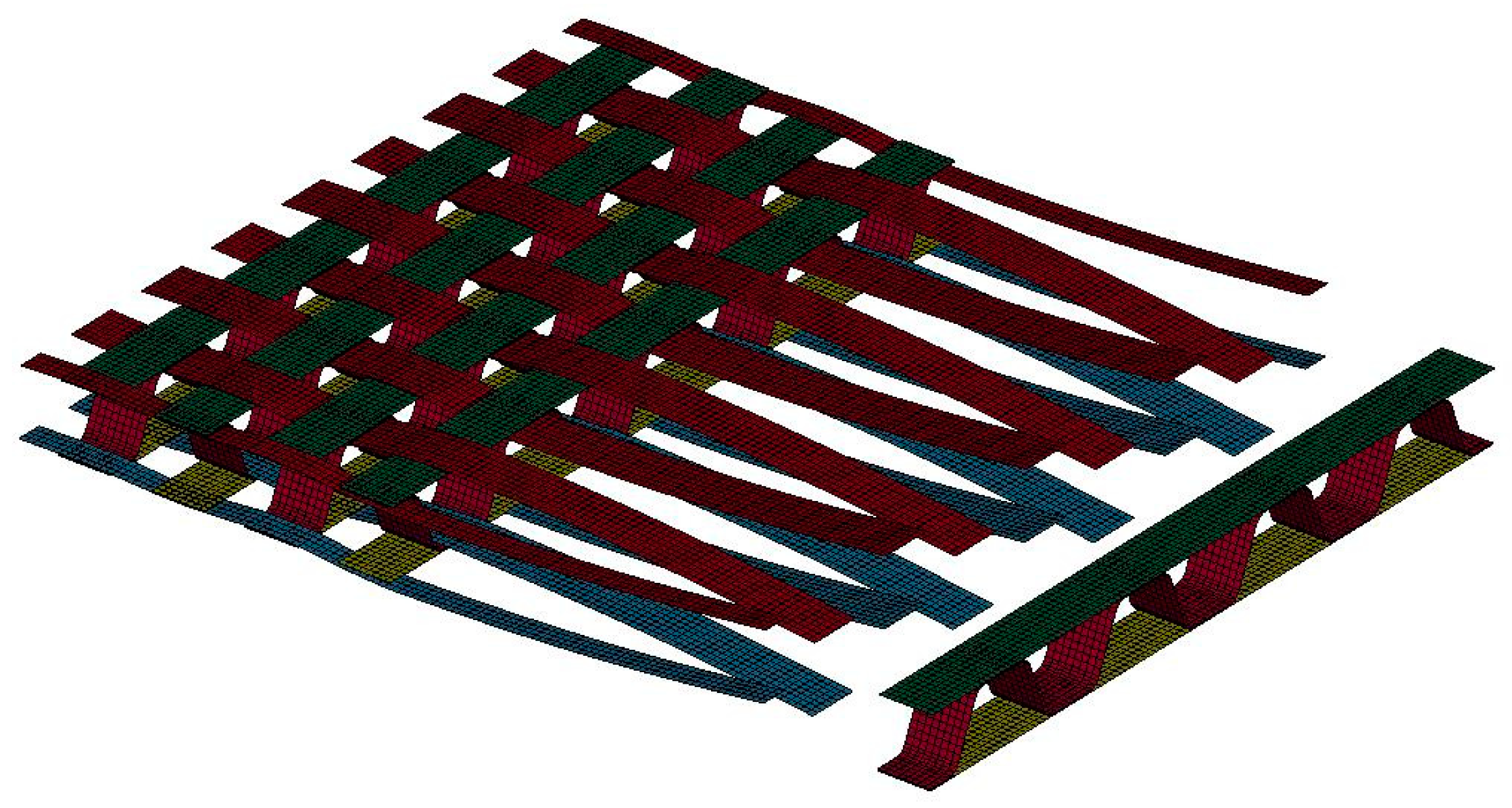
3. Modelling Biaxial Weft-Knitted Fabrics
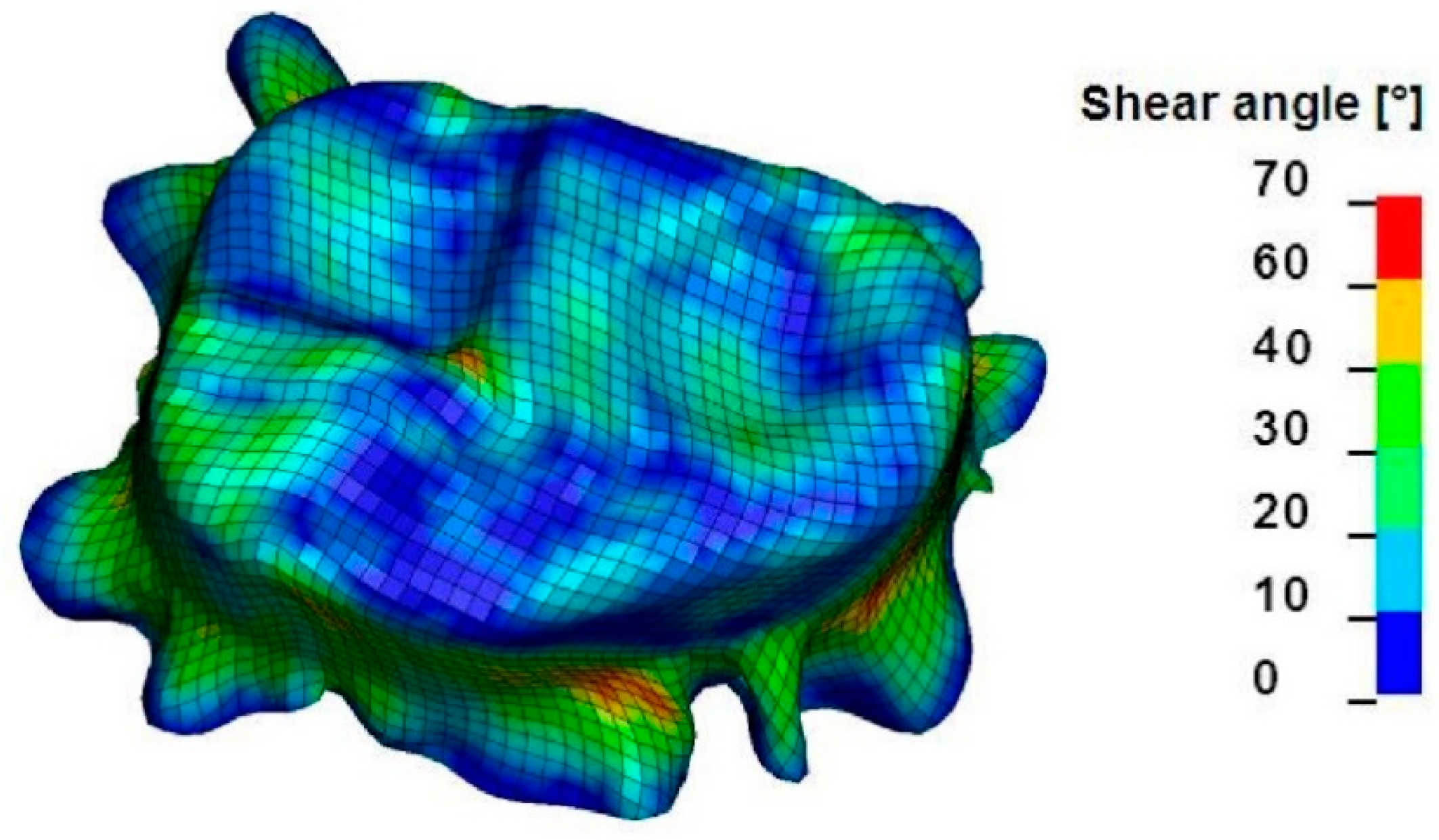
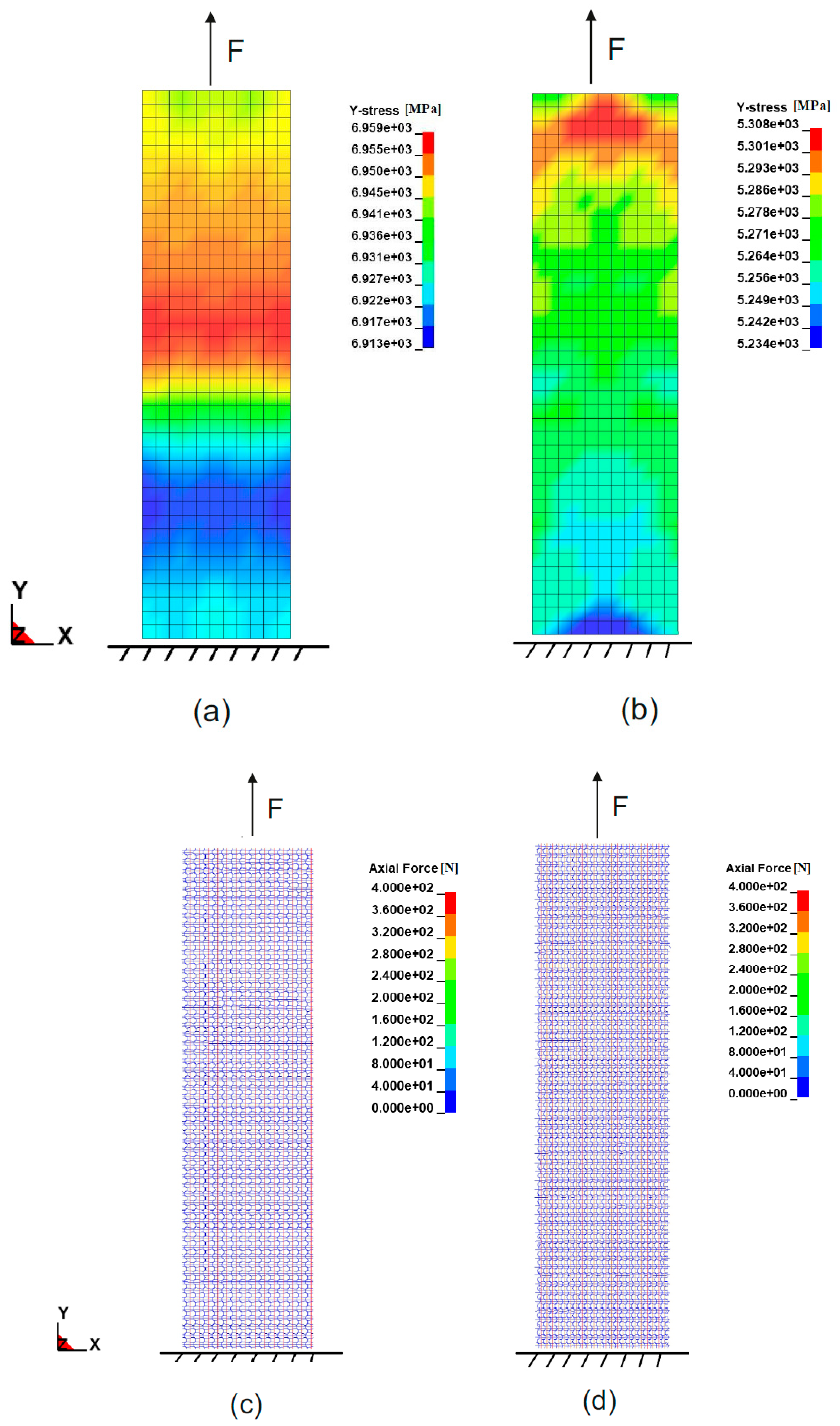
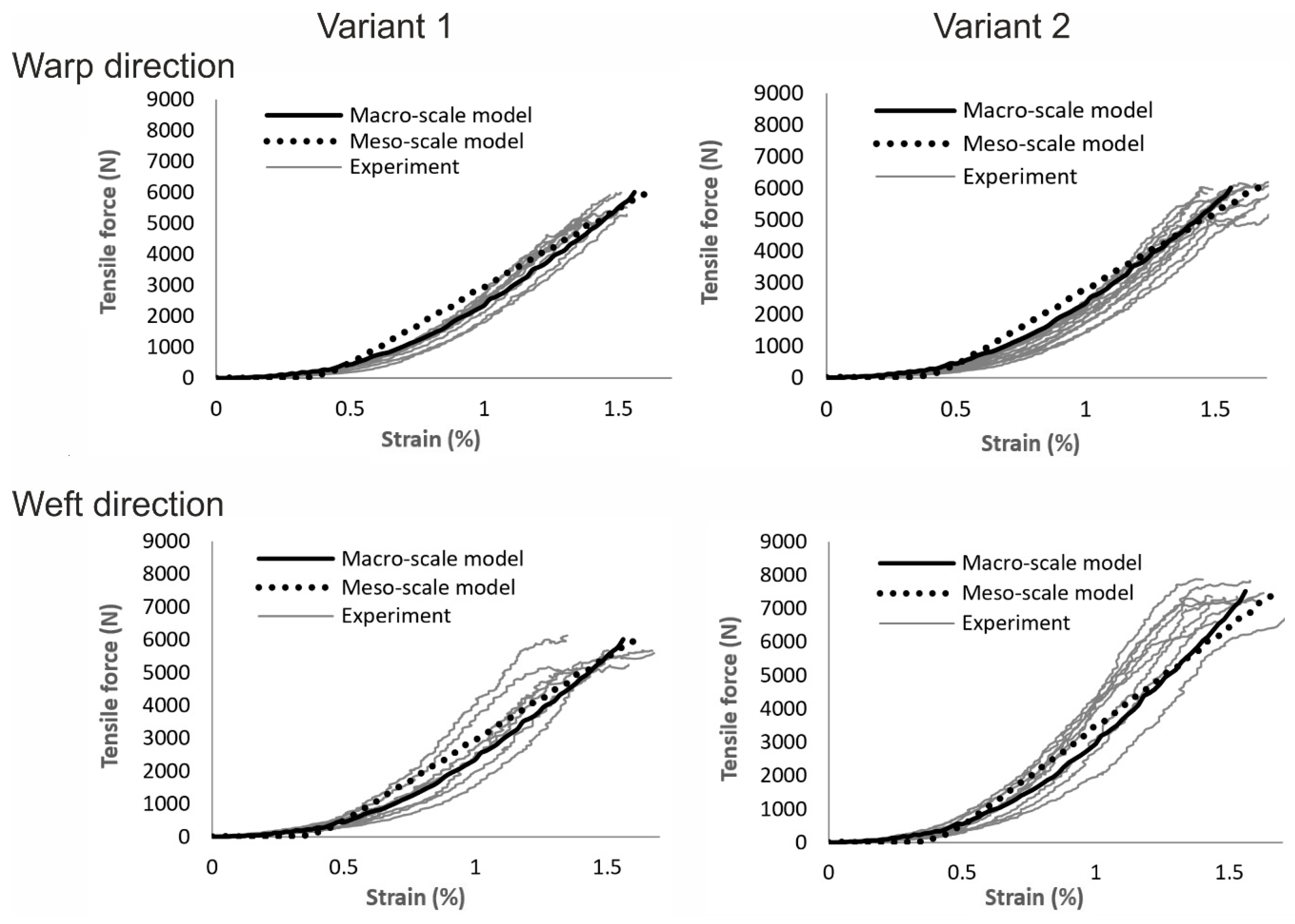
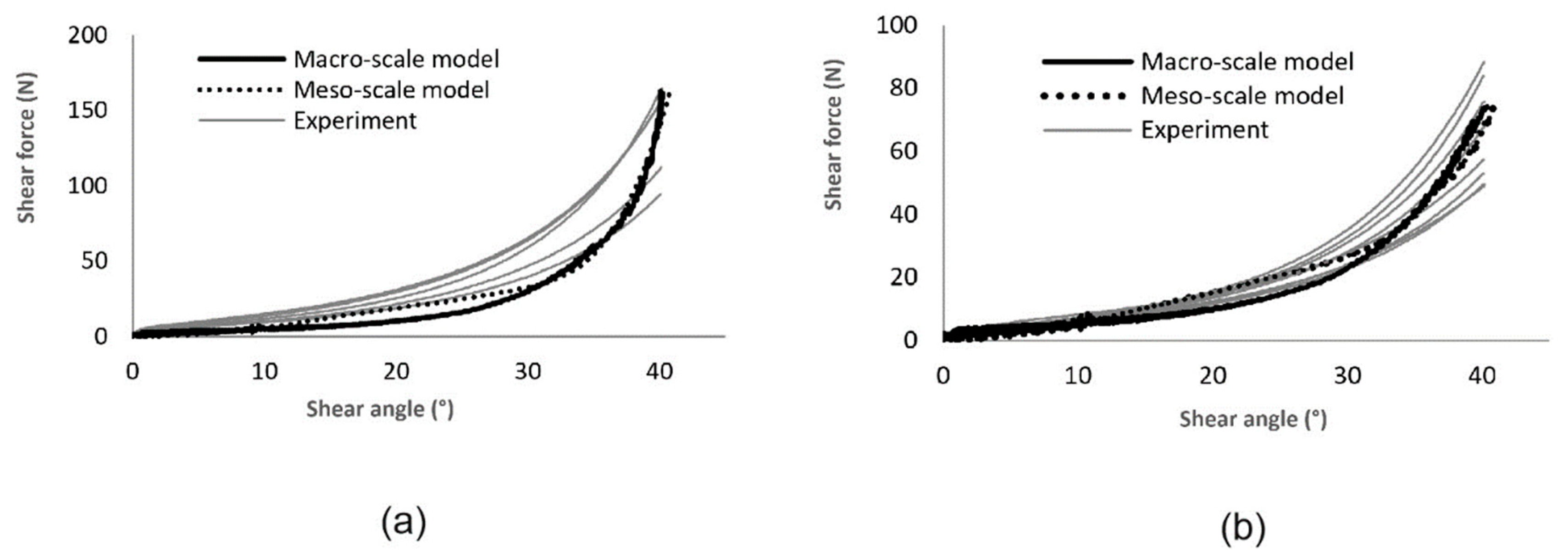
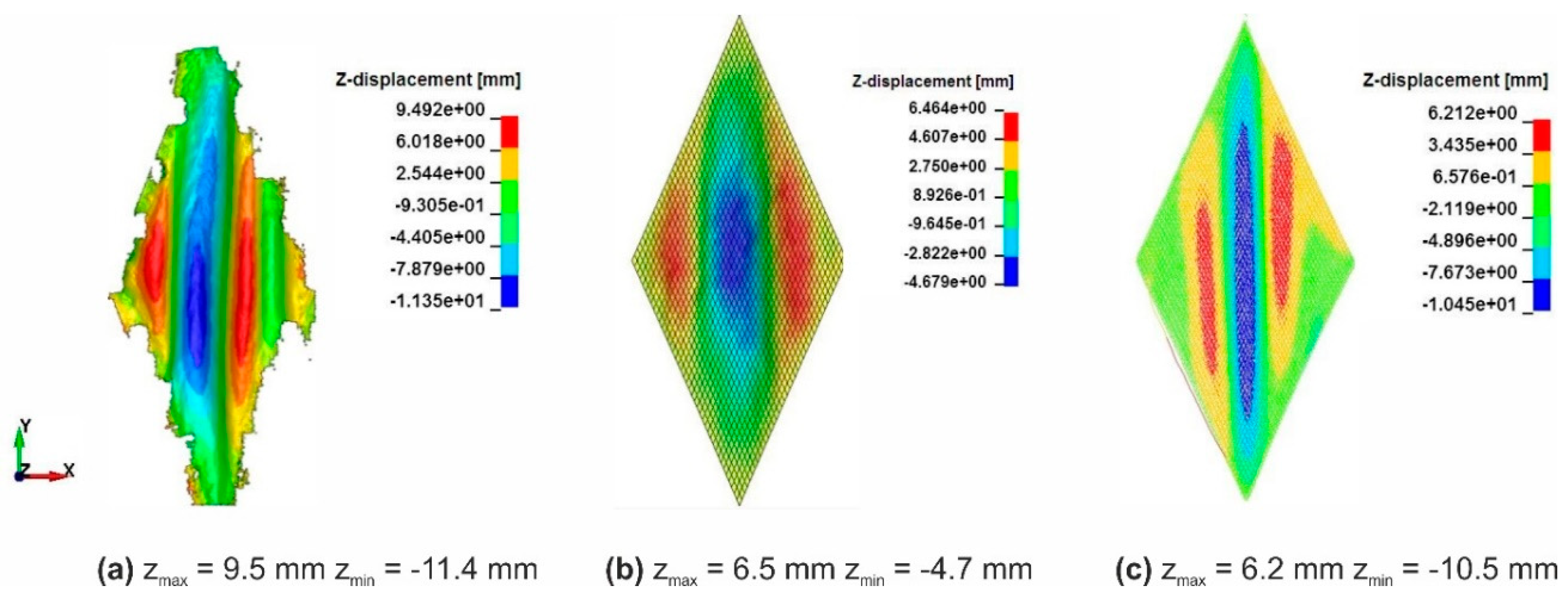
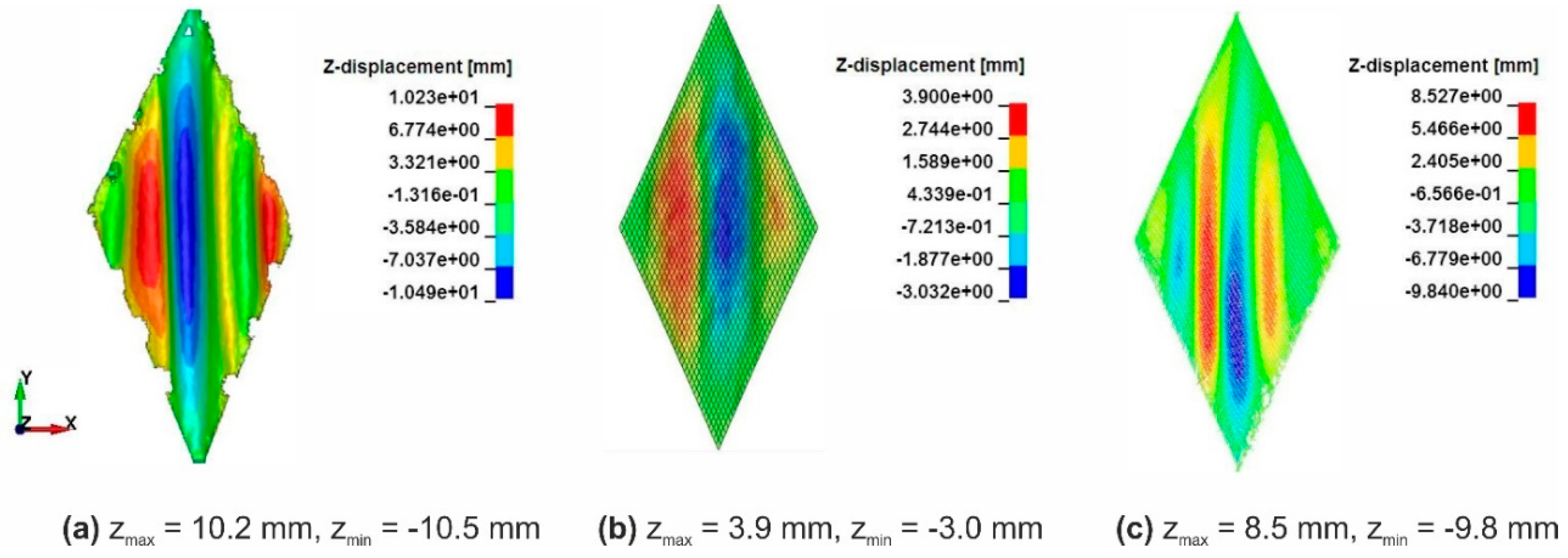
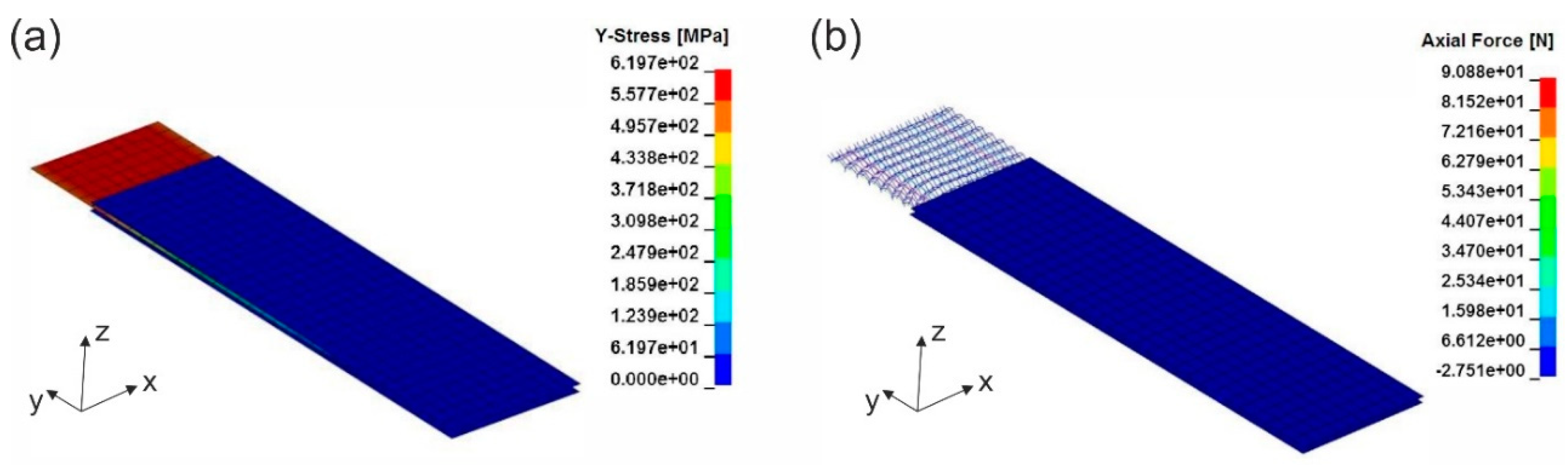
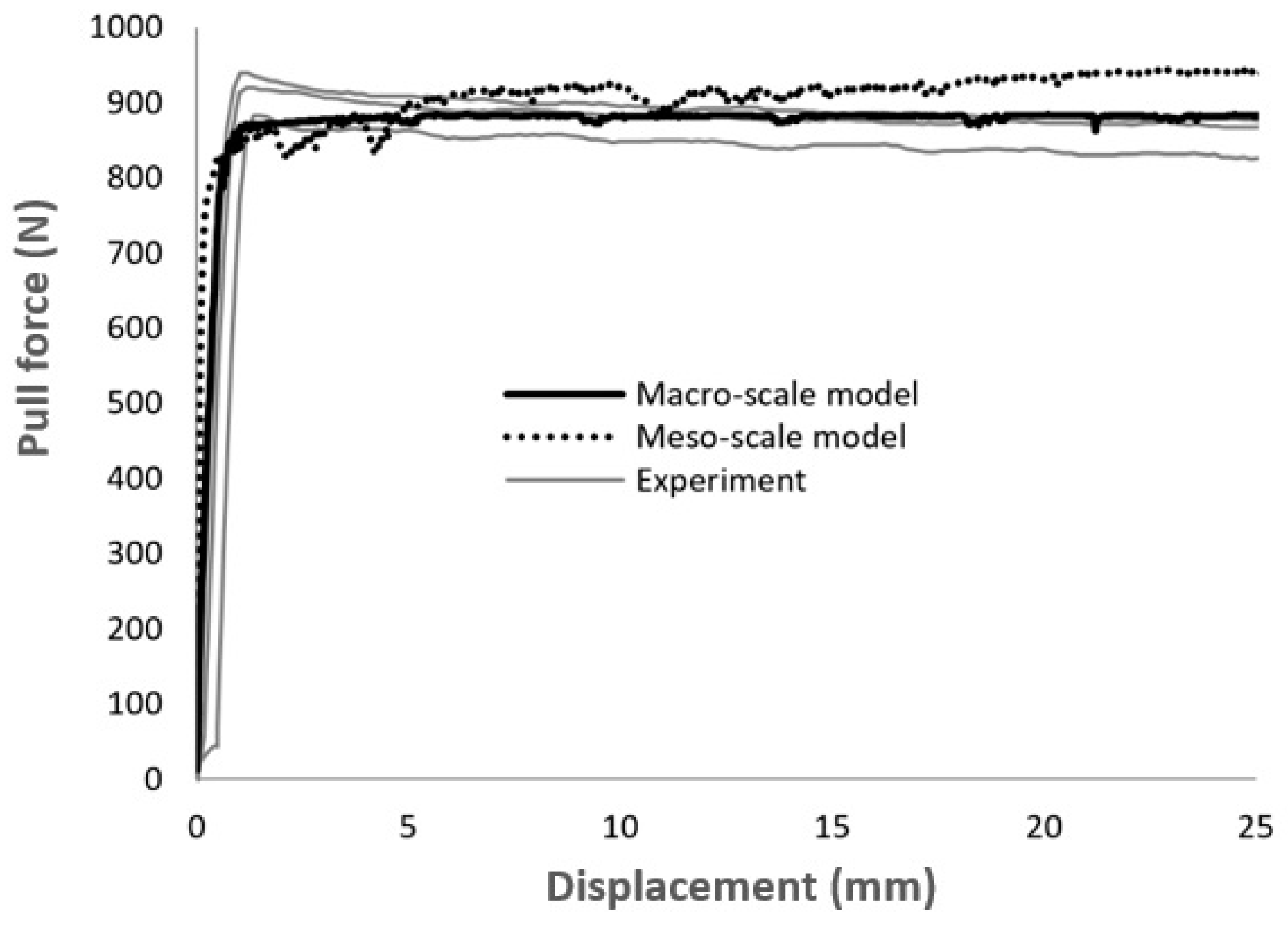
4. Simulation Results
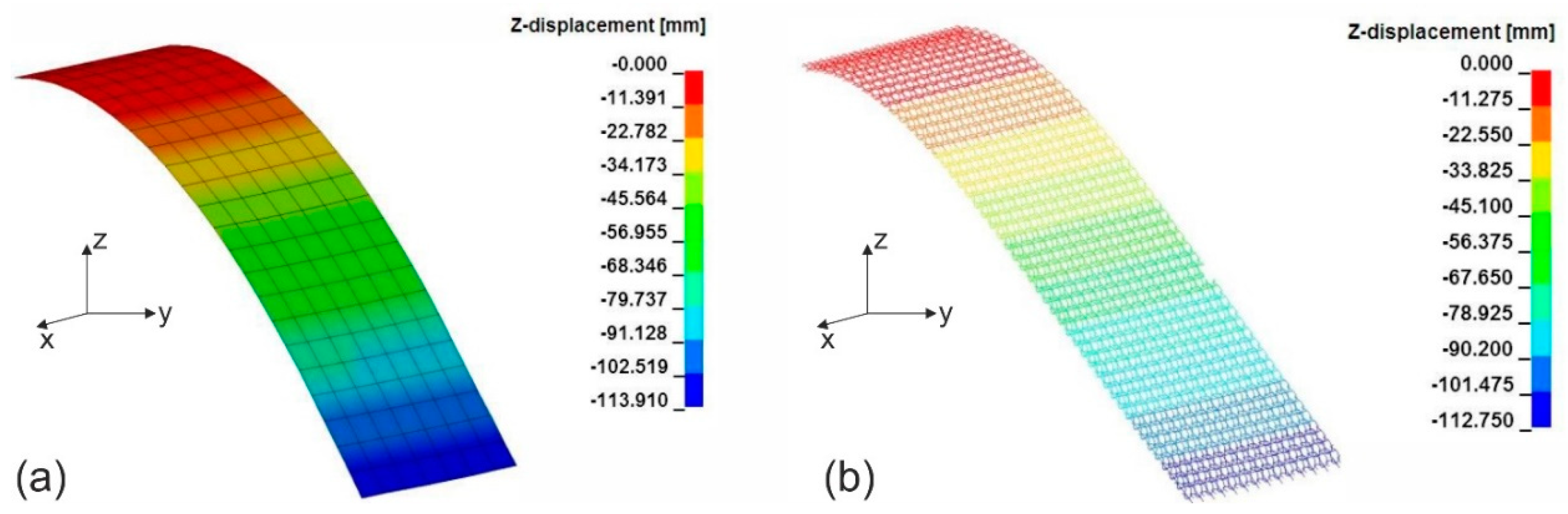
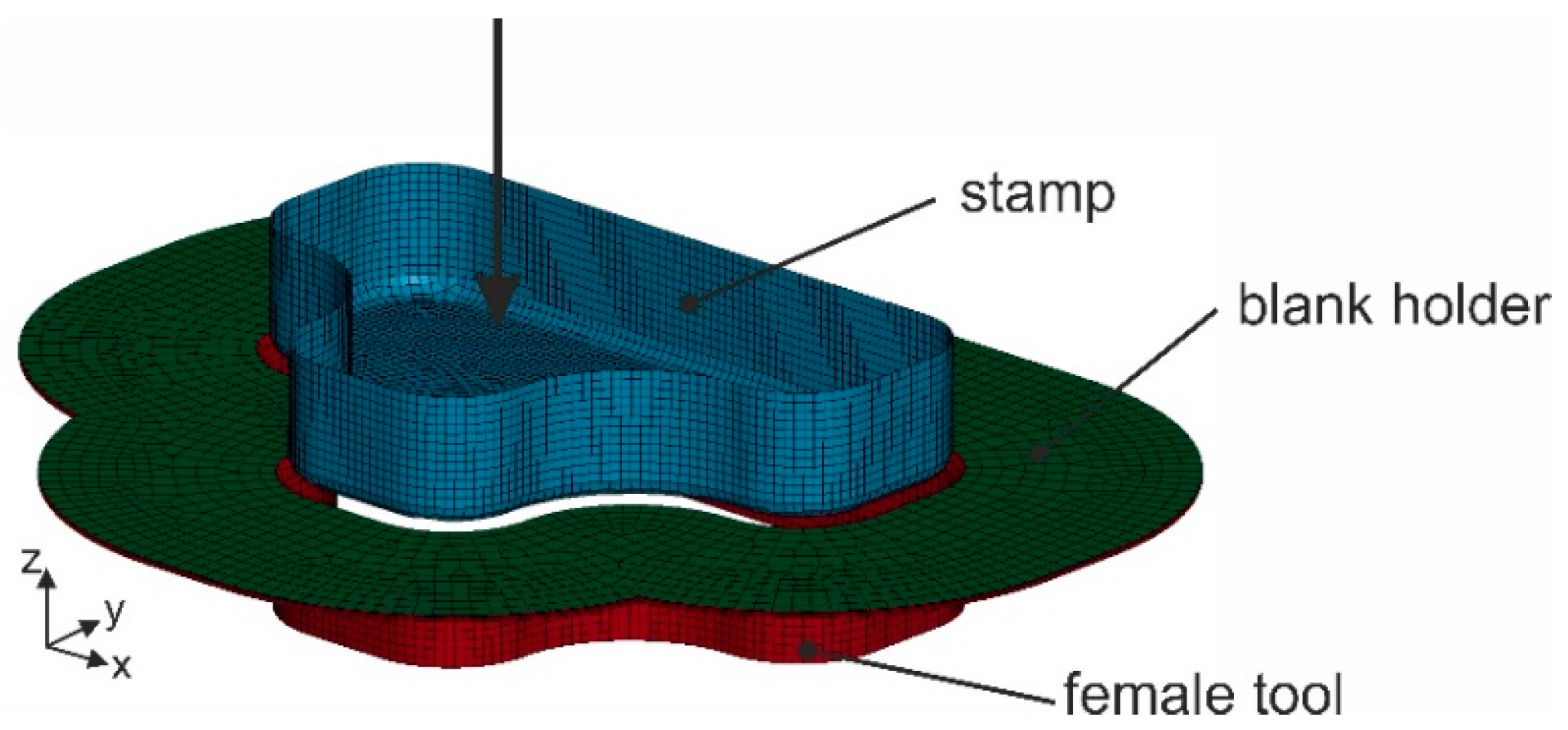
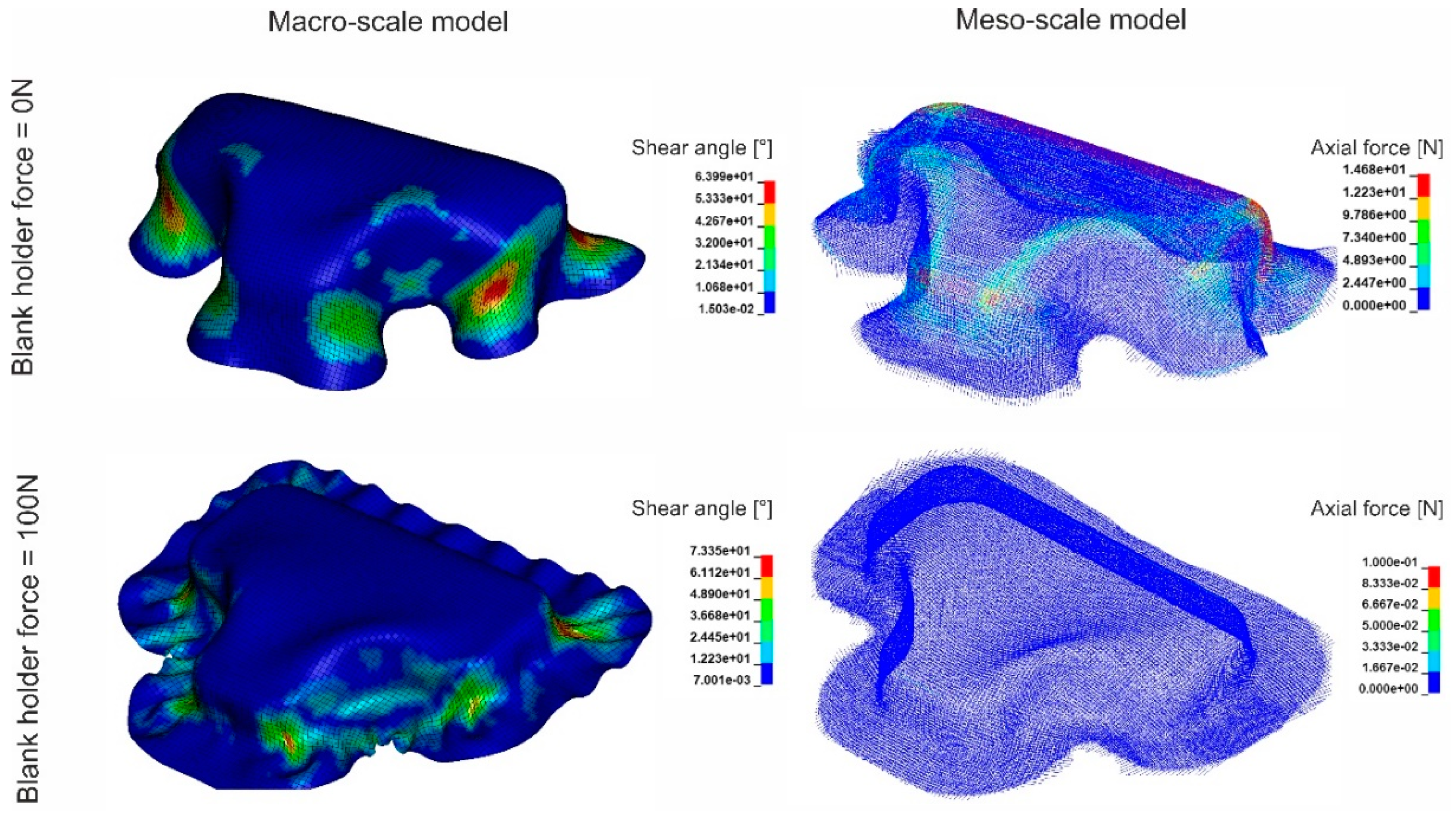
5. Model Application: Forming Simulation
6. Conclusions
Author Contributions
Funding

Acknowledgments
Conflicts of Interest
References
- Mazumdar, S. Composites Manufacturing: Materials, Product, and Process Engineering; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Cherif, C. (Ed.) Textile Materials for Lightweight Constructions; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Golzar, M.; Brünig, H.; Mäder, E. Commingled Hybrid Yarn Diameter Ratio in Continuous Fiber-Reinforced Thermoplastic Composites. J. Thermoplast. Compos. Mater. 2007, 20, 17–26. [Google Scholar] [CrossRef]
- Hasan, M.M.B.; Staiger, E.; Ashir, M.; Cherif, C. Development of Carbon Fibre/Polyamide 6,6 Commingled Hybrid Yarn for Textile-Reinforced Thermoplastic Composites. J. Thermoplast. Compos. Mater. 2015, 28, 1708–1724. [Google Scholar] [CrossRef]
- Abounaim, M.; Diestel, O.; Hoffmann, G.; Cherif, C. High Performance Thermoplastic Composite from Flat Knitted Multi-Layer Textile Preform Using Hybrid Yarn. Compos. Sci. Technol. 2011, 71, 511–519. [Google Scholar] [CrossRef]
- Trümper, W. Semi-Finished Weft Knitted Fabrics and Weft Knitting Techniques. In Textile Materials for Lightweight Constructions; Springer: Berlin/Heidelberg, Germany, 2016; pp. 213–250. [Google Scholar] [CrossRef]
- Trümper, W.; Lin, H.; Callin, T.; Bollengier, Q.; Cherif, C.; Krzywinski, S. Recent Developments in Multi-Layer Flat Knitting Technology for Waste Free Production of Complex Shaped 3D-Reinforcing Structures for Composites. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 141, p. 012015. [Google Scholar] [CrossRef]
- Hasani, H.; Hassanzadeh, S.; Abghary, M.J.; Omrani, E. Biaxial Weft-Knitted Fabrics as Composite Reinforcements: A Review. J. Ind. Text. 2017, 1439–1473. [Google Scholar] [CrossRef]
- Gereke, T.; Döbrich, O.; Hübner, M.; Cherif, C. Experimental and Computational Composite Textile Reinforcement Forming: A Review. Compos. Part A Appl. Sci. Manuf. 2013, 46, 1–10. [Google Scholar] [CrossRef]
- Nosrat Nezami, F.; Gereke, T.; Cherif, C. Analyses of Interaction Mechanisms during Forming of Multilayer Carbon Woven Fabrics for Composite Applications. Compos. Part A Appl. Sci. Manuf. 2016, 84, 406–416. [Google Scholar] [CrossRef]
- Nosrat Nezami, F.; Gereke, T.; Cherif, C. Active Forming Manipulation of Composite Reinforcements for the Suppression of Forming Defects. Compos. Part A Appl. Sci. Manuf. 2017, 99, 94–101. [Google Scholar] [CrossRef]
- Döbrich, O.; Gereke, T.; Diestel, O.; Krzywinski, S.; Cherif, C. Decoupling the Bending Behavior and the Membrane Properties of Finite Shell Elements for a Correct Description of the Mechanical Behavior of Textiles with a Laminate Formulation. J. Ind. Text. 2014, 44, 70–84. [Google Scholar] [CrossRef]
- Boisse, P.; Hamila, N.; Guzman-Maldonado, E.; Madeo, A.; Hivet, G.; dell’Isola, F. The Bias-Extension Test for the Analysis of in-Plane Shear Properties of Textile Composite Reinforcements and Prepregs: A Review. Int. J. Mater. Form. 2017, 10, 473–492. [Google Scholar] [CrossRef]
- Lamers, E.A.D. Shape Distortions in Fabric Reinforced Composite Products Due to Processing Induced Fibre Reorientation. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2004. [Google Scholar]
- Wijskamp, S.; Lamers, E.A.D.; Akkerman, R. Effects of Out-of-Plane Properties on Distortions of Composite Panels. In FRC 2000–Composites for the Millennium; Woodhead Publishing: Sawston, UK, 2014; pp. 361–368. [Google Scholar] [CrossRef]
- Erol, O.; Powers, B.; Keefe, M. A Novel Approach to Investigate the Effect of Meso-Scale Yarn Structure on the in-Plane Mechanical Response of Woven Monofilament Textiles by Numerical Modeling of Experiments. Mech. Adv. Mater. Struct. 2018, 25, 548–558. [Google Scholar] [CrossRef]
- Tran, P.; Ngo, T.; Yang, E.C.; Mendis, P.; Humphries, W. Effects of Architecture on Ballistic Resistance of Textile Fabrics: Numerical Study. Int. J. Damage Mech. 2014, 23, 359–376. [Google Scholar] [CrossRef]
- Grujicic, M.; Bell, W.C.; Arakere, G.; He, T.; Xie, X.; Cheeseman, B.A. Development of a Meso-Scale Material Model for Ballistic Fabric and Its Use in Flexible-Armor Protection Systems. J. Mater. Eng. Perform. 2010, 19, 22–39. [Google Scholar] [CrossRef]
- Hübner, M.; Staiger, E.; Küchler, K.; Gereke, T.; Cherif, C. Simulation of Patched Woven Fabric Composite Structures under Tensile Load. Tekstilec 2016, 59, 175–181. [Google Scholar] [CrossRef]
- Gereke, T.; Döbrich, O.; Malik, S.A.; Kocaman, R.T.; Aibibu, D.; Schmidt, K.; Antonyuk, S.; Ripperger, S.; Cherif, C. Numerical Micro-Scale Modelling of the Mechanical Loading of Woven Fabrics Equipped with Particles. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 460. [Google Scholar] [CrossRef]
- Döbrich, O.; Gereke, T.; Cherif, C. Modelling of Textile Composite Reinforcements on the Micro-Scale. Autex Res. J. 2014, 14, 28–33. [Google Scholar] [CrossRef]
- Nilakantan, G.; Keefe, M.; Bogetti, T.A.; Adkinson, R.; Gillespie, J.W. On the Finite Element Analysis of Woven Fabric Impact Using Multiscale Modeling Techniques. Int. J. Solids Struct. 2010, 47, 2300–2315. [Google Scholar] [CrossRef]
- Boisse, P.; Gasser, A.; Hivet, G. Analyses of Fabric Tensile Behaviour: Determination of the Biaxial Tension-Strain Surfaces and Their Use in Forming Simulations. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1395–1414. [Google Scholar] [CrossRef]
- Cherouat, A.; Billoët, J.L. Mechanical and Numerical Modelling of Composite Manufacturing Processes Deep-Drawing and Laying-up of Thin Pre-Impregnated Woven Fabrics. J. Mater. Process. Technol. 2001, 118, 460–471. [Google Scholar] [CrossRef]
- Lin, H.; Wang, J.; Long, A.C.; Clifford, M.J.; Harrison, P. Predictive Modelling for Optimization of Textile Composite Forming. Compos. Sci. Technol. 2007, 67, 3242–3252. [Google Scholar] [CrossRef]
- Khan, M.A.; Mabrouki, T.; Vidal-Sallé, E.; Boisse, P. Numerical and Experimental Analyses of Woven Composite Reinforcement Forming Using a Hypoelastic Behaviour. Application to the Double Dome Benchmark. J. Mater. Process. Technol. 2010, 210, 378–388. [Google Scholar] [CrossRef]
- Hamila, N.; Wang, P.; Vidal-Sallé, E.; Boisse, P. Simulation of Forming and Wrinkling of Textile Composite Reinforcements. In AIP Conference Proceedings; AIP: College Park, MD, USA, 2011; Volume 1353, pp. 942–947. [Google Scholar] [CrossRef]
- Gelin, J.C.; Cherouat, A.; Boisse, P.; Sabhi, H. Manufacture of Thin Composite Structure by the RTM Process: Numerical Simulation of the Shaping Operation. Compos. Sci. Technol. 1996, 56, 711–718. [Google Scholar] [CrossRef]
- Hamila, N.; Boisse, P. Simulations of Textile Composite Reinforcement Draping Using a New Semi-Discrete Three Node Finite Element. Compos. Part B Eng. 2008, 39, 999–1010. [Google Scholar] [CrossRef]
- Hübner, M.; Rocher, J.E.; Allaoui, S.; Hivet, G.; Gereke, T.; Cherif, C. Simulation-Based Investigations on the Drape Behavior of 3D Woven Fabrics Made of Commingled Yarns. Int. J. Mater. Form. 2016, 9, 591–599. [Google Scholar] [CrossRef]
- Gereke, T.; Cherif, C. A Review of Numerical Models for 3D Woven Composite Reinforcements. Compos. Struct. 2019, 60–66. [Google Scholar] [CrossRef]
- Khan, K.A.; Umer, R. Modeling the Viscoelastic Compaction Response of 3D Woven Fabrics for Liquid Composite Molding Processes. J. Reinf. Plast. Compos. 2017, 36. [Google Scholar] [CrossRef]
- Zeng, X.; Brown, L.P.; Endruweit, A.; Matveev, M.; Long, A.C. Geometrical Modelling of 3D Woven Reinforcements for Polymer Composites: Prediction of Fabric Permeability and Composite Mechanical Properties. Compos. Part A Appl. Sci. Manuf. 2014, 56, 150–160. [Google Scholar] [CrossRef]
- Zeng, X.; Brown, L.P.; Endruweit, A.; Long, A.C. Advanced Geometry Modelling of 3D Woven Reinforcements in Polymer Composites: Processing and Performance Analysis. In Proceedings of the Fourth World Conference on 3D Fabric and Their Applications, Aachen, Germany, 10–11 September 2012. [Google Scholar]
- Yang, X. Dynamic Simulation of 3D Weaving Process. J. Chem. Inf. Model. 2015, 53, 160. [Google Scholar] [CrossRef]
- Russcher, L.; Lamers, E.; Dufour, C.; Boussu, F.; Wang, P.; Soulat, D. Modelling the Microstructure of Multilayer Woven Fabrics. In Proceedings of the 13th AUTEX World Textile Conference, Dresden, Germany, 22–24 May 2013. [Google Scholar]
- Vorobiov, O.; Bischoff, T.; Tulke, A. Micro-Meso Draping Modelling of Non-Crimp Fabrics. In Proceedings of the 10th European LS-DYNA Conference, Würzburg, Germany, 15–17 June 2015. [Google Scholar]
- Demircan, O.; Ashibe, S.; Kosui, T.; Nakai, A. Modeling of Tensile and Bending Properties of Biaxial Weft Knitted Composites. Sci. Eng. Compos. Mater. 2015, 22, 303–313. [Google Scholar] [CrossRef]
- Duhovic, M.; Bhattacharyya, D. Simulating the Deformation Mechanisms of Knitted Fabric Composites. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1897–1915. [Google Scholar] [CrossRef]
- Abghary, M.J.; Hasani, H.; Nedoushan, R.J. Numerical Simulating the Tensile Behavior of 1×1 Rib Knitted Fabrics Using a Novel Geometrical Model. Fibers Polym. 2016, 17, 795–800. [Google Scholar] [CrossRef]
- Lomov, S.V. Modelling the Geometry of Textile Reinforcements for Composites: WiseTex. In Composite Reinforcements for Optimum Performance; Woodhead Publishing: Sawston, UK, 2011; pp. 200–238. [Google Scholar] [CrossRef]
- Weeger, O.; Sakhaei, A.H.; Tan, Y.Y.; Quek, Y.H.; Lee, T.L.; Yeung, S.K.; Kaijima, S.; Dunn, M.L. Nonlinear Multi-Scale Modelling, Simulation and Validation of 3D Knitted Textiles. Appl. Compos. Mater. 2018, 25, 797–810. [Google Scholar] [CrossRef]
- De Araújo, M.; Fangueiro, R.; Hong, H.B. Modelling and Simulation of the Mechanical Behaviour of Weft-Knitted Fabrics for Technical Applications: Part I: General Considerations and Experimental Analyses. Autex Res. J. 2003, 3, 111–123. [Google Scholar]
- Hessami, R.; Yazdi, A.A.; Mazidi, A. Investigation of Tensile and Flexural Behavior of Biaxial and Rib 1 × 1 Weft-Knitted Composite Using Experimental Tests and Multi-Scale Finite Element Modeling. J. Compos. Mater. 2019, 53, 3201–3215. [Google Scholar] [CrossRef]
- Pham, M.Q.; Döbrich, O.; Mersch, J.; Gereke, T.; Cherif, C. Meso-Scale Model for the Forming Process of Biaxial Reinforced Weft-Knitted Fabrics. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 406. [Google Scholar] [CrossRef]
- Dinh, T.D.; Weeger, O.; Kaijima, S.; Yeung, S.K. Prediction of Mechanical Properties of Knitted Fabrics under Tensile and Shear Loading: Mesoscale Analysis Using Representative Unit Cells and Its Validation. Compos. Part B Eng. 2018, 148, 81–92. [Google Scholar] [CrossRef]
- Shekarchizadeh, N.; Abedi, M.M.; Jafari Nedoushan, R. Prediction of Elastic Behavior of Plain Weft-Knitted Composites. J. Reinf. Plast. Compos. 2016, 35, 1613–1622. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, Y. Modeling Formability of Multiaxial Warp Knitted Fabrics on a Hemisphere. Compos. Part A Appl. Sci. Manuf. 2002, 33, 725–734. [Google Scholar] [CrossRef]
- De Araújo, M.; Fangueiro, R.; Hong, H. Modelling and Simulation of the Mechanical Behaviour of Weft-Knitted Fabrics for Technical Applications. Part IV: 3D FEA Model with a Mesh of Tetrahedric Elements. Autex Res. J. 2004, 4, 72–80. [Google Scholar]
- De Araújo, M.; Fangueiro, R.; Hong, H. Modelling and Simulation of the Mechanical Behaviour of Weft-Knitted Fabrics for Technical Applications: Part II: 3D Model Based on the Elastica Theory. Autex Res. J. 2003, 4, 166–172. [Google Scholar]
- De Araújo, M.; Fangueiro, R.; Hong, H. Modelling and Simulation of the Mechanical Behaviour of Weft-Knitted Fabrics for Technical Applications: Part III: 2D Hexagonal FEA Model with Non-Linear Truss Elements. Autex Res. J. 2004, 4, 25–32. [Google Scholar]
- De Araujo, M.; Fangueiro, R.; Hu, H. Weft-Knitted Structures for Industrial Applications. In Advances in Knitting Technology; Woodhead Publishing: Sawston, UK, 2011; pp. 136–170. [Google Scholar] [CrossRef]
- Hamedi, S.; Hasani, H.; Dibajian, S.H. Numerical Simulating the Flexural Properties of 3D Weft-Knitted Spacer Fabric Reinforced Composites. J. Compos. Mater. 2017, 51, 1887–1899. [Google Scholar] [CrossRef]
- Dusserre, G.; Balea, L.; Bernhart, G. Elastic Properties Prediction of a Knitted Composite with Inlaid Yarns Subjected to Stretching: A Coupled Semi-Analytical Model. Compos. Part A Appl. Sci. Manuf. 2014, 64, 185–193. [Google Scholar] [CrossRef]
- Iwata, A.; Inoue, T.; Naouar, N.; Boisse, P.; Lomov, S.V. Coupled Meso-Macro Simulation of Woven Fabric Local Deformation during Draping. Compos. Part A Appl. Sci. Manuf. 2019, 118, 267–280. [Google Scholar] [CrossRef]
- Boufaida, Z.; Boisse, J.; André, S.; Farge, L. A Mechanical Study of a Glass Fabric-Thermoplastic Resin Composite: 3D-DIC and X-Ray Tomographic Observations Explained by Numerical Simulations Based on a Spectral Solver. arXiv 2016, arXiv:1605.00478. [Google Scholar]
- Bilisik, K.; Kaya, G.; Ozdemir, H.; Korkmaz, M.; Erdogan, G. Applications of Glass Fibers in 3D Preform Composites. In Advances in Glass Science and Technology; IntechOpen: London, UK, 2018. [Google Scholar]
- Hufenbach, W.; Böhm, R.; Thieme, M.; Winkler, A.; Mäder, E.; Rausch, J.; Schade, M. Polypropylene/Glass Fibre 3D-Textile Reinforced Composites for Automotive Applications. Mater. Des. 2011, 32, 1468–1476. [Google Scholar] [CrossRef]
- International Organization for Standardization. Textiles-Yarn from Packages-Determination of Linear Density (Mass per Unit Length) by the Skein Method (ISO 2060:1994); German Version EN ISO 2060:1995; ISO: Geneva, Switzerland, 1995. [Google Scholar]
- International Organization for Standardization. Textile Glass-Yarns-Determination of Breaking Force and Breaking Elongation ISO 3341:2000-05; ISO: Geneva, Switzerland, 2000. [Google Scholar]
- Deutsches Institut für Normung. Textilien–Maschenwaren–Bestimmung Der Maschenlänge Und Der Längenbezogenen Garnfeinheit Bei Gestricken; Deutsche Fassung EN 14970:2006; Deutsches Institut für Normung: Berlin, Germany, 2006. [Google Scholar]
- International Organization for Standardization. Textiles-Determination of Thickness of Textiles and Textile Products ISO 5084:1996; ISO: Geneva, Switzerland, 1996. [Google Scholar]
- Deutsches Institut für Normung. DIN EN 12127:1997-12 Textiles-Fabrics-Determination of Mass per Unit Area Using Small Samples; Deutsches Institut für Normung: Berlin, Germany, 1997. [Google Scholar]
- International Organization for Standardization. Textiles-Tensile Properties of Fabrics-Part 1: Determination of Maximum Force and Elongation at Maximum Force Using the Strip Method ISO 13934-1:2013; ISO: Geneva, Switzerland, 2013. [Google Scholar] [CrossRef]
- Orawattanasrikul, S. Experimentelle Analyse der Scherdeformationen Biaxial Verstärkter Mehrlagengestricke. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2006. [Google Scholar]
- Deutsches Institut für Normung. DIN 53362:2003-10 Testing of Plastics Films and Textile Fabrics (Excluding Nonwovens), Coated or Not Coated Fabrics-Determination of Stiffness in Bending-Method According to Cantilever; Deutsches Institut für Normung: Berlin, Germany, 2003. [Google Scholar]
- Reumann, R.-D.; Hempel, P.; Haase, J. Flächengebildeprüfungen. In Prüfverfahren in der Textil-und Bekleidungstechnik; Springer: Berlin/Heidelberg, Germany, 2011; pp. 379–491. [Google Scholar] [CrossRef]
- Boisse, P.; Hamila, N.; Madeo, A. The Difficulties in Modeling the Mechanical Behavior of Textile Composite Reinforcements with Standard Continuum Mechanics of Cauchy. Some Possible Remedies. Int. J. Solids Struct. 2018, 55–65. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual Volume II Material Models; Liver-More Software Technology Corporation: Livermore, CA, USA, 2017. [Google Scholar]
- Choi, K.F.; lo, T.Y. An Energy Model of Plain Knitted Fabric. Text. Res. J. 2003, 73, 739–748. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual Volume I; Liver-More Software Technology Corporation: Livermore, CA, USA, 2017. [Google Scholar]
- Livermore Software Technology Corporation (LSTC). Theory Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2015. [Google Scholar]
- Moustacas, H.; Wielhorski, Y.; Durville, D. A Higher Order Finite Strain Beam Model for the Modelling of Compaction of Textile Tows. In EUROMECH Colloquium 602; AMAC: Lyon, France, 2019. [Google Scholar]



| Parameter | Value |
|---|---|
| Reinforcing yarn (commingled hybrid yarn and folded) | CF/PA 6.6 (4 × 300 tex) |
| E-Modulus of reinforcing yarn [GPa] | 59.3 ± 17.7 |
| Fracture strain of reinforcing yarn [%] | 1.00 ± 0.15 |
| Knitting yarn (folded yarn) | GF (2 x 68 tex)/PA 6.6 (94 tex) |
| E-Modulus of knitting yarn [GPa] | 71.9 ± 6.38 |
| Fracture strain of knitting yarn [%] | 2.69 ± 0.14 |
| Parameter | Unit | Variant 1 | Variant 2 |
|---|---|---|---|
| Warp yarn density | yarn/100 mm | 28 | 28 |
| Weft yarn density | yarn/100 mm | 28 | 41 |
| Knitting loop length | mm | 14.4 ± 0.5 | 13.4 ± 0.5 |
| Area mass density of the fabric | g/m2 | 824.2 ± 45.7 | 1198.8 ± 28.6 |
| Thickness of the fabric | mm | 2.22 ± 0.08 | 2.63 ± 0.15 |
| Parameter | Unit | Direction | Variant 1 | Variant 2 |
|---|---|---|---|---|
| Max. tensile force | N | warp | 5820 ± 461 | 5800 ± 367 |
| weft | 5744 ± 354 | 7332 ± 380 | ||
| Fracture strain | % | warp | 1.6 ± 0.3 | 1.6 ± 0.1 |
| weft | 1.6 ± 0.2 | 1.6 ± 0.2 | ||
| Overhang length | mm | warp | 171 ± 51 | 178 ± 14 |
| weft | 151 ± 15 | 194 ± 8 | ||
| Cantilever bending stiffness per unit width | Ncm2 | warp | 2.53 x 103 | 4.14 x 103 |
| weft | 1.74 x 103 | 5.36 x 103 |
| Simulation | Macro-Scale Model | Meso-Scale Model | ||
|---|---|---|---|---|
| Computational Cost (CPUh) | Number of Shell Elements | Computational Cost (CPUh) | Number of Beam Elements | |
| Tensile stripe test | 0.067 | 440 | 4 | 34,636 |
| Picture-frame-test | 28 | 1600 | 204 | 40,123 |
| Cantilever test | 16 | 300 | 1344 | 29,063 |
| Friction test | 0.67 | 300 | 14 | 25,970 |
| Forming with T-shape tools | 384 | 27,512 | 2016 | 237,192 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, M.Q.; Döbrich, O.; Trümper, W.; Gereke, T.; Cherif, C. Numerical Modelling of the Mechanical Behaviour of Biaxial Weft-Knitted Fabrics on Different Length Scales. Materials 2019, 12, 3693. https://doi.org/10.3390/ma12223693
Pham MQ, Döbrich O, Trümper W, Gereke T, Cherif C. Numerical Modelling of the Mechanical Behaviour of Biaxial Weft-Knitted Fabrics on Different Length Scales. Materials. 2019; 12(22):3693. https://doi.org/10.3390/ma12223693
Chicago/Turabian StylePham, Minh Quang, Oliver Döbrich, Wolfgang Trümper, Thomas Gereke, and Chokri Cherif. 2019. "Numerical Modelling of the Mechanical Behaviour of Biaxial Weft-Knitted Fabrics on Different Length Scales" Materials 12, no. 22: 3693. https://doi.org/10.3390/ma12223693
APA StylePham, M. Q., Döbrich, O., Trümper, W., Gereke, T., & Cherif, C. (2019). Numerical Modelling of the Mechanical Behaviour of Biaxial Weft-Knitted Fabrics on Different Length Scales. Materials, 12(22), 3693. https://doi.org/10.3390/ma12223693







