Elastic Mechanical Properties of 45S5-Based Bioactive Glass–Ceramic Scaffolds †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication of Glass-Derived Scaffolds
2.2. Characterizations
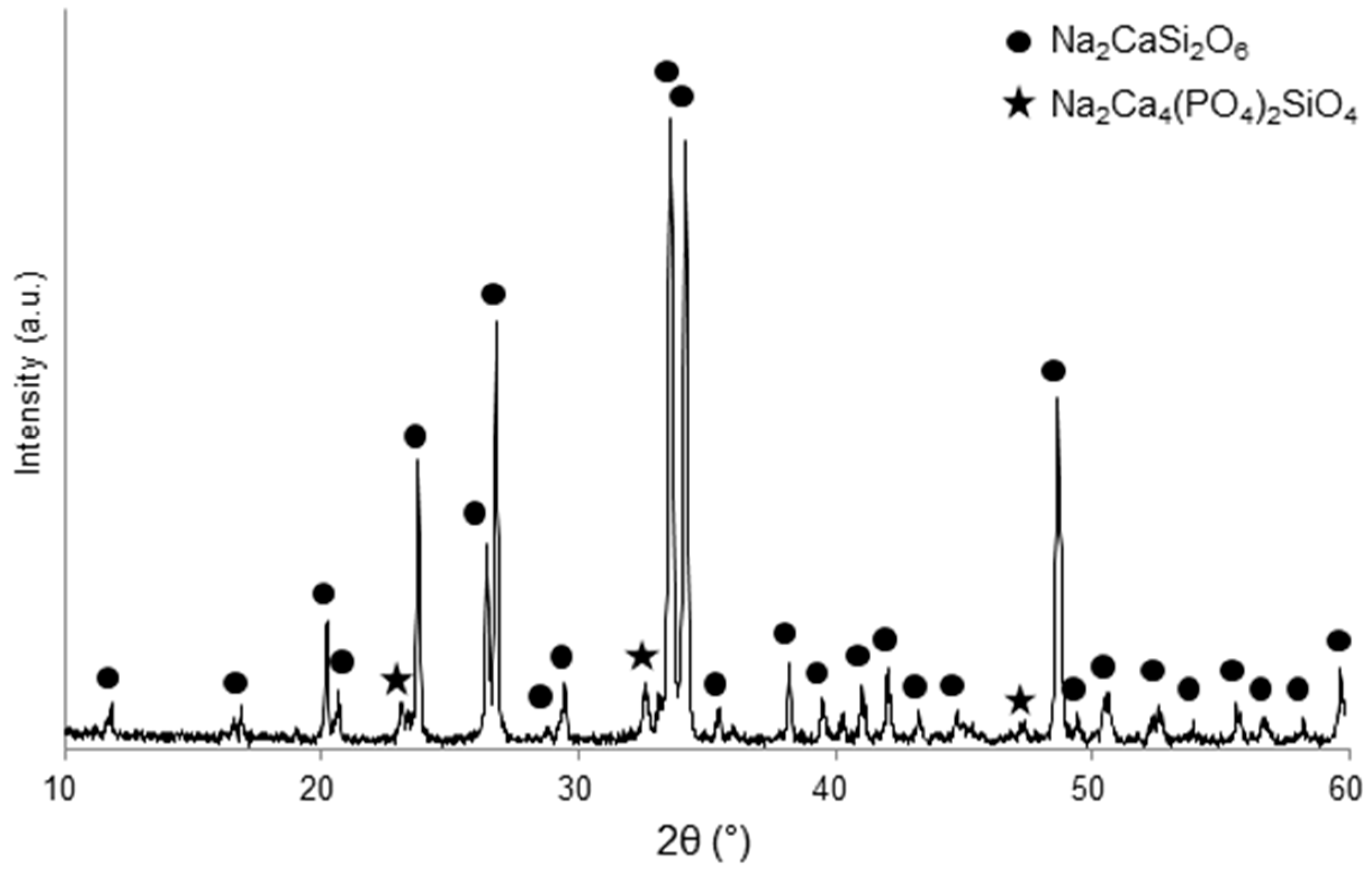
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Campana, V.; Milano, G.; Pagano, E.; Barba, M.; Cicione, C.; Salonna, G.; Lattanzi, W.; Logroscino, G. Bone substitutes in orthopaedic surgery: From basic science to clinical practice. J. Mater. Sci. Mater. Med. 2014, 25, 2445–2461. [Google Scholar] [CrossRef] [PubMed]
- Baino, F.; Novajra, G.; Vitale-Brovarone, C. Bioceramics and scaffolds: A winning combination for tissue engineering. Front. Bioeng. Biotechnol. 2015, 3, 202. [Google Scholar] [CrossRef] [PubMed]
- Hing, K.A. Bioceramic bone graft substitutes: Influence of porosity and chemistry. Int. J. Appl. Ceram. Technol. 2005, 2, 184–199. [Google Scholar] [CrossRef]
- Karageorgiu, V.; Kaplan, D. Porosity of 3D biomaterial scaffolds and osteo-genesis. Biomaterials 2005, 26, 5474–5491. [Google Scholar] [CrossRef] [PubMed]
- Rahaman, M.N.; Day, D.E.; Bal, B.S.; Fu, Q.; Jung, S.B.; Bonewald, L.F.; Tomsia, A.P. Bioactive glass in tissue engineering. Acta Biomater. 2011, 7, 2355–2373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoppe, A.; Güldal, N.S.; Boccaccini, A.R. A review of the biological response to ionic dissolution products from bioactive glasses and glass-ceramics. Biomaterials 2011, 32, 2757–2774. [Google Scholar] [CrossRef]
- Baino, F.; Hamzehlou, S.; Kargozar, S. Bioactive glasses: Where are we and where are we going? J. Funct. Biomater. 2018, 9, 25. [Google Scholar] [CrossRef] [PubMed]
- Miguez-Pacheco, V.; Hench, L.L.; Boccaccini, A.R. Bioactive glasses beyond bone and teeth: Emerging applications in contact with soft tissues. Acta Biomater. 2015, 13, 1–15. [Google Scholar] [CrossRef]
- Kargozar, S.; Hamzehlou, S.; Baino, F. Can bioactive glasses be useful to accelerate the healing of epithelial tissues? Mater. Sci. Eng. C 2019, 97, 1009–1020. [Google Scholar] [CrossRef]
- Chen, Q.Z.; Thompson, I.D.; Boccaccini, A.R. 45S5 Bioglass®-derived glass–ceramic scaffolds for bone tissue engineering. Biomaterials 2006, 27, 2414–2425. [Google Scholar] [CrossRef]
- Hench, L.L. Bioceramics: From concept to clinic. J. Am. Ceram. Soc. 1991, 74, 1487–1510. [Google Scholar] [CrossRef]
- Massera, J.; Fagerlund, S.; Hupa, L.; Hupa, M. Crystallization mechanism of the bioactive glasses, 45S5 and S53P4. J. Am. Ceram. Soc. 2012, 95, 607–613. [Google Scholar] [CrossRef]
- Peitl, O.; LaTorre, G.P.; Hench, L.L. Effect of crystallization on apatite layer formation of bioactive glass 45S5. J. Biomed. Mater. Res. 1996, 30, 509–514. [Google Scholar]
- Bellucci, D.; Chiellini, F.; Ciardelli, G.; Gazzarri, M.; Gentile, P.; Sola, A.; Cannillo, V. Processing and characterization of innovative scaffolds for bone tissue engineering. J. Mater. Sci. Mater. Med. 2012, 23, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.C.; Hsu, H.C.; Hsiao, S.H.; Ho, W.F. Preparation of porous 45S5 Bioglass®-derived glass-ceramic scaffolds by using rice husk as a porogen additive. J. Mater. Sci. Mater. Med. 2009, 20, 1229–1236. [Google Scholar] [CrossRef] [PubMed]
- Eqtesadi, S.; Motealleh, A.; Miranda, P.; Pajares, A.; Lemos, A.; Ferreira, J.M.F. Robocasting of 45S5 bioactive glass scaffolds for bone tissue engineering. J. Eur. Ceram. Soc. 2014, 34, 107–118. [Google Scholar] [CrossRef]
- Motealleh, A.; Eqtesadi, S.; Civantos, A.; Pajares, A.; Miranda, P. Robocast 45S5 bioglass scaffolds: In vitro behaviour. J. Mater. Sci. 2017, 52, 9179–9191. [Google Scholar] [CrossRef]
- Jones, J.R.; Brauer, D.S.; Hupa, L.; Greenspan, D.C. Bioglass and bioactive glasses and their impact on healthcare. Int. J. Appl. Glass Sci. 2016, 7, 423–434. [Google Scholar] [CrossRef]
- Vitale-Brovarone, C.; Baino, F.; Verné, E. High strength bioactive glass-ceramic scaffolds for bone regeneration. J. Mater. Sci. Mater. Med. 2009, 20, 643–653. [Google Scholar] [CrossRef]
- Fu, Q.; Rahaman, M.N.; Bal, B.S.; Brown, R.F.; Day, D.E. Mechanical and in vitro performance of 13–93 bioactive glass scaffolds prepared by a polymer foam replication technique. Acta Biomater. 2008, 4, 1854–1864. [Google Scholar] [CrossRef]
- Baino, F.; Vitale-Brovarone, C. Mechanical properties and reliability of glass-ceramic foam scaffolds for bone repair. Mater. Lett. 2014, 118, 27–30. [Google Scholar] [CrossRef]
- Baino, F.; Verné, E.; Vitale-Brovarone, C. 3-D high strength glass-ceramic scaffolds containing fluoroapatite for load-bearing bone portions replacement. Mater. Sci. Eng. C 2009, 29, 2055–2062. [Google Scholar] [CrossRef]
- Chen, Q.Z.; Mohn, D.; Stark, W.J. Optimization of Bioglass® scaffold fabrication process. J. Am. Ceram. Soc. 2011, 94, 4184–4190. [Google Scholar] [CrossRef]
- Chen, Q.; Baino, F.; Spriano, S.; Pugno, N.; Vitale-Brovarone, C. Modelling of the strength-porosity relationship in glass-ceramic foam scaffolds for bone repair. J. Eur. Ceram. Soc. 2014, 34, 2663–2673. [Google Scholar] [CrossRef]
- Tagliabue, S.; Rossi, E.; Baino, F.; Vitale-Brovarone, G.; Gastaldi, D.; Vena, P. Micro-CT based finite element models for elastic properties of glass-ceramic scaffolds. J. Mech. Behav. Biomed. Mater. 2017, 65, 248–255. [Google Scholar] [CrossRef] [PubMed]
- Baino, F.; Ferraris, M.; Bretcanu, O.; Verné, E.; Vitale-Brovarone, C. Optimization of composition, structure and mechanical strength of bioactive 3-D glass-ceramic scaffolds for bone substitution. J. Biomater. Appl. 2013, 27, 872–890. [Google Scholar] [CrossRef]
- ASTM C1259-14. Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio for Advanced Ceramics by Impulse Excitation of Vibration; ASTM: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Lefebvre, L.; Chevalier, J.; Gremillard, L.; Zenati, R.; Thollet, G.; Bernache-Assolant, D.; Govin, A. Structural transformations of bioactive glass 45S5 with thermal treatments. Acta Mater. 2007, 55, 3305–3313. [Google Scholar] [CrossRef] [Green Version]
- Golovchak, R.; Thapar, P.; Ingram, A.; Savytskii, D.; Jain, H. Influence of phase separation on the devitrification of 45S5 bioglass. Acta Biomater. 2014, 10, 4878–4886. [Google Scholar] [CrossRef] [Green Version]
- Baino, F.; Fiume, E. Quantifying the effect of particle size on the crystallization of 45S5 bioactive glass. Mater. Lett. 2018, 224, 54–58. [Google Scholar] [CrossRef]
- Lefebvre, L.; Gremillard, L.; Chevalier, J.; Zenati, R.; Bernache-Assolant, D. Sintering behaviour of 45S5 bioactive glass. Acta Biomater. 2008, 4, 1894–1903. [Google Scholar] [CrossRef]
- Bellucci, D.; Cannillo, V.; Sola, A.; Chiellini, F.; Gazzarri, M.; Migone, C. Macroporous Bioglass®-derived scaffolds for bone tissue regeneration. Ceram. Int. 2011, 37, 1575–1585. [Google Scholar] [CrossRef]
- Anselme, K.; Davidson, P.; Popa, A.M.; Giazzon, M.; Liley, M.; Ploux, L. The interactions of cells and bacteria with surfaces structured at the nanometre scale. Acta Biomater. 2010, 6, 3824–3846. [Google Scholar] [CrossRef]
- Thompson, J.D.; Hench, L.L. Mechanical properties of bioactive glasses, glass-ceramics and composites. Proc. Inst. Mech. Eng. H J. Eng. Med. 1998, 212, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Foppiano, S.; Marshall, S.J.; Marshall, G.W.; Saiz, E.; Tomsia, A.P. The influence of novel bioactive glasses on in vitro osteoblast behavior. J. Biomed. Mater. Res. A 2004, 71, 242–249. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, F. The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorova, E.; Ticha, G. Elasticity of porous ceramics—A critical study of modulus-porosity relations. J. Eur. Ceram. Soc. 2006, 26, 1085–1097. [Google Scholar] [CrossRef]
- Zivcova, Z.; Cerny, M.; Pabst, W.; Gregorova, E. Elastic properties of porous oxide ceramics prepared using starch as a pore-forming agent. J. Eur. Ceram. Soc. 2009, 29, 2765–2771. [Google Scholar] [CrossRef]
- Pabst, W.; Gregorova, E.; Sedlarova, I.; Cerny, M. Preparation and characterization of porous alumina-zirconia composite ceramics. J. Eur. Ceram. Soc. 2011, 31, 2721–2731. [Google Scholar] [CrossRef]
- Kaur, G.; Kumar, V.; Baino, F.; Mauro, J.C.; Pickrell, G.; Evans, I.; Bretcanu, O. Mechanical properties of bioactive glasses, ceramics, glass-ceramics and composites: State-of-the-art review and future challenges. Mater. Sci. Eng. C 2019, 104, 109895. [Google Scholar] [CrossRef]
- Malasoma, A.; Fritsch, A.; Kohlhauser, C.; Brynk, T.; Vitale-Brovarone, C.; Pakiela, Z.; Eberhardsteiner, J.; Hellmich, C. Micromechanics of bioresorbable porous CEL2 glass ceramic scaffolds for bone tissue engineering. Adv. Appl. Ceram. 2008, 107, 277–286. [Google Scholar] [CrossRef]
- Jones, J.R.; Ehrenfried, L.M.; Hench, L.L. Optimising bioactive glass scaffolds for bone tissue engineering. Biomaterials 2006, 27, 964–973. [Google Scholar] [CrossRef] [PubMed]
- Midha, S.; Kim, T.B.; Van Den Bergh, W.; Lee, P.D.; Jones, J.R.; Mitchell, C.A. Preconditioned 70S30C bioactive glass foams promote osteogenesis in vivo. Acta Biomater. 2013, 9, 9169–9182. [Google Scholar] [CrossRef] [PubMed]
- Baino, F.; Fiume, E.; Miola, M.; Leone, F.; Onida, B.; Verné, E. Fe-doped bioactive glass-derived scaffolds produced by sol-gel foaming. Mater. Lett. 2019, 235, 207–211. [Google Scholar] [CrossRef]
- Arnold, M.; Boccaccini, A.R.; Ondracek, G. Prediction of the Poisson’s ratio of porous materials. J. Mater. Sci. 1996, 31, 1643–1646. [Google Scholar] [CrossRef]
- De With, G.; Van Dijk, H.; Hattu, N.; Prijs, K. Preparation, microstructure and mechanical properties of dense polycrystalline hydroxy apatite. J. Mater. Sci. 1981, 16, 1592–1598. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids—Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; pp. 175–234. [Google Scholar]
- Denry, I.; Goudouri, O.M.; Fredericks, D.C.; Akkouch, A.; Acevedo, M.R.; Holloway, J.A. Strontium-releasing fluorapatite glass-ceramic scaffolds: Structural characterization and in vivo performance. Acta Biomater. 2018, 75, 463–471. [Google Scholar] [CrossRef]
- Baino, F.; Fiume, E. Mechanical characterization of 45S5 bioactive glass-derived scaffolds. Mater. Lett. 2019, 245, 14–17. [Google Scholar] [CrossRef]
- Rezwan, K.; Chen, Q.Z.; Blaker, J.J.; Boccaccini, A.R. Biodegradable and bioactive porous polymer/inorganic composite scaffolds for bone tissue engineering. Biomaterials 2006, 27, 3413–3431. [Google Scholar] [CrossRef]
- Keller, T.S. Predicting the compressive mechanical behavior of bone. J. Biomech. 1994, 27, 1159–1168. [Google Scholar] [CrossRef]

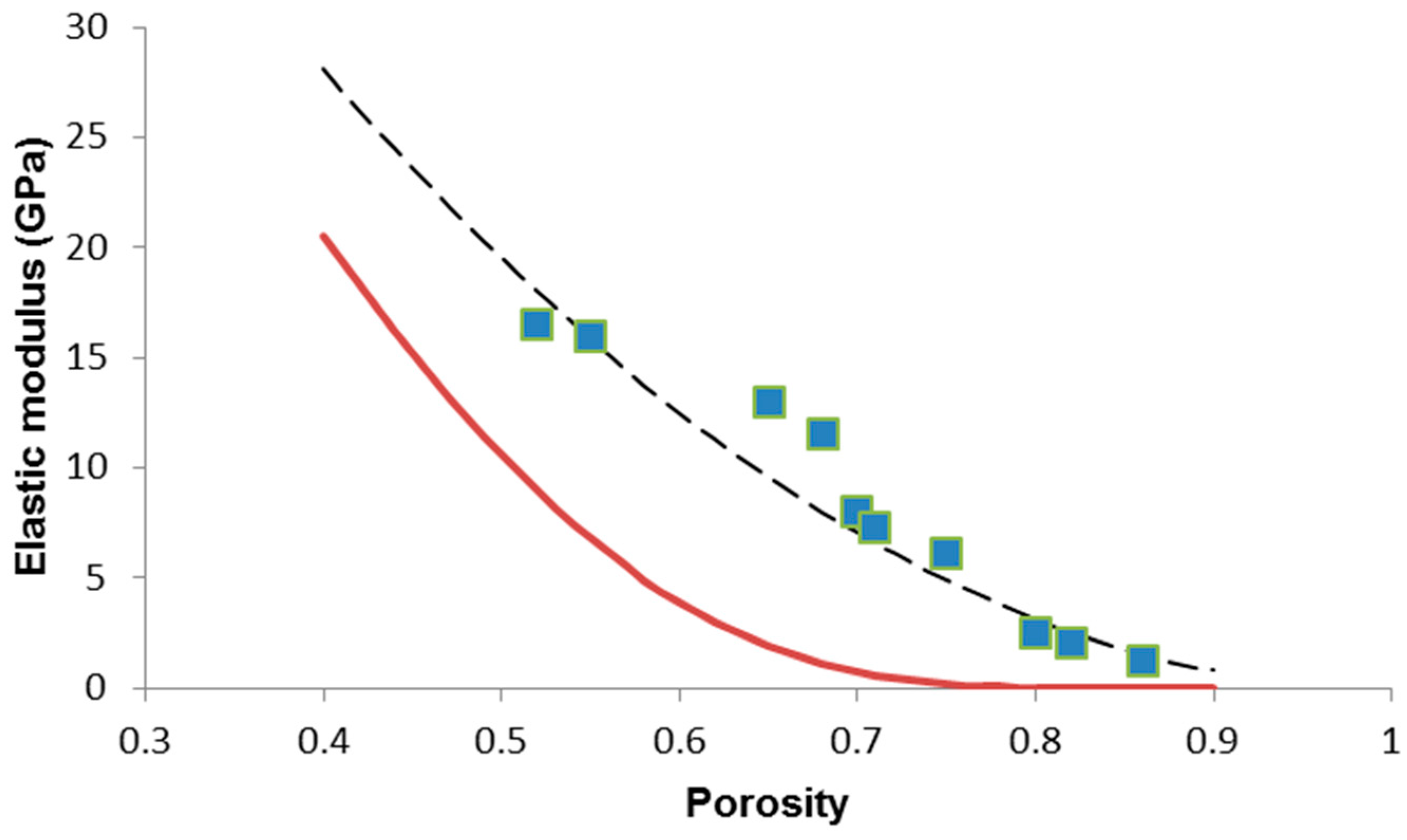
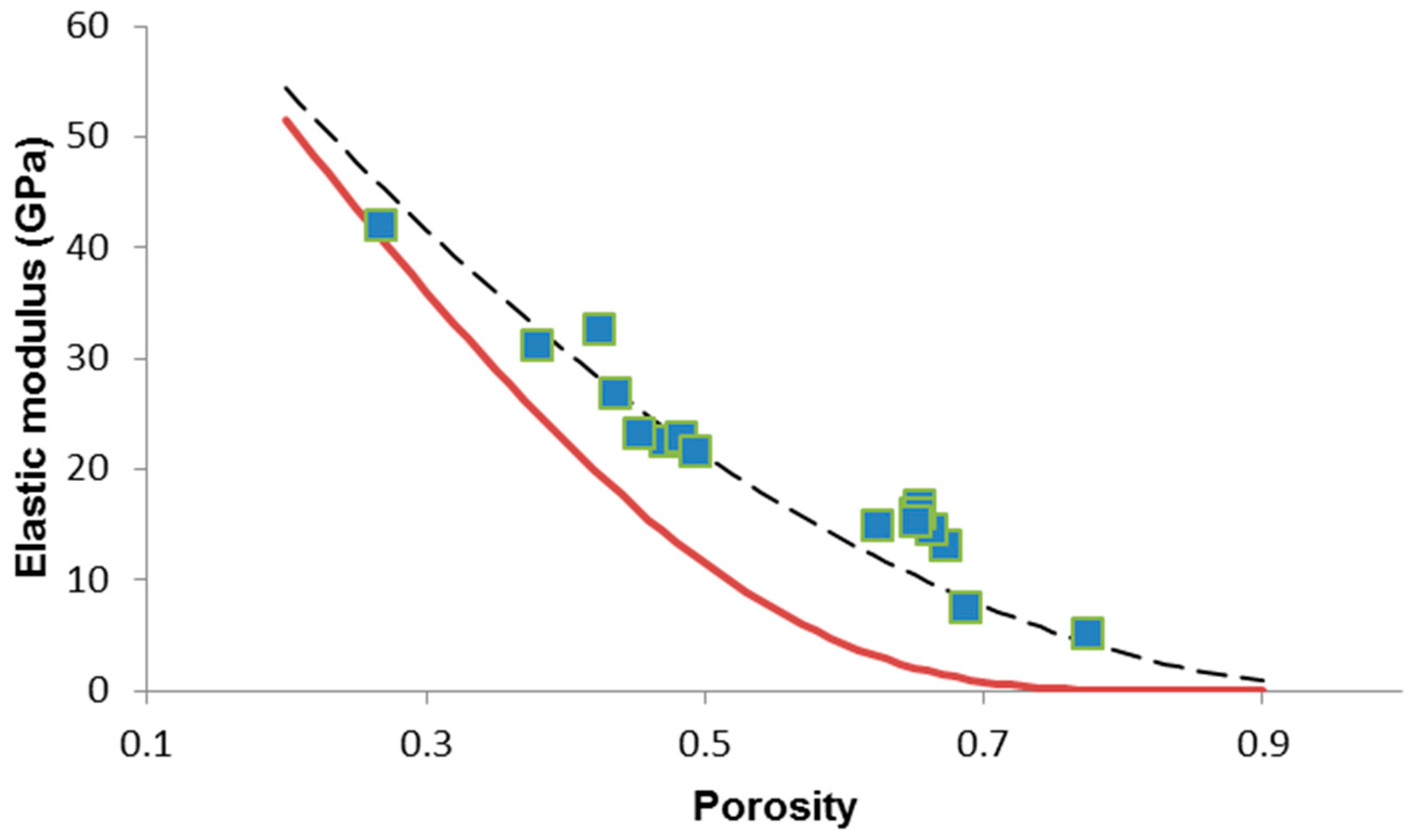
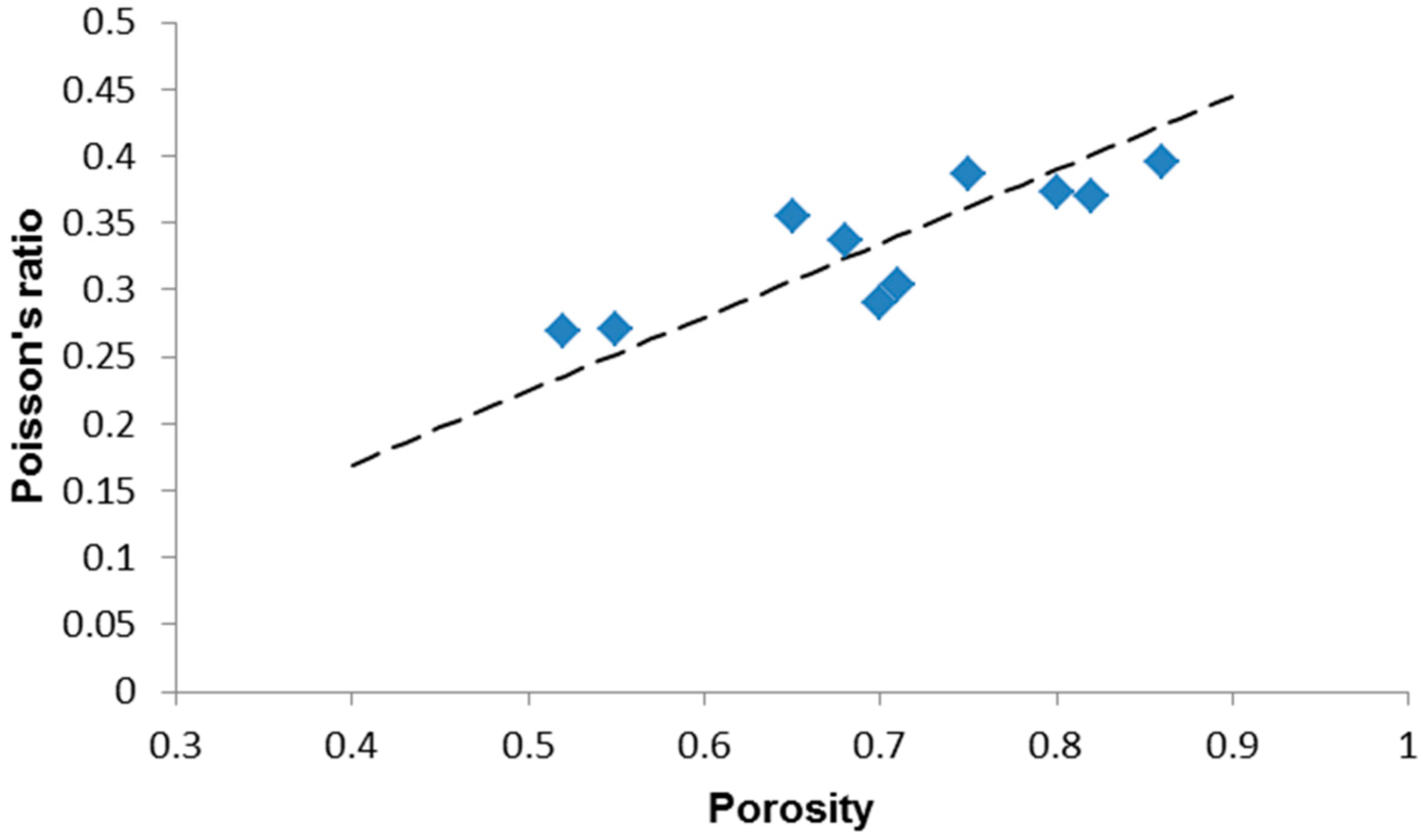
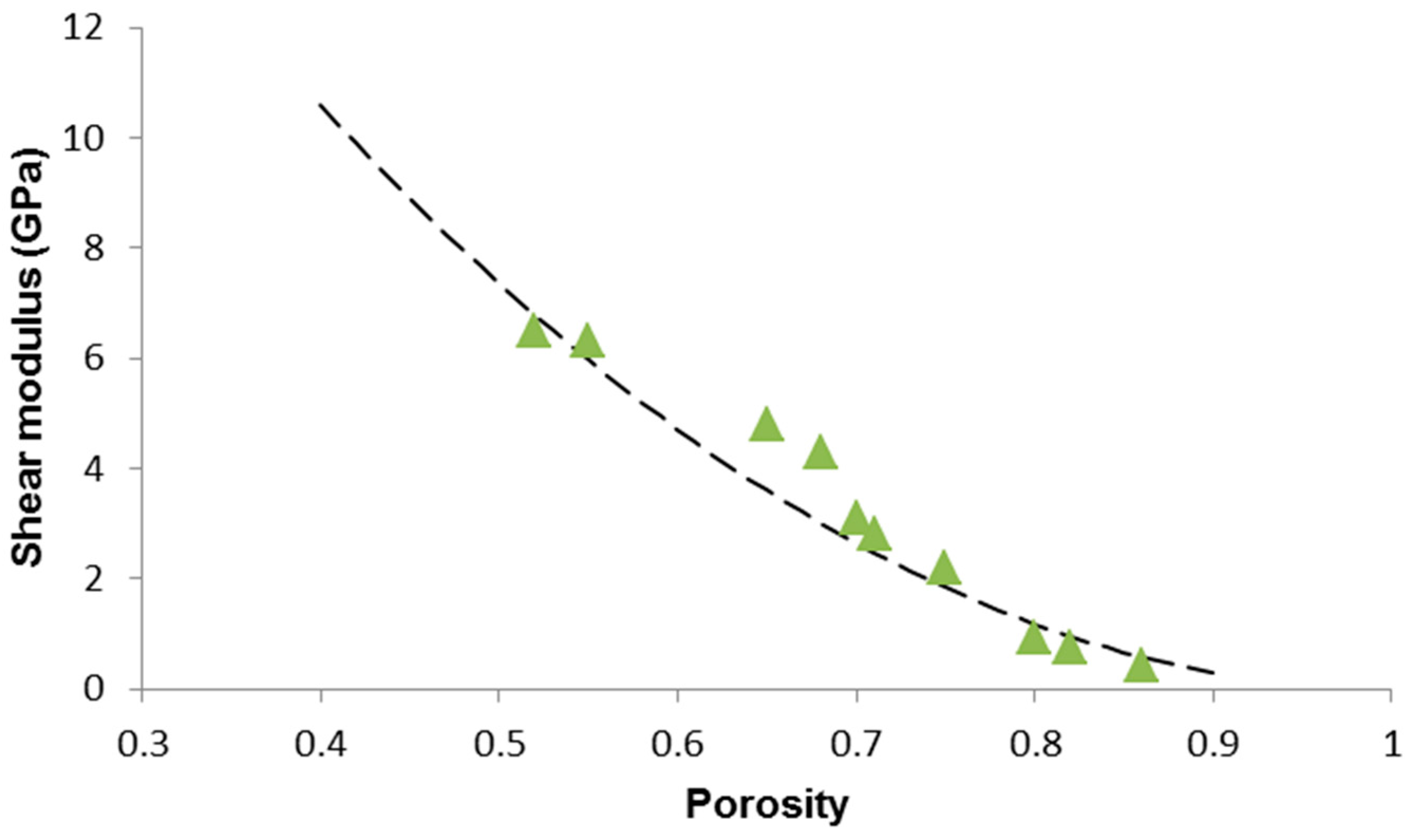
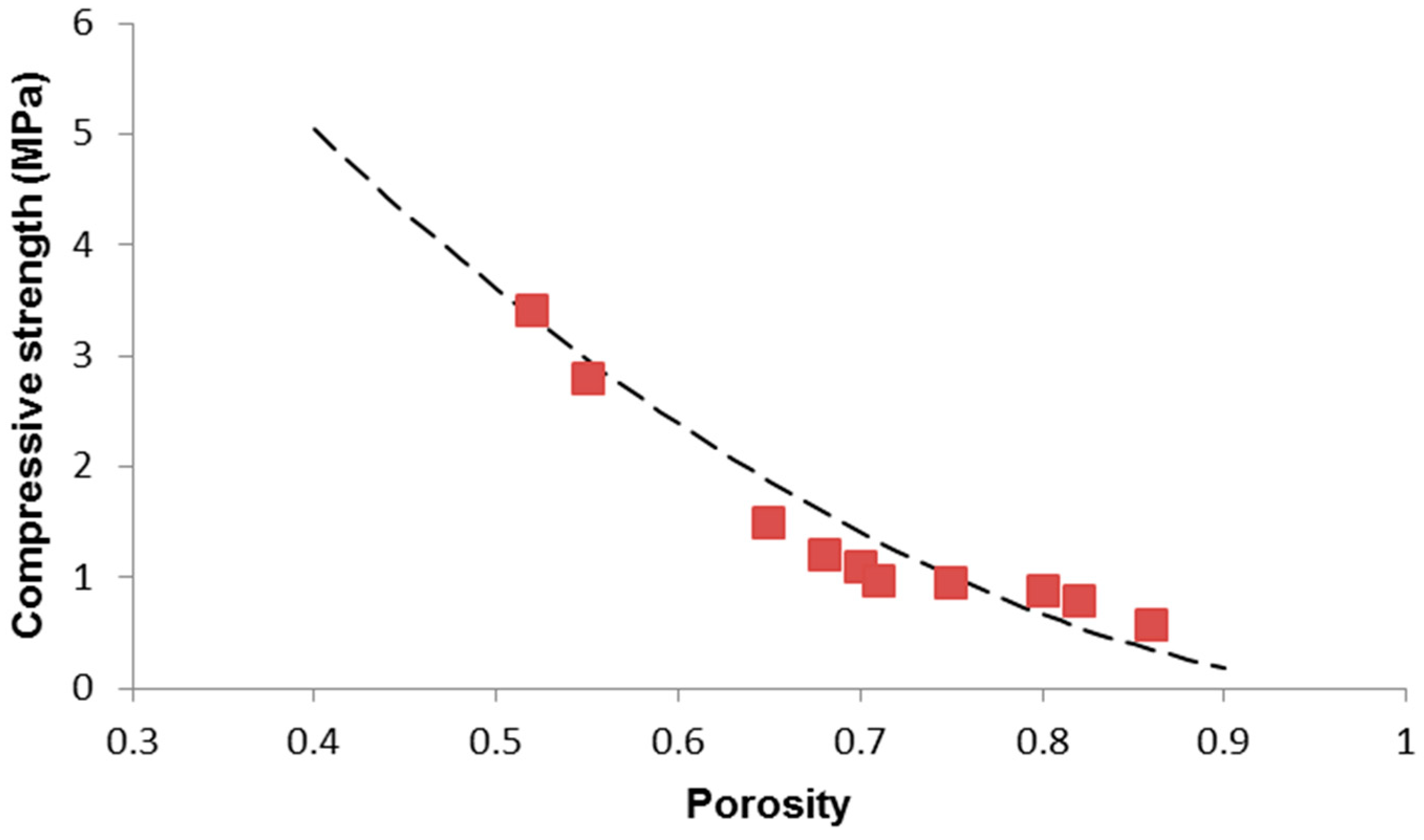
| Scaffold Code (S-x) | p | E (GPa) | G (GPa) | ν | σc (MPa) |
|---|---|---|---|---|---|
| S-27 | 0.86 | 1.2 | 0.43 | 0.3953 | 0.58 |
| S-29 | 0.82 | 2.0 | 0.73 | 0.3698 | 0.78 |
| S-31 | 0.80 | 2.5 | 0.91 | 0.3736 | 0.88 |
| S-33 | 0.75 | 6.1 | 2.2 | 0.3863 | 0.95 |
| S-35 | 0.71 | 7.3 | 2.8 | 0.3035 | 0.96 |
| S-37 | 0.70 | 8.0 | 3.1 | 0.2903 | 1.1 |
| S-39 | 0.68 | 11.5 | 4.3 | 0.3372 | 1.2 |
| S-41 | 0.65 | 13.0 | 4.8 | 0.3541 | 1.5 |
| S-43 | 0.55 | 16.0 | 6.3 | 0.2698 | 2.8 |
| S-45 | 0.52 | 16.5 | 6.5 | 02692 | 3.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baino, F.; Fiume, E. Elastic Mechanical Properties of 45S5-Based Bioactive Glass–Ceramic Scaffolds. Materials 2019, 12, 3244. https://doi.org/10.3390/ma12193244
Baino F, Fiume E. Elastic Mechanical Properties of 45S5-Based Bioactive Glass–Ceramic Scaffolds. Materials. 2019; 12(19):3244. https://doi.org/10.3390/ma12193244
Chicago/Turabian StyleBaino, Francesco, and Elisa Fiume. 2019. "Elastic Mechanical Properties of 45S5-Based Bioactive Glass–Ceramic Scaffolds" Materials 12, no. 19: 3244. https://doi.org/10.3390/ma12193244
APA StyleBaino, F., & Fiume, E. (2019). Elastic Mechanical Properties of 45S5-Based Bioactive Glass–Ceramic Scaffolds. Materials, 12(19), 3244. https://doi.org/10.3390/ma12193244






