Fatigue Assessment Strategy Using Bayesian Techniques
Abstract
:1. Introduction
2. Fundamentals Bases of the Model
2.1. The Probabilistic Fatigue Model
2.2. Bayesian Methods
2.2.1. Prior Distribution
2.2.2. The Prior Predictive Distribution
2.2.3. The Posterior Distribution
2.2.4. The Posterior Predictive Distribution
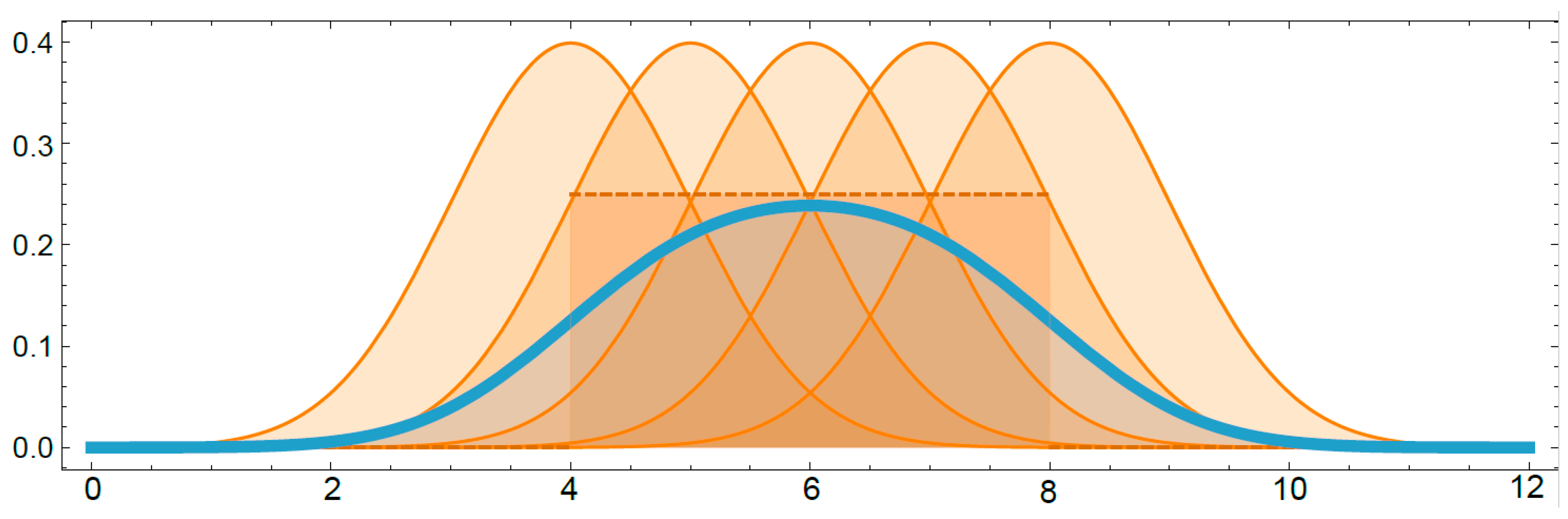
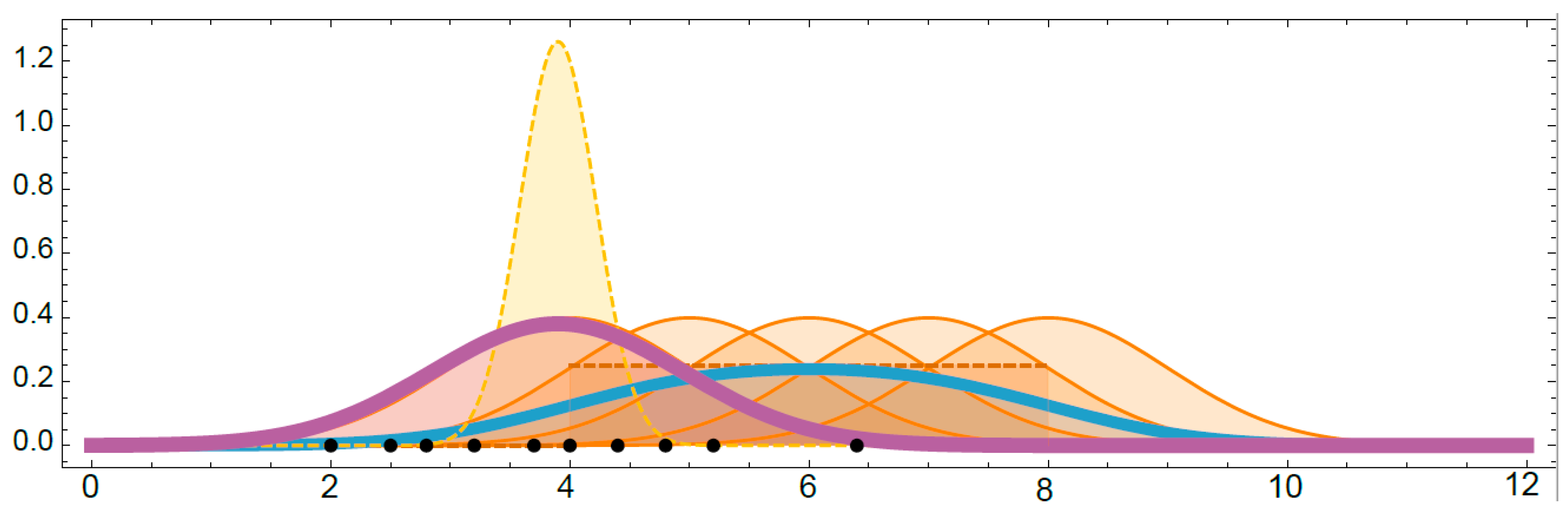
2.2.5. Application Example
3. The Proposed Model
3.1. Model Implementation Through Openbugs Code
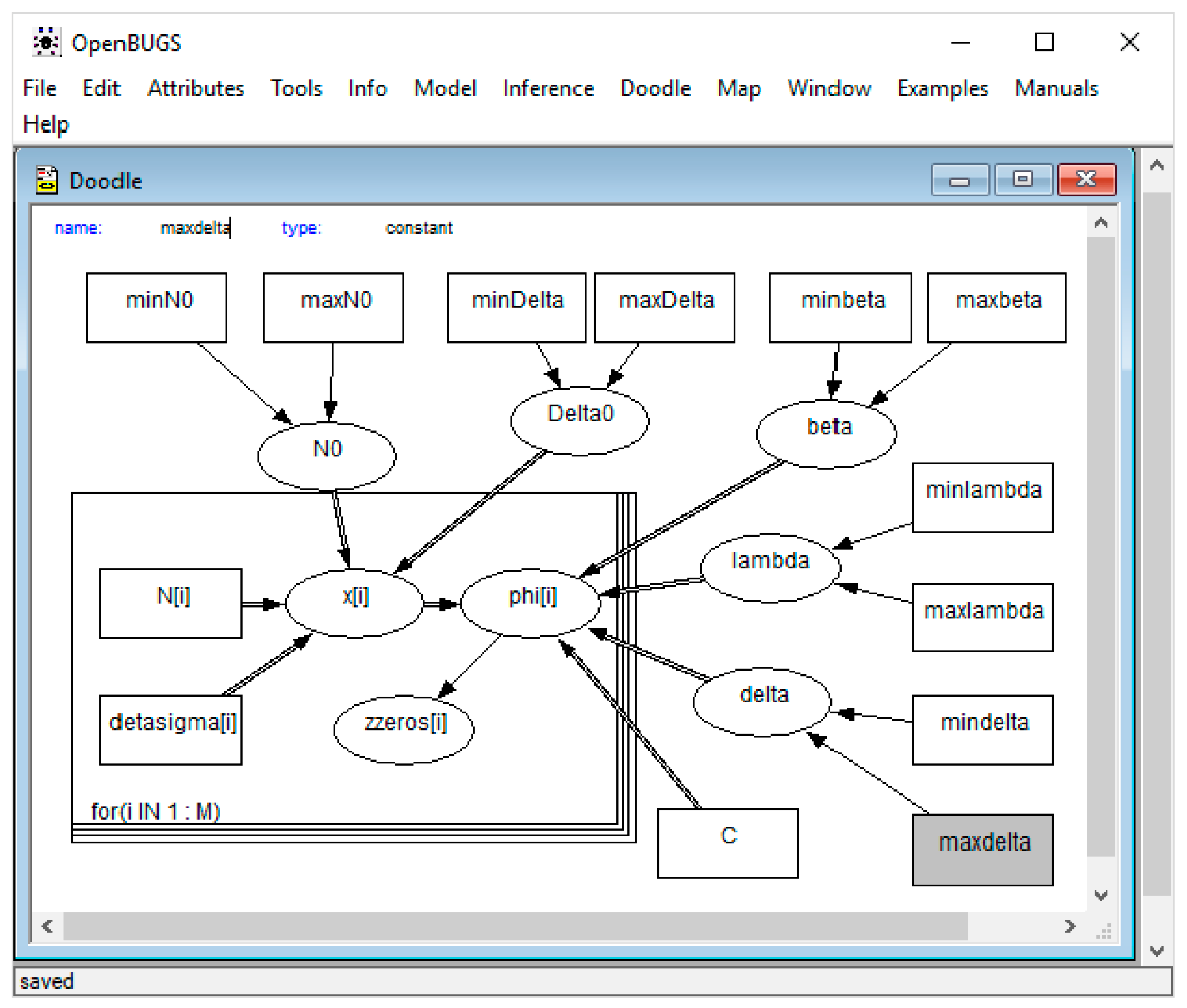
3.2. Model Implementation Using Graphic Doodle in OpenBUGS
3.3. Execution of the Code in OpenBUGS and Analysis of the Results Provided by the Program
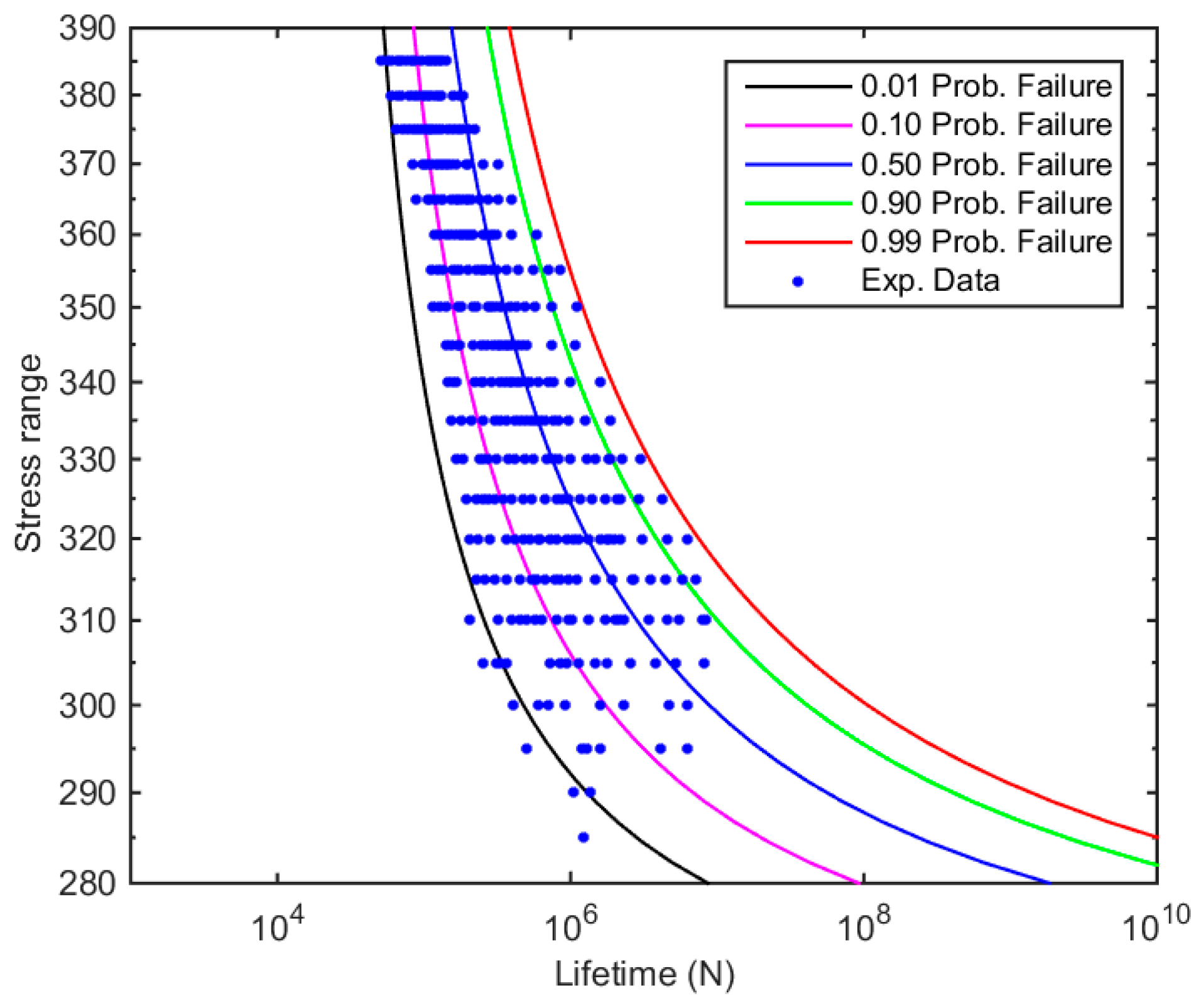
4. Practical Example
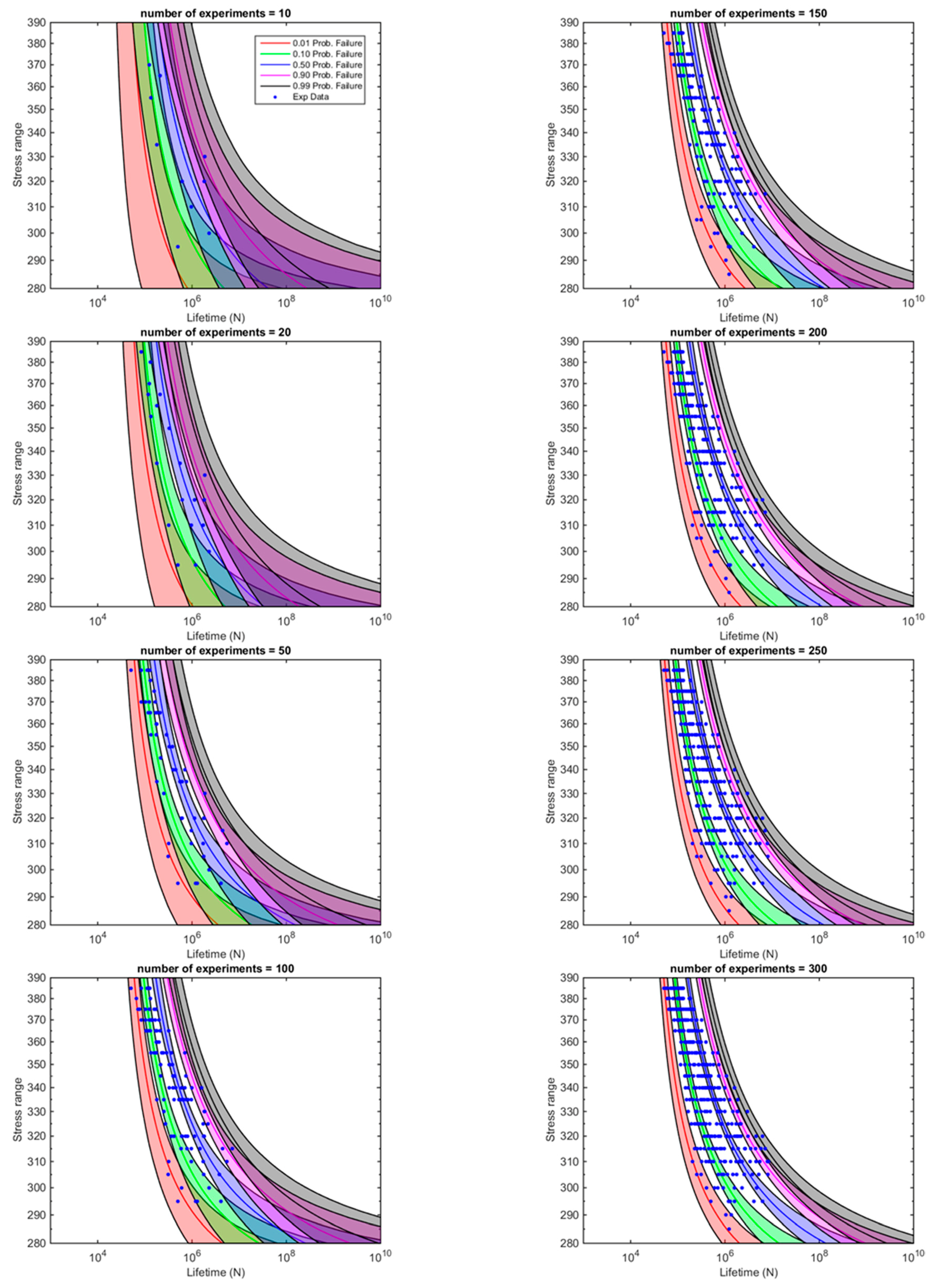
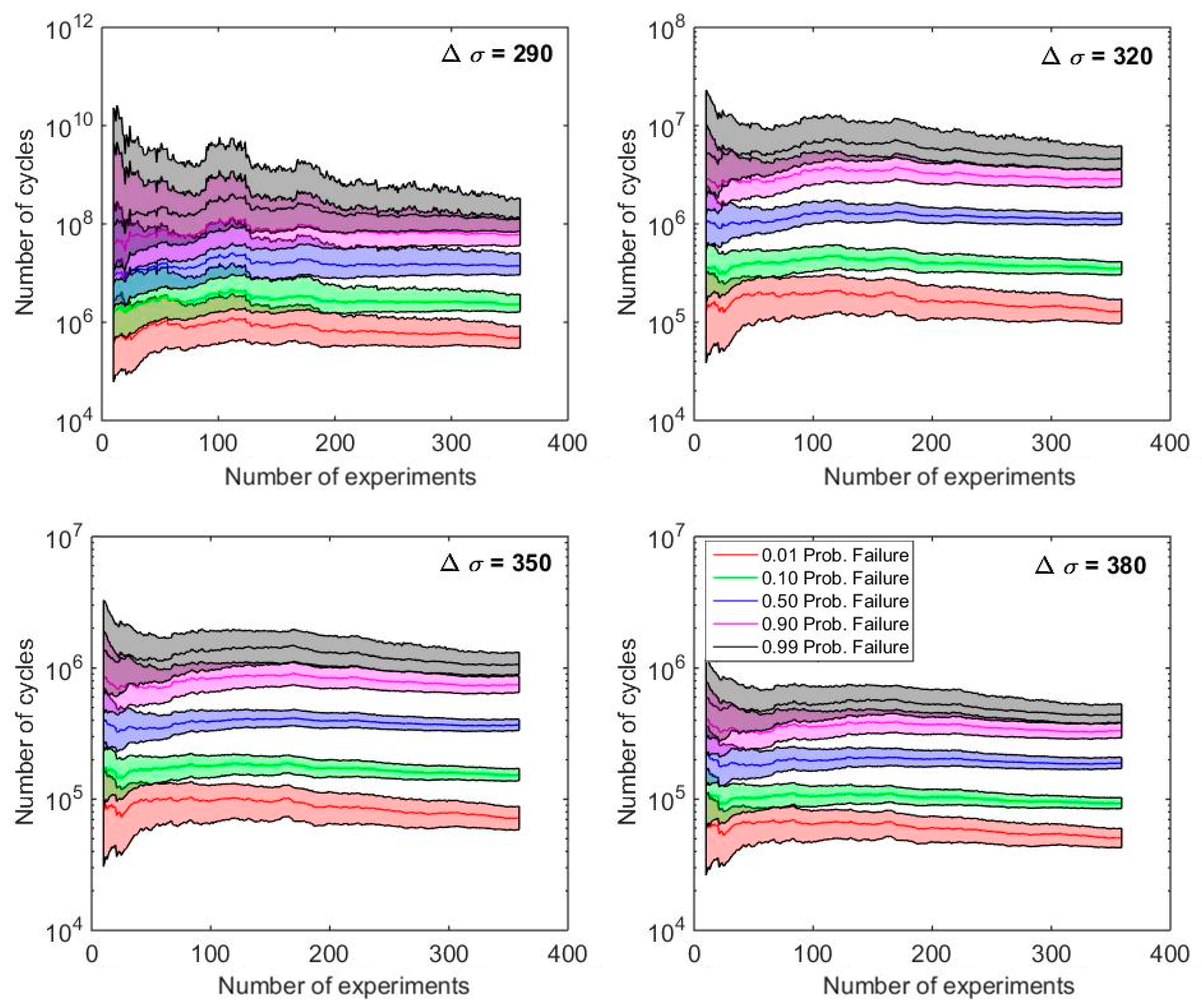
Influence of the Number of Fatigue Tests Performed
5. Conclusions
- (a)
- Concerning the Bayesian model:
- Despite the limited utility of standard Bayesian methods, which utility is generally restricted to specific and simple cases, the Bayesian methods based on Markov Chain Monte Carlo (MCMC) techniques, implemented in the OpenBUGS, can be advantageously used in the analysis of more complex and advanced models, particularly probabilistic ones, thus, opening the applications to a broad spectrum of fracture and fatigue problems to be explored in the future, as the one investigated here.
- The OpenBUGS software allows for the systematic sampling of the model parameters to be integrated into posterior predictive models, once the prior information has been enriched with the experimental data.
- The new Bayesian approach allows very large posterior samples of the model parameters to be obtained and use them to derive the approximate distribution of any variable instead of working with closed complex formulas.
- Bayesian methods, instead of providing point estimates of the variables, provide very large samples of them that can be interpreted as their density functions, which is much more than confidence intervals.
- The application of Bayesian techniques to the probabilistic regression Weibull model proposed by Castillo and Canteli for the analysis of S-N data enables the initial simple probabilistic definition of the five parameters model to be enhanced by providing the probability distribution for any percentile failure curve of the original model (to be interpreted as confidence intervals). Furthermore, the approach enables the subsequent evolution of the confidence intervals to be defined as a function of the number of tests carried out.
- (b)
- Concerning the S-N model:
- The Bayes methodology can be applied at any time during the testing process providing an invaluable contribution to enhance the confidence intervals of the S-N assessment, in particular when using such a probabilistic model as that of Castillo-Canteli.
- The evolution of the confidence bands for the fatigue limit referred to the assessment of the fatigue S-N field of the Maennig example confirms the robustness of the S-N model proposed by Castillo-Canteli. In fact, the confidence bands obtained by applying the Bayes methodology proves to show a near asymptotic trend with quick diminishing for increasing number of evaluated test results evidencing a moderate variation in the ranges of the fatigue limit even for scarce number of test data.
- The confidence intervals in the particular case of the fatigue limit are transcendental because the direct interpretation of the latter, whereas those for the remaining S-N parameter are of less interest when separately interpreted. Instead, the reciprocal interdependence, i.e., the correlation, existing among all the model parameters is better reflected through the representation of the confidence bands (distribution of the particular probability of failure) of the percentiles S-N curves, preferably only for low or very low probability of failure in practical design.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. OpenBugs Codes
| Mode 1 |
 |
| Mode 2 |
 |
References
- ISO. 12107:2012. Metallic Materials-Fatigue Testing-Statistical Planning and Analysis of Data, 2nd ed.; ISO: London, UK, 2018. [Google Scholar]
- ASTM. E739–10 Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data; ASTM: West Conshohocken, PA, USA, 2015. [Google Scholar]
- ASM International. Fatigue and Fracture, Statistical Considerations in Fatigue. In ASM Handbook; ASM International: Cleveland, OH, USA, 1997; Volume 19, ISBN 978-0-87170-385-9. [Google Scholar]
- Castillo, E.; Fernández Canteli, A. A Unified Statistical Methodology for Modeling Fatigue Damage; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Freudenthal, A.M. The statistical aspect of fatigue of materials. Proc. R. Soc. 1946, 187, 416–429. [Google Scholar]
- Freudenthal, A.M.; Gumbel, E.J. Physical and statistical aspects of fatigue. Adv. Appl. Mech. 1956, 4, 117–158. [Google Scholar]
- Bolotin, V.V. Wahrscheinlichkeitsmethoden zur Berechnung von Konstruktionen; Verlag für Bauwesen: Berlin, Germany, 1981. [Google Scholar]
- Bolotin, V.V. Mechanics of Fatigue; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Koller, R.; Ruiz-Ripoll, M.L.; García, A.; Fernández Canteli, A.; Castillo, E. Experimental validation of a statistical model for the Wöhler field corresponding to any stress level and amplitude. Int. J. Fatigue 2009, 31, 231–241. [Google Scholar] [CrossRef]
- Pyttel, B.; Fernández-Canteli, A.; Argente-Ripoll, A. Comparison of different statistical models for description of fatigue including very high cycle fatigue. Int. J. Fatigue 2016, 93, 435–442. [Google Scholar] [CrossRef]
- Correia, J.A.F.O.; Apetre, N.; Arcari, A.; de Jesus, A.; Muniz-Calvente, M.; Calçada, R.; Berto, F.; Fernández Canteli, A. Generalized probabilistic model allowing for various fatigue damage variables. Int. J. Fatigue 2017, 100, 187–194. [Google Scholar] [CrossRef]
- Muniz-Calvente, M.; de Jesus, A.; Correia, J.A.F.O.; Fernández Canteli, A. A methodology for probabilistic prediction of fatigue crack initiation taking into account the scale effect. Eng. Fract. Mech. 2017, 185, 101–113. [Google Scholar] [CrossRef]
- Benjamin, J.; Cornell, C.A. Probability, Statistics and Decisions for Civil Engineers; Mc Graw-Hill Co.: New York, NY, USA, 1970. [Google Scholar]
- Castillo, E. Extreme Value Theory in Engineering; Elsevier: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Efron, B.; Tibshirami, R. An Introduction to the Bootstrap; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Davidson, A.; Hinkley, D. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Chernick, M. A Practitioner’s Guide; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Chao, M.; Fuh, C. Bootstrap methods for the up-and-down test on pyrotechnics sensitivity analysis. Stat. Sin. 2001, 1, 1–21. [Google Scholar]
- Guida, M.; Penta, F. A Bayesian analysis of fatigue data. Struct. Saf. 2010, 32, 64–76. [Google Scholar] [CrossRef]
- Zhu, S.P. Bayesian framework for probabilistic low cycle life prediction and uncertainty modeling of aircraft turbine disk alloys. Probabilistic Eng. Mech. 2013, 34, 114–122. [Google Scholar] [CrossRef]
- Maennig, W.W. Untersuchungen zur Planung und Auswertung von Dauerschwingversuchen an Stahl in den Bereichen der Zeit-und der Dauerfestigkeit. Fortschr-Ber; VDI-ZS Reihe; VDI Verlag: Düsseldorf, Germany, 1967; Volume 5. [Google Scholar]
- Maennig, W.W. Bemerkungen zur Beurteilung des Dauerschwingverhaltens von Stahl und einige Untersuchungen zur Bestimmung des Dauerfestigkeitsbereiches. Materialprüfung 1970, 12, 124–131. [Google Scholar]
- Maennig, W.W. Vergleichende Untersuchung über die Eignung der Treppenstufenmethode zur Berechnung der Dauerschwingfestigkeit. Materialprüfung 1971, 13, 6–11. [Google Scholar]
- Castillo, E.; Iglesias, A.; Ruíz-Cobo, R. Functional Equations in Applied Sciences; Elsevier Science: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Aczel, J. Lectures on Functional Equations and Applications and Their Applications; Mathematics in Science and Engineering; Academic Press: Cambridge, MA, USA, 1966; Volume 19. [Google Scholar]
- Aczel, J. Chapter 1: On history and applications and theory of functional equations (Introduction). In Functional Equations: History, Applications and Theory; Aczel, J., Ed.; Reidel Publishing Company: Dordrecht, The Netherlands, 1984; pp. 3–12. [Google Scholar]
- Fernández-Canteli, A.; Przybilla, C.; Nogal, M.; López-Aenlle, M.; Castillo, E. ProFatigue: A software program for probabilistic assessment of experimental fatigue data sets. Procedia Eng. 2014, 74, 236–241. [Google Scholar] [CrossRef]



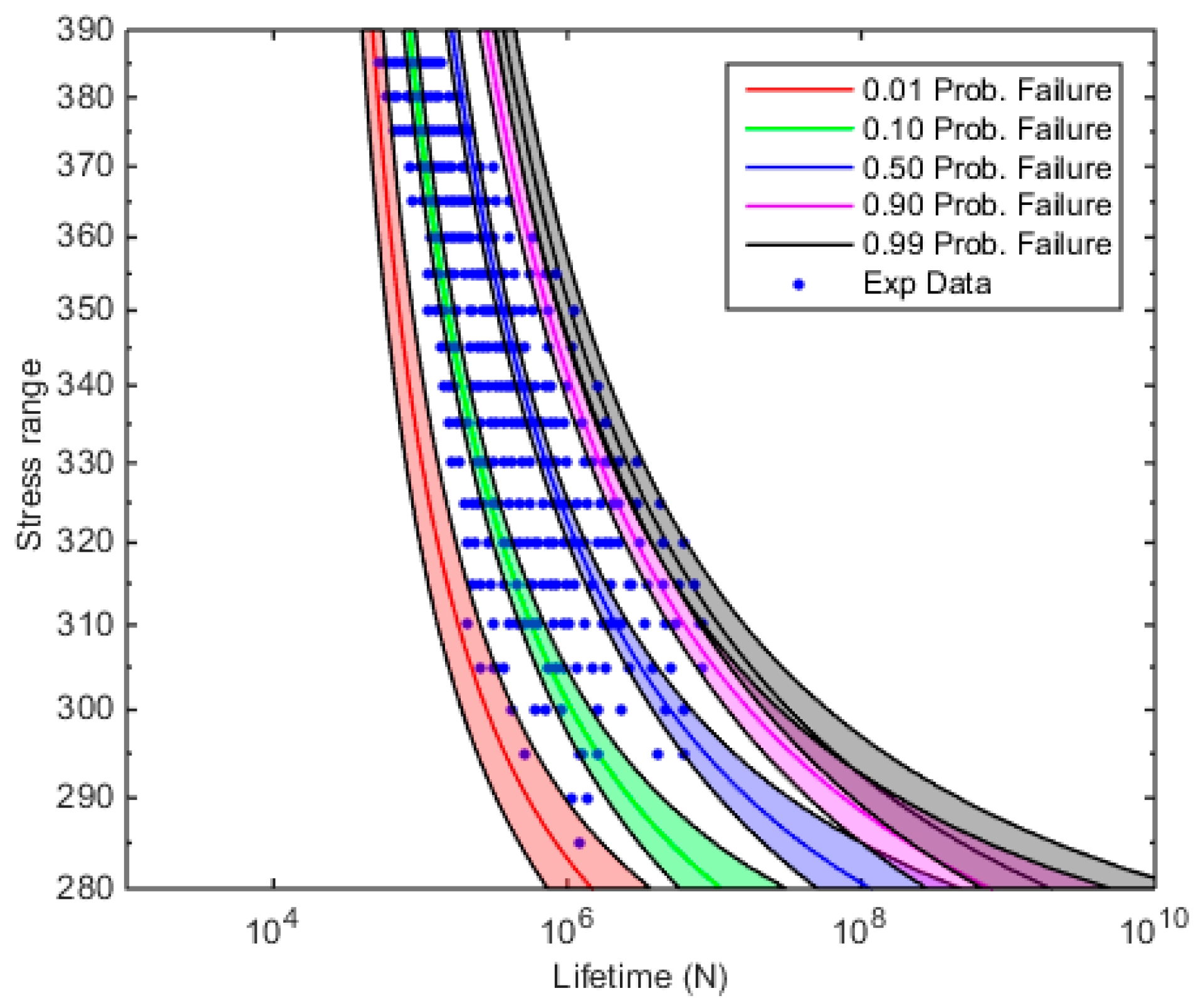

| Lifetime (Thousands of Cycles) (N) | |
|---|---|
| 385 | 51,57,60,67,68,69,75,76,82,83,87,95,106,109,111,119,122,128,132,140 |
| 380 | 59,66,69,80,87,90,97,98,99,100,107,109,117,118,125,128,132,158,177,186 |
| 375 | 65,71,78,84,89,93,98,103,105,109,113,118,124,131,147,156,171,182,199,220 |
| 370 | 83,98,100,104,110,111,122,125,132,136,141,143,146,155,165,194,200,201,251,318 |
| 365 | 89,105,108,118,119,121,130,133,152,164,170,181,182,192,199,211,238,273,324,398 |
| 360 | 117,127,141,151,162,173,181,186,192,198,203,209,218,255,262,288,295,309,394,585 |
| 355 | 112,125,133,156,166,168,173,202,227,247,253,261,285,286,309,365,442,559,702,852 |
| 350 | 115,129,143,169,177,178,218,230,271,280,285,305,326,342,381,431,493,568,734,1101 |
| 345 | 140,155,169,174,218,248,265,293,321,326,348,350,364,374,397,426,461,504,738,1063 |
| 340 | 146,159,168,224,246,253,291,326,358,385,397,425,449,498,532,610,714,763,987,1585 |
| 335 | 154,180,210,254,305,332,363,415,457,482,528,559,593,611,678,767,835,957,1274,1854 |
| 330 | 166,184,241,251,273,312,371,418,493,562,683,760,830,981,1306,1463,1842,1867,2220,2978 |
| 325 | 196,227,250,271,308,347,393,475,548,669,799,879,975,1154,1388,1705,2073,2211,2925,4257 |
| 320 | 206,231,283,370,413,474,523,597,605,619,727,815,935,1056,1144,1336,1580,1786,1826,1943,2214, 3107,4510,6297 |
| 315 | 226,257,307,370,457,549,570,590,672,781,850,974,1093,1460,1477,1936,2662,2731,3487,4396,5803, 7215 |
| 310 | 206,317,393,446,502,570,627,809,956,1022,1327,1745,2001,2139,2314,3425,4576,5453,7868,8297 |
| 305 | 253,311,329,370,726,845,935,954,1139,1456,1792,2578,3776,5161,8131 |
| 300 | 411,606,700,707,919,1587,1595,2295,4628,6280 |
| 295 | 503,1191,1282,1609,4070,6337 |
| 290 | 1055,1369 |
| 285 | 1220 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo, E.; Muniz-Calvente, M.; Fernández-Canteli, A.; Blasón, S. Fatigue Assessment Strategy Using Bayesian Techniques. Materials 2019, 12, 3239. https://doi.org/10.3390/ma12193239
Castillo E, Muniz-Calvente M, Fernández-Canteli A, Blasón S. Fatigue Assessment Strategy Using Bayesian Techniques. Materials. 2019; 12(19):3239. https://doi.org/10.3390/ma12193239
Chicago/Turabian StyleCastillo, Enrique, Miguel Muniz-Calvente, Alfonso Fernández-Canteli, and Sergio Blasón. 2019. "Fatigue Assessment Strategy Using Bayesian Techniques" Materials 12, no. 19: 3239. https://doi.org/10.3390/ma12193239
APA StyleCastillo, E., Muniz-Calvente, M., Fernández-Canteli, A., & Blasón, S. (2019). Fatigue Assessment Strategy Using Bayesian Techniques. Materials, 12(19), 3239. https://doi.org/10.3390/ma12193239







