Synthesis of Intermetallic (Mg1−x,Alx)2Ca by Combinatorial Sputtering
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
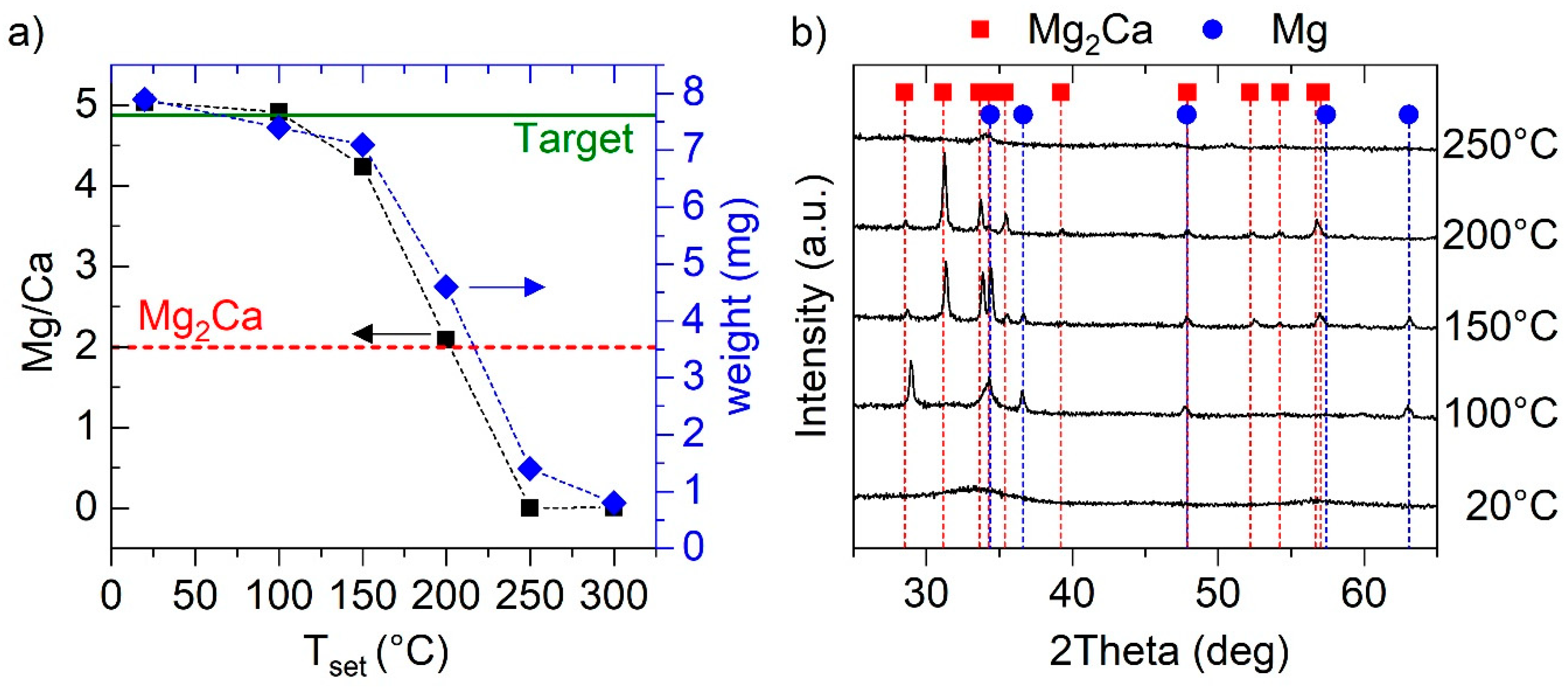
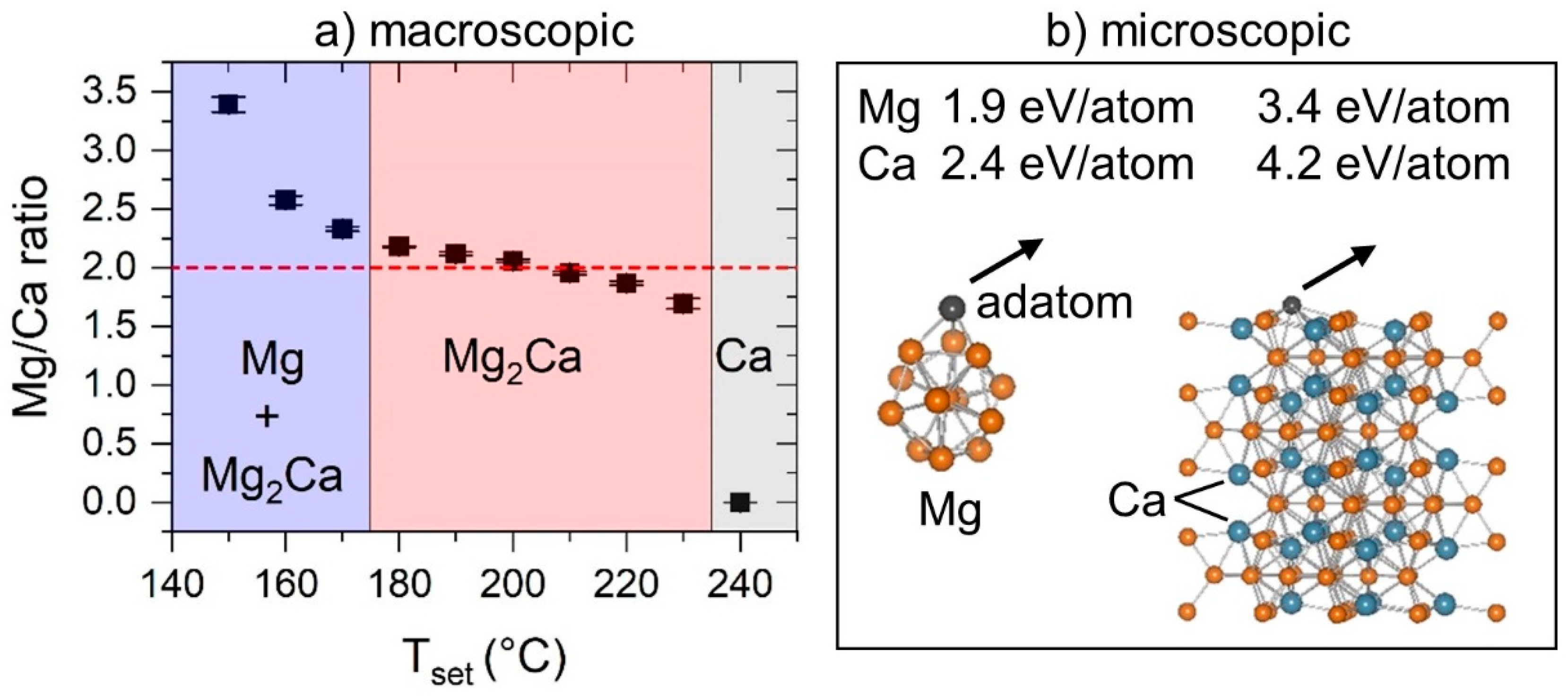
3.1. Binary Mg–Ca
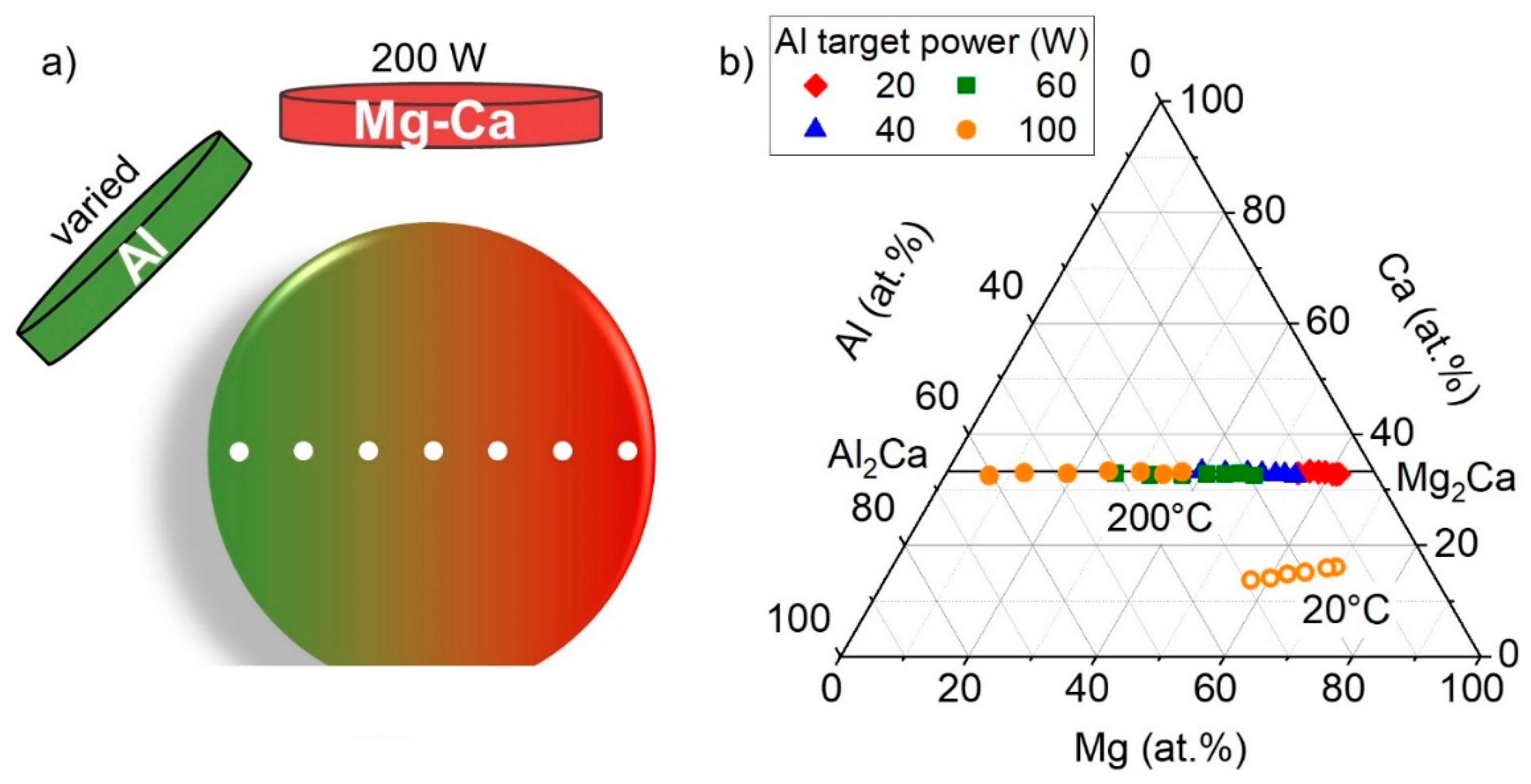
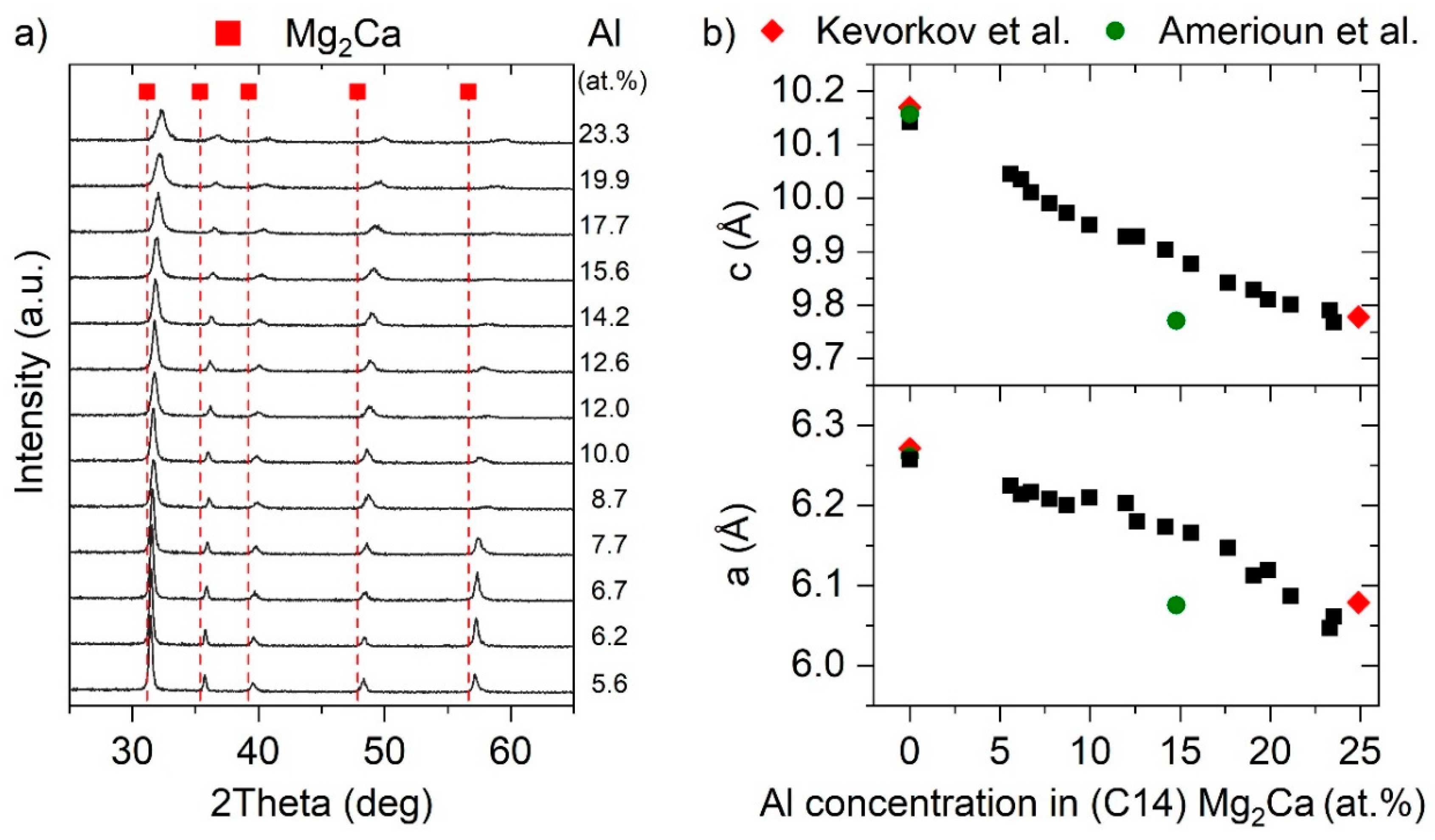
3.2. Ternary Mg–Ca–Al
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mordike, B.L.; Ebert, T. Magnesium: Properties—Applications—Potential. Mater. Sci. Eng. A 2001, 302, 37–45. [Google Scholar] [CrossRef]
- Luo, A.A. Magnesium casting technology for structural applications. J. Magnes. Alloy. 2013, 1, 2–22. [Google Scholar] [CrossRef]
- Song, G.L.; Atrens, A. Corrosion Mechanisms of Magnesium Alloys. Adv. Eng. Mater. 1999, 1, 11–33. [Google Scholar] [CrossRef]
- Amberger, D.; Eisenlohr, P.; Göken, M. On the importance of a connected hard-phase skeleton for the creep resistance of Mg alloys. Acta Mater. 2012, 60, 2277–2289. [Google Scholar] [CrossRef]
- Pekguleryuz, M.O.; Baril, E. Creep Resistant Magnesium Diecasting Alloys Based on Alkaline Earth Elements. Mater. Trans. 2001, 42, 1258–1267. [Google Scholar] [CrossRef]
- Amberger, D.; Eisenlohr, P.; Göken, M. Microstructural evolution during creep of Ca-containing AZ91. Mater. Sci. Eng. A 2009, 510, 398–402. [Google Scholar] [CrossRef]
- Ninomiya, R.; Ojiro, T.; Kubota, K. Improved heat resistance of Mg–Al alloys by the Ca addition. Acta Metall. Et. Mater. 1995, 43, 669–674. [Google Scholar] [CrossRef]
- Han, L.; Hu, H.; Northwood, D.O.; Li, N. Microstructure and nano-scale mechanical behavior of Mg–Al and Mg–Al–Ca alloys. Mater. Sci. Eng. A 2008, 473, 16–27. [Google Scholar] [CrossRef]
- Janz, A.; Gröbner, J.; Cao, H.; Zhu, J.; Chang, Y.A.; Schmid-Fetzer, R. Thermodynamic modeling of the Mg–Al–Ca system. Acta Mater. 2009, 57, 682–694. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, C.; Zhu, J.; Cao, G.; Kou, S.; Schmid-Fetzer, R.; Chang, Y.A. Experiments coupled with modeling to establish the Mg-rich phase equilibria of Mg–Al–Ca. Acta Mater. 2008, 56, 5245–5254. [Google Scholar] [CrossRef]
- Amerioun, S.; Simak, S.I.; Häussermann, U. Laves-Phase Structural Changes in the System CaAl2−xMgx. Lnorg. Chem. 2003, 42, 1467–1474. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Saddock, N.D.; Jones, J.W.; Pollock, T.M. Structure and transition of eutectic (Mg,Al)2Ca Laves phase in a die-cast Mg–Al–Ca base alloy. Scr. Mater. 2004, 51, 1005–1010. [Google Scholar] [CrossRef]
- Suzuki, A.; Saddock, N.D.; Jones, J.W.; Pollock, T.M. Phase equilibria in the Mg–Al–Ca ternary system at 773 and 673 K. Metall. Mater. Trans. A 2006, 37, 975–983. [Google Scholar] [CrossRef]
- Kevorkov, D.; Medraj, M.; Li, J.; Essadiqi, E.; Chartrand, P. The 400 °C isothermal section of the Mg–Al–Ca system. Intermetallics 2010, 18, 1498–1506. [Google Scholar] [CrossRef]
- Gebhardt, T.; Music, D.; Takahashi, T.; Schneider, J.M. Combinatorial thin film materials science: From alloy discovery and optimization to alloy design. Thin Solid Film. 2012, 520, 5491–5499. [Google Scholar] [CrossRef]
- Wu, Z.; Bai, Y.; Qu, W.; Wu, A.; Zhang, D.; Zhao, J.; Jiang, X. Al–Mg–B thin films prepared by magnetron sputtering. Vacuum 2010, 85, 541–545. [Google Scholar] [CrossRef]
- Frodelius, J.; Eklund, P.; Beckers, M.; Persson, P.O.Å.; Högberg, H.; Hultman, L. Sputter deposition from a Ti2AlC target: Process characterization and conditions for growth of Ti2AlC. Thin Solid Film. 2010, 518, 1621–1626. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Efficient projector expansion for the ab initio LCAO method. Phys. Rev. B 2005, 72, 045121. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Chibisov, A.N. Oxygen adsorption on small Ti clusters: A first-principles study. Comput. Mater. Sci. 2014, 82, 131–133. [Google Scholar] [CrossRef]
- Koten, M.A.; Manchanda, P.; Balamurugan, B.; Skomski, R.; Sellmyer, D.J.; Shield, J.E. Ferromagnetism in Laves-phase WFe2 nanoparticles. Apl. Mater. 2015, 3, 076101. [Google Scholar] [CrossRef]
- Alcock, C.B.; Itkin, V.P.; Horrigan, M.K. Vapour Pressure Equations for the Metallic Elements: 298–2500 K. Can. Met. Q 1984, 23, 309–313. [Google Scholar] [CrossRef]
- Reckeweg, O.; Lind, C.; Simon, A.; DiSalvo, F.J. Reactions of alkaline earth metals and nitrogen in sealed niobium ampoules: The formation of MgZn2 type intermetallic phases in the presence of nitrogen and the new compound Ba5[NbN4]N. J. Alloy. Compd. 2004, 384, 98–105. [Google Scholar] [CrossRef]
- Stampfl, C.; Scheffler, M. Theory of Alkali-Metal Adsorption on Close-Packed Metal Surfaces. Surf. Rev. Lett. 1995, 2, 317–343. [Google Scholar] [CrossRef]
- Blomqvist, J.; Salo, P. Adsorption of benzene, phenol, propane and carbonic acid molecules on oxidized Al(111) and α-Al2O3(0001) surfaces: A first-principles study. J. Phys. Condens. Matter 2009, 21, 225001. [Google Scholar] [CrossRef] [PubMed]
- Bragg, W.H.; Bragg, W.L. The reflection of X-rays by crystals. Proceedings of the Royal Society of London. Ser. A Contain. Pap. Math. Phys. Character 1913, 88, 428–438. [Google Scholar] [CrossRef]
- Slater, J.C. Atomic Radii in Crystals. J. Chem. Phys. 1964, 41, 3199–3204. [Google Scholar] [CrossRef]
- Zhong, Y.; Liu, J.; Witt, R.A.; Sohn, Y.-h.; Liu, Z.-K. Al2(Mg,Ca) phases in Mg–Al–Ca ternary system: First-principles prediction and experimental identification. Scr. Mater. 2006, 55, 573–576. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keuter, P.; Karimi Aghda, S.; Music, D.; Kümmerl, P.; Schneider, J.M. Synthesis of Intermetallic (Mg1−x,Alx)2Ca by Combinatorial Sputtering. Materials 2019, 12, 3026. https://doi.org/10.3390/ma12183026
Keuter P, Karimi Aghda S, Music D, Kümmerl P, Schneider JM. Synthesis of Intermetallic (Mg1−x,Alx)2Ca by Combinatorial Sputtering. Materials. 2019; 12(18):3026. https://doi.org/10.3390/ma12183026
Chicago/Turabian StyleKeuter, Philipp, Soheil Karimi Aghda, Denis Music, Pauline Kümmerl, and Jochen M. Schneider. 2019. "Synthesis of Intermetallic (Mg1−x,Alx)2Ca by Combinatorial Sputtering" Materials 12, no. 18: 3026. https://doi.org/10.3390/ma12183026
APA StyleKeuter, P., Karimi Aghda, S., Music, D., Kümmerl, P., & Schneider, J. M. (2019). Synthesis of Intermetallic (Mg1−x,Alx)2Ca by Combinatorial Sputtering. Materials, 12(18), 3026. https://doi.org/10.3390/ma12183026





