Bending Experiment and Mechanical Properties Analysis of Composite Sandwich Laminated Box Beams
Abstract
1. Introduction
2. Experimental Study
2.1. Introduction of Specimens and Experimental Methods
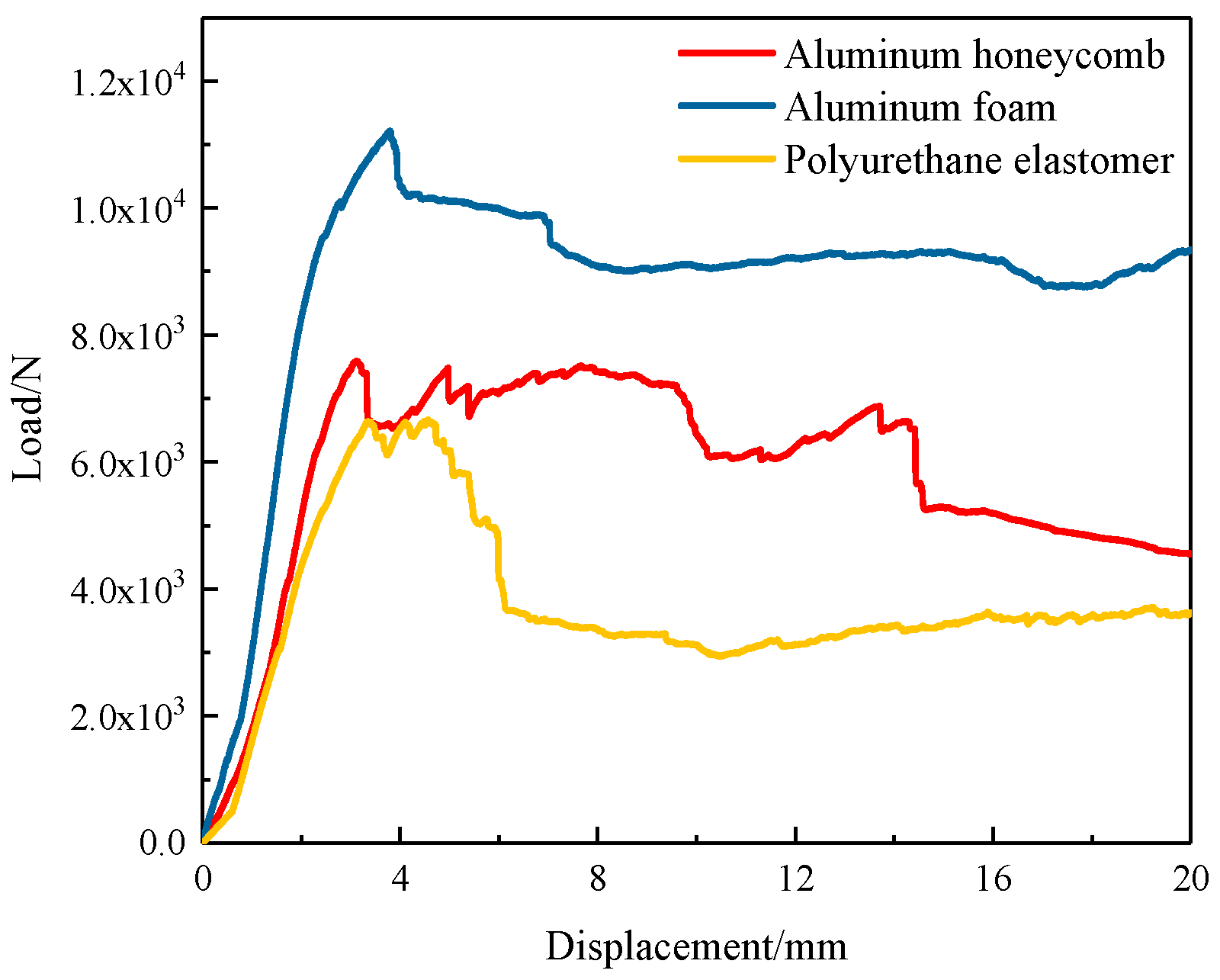
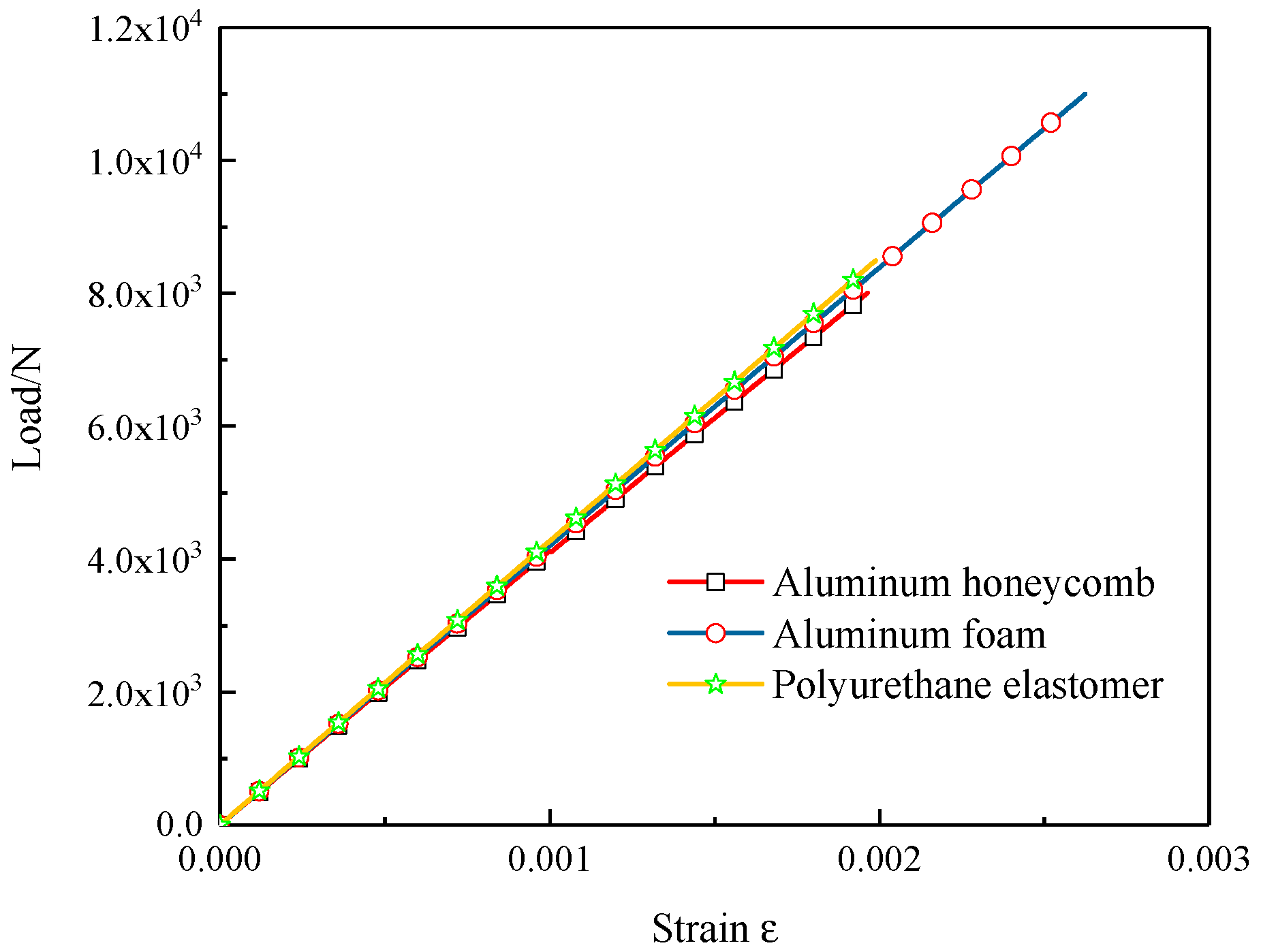
2.2. Three-Point Bending Experiment Process and Results
3. Model of Composite Sandwich Laminated Box Beam
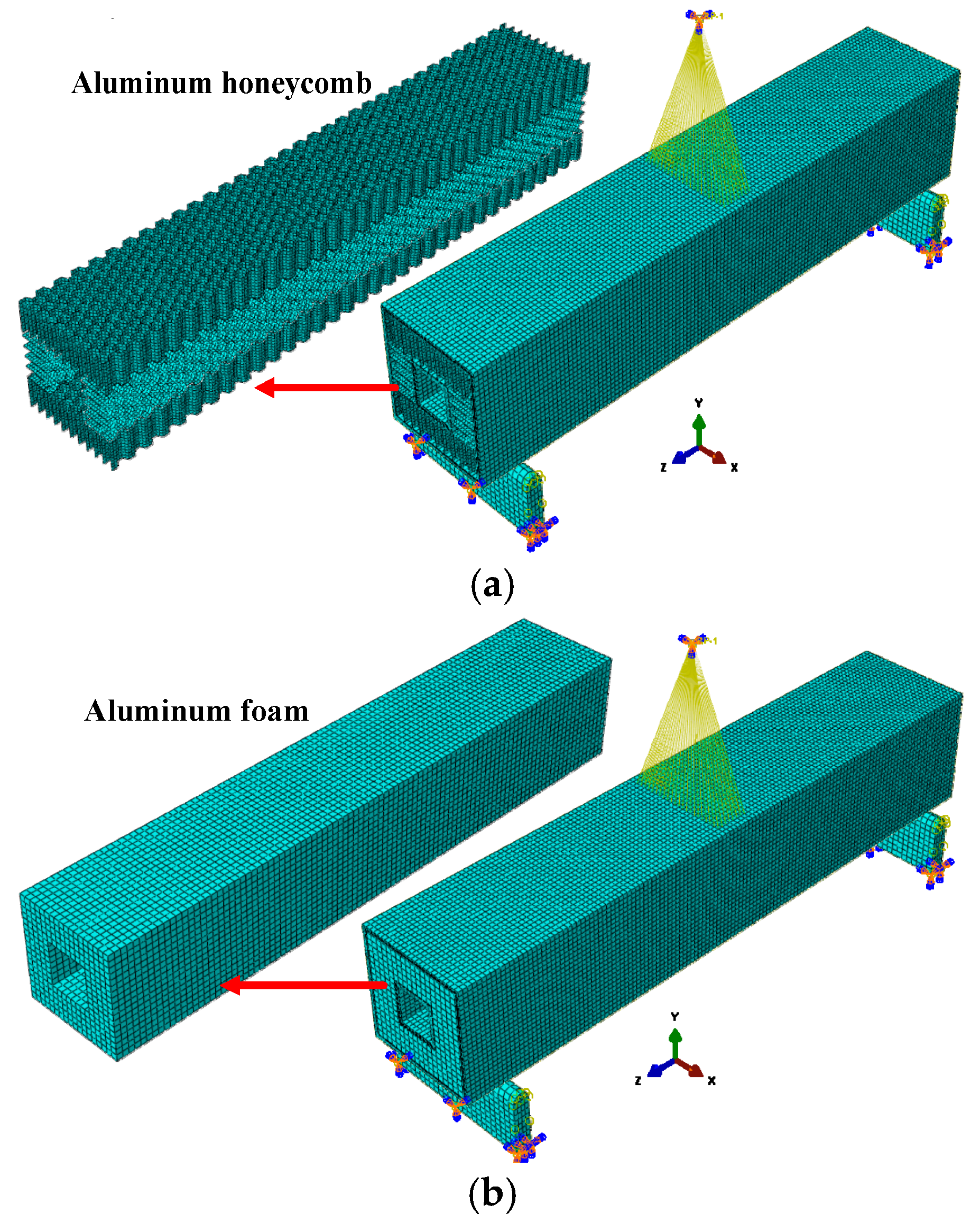
3.1. Finite Element Model of Composite Sandwich Laminated Box Beam
3.1.1. Constitutive Model and Progressive Damage Analysis for Composite Panels
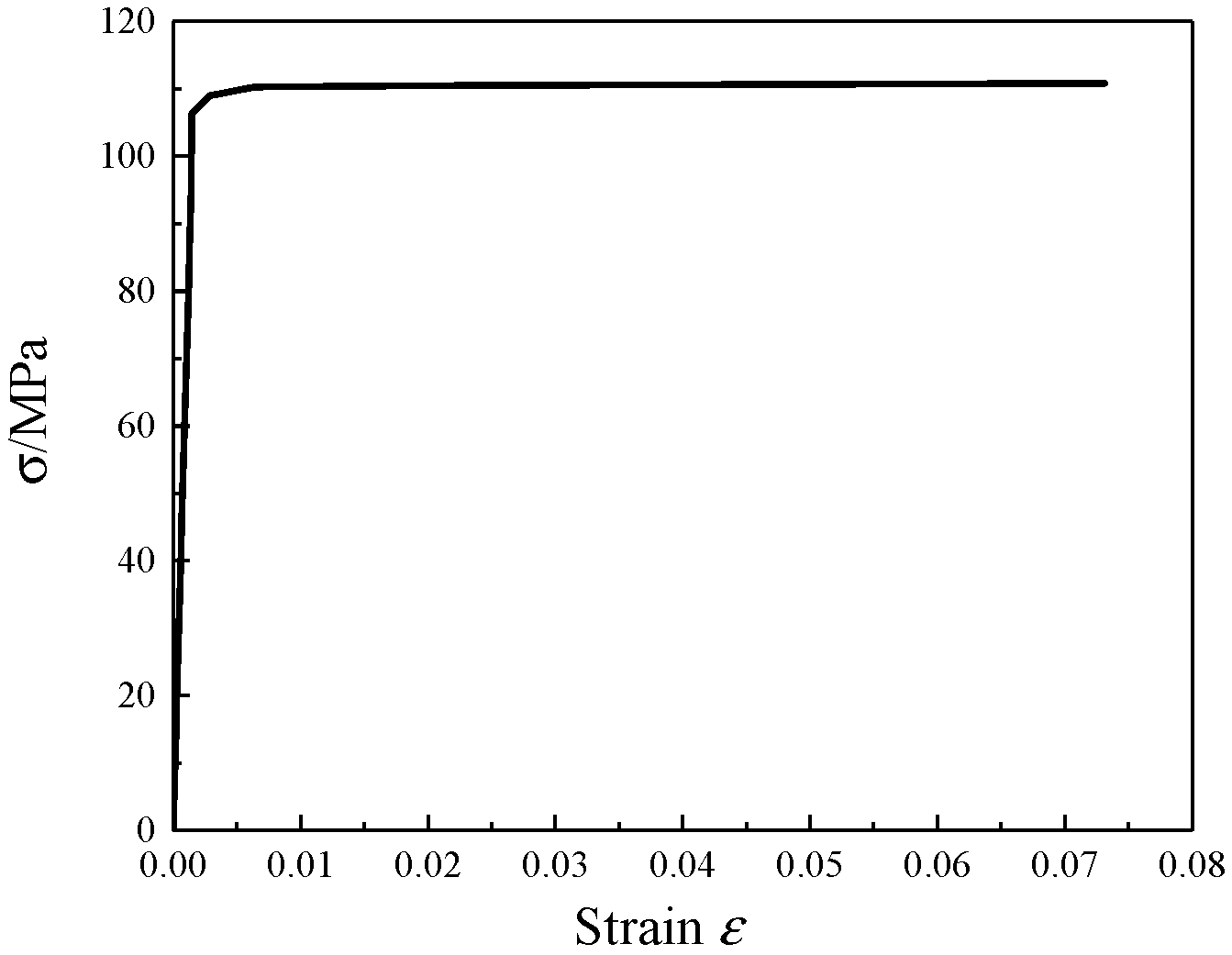
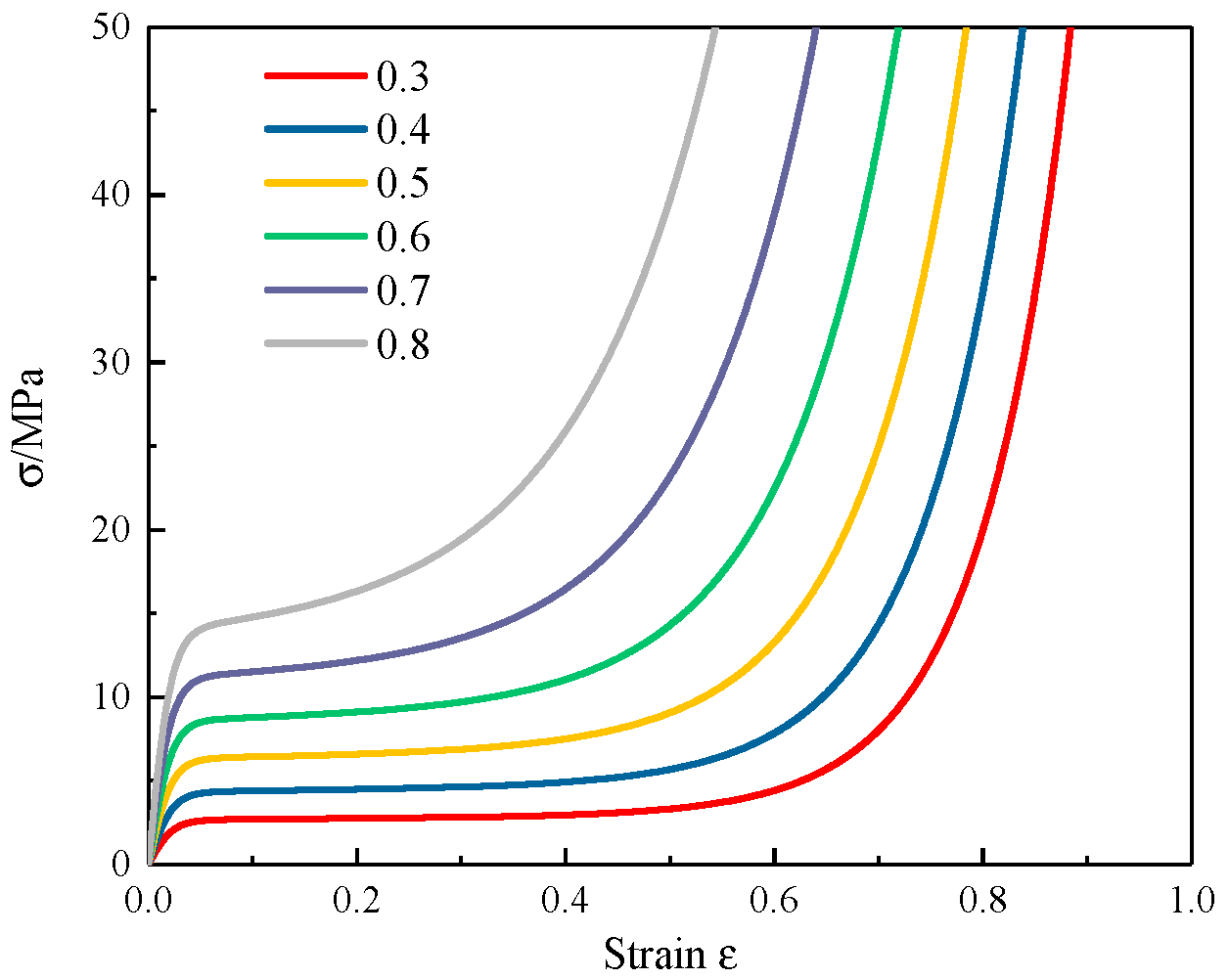
3.1.2. Elastoplastic Constitutive Model of Core Material
3.1.3. Adhesive Interface Element Damage Analysis Model
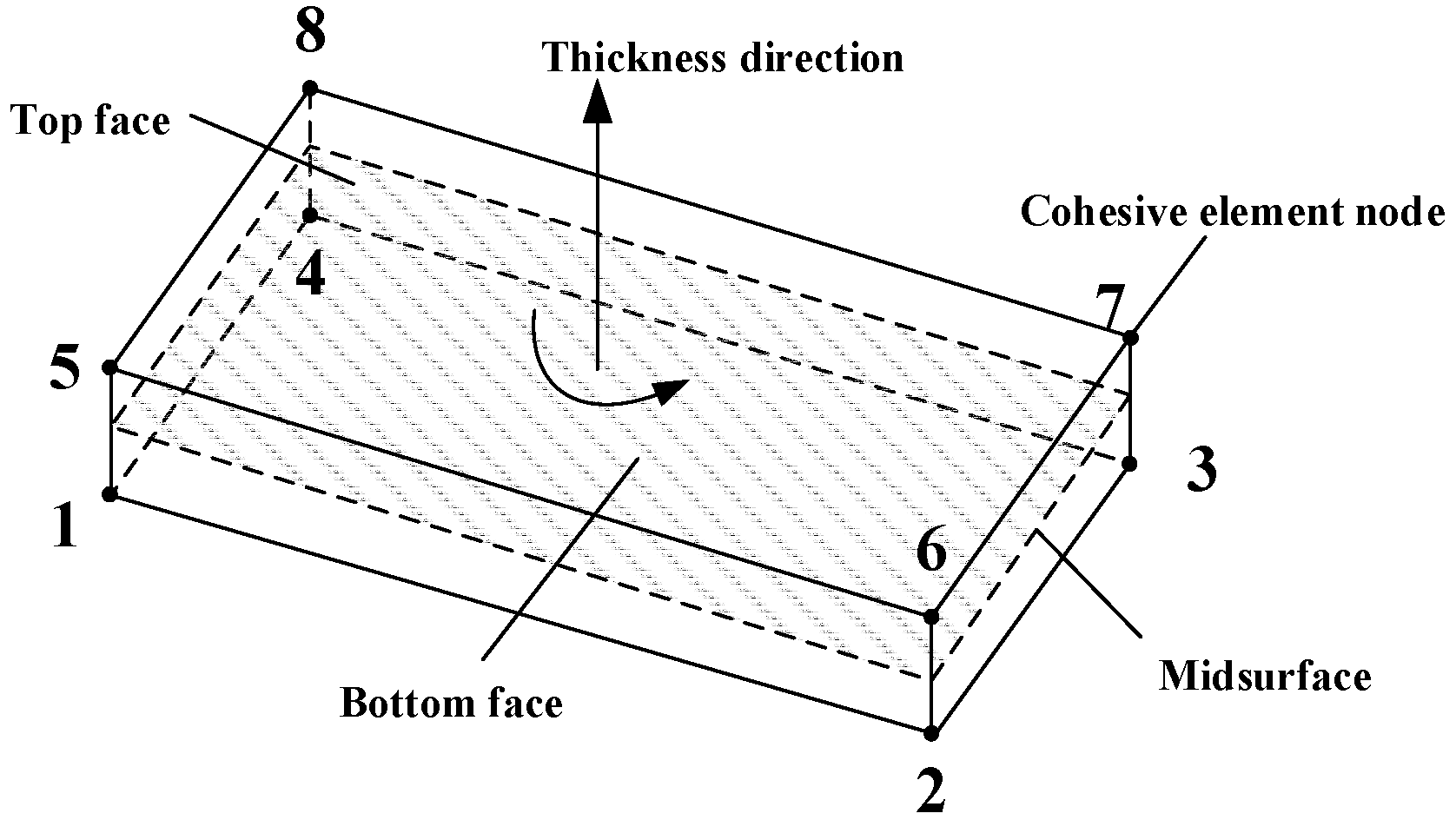
3.1.4. Geometric Model
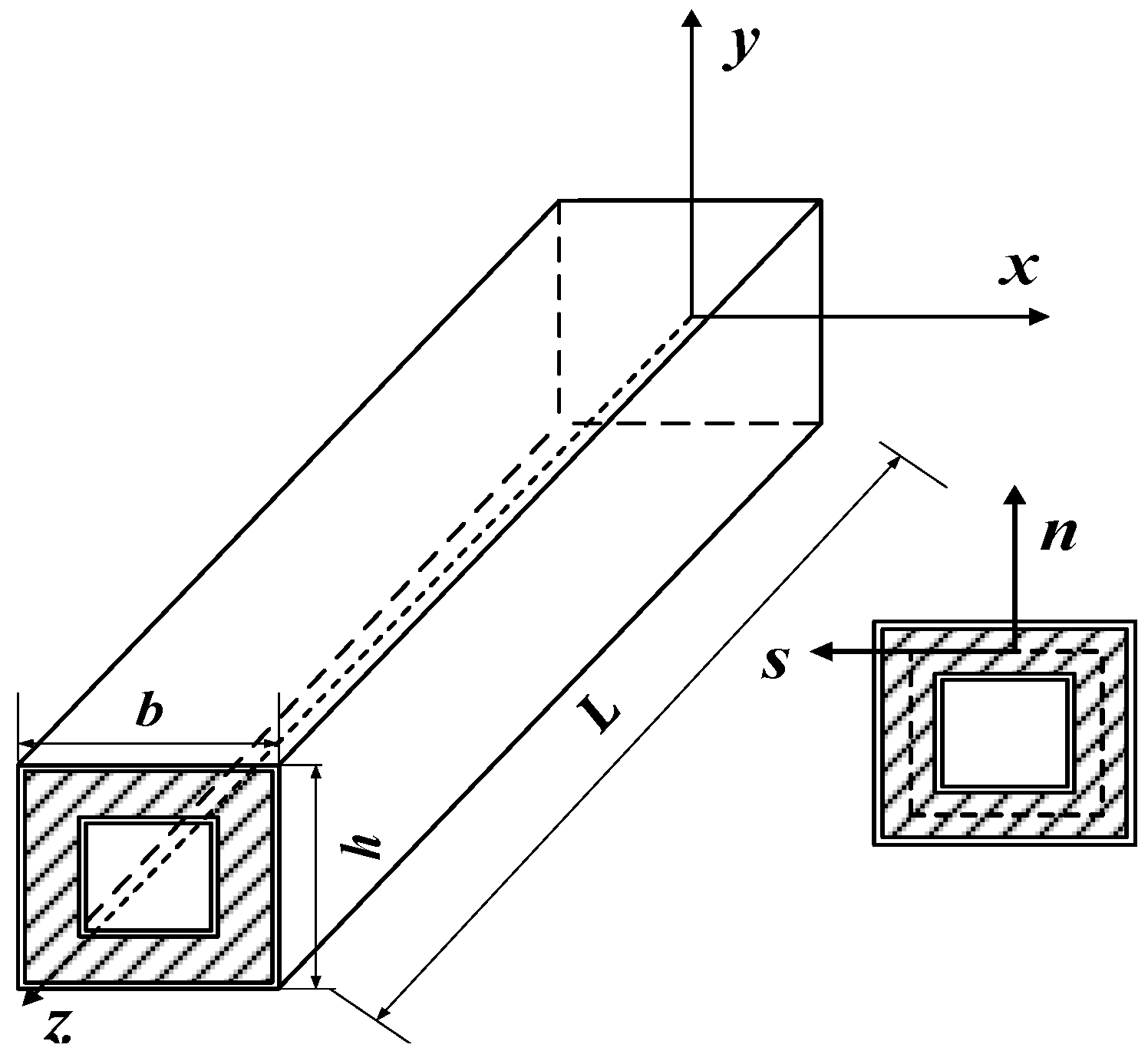
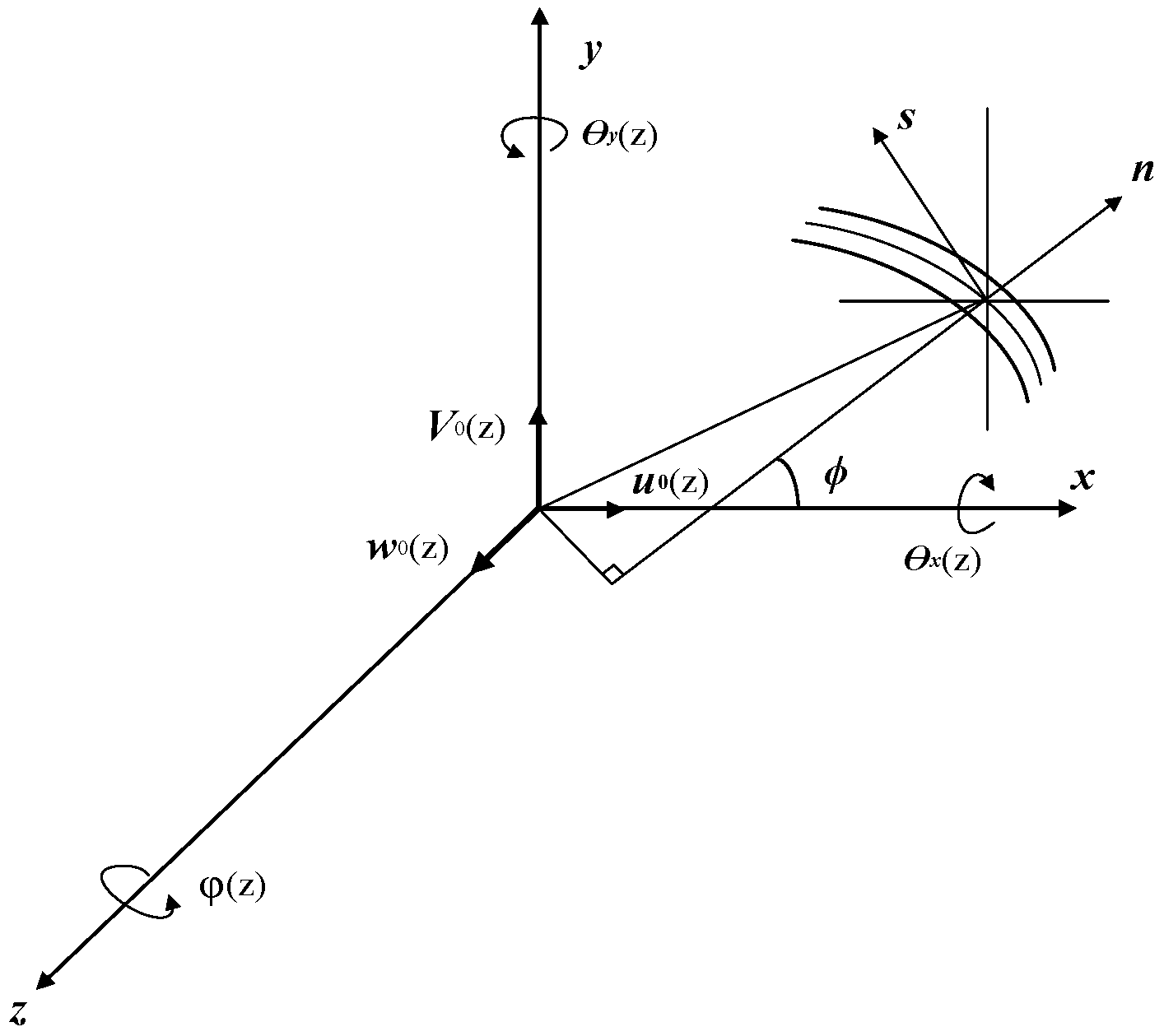
3.2. Analytical Model of Composite Sandwich Laminated Box Beam
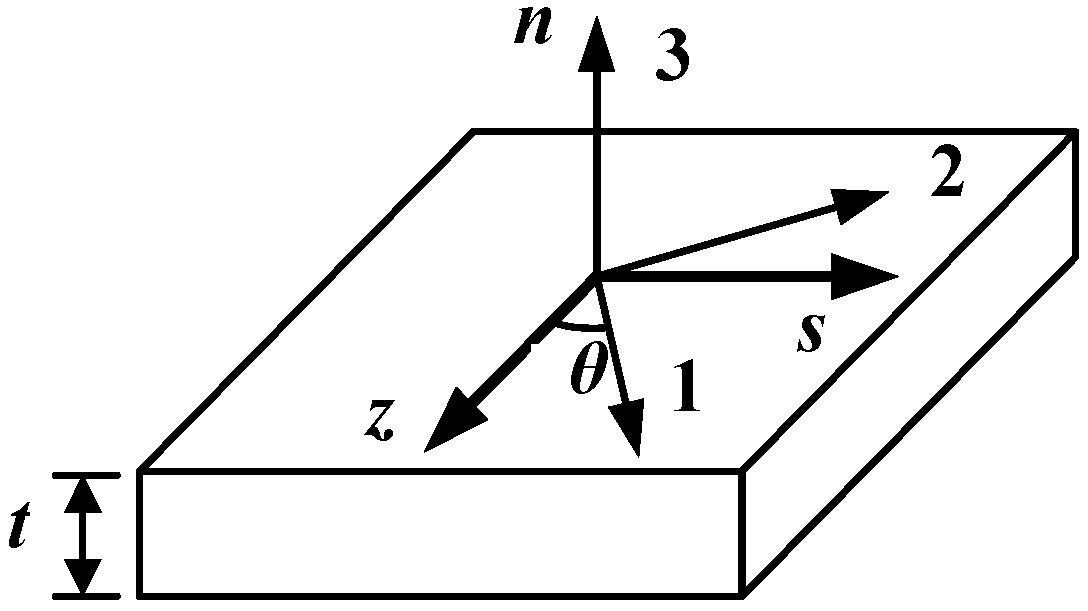
3.2.1. Simplification of Constitutive Equation for Composite Panels and Core Materials
3.2.2. Calculation of Bending Stiffness of Composite Sandwich Laminated Box Beam
3.3. Results, Discussion, and Comparative Analysis
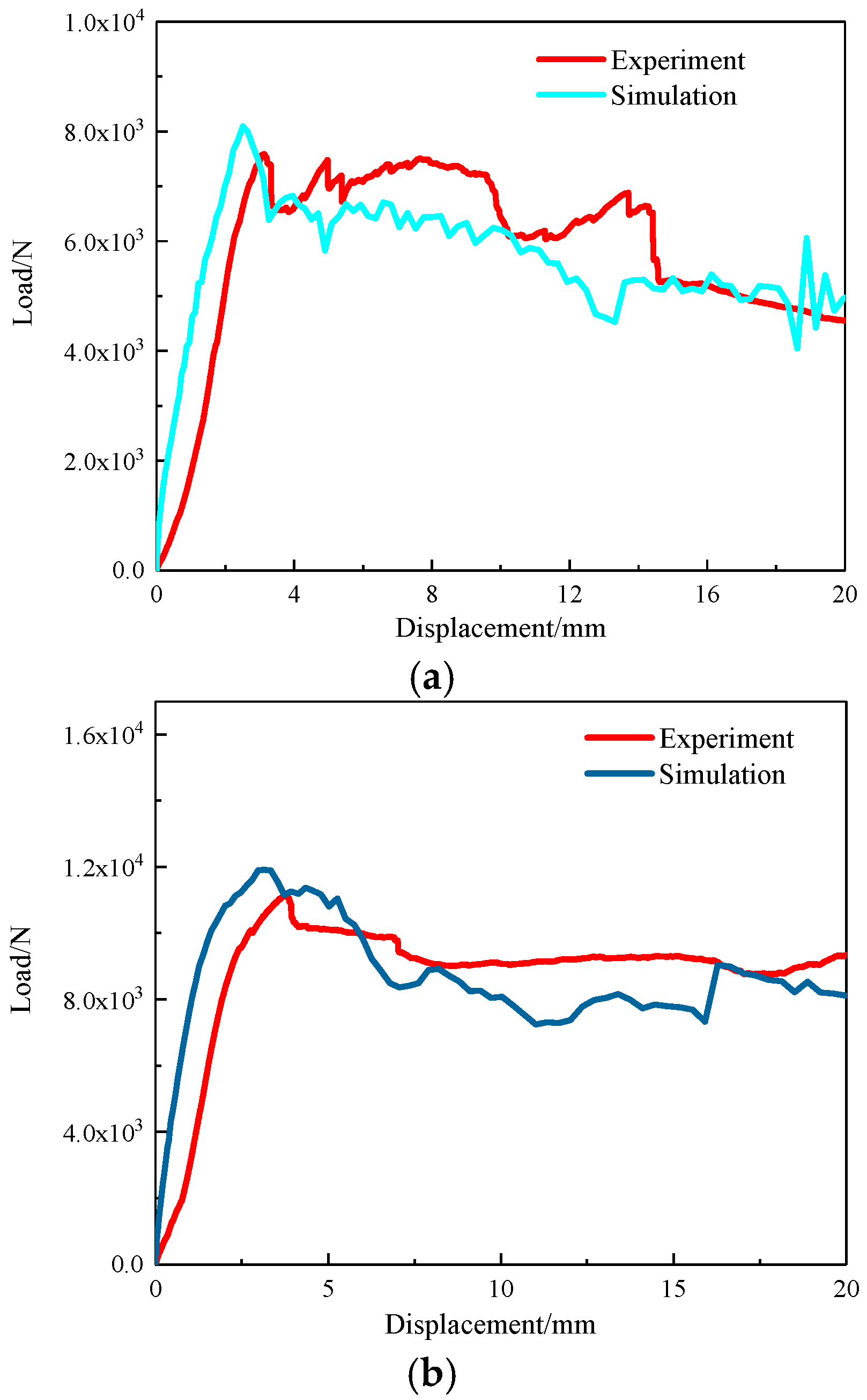
3.3.1. Model Validity Verification
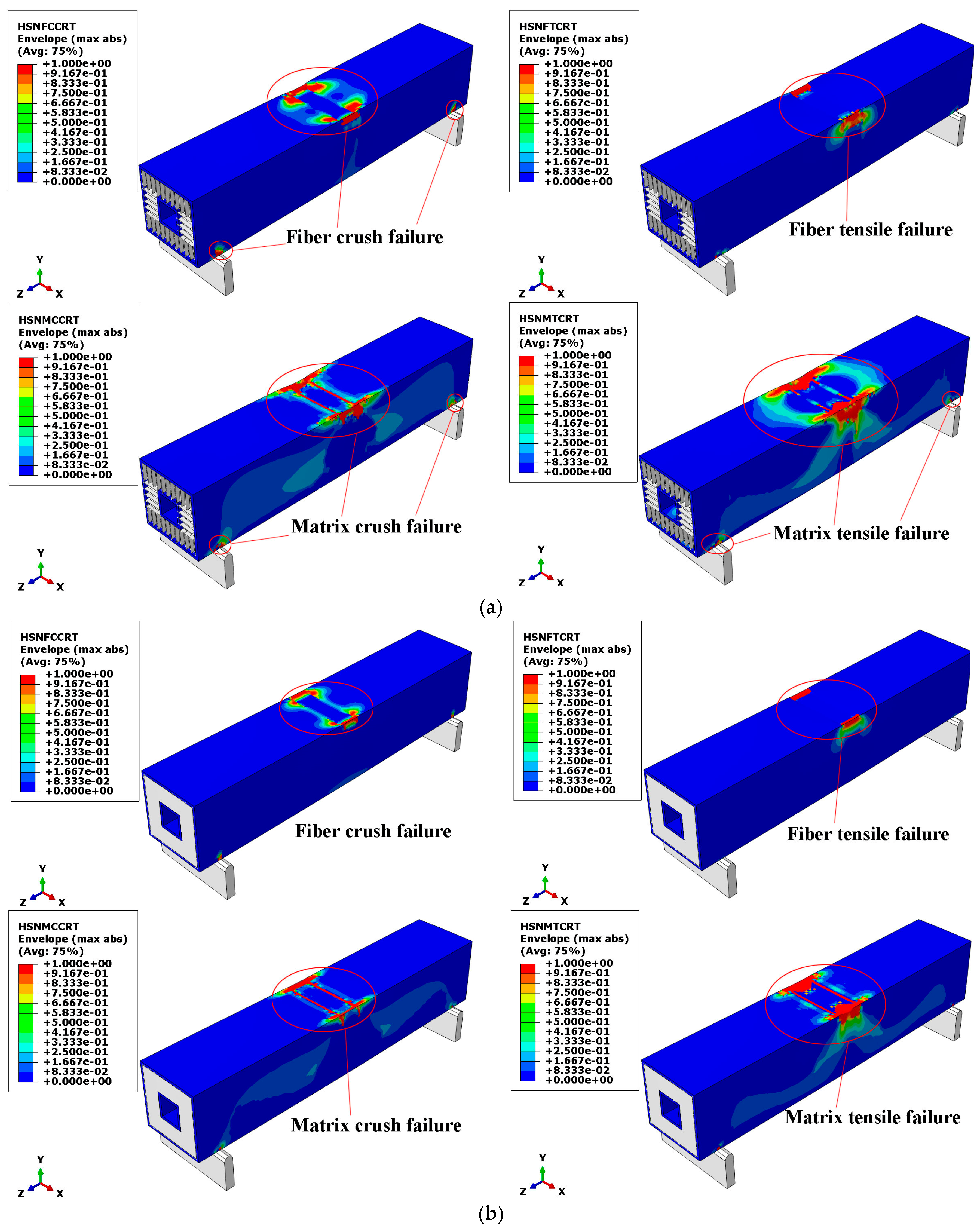
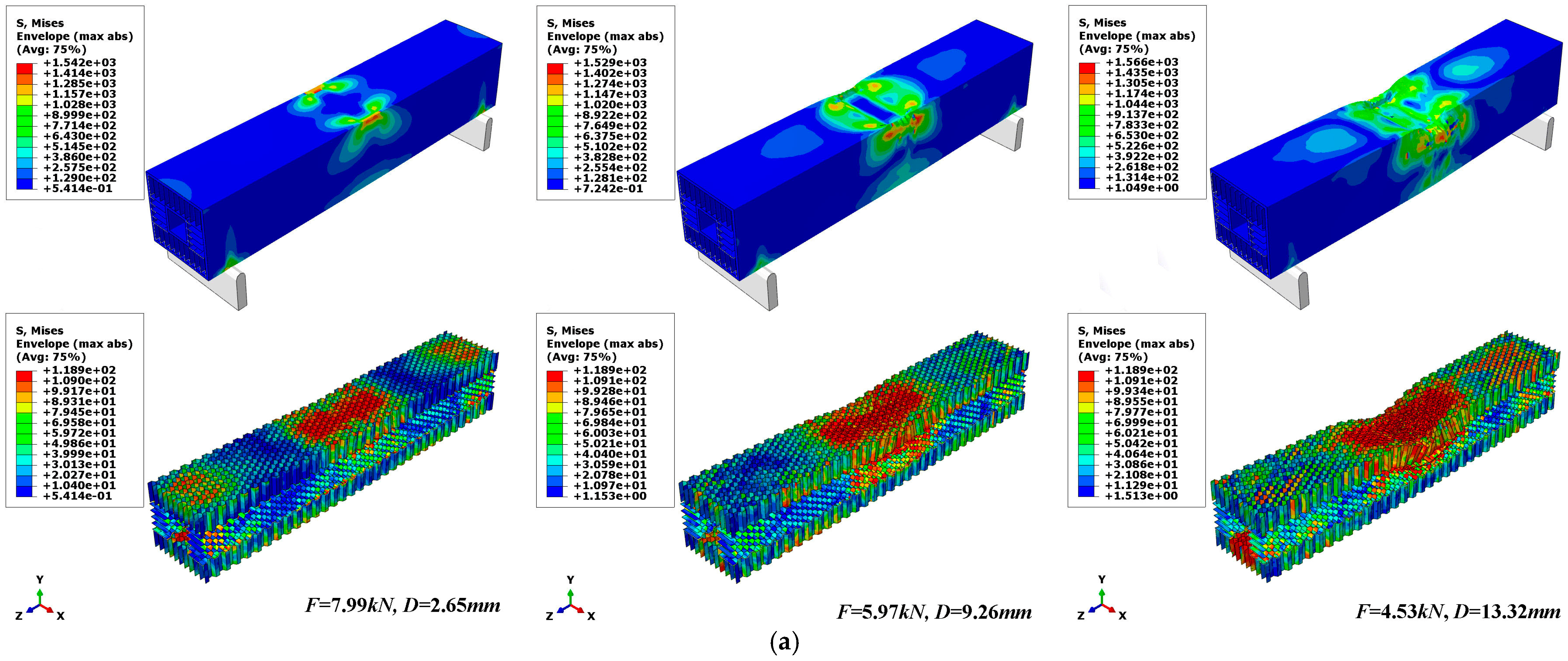
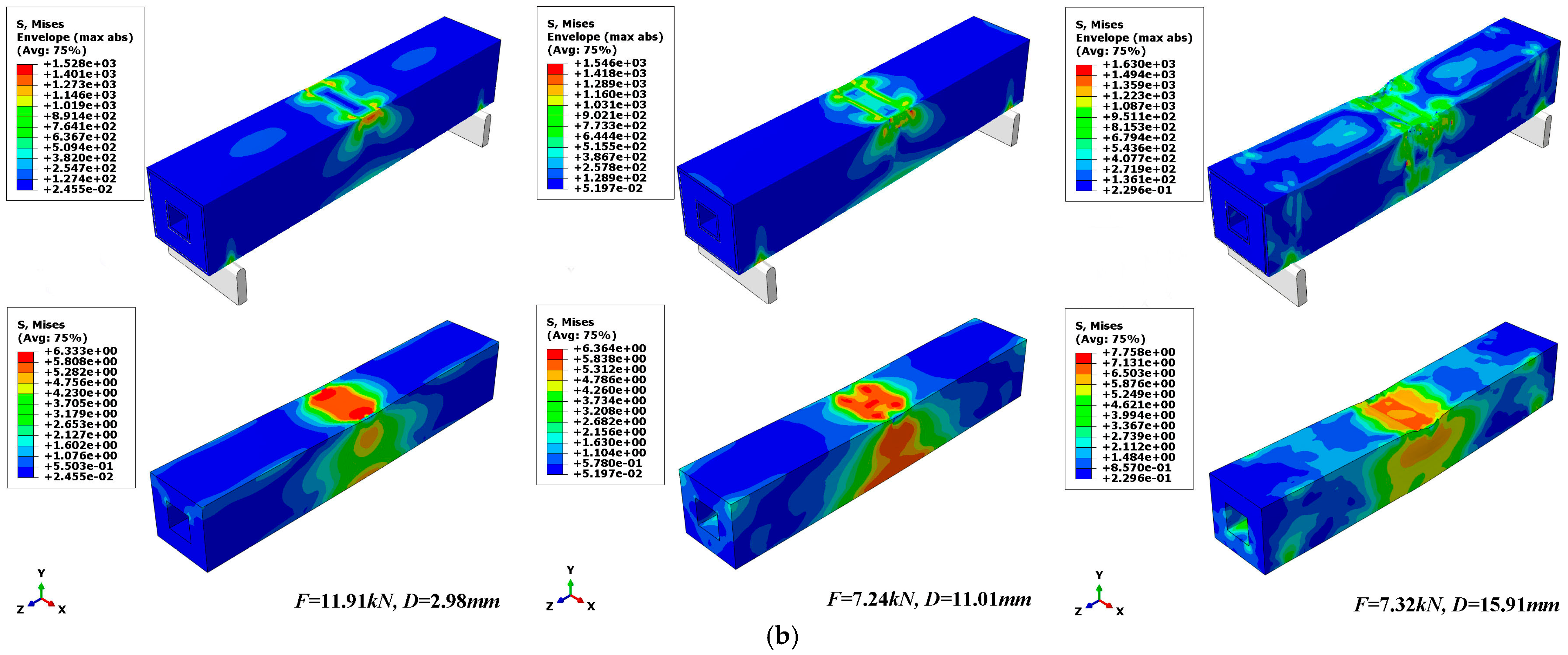
3.3.2. Failure Mechanism Analysis of Composite Sandwich Laminated Box Beams under Three-Point Bending
4. Analysis of Factors Affecting Mechanical Properties of Composite Sandwich Laminated Box Beams
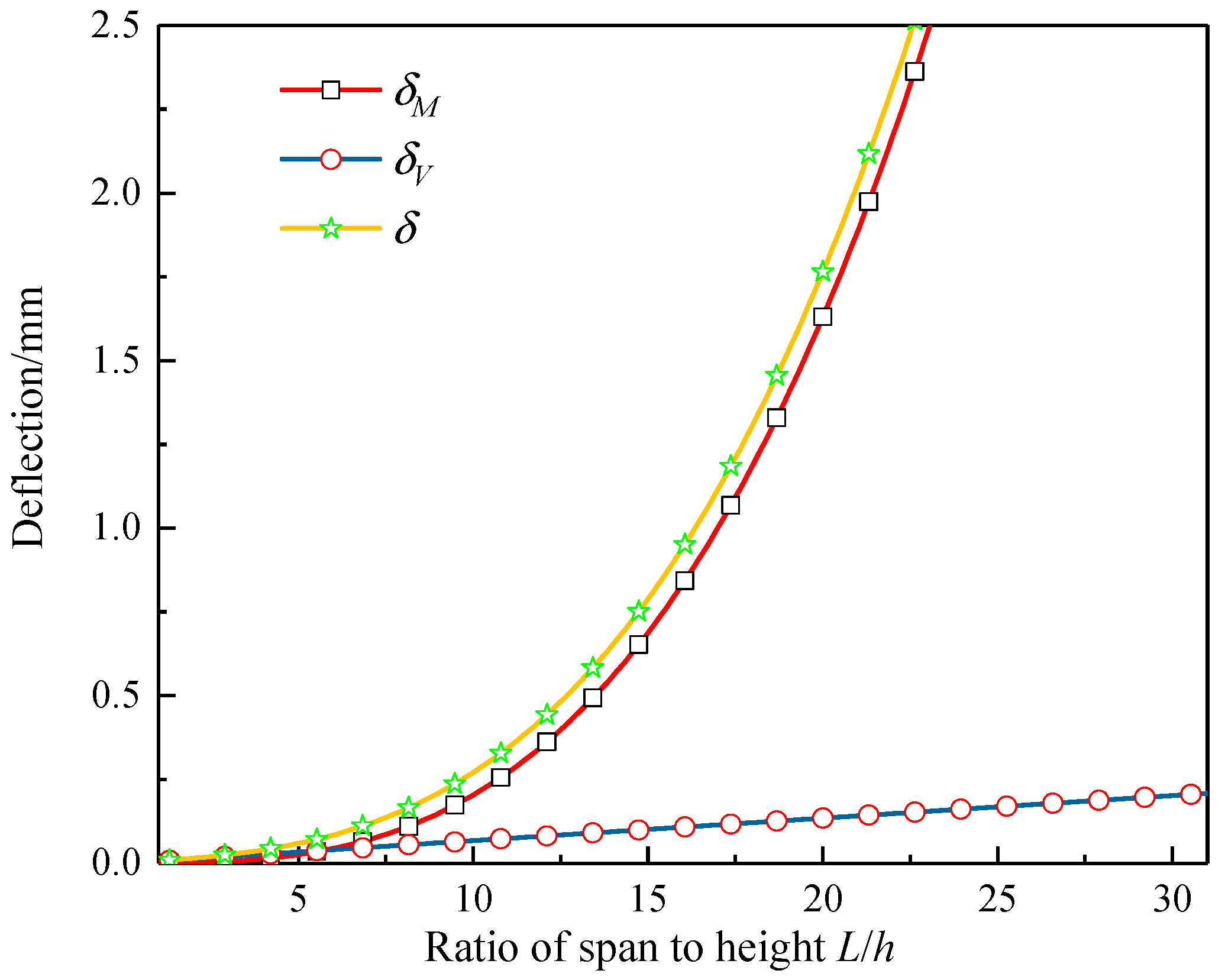
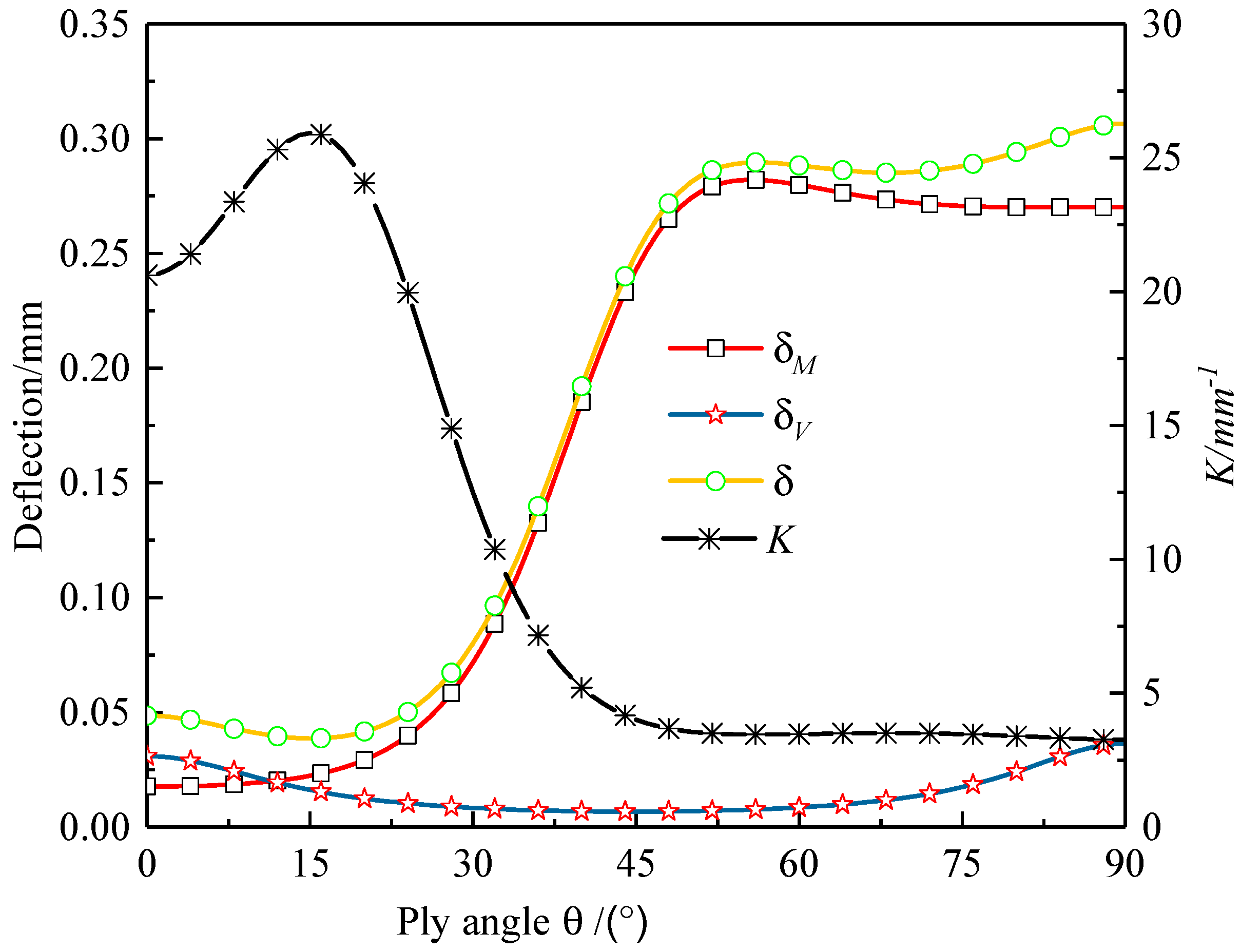
4.1. Influence of the Ratio of Span to Height
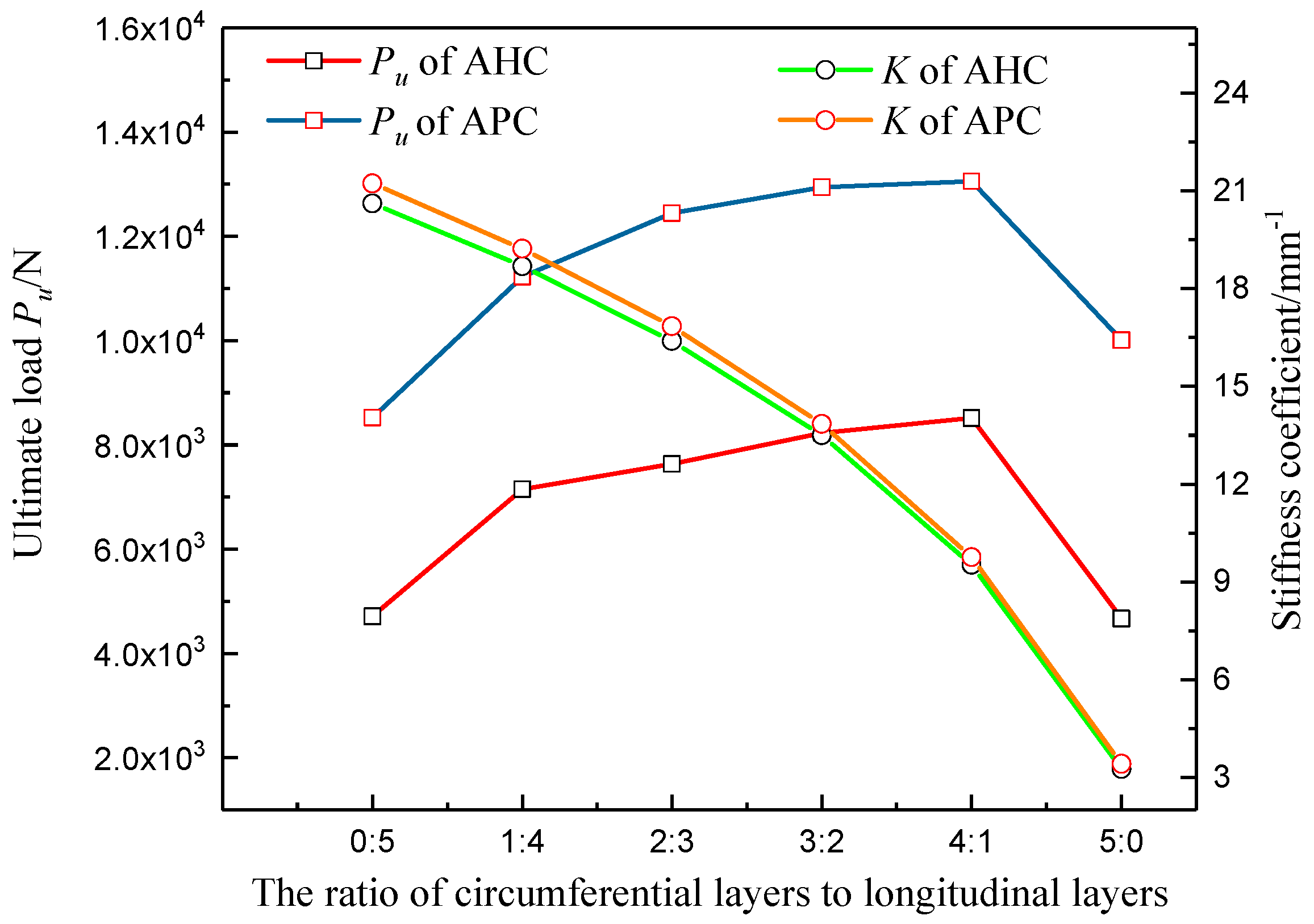
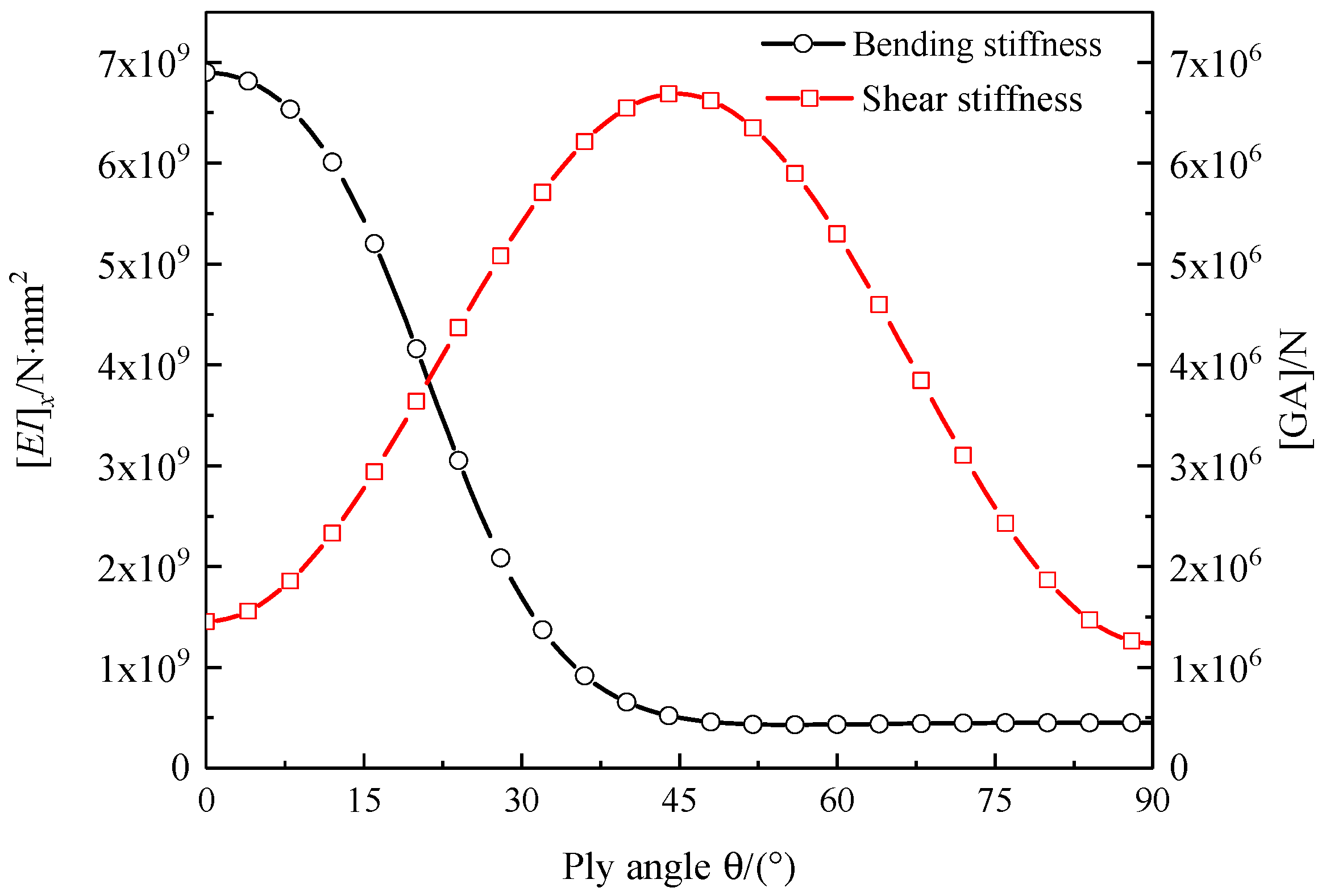
4.2. Influence of Layup Parameters
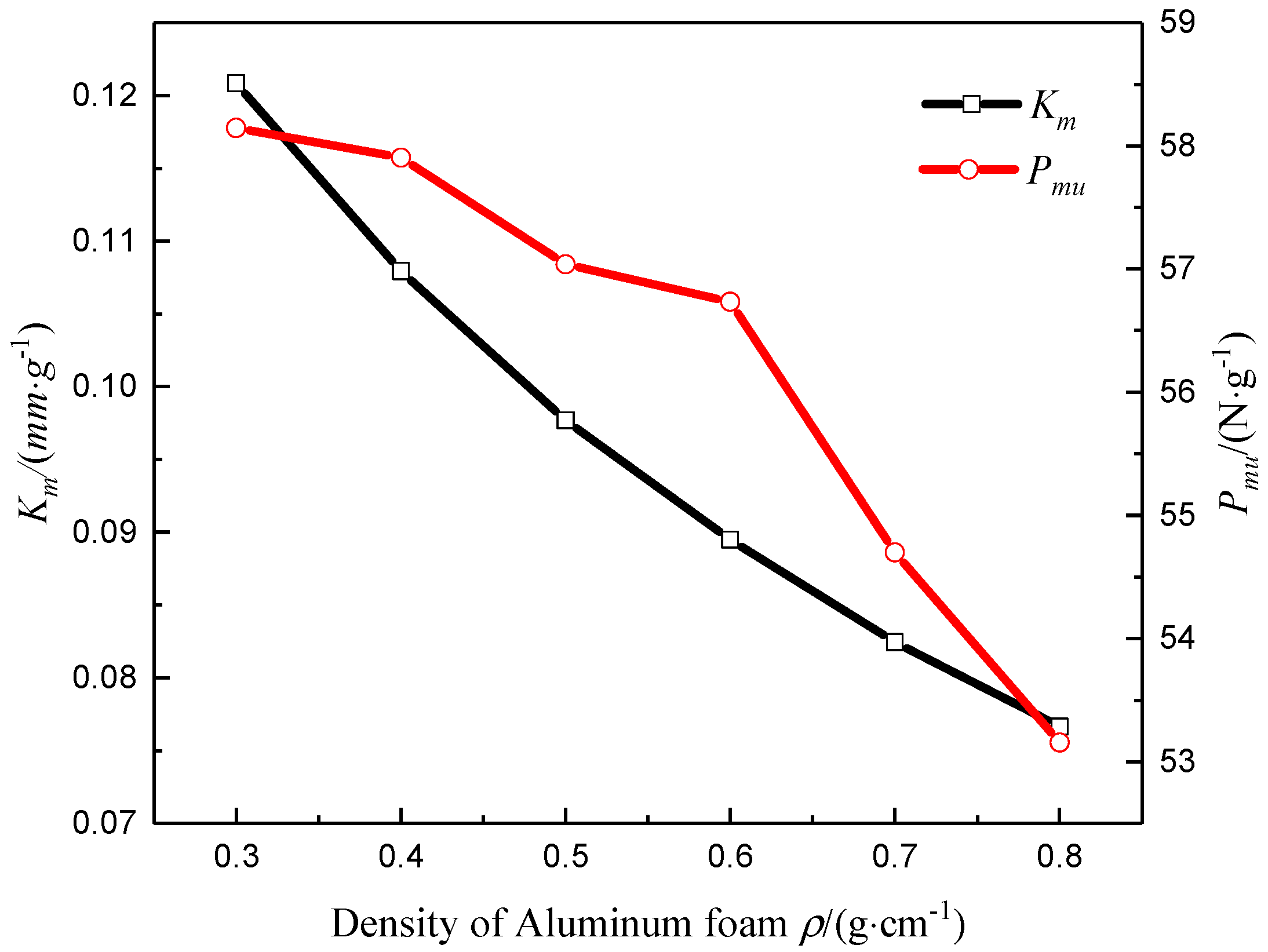
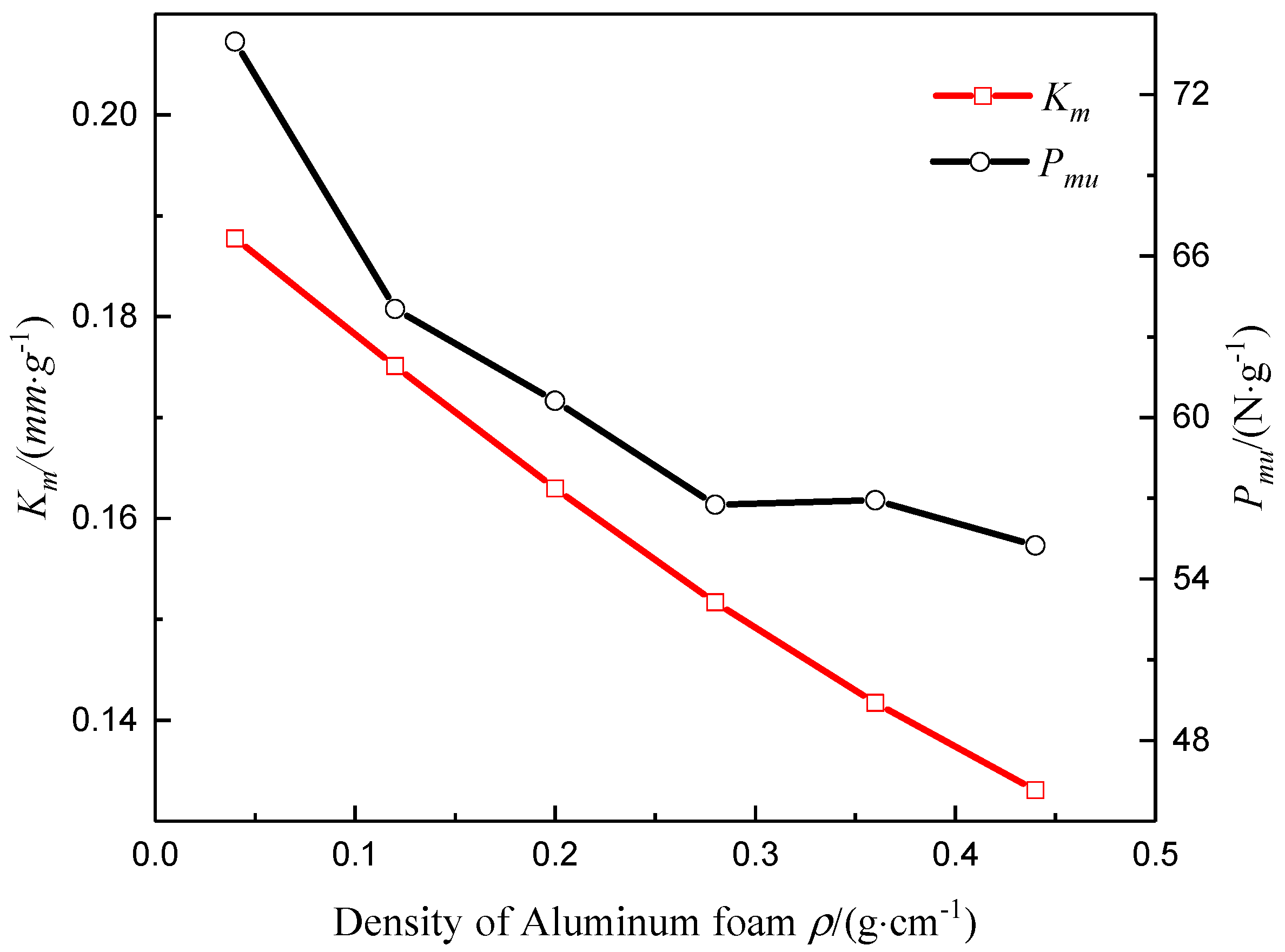
4.3. Influence of Core Material Parameters
5. Conclusions
- (1)
- Composite sandwich laminated box beams with cores of aluminum honeycomb, aluminum foam, and polyurethane elastomer underwent localized crushing damage under three-point bending load. After the ultimate load, the first two kinds of composite sandwich laminated box beams still had a high load-carrying capacity within a certain range. The composite aluminum honeycomb sandwich box laminated beam had the highest ratios of overall stiffness to mass and ultimate load to mass, leading to a better benefit of light weight.
- (2)
- The finite element models of composite sandwich laminated box beams filled with aluminum honeycomb and aluminum foam, established by composite progressive damage analysis and the core elastoplastic constitutive equation, could approximately simulate the three-point bending failure process and predict the ultimate load. The analytical model of the composite sandwich laminated box beam established by the Timoshenko beam theory could approximately calculate the overall stiffness parameters of the composite sandwich laminated box beam.
- (3)
- For composite sandwich laminated box beams with a small ratio of span to height, the additional deflection caused by shear deformation must be considered in the deflection analysis. As the ratio of circumferential layers to longitudinal layers increased, the three-point bending ultimate load of the composite sandwich laminated box beam increased, and the overall bending stiffness decreased. The use of aluminum foam with low density and aluminum honeycomb with a small cell-wall thickness as the core materials can achieve greater benefits of light weight.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Steeves, C.A.; Fleck, N.A. Collapse mechanisms of sandwich beams with composite faces and a foam core, loaded in three-point bending. Part I: Analytical models and minimum weight design. Int. J. Mech. Sci. 2004, 46, 561–583. [Google Scholar] [CrossRef]
- McCormack, T.; Miller, R.; Kesler, O.; Gibson, L. Failure of sandwich beams with metallic foam cores. Int. J. Solids Struct. 2001, 38, 4901–4920. [Google Scholar] [CrossRef]
- Mai, S.; Fleck, N.; Lu, T. Optimal design of box-section sandwich beams in three-point bending. Int. J. Solids Struct. 2007, 44, 4742–4769. [Google Scholar] [CrossRef]
- Xu, W.M.; Yuan, R.C.; Jiang, Z.G.; Hu, P. Analysis of Deflection of Sandwich Beams with Sandwich Composites. Acta Armamentari Sin. 2009, 30, 1061–1066. [Google Scholar]
- Liu, Q.; Xu, X.; Ma, J.; Wang, J.; Shi, Y.; Hui, D. Lateral crushing and bending responses of CFRP square tube filled with aluminum honeycomb. Compos. Part B: Eng. 2017, 118, 104–115. [Google Scholar] [CrossRef]
- Geuchy Ahmad, M.I.; Hoa, S.V. Flexural stiffness of thick walled composite tubes. Compos. Struct. 2016, 149, 125–133. [Google Scholar] [CrossRef]
- Shadmehri, F.; Derisi, B.; Hoa, S.V. On bending stiffness of composite tubes. Compos. Struct. 2011, 93, 2173–2179. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef]
- Aktay, L.; Johnson, A.F.; Krolin, B.H. Numerical modelling of honeycomb core crush behavior. Eng. Fract. Mech. 2008, 75, 2616–2630. [Google Scholar] [CrossRef]
- Liu, Q.; Subhash, G. A phenomenological constitutive model for foams under large deformations. Polym. Eng. Sci. 2004, 44, 463–473. [Google Scholar] [CrossRef]
- ABAQUS Inc., Ltd. Abaqus Theory Manual. Version V 6.12; ABAQUS Inc., Ltd.: Johnston, RI, USA, 2012. [Google Scholar]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Jose, S.; Kumar, R.R.; Jana, M.K.; Rao, G.V. Intralaminar fracture toughness of cross-ply laminate and its constituent sub-laminates. Compos. Sci. Technol. 2001, 61, 1115–1122. [Google Scholar] [CrossRef]
- Cui, H.; Yan, Q.; Wang, X.M.; Bi, S.Q.; Wang, X.F. Assessment of failure analysis method for the bolted structure between selective laser melting aluminum plate and CFRP composite laminate. Acta Mater. Compos. Sin. 2017, 34, 2762–2769. [Google Scholar]
- Tan, C.; Li, Y.L.; Guo, Y.Z. Mechanical property analysis of composite adhesively bonded sandwich pipe joints. Acta Mater. Compos. Sin. 2014, 31, 1532–1542. [Google Scholar]
- Vo, T.P.; Lee, J. Flexural-torsional behavior of thin-walled composite box beams using shear-deformable beam theory. Eng. Struct. 2008, 30, 1958–1968. [Google Scholar] [CrossRef][Green Version]
- Qin, Z.; Librescu, L. On a shear-deformable theory of anisotropic thin-walled beams: Further contribution and validations. Compos. Struct. 2002, 56, 345–358. [Google Scholar] [CrossRef]

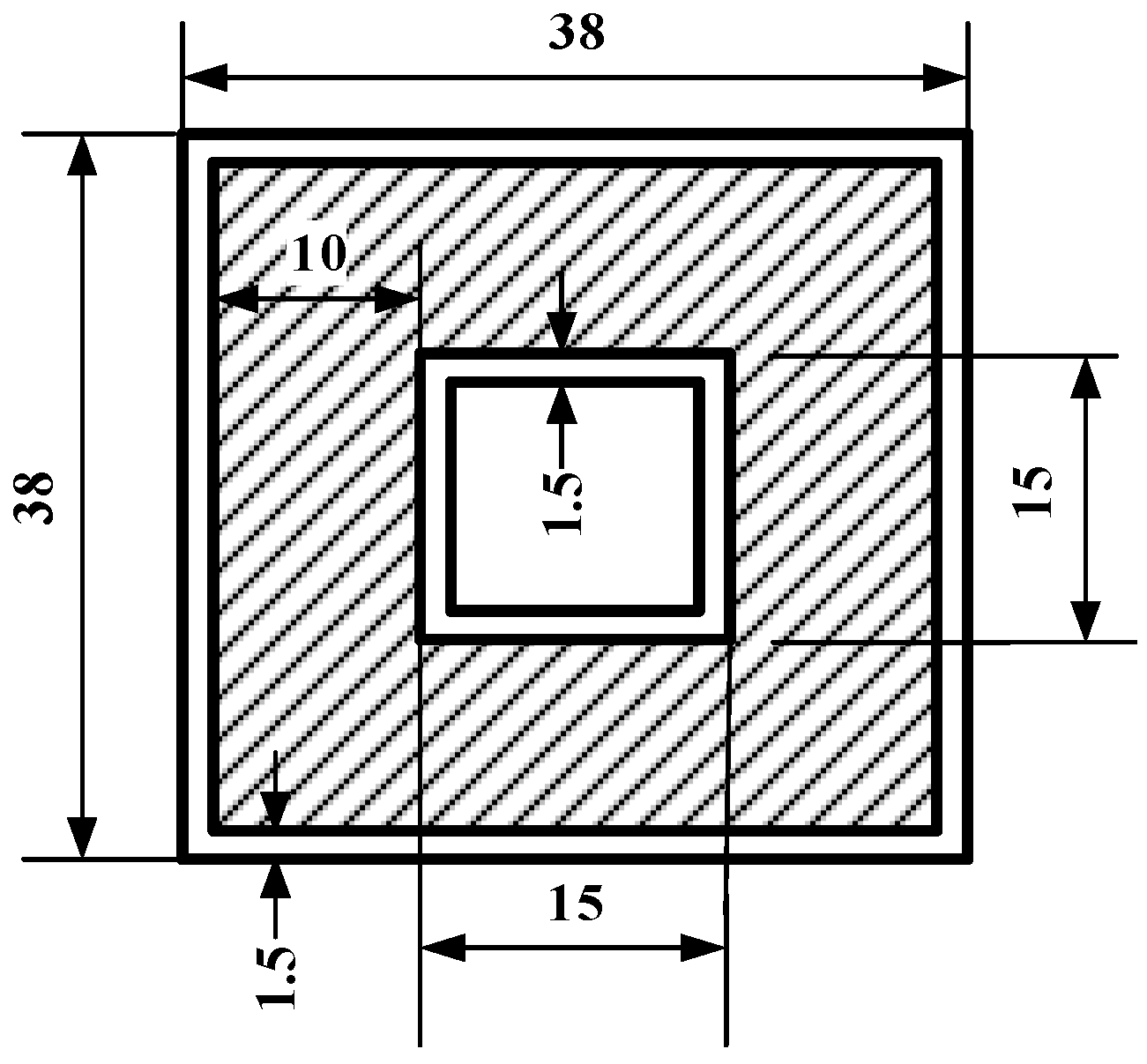



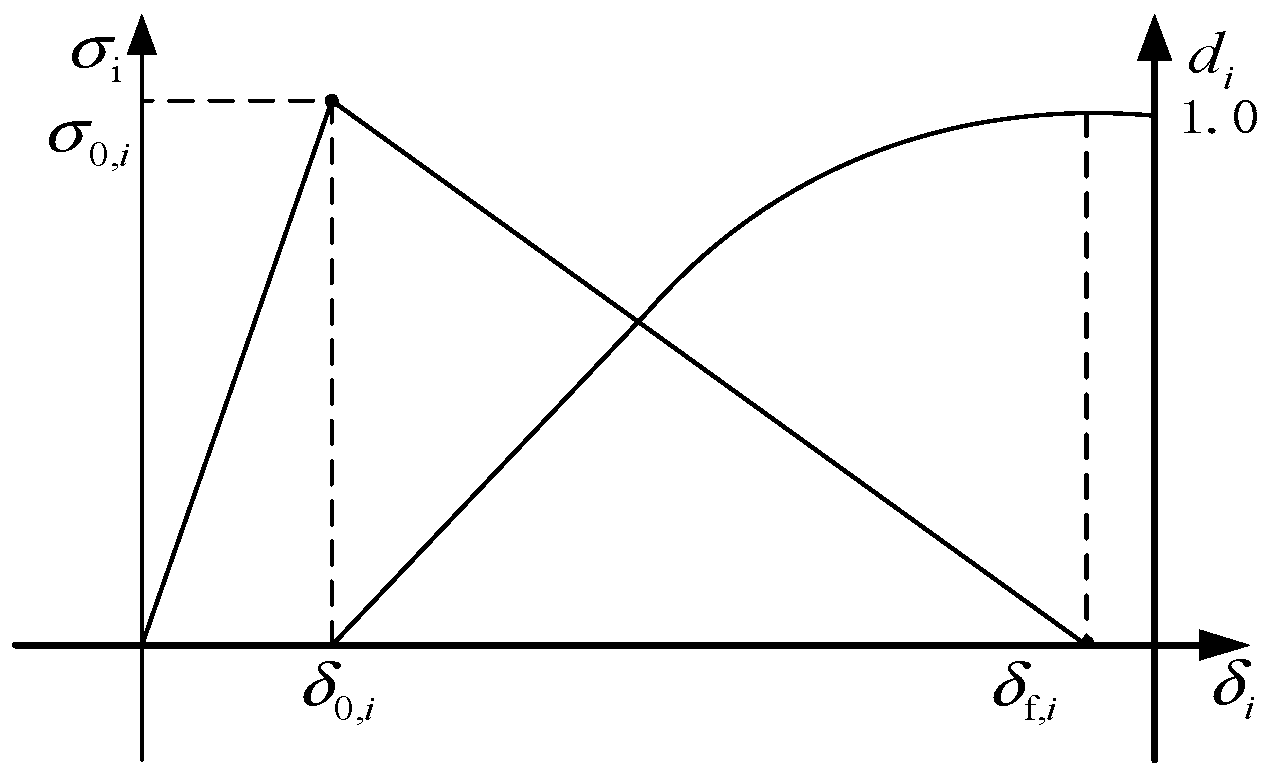
| No. | Type of Core | Total Mass m (g) |
|---|---|---|
| B1 | Aluminum honeycomb | 109.4 |
| B2 | Aluminum foam | 197.6 |
| B3 | Polyurethane elastomer | 349.8 |
| No. | Kb (N∙m2) | Pu (N) | Kmb (N∙m2/g) | Pmu (N/g) |
|---|---|---|---|---|
| B1 | 3686.56 | 7590.15 | 32.42 | 69.51 |
| B2 | 3707.98 | 11,211.87 | 21.25 | 56.74 |
| B3 | 3693.66 | 6670.07 | 10.46 | 19.07 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| E1 (GPa) | 135 | Xt (MPa) | 1673 |
| E2= E3 (GPa) | 8.8 | Xc (MPa) | 1160 |
| G12 = G13 (GPa) | 4.47 | Yt (MPa) | 68 |
| G23 (GPa) | 3.0 | Yc (MPa) | 210 |
| v12 = v13 | 0.33 | SL = ST (MPa) | 112 |
| v23 | 0.33 | ρ (g/cm3) | 1.58 |
| 50.5 | 30.5 | 0.22 | 1.1 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (MPa) | 30 | Knn (GPa) | 1000 |
| (MPa) | 60 | Kss (GPa) | 1000 |
| (MPa) | 60 | Ktt (GPa) | 1000 |
| (N/mm) | 0.2 | η | 1.5 |
| (N/mm) | 1.0 | ρ (g/m3) | 1.2 |
| (N/mm) | 1.002 |
| No. | Theoretical Calculation (N∙m2) | Experiment (N∙m2) | Error (%) |
|---|---|---|---|
| B1 | 3686.56 | 3495.26 | −5.19 |
| B2 | 3707.98 | 3529.02 | −4.83 |
| B3 | 3693.66 | 3544.75 | −4.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Xiong, C.; Yin, J.; Yin, D.; Deng, H. Bending Experiment and Mechanical Properties Analysis of Composite Sandwich Laminated Box Beams. Materials 2019, 12, 2959. https://doi.org/10.3390/ma12182959
Zhu X, Xiong C, Yin J, Yin D, Deng H. Bending Experiment and Mechanical Properties Analysis of Composite Sandwich Laminated Box Beams. Materials. 2019; 12(18):2959. https://doi.org/10.3390/ma12182959
Chicago/Turabian StyleZhu, Xiujie, Chao Xiong, Junhui Yin, Dejun Yin, and Huiyong Deng. 2019. "Bending Experiment and Mechanical Properties Analysis of Composite Sandwich Laminated Box Beams" Materials 12, no. 18: 2959. https://doi.org/10.3390/ma12182959
APA StyleZhu, X., Xiong, C., Yin, J., Yin, D., & Deng, H. (2019). Bending Experiment and Mechanical Properties Analysis of Composite Sandwich Laminated Box Beams. Materials, 12(18), 2959. https://doi.org/10.3390/ma12182959




