A Simplified Calculation Method of Heat Source Model for Induction Heating
Abstract
1. Introduction
2. Simplification of Heat Source
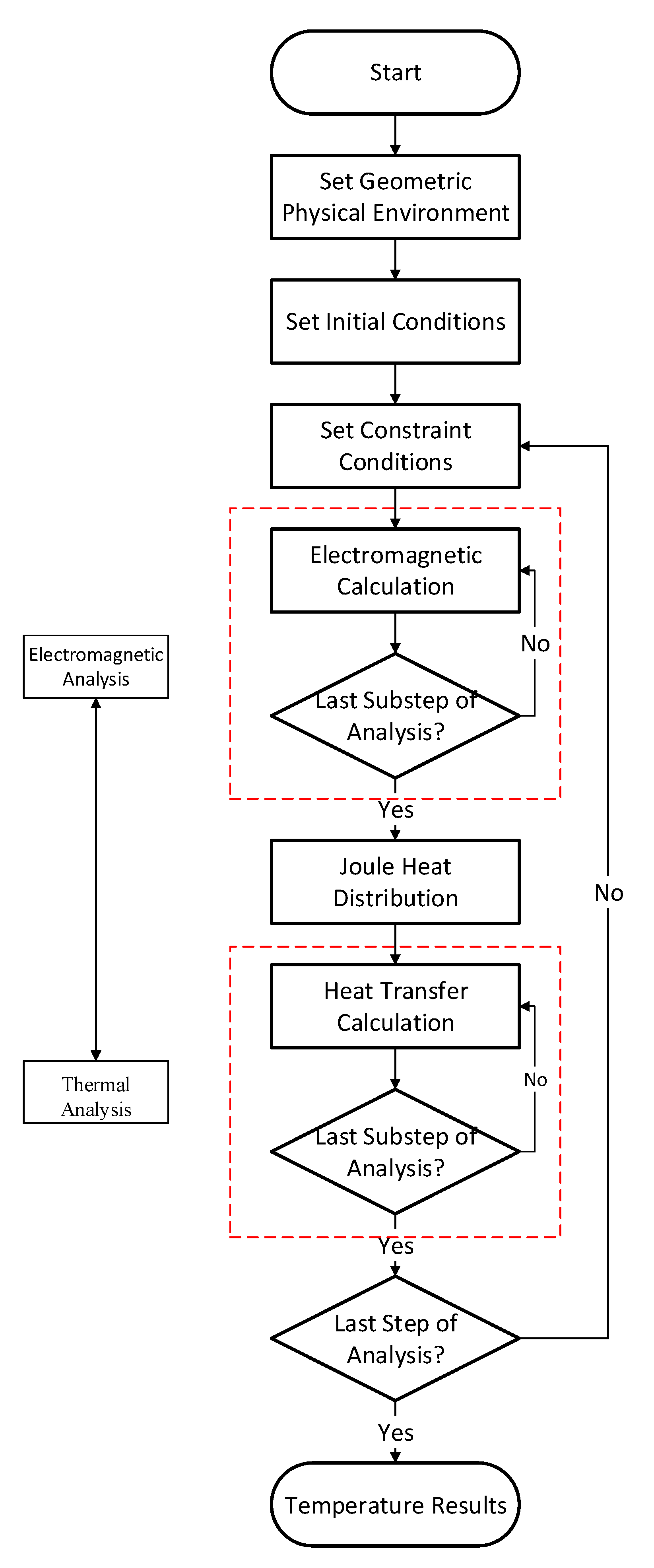
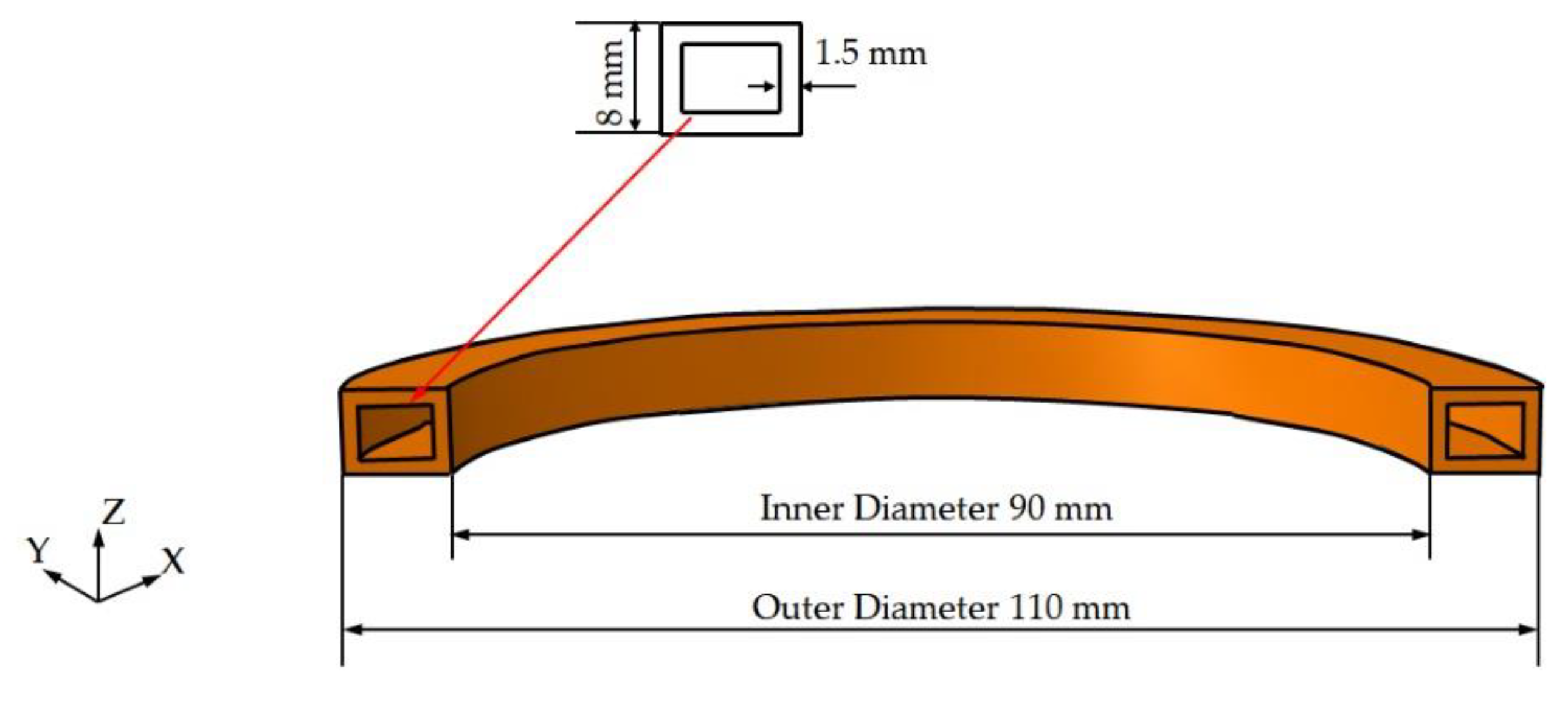
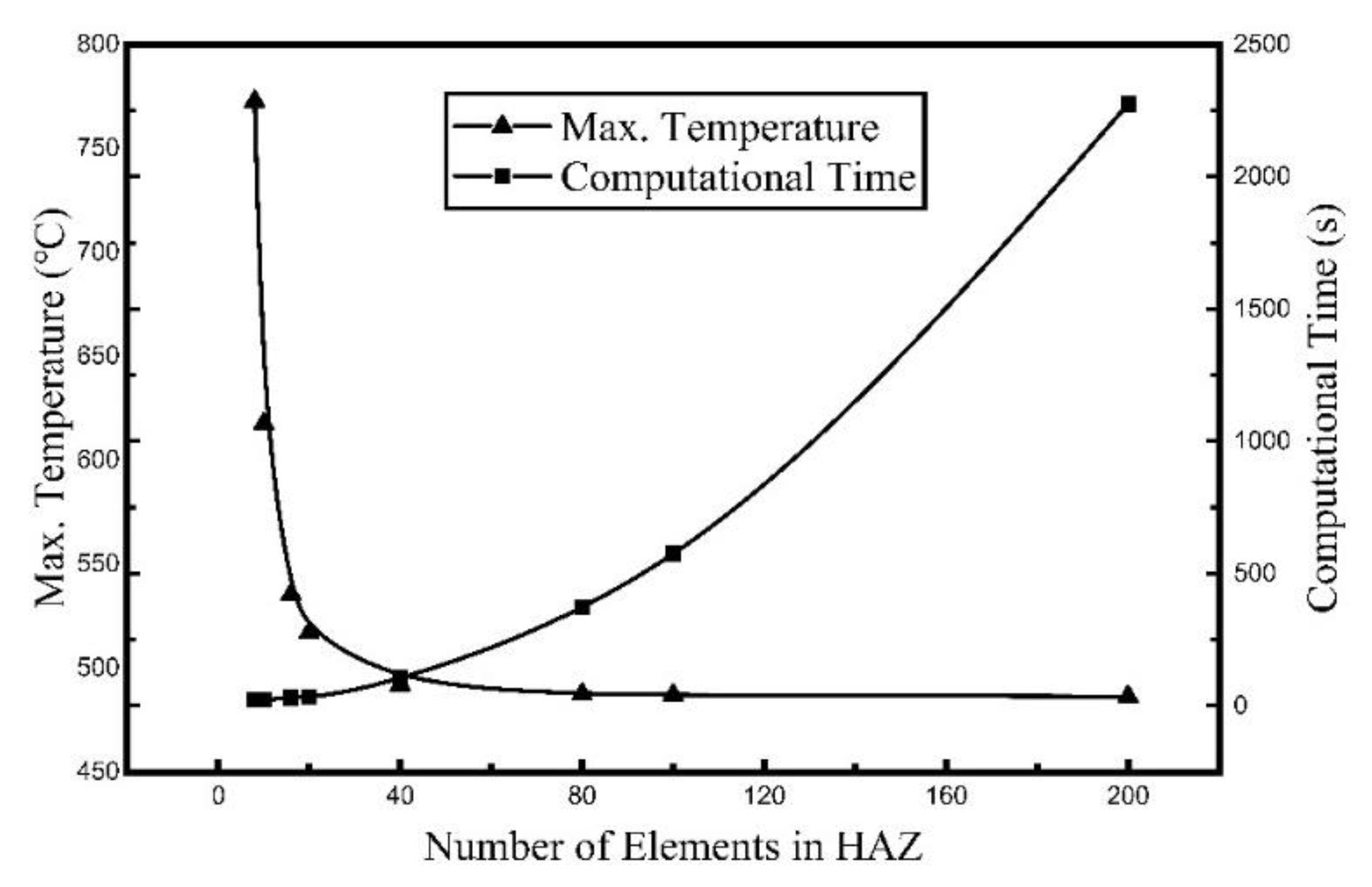
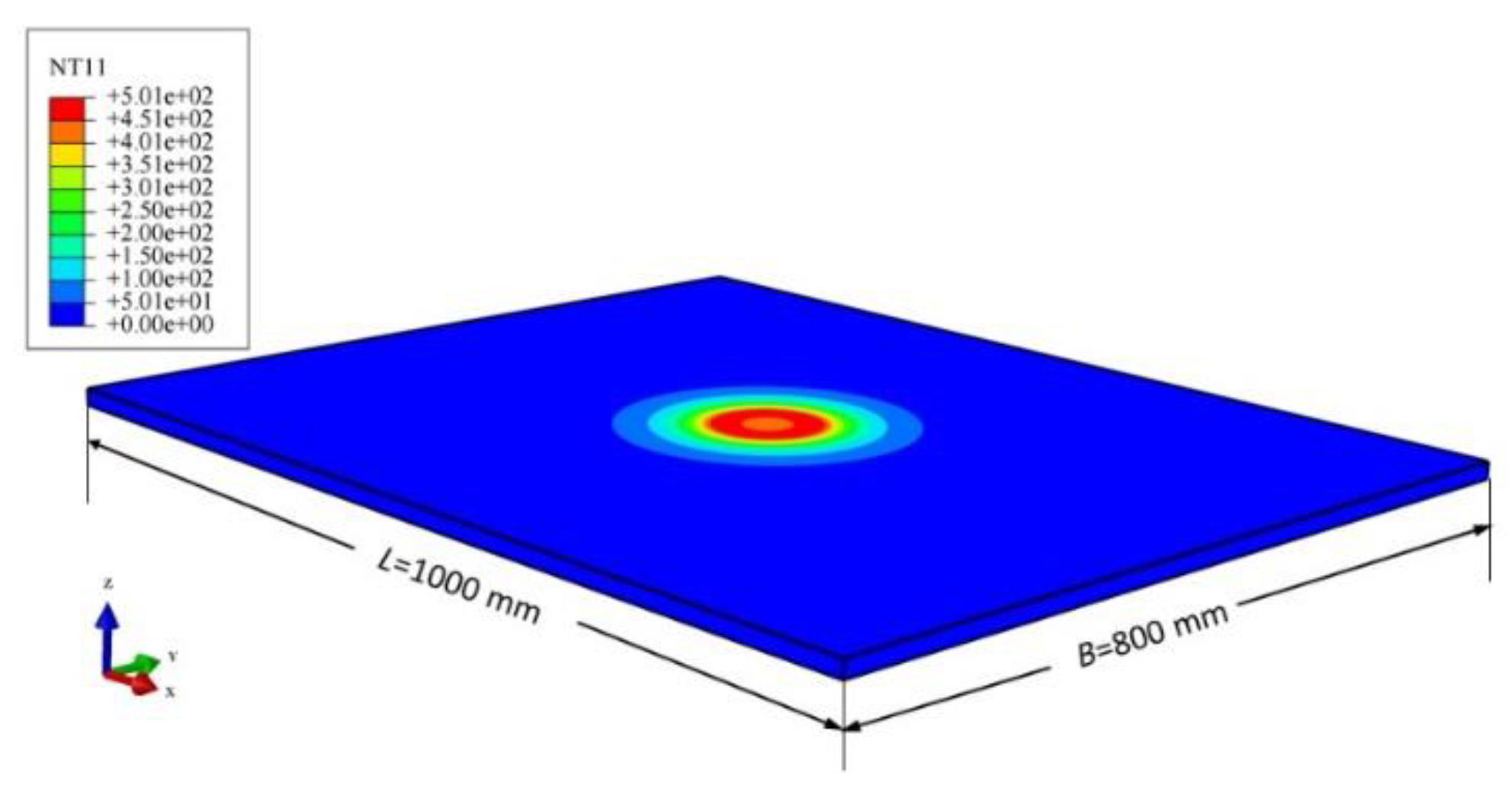
2.1. Finite Element Calculation
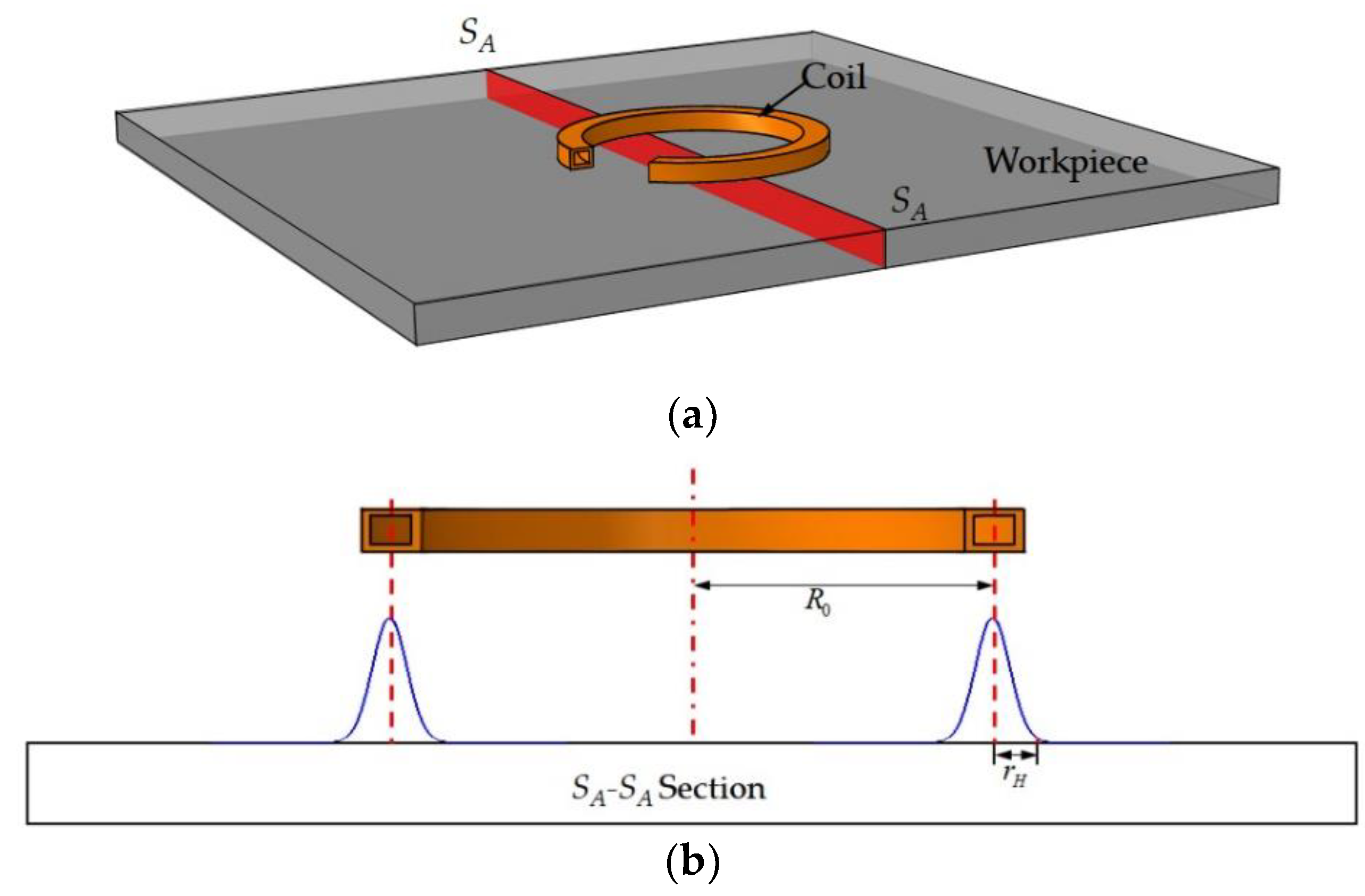
2.2. Simplification of Heat Source Model
3. Verifications of Heat Source Model
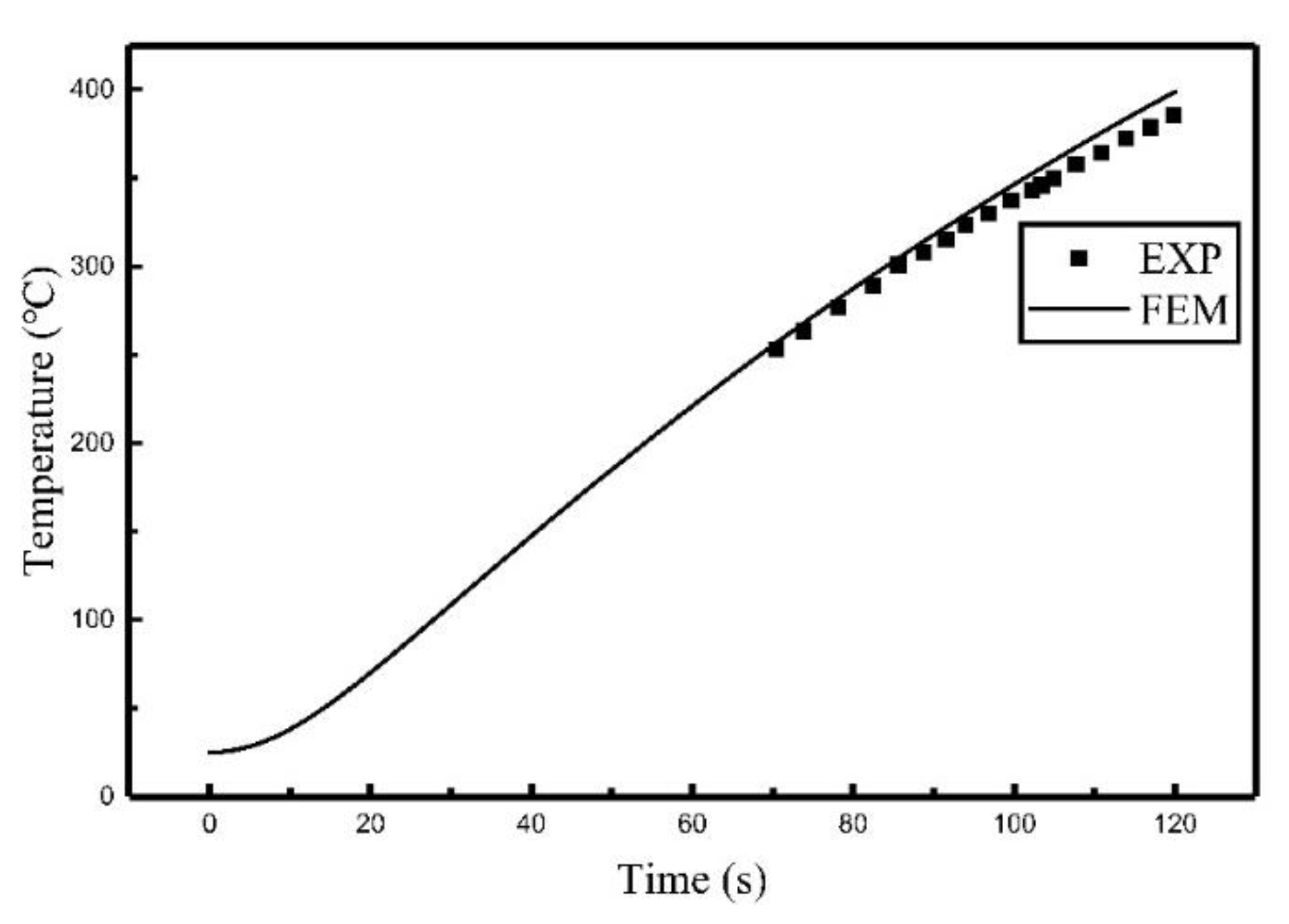
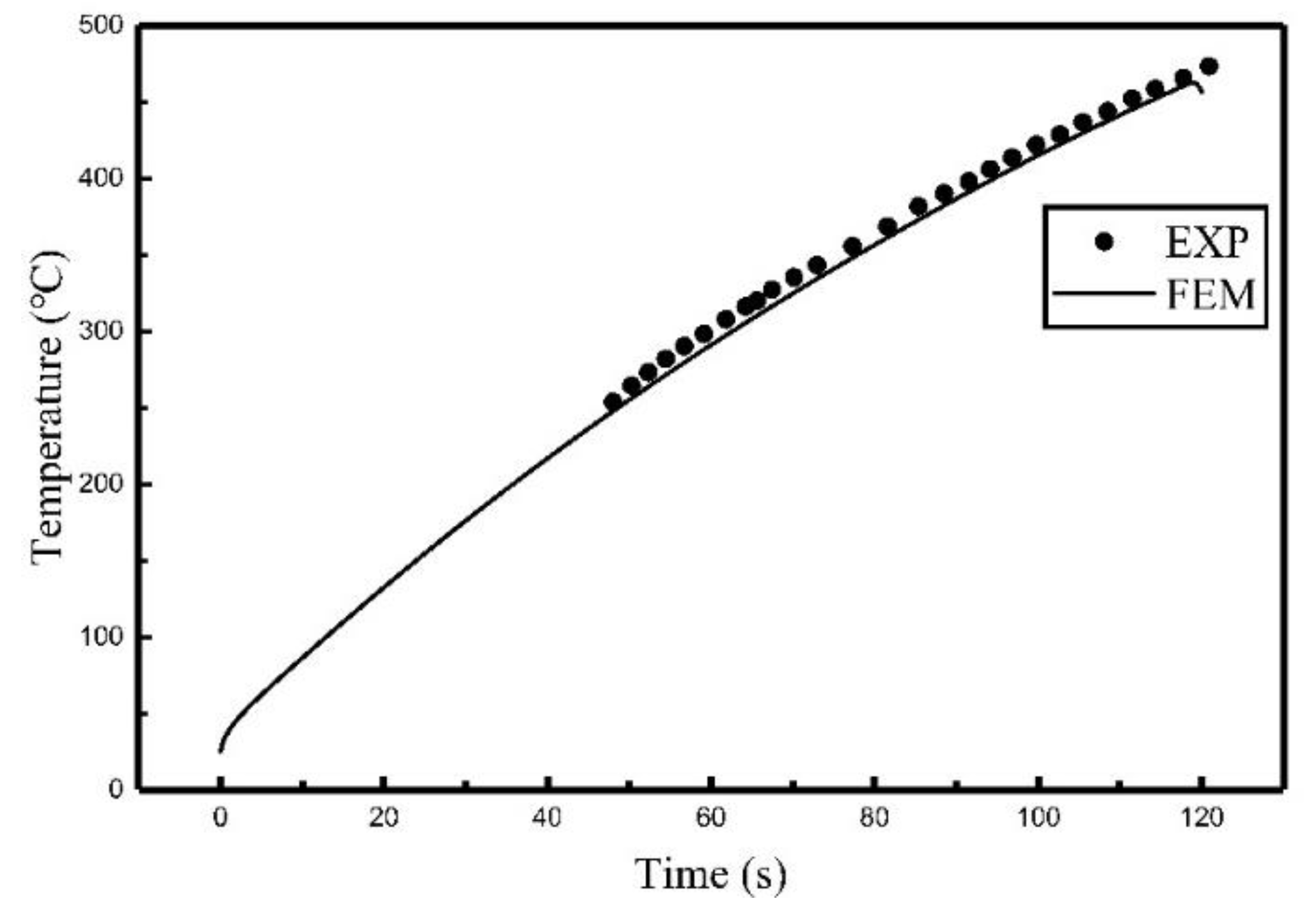
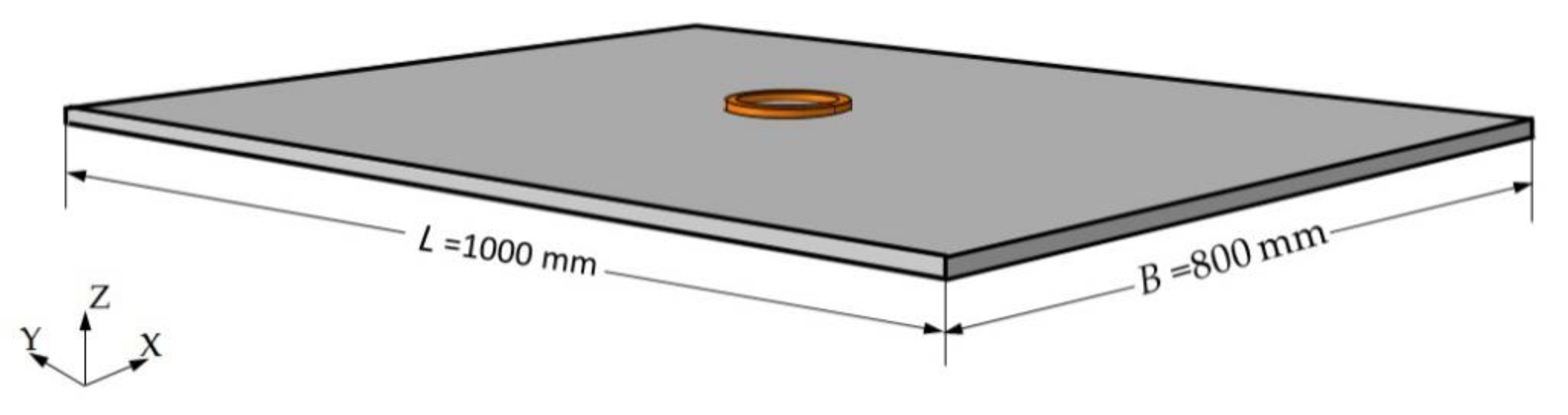
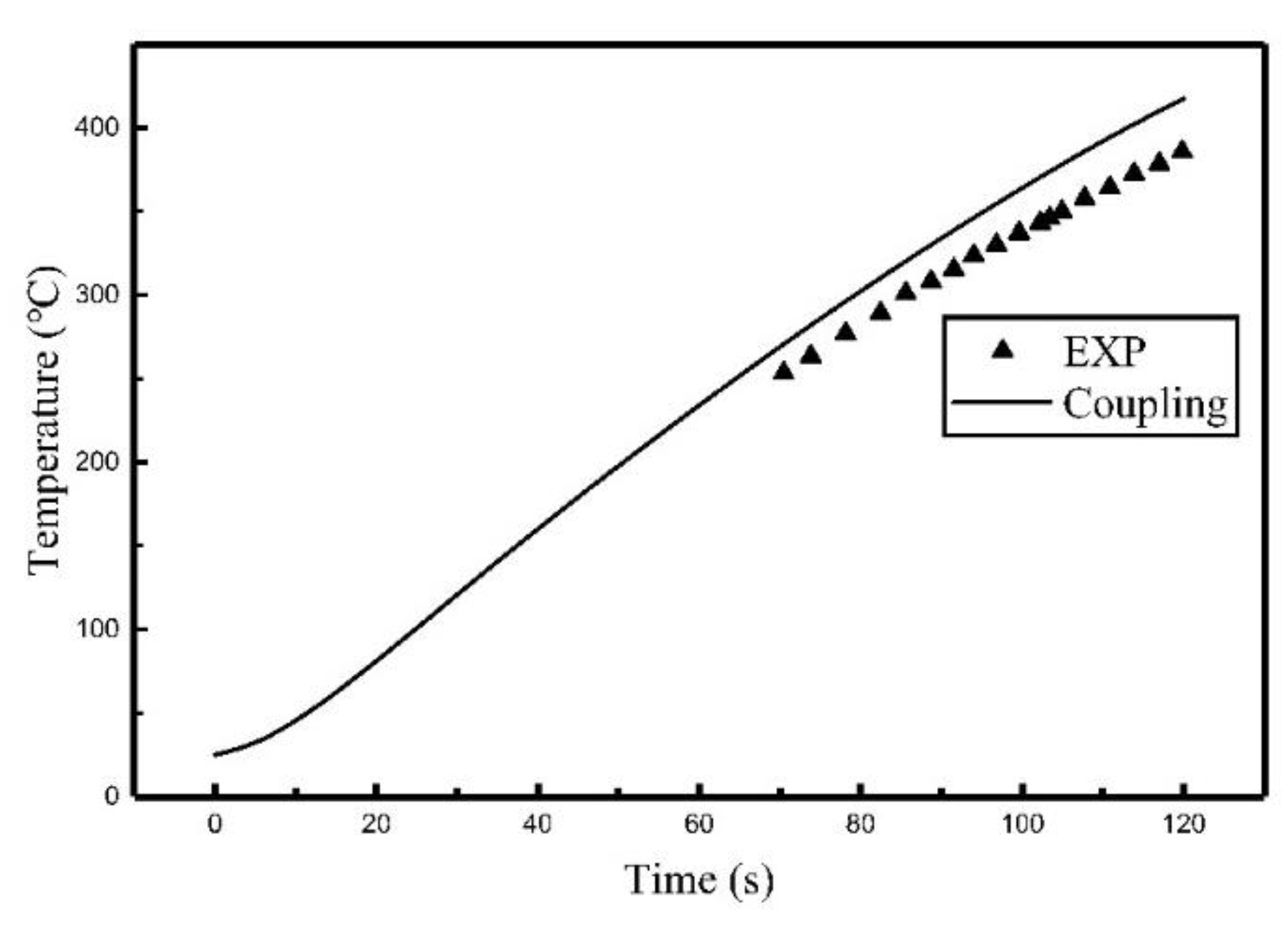
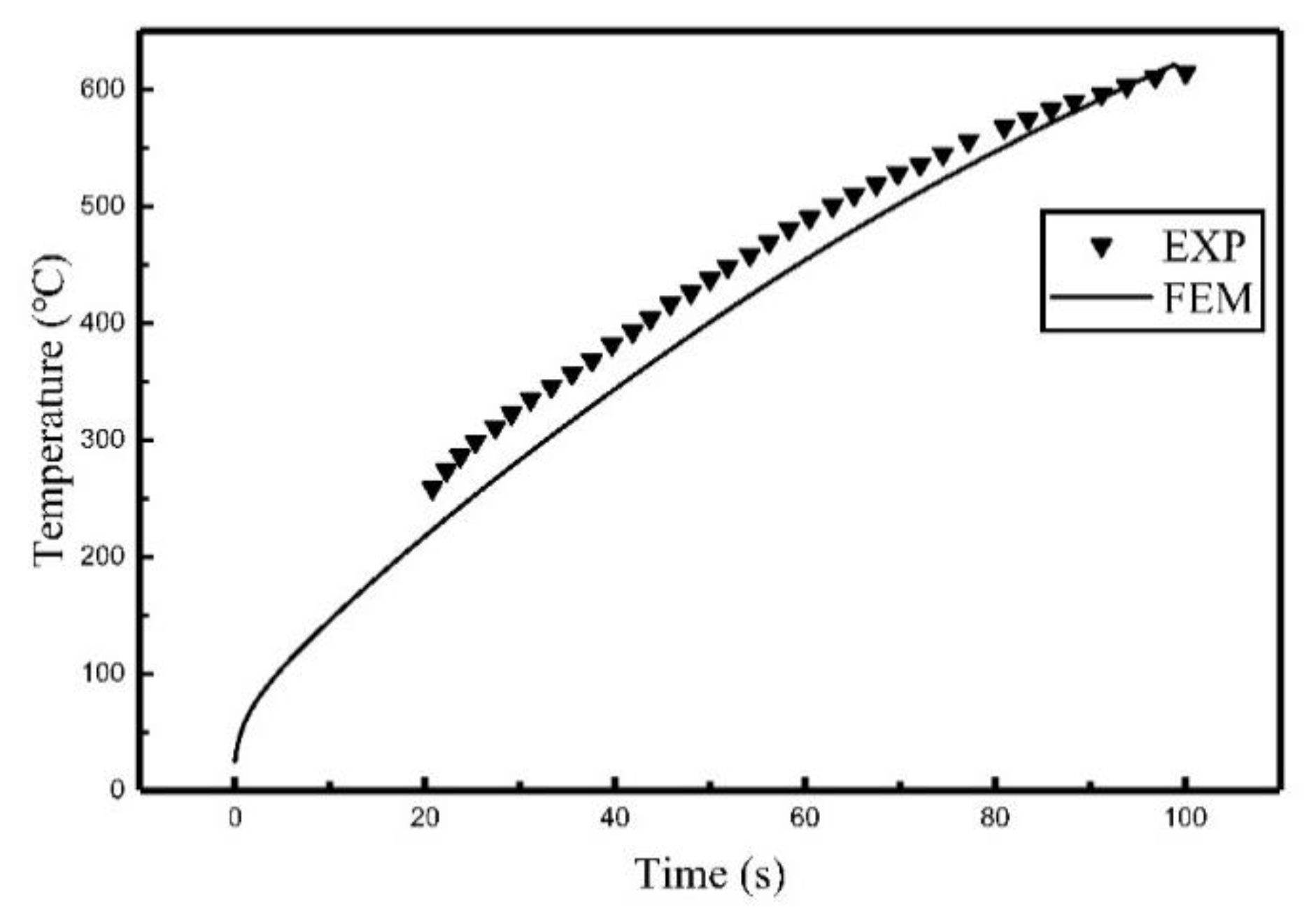
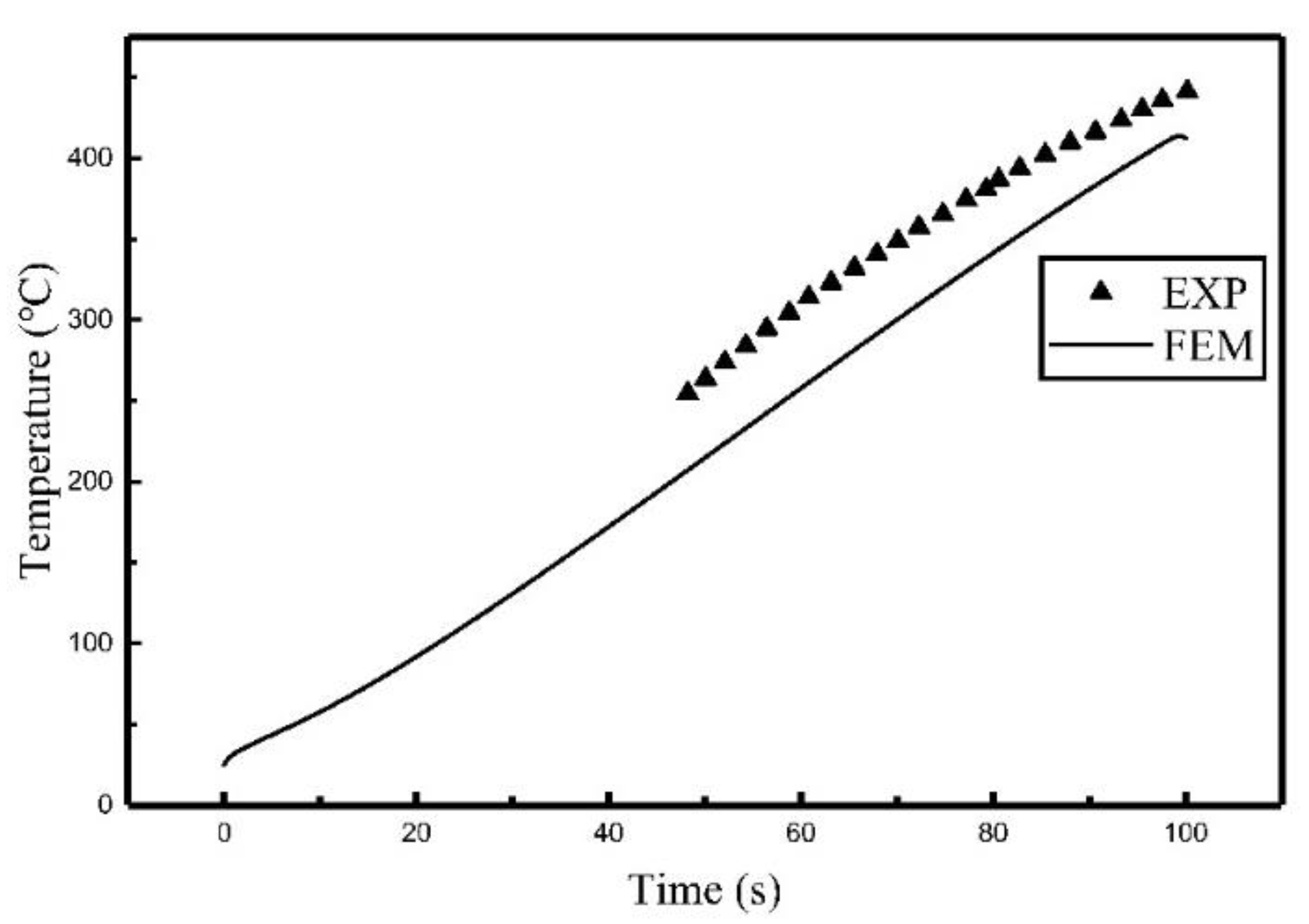
3.1. Experimental Verification for Single Coil
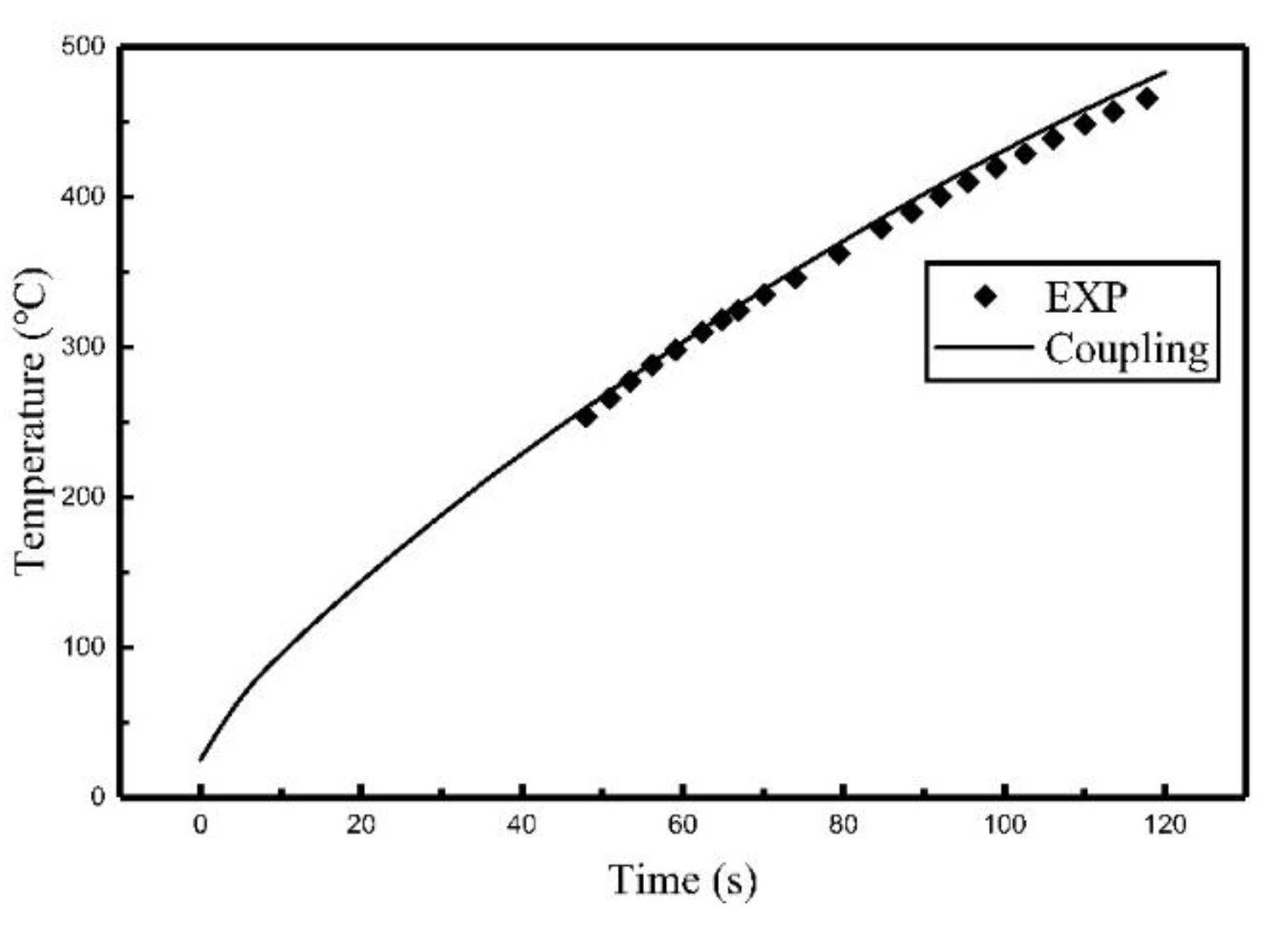
3.2. FEM Calculation and Comparison
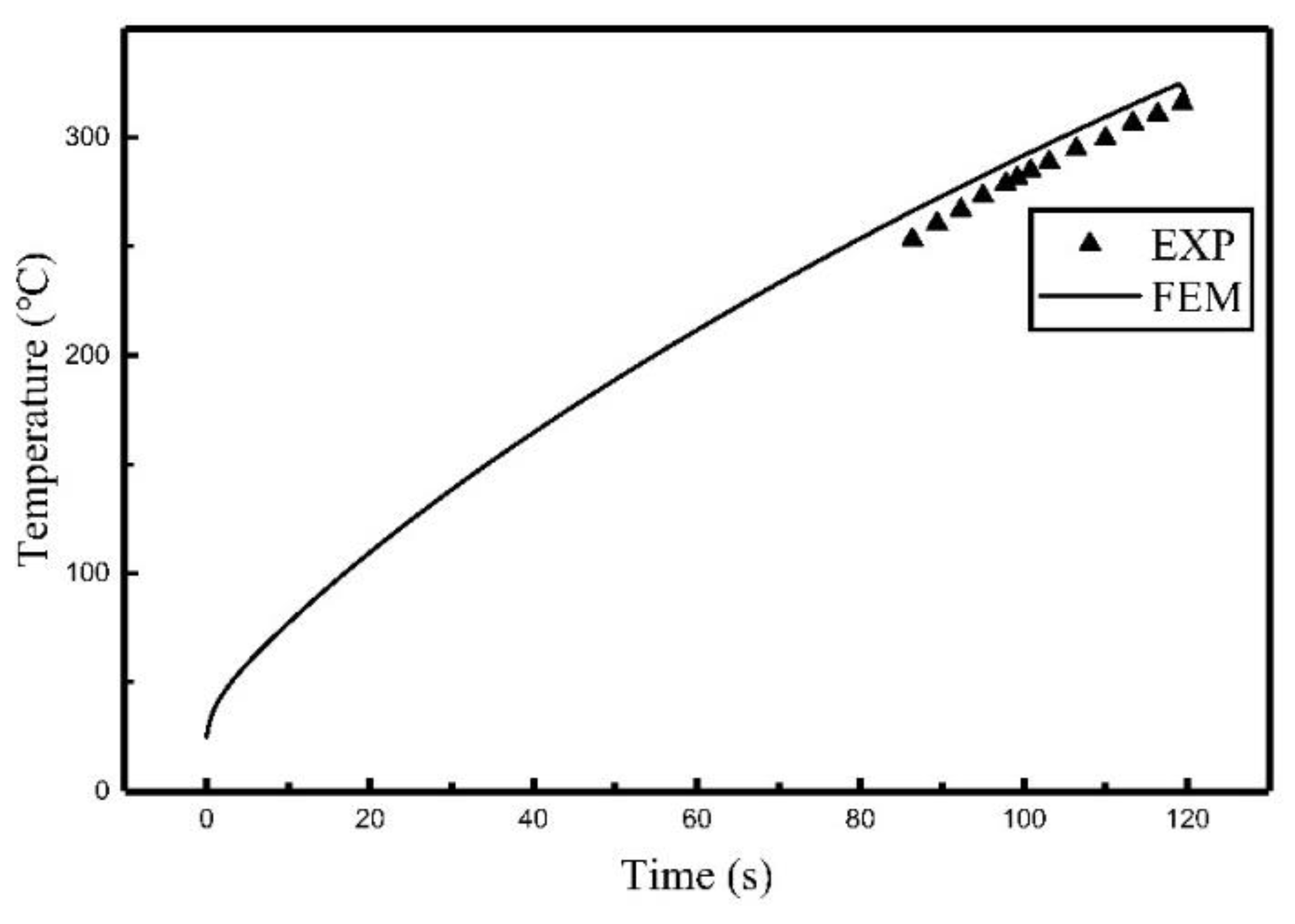
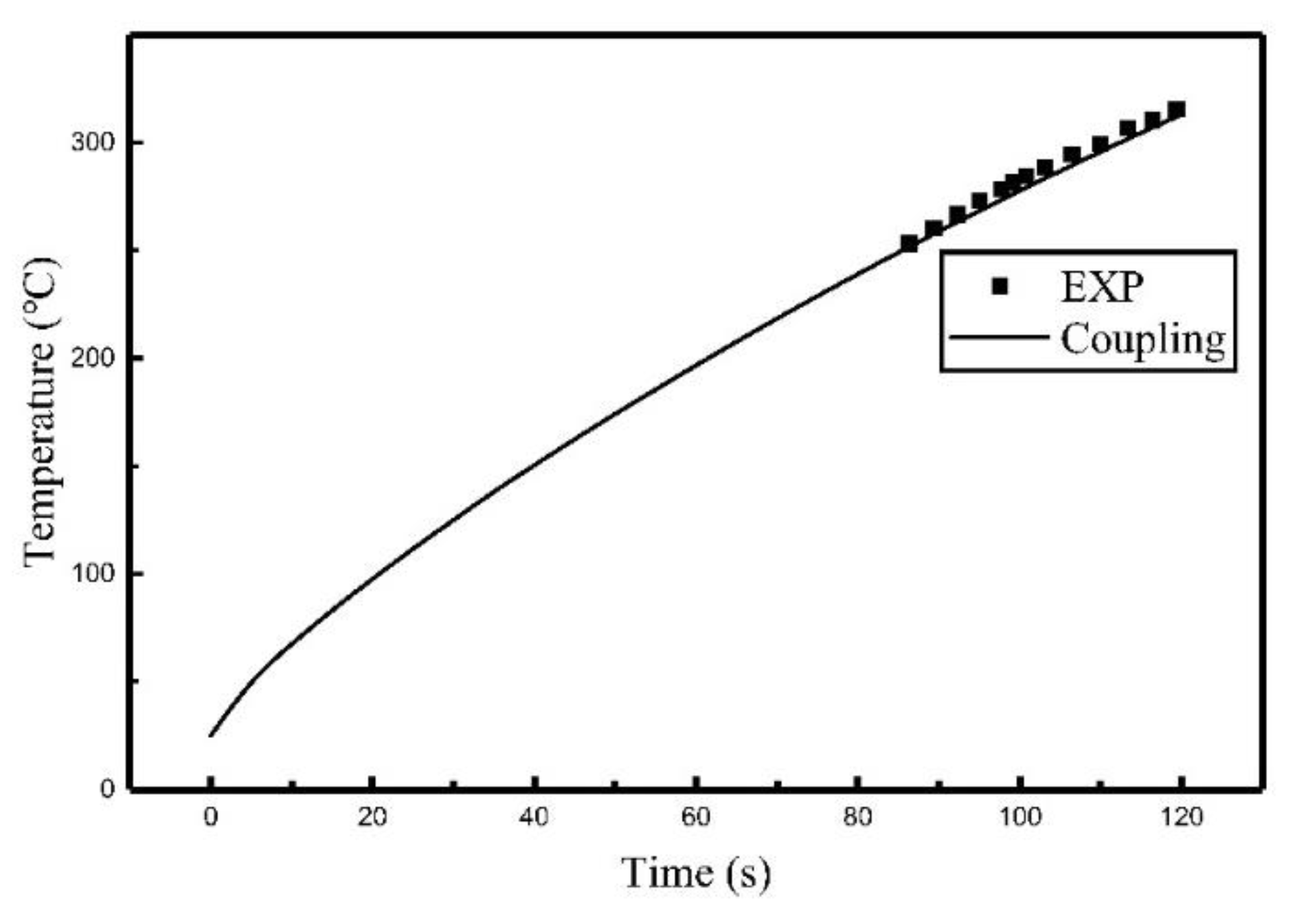
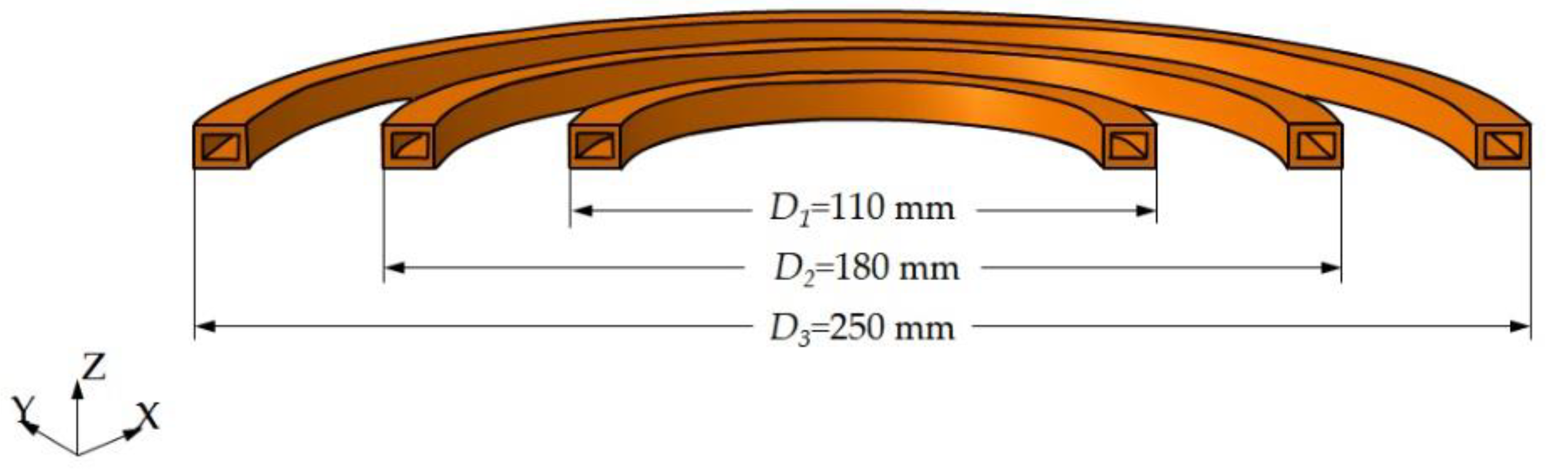
3.3. Application to Multi-Coil
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Monzel, C.; Henneberger, G. Optimizing heat source distribution for transverse flux inductive heating devices for thin strips with genetic algorithms. In Proceedings of the Power Electronics and Variable Speed Drives, London, UK, 18–19 September 2000; pp. 426–430. [Google Scholar]
- Bay, F.; Labbe, V.; Favennec, Y.; Chenot, J.L. A numerical model for induction heating processes coupling electromagnetism and thermomechanics. Int. J. Numer. Methods Eng. 2003, 58, 839–867. [Google Scholar] [CrossRef]
- Shuai, K.; Luo, Y.; Sha, W.; Xie, L. FEM Analysis of the Temperature Field of High Frequency Induction Heating in Plate Bend Molding. Boil. Technol. 2004, 35, 52–54. [Google Scholar]
- Luo, Y.; Ishiyama, M.; Murakawa, H. Study of Temperature Field and Inherent Strain Produced by High Frequency Induction Heating on Flat Plate. Trans. JWRI 2004, 33, 59–63. [Google Scholar]
- Zhou, H.; Jiang, Z.; Luo, Y.; Luo, P. Research on Hull Plate Bending Based on the Technology of High-Frequency Induction. Shipbuild. China 2014, 55, 128–138. [Google Scholar]
- Zhou, H.; Jiang, Z.; Luo, Y.; Luo, P. Influence of Thermal Properties of Plate on Its High-Frequency Induction Bending in Forming Ship Hulls. Shipbuild. China 2015, 56, 101–108. [Google Scholar]
- Liu, F.; Shi, Y.; Lei, X. Numerical investigation of the temperature field of a metal plate during high-frequency induction heat forming. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 223, 979–986. [Google Scholar] [CrossRef]
- Hu, X. A Study on Heating Source Model and Deformation Law for Line Heating by High Frequency Induction Based on Numerical Experiment. Master’s Thesis, Dalian University of Technology, Dalian, China, November 2008. [Google Scholar]
- Zhang, X.; Yang, Y.; Liu, Y. Feasibility research on application of a high frequency induction heat to line heating technology. J. Mar. Sci. Appl. 2011, 10, 456–464. [Google Scholar] [CrossRef]
- Bae, K.Y.; Yang, Y.S.; Hyun, C.M. Analysis of Triangle Heating Technique using High Frequency Induction Heating in Forming Process of Steel Plate. Int. J. Precis. Eng. Manuf. 2012, 13, 539–545. [Google Scholar] [CrossRef]
- Jeong, C.M.; Yang, Y.S.; Bae, K.Y.; Hyun, C.M. Prediction of deformation of steel plate with forced displacement and initial curvature in a forming process with high frequency induction heating. Int. J. Precis. Eng. Manuf. 2013, 14, 785–790. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, H.; Wang, G. Modeling of the moving induction heating used as secondary heat source in weld-based additive manufacturing. Int. J. Adv. Manuf. Technol. 2014, 77, 717–727. [Google Scholar] [CrossRef]
- Kubota, H.; Tomizawa, A.; Yamamoto, K.; Okada, N.; Hama, T.; Takuda, H. Finite Element Analysis of Three-Dimensional Hot Bending and Direct Quench Process Considering Phase Transformation and Temperature Distribution by Induction Heating. ISIJ Int. 2014, 54, 1856–1865. [Google Scholar] [CrossRef]
- Yang, S. Research on Heat Source Model and Numerical Simulation of High Frequency Induction Heating Forming. Dev. Appl. Mater. 2015, 30, 20–23. [Google Scholar]
- Li, J. Numerical Studies on the Induction Quenching Process of Crankshaft. Doctor’s Thesis, Beijing Institute of Technology, Beijing, China, January 2015. [Google Scholar]
- Aung, M.P.; Nakamura, M.; Hirohata, M. Characteristics of Residual Stresses Generated by Induction Heating on Steel Plates. Metals 2018, 8, 25. [Google Scholar] [CrossRef]
- Riccio, A.; Russo, A.; Raimondo, A.; Cirillo, P.; Caraviello, A. A numerical/experimental study on the induction heating of adhesives for composite materials bonding. Mater. Today Commun. 2018, 15, 203–213. [Google Scholar] [CrossRef]
- Bao, L.; Qi, X.W.; Mei, R.B.; Zhang, X.; Li, G.L. Investigation and modeling of work roll temperature in induction heating by finite element method. J. S. Afr. Inst. Min. Met. 2018, 118, 735–743. [Google Scholar]
- Li, F.; Li, X.K.; Qin, X.F.; Rong, Y. Study on the plane induction heating process strengthened by magnetic flux concentrator based on response surface methodology. J. Mech. Sci. Technol. 2018, 32, 2347–2356. [Google Scholar] [CrossRef]
- Sun, R.; Shi, Y.J.; Pei, Z.F.; Li, Q.; Wang, R.H. Heat transfer and temperature distribution during high-frequency induction cladding of 45 steel plate. Appl. Therm. Eng. 2018, 139, 1–10. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Hu, X.; Yang, Z. Simplified calculation method for high frequency induction heating source of ship plate. Chin. J. Ship Res. 2018, 5, 18–24. [Google Scholar]
- Li, Y. Steel Structure Welding Residual Stress Analysis. Master’s Thesis, Wuhan University of Technology, Wuhan, China, April 2007. [Google Scholar]

| Temperature (°C) | Density (kg/m3) | Specific Heat (J/(kg·°C)) | Heat Conductivity Coefficient (W/(m·°C)) |
|---|---|---|---|
| 0 | 7842 | 450.36 | 66.97 |
| 50 | - | 464.6 | 65.21 |
| 200 | 7822 | 498.1 | 57.38 |
| 250 | - | 502.26 | 54.91 |
| 300 | - | 514.82 | 53 |
| 400 | 7802 | 537.42 | 47.92 |
| 450 | - | 623.64 | 45.83 |
| 500 | - | 707.35 | 43.53 |
| 600 | 7782 | 812 | 39.3 |
| 650 | - | 904.07 | 36.37 |
| 700 | - | 967.69 | 34.74 |
| 800 | 7761 | 1026.32 | 31.02 |
| Temperature (°C) | Young‘s Modulus (GPa) | Poisson Ratio | Heat Expansion Coefficient (1/°C) | Yield Strength (MPa) |
|---|---|---|---|---|
| 0 | 206 | 0.267 | 1.20 × 10−5 | 235 |
| 50 | 196 | 0.29 | 1.25 × 10−5 | - |
| 200 | 196 | 0.322 | 1.40 × 10−5 | 163 |
| 250 | 186 | 0.296 | 1.43 × 10−5 | - |
| 300 | 186 | 0.262 | 1.47 × 10−5 | - |
| 400 | 166 | 0.24 | 1.54 × 10−5 | 130 |
| 450 | 157 | 0.229 | 1.57 × 10−5 | - |
| 500 | 157 | 0.223 | 1.59 × 10−5 | - |
| 600 | 135 | 0.223 | 1.64 × 10−5 | 119 |
| 650 | 117 | 0.223 | 1.66 × 10−5 | - |
| 700 | 112 | 0.223 | 1.67 × 10−5 | - |
| 800 | 113 | 0.223 | 1.69 × 10−5 | 109 |
| Sensor | Maximum Relative Error | Average Relative Error | Minimum Relative Error |
|---|---|---|---|
| C1 | 3.55% | 2.43% | 1.15% |
| C2 | 3.84% | 2.42% | 1.16% |
| C3 | 5.42% | 3.64% | 2.46% |
| Sensor | Maximum Relative Error | Average Relative Error | Minimum Relative Error |
|---|---|---|---|
| C1 | 8.65% | 7.55% | 6.38% |
| C2 | 2.71% | 1.68% | 0.50% |
| C3 | 1.61% | 1.17% | 0.27% |
| Number of Degrees of Freedom | Computation Time/Min | |
|---|---|---|
| Full-coupling model | 230,917 | 6.7 |
| Heat source model | 86,399 | 3.7 |
| Sensor | Maximum Relative Error | Average Relative Error | Minimum Relative Error |
|---|---|---|---|
| C2 | 18.63% | 12.72% | 4.82% |
| C3 | 15.42% | 7.65% | 0.15% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Zhao, Y.; Yuan, H.; Hu, X.; Yang, Z. A Simplified Calculation Method of Heat Source Model for Induction Heating. Materials 2019, 12, 2938. https://doi.org/10.3390/ma12182938
Dong H, Zhao Y, Yuan H, Hu X, Yang Z. A Simplified Calculation Method of Heat Source Model for Induction Heating. Materials. 2019; 12(18):2938. https://doi.org/10.3390/ma12182938
Chicago/Turabian StyleDong, Hongbao, Yao Zhao, Hua Yuan, Xiaocai Hu, and Zhen Yang. 2019. "A Simplified Calculation Method of Heat Source Model for Induction Heating" Materials 12, no. 18: 2938. https://doi.org/10.3390/ma12182938
APA StyleDong, H., Zhao, Y., Yuan, H., Hu, X., & Yang, Z. (2019). A Simplified Calculation Method of Heat Source Model for Induction Heating. Materials, 12(18), 2938. https://doi.org/10.3390/ma12182938





