Constitutive Modeling of the Tensile Behavior of Recycled Polypropylene-Based Composites
Abstract
1. Introduction
2. Experimental Study
2.1. Materials and Processing
2.2. Experimental Procedures
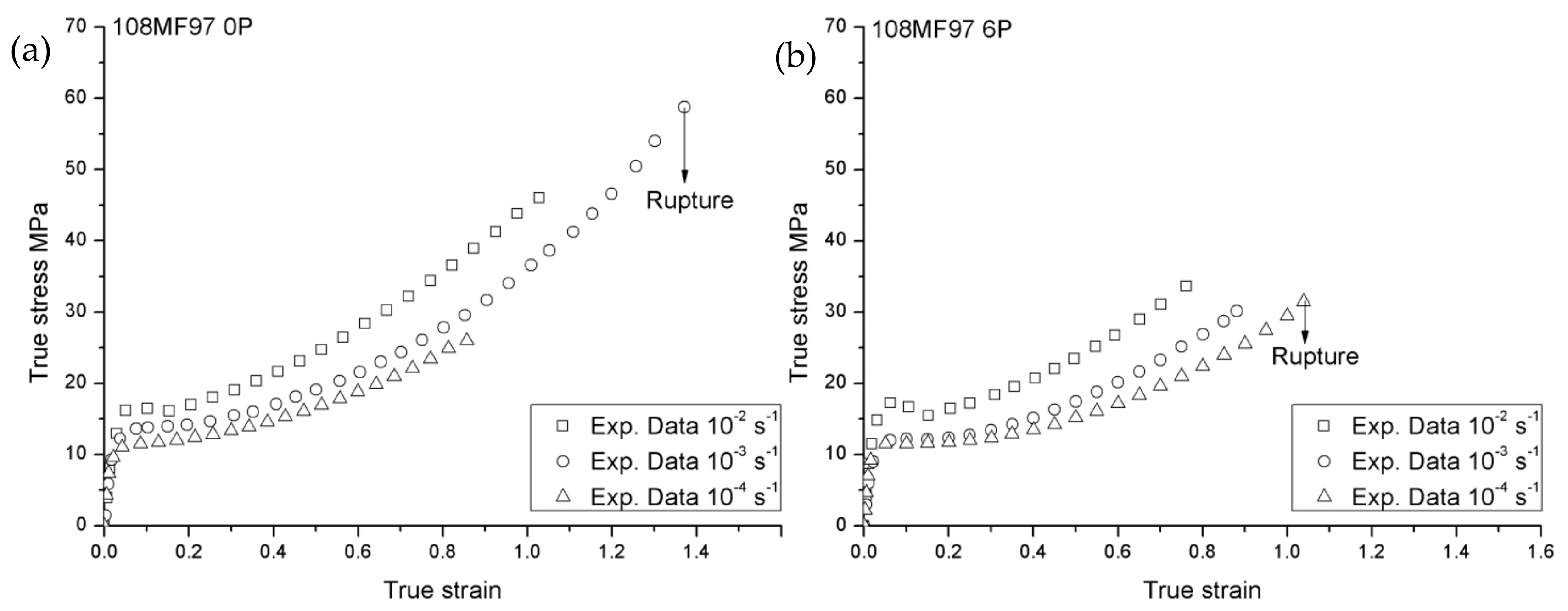
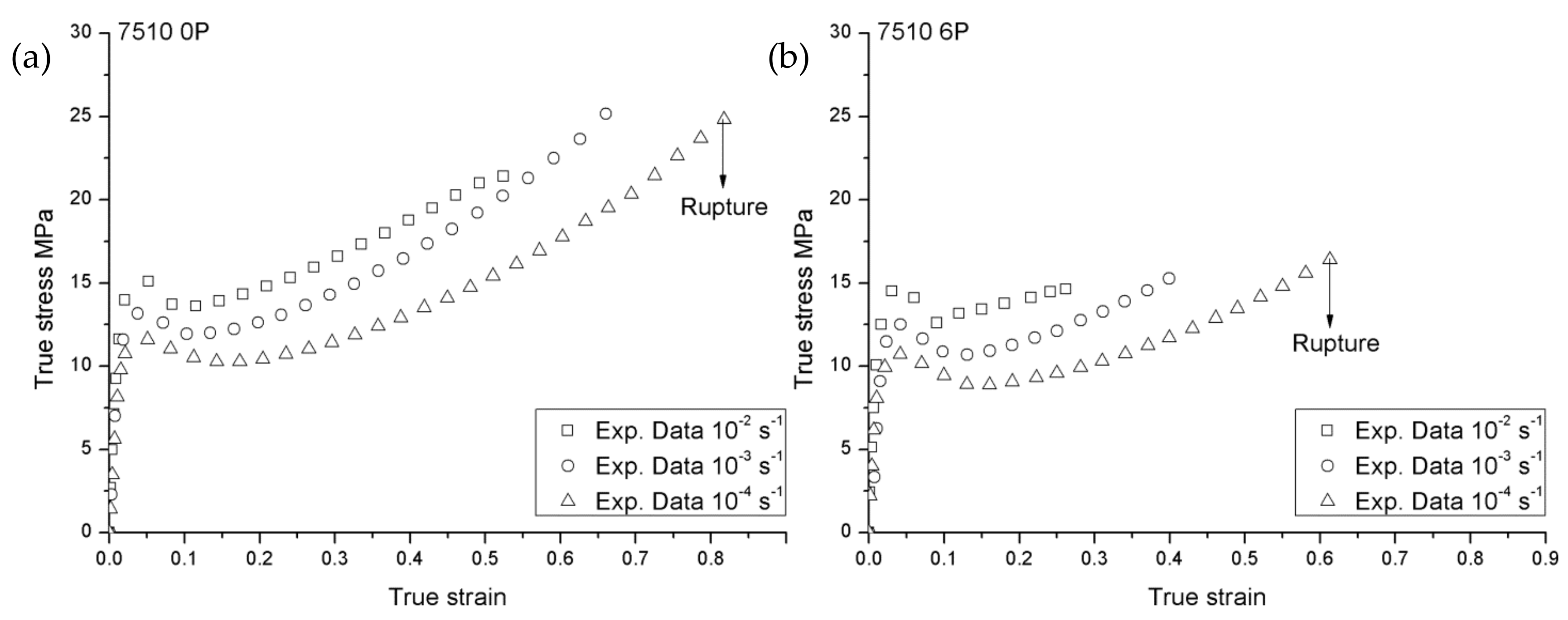
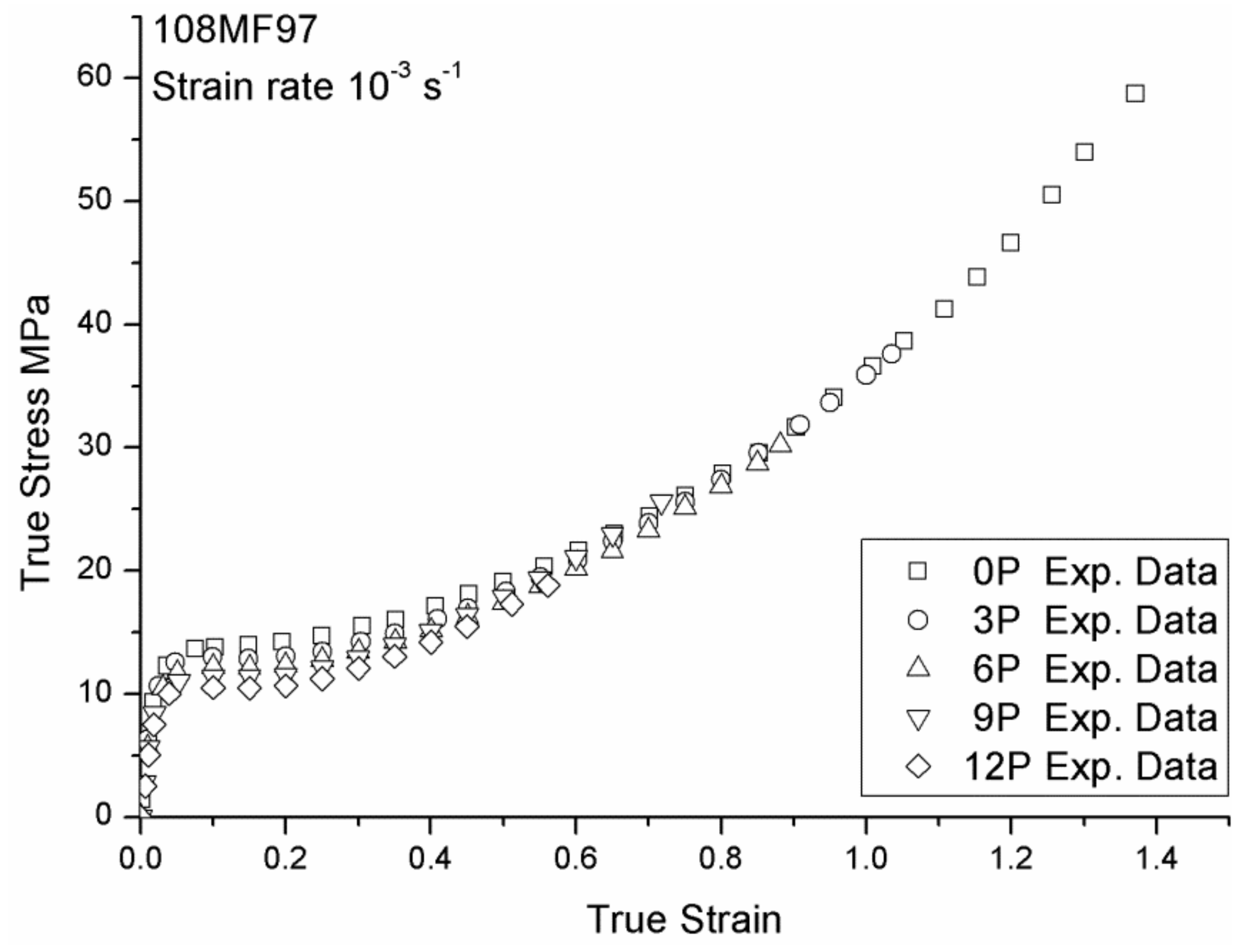
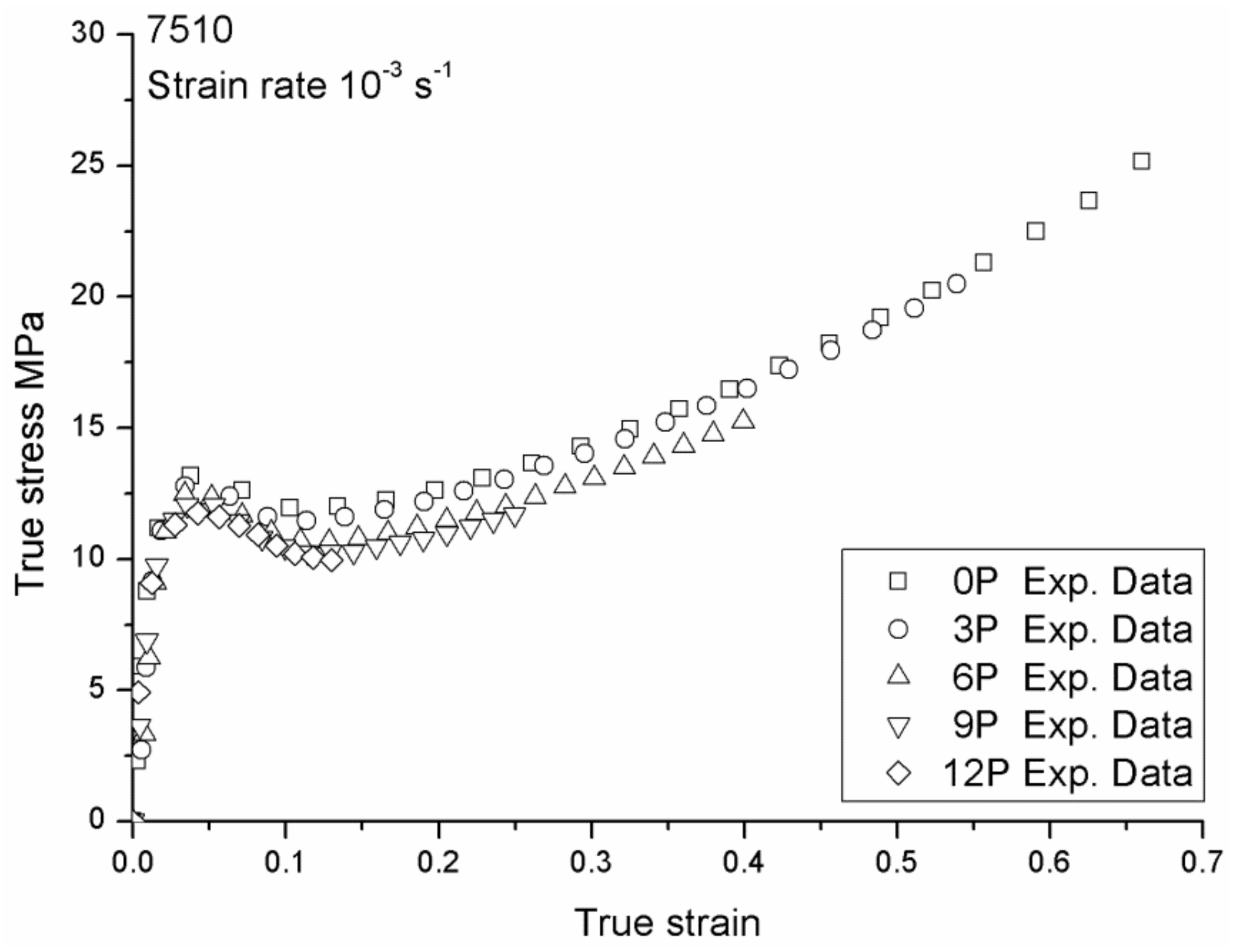
2.3. Experimental Results
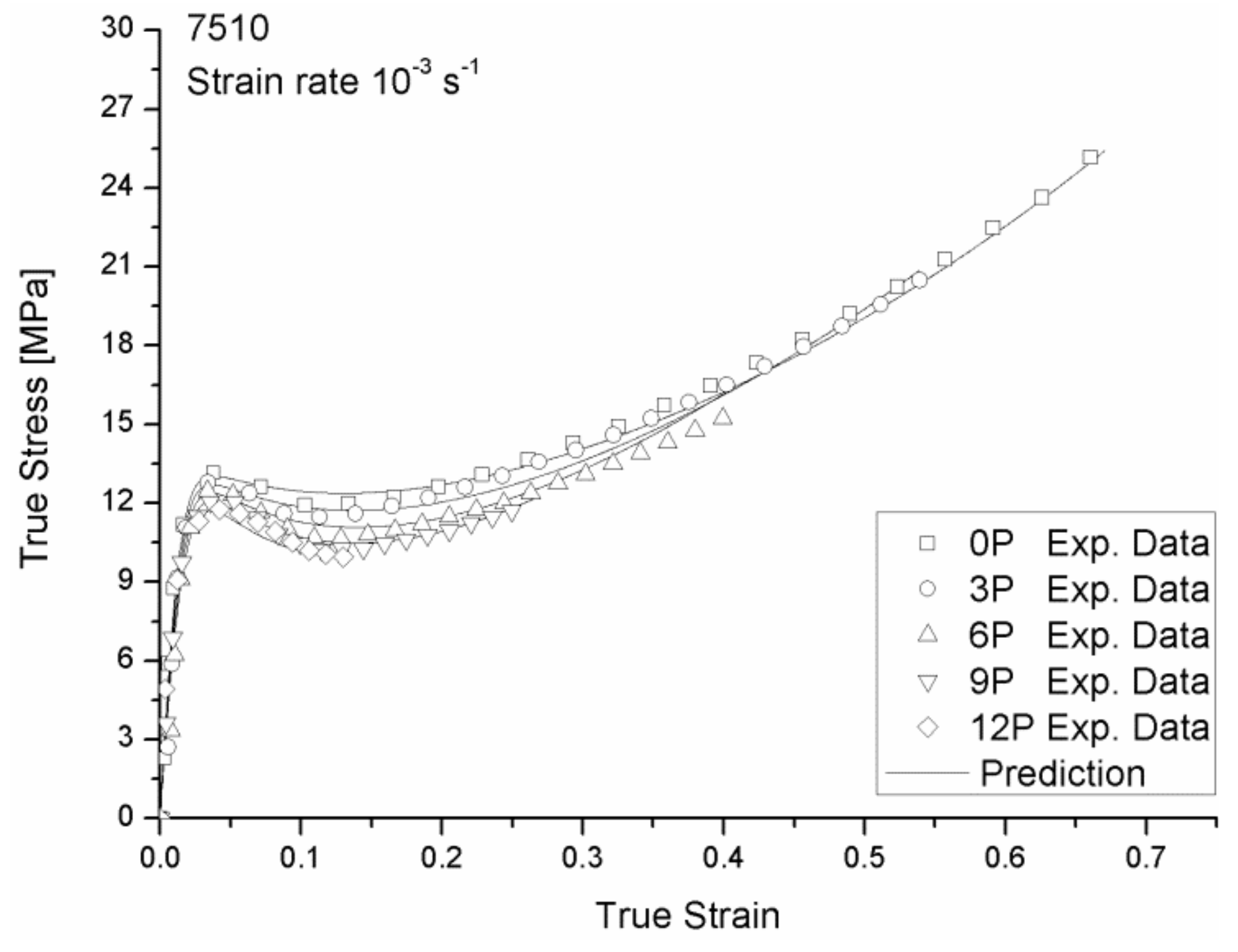
3. Constitutive Relation
3.1. Strain Rate Dependent of Young’s Modulus and Failure Strain
3.2. Flow Rule
3.3. Strain Softening
3.4. Orientational Hardening
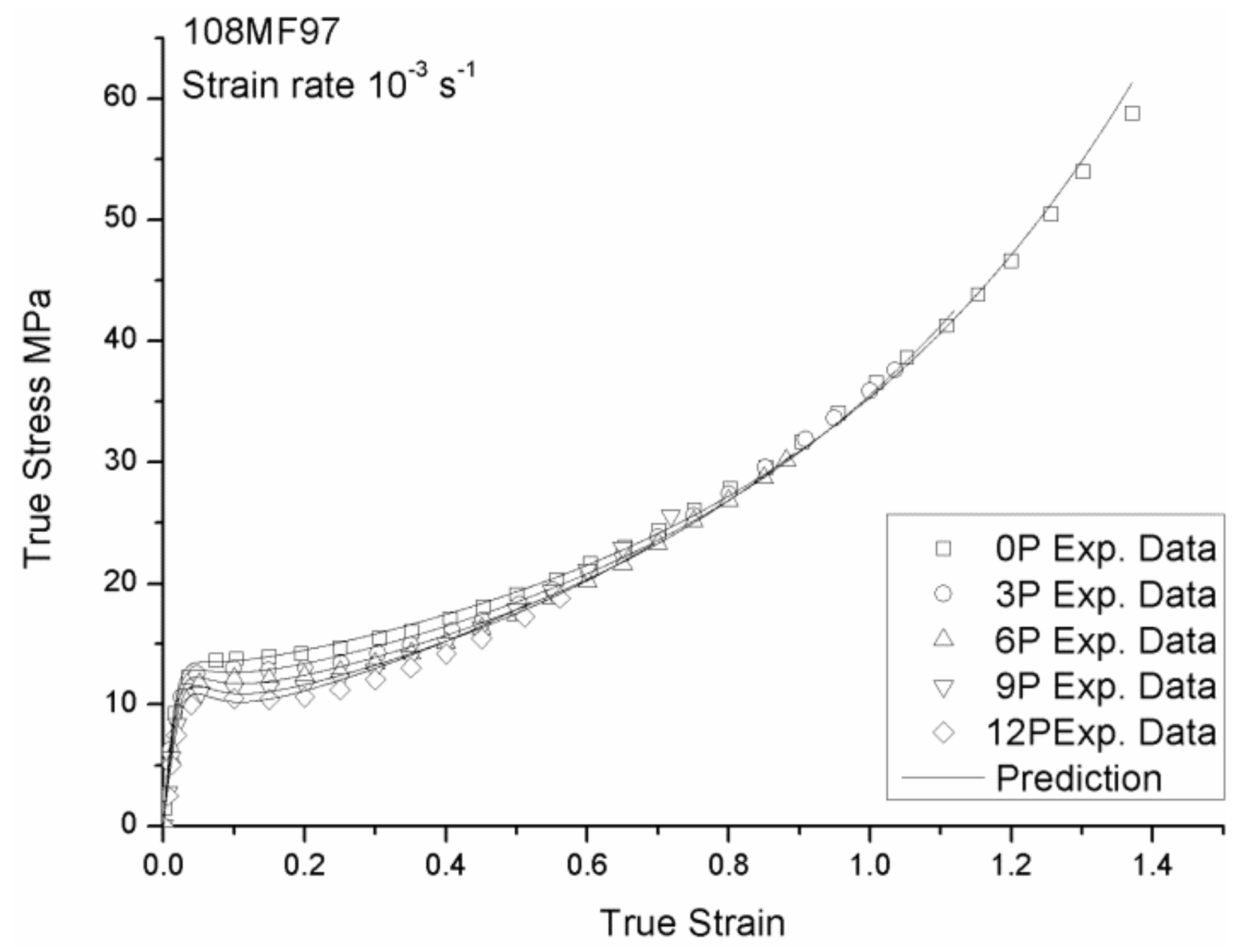
3.5. Recycling Effect
4. Constitutive Modeling
4.1. Kinematics of Finite Strain
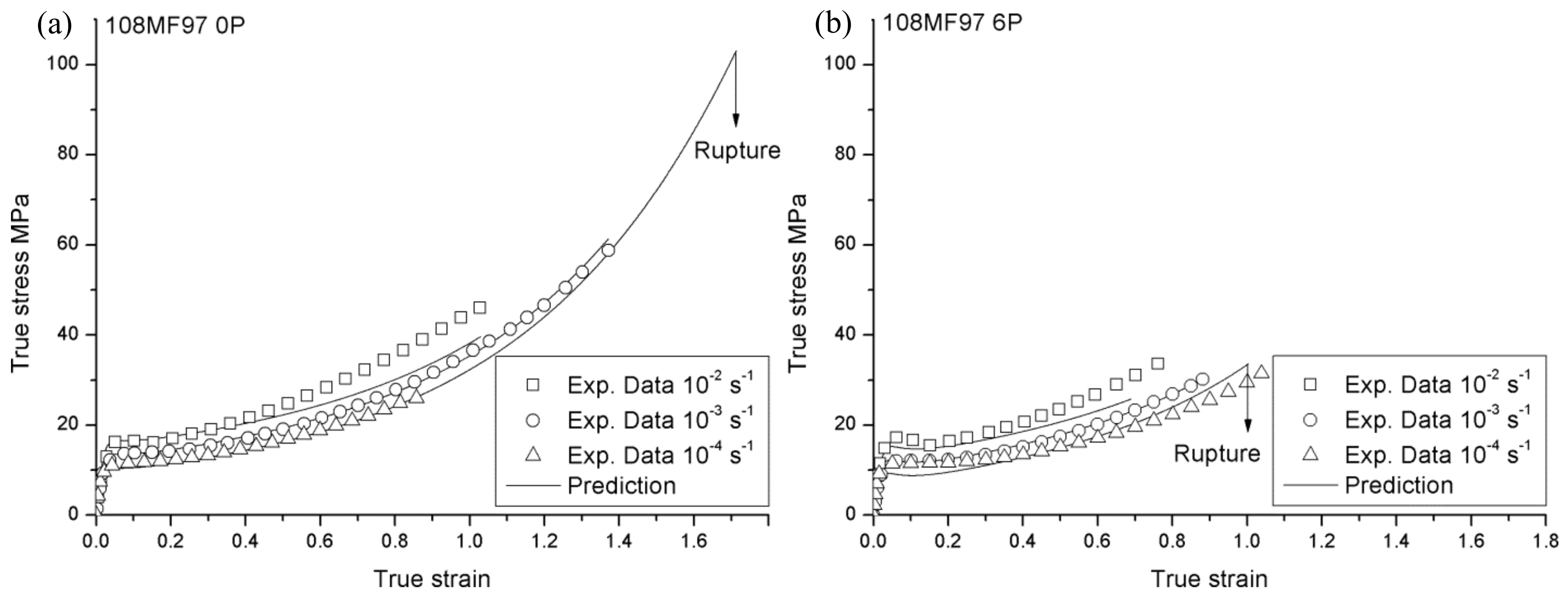
4.2. Modeling Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chirayil, C.J.; Joy, J.; Maria, H.J.; Krupa, I.; Thomas, S. Polyolefins in automotive industry. In Polyolefin Compounds and Materials; Springer: Cham, Switzerland, 2016; pp. 265–283. [Google Scholar]
- Chow, W.S. Polypropylene blends: Properties control by design. In Polypropylene Handbook; Springer: Cham, Switzerland, 2019; pp. 419–480. [Google Scholar]
- Wu, J.H.; Chen, C.W.; Wu, Y.T.; Wu, G.T.; Kuo, M.; Tsai, Y. Mechanical properties, morphology, and crystallization behavior of polypropylene/elastomer/talc composites. Polym. Compos. 2015, 36, 69–77. [Google Scholar] [CrossRef]
- Sardon, H.; Dove, A.P. Plastics recycling with a difference. Science 2018, 360, 380–381. [Google Scholar] [CrossRef] [PubMed]
- Bahlouli, N.; Pessey, D.; Raveyre, C.; Guillet, J.; Ahzi, S.; Dahoun, A.; Hiver, J.M. Recycling effects on the rheological and thermomechanical properties of polypropylene-based composites. Mater. Des. 2012, 33, 451–458. [Google Scholar] [CrossRef]
- Stan, F.; Sandu, L.I.; Fetecau, C.; Rosculet, R. Effect of reprocessing on the rheological, electrical, and mechanical properties of polypropylene/carbon nanotube composites. J. Micro Nano Manuf. 2017, 5, 021005. [Google Scholar] [CrossRef]
- Martín-Alfonso, J.; Franco, J. Influence of polymer reprocessing cycles on the microstructure and rheological behavior of polypropylene/mineral oil oleogels. Polym. Test. 2015, 45, 12–19. [Google Scholar] [CrossRef]
- Soccalingame, L.; Perrin, D.; Bénézet, J.-C.; Mani, S.; Coiffier, F.; Richaud, E.; Bergeret, A. Reprocessing of artificial UV-weathered wood flour reinforced polypropylene composites. Polym. Degrad. Stab. 2015, 120, 313–327. [Google Scholar] [CrossRef]
- Spicker, C.; Rudolph, N.; Kühnert, I.; Aumnate, C. The use of rheological behavior to monitor the processing and service life properties of recycled polypropylene. J. Food Packag. Shelf 2019, 19, 174–183. [Google Scholar] [CrossRef]
- Da Costa, H.M.; Ramos, V.D.; De Oliveira, M.G. Degradation of polypropylene (PP) during multiple extrusions: Thermal analysis, mechanical properties and analysis of variance. Polym. Test. 2007, 26, 676–684. [Google Scholar] [CrossRef]
- Martins, M.H.; De Paoli, M.A. Polypropylene compounding with post-consumer material: II. Reprocessing. Polym. Degrad. Stab. 2002, 78, 491–495. [Google Scholar] [CrossRef]
- Sarrionandia, M.; Lopez-Arraiza, A.; Aurrekoetxea, J.; Arostegui, A. Structure and mechanical properties of a talc-filled polypropylene/ethylene-propylene-diene composite after reprocessing in the melt state. J. Appl. Polym. Sci. 2009, 114, 1195–1201. [Google Scholar] [CrossRef]
- Jiménez, A.; Torre, L.; Kenny, J.M. Processing and properties of recycled polypropylene modified with elastomers. Plast. Rubber Compos. 2003, 32, 357–367. [Google Scholar] [CrossRef]
- Wang, K.; Addiego, F.; Bahlouli, N.; Ahzi, S.; Rémond, Y.; Toniazzo, V.; Muller, R. Analysis of thermomechanical reprocessing effects on polypropylene/ethylene octene copolymer blends. Polym. Degrad. Stab. 2012, 97, 1475–1484. [Google Scholar] [CrossRef]
- Wang, K.; Bahlouli, N.; Addiego, F.; Ahzi, S.; Rémond, Y.; Ruch, D.; Muller, R. Effect of talc content on the degradation of re-extruded polypropylene/talc composites. Polym. Degrad. Stab. 2013, 98, 1275–1286. [Google Scholar] [CrossRef]
- Wang, K.; Addiego, F.; Bahlouli, N.; Ahzi, S.; Rémond, Y.; Toniazzo, V. Impact response of recycled polypropylene-based composites under a wide range of temperature: Effect of filler content and recycling. Compos. Sci. Technol. 2014, 95, 89–99. [Google Scholar] [CrossRef]
- Wang, K.; Bahlouli, N.; Addiego, F.; Ahzi, S. Elastic and yield behaviors of recycled polypropylene-based composites: Experimental and modeling study. Compos. Part B Eng. 2016, 99, 132–153. [Google Scholar] [CrossRef]
- Addiego, F.; Dahoun, A.; G’Sell, C.; Hiver, J.-M. Characterization of volume strain at large deformation under uniaxial tension in high-density polyethylene. Polymer 2006, 47, 4387–4399. [Google Scholar] [CrossRef]
- Wang, K.; Boumbimba, R.M.; Bahlouli, N.; Ahzi, S.; Muller, R.; Bouquey, M. Dynamic behaviour of a melt mixing polypropylene organoclay nanocomposites. J. Eng. Mater. Technol. 2012, 134, 010905. [Google Scholar] [CrossRef]
- Wang, Y.; Arruda, E.M. Constitutive modeling of a thermoplastic olefin over a broad range of strain rates. J. Eng. Mater. Technol. 2006, 128, 551–558. [Google Scholar] [CrossRef]
- Ahzi, S.; Ganesan, A.; Arruda, E. Modeling and simulation of deformation texture in semi-crystalline polymers: Application to polypropylene and nylon-6. In Materials Science Forum; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2002; pp. 1723–1728. [Google Scholar]
- Gensler, R.; Plummer, C.J.G.; Grein, C.; Kausch, H.H. Influence of the loading rate on the fracture resistance of isotactic polypropylene and impact modified isotactic polypropylene. Polymer 2000, 41, 3809–3819. [Google Scholar] [CrossRef]
- Wu, Z.; Ahzi, S.; Arruda, E.; Makradi, A. Modeling the large inelastic deformation response of non-filled and silica filled SL5170 cured resin. J. Mater. Sci. 2005, 40, 4605–4612. [Google Scholar] [CrossRef][Green Version]
- Zhou, Y.; Rangari, V.; Mahfuz, H.; Jeelani, S.; Mallick, P.K. Experimental study on thermal and mechanical behavior of polypropylene, talc/polypropylene and polypropylene/clay nanocomposites. Mater. Sci. Eng. A Struct. 2005, 402, 109–117. [Google Scholar] [CrossRef]
- Boyce, M.C.; Parks, D.M.; Argon, A.S. Large inelastic deformation of glassy polymers. Part I: Rate dependent constitutive model. Mech. Mater. 1988, 7, 15–33. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Boumbimba, R.M.; Wang, K.; Hablot, E.; Bahlouli, N.; Ahzi, S.; Avérous, L. Renewable biocomposites based on cellulose fibers and dimer fatty acid polyamide: Experiments and modeling of the stress–strain behavior. Polym. Eng. Sci. 2017, 57, 95–104. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C.; Jayachandran, R. Effects of strain rate, temperature and thermomechanical coupling on the finite strain deformation of glassy polymers. Mech. Mater. 1995, 19, 193–212. [Google Scholar] [CrossRef]
- Teegarden, D.M. Polymer Chemistry: Introduction to an Indispensable Science; Illustrated edition; National Science Teachers Association: Arlington, VA, USA, 2004; p. 280. [Google Scholar]
- Richeton, J.; Ahzi, S.; Vecchio, K.S.; Jiang, F.C.; Makradi, A. Modeling and validation of the large deformation inelastic response of amorphous polymers over a wide range of temperatures and strain rates. Int. J. Solids Struct. 2007, 44, 7938–7954. [Google Scholar] [CrossRef]
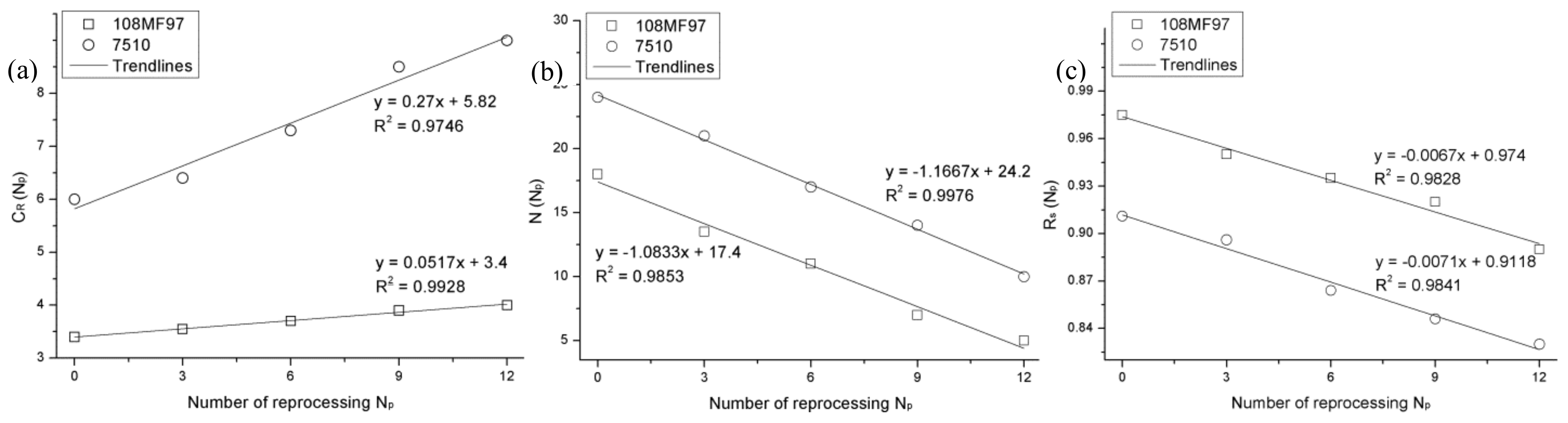

| Np | E (MPa) | εR | CR | N | Rs | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 108MF97 | 7510 | 108MF97 | 7510 | 108MF97 | 7510 | 108MF97 | 7510 | 108MF97 | 7510 | |
| 0 | 850 | 1100 | 1.37 | 0.66 | 3.4 | 6 | 18 | 24 | 0.975 | 0.911 |
| 3 | 790 | 1050 | 1.04 | 0.54 | 3.55 | 6.4 | 13.5 | 21 | 0.95 | 0.896 |
| 6 | 730 | 1000 | 0.88 | 0.40 | 3.7 | 7.3 | 11 | 17 | 0.935 | 0.864 |
| 9 | 650 | 950 | 0.72 | 0.25 | 3.9 | 8.5 | 7 | 14 | 0.92 | 0.846 |
| 12 | 590 | 920 | 0.56 | 0.13 | 4 | 9 | 5 | 10 | 0.89 | 0.83 |
| 108MF97 | –31.11 | –0.01 | 0.05 | –1.08 | –0.01 | 977.51 | 0.34 | 3.4 | 17.4 | 0.97 | –0.001 | 0.02 | 0.019 | –0.43 |
| 7510 | –9.87 | –0.02 | 0.27 | –1.17 | –0.01 | 1250 | 0.23 | 5.82 | 24.2 | 0.91 | 0.001 | –0.001 | 0.017 | –0.28 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Peng, Y.; Matadi Boumbimba, R.; Bahlouli, N.; Pessey, D.; Ahzi, S.; Addiego, F.; Rémond, Y. Constitutive Modeling of the Tensile Behavior of Recycled Polypropylene-Based Composites. Materials 2019, 12, 2419. https://doi.org/10.3390/ma12152419
Wang K, Peng Y, Matadi Boumbimba R, Bahlouli N, Pessey D, Ahzi S, Addiego F, Rémond Y. Constitutive Modeling of the Tensile Behavior of Recycled Polypropylene-Based Composites. Materials. 2019; 12(15):2419. https://doi.org/10.3390/ma12152419
Chicago/Turabian StyleWang, Kui, Yong Peng, Rodrigue Matadi Boumbimba, Nadia Bahlouli, Daniel Pessey, Said Ahzi, Frédéric Addiego, and Yves Rémond. 2019. "Constitutive Modeling of the Tensile Behavior of Recycled Polypropylene-Based Composites" Materials 12, no. 15: 2419. https://doi.org/10.3390/ma12152419
APA StyleWang, K., Peng, Y., Matadi Boumbimba, R., Bahlouli, N., Pessey, D., Ahzi, S., Addiego, F., & Rémond, Y. (2019). Constitutive Modeling of the Tensile Behavior of Recycled Polypropylene-Based Composites. Materials, 12(15), 2419. https://doi.org/10.3390/ma12152419