Part I: The Analytical Model Predicting Post-Yield Behavior of Concrete-Encased Steel Beams Considering Various Confinement Effects by Transverse Reinforcements and Steels
Abstract
:1. Introduction
1.1. Literature Review
1.2. Motivations and Objectives in This Study; Methodology for the Prediction of Nonlinear Structural Behavior of Steel–Concrete Composite Beams
2. Materials and Methods
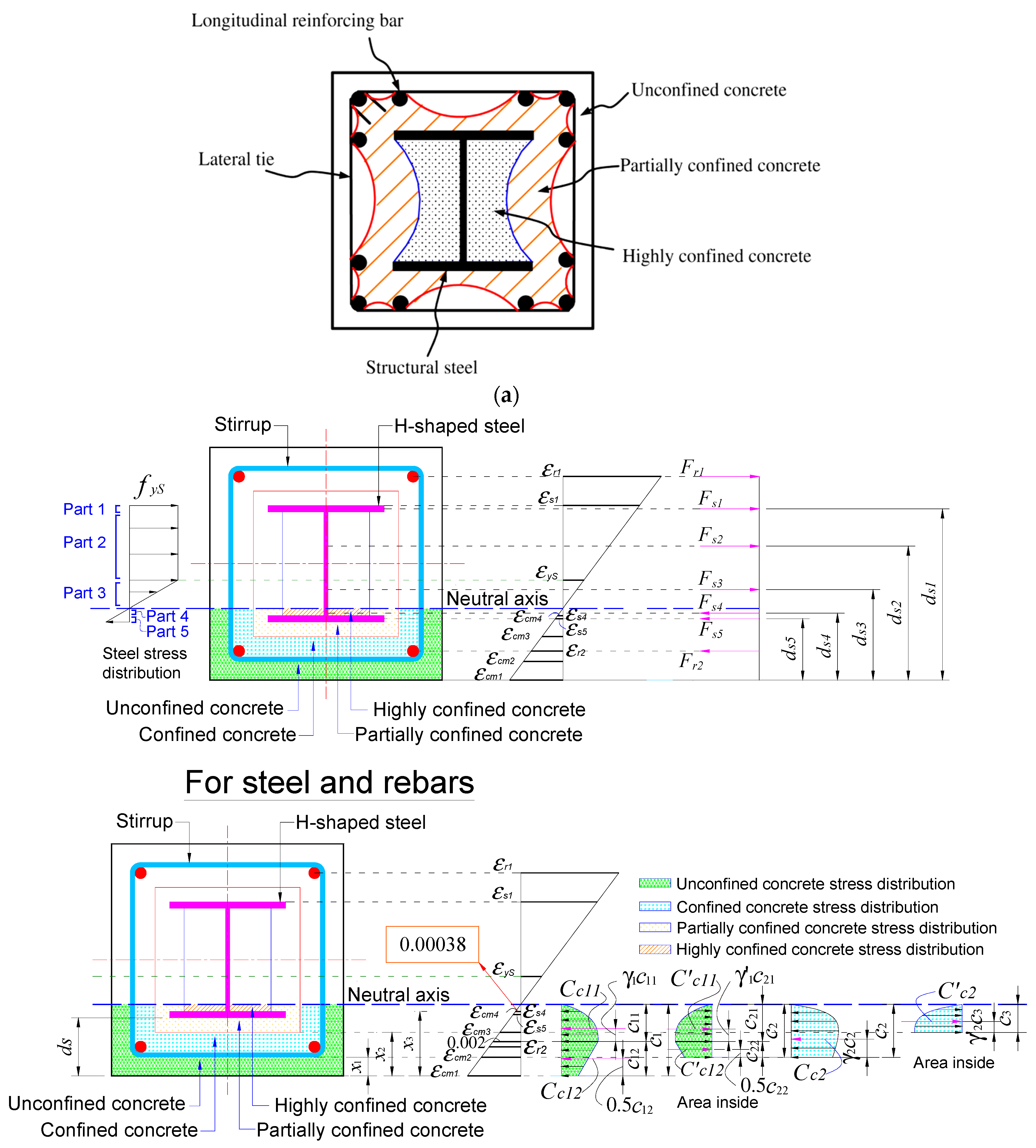
2.1. Analytical Model of Concrete Confined by a Wide-Flange Steel Section
2.1.1. A Confinement Effect Caused by the Structural Steel Sections
2.1.2. Local Buckling of the Longitudinal Bars and the Structural Steel
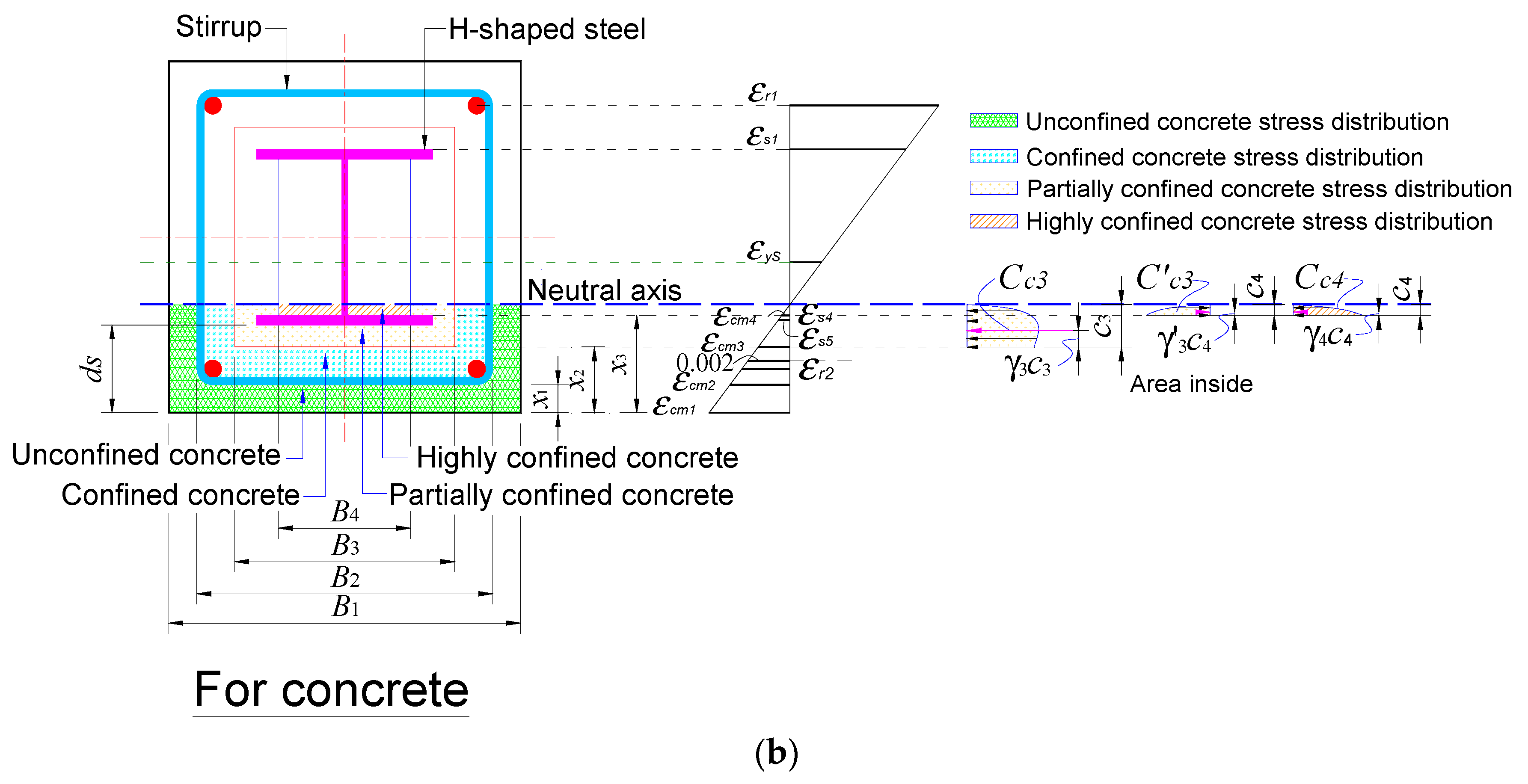
2.2. Analytical Model of Confinement by Transverse Reinforcements and Wide Flange Steel Sections
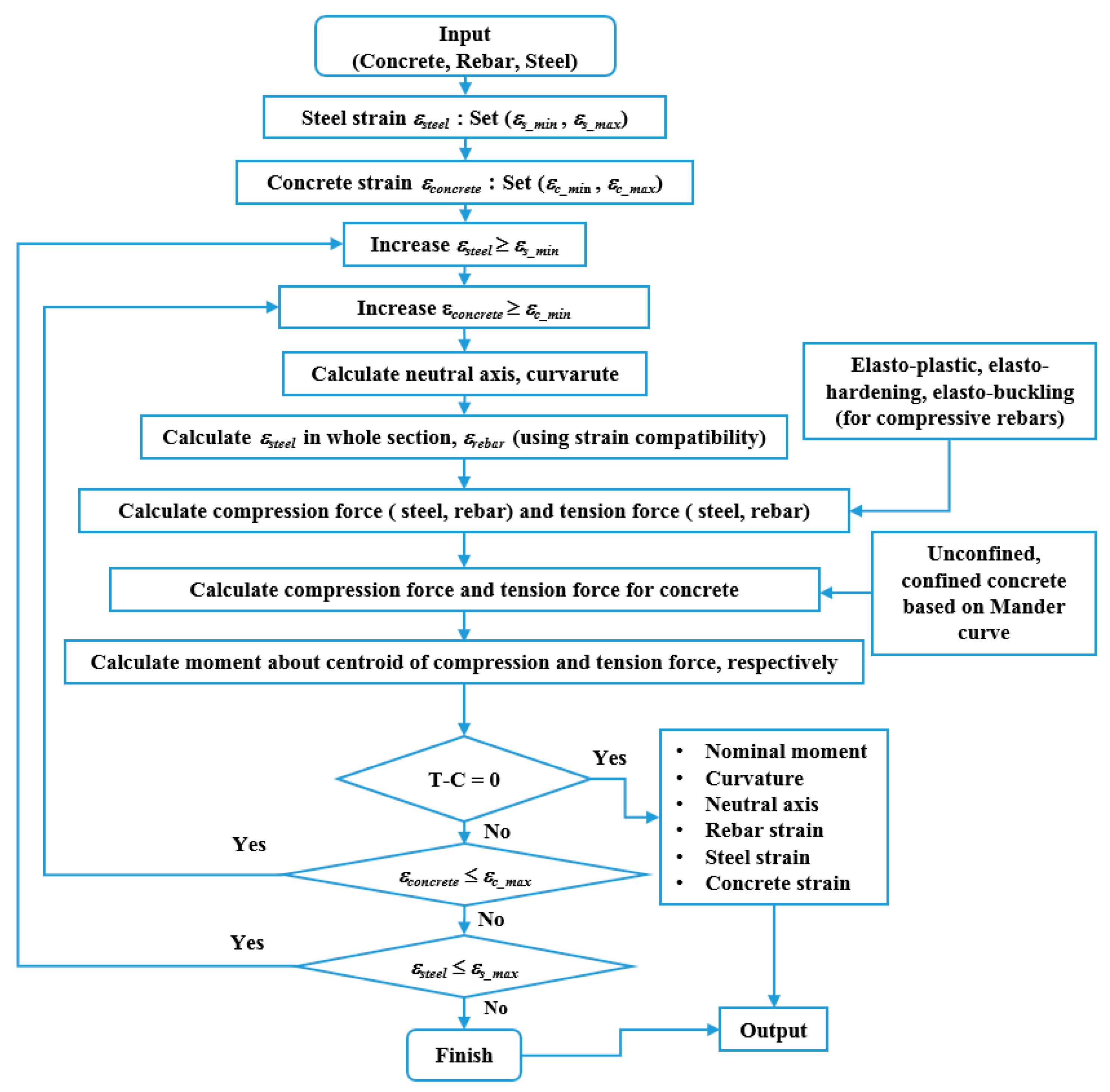
2.2.1. Strain Compatibility-Based Model
2.2.2. At the Maximum Load Limit State
- .
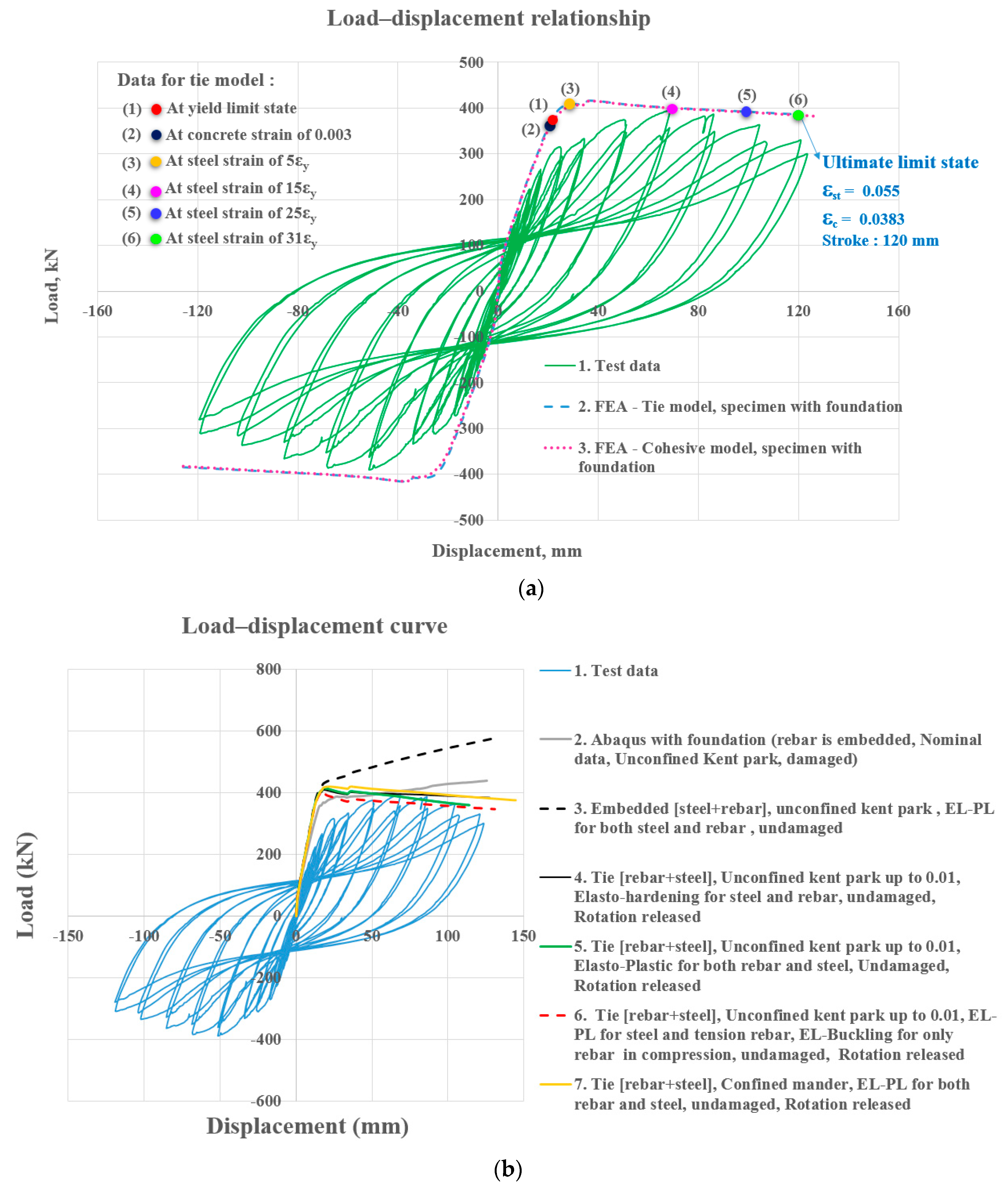
2.2.3. Validation of Analytical Model Based on Non-Linear Finite Element Analysis
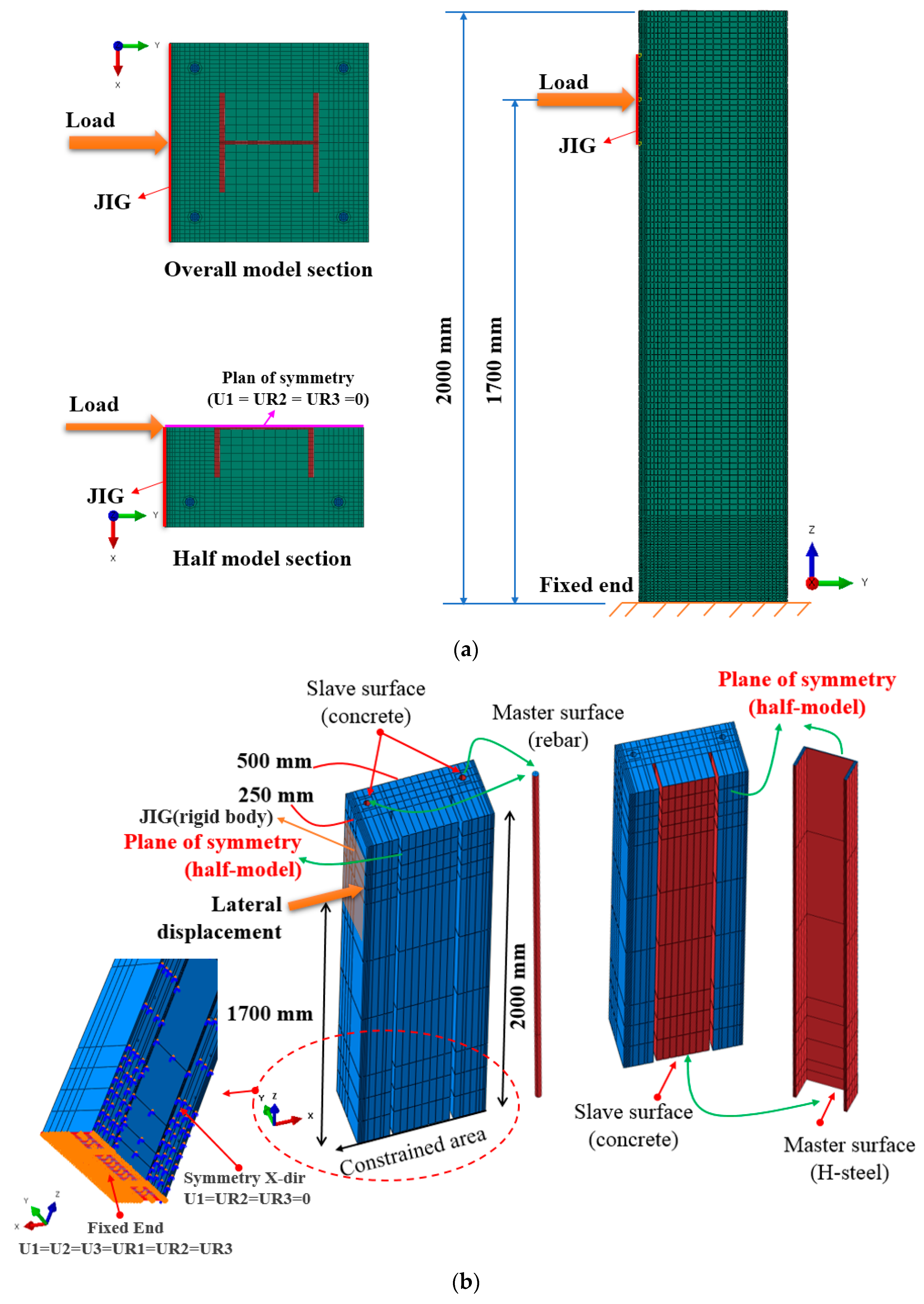
2.3. Finite Element Analysis of the Composite Beams
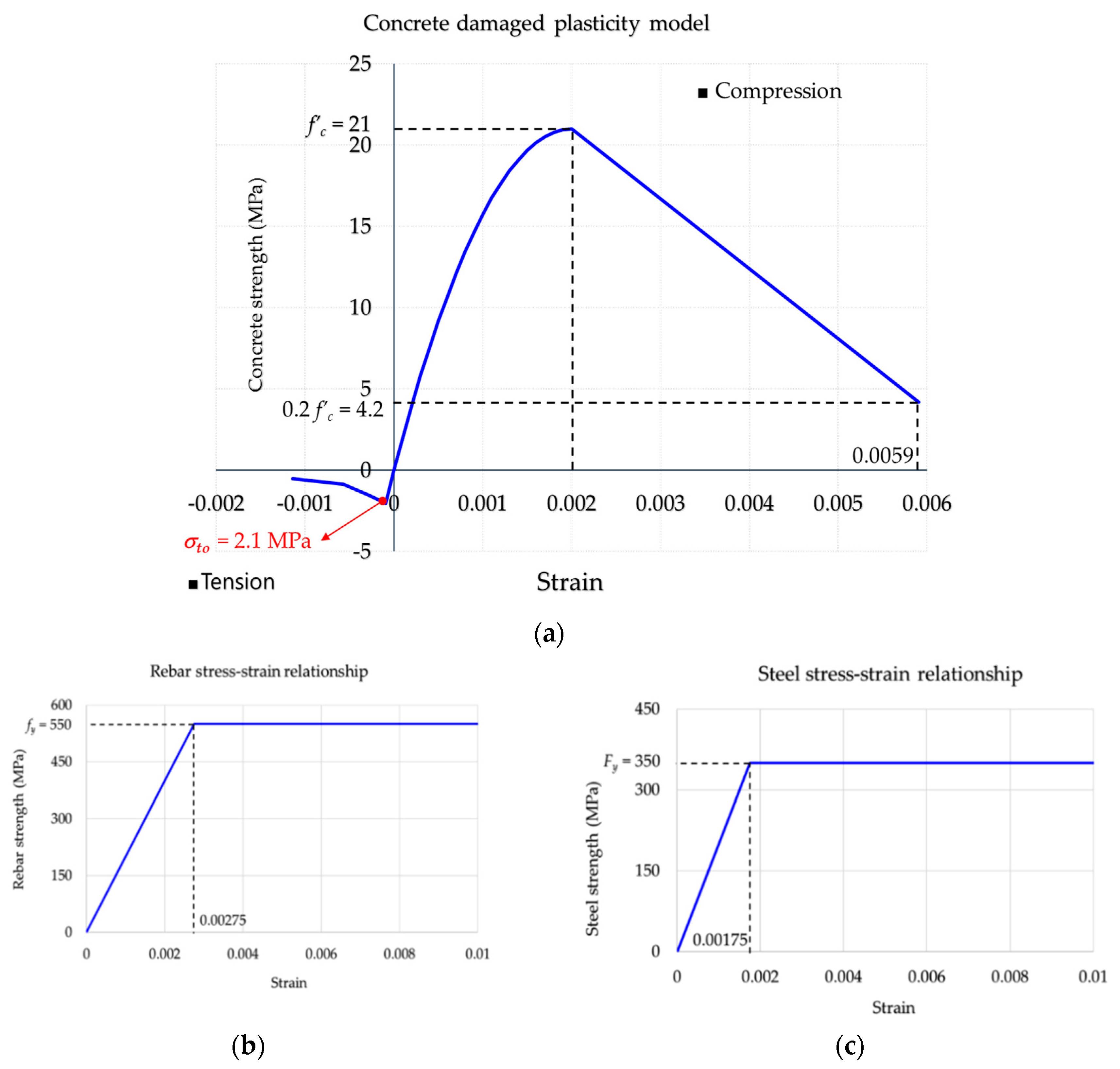
2.3.1. Material Properties and Parameters
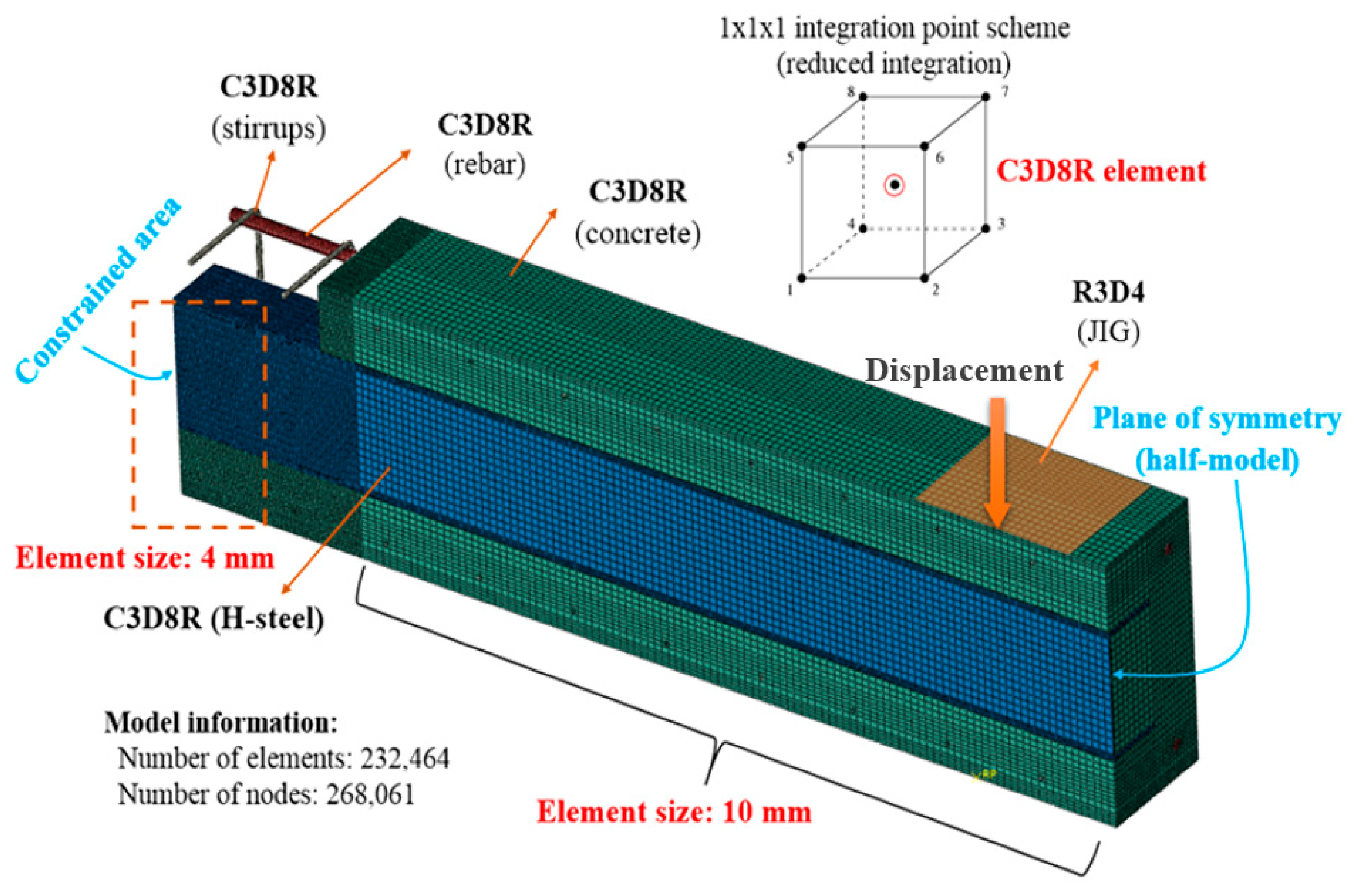
2.3.2. Element Descriptions
2.3.3. Modeling of Reinforcing Bars and H-Steels for Composite Beams
2.3.4. Non-Linear Finite Element Analysis Based on Concrete Plasticity
3. Results and Discussion
3.1. Verification of the Analytical Model with Finite Element Analysis Results
3.2. Influence of Buckling Effect of Reinforcing Steels on the Flexural Strength
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Ari | Area of rebar layer i (i = 1,2), mm2 |
| Asi | Area of part i of H-steel section, mm2 |
| B | Width of the beam section, mm |
| Bi | Width of unconfined, confined, partially, highly confined concrete area (i = 1–4), mm |
| ci | Height of concrete compression zone of unconfined, confined, partially, highly confined concrete area (i = 1–4), mm |
| c11, c12 | Height of components of unconfined area, mm |
| c21, c22 | Height of components of unconfined area inside, mm |
| Cci | Compressive force given by unconfined, confined, partially, highly confined concrete area, kN |
| C’ci | Compressive force given by unconfined, confined, partially, highly confined concrete area inside, kN |
| Cc11, Cc12 | Components of compressive force given by unconfined area, kN |
| C’c11, C’c12 | Components of compressive force given by unconfined area inside, kN |
| D | Depth of the beam section, mm |
| di | Distance from rebar layer i (i = 1,2) to bottom of beam, mm |
| dc | Distance from centroid to bottom of the beam, mm |
| ds | Distance from bottom flange of H-steel to bottom of the beam, mm |
| Es | Young’s modulus of steel, MPa |
| Er | Young’s modulus of rebar, MPa |
| The external axial forces, kN | |
| The internal forces contributed by rebar in tension, kN | |
| The internal forces contributed by rebar in compression, kN | |
| The internal forces contributed by steel in tension, kN | |
| The internal forces contributed by steel in compression, kN | |
| Fri | Force given by rebar layer i (i = 1,2), kN |
| Fsi | Force given by part i of L-steel section, kN |
| εcmi | Strain at fiber of unconfined, confined, partially, highly confined concrete area (i = 1–4) |
| εyR | Yield strain of rebar |
| εyS | Yield strain of steel |
| εri | Strain of rebar layer i (i = 1, 2) |
| εsi | Strain respect to part i of H-steel section |
| fyR | Yield strength of rebar, MPa |
| fyS | Yield strength of steel, MPa |
| f 'c | Compressive strength of unconfined concrete, MPa |
| f 'cc | Compressive strength of confined concrete, MPa |
| fc1 | Concrete compressive stress in term of concrete strain of unconfined area, MPa |
| fc2 | Concrete compressive stress in term of concrete strain of confined area, MPa |
| Concrete compressive strength at extreme fiber of unconfined region, MPa | |
| Concrete compressive strength at extreme fiber of confined region, MPa | |
| h | Depth of H-steel section, mm |
| Kh | Confinement factors for highly confined concrete |
| Kp | Confinement factors for partially confined concrete |
| tf1 | Top flange thickness of H-steel section, mm |
| tf2 | Bottom flange thickness of H-steel section, mm |
| tw | Web thickness of H-steel section, mm |
| xi | Distance from the edge of the concrete confined areas to the bottom of the beam (i = 1–3), mm |
| w | Width of H-steel section, mm |
| αi | Stress factors for the concrete areas i |
| α’i | Stress factors for the concrete areas inside i |
| Uniaxial tensile stress, MPa | |
| γi | Centroid factor for the concrete areas i |
| γ’i | Centroid factor for the concrete areas inside i |
| Eccentricity | |
| fb0 | Initial equibiaxial compressive yield stress of concrete, MPa |
| fc0 | Initial uniaxial compressive yield stress of concrete, MPa |
| K | The ratio of the second stress invariant on the tensile meridian |
| G(σ) | Non-associated plastic flow potential, Druker-Prager formulation |
| , | The plane in which plastic potential function is defined. |
| Dilation angle |
Appendix A
References
- Brettle, H.J. Ultimate strength design of composite columns. J. Struct. Div. ASCE 1973, 99, 1931–1948. [Google Scholar]
- Bridge, R.Q.; Roderick, J.W. Behavior of built-up composite columns. J. Struct. Div. ASCE 1978, 104, 1141–1155. [Google Scholar]
- Furlong, R.W. Concrete encased steel columns-design tables. J. Struct. Div. ASCE 1974, 100, 1865–1882. [Google Scholar]
- Mirza, S.A.; Skrabek, B.W. Statistical analysis of slender composite beam–column strength. J. Struct. Eng. 1992, 118, 1312–1332. [Google Scholar] [CrossRef]
- El-Tawil, S.; Deierlein, G.G. Strength and ductility of concrete encased composite columns. J. Struct. Eng. 1999, 125, 1009–1019. [Google Scholar] [CrossRef]
- Mirza, S.A.; Hyttinen, V.; Hyttinen, E. Physical tests and analyses of composite steel–concrete beam–columns. J. Struct. Eng. 1996, 122, 1317–1326. [Google Scholar] [CrossRef]
- Focacci, F.; Foraboschi, P.; De Stefano, M. Composite beam generally connected: Analytical model. Compos. Struct. 2015, 133, 1237–1248. [Google Scholar] [CrossRef]
- Foraboschi, P. Three-layered plate: Elasticity solution. Compos. Part B Eng. 2014, 60, 764–776. [Google Scholar] [CrossRef]
- Foraboschi, P. Versatility of steel in correcting construction deficiencies and in seismic retrofitting of RC buildings. J. Build. Eng. 2016, 8, 107–122. [Google Scholar] [CrossRef]
- Chen, C.C.; Lin, N.J. Analytical model for predicting axial capacity and behavior of concrete encased steel composite stub columns. J. Constr. Steel Res. 2006, 62, 424–433. [Google Scholar] [CrossRef]
- AISC Committee. Specification for Structural Steel Buildings (ANSI/AISC 360-10); American Institute of Steel Construction: Chicago, IL, USA, 2010. [Google Scholar]
- Chen, C. Accuracy of AISC methods in predicting flexural strength of concrete-encased members. J. Struct. Eng. ASCE 2013, 139, 338–349. [Google Scholar] [CrossRef]
- Hong, W.K.; Lee, Y.; Kim, S.; Kim, S.I.; Yun, Y.J. Analytical investigation of hybrid composite precast beams with modified strain compatibility for entire history of nominal flexural capacity. Struct. Des. Tall Spec. Build. 2015, 24, 835–852. [Google Scholar] [CrossRef]
- Sheikh, S.A.; Uzumeri, S.M. Analytical model for concrete confinement in tied columns. J. Struct. Div. ASCE 1982, 108, 2703–2722. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress–strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Bayrak, O.; Sheikh, S.A. Plastic hinge analysis. J. Struct. Eng. 2001, 127, 1092–1100. [Google Scholar] [CrossRef]
- Nzabonimpa, J.D.; Hong, W.K. Experimental investigation of “L”-shaped precast concrete column joints with laminated mechanical plates. Struct. Des. Tall Special Build. 2019. under review. [Google Scholar]
- Malm, R. Shear Cracks in Concrete Structures Subjected to In-Plane Stresses. Ph.D. Thesis, KTH, Stockholm, Sweden, 2006. [Google Scholar]
- Birtel, V.; Mark, P. Parameterised finite element modelling of RC beam shear failure. In Proceedings of the ABAQUS Users’ Conference, Boston, MA, USA, 23–25 May 2006; pp. 95–108. [Google Scholar]
- Niza, M.S. Computational analysis of reinforced concrete slabs subjected to impact loads. Int. J. Integr. Eng. 2012, 4, 70–76. [Google Scholar]
- Ahmed, A. Modeling of a reinforced concrete beam subjected to impact vibration using ABAQUS. Int. J. Civ. Struct. Eng. 2014, 4, 227–236. [Google Scholar] [CrossRef]
- Nazem, M.; Rahmani, I.; Rezaee-Pajand, M. Nonlinear FE analysis of reinforced concrete structures using a tresca-type yield surface. Sci. Iran. A 2009, 16, 512–519. [Google Scholar]
- Genikomsou, A.S.; Polak, M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- Hu, J.Y.; Hong, W.K.; Park, S.C. Experimental investigation of precast concrete based dry mechanical column–column joints for precast concrete frames”. Struct. Des. Tall Spec. Build. 2017, 26. [Google Scholar] [CrossRef]
- Nzabonimpa, J.D.; Hong, W.K.; Nguyen, D.H. Post-yield behavior of fixed steel beams encased in concrete with plastic rotation capability under monotonic loads. Mater. Struct. 2018, 51, 70. [Google Scholar] [CrossRef]
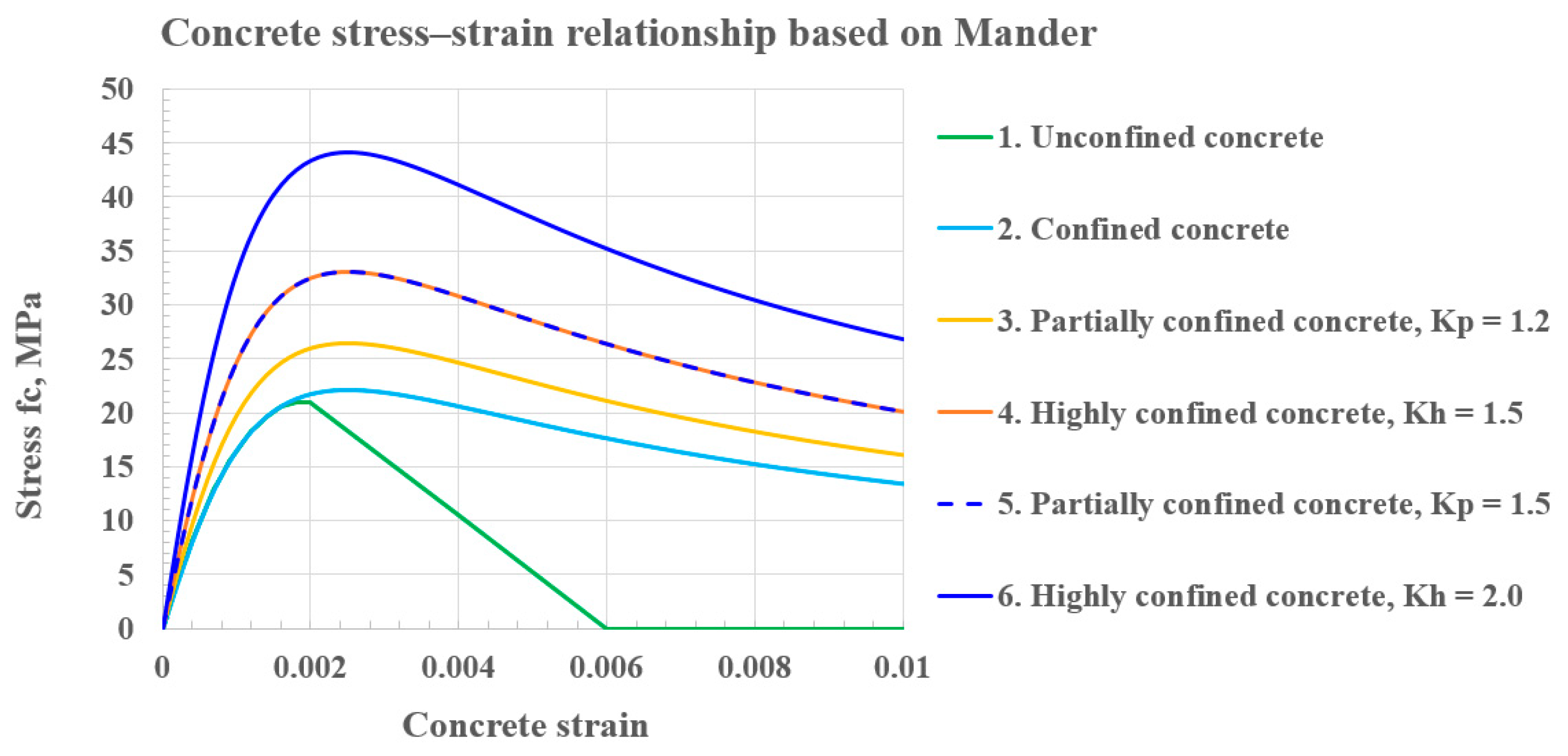



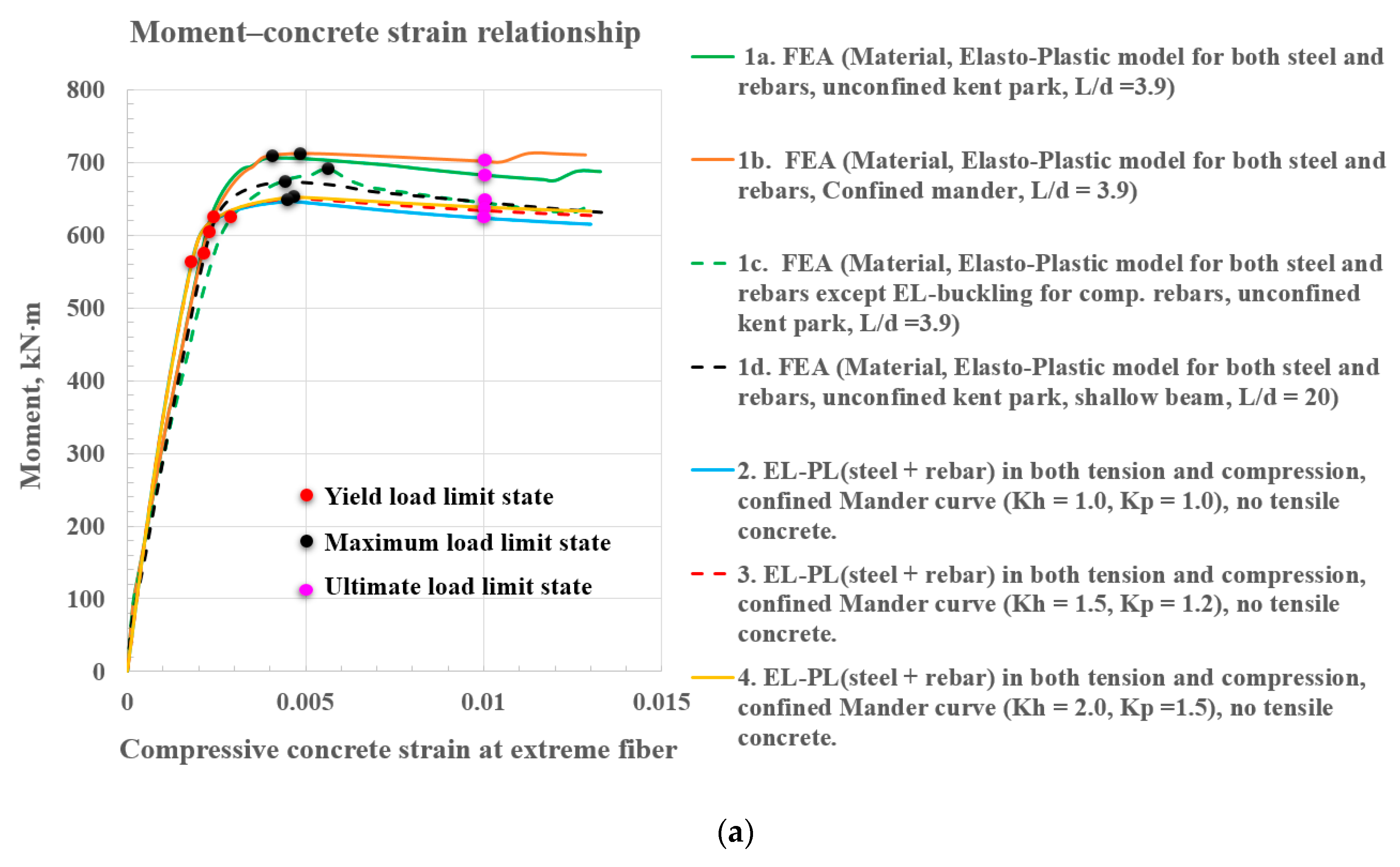
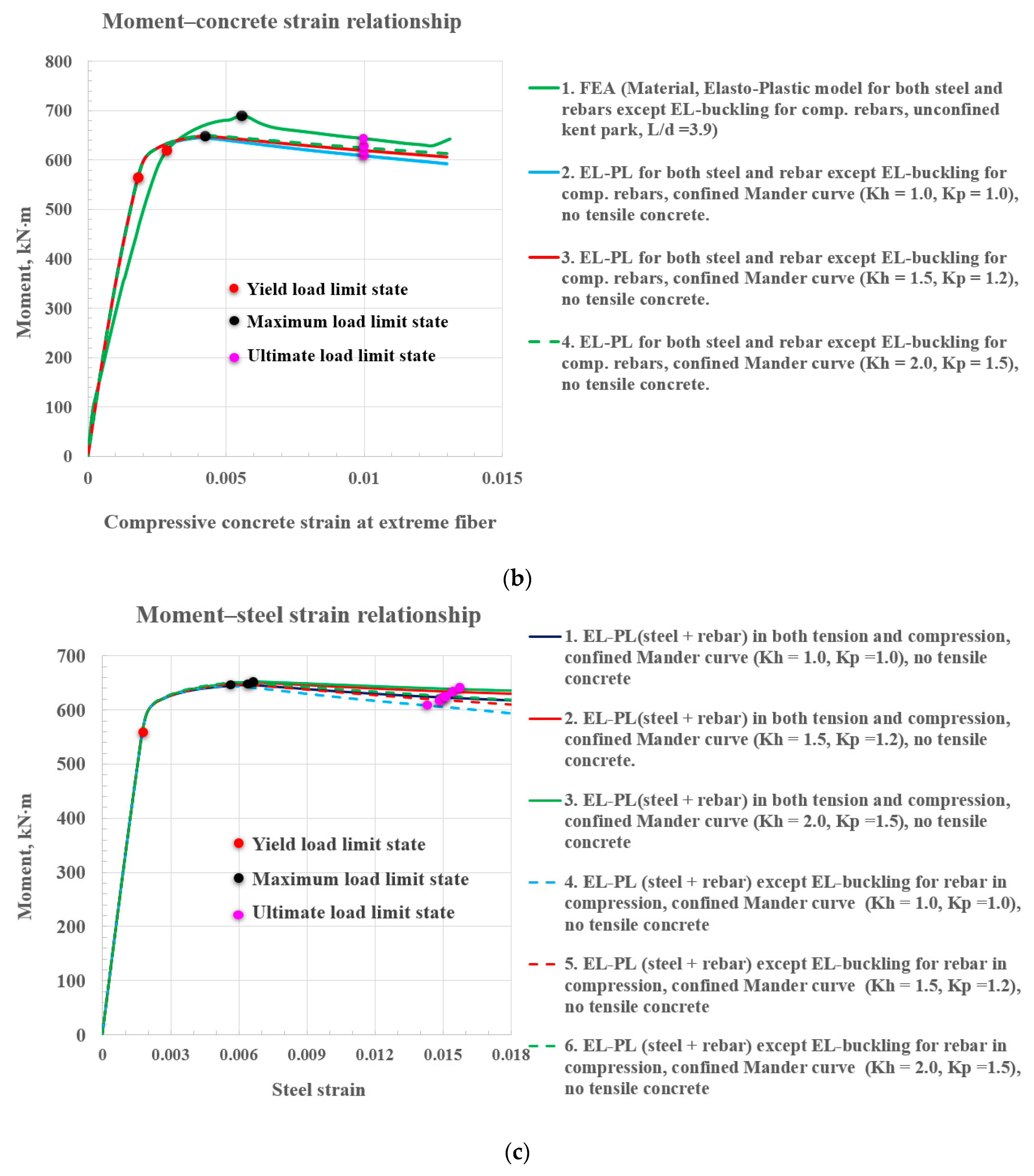
| Kp | Kh | Maximum Load/Concrete Strain | Maximum Moment/Concrete Strain | Design Load (Concrete Strain = 0.003) | Design Moment (Concrete Strain = 0.003) | |
|---|---|---|---|---|---|---|
| Elasto-Plastic (Steel + Rebar) in Both Tension and Compression, Confined Mander Curve, Figure 11a | ||||||
| Legend 2 | 1.0 | 1.0 | 380.6 kN/0.0046 | 647.0 kN∙m/0.0046 | 373.0 kN | 634.1 kN∙m |
| Legend 3 | 1.2 | 1.5 | 382.7 kN/0.0046 | 650.5 kN∙m/0.0046 | 373.5 kN | 634.9 kN∙m |
| Legend 4 | 1.5 | 2.0 | 384.1 kN/0.0046 | 652.9 kN∙m/0.0046 | 374.3 kN | 636.3 kN∙m |
| Elasto-Plastic (Steel + Rebar) in both Tension and Compression except EL-Buckling for Rebar in Compression, Confined Mander Curve, Figure 11b | ||||||
| Legend 2 | 1.0 | 1.0 | 379.7 kN/0.0042 | 645.5 kN∙m/0.0042 | 373.5 kN | 635.0 kN∙m |
| Legend 3 | 1.2 | 1.5 | 381.5 kN/0.0042 | 648.5 kN∙m/0.0042 | 374.1 kN | 635.9 kN∙m |
| Legend 4 | 1.5 | 2.0 | 382.8 kN/0.0042 | 650.8 kN∙m/0.0042 | 374.9 kN | 637.3 kN∙m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.H.; Hong, W.-K. Part I: The Analytical Model Predicting Post-Yield Behavior of Concrete-Encased Steel Beams Considering Various Confinement Effects by Transverse Reinforcements and Steels. Materials 2019, 12, 2302. https://doi.org/10.3390/ma12142302
Nguyen DH, Hong W-K. Part I: The Analytical Model Predicting Post-Yield Behavior of Concrete-Encased Steel Beams Considering Various Confinement Effects by Transverse Reinforcements and Steels. Materials. 2019; 12(14):2302. https://doi.org/10.3390/ma12142302
Chicago/Turabian StyleNguyen, Dinh Han, and Won-Kee Hong. 2019. "Part I: The Analytical Model Predicting Post-Yield Behavior of Concrete-Encased Steel Beams Considering Various Confinement Effects by Transverse Reinforcements and Steels" Materials 12, no. 14: 2302. https://doi.org/10.3390/ma12142302
APA StyleNguyen, D. H., & Hong, W.-K. (2019). Part I: The Analytical Model Predicting Post-Yield Behavior of Concrete-Encased Steel Beams Considering Various Confinement Effects by Transverse Reinforcements and Steels. Materials, 12(14), 2302. https://doi.org/10.3390/ma12142302





