Reliability Analysis of CFRP-Strengthened RC Bridges Considering Size Effect of CFRP
Abstract
1. Introduction
2. Size Effect Model of CFRP
2.1. Mean CFRP Strength
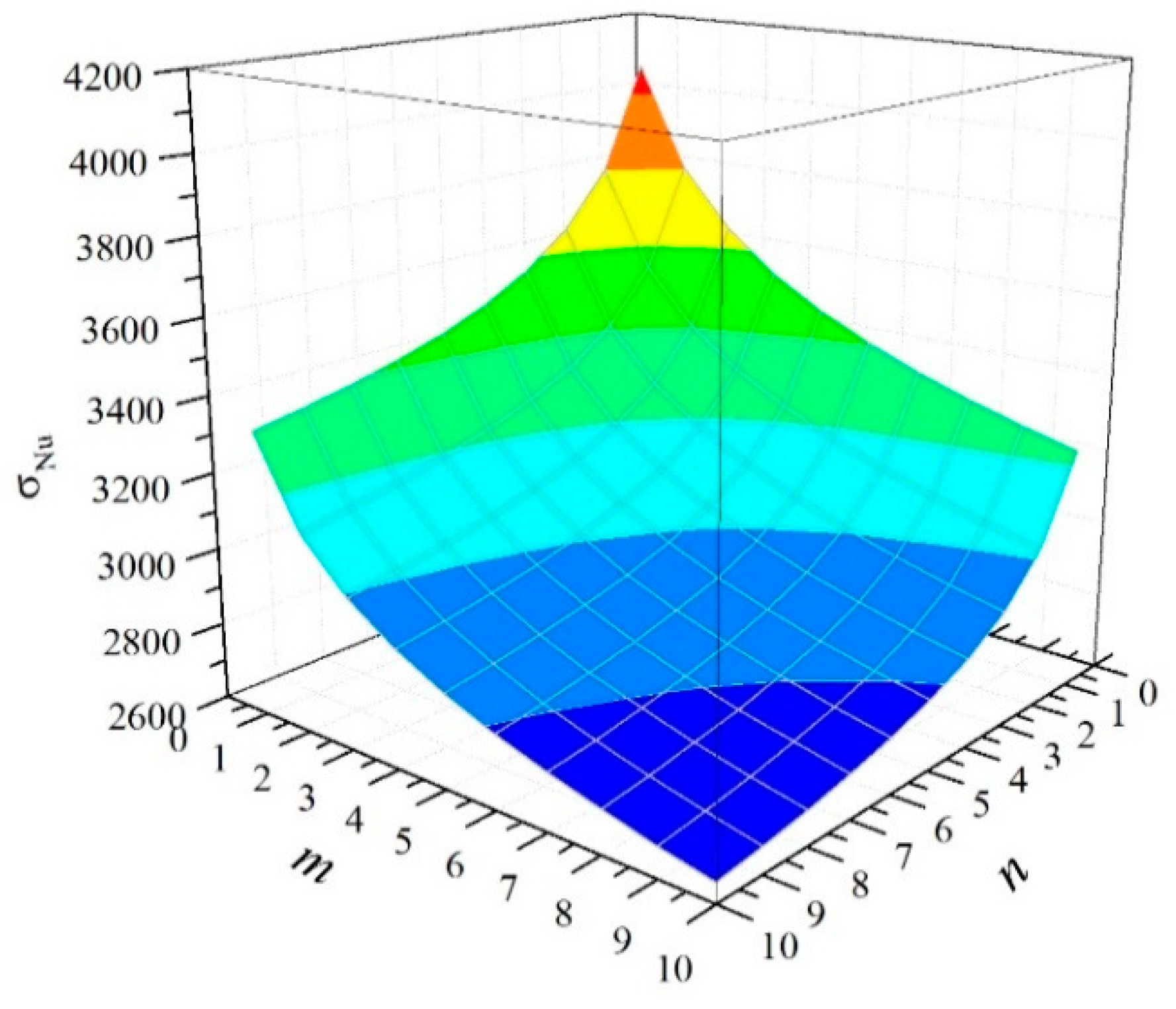
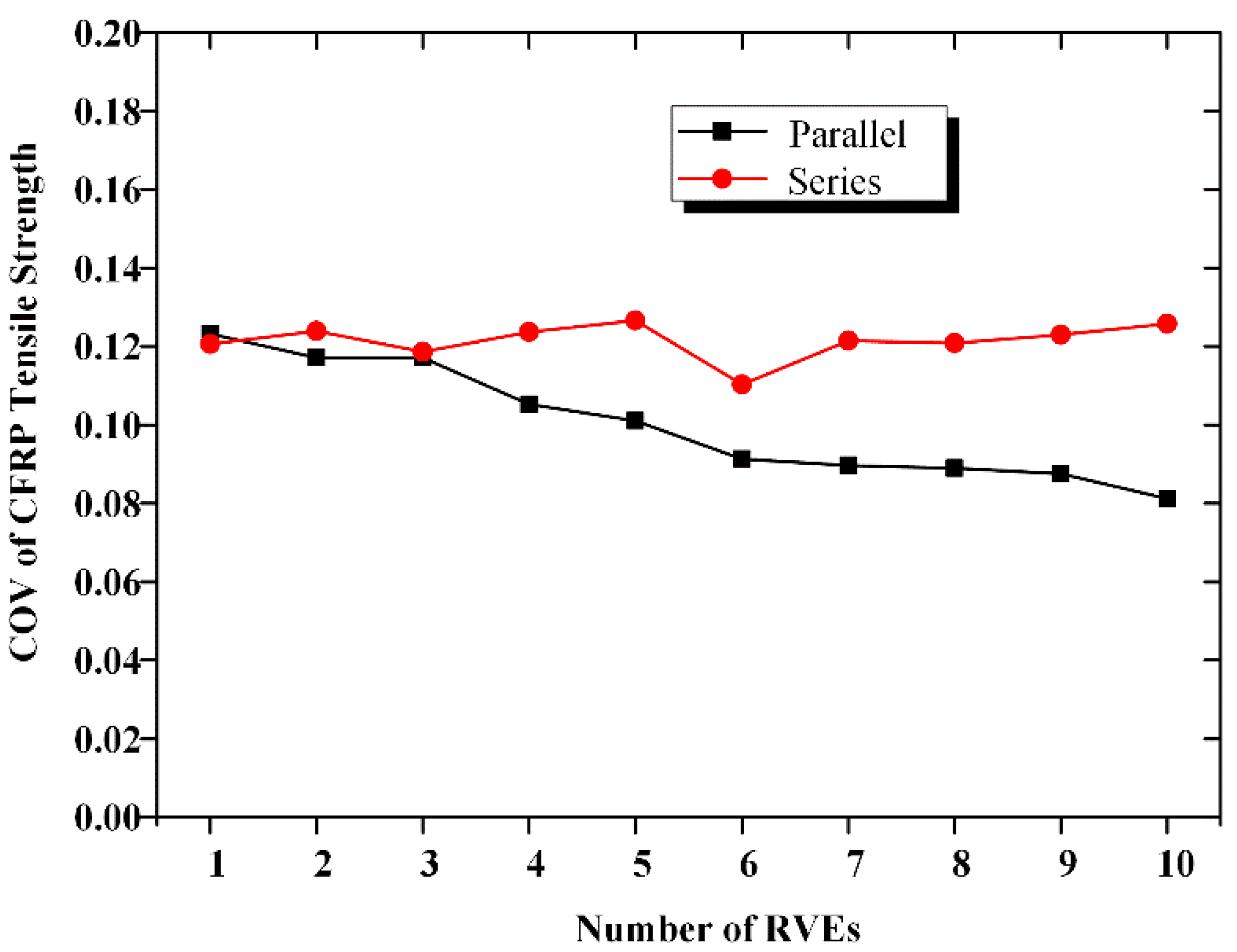
2.2. COV of CFRP Strength
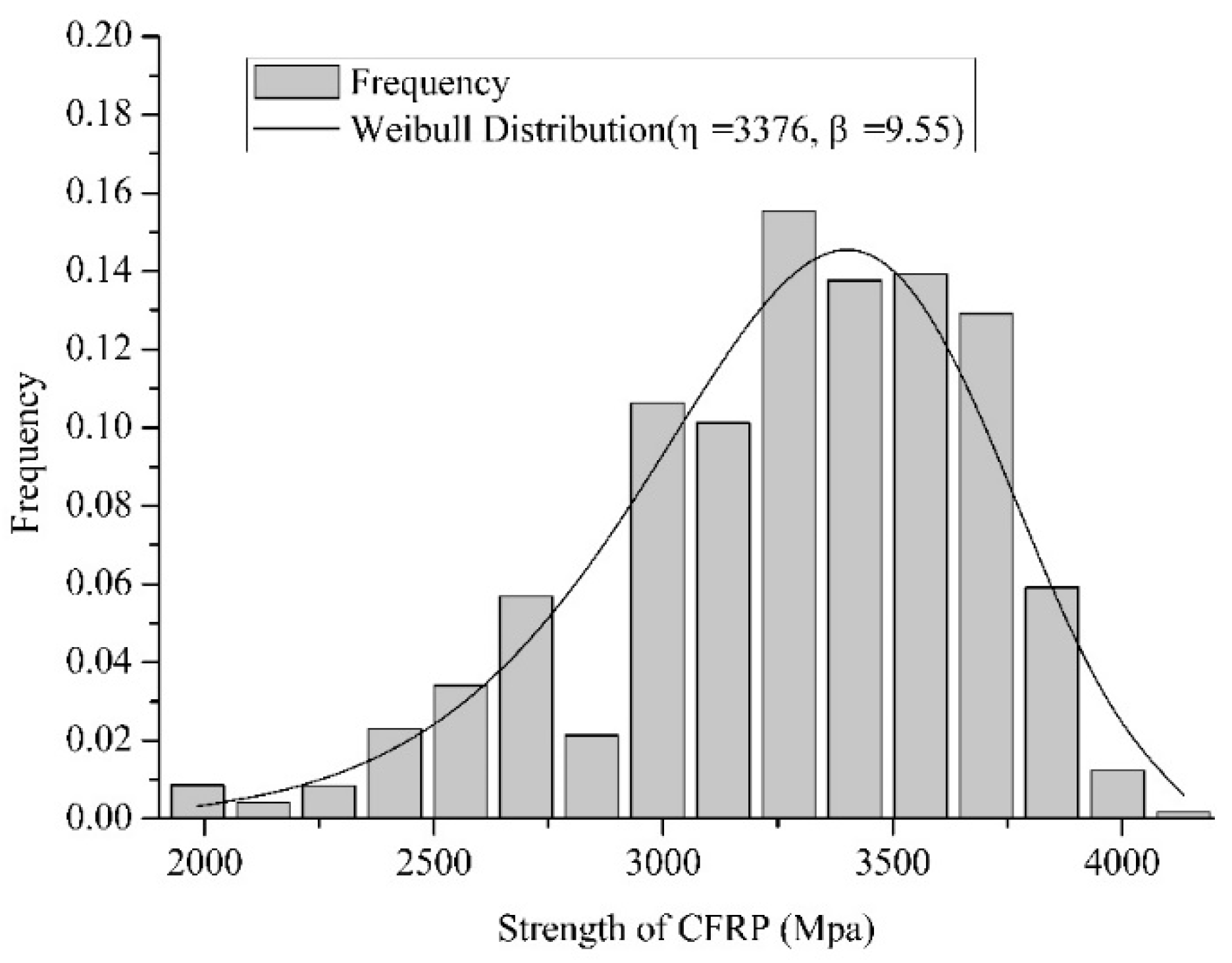
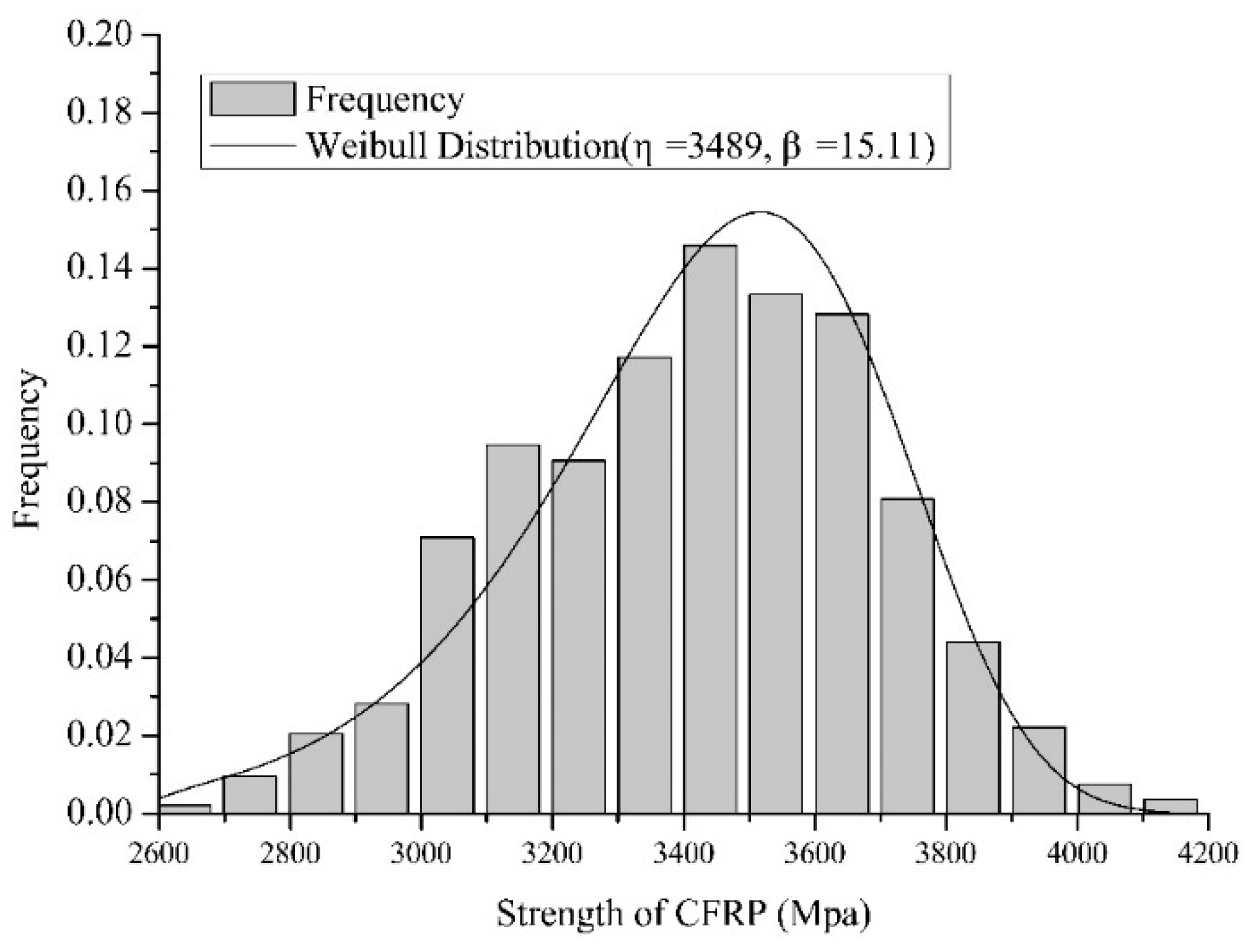
2.3. Distribution Type of CFRP Strength
3. Case Study
3.1. Project Overview
- (1)
- Crushing of the concrete in compression before yielding of the reinforcing steel;
- (2)
- Yielding of the steel in tension followed by rupture of the FRP laminate;
- (3)
- Yielding of the steel in tension followed by concrete crushing;
- (4)
- Shear/tension delamination of the concrete cover;
- (5)
- Debonding of the FRP from the concrete substrate.
- 1.
- Steel-yielding concrete crushing. In this mode, the tensile strain of the CFRP laminate is less than the allowable tensile strain when a failure occurrs. The flexural capacity of the strengthened RC beam can be expressed by equilibrium of the moment at the mid-span cross-section, as Equation (13) [31]:
- 2.
- Steel-yielding FRP rupture. In this mode, the concrete has not yet reached its ultimate capacity when the failure occurrs. This is the most common failure mode of a well-designed CFRP-strengthened RC beam. The flexural capacity of the strengthened RC beam can be expressed as Equation (15):
3.2. Performance Function
3.3. Reliability Evaluation of the CFRP-Strengthened Bridge
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FRP | fiber-reinforced plastic |
| CFRP | carbon fiber-reinforced plastic |
| GFRP | glass fiber-reinforced plastic |
| MC | Monte-Carlo |
| COV | coefficient of variation |
| RC | Reinforced concrete |
| RVE | representative volume element |
| CDF | cumulative distribution function |
| ELS | Equal Load Sharing |
| SD | standard deviation |
| probability density function | |
| FORM | first-order reliability method |
Symbols
| Pf,e(f) | is the failure probability of a link under stress f; |
| Pf,s(f) | is the failure probability of the chain; |
| N | is the number of links in the chain; |
| f | is the mean deviation of CFRP RVEs’ tensile strength; |
| is the standard deviation of CFRP RVEs’ tensile strength; | |
| xi | is the number of failed specimens under load ; |
| N | is the total number of virtual specimens; |
| is the failure probability of the system; | |
| e | is the failure probability of the element; |
| is the system reliability; | |
| is the failure probability of the components after stress redistribution; | |
| is the reliability of the components after stress redistribution; | |
| η | is the scale parameter; |
| β | is the shape parameter; |
| n | is the number of the parallel elements; |
| m | is the number of series elements; |
| fFRP | is the mean strength of the RVEs; |
| fc | is the 28-day yield strength of concrete; |
| b | is the width of the girder web; |
| x | is the height of the compression zone; |
| h0 | is the effective height of the girder cross section; |
| is the yield strength of compression reinforcement; | |
| is the yield strength of tension reinforcement; | |
| α | is the corrosion rate of the reinforcement; |
| as | is the thickness of the concrete cover; |
| Ef | is the elastic module of the CFRP laminate, |
| is the CFRP strain when the failure occurred; | |
| Af | is the sectional area of the CFRP laminate; |
| is the sectional area of compression reinforcement; | |
| is the sectional area of tension reinforcement; | |
| is the relative height of the compression zone during a CFRP rupture; | |
| is the ultimate strain in the FRP; | |
| is the model uncertainty factor for the flexural capacity of CFRP-strengthened RC beams; | |
| is the bending moment generated by permanent loads; | |
| is the bending moment generated by live loads; | |
| l | is the span length of the RC girder; |
| g1 | is the weight of the precast RC girder per unit length; |
| g2 | is the equivalent dead load of the RC diaphragm per unit length; |
| is the weight of the asphalt concrete pavement per unit length; | |
| λconc | is the uncertainty factor of the RC dead load; |
| λasph | is the uncertainty factor of the asphalt concrete dead load; |
| Ibeam | is the impact coefficient of the vehicle load; |
| ξ | is the girder distribution factor, c is the overload rate; |
| mcq | is the transverse distribution coefficient of the vehicle load; |
| is the uniform lane load; | |
| Pk | is the concentrated lane load; |
| mcr | is the transverse distribution coefficient of the crowd load; |
| is the crowd load; | |
| λmtrk-i | is the uncertainty factor of the moment generated by the live loads on the beam. |
| is the stress distribution function in compressive concrete; | |
| is the strain distribution function in compressive concrete; | |
| is the strain corresponding to ultimate strength of concrete; | |
| is the strain of concrete while failure occurs; c is the depth to the neutral axis; | |
| is the initial strain in the concrete before strengthened; | |
| is the initial moment; | |
| is the relative height of the compression zone of the cracked cross section; | |
| is elastic modulus of concrete; | |
| is the inertia moment of cracked cross section. |
References
- Günaydin, M.; Adanur, S.; Altunişik, A.; Sevim, B. Static and dynamic responses of Halgavor Footbridge using steel and FRP materials. Steel Compos. Struct. 2015, 18, 51–69. [Google Scholar] [CrossRef]
- Park, J.-W.; Yoo, J.-H. Flexural and compression behavior for steel structures strengthened with carbon fiber reinforced polymers (CFRPs) sheet. Steel Compos. Struct. 2015, 19, 441–465. [Google Scholar] [CrossRef]
- Plevris, N.; Triantafillou, T.C.; Veneziano, D. Reliability of RC members strengthened with CFRP laminates. J. Struct. Eng. 1995, 121, 1037–1044. [Google Scholar] [CrossRef]
- Okeil, A.M.; El-Tawil, S.; Shahawy, M. Flexural reliability of reinforced concrete bridge girders strengthened with carbon fiber-reinforced polymer laminates. J. Bridg. Eng. 2002, 7, 290–299. [Google Scholar] [CrossRef]
- Atadero, R.; Lee, L.; Karbhari, V.M. Consideration of material variability in reliability analysis of FRP strengthened bridge decks. Compos. Struct. 2005, 70, 430–443. [Google Scholar] [CrossRef]
- Zureick, A.-H.; Bennett, R.M.; Ellingwood, B.R. Statistical characterization of fiber-reinforced polymer composite material properties for structural design. J. Struct. Eng. 2006, 132, 1320–1327. [Google Scholar] [CrossRef]
- Zhou, J.; Bi, F.; Wang, Z.; Zhang, J. Experimental investigation of size effect on mechanical properties of carbon fiber reinforced polymer (CFRP) confined concrete circular specimens. Constr. Build. Mater. 2016, 127, 643–652. [Google Scholar] [CrossRef]
- Barbieri, G.; Biolzi, L.; Bocciarelli, M.; Cattaneo, S. Size and shape effect in the pull-out of FRP reinforcement from concrete. Compos. Struct. 2016, 143, 395–417. [Google Scholar] [CrossRef]
- Ben Dror, E.; Rabinovitch, O. Size effect in the debonding failure of FRP strengthened beams. Eng. Fract. Mech. 2016, 156, 161–181. [Google Scholar] [CrossRef]
- Mahmoud, K.; El-Salakawy, E. Size effect on shear strength of glass fiber-reinforced polymer-reinforced concrete continuous beams. ACI Struct. J. 2016, 113, 125. [Google Scholar] [CrossRef]
- Weibull, W. The Phenomenon of Rupture in Solids; (Ingenioersvetenskaps Akad. Handl.); Royal Swedish Institute of Engineering Research: Stockholm, Sweden, 1939; Volume 153, pp. 1–55. [Google Scholar]
- Bazant, Z.P.; Frangopol, D.M. Size effect hidden in excessive dead load factor. J. Struct. Eng. 2002, 128, 80–86. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Novák, D. Probabilistic nonlocal theory for quasibrittle fracture initiation and size effect. I: Theory. J. Eng. Mech. 2000, 126, 166–174. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Pang, S.D. Mechanics-based statistics of failure risk of quasibrittle structures and size effect on safety factors. Proc. Natl. Acad. Sci. USA 2006, 103, 9434–9439. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Pang, S.-D. Activation energy based extreme value statistics and size effect in brittle and quasibrittle fracture. J. Mech. Phys. Solids 2007, 55, 91–131. [Google Scholar] [CrossRef]
- Le, J.L. Size effect on reliability indexes and safety factors of quasibrittle structures. Struct. Saf. 2015, 52, 20–28. [Google Scholar] [CrossRef]
- Lei, W.-S.; Su, P. An approach to scaling size effect on strength of quasi-brittle biomedical materials. J. Mech. Behav. Biomed. Mater. 2016, 62, 428–432. [Google Scholar] [CrossRef] [PubMed]
- Batdorf, S. Tensile strength of unidirectionally reinforced composites—I. J. Reinf. Plast. Compos. 1982, 1, 153–164. [Google Scholar] [CrossRef]
- Harlow, D.G.; Phoenix, S.L. The chain-of-bundles probability model for the strength of fibrous materials I: Analysis and conjectures. J. Compos. Mater. 1978, 12, 195–214. [Google Scholar] [CrossRef]
- Harlow, D.G.; Phoenix, S.L. Bounds on the probability of failure of composite materials. Int. J. Fract. 1979, 15, 321. [Google Scholar]
- Bergman, B. On the probability of failure in the chain-of-bundles model. J. Compos. Mater. 1981, 15, 92–98. [Google Scholar] [CrossRef]
- Ruggieri, C.; Minami, F.; Toyoda, M. A statistical approach for fracture of brittle materials based on the chain-of-bundles model. J. Appl. Mech. 1995, 62, 320–328. [Google Scholar] [CrossRef]
- Moshtaghin, A.F.; Franke, S.; Keller, T.; Vassilopoulos, A.P. Random field-based modeling of size effect on the longitudinal tensile strength of clear timber. Struct. Saf. 2016, 58, 60–68. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Daniel, I.M.; Li, Z. Size Effect and fracture characteristics of composite laminates. J. Eng. Mater. Technol. 1996, 118, 317–324. [Google Scholar]
- Maimí, P.; González, E.V.; Gascons, N.; Ripoll, L. Size effect law and critical distance theories to predict the nominal strength of quasibrittle structures. Appl. Mech. Rev. 2013, 65, 020803. [Google Scholar] [CrossRef]
- Caner, F.C.; Bazant, Z.P. Size effect on strength of laminate-foam sandwich plates: Finite element analysis with interface fracture. Compos. Part B Eng. 2009, 40, 337–348. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Zhou, Y.; Daniel, I.M.; Caner, F.C.; Yu, Q. Size effect on strength of laminate-foam sandwich plates. J. Eng. Mater. Technol. 2006, 128, 366–374. [Google Scholar] [CrossRef]
- Bazant Z, P. Probabilistic modeling of quasibrittle fracture and size effect. In Proc. 8th Int. Conf. on Structural Safety and Reliability (ICOSSAR); Swets and Zeitinger, Balkema: Boca Raton, FL, USA, 2001; pp. 1–23. [Google Scholar]
- Laffan, M.; Pinho, S.; Robinson, P.; Iannucci, L.; Pinho, S. Measurement of the in situ ply fracture toughness associated with mode I fibre tensile failure in FRP. Part II: Size and lay-up effects. Compos. Sci. Technol. 2010, 70, 614–621. [Google Scholar] [CrossRef]
- Okabe, T. Size effect on tensile strength of unidirectional CFRP composites—Experiment and simulation. Compos. Sci. Technol. 2002, 62, 2053–2064. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China (MOT). JTG/T J22-2008, Specifications for Strengthening Design of Highway Bridges; China Communications Press: Beijing, China, 2008. (In Chinese)
- China State Bureau of Quality Technical Supervision (CSBTS). Test Method for Tensile Properties of Oriented Fiber Reinforced Plastics; GB/T 3354-1999; China Standards Press: Beijing, China, 1999. (In Chinese)
- Yue, Q.; Cao, J.; Yang, Y.; Zhan, Y. Normative specimen of carbon fiber reinforced polymer sheets for checking property. Ind. Construct. 2005, 35, 1–4. (In Chinese) [Google Scholar]
- Daniels, H.E. The statistical theory of the strength of bundles of threads. I. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1945, 183, 405–435. [Google Scholar]
- Scop, P.M.; Argon, A.S. Statistical theory of strength of laminated composites II. J. Compos. Mater. 1969, 3, 30–47. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Smalley, R.F.; Solla, S.A. Collapse of loaded fractal trees. Nature 1985, 313, 671–672. [Google Scholar] [CrossRef]
- Smalley, R.F.; Turcotte, D.L.; Solla, S.A. A renormalization group approach to the stick-slip behavior of faults. J. Geophys. Res. Space Phys. 1985, 90, 1894. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China (MOT). JTG H11-2004 Code for Maintenance of Highway Bridges and Culvers; China Plan Press: Beijing, China, 2004. (In Chinese)
- American Concrete Institute (ACI). Guide for Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; ACI 440.2R-08; ACI Committee: Farmington Hills, MI, USA, 2008; Volume 440. [Google Scholar]
- Ministry of Transport of the People’s Republic of China (MOT). GB/T 50283-1999 Unified Standard for the Reliability Design of Highway Engineering Structures; China Plan Press: Beijing, China, 1999. (In Chinese)

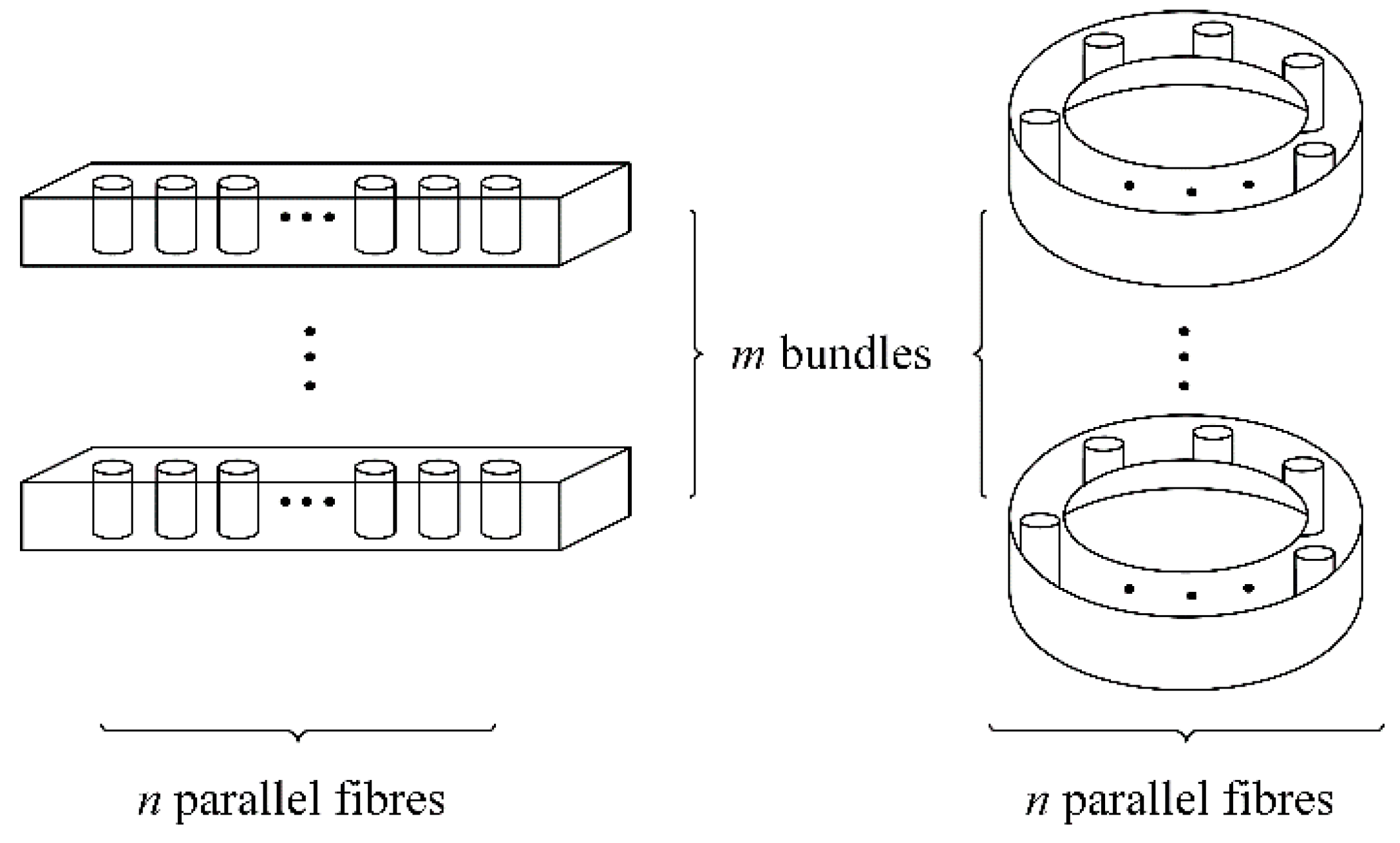

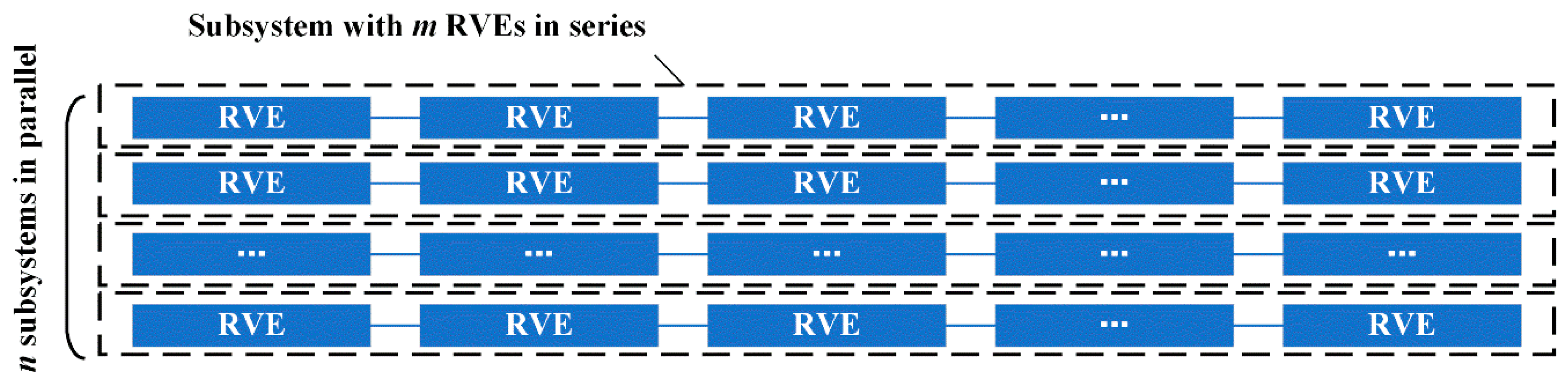
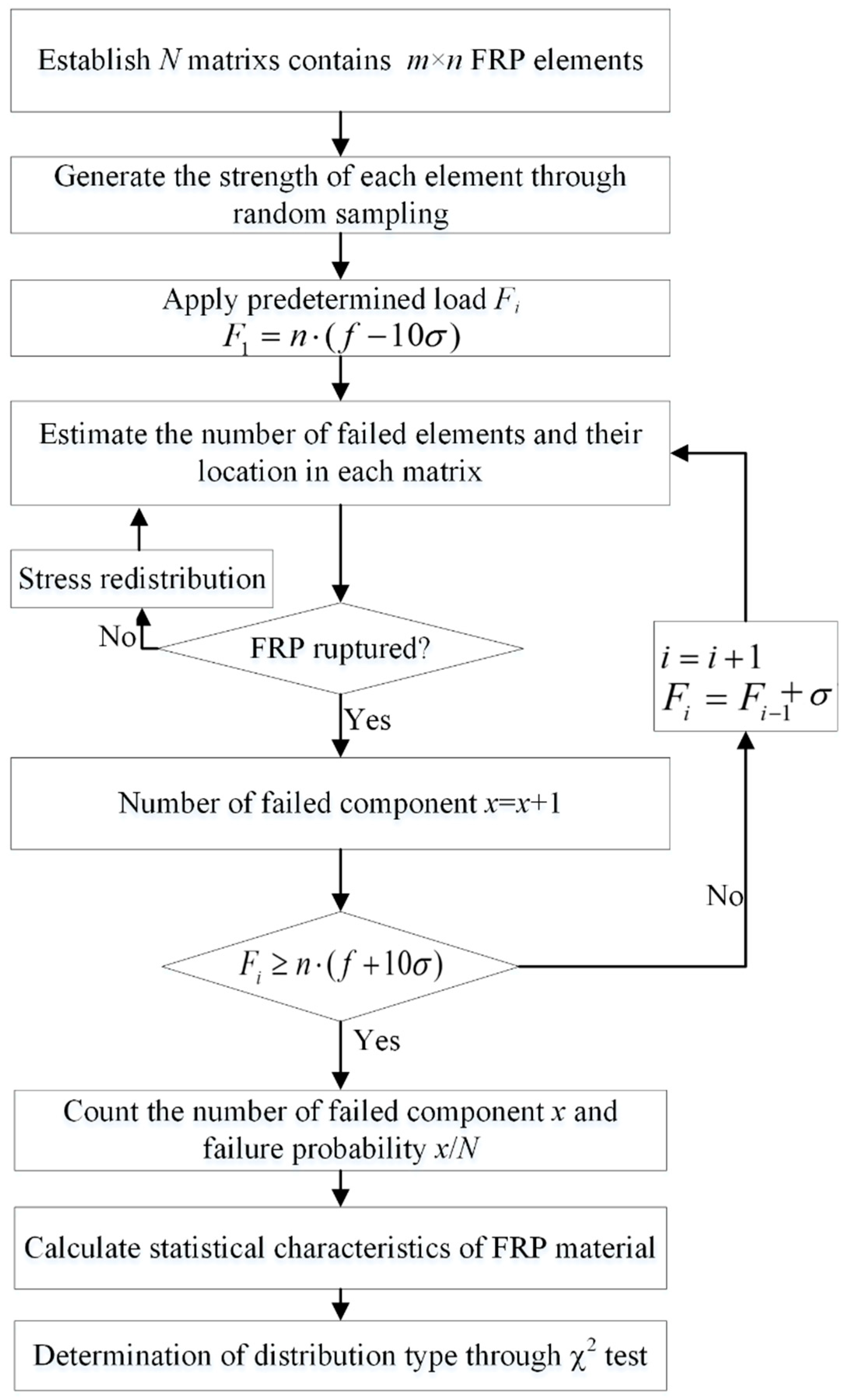
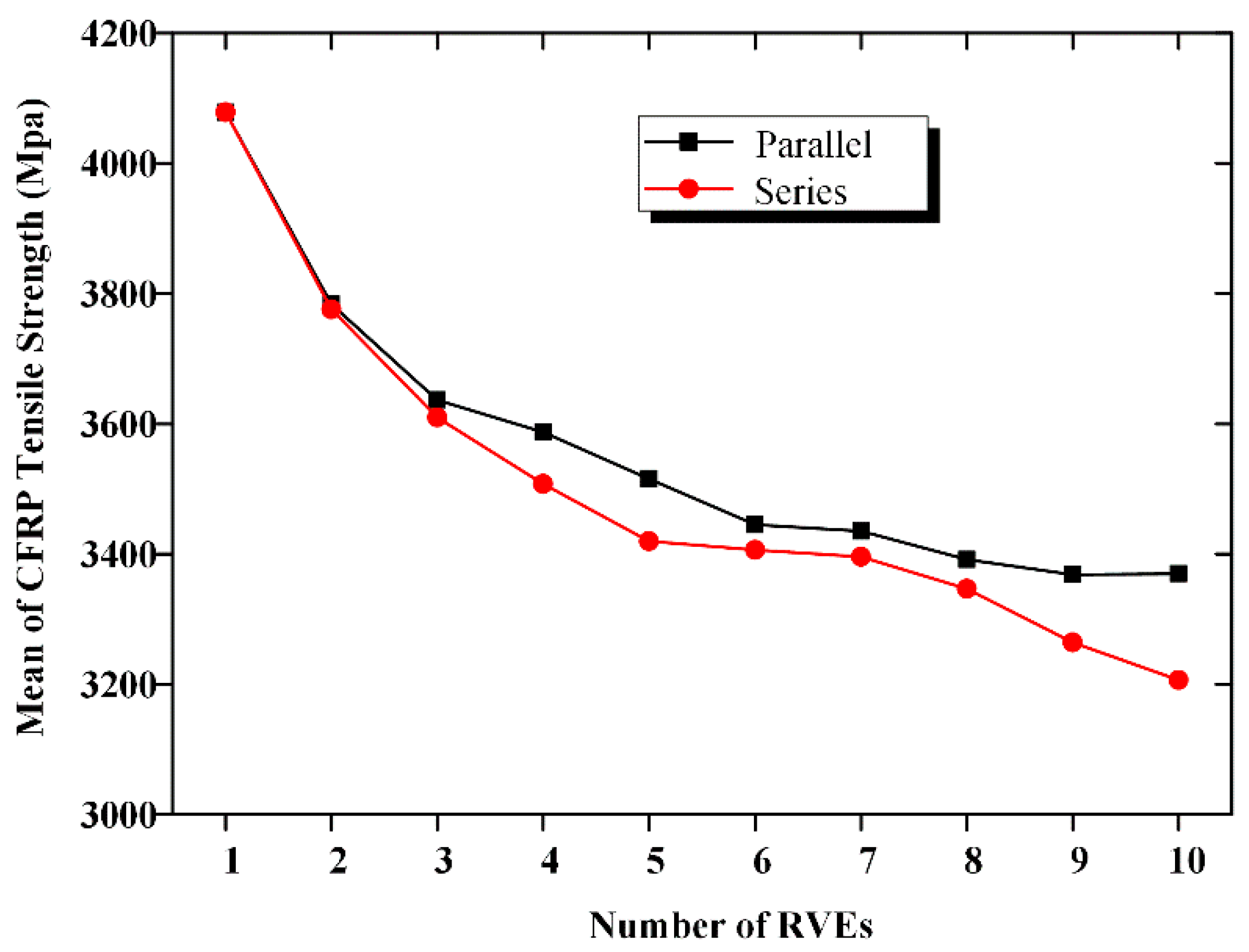

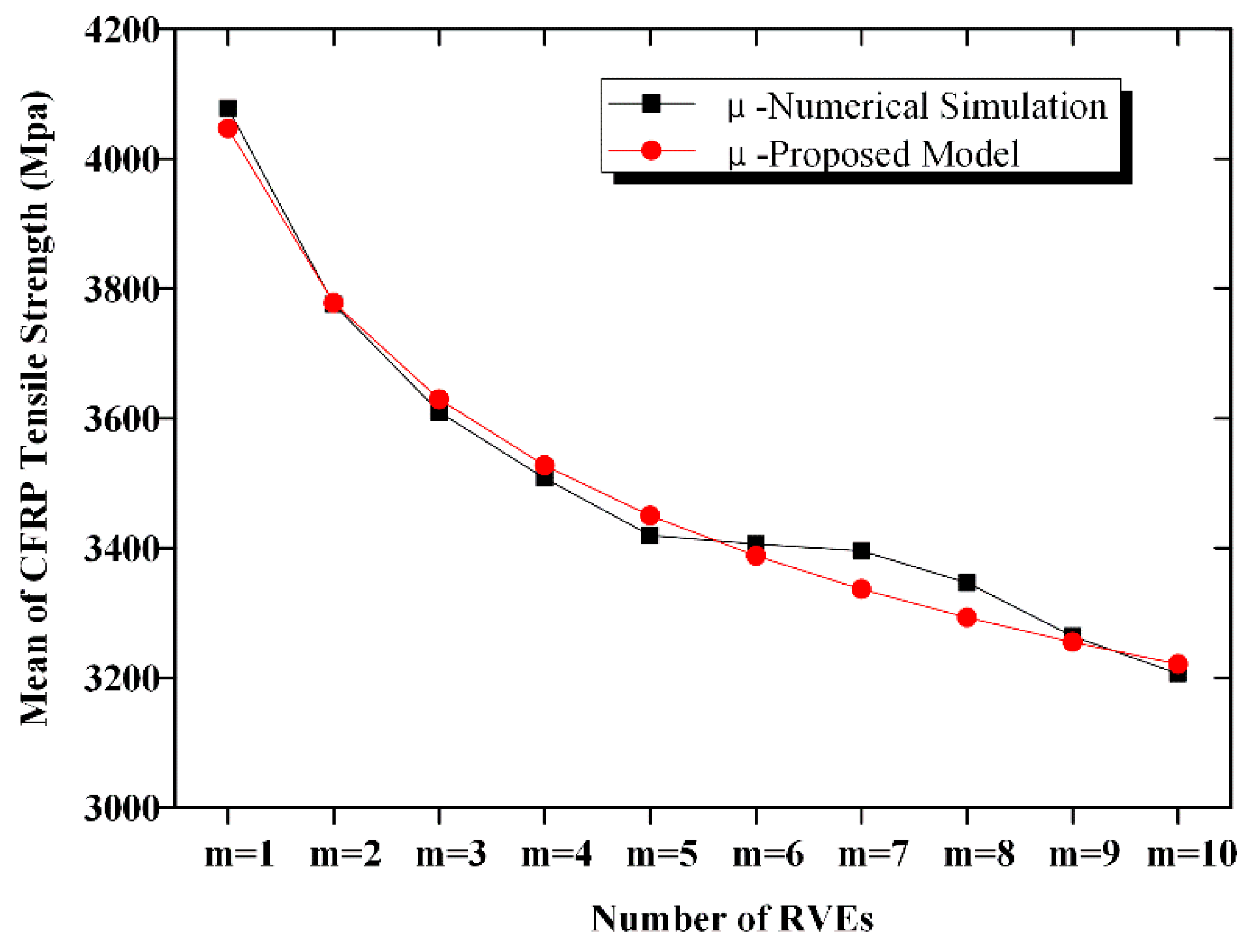
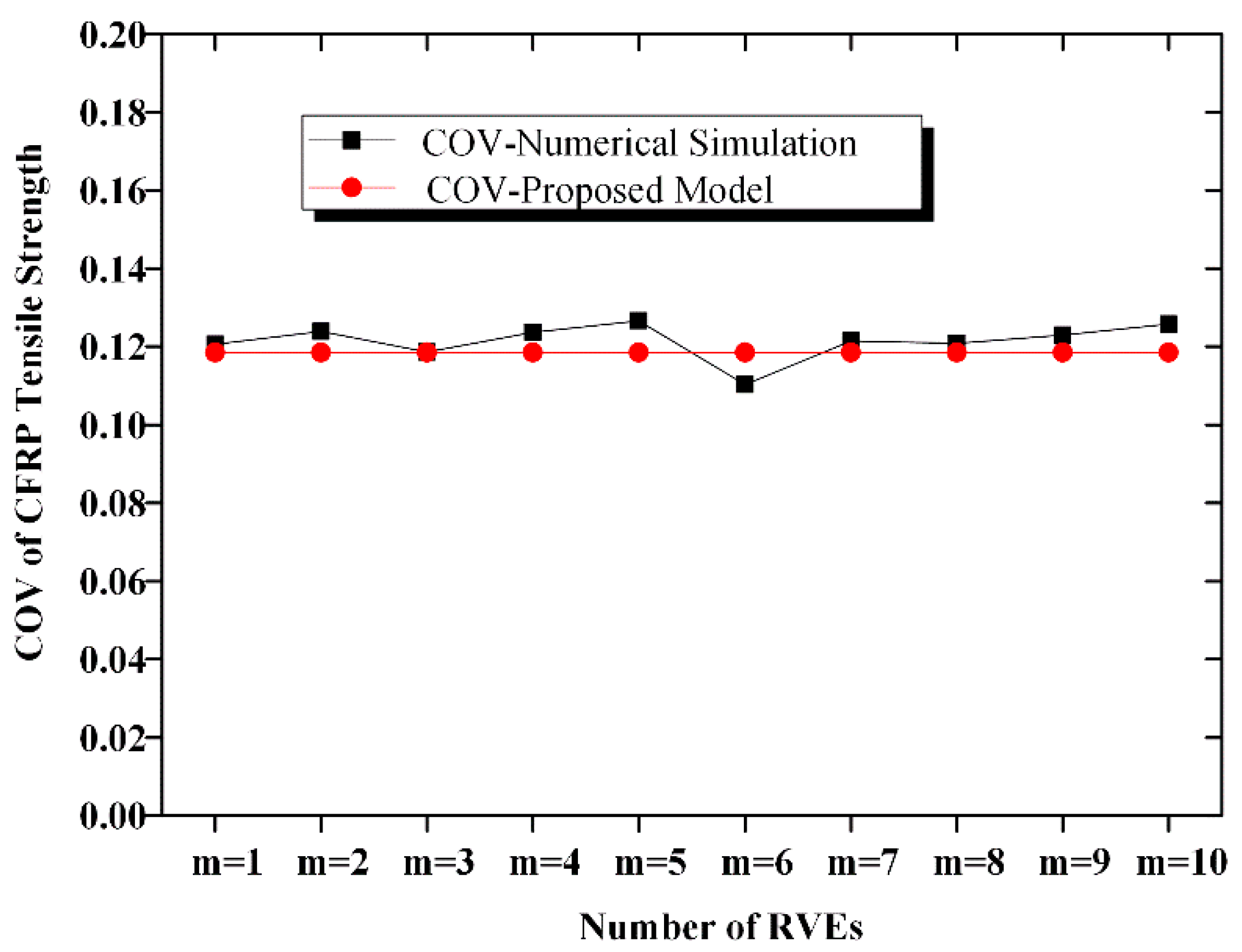

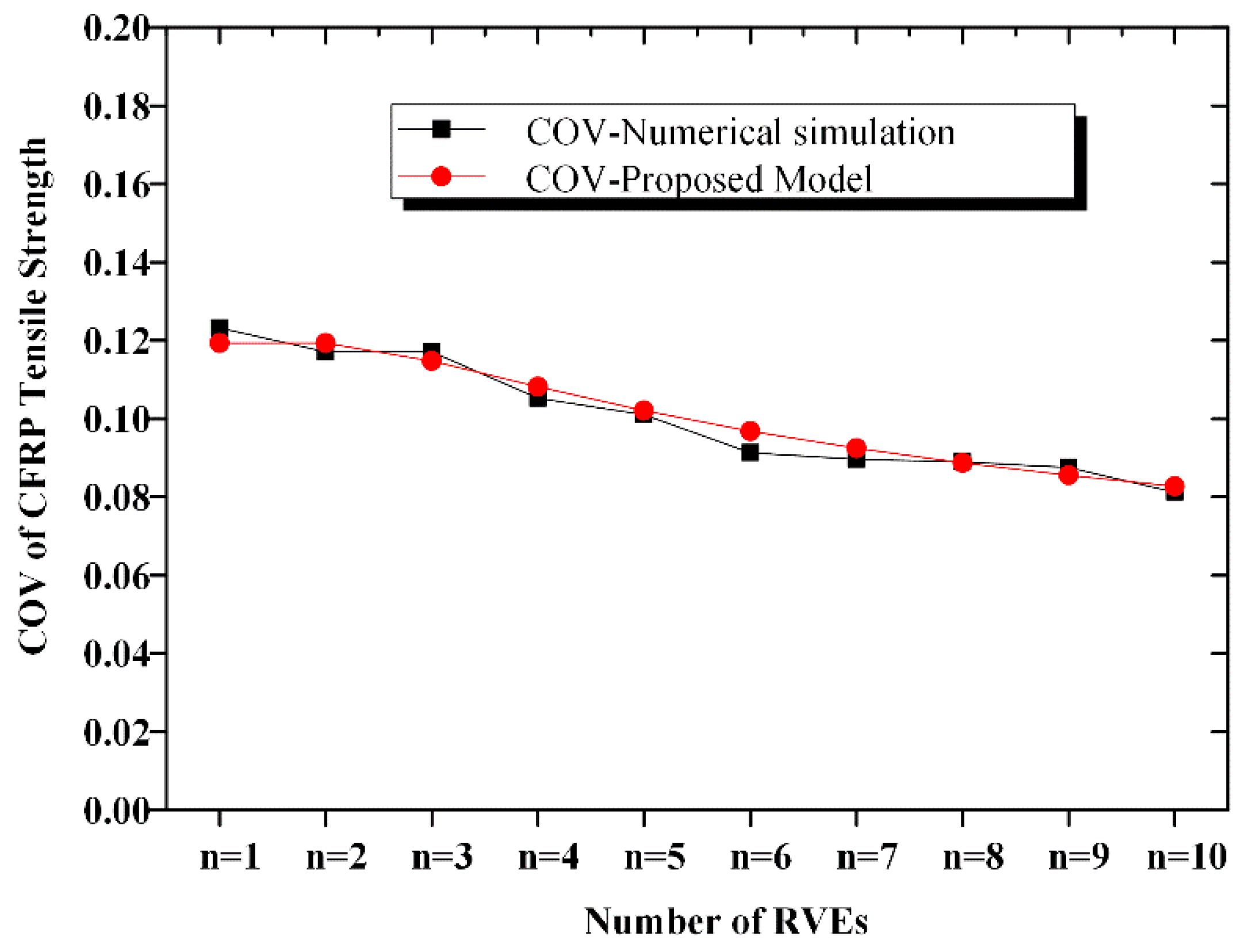


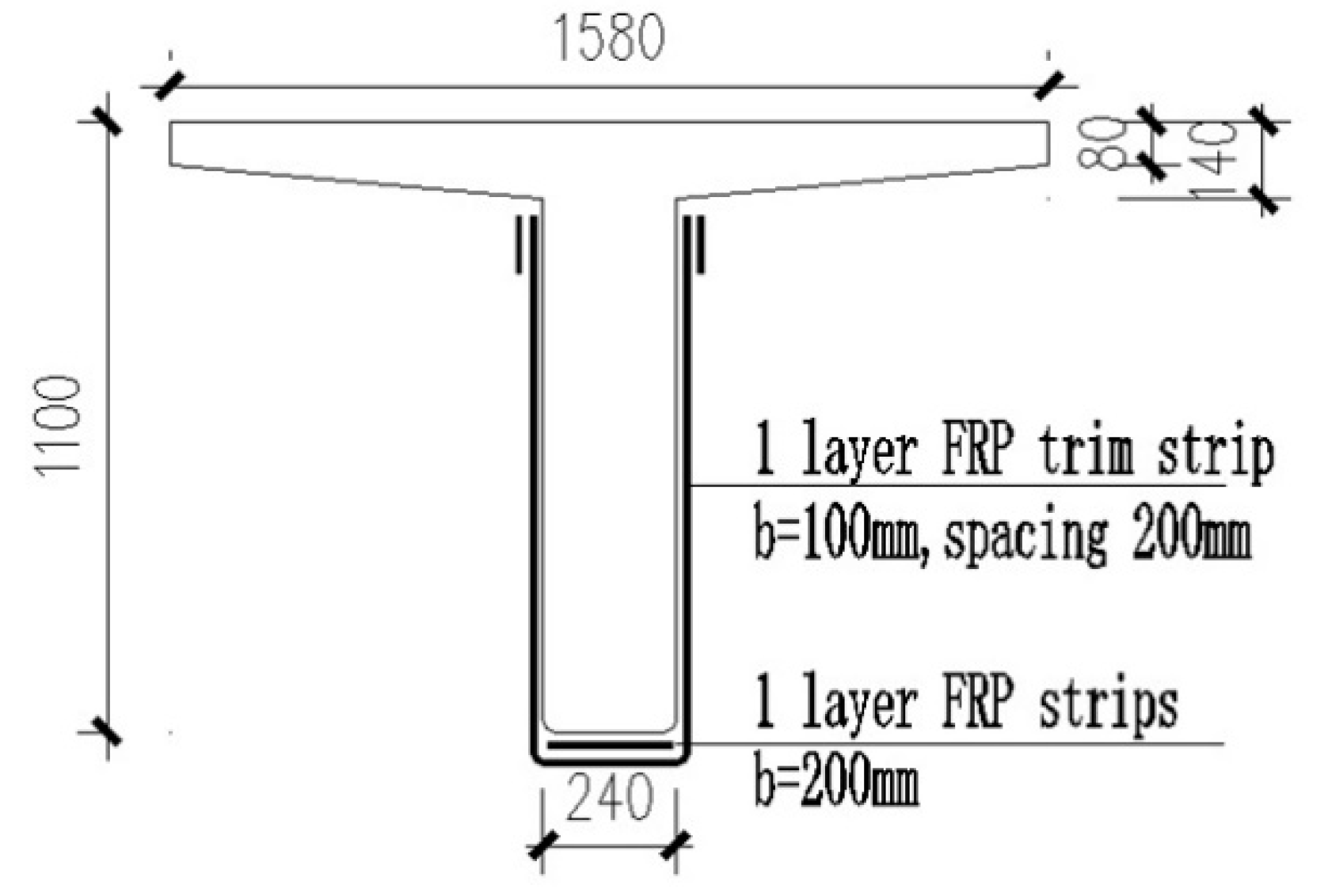
| Statistical Characteristics | Mean (MPa) | COV | Distribution Type |
|---|---|---|---|
| Value | 4078 | 0.12 | Weibull’s distribution |
| m | n | (16-2-1) | Normal Distribution | Log-Normal Distribution | Weibull’s Distribution | Gamma Distribution |
|---|---|---|---|---|---|---|
| 1 | 1 | 29.819 | 3.450 | 8.599 | 3.368 | 4.400 |
| 2 | 1 | 29.819 | 9.200 | 15.326 | 3.766 | 11.615 |
| 3 | 1 | 29.819 | 6.097 | 9.519 | 4.081 | 8.396 |
| 4 | 1 | 29.819 | 9.892 | 13.070 | 7.251 | 11.684 |
| 5 | 1 | 29.819 | 11.219 | 14.616 | 7.295 | 12.863 |
| 6 | 1 | 29.819 | 9.236 | 12.792 | 5.531 | 11.287 |
| 7 | 1 | 29.819 | 8.987 | 9.544 | 12.003 | 9.368 |
| 8 | 1 | 29.819 | 14.790 | 14.281 | 24.031 | 14.394 |
| 9 | 1 | 29.819 | 14.349 | 12.158 | 33.040 | 12.845 |
| 10 | 1 | 29.819 | 6.466 | 7.619 | 6.974 | 6.867 |
| 1 | 2 | 29.819 | 4.027 | 6.265 | 4.708 | 5.273 |
| 1 | 3 | 29.819 | 7.315 | 12.884 | 2.717 | 9.794 |
| 1 | 4 | 29.819 | 12.472 | 16.008 | 9.961 | 14.372 |
| 1 | 5 | 29.819 | 10.716 | 16.062 | 5.845 | 13.210 |
| 1 | 6 | 29.819 | 15.178 | 25.477 | 6.651 | 23.487 |
| 1 | 7 | 29.819 | 2.854 | 1.651 | 16.599 | 1.898 |
| 1 | 8 | 29.819 | 27.733 | 33.521 | 24.190 | 30.065 |
| 1 | 9 | 29.819 | 11.805 | 19.860 | 6.321 | 14.722 |
| 1 | 10 | 29.819 | 16.747 | 21.015 | 13.123 | 18.953 |
| Variables | Bias | COV | Distribution Type |
|---|---|---|---|
| Model uncertainty factor of CFRP-strengthened RC beam in flexure γmfc | 1.0980 | 0.1190 | Normal |
| Yield stress of steel reinforcing fy | 1.0900 | 0.0606 | Normal |
| Reinforced steel area in concrete As | 1.0000 | 0.0350 | Normal |
| 28-day yield strength of concrete fc | 1.2510 | 0.1464 | Normal |
| Uncertainty factor: weight of concrete λconc | 0.9865 | 0.0980 | Normal |
| Uncertainty factor: weight of asphalt λasph | 0.9891 | 0.1114 | Normal |
| Impact on girders Ibeam | 1.0000 | 0.0500 | Gumbel |
| Uncertainty factor: live load moment on girder | 1.3500 | 0.162 | Gumbel |
| Width of cross section b | 1.0013 | 0.0081 | Normal |
| Height of cross section h0 | 1.0124 | 0.0229 | Normal |
| Design distribution of lane load qk | 0.7882 | 0.1082 | Gumbel |
| Crowd load qr | 0.5786 | 0.3911 | Gumbel |
| Tensile strength of CFRP laminates fFRP (size effect not considered) | 1.1900 | 0.1260 | Weibull |
| Tensile strength of CFRP laminates fFRP (size effect considered) | 0.7512 | 0.0805 | Weibull |
| Thickness of CFRP strips t | 0.8250 | 0.0400 | Normal |
| Elasticity modulus of CFRP laminates Ef | 1.1800 | 0.1040 | Normal |
| Existing Bridge | Reference Scheme | Reinforcement Scheme Considering Size Effect | |
|---|---|---|---|
| Reliability index | 4.1 | 5.4 | 5.0 |
| Failure probability | 2.07 × 10−5 | 3.33 × 10−8 | 2.87 × 10-7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, H.-B.; Wang, Y.-F. Reliability Analysis of CFRP-Strengthened RC Bridges Considering Size Effect of CFRP. Materials 2019, 12, 2247. https://doi.org/10.3390/ma12142247
Xie H-B, Wang Y-F. Reliability Analysis of CFRP-Strengthened RC Bridges Considering Size Effect of CFRP. Materials. 2019; 12(14):2247. https://doi.org/10.3390/ma12142247
Chicago/Turabian StyleXie, Hui-Bing, and Yuan-Feng Wang. 2019. "Reliability Analysis of CFRP-Strengthened RC Bridges Considering Size Effect of CFRP" Materials 12, no. 14: 2247. https://doi.org/10.3390/ma12142247
APA StyleXie, H.-B., & Wang, Y.-F. (2019). Reliability Analysis of CFRP-Strengthened RC Bridges Considering Size Effect of CFRP. Materials, 12(14), 2247. https://doi.org/10.3390/ma12142247





