Graphene Oxide and Its Inorganic Composites: Fabrication and Electrorheological Response
Abstract
1. Introduction
2. Fabrication and Morphologies
2.1. Electrostatic Interaction
2.1.1. Adjustment of the pH
2.1.2. Ultrasonic-Assisted Synthesis
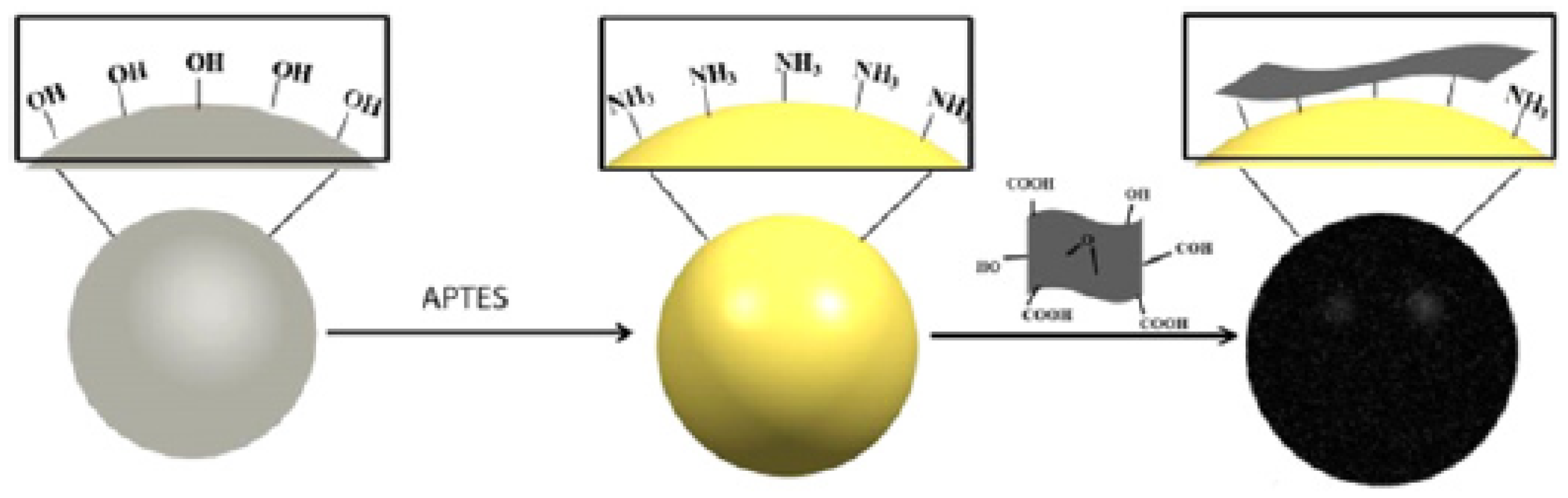
2.1.3. Surface Modification
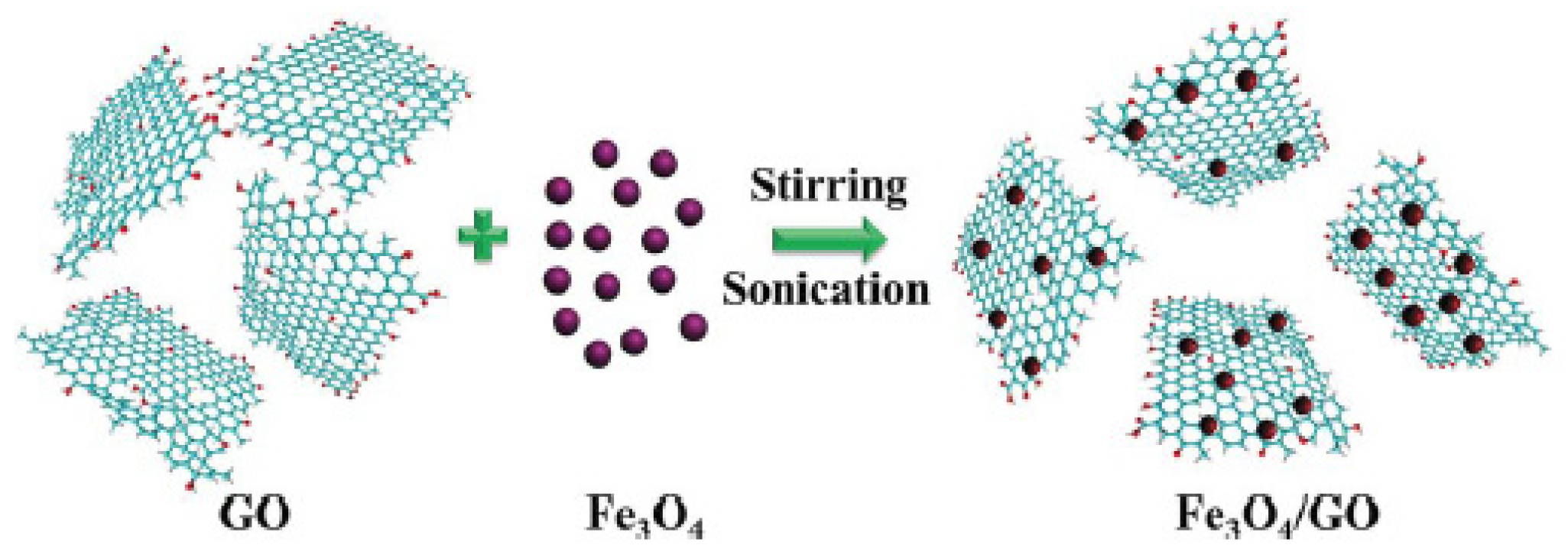
2.2. In-situ Growth
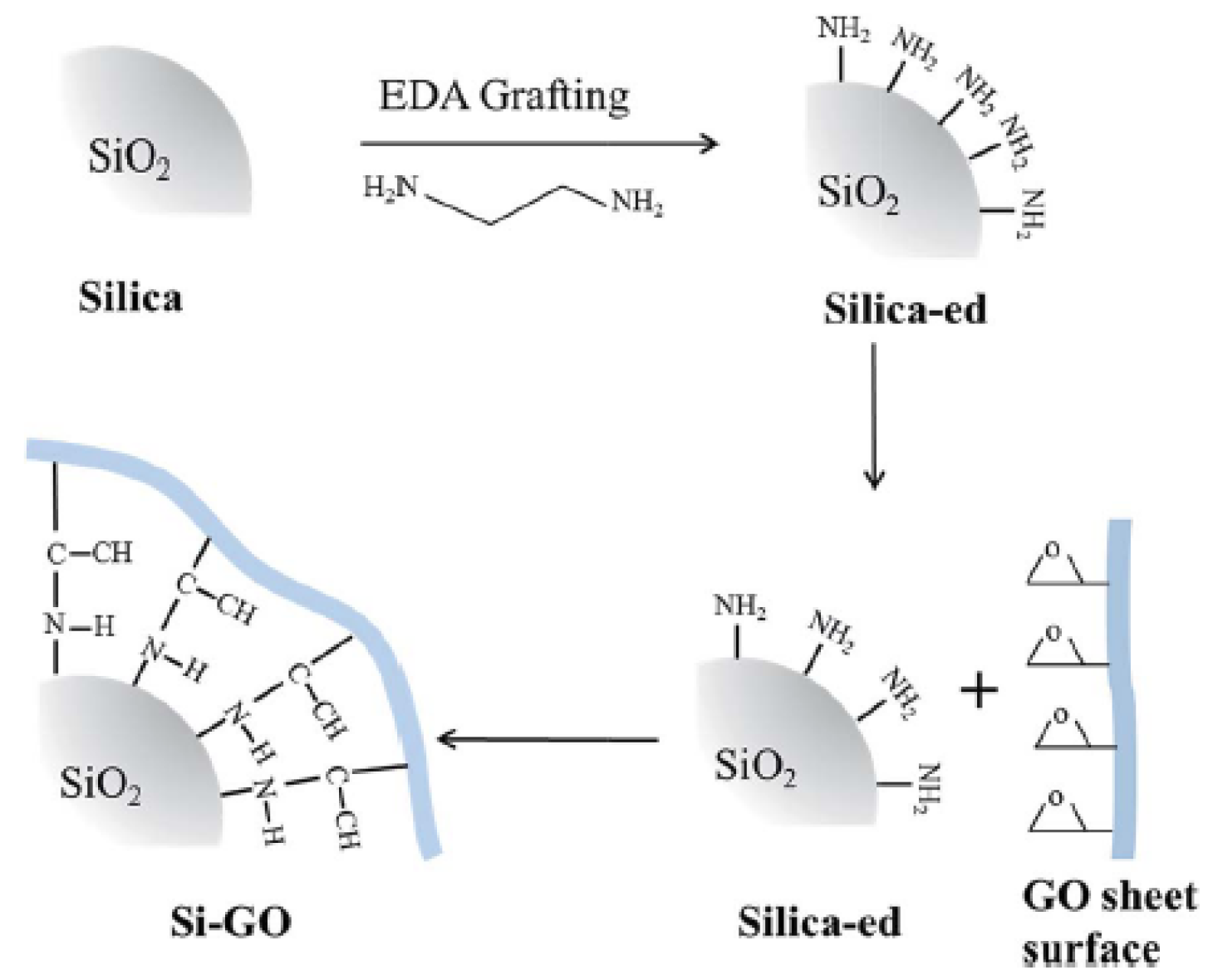
2.3. Chemical Grafting
3. Electrorheological Characteristics
3.1. Formation of Chain-Like Structures
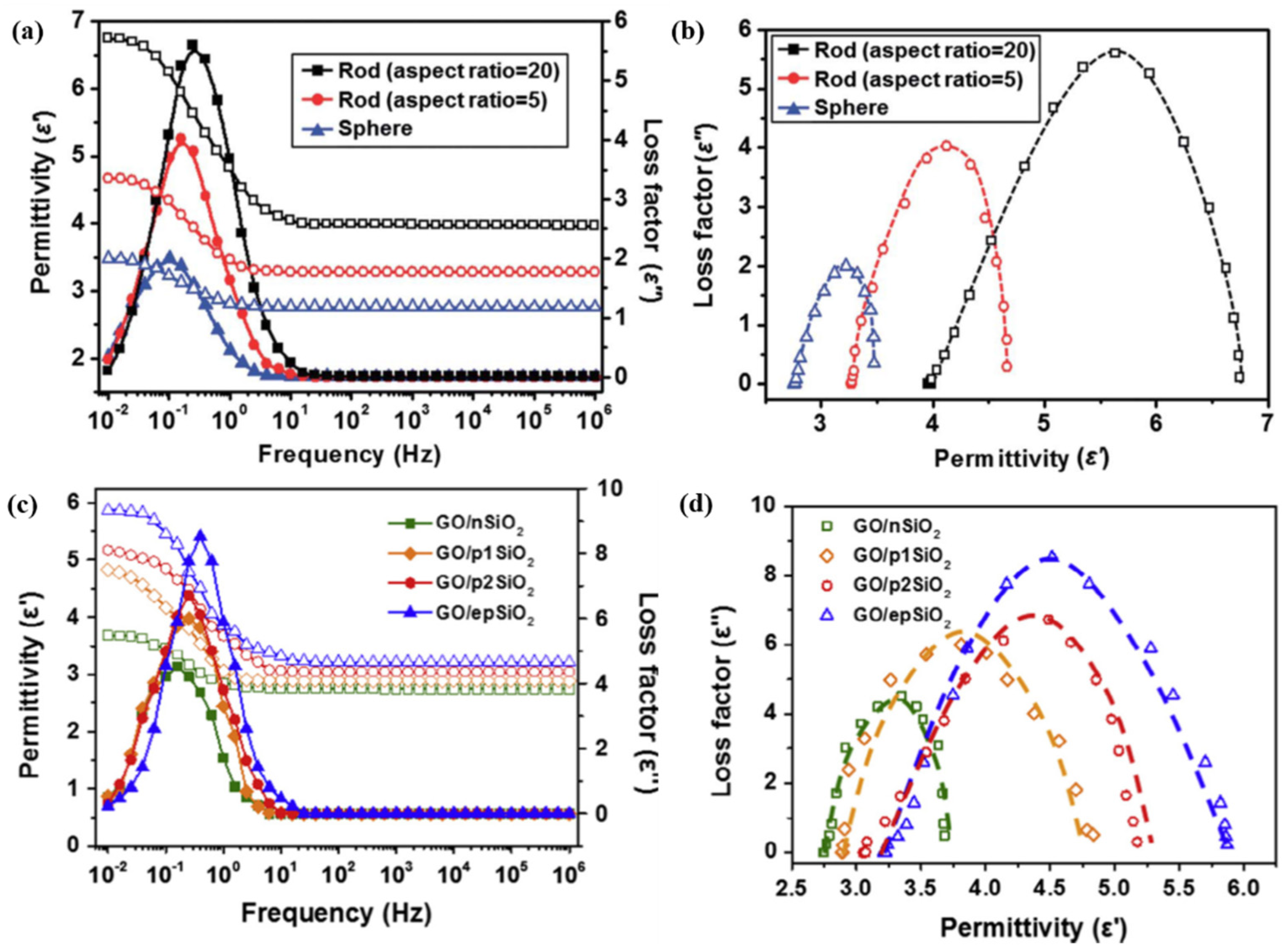
3.2. Dielectric Properties
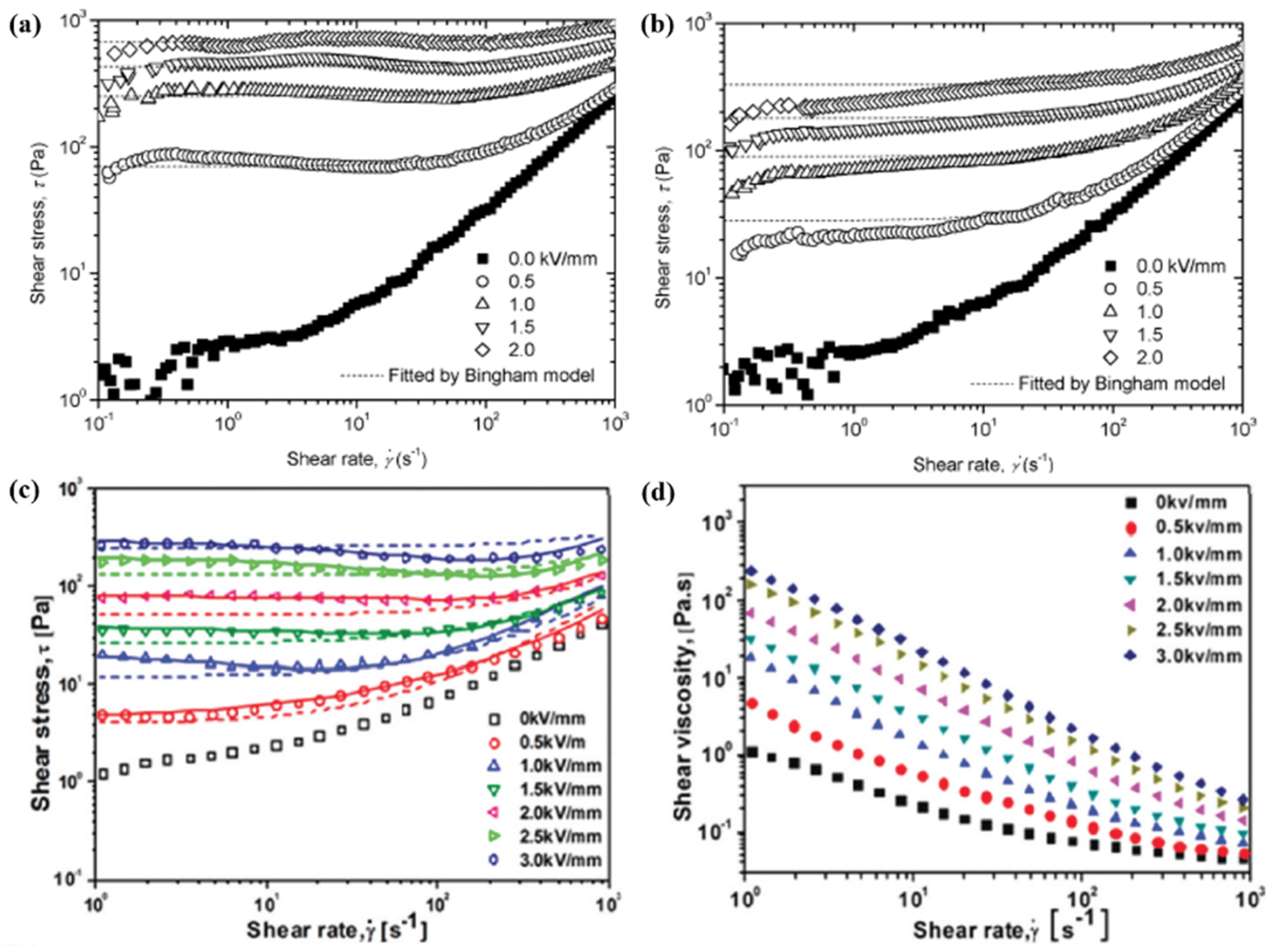
3.3. Steady-Shear Flow Curves
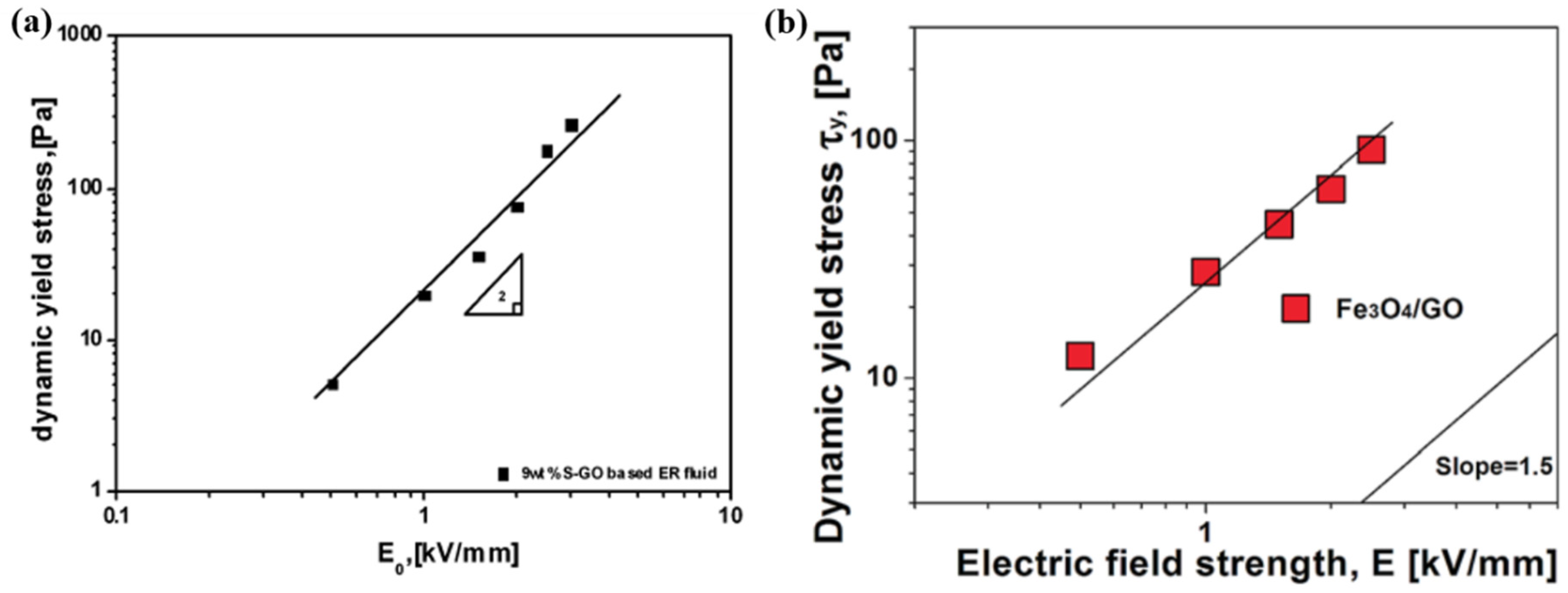
3.4. Dynamic Yield Stress
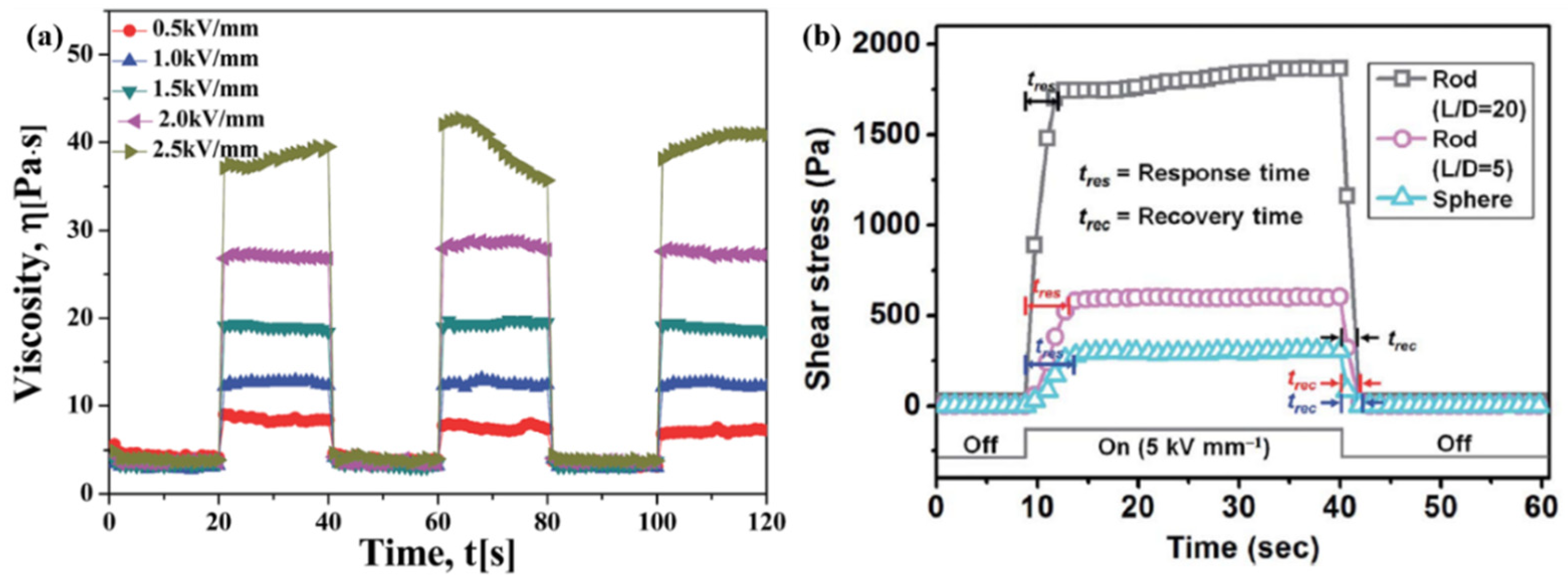
3.5. Response Sensibility
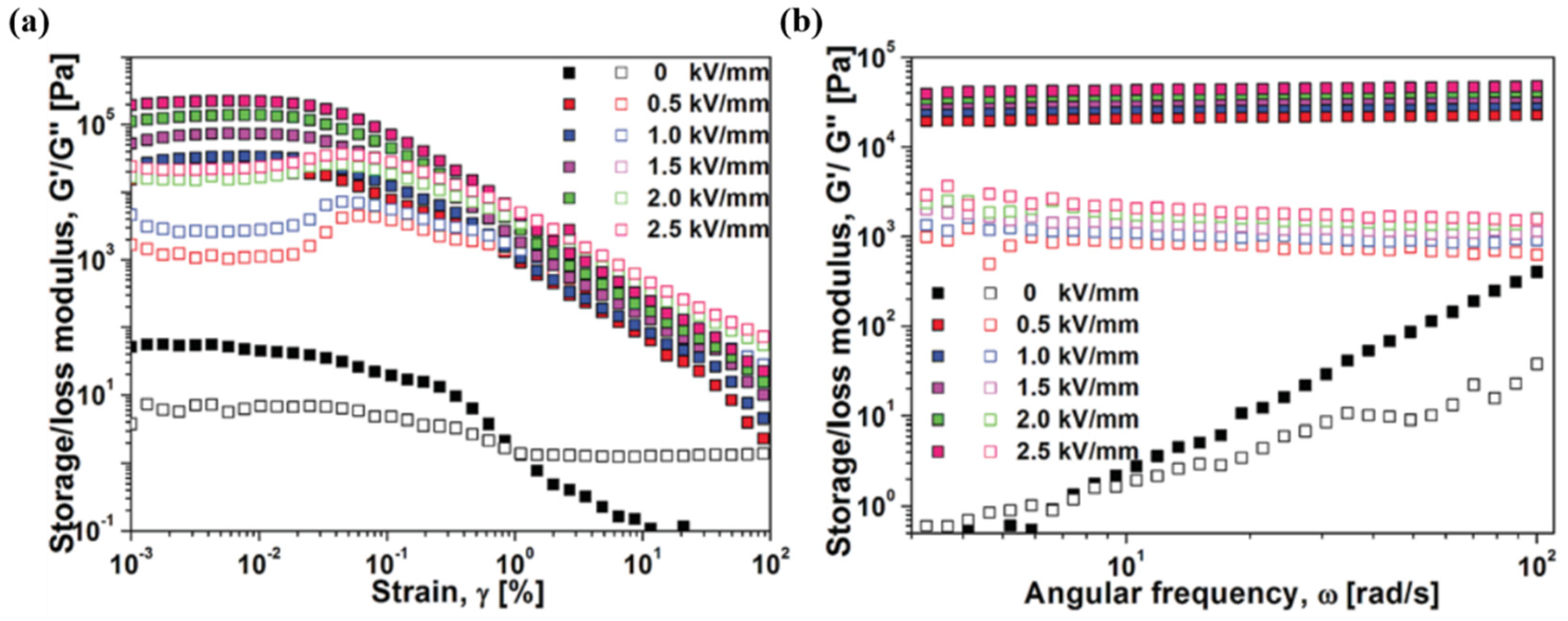
3.6. Dynamic Oscillation Analysis
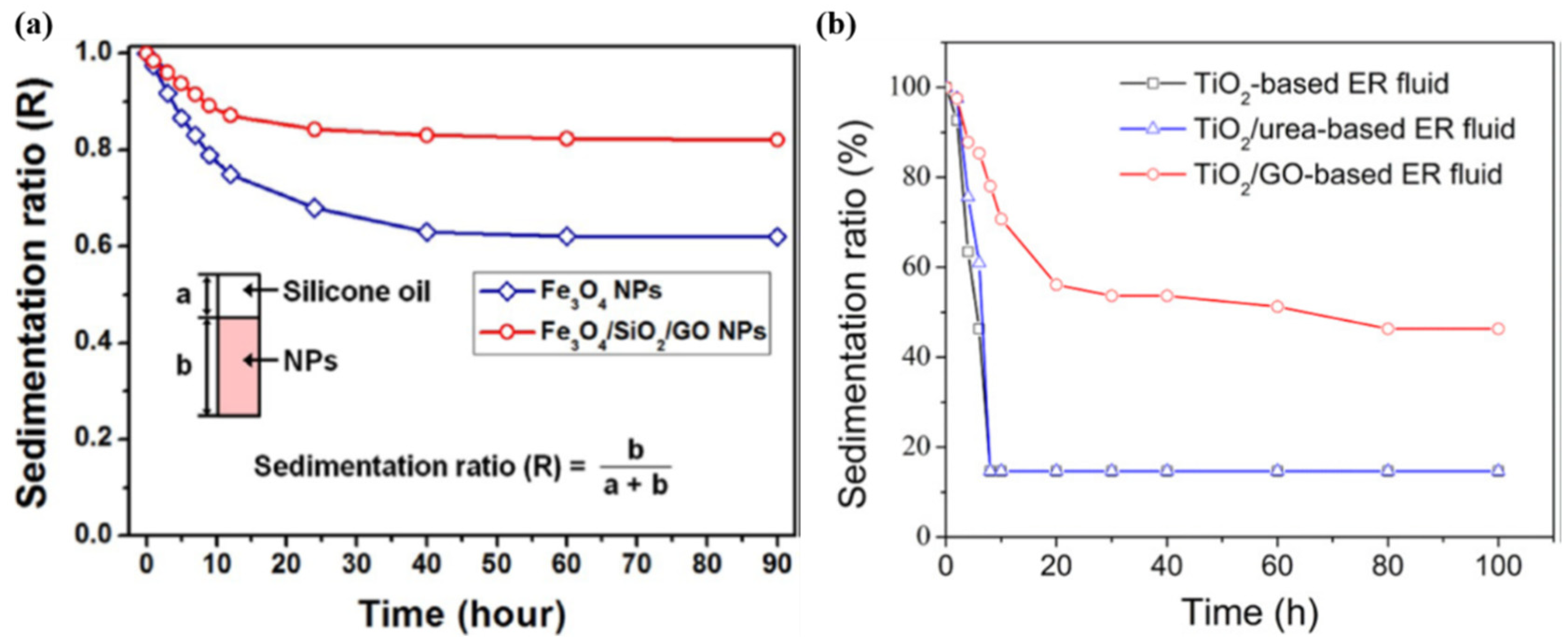
3.7. Sedimentation Stability
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rathinam, K.; Singh, S.P.; Li, Y.; Kasher, R.; Tour, J.M.; Arnusch, C.J. Polyimide derived laser-induced graphene as adsorbent for cationic and anionic dyes. Carbon 2017, 124, 515–524. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, Y.; Yang, K.; Zhang, B.; Zhao, K.; Xiong, G.; Zhang, X. Mechanically robust and electrically conductive graphene-paper/glass-fibers/epoxy composites for stimuli-responsive sensors and Joule heating deicers. Carbon 2017, 124, 296–307. [Google Scholar] [CrossRef]
- Wu, G.; Meyyappan, M.; Lai, K. Simulation of graphene field-effect transistor biosensors for bacterial detection. Sensors 2018, 18, 1715. [Google Scholar] [CrossRef]
- He, C.; Tao, J. Two-dimensional Co3W3C nanosheets on graphene nanocomposition: An Pt-like electrocatalyst toward hydrogen evolution reaction in wide pH range. Mater. Today Energy 2018, 8, 65–72. [Google Scholar] [CrossRef]
- Ghosh, S.; Polaki, S.R.; Sahoo, G.; Jin, E.-M.; Kamruddin, M.; Cho, J.S.; Jeong, S.M. Designing metal oxide-vertical graphene nanosheets structures for 2.6 V aqueous asymmetric electrochemical capacitor. J. Ind. Eng. Chem. 2019, 72, 107–116. [Google Scholar] [CrossRef]
- Lin, S.; Ju, S.; Shi, G.; Zhang, J.; He, Y.; Jiang, D. Ultrathin nitrogen-doping graphene films for flexible and stretchable EMI shielding materials. J. Mater. Sci. 2019, 54, 7165–7179. [Google Scholar] [CrossRef]
- Ranjan, P.; Agrawal, S.; Sinha, A.; Rao, T.R.; Balakrishnan, J.; Thakur, A.D. A low-cost non-explosive synthesis of graphene oxide for scalable applications. Sci. Rep. UK 2018, 8, 12007. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Fugetsu, B. Mass production of graphene oxide from expanded graphite. Mater. Lett. 2013, 109, 207–210. [Google Scholar] [CrossRef]
- Pei, S.; Cheng, H.-M. The reduction of graphene oxide. Carbon 2012, 50, 3210–3228. [Google Scholar] [CrossRef]
- Guex, L.G.; Sacchi, B.; Peuvot, K.F.; Andersson, R.L.; Pourrahimi, A.M.; Ström, V.; Farris, S.; Olsson, R.T. Experimental review: Chemical reduction of graphene oxide (GO) to reduced graphene oxide (rGO) by aqueous chemistry. Nanoscale 2017, 9, 9562–9571. [Google Scholar] [CrossRef]
- Wu, S.-Y.; An, S.S.A.; Hulme, J. Current applications of graphene oxide in nanomedicine. Int. J. Nanomed. 2015, 10, 9–24. [Google Scholar]
- Wang, X.; Yu, S.; Jin, J.; Wang, H.; Alharbi, N.S.; Alsaedi, A.; Hayat, T.; Wang, X. Application of graphene oxides and graphene oxide-based nanomaterials in radionuclide removal from aqueous solutions. Sci. Bull. 2016, 61, 1583–1593. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, C.; Chen, Y.; Wang, J.; Wang, C.; Zhu, X. Lithium storage performance and mechanism of VS4/rGO as an electrode material associated with lithium-sulfur batteries. J. Alloy Compd. 2019, 785, 855–861. [Google Scholar] [CrossRef]
- Abdullah, M.F.; Hashim, A.M. Improved coverage of rGO film on Si inverted pyramidal microstructures for enhancing the photovoltaic of rGO/Si heterojunction solar cell. Mater. Sci. Semicon. Proc. 2019, 96, 137–144. [Google Scholar] [CrossRef]
- Yang, M.; Wang, L.; Cheng, Y.; Ma, K.; Wei, X.; Jia, P.; Gong, Y.; Zhang, Y.; Yang, J.; Zhao, J. Light- and pH-responsive self-healing hydrogel. J. Mater. Sci. 2019, 54, 9983–9994. [Google Scholar] [CrossRef]
- Li, Q.; Wu, J.; Huang, L.; Gao, J.; Zhou, H.; Shi, Y.; Pan, Q.; Zhang, G.; Du, Y.; Liang, W. Sulfur dioxide gas-sensitive materials based on zeolitic imidazolate framework-derived carbon nanotubes. J. Mater. Chem. A 2018, 6, 12115–12124. [Google Scholar] [CrossRef]
- Sagi, R.; Akerman, M.; Ramakrishnan, S.; Asscher, M. Temperature effect on transport, charging, and binding of low-energy electrons interacting with amorphous solid water films. J. Phys. Chem. C 2018, 122, 9985–9996. [Google Scholar] [CrossRef]
- Miclos, S.; Savastru, D.; Savastru, R.; Lancranjan, I.I. Transverse mechanical stress and optical birefringence induced into single-mode optical fibre embedded in a smart polymer composite material. Compos. Struct. 2019, 218, 15–26. [Google Scholar] [CrossRef]
- Stanway, R. Smart fluids: Current and future developments. Mater. Sci. Technol. 2004, 20, 931–939. [Google Scholar] [CrossRef]
- Liu, Y.D.; Choi, H.J. Electrorheological fluids: Smart soft matter and characteristics. Soft Matter. 2012, 8, 11961–11978. [Google Scholar] [CrossRef]
- Genç, S.; Phulé, P.P. Rheological properties of magnetorheological fluids. Smart Mater. Struct. 2002, 11, 140–146. [Google Scholar] [CrossRef]
- Son, K.J. A discrete element model for the influence of surfactants on sedimentation characteristics of magnetorheological fluids. Korea Austral. Rheol. J. 2018, 30, 29–39. [Google Scholar] [CrossRef]
- Abed, A.; Bouzidane, A.; Thomas, M.; Zahloul, H. Performance characteristics of a three-pad hydrostatic squeeze film damper compensated with new electrorheological valve restrictors. Proc. Inst. Mech. Eng. Part J J. Eng. 2016, 231, 889–899. [Google Scholar] [CrossRef]
- Bilyk, V.A.; Korobko, E.V. Research of the influence of dissipative heating on the performance characteristics of electrorheological shock absorbers. J. Intell. Mater. Sys. Struct. 2015, 26, 1906–1912. [Google Scholar] [CrossRef]
- Behbahani, S.B.; Tan, X. Design and dynamic modeling of electrorheological fluid-based variable-stiffness fin for robotic fish. Smart Mater. Struct. 2017, 26, 085014. [Google Scholar] [CrossRef]
- Tonazzini, A.; Sadeghi, A.; Mazzolai, B. Electrorheological valves for flexible fluidic actuators. Soft Robot. 2016, 3, 34–41. [Google Scholar] [CrossRef]
- Madeja, J.; Kesy, Z.; Kesy, A. Application of electrorheological fluid in a hydrodynamic clutch. Smart Mater. Struct. 2011, 20, 105005. [Google Scholar] [CrossRef]
- Davis, L. Polarization forces and conductivity effects in electrorheological fluids. J. Appl. Phys. 1992, 72, 1334–1340. [Google Scholar] [CrossRef]
- Khusid, B.; Acrivos, A. Effects of conductivity in electric-field-induced aggregation in electrorheological fluids. Phys. Rev. E 1995, 52, 1669–1693. [Google Scholar] [CrossRef]
- Clercx, H.; Bossis, G. Many-body electrostatic interactions in electrorheological fluids. Phys. Rev. E 1993, 48, 2721–2738. [Google Scholar] [CrossRef]
- Sung, J.H.; Cho, M.S.; Choi, H.J.; Jhon, M.S. Electrorheology of semiconducting polymers. J. Ind. Eng. Chem. 2004, 10, 1217–1229. [Google Scholar]
- Tangboriboon, N.; Uttanawanit, N.; Longtong, M.; Wongpinthong, P.; Sirivat, A.; Kunanuruksapong, R. Electrical and electrorheological properties of alumina/natural rubber (STR XL) composites. Materials 2010, 3, 656–671. [Google Scholar] [CrossRef]
- He, K.; Wen, Q.; Wang, C.; Wang, B.; Yu, S.; Hao, C.; Chen, K. The preparation and electrorheological behavior of bowl-like titanium oxide nanoparticles. Soft Matter. 2017, 13, 7677–7688. [Google Scholar] [CrossRef] [PubMed]
- Jang, W.H.; Kim, J.W.; Choi, H.J.; Jhon, M.S. Synthesis and electrorheology of camphorsulfonic acid doped polyaniline suspensions. Colloid Polym. Sci. 2001, 279, 823–827. [Google Scholar] [CrossRef]
- Park, I.H.; Kwon, S.H.; Choi, H.J. Emulsion-polymerized polyindole nanoparticles and their electrorheology. J. Appl. Polym. Sci. 2018, 135, 46384. [Google Scholar] [CrossRef]
- Kim, M.H.; Bae, D.H.; Choi, H.J.; Seo, Y. Synthesis of semiconducting poly(diphenylamine) particles and analysis of their electrorheological properties. Polymer 2017, 119, 40–49. [Google Scholar] [CrossRef]
- Parmar, K.P.S.; Méheust, Y.; Schjelderupsen, B.; Fossum, J.O. Electrorheological Suspensions of Laponite in Oil: Rheometry Studies. Langmuir 2008, 24, 1814–1822. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.D.; Song, I.C. Electrorheological and dielectric properties of polypyrrole dispersions. J. Mater. Sci. 2002, 37, 5051–5055. [Google Scholar] [CrossRef]
- Otsubo, Y.; Sekine, M.; Katayama, S. Electrorheological properties of silica suspensions. J. Rheol. 1992, 36, 479–496. [Google Scholar] [CrossRef]
- Dhar, P.; Katiyar, A.; Pattamatta, A.; Das, S.K. Large electrorheological phenomena in graphene nano-gels. Nanotechnology 2017, 28, 035702. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, Y.; Yin, J.; Zhao, X. Preparation and enhanced electro-responsive characteristic of graphene/layered double-hydroxide composite dielectric nanoplates. J. Mater. Chem. C 2014, 2, 10386–10394. [Google Scholar] [CrossRef]
- Yin, J.; Chang, R.; Shui, Y.; Zhao, X. Preparation and enhanced electro-responsive characteristic of reduced graphene oxide/polypyrrole composite sheet suspensions. Soft Matter. 2013, 9, 7468–7478. [Google Scholar] [CrossRef]
- Zhang, W.L.; Liu, Y.D.; Choi, H.J.; Kim, S.G. Electrorheology of graphene oxide. ACS Appl. Mater. Interf. 2012, 4, 2267–2272. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.-Y.; Jang, J. Highly stable, concentrated dispersions of graphene oxide sheets and their electro-responsive characteristics. Soft Matter. 2012, 8, 7348–7350. [Google Scholar] [CrossRef]
- Shin, K.-Y.; Lee, S.; Hong, S.; Jang, J. Graphene size control via a mechanochemical method and electroresponsive properties. ACS Appl. Mater. Interf. 2014, 6, 5531–5537. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.L.; Park, B.J.; Choi, H.J. Colloidal graphene oxide/polyaniline nanocomposite and its electrorheology. Chem. Commun. 2010, 46, 5596–5598. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Wang, X.; Wang, J.; Liu, F.; Zhang, M.; Xu, C. Microwave-assisted covalent modification of graphene nanosheets with chitosan and its electrorheological characteristics. Appl. Surf. Sci. 2011, 257, 2637–2642. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, W.L.; Choi, H.J. Facile fabrication of self-assembled PMMA/graphene oxide composite particles and their electroresponsive properties. Colloid Polym. Sci. 2013, 291, 955–962. [Google Scholar] [CrossRef]
- Li, Y.; Guan, Y.; Liu, Y.; Yin, J.; Zhao, X. Highly stable nanofluid based on polyhedral oligomeric silsesquioxane-decorated graphene oxide nanosheets and its enhanced electro-responsive behavior. Nanotechnology 2016, 27, 195702. [Google Scholar] [CrossRef]
- Ilčíková, M.; Mrlík, M.; Babayan, V.; Kasák, P. Graphene oxide modified by betaine moieties for improvement of electrorheological performance. RSC Adv. 2015, 5, 57820–57827. [Google Scholar] [CrossRef]
- Kosmulski, M. Oxide/electrolyte interface: Electric double layer in mixed solvent systems. Colloids Surf. A 1995, 95, 81–100. [Google Scholar] [CrossRef]
- Tombácz, E. pH-dependent surface charging of metal oxides. Period. Polytech. Chem. Eng. 2009, 53, 77–86. [Google Scholar] [CrossRef]
- Zhang, W.L.; Choi, H.J. Fast and facile fabrication of a graphene oxide/titania nanocomposite and its electro-responsive characteristics. Chem. Commun. 2011, 47, 12286–12288. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.L.; Choi, H.J.; Leong, Y.K. Facile fabrication of graphene oxide-wrapped alumina particles and their electrorheological characteristics. Mater. Chem. Phys. 2014, 145, 151–155. [Google Scholar] [CrossRef]
- Zhang, W.L.; Tian, Y.; Liu, Y.D.; Song, Z.Q.; Liu, J.Q.; Choi, H.J. Large scale and facile sonochemical synthesis of magnetic graphene oxide nanocomposites and their dual electro/magneto-stimuli responses. RSC Adv. 2016, 6, 77925–77930. [Google Scholar] [CrossRef]
- Yin, J.; Shui, Y.; Dong, Y.; Zhao, X. Enhanced dielectric polarization and electro-responsive characteristic of graphene oxide-wrapped titania microspheres. Nanotechnology 2014, 25, 045702. [Google Scholar] [CrossRef]
- Acres, R.G.; Ellis, A.V.; Alvino, J.; Lenahan, C.E.; Khodakov, D.A.; Metha, G.F.; Andersson, G.G. Molecular structure of 3-aminopropyltriethoxysilane layers formed on silanol-terminated silicon surfaces. J. Phys. Chem. C 2012, 116, 6289–6297. [Google Scholar] [CrossRef]
- Dong, X.; Huo, S.; Qi, M. Comparison of electrorheological performance between urea-coated and graphene oxide-wrapped core-shell structured amorphous TiO2 nanoparticles. Smart Mater. Struct. 2015, 25, 015033. [Google Scholar] [CrossRef]
- Yoon, C.-M.; Lee, S.; Hong, S.H.; Jang, J. Fabrication of density-controlled graphene oxide-coated mesoporous silica spheres and their electrorheological activity. J. Colloid Interf. Sci. 2015, 438, 14–21. [Google Scholar] [CrossRef]
- Lee, S.; Yoon, C.-M.; Hong, J.-Y.; Jang, J. Enhanced electrorheological performance of a graphene oxide-wrapped silica rod with a high aspect ratio. J. Mater. Chem. C 2014, 2, 6010–6016. [Google Scholar] [CrossRef]
- Yin, J.; Zhao, X. Electrorheological properties of titanate nanotube suspensions. Colloids Surf. A 2008, 329, 153–160. [Google Scholar] [CrossRef]
- Yin, J.; Zhao, X.; Xia, X.; Xiang, L.; Qiao, Y. Electrorheological fluids based on nano-fibrous polyaniline. Polymer 2008, 49, 4413–4419. [Google Scholar] [CrossRef]
- Yoon, C.-M.; Noh, J.; Jang, Y.; Jang, J. Fabrication of a silica/titania hollow nanorod and its electroresponsive activity. RSC Adv. 2017, 7, 19754–19763. [Google Scholar] [CrossRef]
- Xia, X.; Yin, J.; Qiang, P.; Zhao, X. Electrorheological properties of thermo-oxidative polypyrrole nanofibers. Polymer 2011, 52, 786–792. [Google Scholar] [CrossRef]
- Lee, S.; Noh, J.; Hong, S.; Kim, Y.K.; Jang, J. Dual stimuli-responsive smart fluid of graphene oxide-coated Iron oxide/silica core/shell nanoparticles. Chem. Mater. 2016, 28, 2624–2633. [Google Scholar] [CrossRef]
- Zhang, W.L.; Choi, H.J. Silica-graphene oxide hybrid composite particles and their electroresponsive characteristics. Langmuir 2012, 28, 7055–7062. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Yin, J.; Liu, Y.; Zhao, X. Graphene oxide vs. reduced graphene oxide as core substrate for core/shell-structured dielectric nanoplates with different electro-responsive characteristics. J. Mater. Chem. C 2015, 3, 5098–5108. [Google Scholar] [CrossRef]
- Kim, S.D.; Zhang, W.L.; Choi, H.J.; Seo, Y.P.; Seo, Y. Electrorheological activity generation by graphene oxide coating on low-dielectric silica particles. RSC Adv. 2014, 4, 62644–62650. [Google Scholar] [CrossRef]
- Kim, J.W.; Kim, S.G.; Choi, H.J.; Suh, M.S.; Shin, M.J.; Jhon, M.S. Synthesis and electrorheological characterization of polyaniline and Na+-montmorillonite clay nanocomposite. Int. J. Mod. Phys. B 2001, 15, 657–664. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Seo, Y.P.; Seo, Y. Modeling and analysis of electrorheological suspensions in shear flow. Langmuir 2012, 28, 3077–3084. [Google Scholar] [CrossRef] [PubMed]
- Spaggiari, A.; Dragoni, E. Effect of pressure on the flow properties of magnetorheological fluids. J. Fluids Eng. 2012, 134, 091103. [Google Scholar] [CrossRef]
- Cho, M.; Choi, H.; Jhon, M. Shear stress analysis of a semiconducting polymer based electrorheological fluid system. Polymer 2005, 46, 11484–11488. [Google Scholar] [CrossRef]
- Klingenberg, D.; Van Swol, F.; Zukoski, C. The small shear rate response of electrorheological suspensions. I. Simulation in the point–dipole limit. J. Chem. Phys. 1991, 94, 6160–6169. [Google Scholar] [CrossRef]
- Seo, Y.P.; Choi, H.J.; Seo, Y. Analysis of the static yield stress for giant electrorheological fluids. Korea Austral. Rheol. J. 2017, 29, 215–218. [Google Scholar] [CrossRef]
- Wu, C.; Conrad, H. A modified conduction model for the electrorheological effect. J. Phys. D Appl. Phys. 1996, 29, 3147–3153. [Google Scholar] [CrossRef]
- Schwarzl, F. Numerical calculation of stress relaxation modulus from dynamic data for linear viscoelastic materials. Rheol. Acta 1975, 14, 581–590. [Google Scholar] [CrossRef]
- Emri, I.; Von Bernstorff, B.; Cvelbar, R.; Nikonov, A. Re-examination of the approximate methods for interconversion between frequency-and time-dependent material functions. J. Non-Newton. Fluid Mech. 2005, 129, 75–84. [Google Scholar] [CrossRef]
- Zhang, W.L.; Liu, Y.D.; Choi, H.J. Fabrication of semiconducting graphene oxide/polyaniline composite particles and their electrorheological response under an applied electric field. Carbon 2012, 50, 290–296. [Google Scholar] [CrossRef]
- Zhang, W.L.; Choi, H.J. Fabrication and electrorheology of graphene oxide/ionic N-substituted copolyaniline composite. Colloid Polym. Sci. 2013, 291, 1401–1408. [Google Scholar] [CrossRef]
- Sim, B.; Zhang, W.L.; Choi, H.J. Graphene oxide/poly(2-methylaniline) composite particle suspension and its electro-response. Mater. Chem. Phys. 2015, 153, 443–449. [Google Scholar] [CrossRef]
- Cao, Y.; Choi, H.J.; Zhang, W.L.; Wang, B.; Hao, C.; Liu, J. Eco-friendly mass production of poly (p-phenylenediamine)/graphene oxide nanoplatelet composites and their electrorheological characteristics. Compos. Sci. Technol. 2016, 122, 36–41. [Google Scholar] [CrossRef]
- Kim, S.D.; Zhang, W.L.; Choi, H.J. Pickering emulsion-fabricated polystyrene–graphene oxide microspheres and their electrorheology. J. Mater. Chem. C 2014, 2, 7541–7546. [Google Scholar] [CrossRef]
- Min, T.H.; Lee, C.J.; Choi, H.J. Pickering emulsion polymerized core-shell structured poly(methyl methacrylate)/graphene oxide particles and their electrorheological characteristics. Polym. Test. 2018, 66, 195–202. [Google Scholar] [CrossRef]
- Lee, C.J.; Choi, H.J. Graphene oxide as a Pickering emulsifier for poly(glycidyl methacrylate) composite particles and their suspension rheology under applied electric fields. Colloids Surf. A 2018, 550, 56–64. [Google Scholar] [CrossRef]
- Mrlík, M.; Ilčíková, M.; Plachý, T.; Moučka, R.; Pavlínek, V.; Mosnáček, J. Tunable electrorheological performance of silicone oil suspensions based on controllably reduced graphene oxide by surface initiated atom transfer radical polymerization of poly(glycidyl methacrylate). J. Ind. Eng. Chem. 2018, 57, 104–112. [Google Scholar] [CrossRef]
- Mrlik, M.; Ilcikova, M.; Osicka, J.; Kutalkova, E.; Minarik, A.; Vesel, A.; Mosnacek, J. Electrorheology of SI-ATRP-modified graphene oxide particles with poly(butyl methacrylate): Effect of reduction and compatibility with silicone oil. RSC Adv. 2019, 9, 1187–1198. [Google Scholar] [CrossRef]
- Kutalkova, E.; Mrlik, M.; Ilcikova, M.; Osicka, J.; Sedlacik, M.; Mosnacek, J. Enhanced and Tunable Electrorheological Capability using Surface Initiated Atom Transfer Radical Polymerization Modification with Simultaneous Reduction of the Graphene Oxide by Silyl-Based Polymer Grafting. Nanomaterials 2019, 9, 308. [Google Scholar] [CrossRef]
- Mrlik, M.; Cvek, M.; Osicka, J.; Moucka, R.; Sedlacik, M.; Pavlinek, V. Surface-initiated atom transfer radical polymerization from graphene oxide: A way towards fine tuning of electric conductivity and electro-responsive capabilities. Mater. Lett. 2018, 211, 138–141. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Zheng, C.; Lei, Q.; Dong, Y.; Zhao, X.; Yin, J. Pickering emulsion polymerization of poly(ionic liquid)s encapsulated nano-SiO2 composite particles with enhanced electro-responsive characteristic. Polymer 2018, 146, 109–119. [Google Scholar] [CrossRef]







| Materials | Synthesis Method | Morphology | ρ (g/cm3) | Particle Concent-Ration | Slope | (Pa) | λ (s) | Sedimen-Tation Ratio | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GO [43] | Modified Hummers method | Sheet | 1.78 | 6.02 × 10−6 | 5 wt.% | 2.5 | _ | ~0.1 | _ | _ | _ | _ | 0.45 | 1.3 × 10−5 | _ |
| GO/TiO2 [53] | Electrostatic interaction | Sheet | _ | 5.5 × 10−10 | 15 wt.% | 3.0 | _ | _ | 160 | _ | _ | _ | _ | _ | _ |
| GO-wrapped titania [56] | Sphere | _ | _ | 10 vol.% | 3.0 | 1 | ~0.2 | 600 | 1.47 | ~30/90 | ~2 × 105 2 × 104 | 2.7 | 5 × 10−3 | 45% | |
| TiO2/GO [58] | Sphere | 1.978 | _ | 37 vol.% | 5.0 | <10 | _ | ~8 × 103 | _ | _ | _ | _ | _ | 50% | |
| Fe3O4/GO [55] | Sphere | _ | 10−7 | 15 wt.% | 3.0 | _ | ~0.2 | 100 | 1.5 | ~50/10 | ~2 × 105 2 × 104 | _ | _ | _ | |
| Fe3O4//SiO2/GO [65] | Sphere | _ | _ | 25 vol.% | 3.0 | _ | ~0.08 | 15 | _ | _ | _ | _ | _ | 82% | |
| GO/Al2O3 [54] | Sphere | _ | 1.24 × 10−13 | 20 wt.% | 5.0 | _ | ~0.07 | 92 | 1.0 | _ | ~3 × 104 3 × 103 | _ | _ | _ | |
| GO-wrapped silica [60] | Sphere | _ | _ | 5 wt.% | 5.0 | _ | _ | ~100 | 2.0–1.5 | _ | _ | 0.71 | 1.592 | _ | |
| Rod (1:5) | _ | _ | 5 wt.% | 5.0 | _ | _ | ~250 | 2.0–1.5 | _ | _ | 1.4 | 1.007 | _ | ||
| Rod (1:20) | _ | _ | 5 wt.% | 5.0 | _ | _ | ~800 | 2.0–1.5 | _ | _ | 2.78 | 0.634 | _ | ||
| GO-coated silica spheres [59] | GO/nSiO2 | 2.67 | _ | 3 wt.% | 4.0 | _ | _ | 9.88 | _ | _ | _ | 0.94 | 1 | 65% | |
| GO/p1SiO2 | 2.52 | _ | 3 wt.% | 4.0 | _ | _ | 17.08 | _ | _ | _ | 1.94 | 0.64 | 60% | ||
| GO/p2SiO2 | 2.28 | _ | 3 wt.% | 4.0 | _ | _ | 20.43 | _ | _ | _ | 2.12 | 0.64 | 50% | ||
| GO/epSiO2 | 2.03 | _ | 3 wt.% | 4.0 | _ | _ | 30.18 | _ | _ | _ | 2.65 | 0.4 | 45% | ||
| GO/SiO2 [67] | Sheet | _ | _ | 3 vol.% | 2.0 | _ | _ | _ | _ | _ | _ | 0.9 | 4.5 × 10−7 | _ | |
| Si-GO [66] | In-situ growth | Sheet | _ | _ | 9 wt.% | 3.0 | _ | ~0.05 | 264 | 2 | _ | ~5 × 104 5 × 103 | 2.3 | 5 × 10−2 | _ |
| GO-Si [68] | Chemical grafting | Sphere | 2.003 | _ | 15 wt.% | 2.5 | _ | ~0.05 | _ | 1.5 | ~30/10 | _ | 0.06 | 6 × 10−6 | _ |
| GO/PANI [79] | In-situ polymerization | Sheet | _ | _ | 10 vol.% | 2.5 | _ | ~4 | _ | 2.0–1.5 | _ | _ | _ | _ | _ |
| GO/NCOPA [80] | Sheet | _ | _ | 10 wt.% | 5.0 | _ | ~0.1 | ~200 | 2.0–1.5 | ~7 × 103 2 × 102 | _ | 1.98 | 1 × 10−3 | _ | |
| GO/P2MAN [81] | Sheet | 1.43 | _ | 10 vol.% | 2.0 | _ | ~0.1 | _ | 1.5 | ~0.5/2 | _ | _ | _ | ~85% | |
| PPDA/GO [82] | Sheet | _ | _ | 8 wt.% | 2.5 | _ | ~103 | _ | _ | _ | _ | 1.71 | _ | _ | |
| POSS-GO [49] | Chemical grafting | Sheet | _ | _ | ~3 wt.% | 3.0 | <0.5 | ~0.7 | ~600 | 1.53 | _ | ~5.8 × 103 1 × 103 | _ | _ | _ |
| PS/GO [83] | Pickering emulsion polymerization | Sphere | _ | _ | 10 vol.% | 2.0 | _ | _ | _ | 1.5 | ~20/200 | _ | 2.54 | 2.54 × 10−4 | _ |
| PMMA/GO [84] | Sphere | 1.27 | - | 10 vol.% | 2.5 | _ | _ | _ | 1.5 | ~4/5 | _ | 0.51 | 5 × 10−3 | _ | |
| PGMA/GO [85] | Sphere | 1.41 | 8.7 × 10−12 | 10 vol.% | 2.0 | _ | ~0.07 | _ | 1.5–1.0 | ~1/1 | _ | 2.6 | 2.6 × 10−3 | _ | |
| GO-PGMA [86] | SI-ATRP | Sheet | _ | 6.17 × 10−7 | 10 wt.% | 2.0 | _ | _ | _ | 1.46 | _ | _ | 1.81 | 9 × 10−3 | 90% |
| GO-PBMA [87] | SI-ATRP | Sheet | 2.21 | 6 × 10−7 | 5 wt.% | 2.5 | _ | _ | _ | 1.48 | _ | _ | 1.37 | 5 × 10−3 | 60% |
| GO-PHEMATMS [88] | SI-ATRP | Sheet | _ | 6 × 10−6 | 5 wt.% | 2.5 | _ | _ | _ | 1.44 | _ | _ | 2.11 | 2 × 10−3 | 90% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.Z.; Kim, J.N.; Choi, H.J. Graphene Oxide and Its Inorganic Composites: Fabrication and Electrorheological Response. Materials 2019, 12, 2185. https://doi.org/10.3390/ma12132185
Dong YZ, Kim JN, Choi HJ. Graphene Oxide and Its Inorganic Composites: Fabrication and Electrorheological Response. Materials. 2019; 12(13):2185. https://doi.org/10.3390/ma12132185
Chicago/Turabian StyleDong, Yu Zhen, Joo Nyeon Kim, and Hyoung Jin Choi. 2019. "Graphene Oxide and Its Inorganic Composites: Fabrication and Electrorheological Response" Materials 12, no. 13: 2185. https://doi.org/10.3390/ma12132185
APA StyleDong, Y. Z., Kim, J. N., & Choi, H. J. (2019). Graphene Oxide and Its Inorganic Composites: Fabrication and Electrorheological Response. Materials, 12(13), 2185. https://doi.org/10.3390/ma12132185






