An Ab Initio Study of Thermodynamic and Mechanical Stability of Heusler-Based Fe2AlCo Polymorphs
Abstract
1. Introduction
2. Materials and Methods
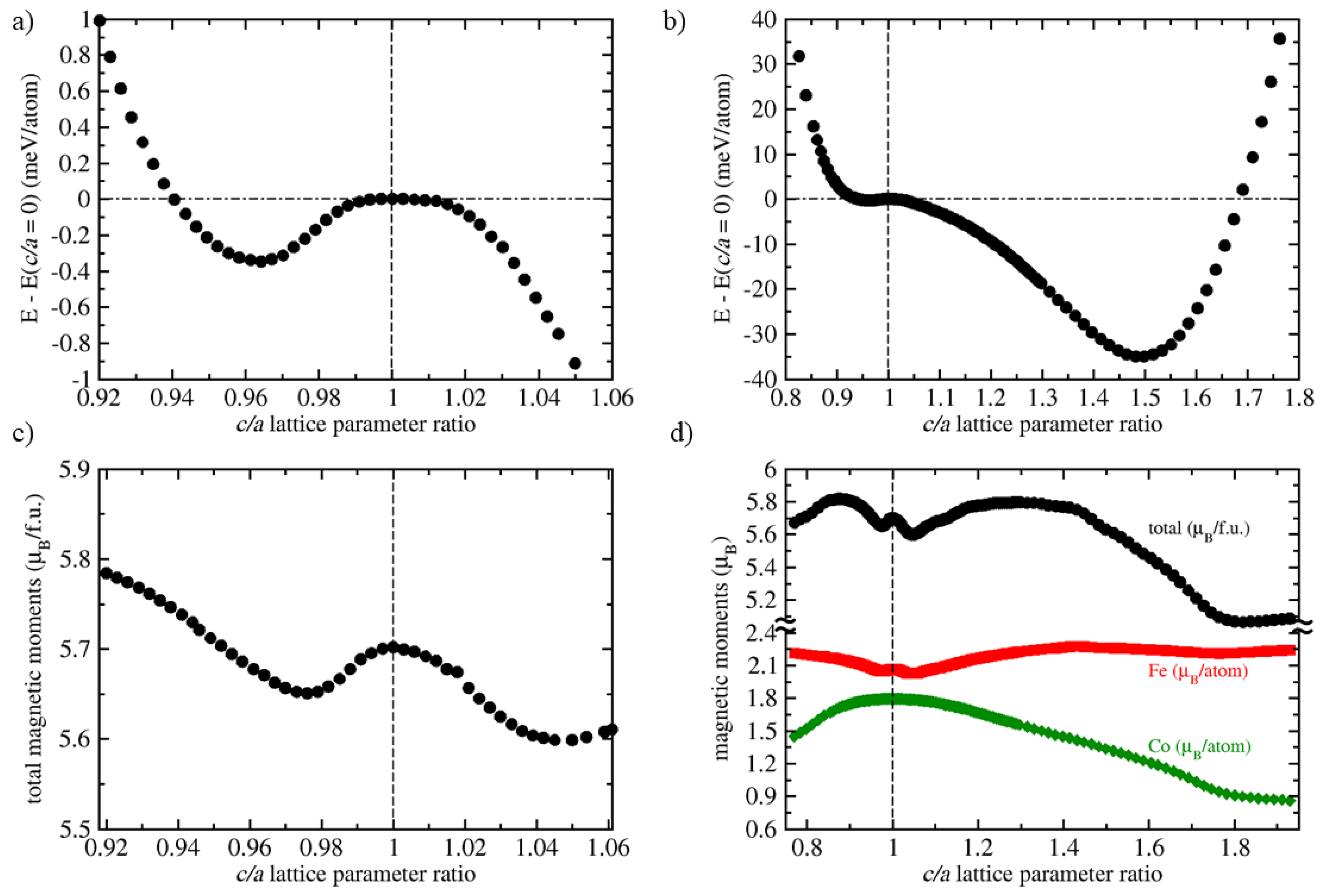
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heusler, F.; Starck, W.; Haupt, E. Magnetisch-chemische Studien. Verh. Dtsch. Phys. Ges. 1903, 5, 219–232. [Google Scholar]
- Webster, P. Heusler Alloys. Contemp. Phys. 1969, 10, 559–577. [Google Scholar] [CrossRef]
- Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Sol. State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Picozzi, S.; Continenza, A.; Freeman, A. Co2MnX (X = Si, Ge, Sn) Heusler compounds: An ab initio study of their structural, electronic, and magnetic properties at zero and elevated pressure. Phys. Rev. B 2002, 66, 094421. [Google Scholar] [CrossRef]
- Webster, P. Magnetic and chemical order in Heusler alloys containing cobalt and manganese. J. Phys. Chem. Sol. 1971, 32, 1221. [Google Scholar] [CrossRef]
- Kübler, J.; Williams, A.; Sommers, C. Formation and coupling of magnetic-moments in Heusler alloys. Phys. Rev. B 1983, 28, 1745–1755. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef]
- Miura, Y.; Nagao, K.; Shirai, M. Atomic disorder effects on half-metallicity of the full-Heusler alloys Co2(Cr1-xFex)Al: A first-principles study. Phys. Rev. B 2004, 69, 144413. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.; Papanikolaou, N. Origin and properties of the gap in the half-ferromagnetic Heusler alloys. Phys. Rev. B 2002, 66, 134428. [Google Scholar] [CrossRef]
- Kandpal, H.C.; Fecher, G.H.; Felser, C. Calculated electronic and magnetic properties of the half-metallic, transition metal based Heusler compounds. J. Phys. D Appl. Phys. 2007, 40, 1507–1523. [Google Scholar] [CrossRef]
- Galanakis, I.; Mavropoulos, P.; Dederichs, P. Electronic structure and Slater-Pauling behaviour in half-metallic Heusler alloys calculated from first principles. J. Phys. D Appl. Phys. 2006, 39, 765–775. [Google Scholar] [CrossRef]
- Picozzi, S.; Continenza, A.; Freeman, A. Role of structural defects on the half-metallic character of Co2MnGe and Co2MnSi Heusler alloys. Phys. Rev. B 2004, 69, 094423. [Google Scholar] [CrossRef]
- Buschow, K.; Van Engen, P. Magnetic and magneto-optical properties of Heusler alloys based on aluminum and gallium. J. Mag. Mag. Mat. 1981, 25, 90–96. [Google Scholar] [CrossRef]
- Nishino, Y.; Kato, M.; Asano, S.; Soda, K.; Hayasaki, M.; Mizutani, U. Semiconductor-like behavior of electrical resistivity in Heusler-type Fe2VAl compound. Phys. Rev. Lett. 1997, 79, 1909–1912. [Google Scholar] [CrossRef]
- Sakurada, S.; Shutoh, N. Effect of Ti substitution on the thermoelectric properties of (Zr,Hf)NiSn half-Heusler compounds. Appl. Phys. Lett. 2005, 86, 082105. [Google Scholar] [CrossRef]
- Shen, Q.; Chen, L.; Goto, T.; Hirai, T.; Yang, J.; Meisner, G.; Uher, C. Effects of partial substitution of Ni by Pd on the thermoelectric properties of ZrNiSn-based half-Heusler compounds. Appl. Phys. Lett. 2001, 79, 4165–4167. [Google Scholar] [CrossRef]
- Chadov, S.; Qi, X.; Kuebler, J.; Fecher, G.H.; Felser, C.; Zhang, S.C. Tunable multifunctional topological insulators in ternary Heusler compounds. Nat. Mat. 2010, 9, 541–545. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Wray, L.A.; Xia, Y.; Xu, S.; Jia, S.; Cava, R.J.; Bansil, A.; Hasan, M.Z. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 2010, 9, 546–549. [Google Scholar] [CrossRef] [PubMed]
- Planes, A.; Manosa, L.; Acet, M. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Phys. Cond. Matter 2009, 21, 233201. [Google Scholar] [CrossRef] [PubMed]
- Entel, P.; Buchelnikov, V.; Khovailo, V.; Zayak, A.; Adeagbo, W.; Gruner, M.; Herper, H.; Wassermann, E. Modelling the phase diagram of magnetic shape memory Heusler alloys. J. Phys. D Appl. Phys. 2006, 39, 865–889. [Google Scholar] [CrossRef]
- Kainuma, R.; Imano, Y.; Ito, W.; Morito, H.; Sutou, Y.; Oikawa, K.; Fujita, A.; Ishida, K.; Okamoto, S.; Kitakami, O. Metamagnetic shape memory effect in a Heusler-type Ni43Co7Mn39Sn11 polycrystalline alloy. Appl. Phys. Lett. 2006, 88, 192513. [Google Scholar] [CrossRef]
- Gilleßen, M.; Dronskowski, R. A combinatorial study of full Heusler alloys by first-principles computational methods. J. Comput. Chem. 2009, 30, 1290–1299. [Google Scholar] [CrossRef] [PubMed]
- Gilleßen, M.; Dronskowski, R. A combinatorial study of inverse Heusler alloys by first-principles computational methods. J. Comput. Chem. 2010, 31, 612–619. [Google Scholar] [CrossRef] [PubMed]
- Grover, A.K.; Pillay, R.G.; Nagarajan, V.; Tandon, P.N. Site preference and local environment effects in ferromagnetic ternary alloys. J. Magn. Magn. Mater. 1980, 15, 699–700. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
- Zhou, L.; Holec, D.; Mayrhofer, P.H. First-principles study of elastic properties of cubic Cr1-xAlxN alloys. J. Appl. Phys. 2013, 113, 043511. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Jain, V.; Nehra, J.; Sudheesh, V.D.; Lakshmi, N.; Venugopalan, K. Comparative study of the structural and magnetic properties of bulk and nano-sized Fe2CoAl. AIP Conf. Proc. 2013, 1536, 935–936. [Google Scholar] [CrossRef]
- Titrian, H.; Aydin, U.; Friák, M.; Ma, D.; Raabe, D.; Neugebauer, J. Self-consistent Scale-bridging Approach to Compute the Elasticity of Multi-phase Polycrystalline Materials. Mater. Res. Soc. Symp. Proc. 2013, 1524. [Google Scholar] [CrossRef]
- Friák, M.; Counts, W.A.; Ma, D.; Sander, B.; Holec, D.; Raabe, D.; Neugebauer, J. Theory-guided materials design of multi-phase Ti-Nb alloys with bone-matching elastic properties. Materials 2012, 5, 1853–1872. [Google Scholar] [CrossRef]
- Raghavan, V. Ternary and aluminum phase higher order diagram updates. J. Phase Equi. Diff. 2005, 26, 623. [Google Scholar]
- Raghavan, V. Ternary and higher order aluminum phase diagram updates. J. Phase Equi. Diff. 2005, 26, 348. [Google Scholar] [CrossRef]
- Ducher, R.; Kainuma, R.; Ohnuma, I.; Ishida, K. Phase equilibria and stability of B2 and L21 ordered phases in the Co-Fe-Ga Heusler alloy system. J. Alloys Compd. 2007, 437, 93–101. [Google Scholar] [CrossRef]
- Kumar, A.; Srivastava, P.C. Synthesis and characterization of Co2FeAl Heusler alloy nanoparticles. Mater. Sci. Pol. 2013, 31, 501–505. [Google Scholar] [CrossRef]
- Zhu, L.F.; Friák, M.; Dick, A.; Grabowski, B.; Hickel, T.; Liot, F.; Holec, D.; Schlieter, A.; Kuehn, U.; Eckert, J.; Ebrahimi, Z.; Emmerich, H.; Neugebauer, J. First-principles study of the thermodynamic and elastic properties of eutectic Fe-Ti alloys. Acta Mater. 2012, 60, 1594–1602. [Google Scholar] [CrossRef]
- Hemzalová, P.; Friák, M.; Šob, M.; Ma, D.; Udyansky, A.; Raabe, D.; Neugebauer, J. Ab initio study of thermodynamic, electronic, magnetic, structural, and elastic properties of Ni4N allotropes. Phys. Rev. B 2013, 88, 174103. [Google Scholar] [CrossRef]
- Maisel, S.B.; Hoefler, M.; Mueller, S. A canonical stability-elasticity relationship verified for one million face-centred-cubic structures. Nature 2012, 491, 740. [Google Scholar] [CrossRef] [PubMed]
- Friák, M.; Všianská, M.; Holec, D.; Zelený, M.; Šob, M. Tensorial elastic properties and stability of interface states associated with Σ 5(210) grain boundaries in Ni3(Al,Si). Sci. Technol. Adv. Mater. 2017, 18, 273–282. [Google Scholar] [CrossRef] [PubMed]
- Craievich, P.J.; Weinert, M.; Sanchez, J.M.; Watson, R.E. Local stability of nonequilibrium phases. Phys. Rev. Lett. 1994, 72, 3076–3079. [Google Scholar] [CrossRef] [PubMed]
- Šob, M.; Wang, L.G.; Vitek, V. Local stability of higher-energy phases in metallic materials and its relation to the structure of extended defects. Comput. Mater. Sci. 1997, 8, 100–106. [Google Scholar] [CrossRef]
- Wang, L.G.; Šob, M.; Zhang, Z. Instability of higher-energy phases in simple and transition metals. J. Phys. Chem. Solids 2003, 64, 863–872. [Google Scholar] [CrossRef]
- Friák, M.; Šob, M.; Vitek, V. Ab initio calculation of phase boundaries in iron along the bcc-fcc transformation path and magnetism of iron overlayers. Phys. Rev. B 2001, 63, 052405. [Google Scholar] [CrossRef]
- Qiu, S.L.; Marcus, P.M.; Ma, H. Tetragonal equilibrium states of Mn and Fe. J. Appl. Phys. 2000, 87, 5932–5934. [Google Scholar] [CrossRef]
- Spišák, D.; Hafner, J. Complex reconstruction of γ-iron multilayers on Cu(100): Ab initio local-spin-density investigations. Phys. Rev. B 2000, 61, 16129–16136. [Google Scholar] [CrossRef]
- Friák, M.; Hickel, T.; Körmann, F.; Udyansky, A.; Dick, A.; von Pezold, J.; Ma, D.; Kim, O.; Counts, W.A.; Šob, M.; et al. Determining the elasticity of materials employing quantum-mechanical approaches: From the electronic ground state to the limits of materials stability. Steel Res. Int. 2011, 82, 86–100. [Google Scholar] [CrossRef]
- Friák, M.; Šob, M.; Vitek, V. Ab initio calculation of tensile strength in iron. Phil. Mag. 2003, 83, 3529–3537. [Google Scholar] [CrossRef]
- Legut, D.; Friák, M.; Šob, M. Phase stability, elasticity, and theoretical strength of polonium from first principles. Phys. Rev. B 2010, 81, 214118. [Google Scholar] [CrossRef]
- Legut, D.; Friák, M.; Šob, M. Why is polonium simple cubic and so highly anisotropic? Phys. Rev. Lett. 2007, 99, 016402. [Google Scholar] [CrossRef] [PubMed]
- Šob, M.; Friák, M.; Legut, D.; Vitek, V. Theoretical strength, magnetism and stability of metals and intermetallics. In Complex Inorganic Solids; Turchi, P., Gonis, A., Rajan, K., Meike, A., Eds.; Springer: New York, NY, USA, 2005; pp. 307–325. [Google Scholar]
- Šob, M.; Legut, D.; Friák, M.; Fiala, J. Magnetism of Ni3Al and Fe3Al under extreme pressure and shape deformation: An ab initio study. J. Mag. Mag. Mat. 2004, 272, E205. [Google Scholar] [CrossRef]
- Friák, M.; Šob, M. Ab initio study of the bcc-hcp transformation in iron. Phys. Rev. B 2008, 77, 174117. [Google Scholar] [CrossRef]
- Zelený, M.; Friák, M.; Šob, M. Ab initio study of energetics and magnetism of Fe, Co, and Ni along the trigonal deformation path. Phys. Rev. B 2011, 83, 184424. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
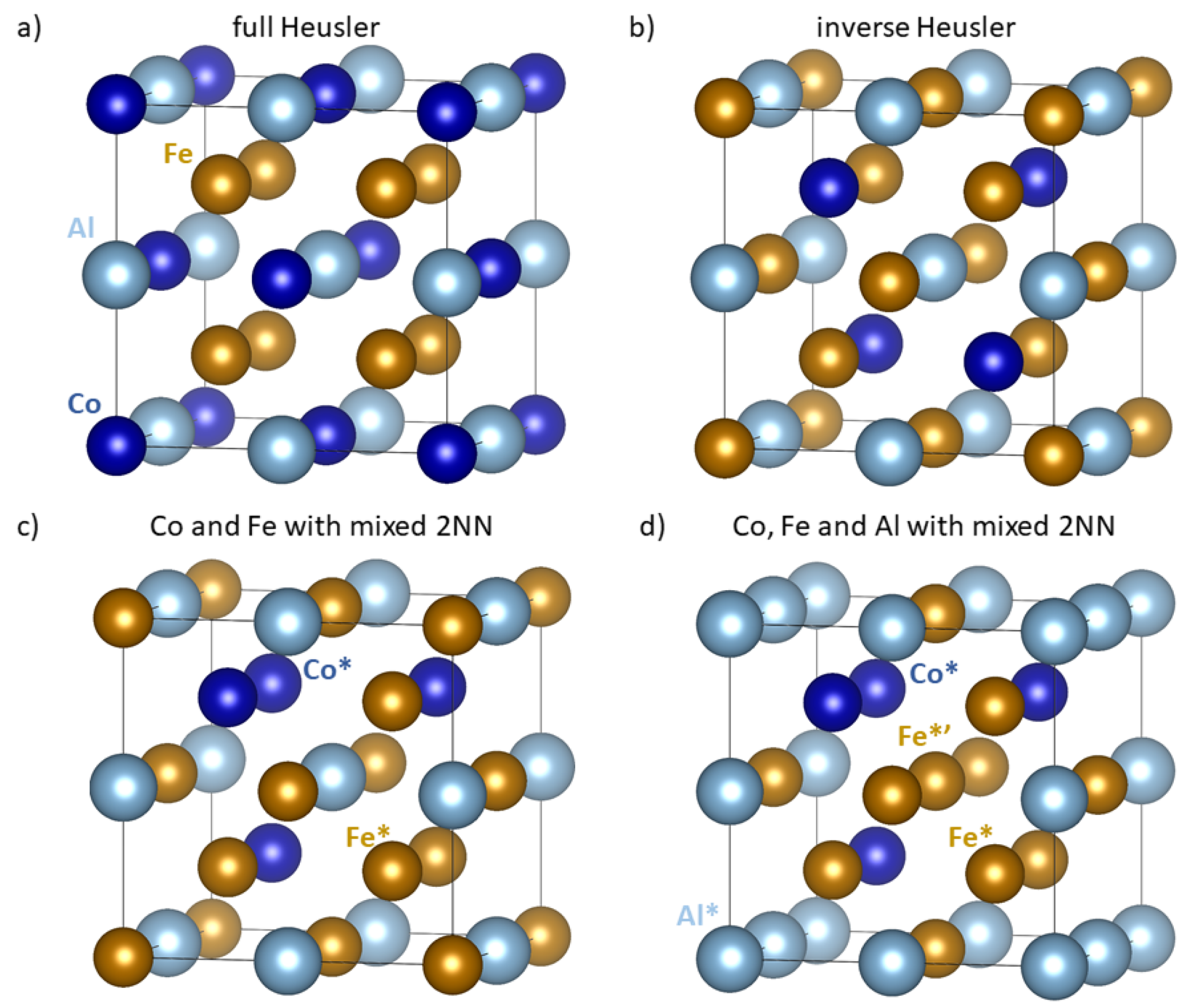
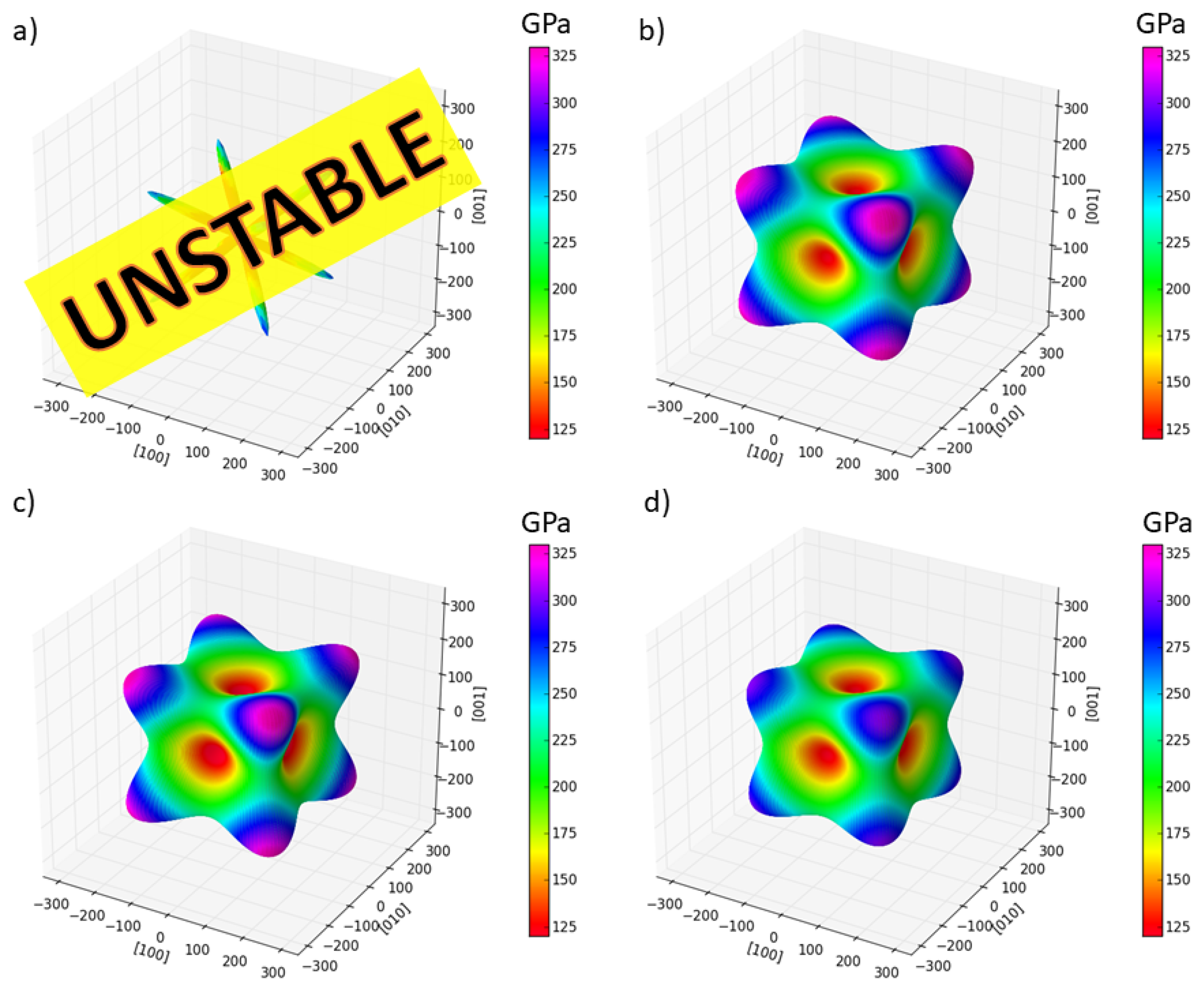
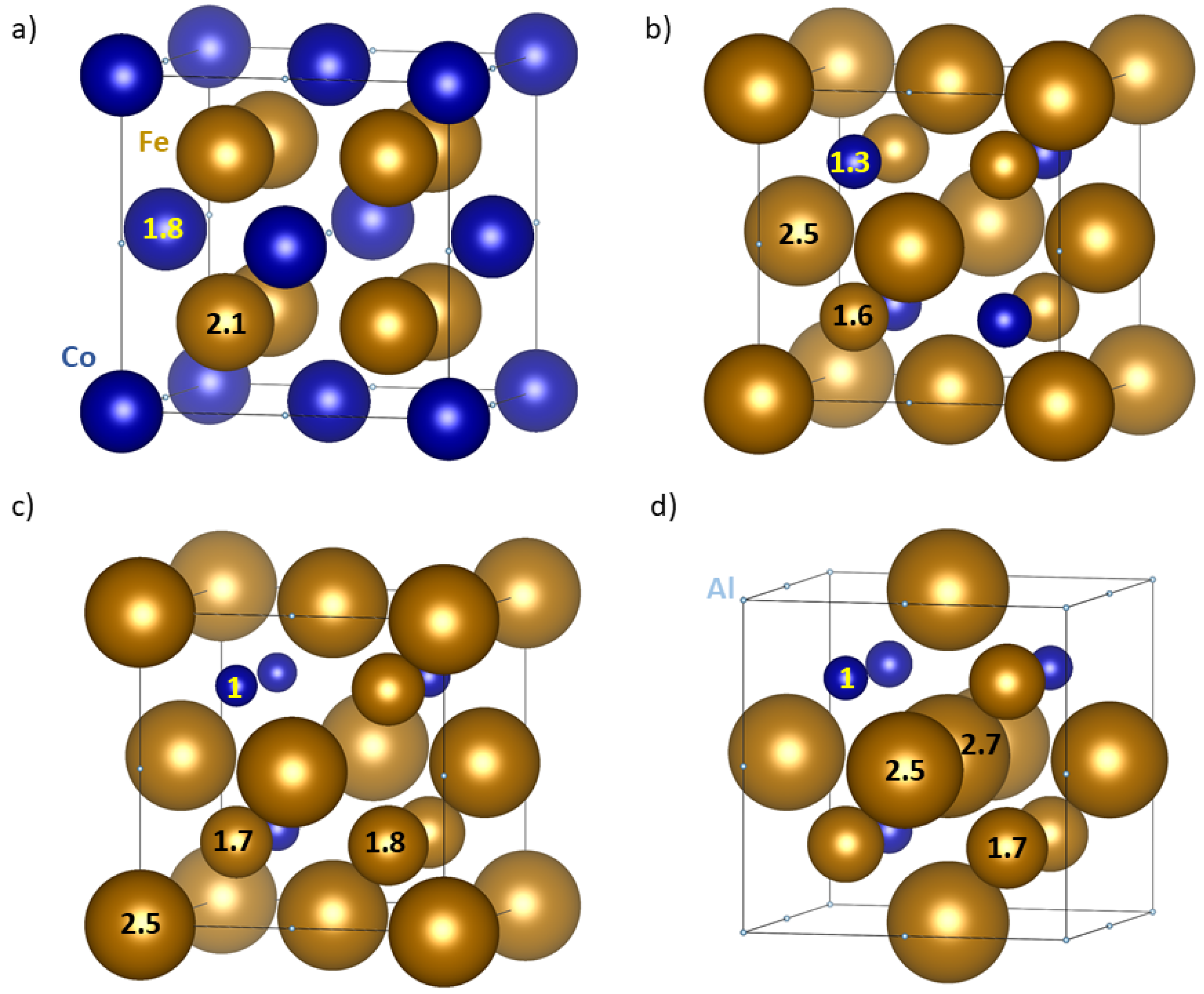
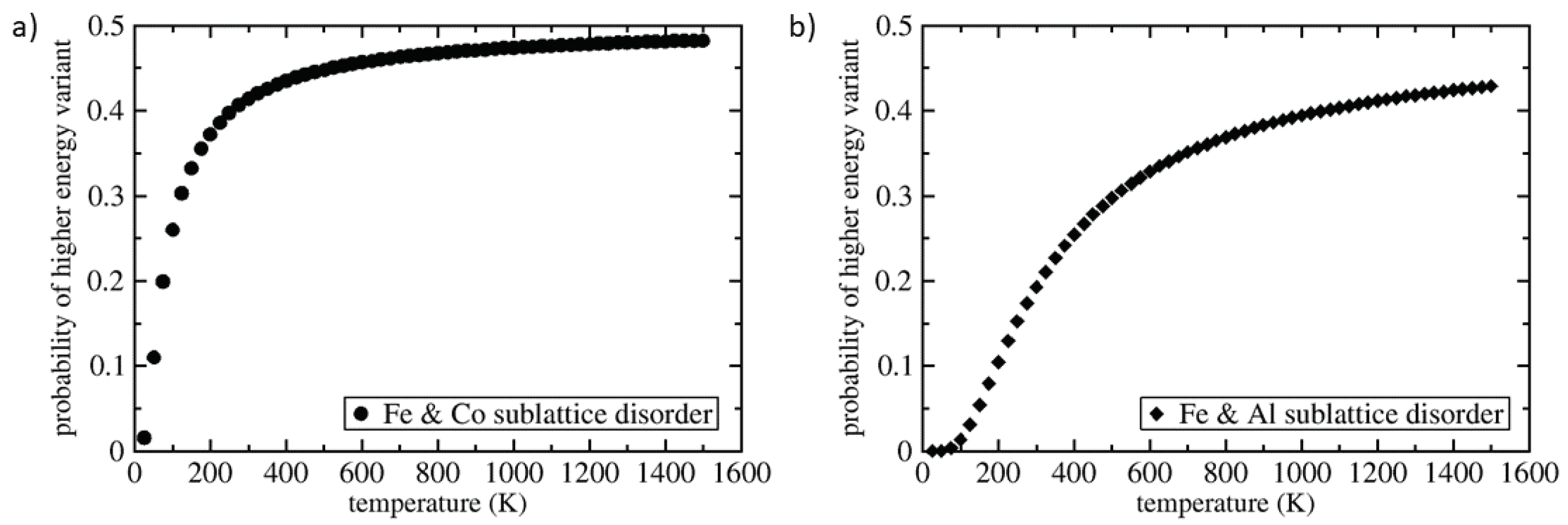
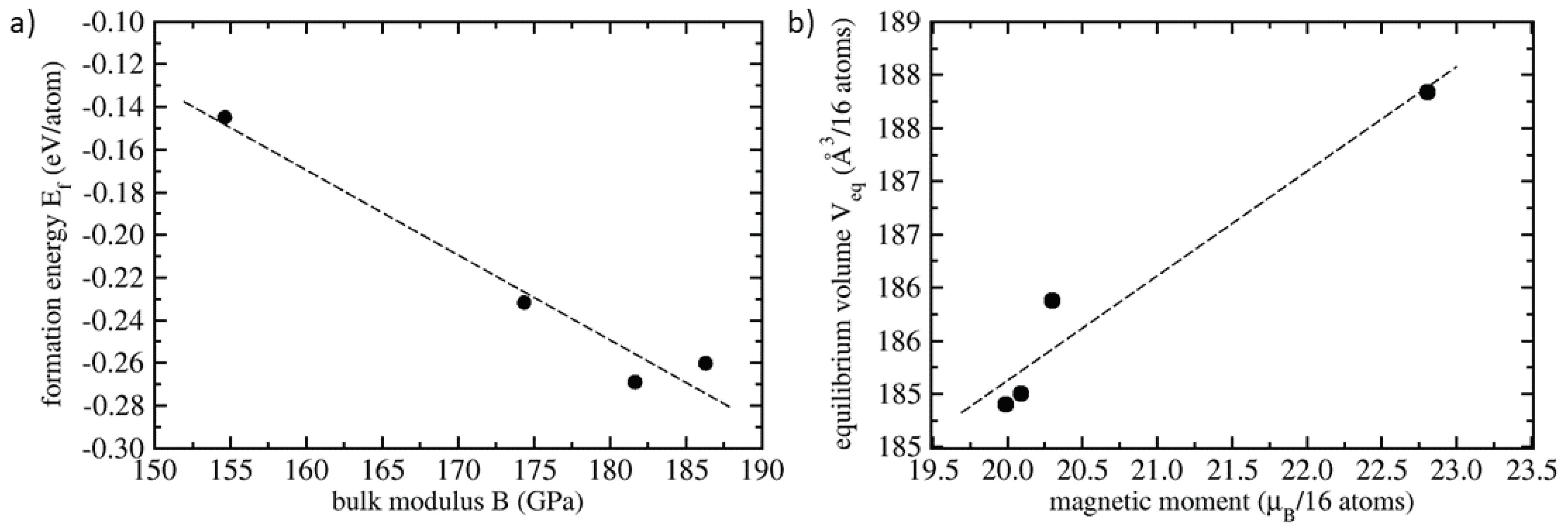
| Polymorph | E | V | a | C | C | C | B | |
|---|---|---|---|---|---|---|---|---|
| (eV/atom) | (Å/atom) | (Å) | (/f.u.) | (GPa) | (GPa) | (GPa) | (GPa) | |
| full Heusler | −0.145 | 11.740 | 5.727 | 5.70 | 148 | 158 | 115 | 155 |
| inverse Heusler | −0.260 | 11.556 | 5.697 | 4.99(8) | 245 | 157 | 139 | 186 |
| Co & Fe with mixed 2NN | −0.269 | 11.562 | 5.698 | 5.02 | 235 | 155 | 139 | 182 |
| Co, Fe & Al with mixed 2NN | −0.232 | 11.617 | 5.707 | 5.08 | 233 | 145 | 125 | 174 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friák, M.; Oweisová, S.; Pavlů, J.; Holec, D.; Šob, M. An Ab Initio Study of Thermodynamic and Mechanical Stability of Heusler-Based Fe2AlCo Polymorphs. Materials 2018, 11, 1543. https://doi.org/10.3390/ma11091543
Friák M, Oweisová S, Pavlů J, Holec D, Šob M. An Ab Initio Study of Thermodynamic and Mechanical Stability of Heusler-Based Fe2AlCo Polymorphs. Materials. 2018; 11(9):1543. https://doi.org/10.3390/ma11091543
Chicago/Turabian StyleFriák, Martin, Sabina Oweisová, Jana Pavlů, David Holec, and Mojmír Šob. 2018. "An Ab Initio Study of Thermodynamic and Mechanical Stability of Heusler-Based Fe2AlCo Polymorphs" Materials 11, no. 9: 1543. https://doi.org/10.3390/ma11091543
APA StyleFriák, M., Oweisová, S., Pavlů, J., Holec, D., & Šob, M. (2018). An Ab Initio Study of Thermodynamic and Mechanical Stability of Heusler-Based Fe2AlCo Polymorphs. Materials, 11(9), 1543. https://doi.org/10.3390/ma11091543







