Analysis of Surface Extraction Methods Based on Gradient Operators for Computed Tomography in Metrology Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Surface Extraction Procedure
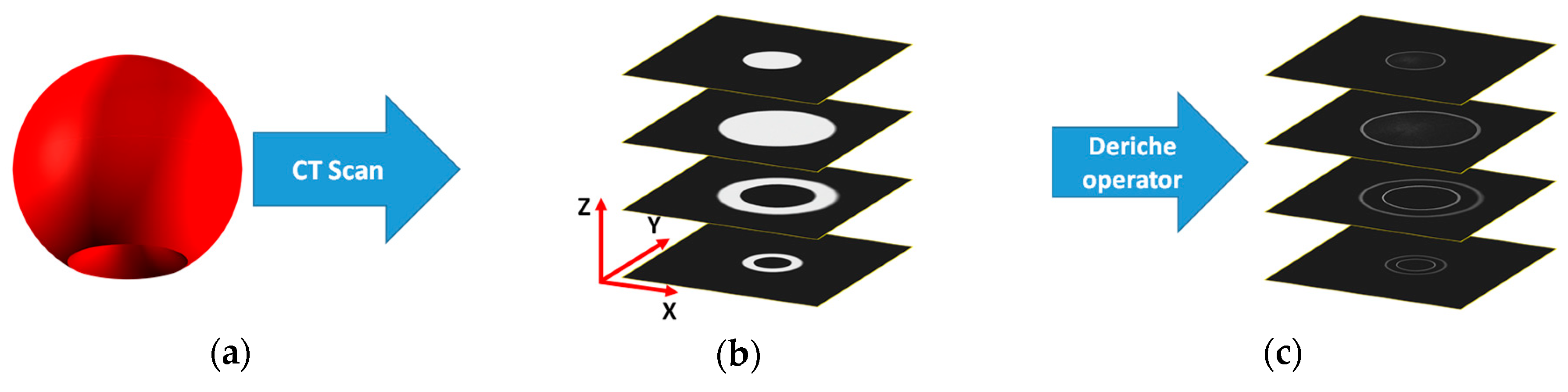
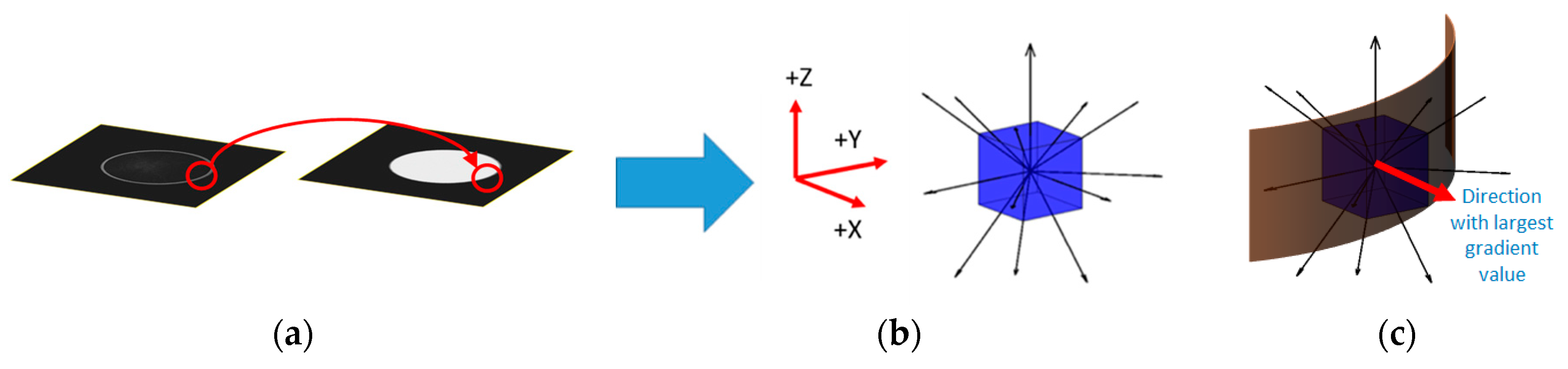
2.1.1. 3D Adapted Deriche Algorithm
- Preliminary edge detection.
- Sub-voxel refinement.
- Suppression of no-maximum points.
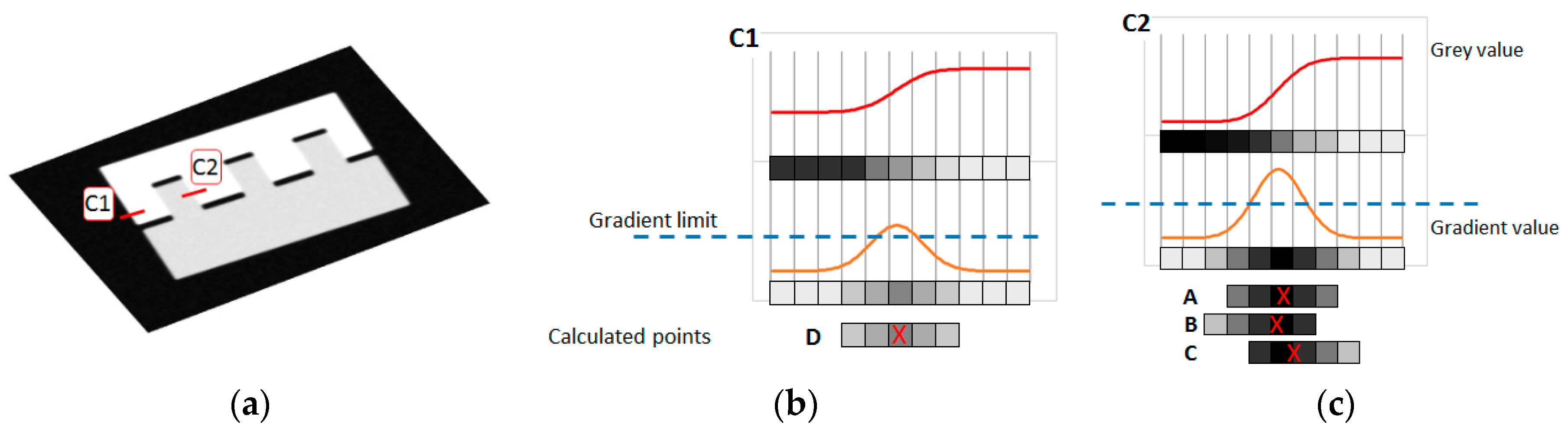
2.1.2. Canny Algorithm (CA)
- The preliminary edge detection in the Canny algorithm is based on the application of the Canny filter to the images along each of the three Cartesian directions, using a 1 × 10 convolution mask, oriented along the direction. This process leads to a precise determination of the gradient, but it requires significant computational resources.
- The second main difference is in the sub-voxel refinement step. In the Deriche algorithm, the point is calculated along a direction perpendicular to the part surface, while in the Canny algorithm, the calculation of the optimal position of the point with sub-voxel definition is carried out by applying Equation (6):where Xi, Yj, and Zk are the coordinates of the voxels inside the search window; and i, j, and k are the voxel indices within the search window. GX,i, GY,j, and GZ,k, with possible values from 0 to 65,535, i.e., 16 bits, are the gray value transitions obtained in the preliminary surface detection phase for the X, Y, and Z directions, respectively. This refinement is carried out separately and independently along the three directions, providing the three dimensional coordinates of each surface point. In order to obtain each of the coordinates, only the 3D image along that direction, obtained from the previous step, is used.
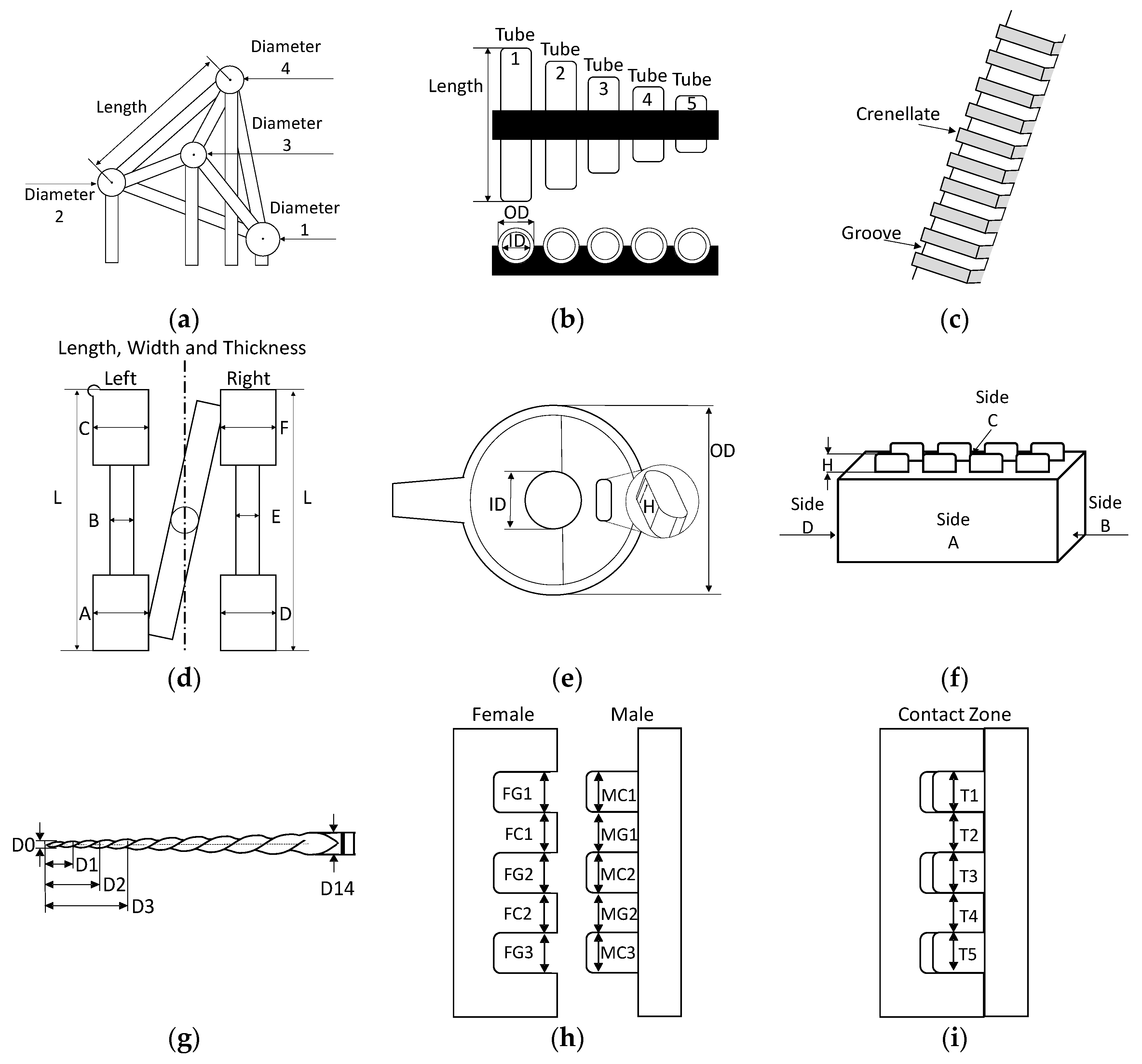
2.2. Workpieces
2.3. Computed Tomography System
2.4. Calibration Systems
2.4.1. Coordinate Measuring Machines (CMM)
2.4.2. Optical Coordinate Measuring Machines (OCMM)
3. Results
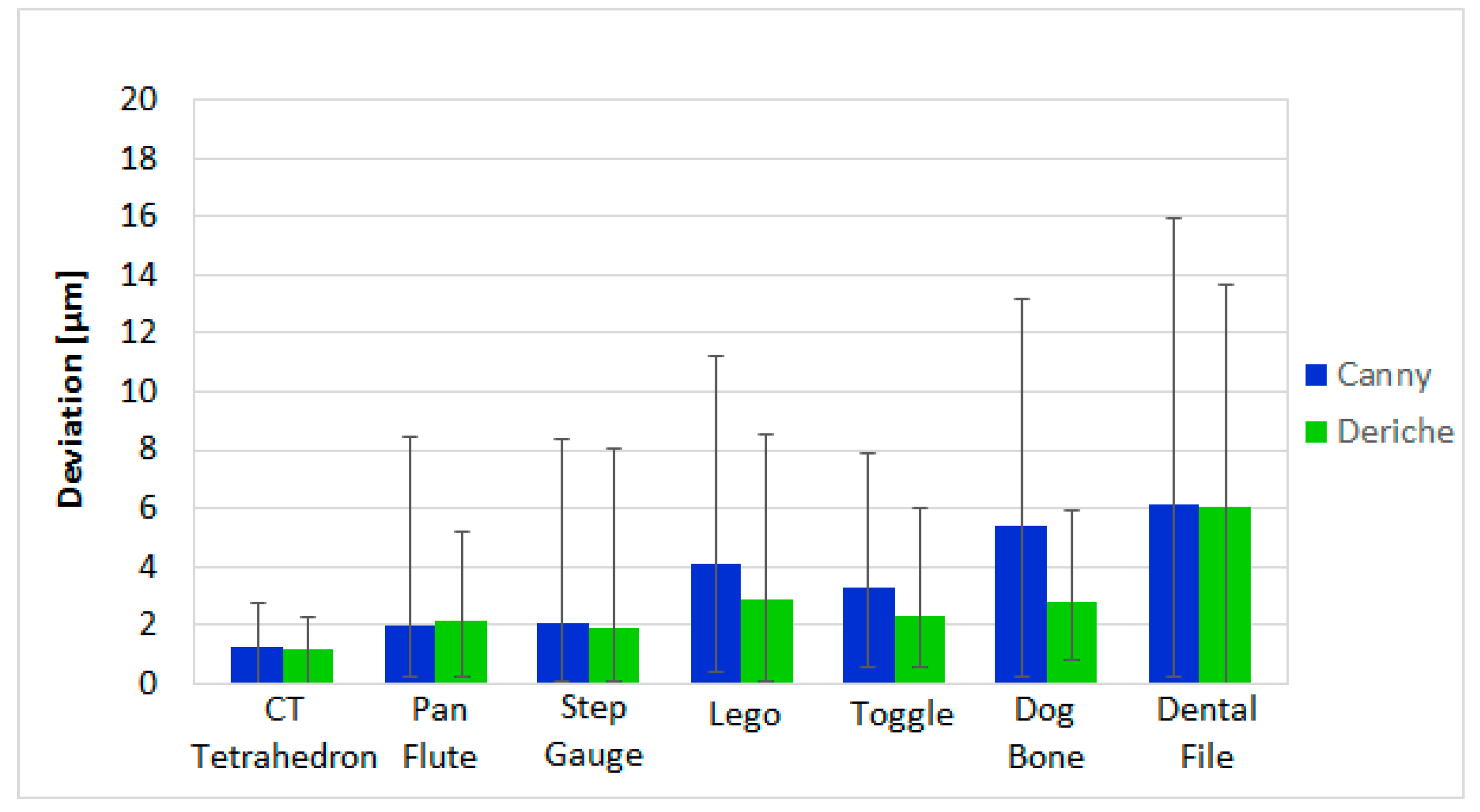
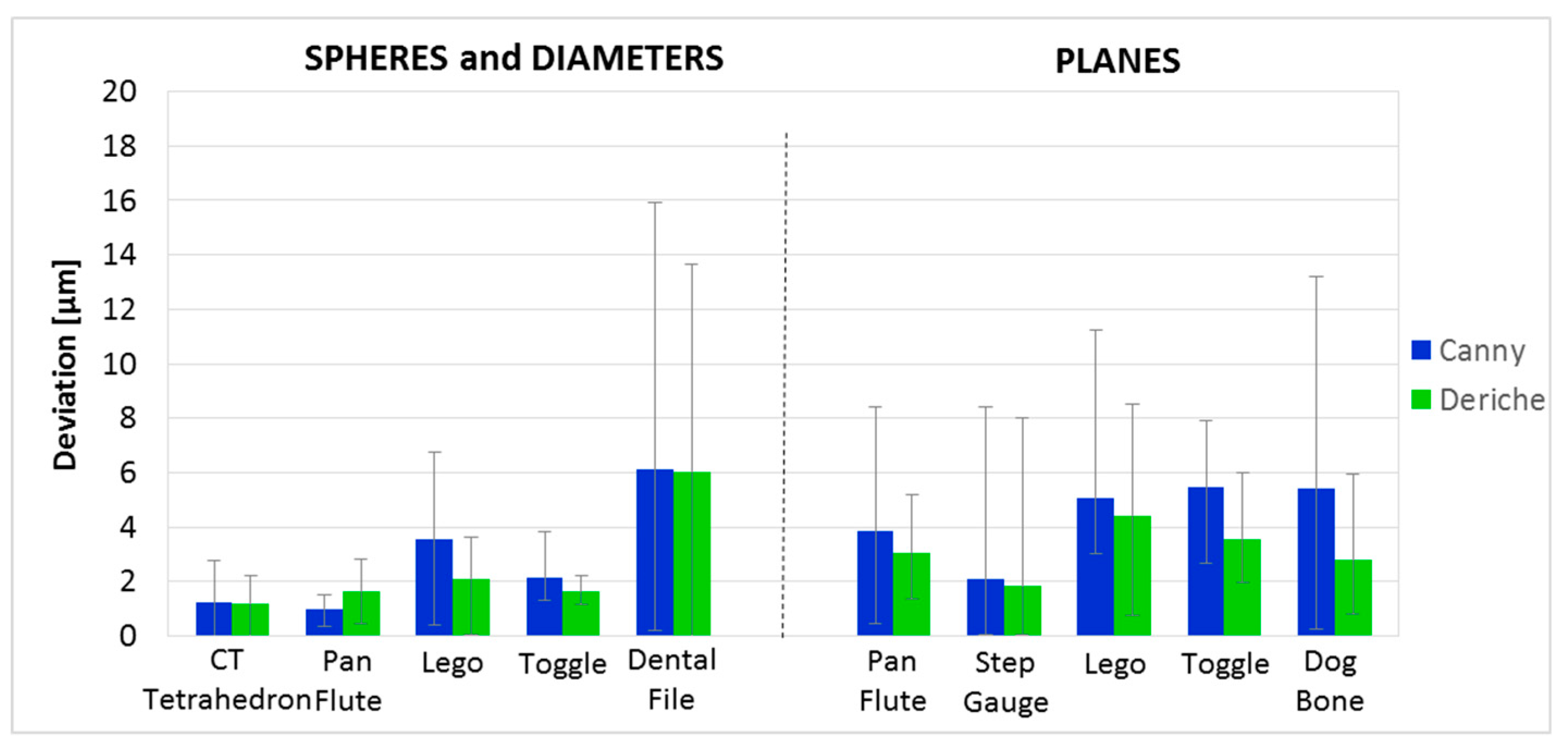
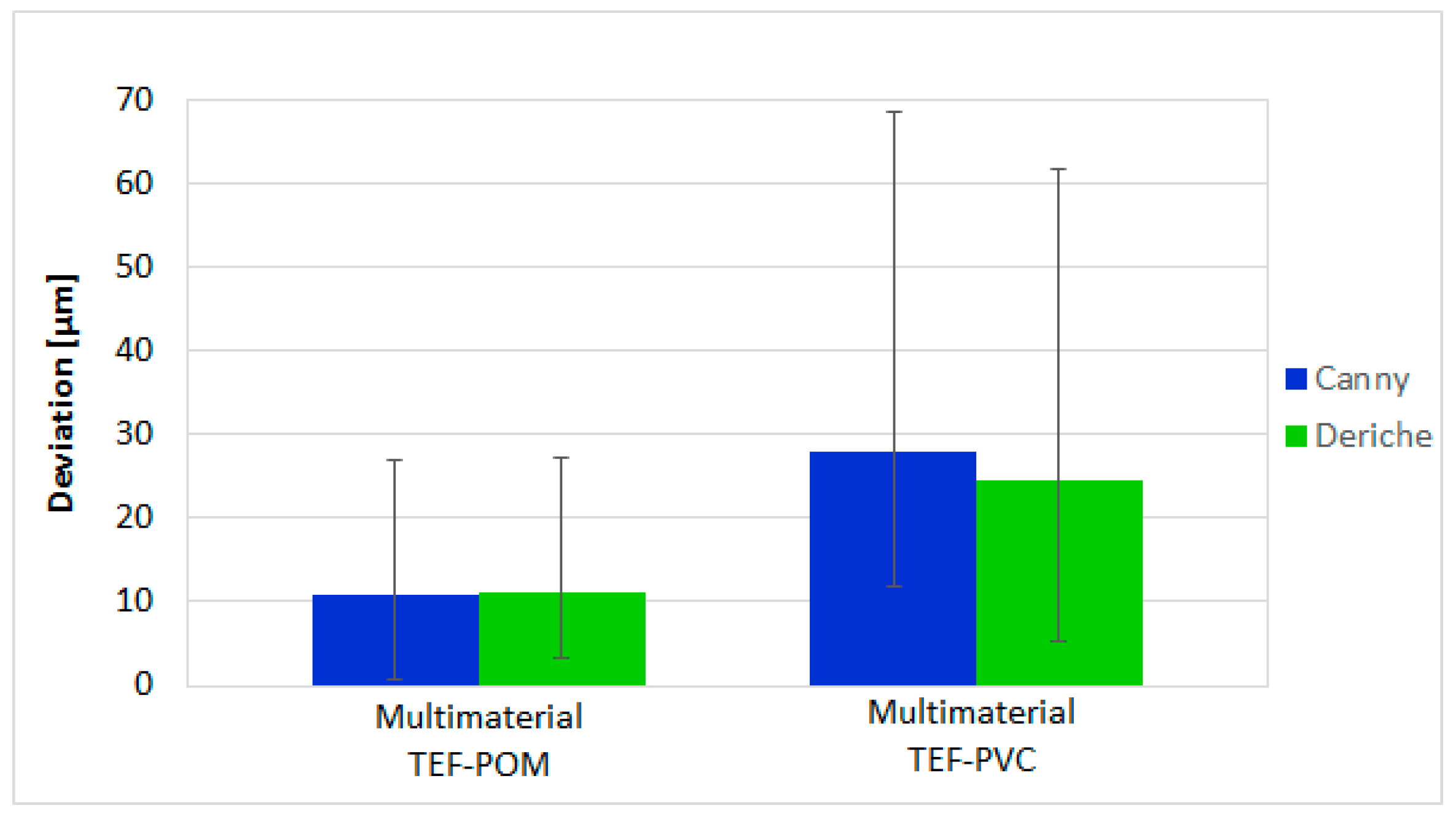
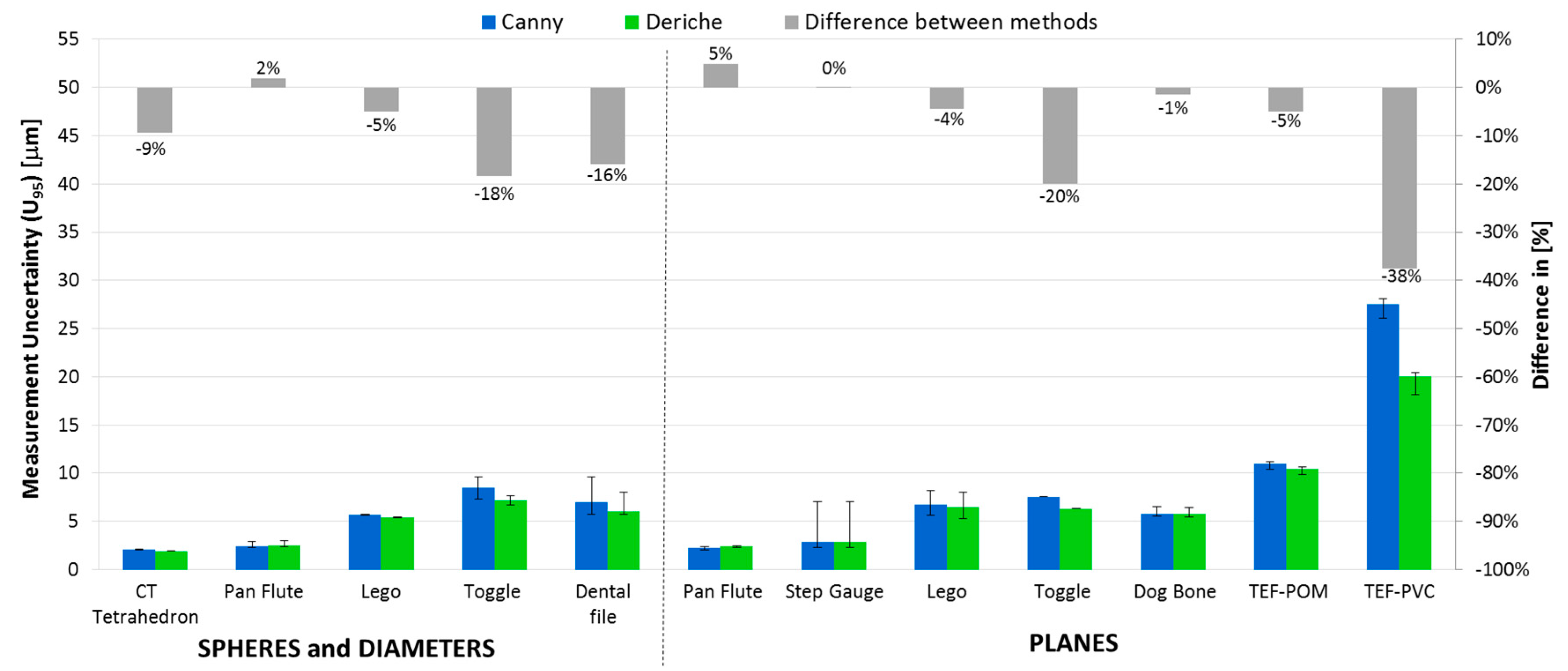
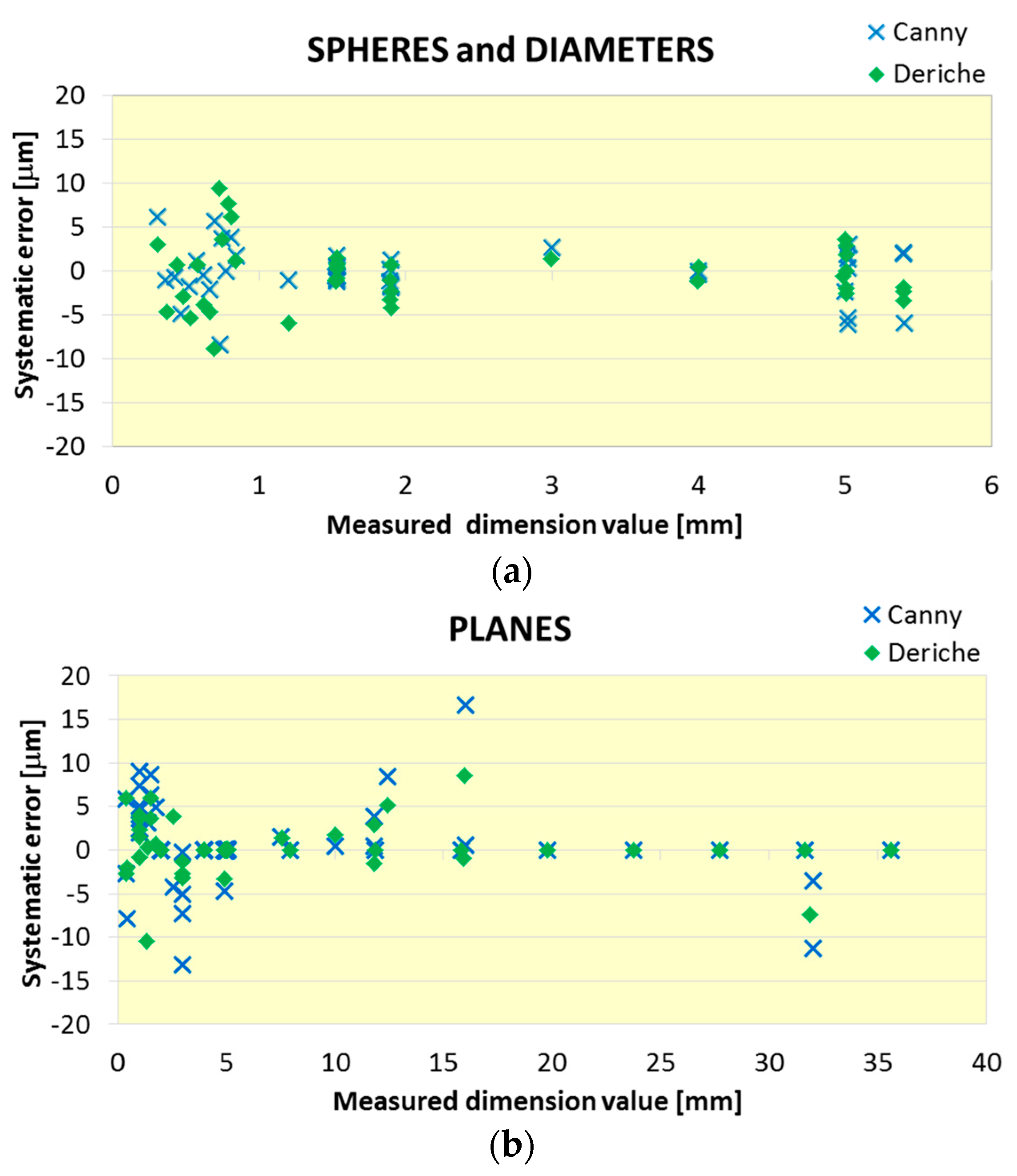
3.1. CT Comparison Results
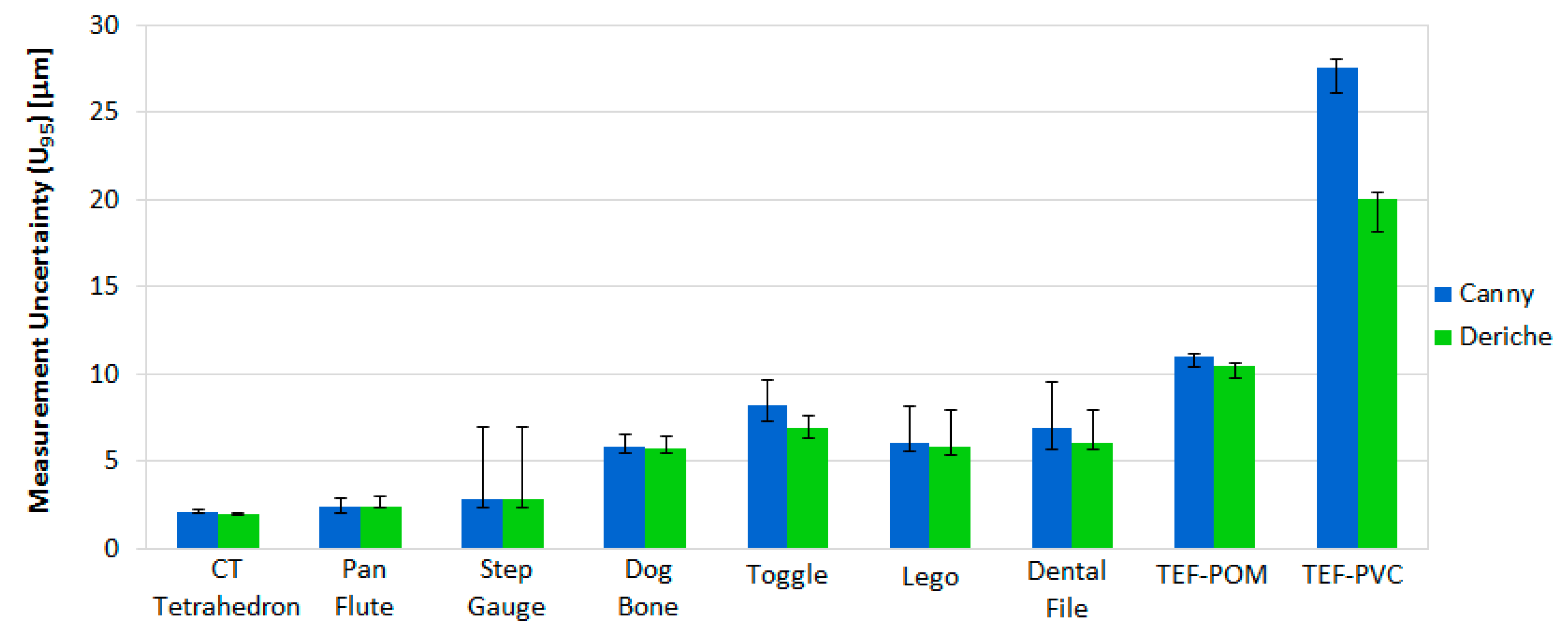
3.2. Uncertainty Estimation for CT Measurements
- ▪
- The term ucal represents the standard uncertainty of calibration of the workpiece determined by a CMS (coordinate measuring system).
- ▪
- The term up is the standard uncertainty of the measurement procedure (repeatability).
- ▪
- The term uw is the standard uncertainty of the material and manufacturing variations of the measured process. It is specifically associated with two uncertainty sources: variations in the mechanical properties of the workpiece (uw1); and variations in the CTEs (coefficient of thermal expansion) of the workpiece (uw2). In this work, the first factor has been previously included in up (effects of material composition and shape). A rectangular statistical distribution for 20% of CTE variation has been established for the second term.
- ▪
- The term ub is the standard uncertainty associated with the systematic error of the measurement process: the influence of the temperature variation during the CT measurement (ub1 when ∆T = ±2 °C); and the estimation of the systematic error related to the surface detection technique: Canny and Deriche (ub2).
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CMM | Coordinate measuring machine |
| CMS | Coordinate measuring system |
| CT | Computed Tomography |
| DTU | Danmarks Tekniske Universitet (Technical University of Denmark) |
| ID | Inside Diameters |
| LCP | Liquid Crystal Polymer |
| OCMM | Optical Coordinate Measuring Machine |
| OD | Outside Diameters |
| POM | Polyoxymethylene |
| PTFE | Polytetrafluoroethylene (Teflon®) |
| PVC | Polyvinyl chloride |
| TEF-POM | Multi-material part made of PTFE and POM |
| TEF-PVC | Multi-material part made of PTFE and PVC |
| VDI/VDE | Verein Deutscher Ingenieure/Verband Deutscher Elektrotechniker |
References
- Ametova, E.; Ferrucci, M.; Chilingaryan, S.; Dewulf, W. A computationally inexpensive model for estimating dimensional measurement uncertainty due to X-ray computed tomography instrument misalignments. Meas. Sci. Technol. 2018, 29, 065007. [Google Scholar] [CrossRef]
- Carmignato, S.; Pierobon, S.; Rampazzo, P.; Parisatto, M.; Savio, E. CT for Industrial Metrology—Accuracy and Structural Resolution of CT Dimensional Measurements. In Proceedings of the Conference on Industrial Computed Tomography (ICT), Wels, Austria, 19–21 September 2012; pp. 161–172. [Google Scholar]
- Carmignato, S.; Aloisi, V.; Medeossi, F.; Zanini, F.; Savio, E. Influence of surface roughness on computed tomography dimensional measurements. CIRP Ann. Manuf. Technol. 2017, 66, 499–502. [Google Scholar] [CrossRef]
- De Chiffre, L.; Carmignato, S.; Kruth, J.P.; Schmitt, R.; Weckenmann, A. Industrial applications of computed tomography. CIRP Ann. Manuf. Technol. 2014, 63, 655–677. [Google Scholar] [CrossRef]
- Kruth, J.P.; Bartscher, M.; Carmignato, S.; Schmitt, R.; De Chiffre, L.; Weckenmann, A. Computed tomography for dimensional metrology. CIRP Ann. Manuf. Technol. 2011, 60, 821–842. [Google Scholar] [CrossRef]
- Carvalho, L.E.; Sobieranski, A.C.; Wangenheim, A. 3D Segmentation Algorithms for Computerized Tomographic Imaging: A Systematic Literature Review. J. Digit. Imaging 2018, 31, 1–52. [Google Scholar] [CrossRef] [PubMed]
- Kiekens, K.; Welkenhuyzen, F.; Tan, Y.; Bleys, P.; Voet, A.; Kruth, J.P.; Dewulf, W. A test object with parallel grooves for calibration and accuracy assessment of industrial computed tomography (CT) metrology. Meas. Sci. Technol. 2011, 22, 115502. [Google Scholar] [CrossRef]
- Obrist, A.F.; Flisch, A.; Hofmann, J. Point cloud reconstruction with sub-pixel accuracy by slice-adaptive thresholding of X-ray computed tomography images. NDT E Int. 2004, 37, 373–380. [Google Scholar] [CrossRef]
- Kowaluk, T.; Wozniak, A. A new threshold selection method for X-ray computed tomography for dimensional metrology. Precis. Eng. 2017, 50, 449–454. [Google Scholar] [CrossRef]
- Shapiro, L.G.; Stockman, G.C. Computer Vision, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001; ISBN 0130307963. [Google Scholar]
- Hermanek, P.; de Oliveira, F.B.; Bartscher, M.; Carmignato, S. Experimental Investigation of new multi-material gap reference standard for testing computed tomography systems. In Proceedings of the 7th Conference on Industrial Computed Tomography, Leuven, Belgium, 7–9 February 2017. [Google Scholar]
- De Oliveira, F.B.; Stolfi, A.; Bartscher, M.; De Chiffre, L.; Neuschaefer-Rube, U. Experimental investigation of surface determination process on multi-material components for dimensional computed tomography. Case Stud. Nondestruct. Test. Eval. 2016, 6, 93–103. [Google Scholar] [CrossRef]
- Venkatachalam, V.; Wasswerman, R.M. Comprehensive Investigation of Subpixel Edge Detection Schemes in Metrology. Mach. Vis. Appl. Ind. Insp. 2003, 5011, 200–212. [Google Scholar] [CrossRef]
- Walkenburg, R.J.; Mclvor, A.M.; Power, P.W. An Evaluation of Subpixel Feature Localization Methods for Precision Measurements. Videom. III Proc. SPIE 1994, 2350, 229–238. [Google Scholar] [CrossRef]
- West, G.; Clarke, T.A. A Survey and Examination of Subpixel Measurement Techniques. Close Range Photogramm. Meets Mach. Vis. 1990, 1395, 456–463. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Yagüe-Fabra, J.A.; Ontiveros, S.; Jiménez, R.; Chitchian, S.; Tosello, G.; Carmignato, S. A 3D edge detection technique for surface extraction in computed tomography for dimensional metrology applications. CIRP Ann. Manuf. Technol. 2013, 62, 531–534. [Google Scholar] [CrossRef]
- Deriche, R. Using Canny’s Criteria to derive a recursively implemented optimal edge detector. Int. J. Comput. Vis. 1987, 1, 167–187. [Google Scholar] [CrossRef]
- Carmignato, S. Accuracy of industrial computed tomography measurements: Experimental results from an international comparison. CIRP Ann. Manuf. Technol. 2012, 61, 491–494. [Google Scholar] [CrossRef]
- De Chiffre, L.; Carmignato, S.; Cantatore, A.; Jensen, J. Replica calibration artefacts for optical 3d scanning of micro parts. In Proceedings of the 9th Euspen International Conference of the EUSPEN, San Sebastian, Spain, 2–5 June 2009; pp. 352–355. [Google Scholar]
- Massey, L.K. Permeability Properties of Plastics and Elastomers, 2nd ed.; William Andrew Publishing: Norwich, NY, USA, 2003; ISBN 1-884207-97-9. [Google Scholar]
- Gasparin, S.; Tosello, G.; Hansen, H.N.; Islam, A. Quality control and process capability assessment for injection-moulded micro mechanical parts. Int. J. Adv. Manuf. Technol. 2013, 66, 1295–1303. [Google Scholar] [CrossRef]
- Carmignato, S.; Voltan, A.; Savio, E. Metrological performance of optical coordinate measuring machines under industrial conditions. CIRP Ann. Manuf. Technol. 2010, 59, 497–500. [Google Scholar] [CrossRef]
- Ruddle, C.J. The ProTaper technique. Endod. Top. 2005, 10, 187–190. [Google Scholar] [CrossRef]
- Industrias, J.Q. Available online: http://www.jq.com.ar/Imagenes/Productos/Teflon/Virgen/teflonvirgen.htm (accessed on 10 June 2018).
- Habasit. Available online: http://www.habasit.com/en/pom.htm (accessed on 10 June 2018).
- British Plastics Federation (BPF). Available online: http://www.bpf.co.uk/plastipedia/polymers/pvc.aspx (accessed on 10 June 2018).
- Jiménez-Pacheco, R.; Ontiveros, S.; Yagüe-Fabra, J.A. A surface extraction analysis in a multi-material test part for computed tomography in metrology applications. Procedia Manuf. 2017, 13, 487–494. [Google Scholar] [CrossRef]
- Schut. Available online: http://www.schut.com/Products/DeMeet/index_Specifications.htm (accessed on 10 June 2018).
- The Association of German Engineers. VDI/VDE 2630 Part 2.1. Determination of the Uncertainty of Measurement and the Test Process Suitability of Coordinate Measurement Systems with CT Sensors; Verein Deutscher Ingenieure e.V.: Düsseldorf, Germany, 2015. [Google Scholar]



| Parameter | CT Tetrahedron | Pan Flute | Step Gauge | Dog Bone | Toggle | Lego | Endodontic File | TEF-POM | TEF-PVC |
|---|---|---|---|---|---|---|---|---|---|
| Voltage (kV) | 90 | 90 | 45 | 80 | 80 | 45 | 90 | 45 | 45 |
| Current (µA) | 80 | 80 | 120 | 95 | 95 | 120 | 80 | 120 | 120 |
| Angular indexing step (degrees) | 0.2 | 0.35 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.3 | 0.3 |
| Voxel size (µm) | 45.5 | 16.5 | 47 | 8 | 8 | 34 | 28 | 28 | 56 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ontiveros, S.; Jiménez, R.; Yagüe-Fabra, J.A.; Torralba, M. Analysis of Surface Extraction Methods Based on Gradient Operators for Computed Tomography in Metrology Applications. Materials 2018, 11, 1461. https://doi.org/10.3390/ma11081461
Ontiveros S, Jiménez R, Yagüe-Fabra JA, Torralba M. Analysis of Surface Extraction Methods Based on Gradient Operators for Computed Tomography in Metrology Applications. Materials. 2018; 11(8):1461. https://doi.org/10.3390/ma11081461
Chicago/Turabian StyleOntiveros, Sinué, Roberto Jiménez, José A. Yagüe-Fabra, and Marta Torralba. 2018. "Analysis of Surface Extraction Methods Based on Gradient Operators for Computed Tomography in Metrology Applications" Materials 11, no. 8: 1461. https://doi.org/10.3390/ma11081461
APA StyleOntiveros, S., Jiménez, R., Yagüe-Fabra, J. A., & Torralba, M. (2018). Analysis of Surface Extraction Methods Based on Gradient Operators for Computed Tomography in Metrology Applications. Materials, 11(8), 1461. https://doi.org/10.3390/ma11081461






