Effects of Loading Frequency and Loading Type on High-Cycle and Very-High-Cycle Fatigue of a High-Strength Steel
Abstract
1. Introduction
2. Material and Methods
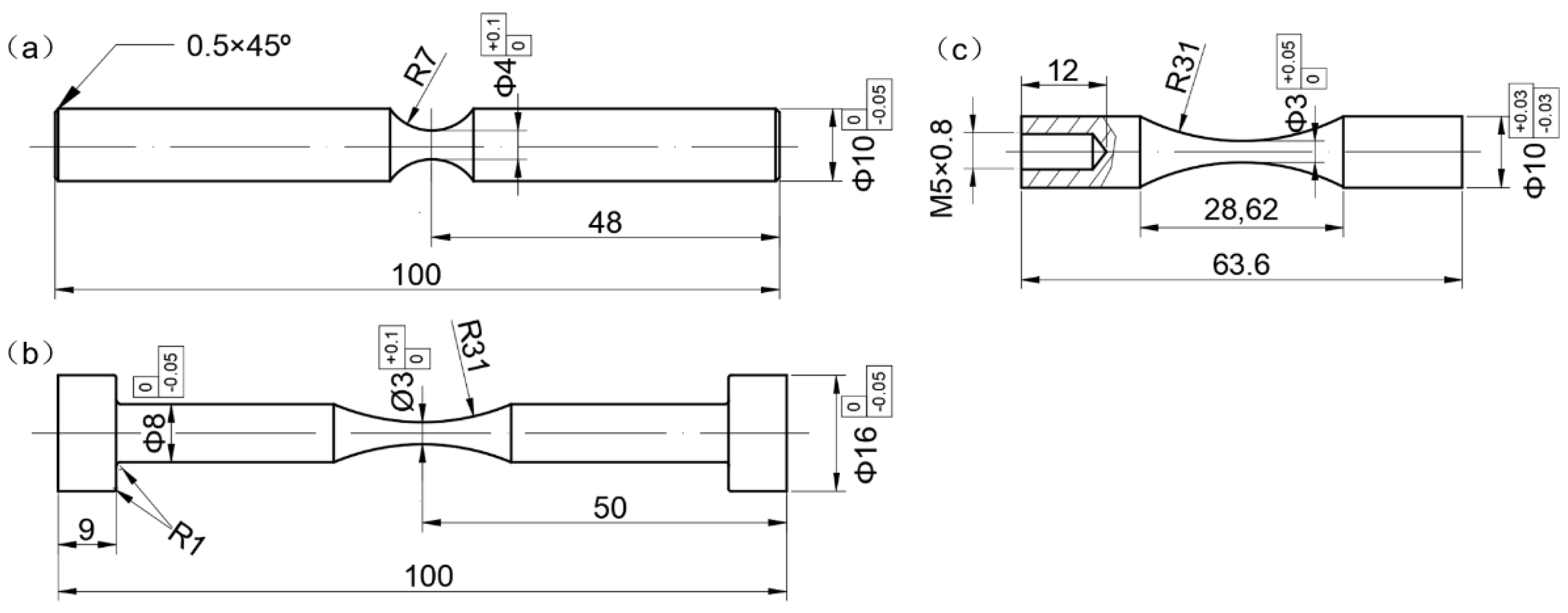
2.1. Test Material
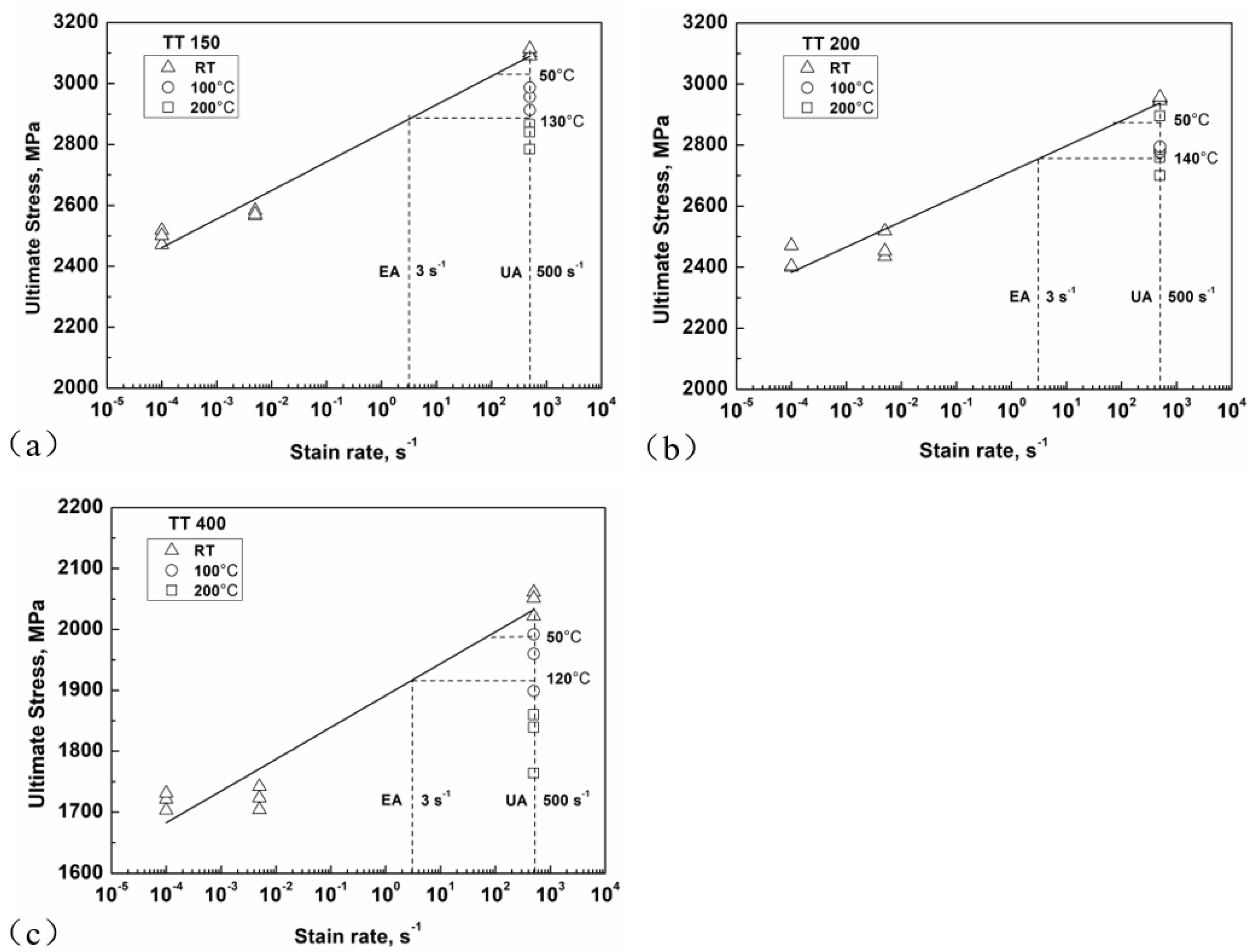
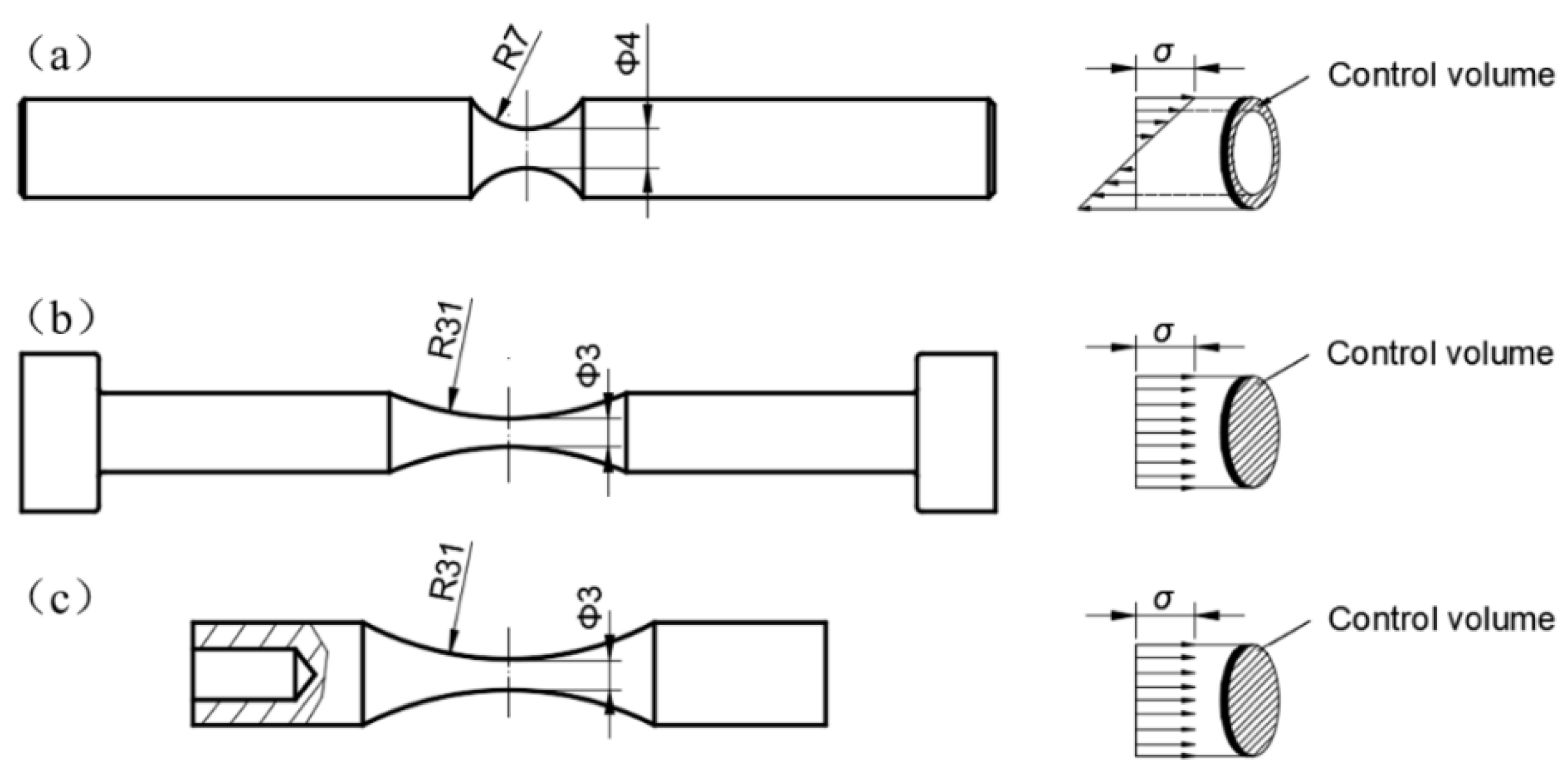
2.2. Experimental Methods
3. Fatigue Testing Results
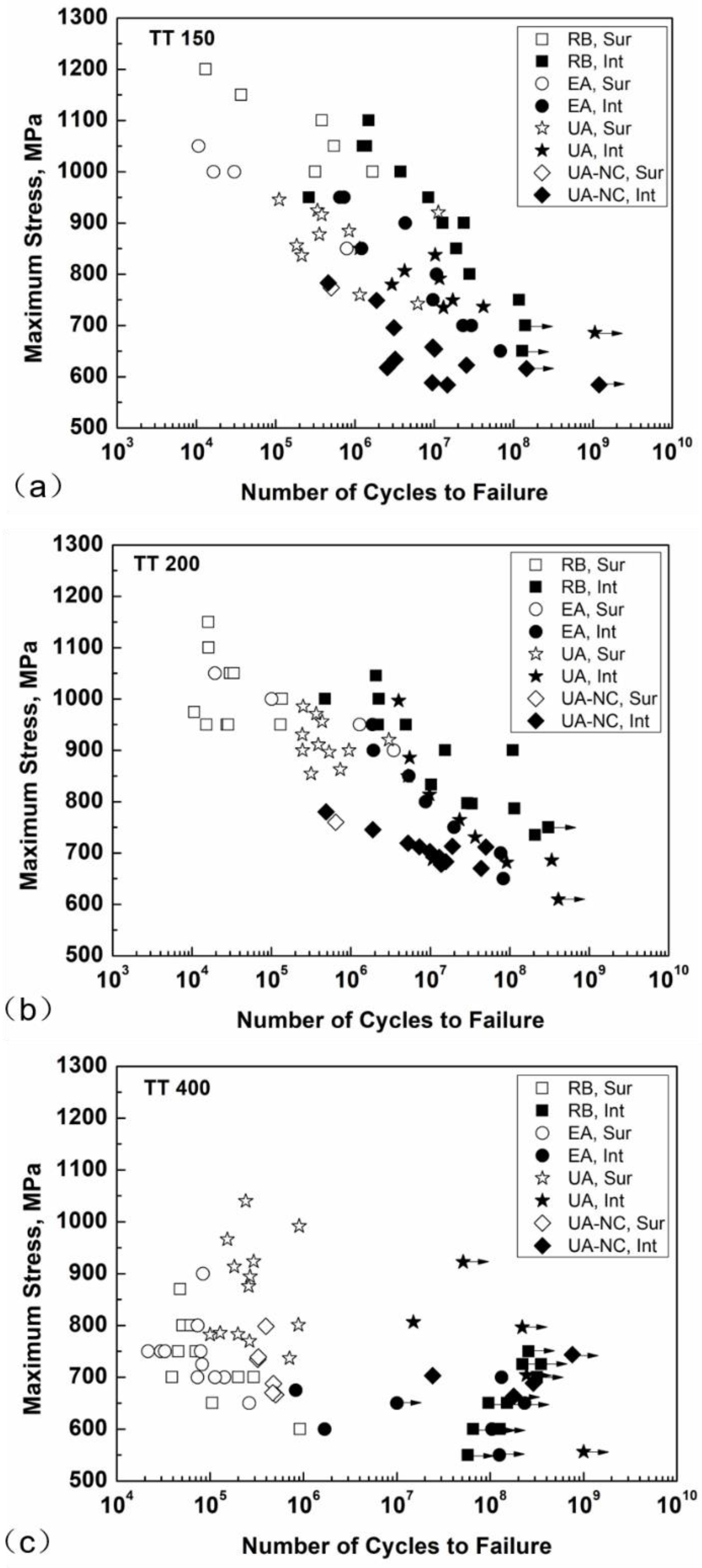
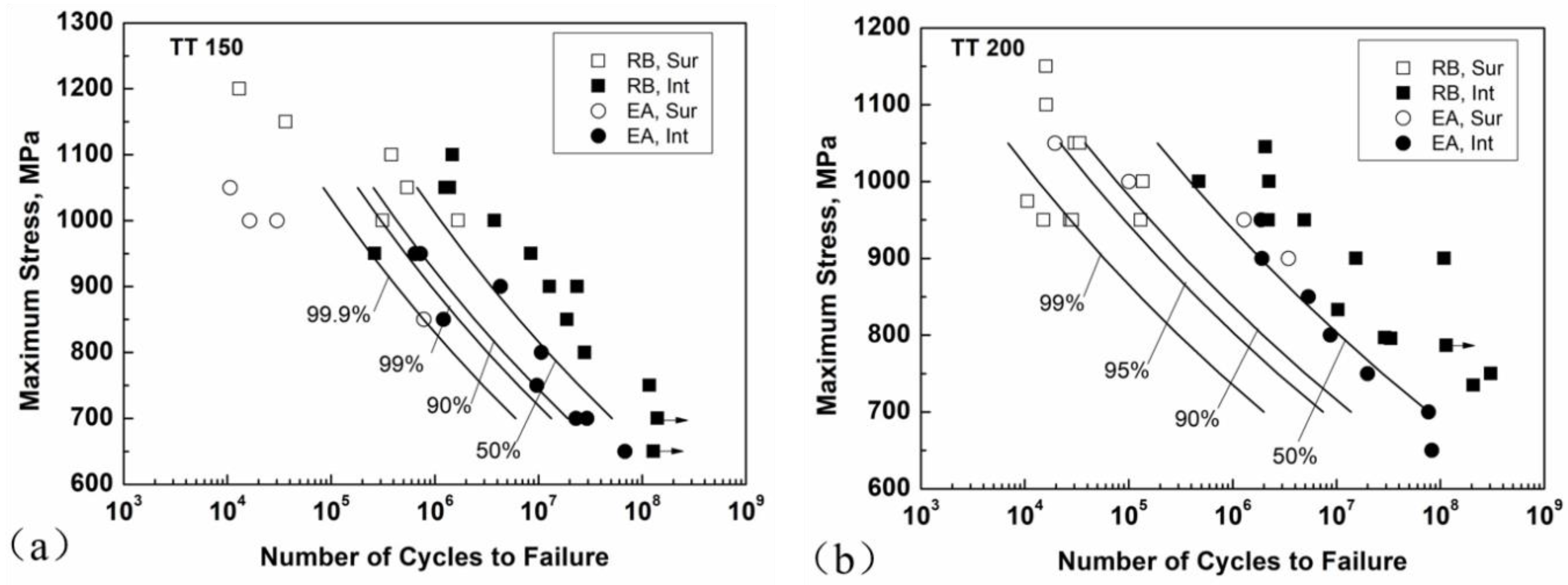
3.1. S-N Data
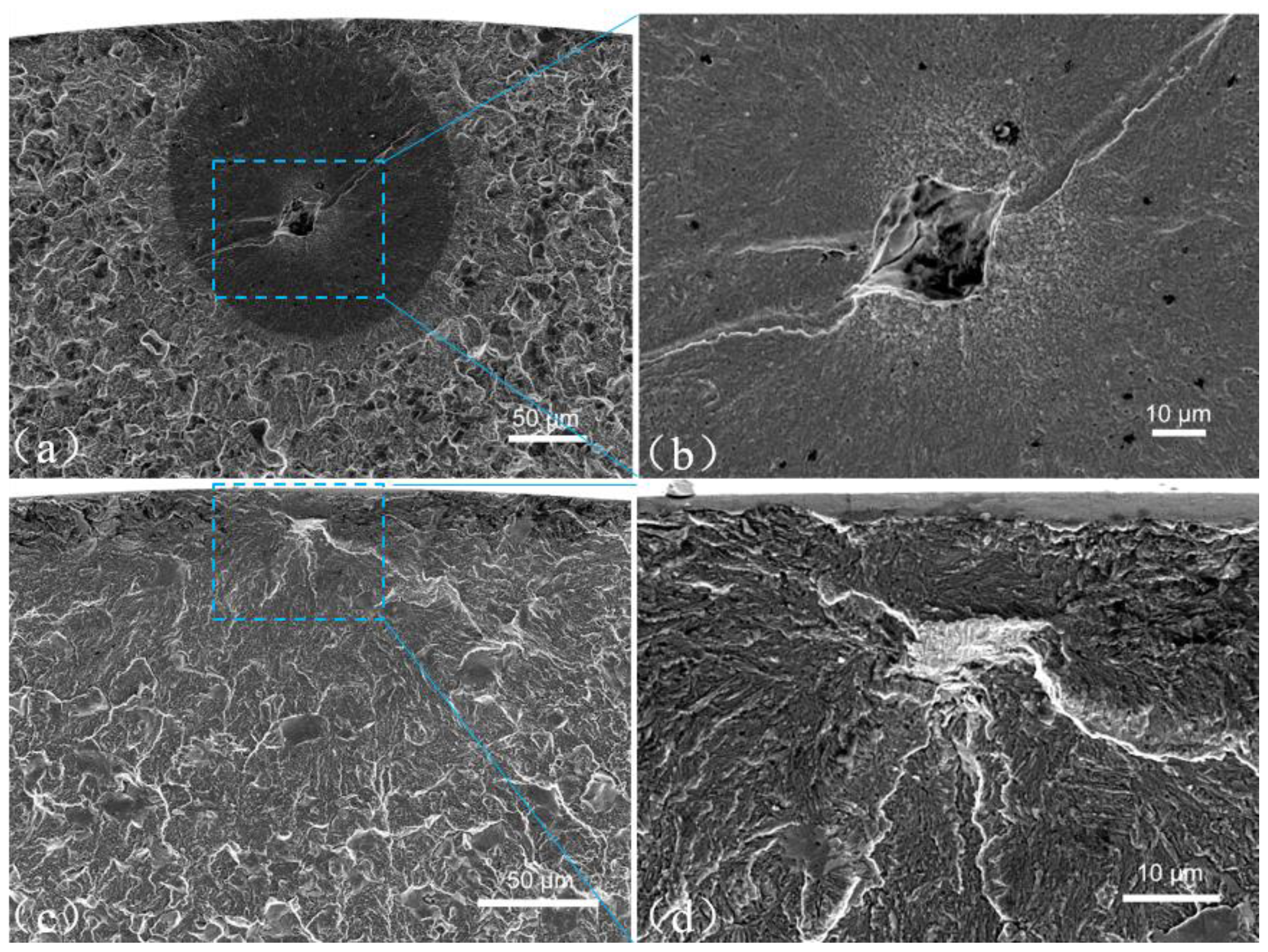
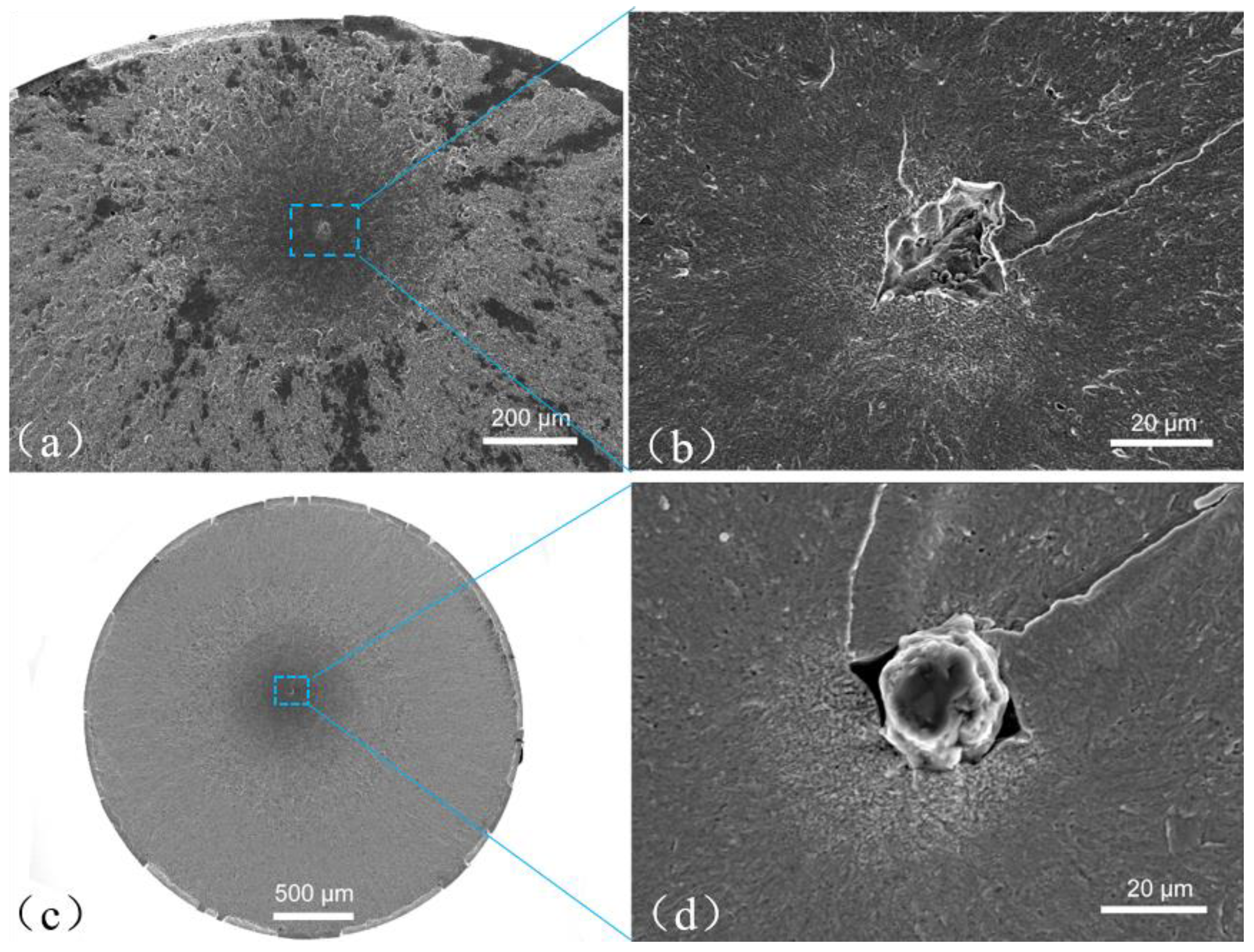
3.2. Fracture Surface Morphology
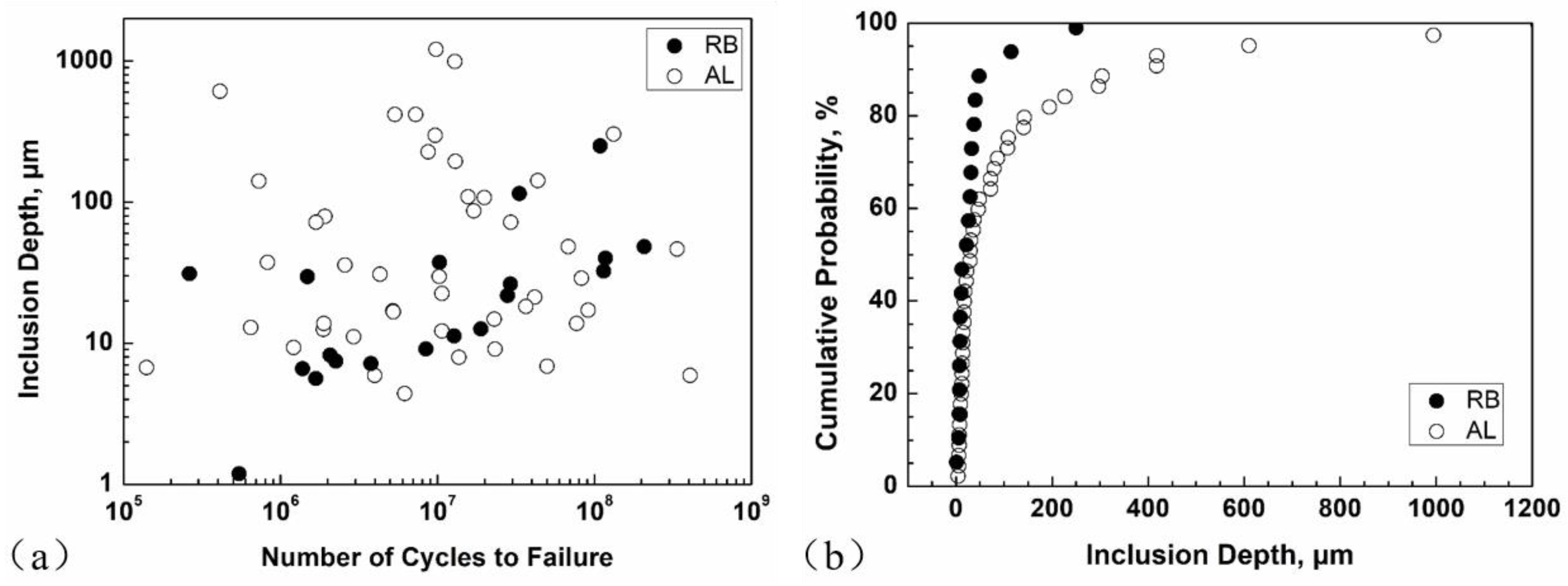
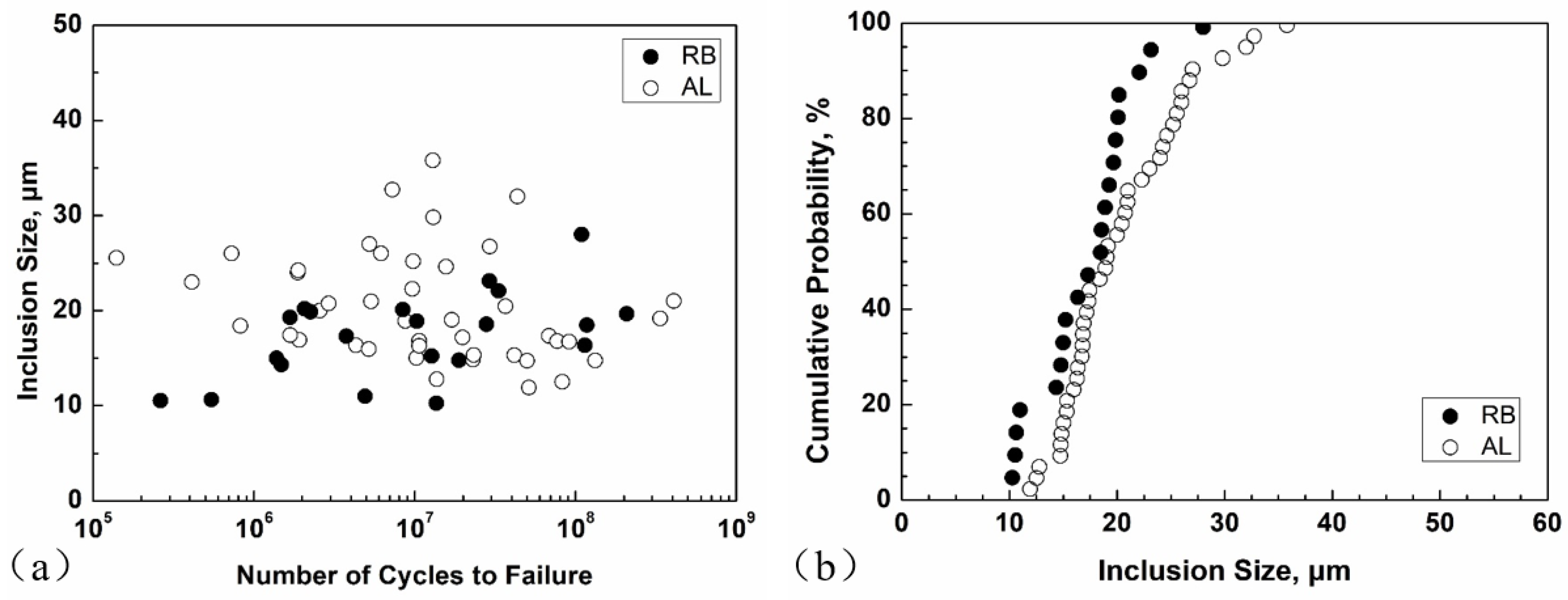
4. Discussion
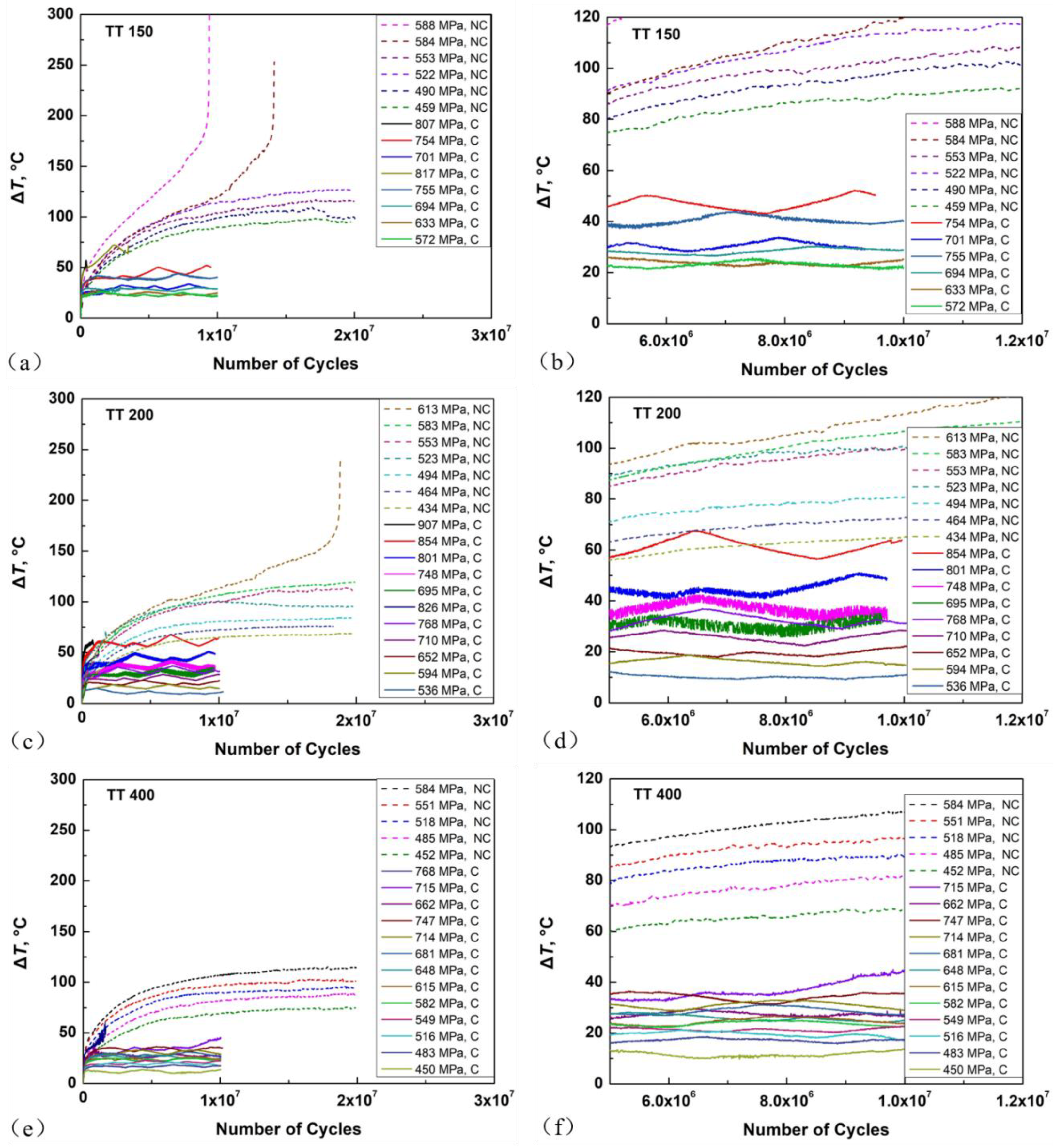
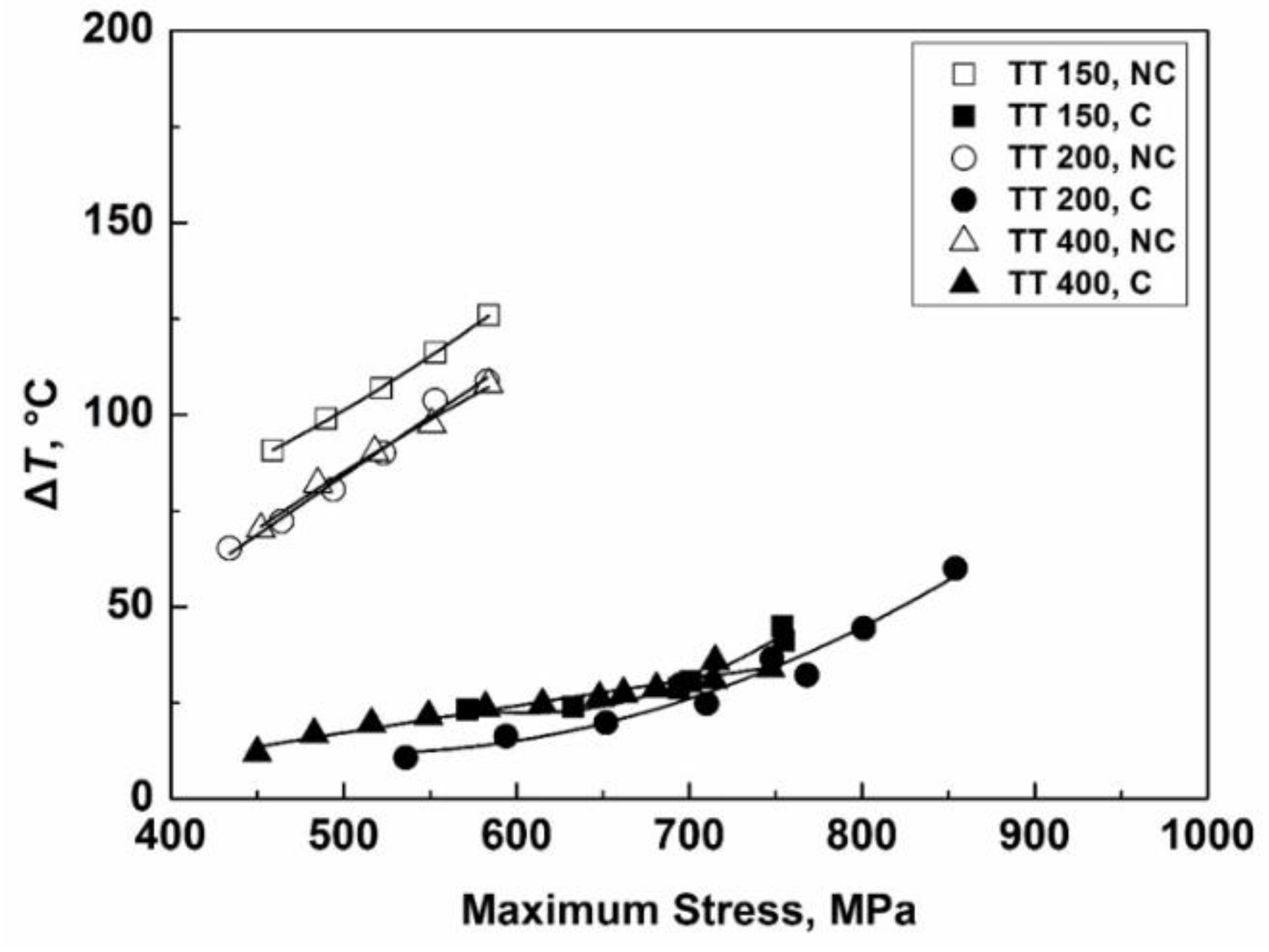
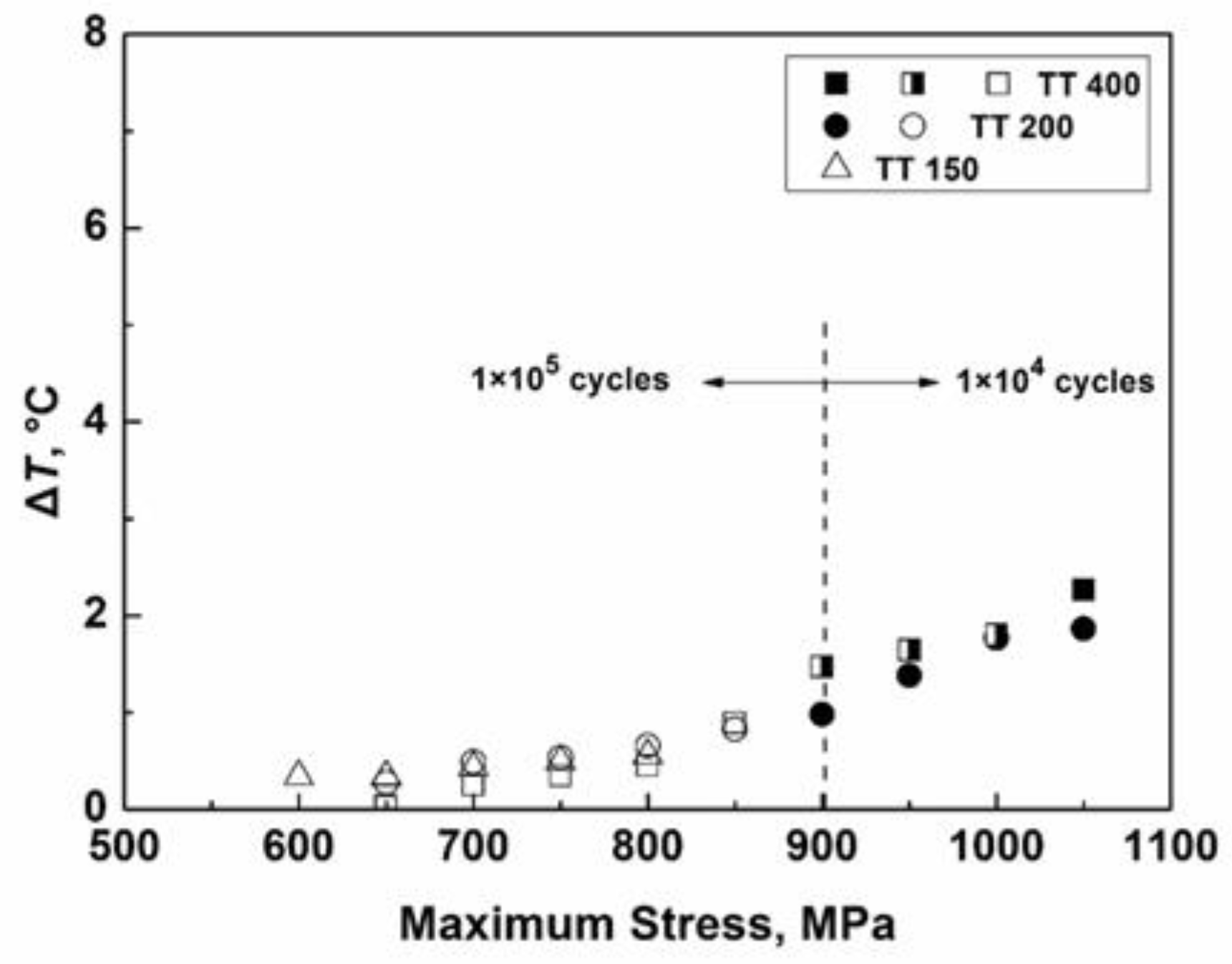
4.1. Effect of Loading Frequency
4.2. Effect of Loading Type
5. Conclusions
- (1)
- For the specimens of the two high strength conditions, the fatigue strength with interior crack initiation mode for the RB method is superior to that for the EA and UA methods because of the small control volume for the former; the fatigue strength for the UA method is slightly higher than that for the EA method in the VHCF regime, suggesting the existence of a loading frequency effect; and the fatigue strength of the UA-NC method is substantially lower than that of the EA and UA methods due to the temperature rise of the specimen for the former.
- (2)
- For the specimens in the low strength condition, the fatigue strength for the RB method is almost the same as that for the EA method because fatigue cracking almost initiates from the specimen surface; thus, the loading type effect is diminishing. The fatigue strength for the UA method is higher than that for the UA-NC method, and the fatigue strength for both the UA and UA-NC methods is higher than that for the EA method, showing an evident loading frequency effect.
- (3)
- The combined response of strain rate and the induced temperature rise is the reason for the loading frequency effect. A parameter η was proposed to judge whether the loading frequency effect may occur, and the calculated results are in agreement with the experimental data.
- (4)
- The statistical method used based on the control volume is suitable for reconciling the effect of loading type. The predicted P-S-N curves of the EA specimen are consistent with the experimental data for the specimens of the two high strength conditions.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Marines, I.; Bin, X.; Bathias, C. An understanding of very high cycle fatigue of metals. Int. J. Fatigue 2003, 25, 1101–1107. [Google Scholar] [CrossRef]
- Mughrabi, H. Specific features and mechanisms of fatigue in the ultrahigh-cycle regime. Int. J. Fatigue 2006, 28, 1501–1508. [Google Scholar] [CrossRef]
- Sakai, T. Review and Prospects for current studies on very high cycle fatigue of metallic materials for machine structural use. J. Solid Mech. Mater. Eng. 2009, 3, 425–439. [Google Scholar] [CrossRef]
- Stanzl-Tschegg, S.E. Fracture mechanical characterization of the initiation and growth of interior fatigue cracks. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1741–1751. [Google Scholar] [CrossRef]
- Mayer, H. Recent developments in ultrasonic fatigue. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 3–29. [Google Scholar] [CrossRef]
- Jeddi, D.; Palin-Luc, T. A review about the effects of structural and operational factors on the gigacycle fatigue of steels. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 969–990. [Google Scholar] [CrossRef]
- Naito, T.; Ueda, H.; Kikuchi, M. Fatigue behavior of carburized steel with internal oxides and nonmartensitic microstructure near the surface. Metall. Trans. A. 1984, 15, 1431–1436. [Google Scholar] [CrossRef]
- Mughrabi, H. Fatigue, an everlasting materials problem—still en vogue. Procedia Eng. 2010, 2, 3–26. [Google Scholar] [CrossRef]
- Sakai, T.; Sato, Y.; Oguma, N. Characteristic S-N properties of high-carbon-chromium-bearing steel under axial loading in long-life fatigue. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 765–773. [Google Scholar] [CrossRef]
- Hong, Y.; Lei, Z.; Sun, C.; Zhao, A. Propensities of crack interior initiation and early growth for very-high-cycle fatigue of high strength steels. Int. J. Fatigue 2014, 58, 144–151. [Google Scholar] [CrossRef]
- Ebara, R. Some influencing variables on internal fatigue crack initiation in structural materials. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1752–1761. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T.; Murakami, Y. On the mechanism of fatigue failure in the superlong life regime (N > 10(7) cycles). Part I: Influence of hydrogen trapped by inclusions. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 893–902. [Google Scholar] [CrossRef]
- Murakami, Y.; Nomoto, T.; Ueda, T.; Murakami, Y. On the mechanism of fatigue failure in the superlong life regime (N > 10(7) cycles). Part II: A fractographic investigation. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 903–910. [Google Scholar] [CrossRef]
- Shiozawa, K.; Morii, Y.; Nishino, S.; Lu, L. Subsurface crack initiation and propagation mechanism under the super-long fatigue regime for high speed tool steel (JIS SKH51) by fracture surface topographic analysis. Int. J. Fatigue 2006, 28, 1521–1532. [Google Scholar] [CrossRef]
- Sakai, T.; Oguma, N.; Morikawa, A. Microscopic and nanoscopic observations of metallurgical structures around inclusions at interior crack initiation site for a bearing steel in very high-cycle fatigue. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1305–1314. [Google Scholar] [CrossRef]
- Grad, P.; Reuscher, B.; Brodyanski, A.; Kopnarski, M.; Kerscher, E. Mechanism of fatigue crack initiation and propagation in the very high cycle fatigue regime of high-strength steels. Scripta Mater. 2012, 67, 838–841. [Google Scholar] [CrossRef]
- Shanyavskiy, A.A. Mechanisms and modeling of subsurface fatigue cracking in metals. Eng. Fract. Mech. 2013, 110, 350–363. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, X.; Lei, Z.; Sun, C. The formation mechanism of characteristic region at crack initiation for very-high-cycle fatigue of high-strength steels. Int. J. Fatigue 2016, 89, 108–118. [Google Scholar] [CrossRef]
- Hong, Y.; Sun, C. The nature and the mechanism of crack initiation and early growth for very-high-cycle fatigue of metallic materials—An overview. Theor. Appl. Fract. Mech. 2017, 92, 331–350. [Google Scholar] [CrossRef]
- Su, H.; Liu, X.; Sun, C.; Hong, Y. Nanograin layer formation at crack initiation region for very-high-cycle fatigue of a Ti-6Al-4V alloy. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 979–993. [Google Scholar] [CrossRef]
- Morrissey, R.J.; McDowell, D.L.; Nicholas, T. Frequency and stress ratio effects in high cycle fatigue of Ti-6Al-4V. Int. J. Fatigue 1999, 21, 679–685. [Google Scholar] [CrossRef]
- Furuya, Y.; Matsuoka, S.; Abe, T.; Yamaguchi, K. Gigacycle fatigue properties for high-strength low-alloy steel at 100 Hz, 600 Hz, and 20 kHz. Scripta Mater. 2002, 46, 157–162. [Google Scholar] [CrossRef]
- Takeuchi, E.; Furuya, Y.; Nagashima, N.; Matsuoka, S. The effect of frequency on the giga-cycle fatigue properties of a Ti-6Al-4V alloy. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 599–605. [Google Scholar] [CrossRef]
- Zhu, X.; Jones, J.W.; Allison, J.E. Effect of frequency, environment, and temperature on fatigue behavior of E319 cast-aluminum alloy: Small-crack propagation. Metall. Mater. Trans. A 2008, 39, 2666–2680. [Google Scholar] [CrossRef]
- Zhu, X.; Jones, J.W.; Allison, J.E. Effect of frequency, environment, and temperature on fatigue behavior of E319 cast aluminum alloy: Stress-controlled fatigue life response. Metall. Mater. Trans. A 2008, 39, 2681–2688. [Google Scholar] [CrossRef]
- Tsutsumi, N.; Murakami, Y.; Doquet, V. Effect of test frequency on fatigue strength of low carbon steel. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 473–483. [Google Scholar] [CrossRef]
- Li, W.; Sakai, T.; Li, Q.; Lu, L.; Wang, P. Effect of loading type on fatigue properties of high strength bearing steel in very high cycle regime. Mater. Sci. Eng. A 2011, 528, 5044–5052. [Google Scholar] [CrossRef]
- Guennec, B.; Akira, U.; Sakai, T.; Takanashi, M.; Itabashi, Y. Effect of the loading frequency on fatigue properties of JIS S15C low carbon steel and some discussions based on micro-plasticity behavior. Int. J. Fatigue 2014, 66, 29–38. [Google Scholar] [CrossRef]
- Schmid, S.; Hahn, M.; Issler, S.; Bacher-Hoechst, M.; Furuya, Y.; Mehner, A.; Bomas, H.; Zoch, H.W. Effect of frequency and biofuel E85 on very high cycle fatigue behaviour of the high strength steel X90CrMoV18. Int. J. Fatigue 2014, 60, 90–100. [Google Scholar] [CrossRef]
- Schneider, N.; Pyttel, B.; Berger, C.; Oechsner, M. Influence of Frequency and Testing Technique on the Fatigue Behaviour of Quenched and Tempered Steel in the VHCF-Regime. In Proceedings of the 11th International Fatigue Congress, Melbourne, Australia, 2–7 March 2014; Clark, G., Wang, C., Eds.; Trans Tech Publications: Zürich, Switzerland, 2014; Volumes 891–892, pp. 1430–1435, ISBN 978-3-03835-008-8. [Google Scholar]
- Zhu, M.; Liu, L.; Xuan, F. Effect of frequency on very high cycle fatigue behavior of a low strength Cr-Ni-Mo-V steel welded joint. Int. J. Fatigue 2015, 77, 166–173. [Google Scholar] [CrossRef]
- Fargione, G.; Giudice, F.; Risitano, A. The influence of the load frequency on the high cycle fatigue behaviour. Theor. Appl. Fract. Mech. 2017, 88, 97–106. [Google Scholar] [CrossRef]
- Wang, S.Q.; Zhang, D.K.; Hu, N.N.; Zhang, J.L. Effect of stress ratio and loading frequency on the corrosion fatigue behavior of smooth steel wire in different solutions. Materials 2016, 9, 750. [Google Scholar] [CrossRef] [PubMed]
- Zhao, A.; Xie, J.; Sun, C.; Lei, Z.; Hong, Y. Effects of strength level and loading frequency on very-high-cycle fatigue behavior for a bearing steel. Int. J. Fatigue 2012, 38, 46–56. [Google Scholar] [CrossRef]
- Laird, C.; Charsley, P. Strain rate sensitivity effects in cyclic deformation and fatigue fracture. Int. J. Fatigue 1982, 4, 239. [Google Scholar]
- Mayer, H. Fatigue crack growth and threshold measurements at very high frequencies. Mater. Sci. Res. 1999, 44, 1–34. [Google Scholar] [CrossRef]
- Papakyriacou, M.; Mayer, H.; Pypen, C.; Plenk, H.; Stanzl-Tschegg, S. Influence of loading frequency on high cycle fatigue properties of b.c.c. and h.c.p. metals. Mater. Sci. Eng. A 2001, 308, 143–152. [Google Scholar] [CrossRef]
- Murakami, Y.; Yokoyama, N.N.; Nagata, J. Mechanism of fatigue failure in ultralong life regime. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 735–746. [Google Scholar] [CrossRef]
- Shiozawa, K.; Hasegawa, T.; Kashiwagi, Y.; Lu, L. Very high cycle fatigue properties of bearing steel under axial loading condition. Int. J. Fatigue 2009, 31, 880–888. [Google Scholar] [CrossRef]
- Nakajima, M.; Tokaji, K.; Itoga, H.; Shimizu, T. Effect of loading condition on very high cycle fatigue behavior in a high strength steel. Int. J. Fatigue 2010, 32, 475–480. [Google Scholar] [CrossRef]
- Li, W.; Deng, H.L.; Liu, P.F. Interior Fracture mechanism analysis and fatigue life prediction of surface-hardened gear steel under axial loading. Materials 2016, 9, 843. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Lei, Z.; Xie, J.; Hong, Y. Effects of inclusion size and stress ratio on fatigue strength for high-strength steels with fish-eye mode failure. Int. J. Fatigue 2013, 48, 19–27. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Liu, X.; Hong, Y. Effects of specimen size on fatigue life of metallic materials in high-cycle and very-high-cycle fatigue regimes. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 770–779. [Google Scholar] [CrossRef]
- Zhang, Z.; Qian, X. Effect of experimental sample size on local Weibull assessment of cleavage fracture for steel. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1128–1142. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, H.; Wang, C.; Wang, Q. Fatigue life dispersion and thermal dissipation investigations for titanium alloy TC17 in very high cycle regime. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1285–1293. [Google Scholar] [CrossRef]
- Lei, Z.; Xie, J.; Sun, C.; Hong, Y. Effect of loading condition on very-high-cycle fatigue behavior and dominant variable analysis. Sci. China–Phys. Mech. Astron. 2014, 57, 74–82. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
| Heat Treatment Condition | Tensile Strength, MPa | Yield Strength, MPa | Microhardness, Hv |
|---|---|---|---|
| TT 150 | 2497 | NA | 828 |
| TT 200 | 2425 | 1764 | 754 |
| TT 400 | 1718 | 1583 | 526 |
| Specimen Condition | σ, MPa | T, °C | η | ||||
|---|---|---|---|---|---|---|---|
| UA | EA | UA | EA | UA | EA | ||
| TT 150 | 700 | 700 | 419 | 2.5 | 51.7 | 20 | 1.103 |
| TT 200 | 700 | 700 | 419 | 2.5 | 46.0 | 20 | 1.108 |
| TT 400 | 700 | 700 | 419 | 2.5 | 51.1 | 20 | 1.080 |
| Specimen Condition | σ, MPa | T, °C | σUA/σUA-NC | ||
|---|---|---|---|---|---|
| UA | UA-NC | ||||
| TT 150 | 584 | 628 | 43.1 | 145.9 | 1.134 |
| TT 200 | 584 | 628 | 36.3 | 128.7 | 1.107 |
| TT 400 | 584 | 628 | 43.7 | 127.9 | 1.106 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Sun, C.; Xie, J.; Hong, Y. Effects of Loading Frequency and Loading Type on High-Cycle and Very-High-Cycle Fatigue of a High-Strength Steel. Materials 2018, 11, 1456. https://doi.org/10.3390/ma11081456
Hu Y, Sun C, Xie J, Hong Y. Effects of Loading Frequency and Loading Type on High-Cycle and Very-High-Cycle Fatigue of a High-Strength Steel. Materials. 2018; 11(8):1456. https://doi.org/10.3390/ma11081456
Chicago/Turabian StyleHu, Yuanpei, Chengqi Sun, Jijia Xie, and Youshi Hong. 2018. "Effects of Loading Frequency and Loading Type on High-Cycle and Very-High-Cycle Fatigue of a High-Strength Steel" Materials 11, no. 8: 1456. https://doi.org/10.3390/ma11081456
APA StyleHu, Y., Sun, C., Xie, J., & Hong, Y. (2018). Effects of Loading Frequency and Loading Type on High-Cycle and Very-High-Cycle Fatigue of a High-Strength Steel. Materials, 11(8), 1456. https://doi.org/10.3390/ma11081456





