Mechanical Properties Study of Fe-Mn-Si Shape Memory Alloys Welding Seam Formed by Laser Welding with Filler Powder
Abstract
1. Introduction
2. Materials and Methods
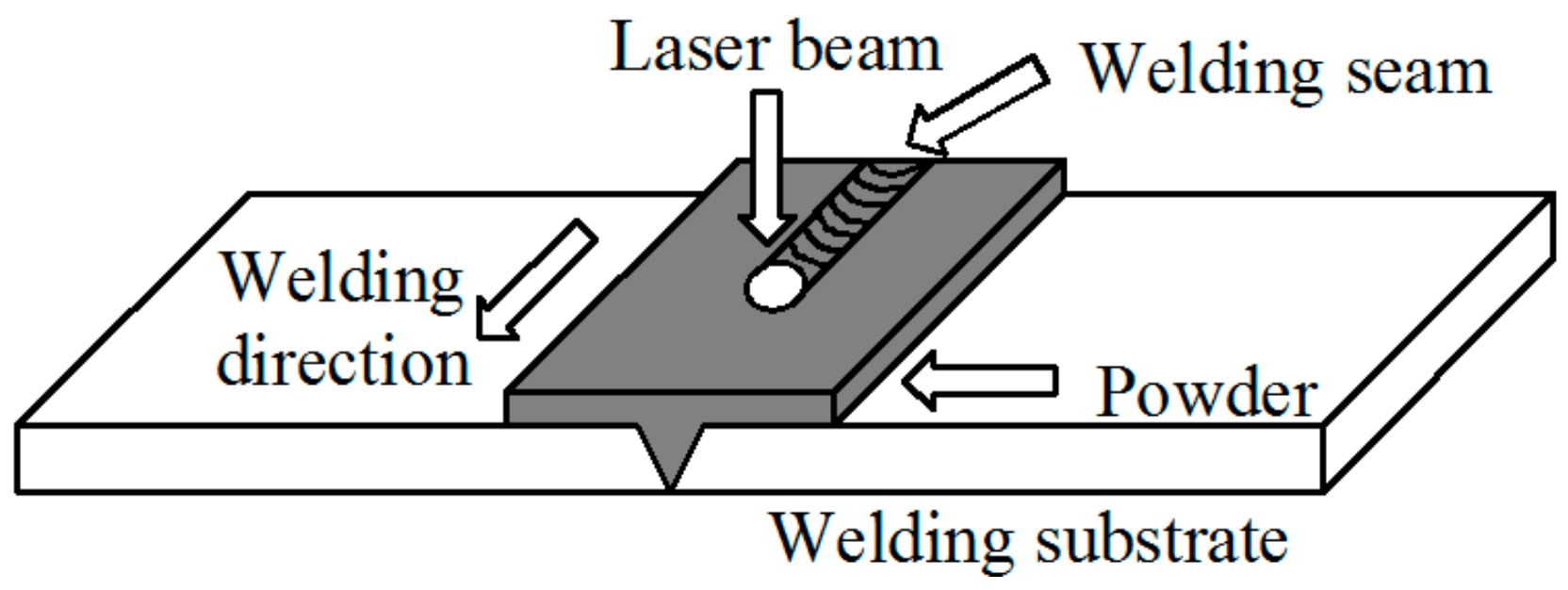
2.1. Experiment of Laser Welding with Powder Filler
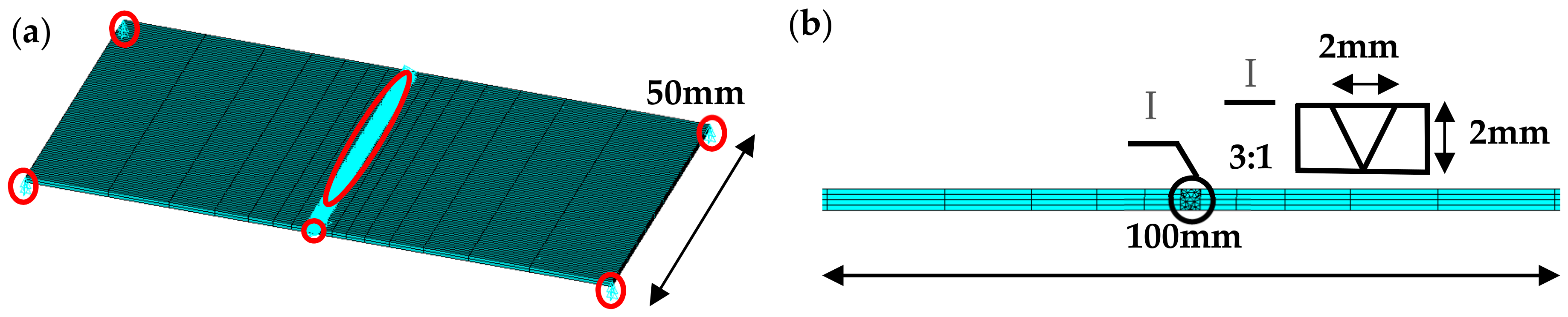
2.2. Numerical Simulation of Laser Welding with Powder Filler
- (1)
- Type of heat source: The energy distribution in the middle of the spot is more than that of the edges in the laser processing, which is similar to the Gaussian mathematical model. Thus, the Gaussian heat source model was used as the heat source, and the “birth and death unit” technology was adopted to simulate the metallurgical bonding between the filler powder and the substrate in the movement process of the laser spot [18].
- (2)
- Material parameters: The thermo-mechanical indirect coupling method was adopted to simulate the laser welding stress field. That is, the temperature unit was converted into the stress unit when the simulation of the temperature field was completed, and the node temperature of each load step (time point) in the thermal analysis was regarded as a load of the stress field. The necessary material parameters for the simulation include: thermal conductivity (W/m·°C), density (kg/m3), specific heat capacity (J/kg·°C), enthalpy (J/m3), Poisson’s ratio, coefficient of thermal expansion (μm /m·K), elastic Modulus (Pa), yield Stress (Pa), etc. The material properties of 304 stainless steel and Fe-Mn-Si memory alloys were obtained by related literatures [19,20] and JMatpro software.
- (3)
- Boundary conditions of temperature field: The boundary conditions of temperature field included radiation, convection and heat conduction. Because the size of the welding seam is small, the heat loss caused by the radiation can be ignored. The convective heat transfer coefficient was applied on the model surface to simulate the convection among the welding seam, the substrate and the surrounding media, and the temperature-dependent convection coefficient is achieved by the TABLE mode in the ANSYS software [21]. The heat conductivity coefficient was defined to simulate the heat conduction between the welding seam and the substrate.
- (4)
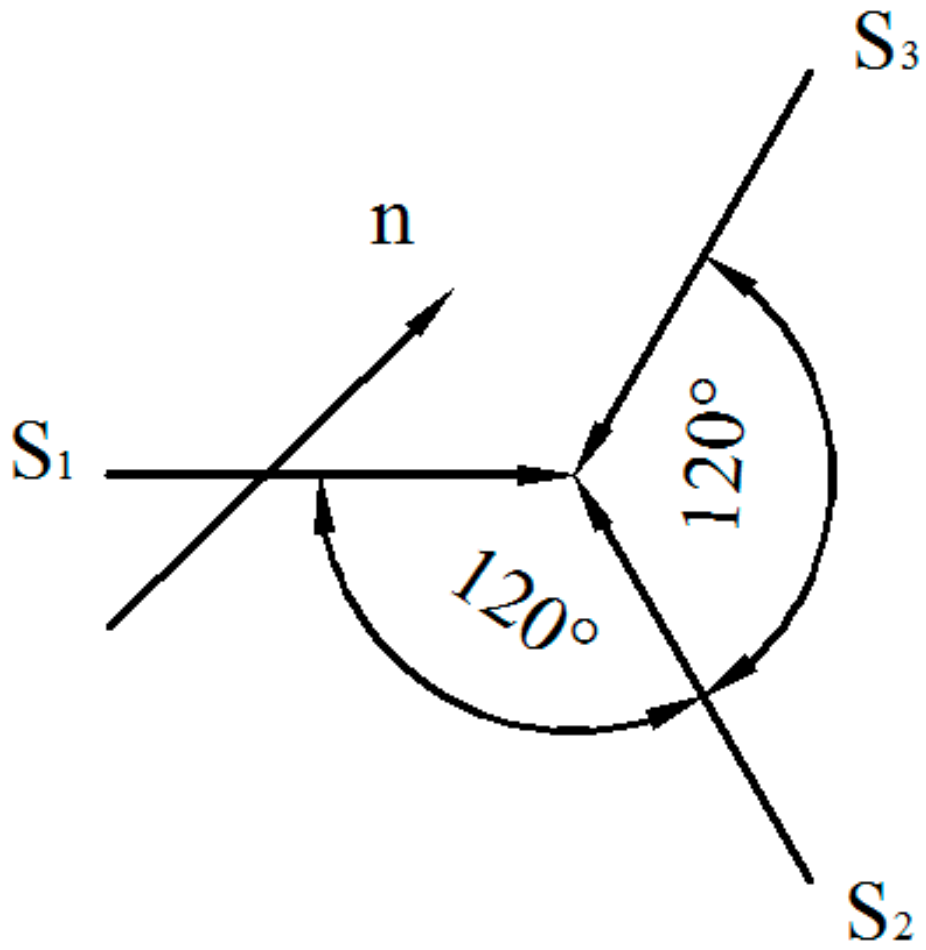
- Boundary conditions of stress field: The boundary conditions of stress field were the constraints on the degree freedoms in the model (displacements in three directions). To avoid stress concentration and simulate a situation where the weldment was freely placed on the workbench, the displacement constraints were set as follows: the nodes in the refined unit of the welding seam were applied as a restraint in the vertical direction to the welding seam; the node in the initial position on the bottom of the welding seam was applied a restraint in the horizontal direction of the welding seam; 8 vertices in the substrate furthest away from the welding seam were set as the constraint in the vertical direction of the substrate surface. The schematic diagram of the displacement constraint is shown in Figure 7a.
3. Results and Discussions
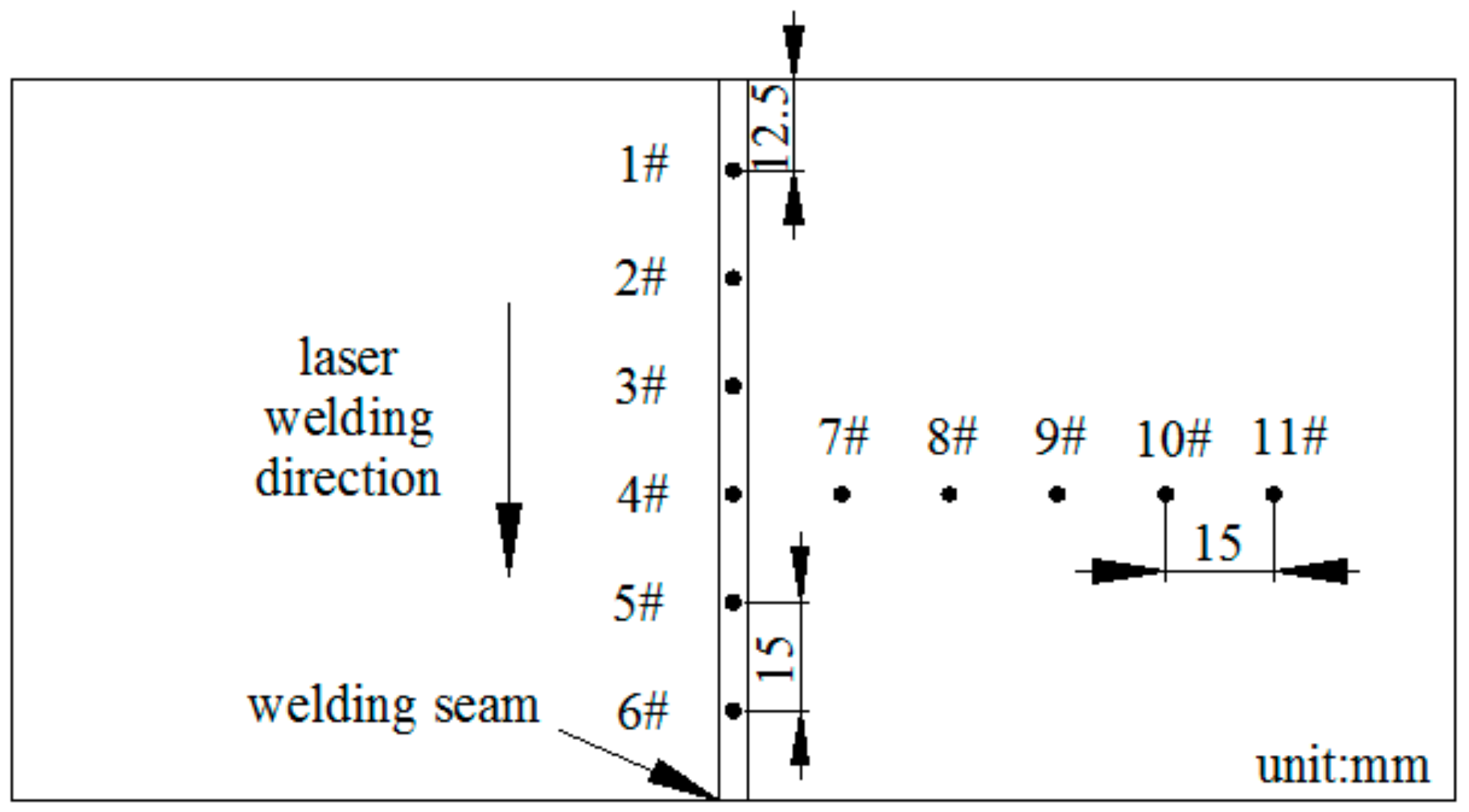
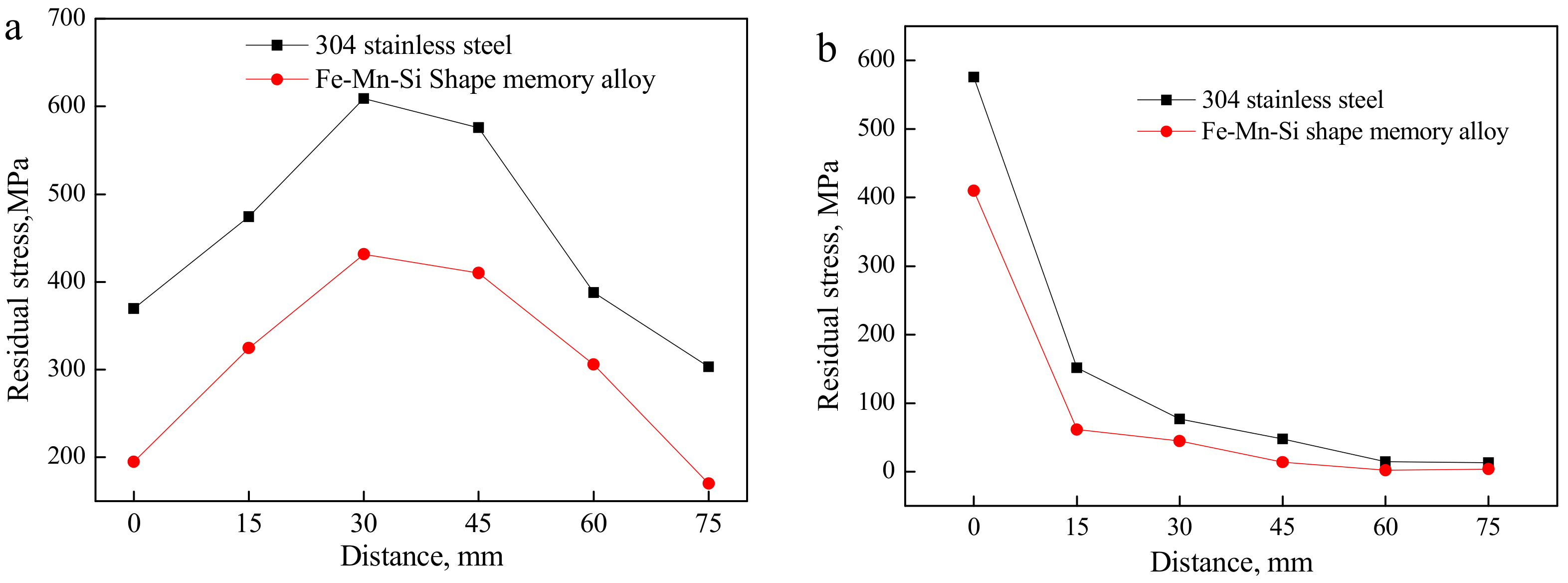
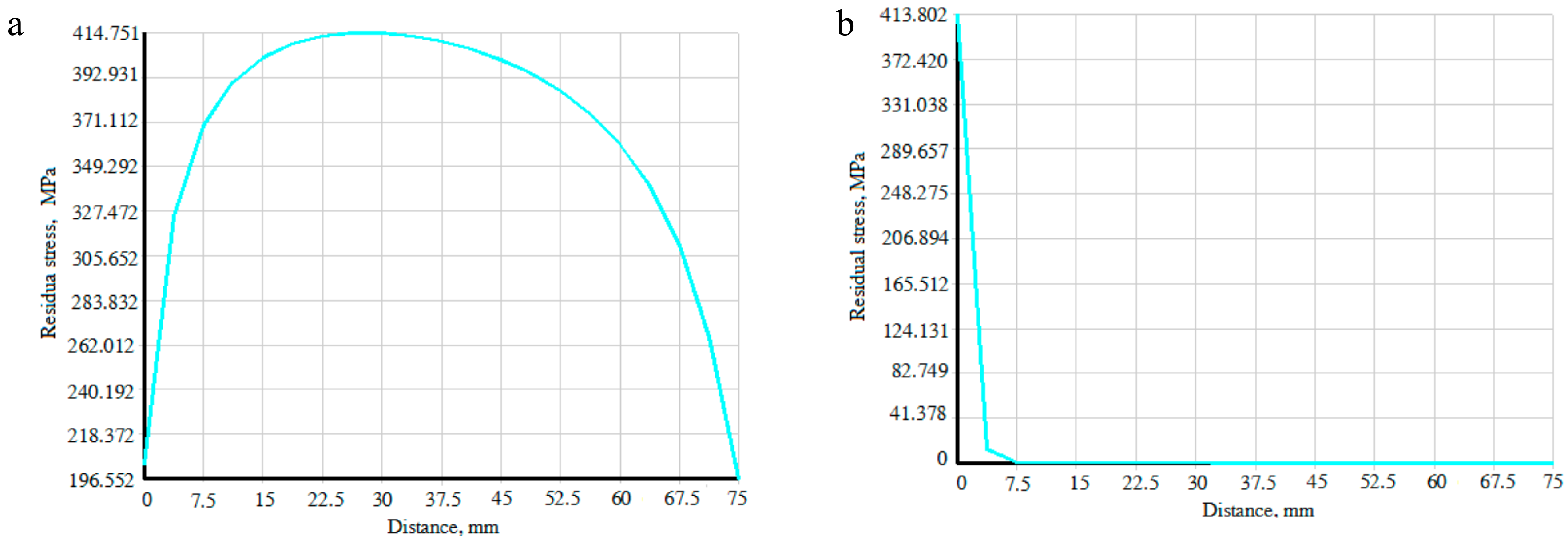
3.1. Residual Stress Distribution of Welding Specimens
3.2. Bending Fatigue Life of Welding Specimens
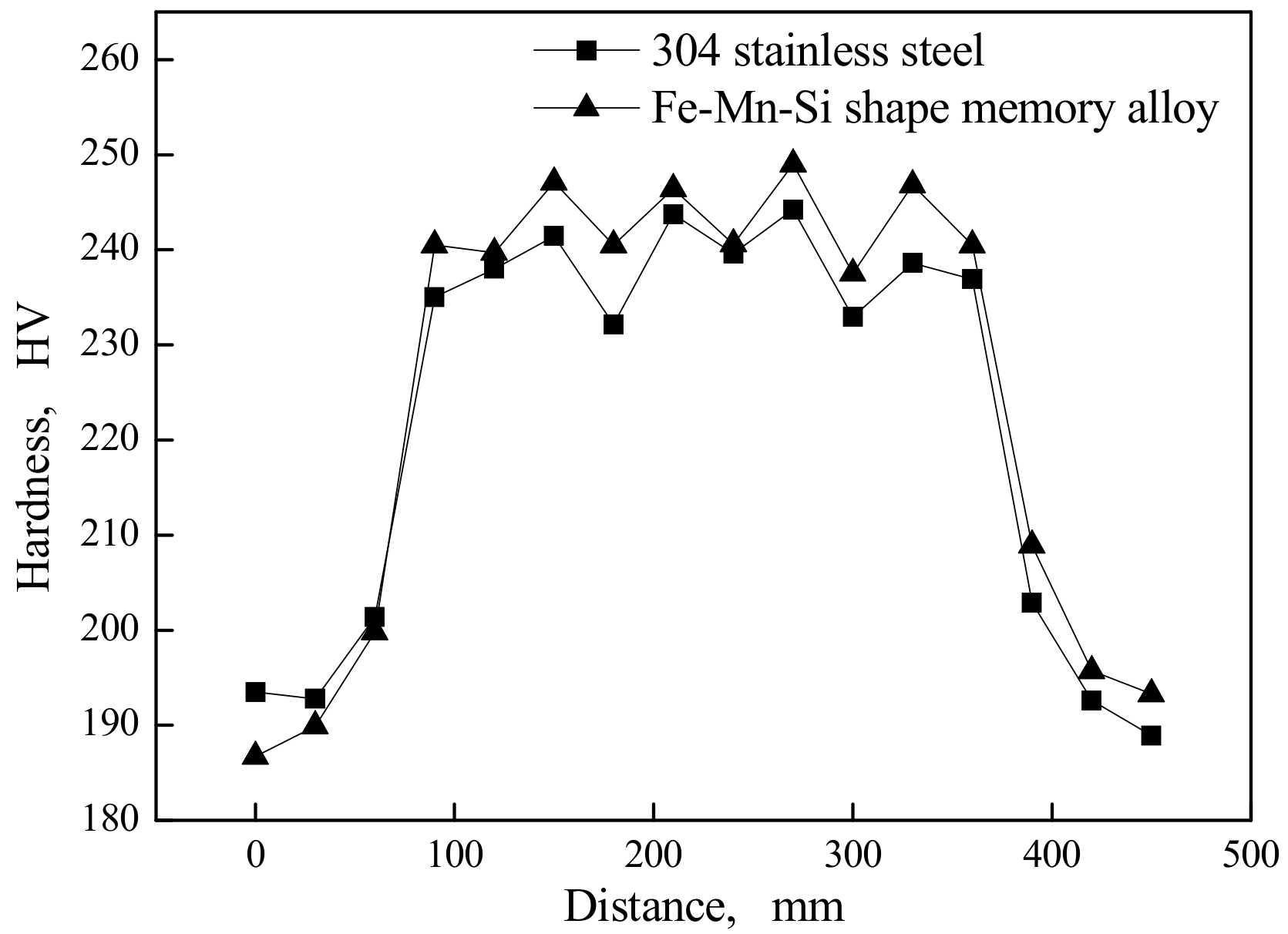
3.3. Microhardness Distribution of Welding Specimens
4. Conclusions
- Under the optimal technological conditions (the laser power is 2.7 KW, the scanning speed is 160 mm/min, the defocus amount is +5 mm) and the mass ratio of Fe/Mn/Si powder (21.118:57.207:21.675), the Fe15Mn5Si12Cr6Ni SMAs welding seam was formed in situ in laser welding of 304 stainless steel with the Fe/Mn/Si powder.
- In the parallel direction to the laser welding, the residual stress of the measuring points in the middle of the welding seam is greater than that in the two sides. In the perpendicular direction to the welding seam, the peak value of the residual stress exists in the narrow area of the welding seam. As the distance between the measuring points and the welding seam increases, the stress rapidly decreases and gradually approaches zero MPa. Although the distribution law of residual stress in the test materials and the comparative materials is similar, the former residual stress at the corresponding measurement points is smaller. Furthermore, the results of the numerical simulation and the experiment are mutually consistent.
- The weldment with Fe-Mn-Si SMAs welding seam and 304 stainless steel welding seam possess 249 and 136 bending fatigue cycles, respectively, and the fatigue cycle of the experimental materials and comparative materials is 90.9% and 49.6% of the base metal, respectively. The macro fracture morphology of the comparative materials is smoother than that of the test materials, and their appearance of fatigue final rupture zone are dense tearing ridges and large number of dimples in turn, which indicates that the Fe-Mn-Si SMAs welding seam significantly improved the bending fatigue characteristics of the weldments.
- The experimental materials have slightly greater microhardness than the comparative material, and the microhardness jumps from the substrate to the welding seam.
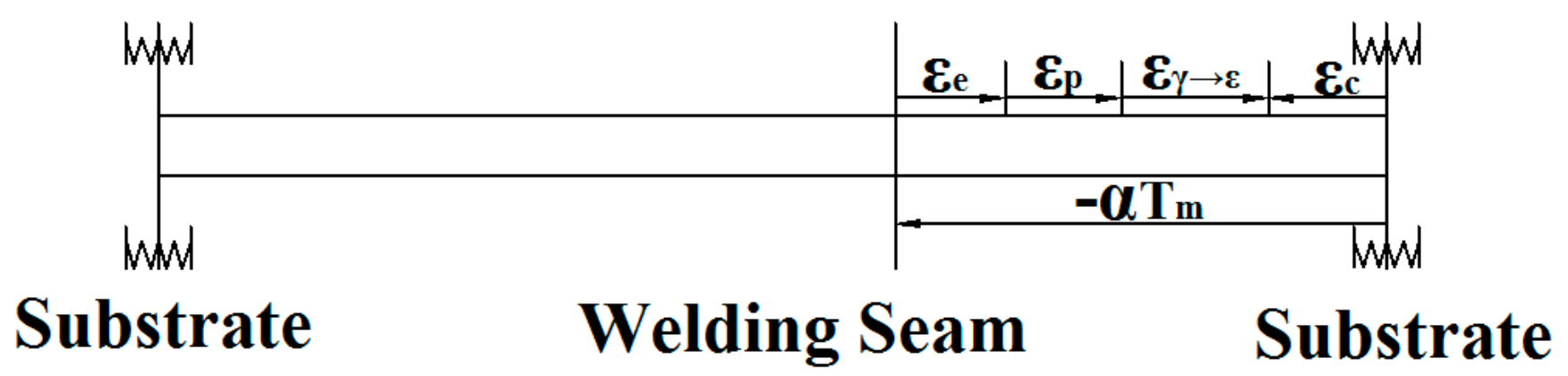
- The residual stress can induce γ→ε martensitic phase transformation in Fe-Mn-Si SMAs welding seam. In addition, the strengthening mechanism of experimental materials is shown as follows: (1) the deformation in the γ→ε martensitic phase transformation can resist residual compression strain, which relaxes the residual strain; (2) the residual stress, as the phase transformation driving force, can be released in the process of shear deformation.
Author Contributions
Funding
Conflicts of Interest
References
- Hong, K.M.; Shin, Y.C. Prospects of laser welding technology in the automotive industry: A review. J. Matel. Process. Technol. 2017, 245, 46–69. [Google Scholar] [CrossRef]
- Wang, P.; Chen, X.; Pan, Q.; Madigan, B.; Long, J. Laser welding dissimilar materials of aluminum to steel: An overview. Int. J. Manuf. Technol. 2016, 87, 3081–3090. [Google Scholar] [CrossRef]
- Caiazzo, F.; Caggiano, A. Investigation of laser welding of Ti alloys for cognitive process parameters selection. Materials 2018, 11, 632. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Jahazi, M.; Immarigron, J.P.; Wallace, W. A review of laser welding techniques for magnesium alloys. J. Matel. Process. Technol. 2006, 171, 188–204. [Google Scholar] [CrossRef]
- Rong, Y.; Zhang, G.; Huang, Y. Study of deformation and residual stress of laser welding 316L T-joint using 3D/shell finite element analysis and experiment verification. Int. J. Manuf. Technol. 2017, 89, 2077–2085. [Google Scholar] [CrossRef]
- Oliveira, J.P.; Fernandes, F.M.B.; Miranda, R.M.; Schell, N.; Ocana, J.L. Residual stress analysis in laser welded NiTi sheets using synchrotron X-ray diffraction. Mater. Design 2016, 100, 180–187. [Google Scholar] [CrossRef]
- Rendler, N.J.; Vigness, I. Hole-drilling strain-gage method of measuring residual stresses. Exp. Mech. 1966, 6, 577–586. [Google Scholar] [CrossRef]
- He, W.F.; Li, X.; Nie, X.F.; Li, Y.H.; Luo, S.H. Study on stability of residual stress induced by laser shock processing in Titanium alloy thin-components. Acta Metall. Sin. 2018, 54, 411–418. [Google Scholar] [CrossRef]
- Xie, G.F.; Luo, Y.; Yang, M. Effect of ultrasonic impact treatment on welding residual stress in 304L welded joint. Hot Work. Technol. 2016, 45, 31–34. [Google Scholar]
- Zhang, Y.; Li, F.; Guo, G.; Wang, G.; Wei, H. Effects of different powders on the micro-gap laser welding-brazing of an aluminium-steel butt joint using a coaxial feeding method. Mater. Design 2016, 109, 10–18. [Google Scholar] [CrossRef]
- Zhou, D.; Peng, Y.; Xu, S.H.; Liu, J.S. Microstructure and mechanical property of steel/Al alloy laser welding with Sn powder addition. Acta Metall. Sin. 2013, 49, 959–968. [Google Scholar] [CrossRef]
- Kuo, M. Laser welding with powder feed. Sci. Technol. Weld. Join. 2014, 3, 279–285. [Google Scholar] [CrossRef]
- Awd, M.; Tenkamp, J.; Hirtler, M.; Siddique, S.; Bambach, M.; Walther, F. Comparison of microstructure and mechanical properties of Scalmalloy® produced by selective laser melting and laser metal deposition. Materials 2018, 11, 12. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.L.; Panwisawas, C.; Ward, M.; Basoalto, H.C.; Brooks, J.W.; Attallah, M.M. On the role of melt flow into the surface structure and porosity development during selective laser melting. Acta Mater. 2015, 96, 72–79. [Google Scholar] [CrossRef]
- Xu, P.; Ju, H.; Lin, C.X.; Zhou, C.Y.; Pan, D.W. In-situ synthesis of Fe-Mn-Si-Cr-Ni shape memory alloy functional coating by laser cladding. Chin. Opt. Lett. 2014, 12, 48–50. [Google Scholar]
- Caenegem, N.V.; Duprez, L.; Verbeken, K.; Segers, D.; Houbaert, Y. Stresses related to the shape memory effect in Fe-Mn-Si based shape memory alloys. Mater. Sci. Eng. A 2008, 481–482, 183–189. [Google Scholar] [CrossRef]
- Li, J.F.; Liao, H.; Normand, B.; Cordier, C.; Maurin, G.; Foct, J.; Coddet, C. Uniform design method for optimization of process parameters of plasma sprayed TiN coatings. Surf. Coat. Technol. 2003, 176, 1–13. [Google Scholar] [CrossRef]
- Derakhshan, E.D.; Yazdian, N.; Craft, B.; Smith, S.; Kovacevic, R. Numerical simulation and experimental validation of residual stress and welding distortion induced by laser-based welding processes of thin structural steel plates in butt joint configuration. Opt. Laser Technol. 2018, 104, 170–182. [Google Scholar] [CrossRef]
- Zhu, X.K.; Chao, Y.J. Numerical simulation of transient temperature and residual stresses in friction stir welding of 304L stainless steel. J. Mater. Process. Technol. 2004, 146, 263–272. [Google Scholar] [CrossRef]
- Suárez, A.; Amado, J.M.; Tobar, M.J.; Yáñez, A.; Fraga, E.; Peel, M.J. Study of residual stresses generated inside laser cladded plates using fem and diffraction of synchrotron radiation. Surf. Coat. Technol. 2010, 204, 1983–1988. [Google Scholar] [CrossRef]
- Brown, S.; Song, H. Finite element simulation of welding of large structures. Trans Asme J. Eng. Ind. 1992, 114, 441–451. [Google Scholar] [CrossRef]
- He, X.D.; Zhang, J.X.; Pei, Y. Effect of input on laser welding residual stress and distortion of TC4 Titanium alloy. Rare Metal Mater. Eng. 2007, 36, 774–777. [Google Scholar]
- Wang, J.; Lu, H. Some discussion on principle of casuing and relieving welding residual stress. China Weld. Inst. 2002, 23, 75–77. [Google Scholar]
- Wang, D.F. Study on the Martensitic Transformation and Shape Memory Mechanism in FeMnSi Based Alloys. Doctoral Thesis, Tianjin University, Tianjin, China, 2000. [Google Scholar]
- Zhou, C.Y.; Lin, C.X.; Xu, P.; Sun, D.P.; Ju, H. In-situ synthesis of Fe-Mn-Si memory alloy on the surface of stainless steel by laser cladding. Rare. Metal Mater. Eng. 2014, 43, 3042–3046. [Google Scholar]
- Zhao, X.Q. The kinetics of martensitic nucleation by thermal and stress activation in iron based alloys. Acta Metall. Sin. 2001, 37, 1153–1158. [Google Scholar]
- Inohara, M.; Akebono, H.; Kato, M.; Sugeta, A. Effects of loading mode on the fatigue behavior of laser welds in automobile mild steel sheet. Weld. World 2016, 60, 535–545. [Google Scholar] [CrossRef]





| Material | Chemical Composition (%) | |||||
|---|---|---|---|---|---|---|
| Cr | Ni | Mn | Si | C | Fe | |
| 304 stainless steel | 19.14 | 8.71 | 1.15 | 0.40 | 0.061 | Bal. |
| 304 stainless steel powder | 18.75 | 10.45 | 1.54 | 0.93 | 0.039 | Bal. |
| Fe/Mn/Si mixed powder | - | - | 57.20 | 21.68 | - | 21.12 |
| Strain and Stress | ε1/10−6 | ε2/10−6 | ε2/10−6 | σ/MPa | |
|---|---|---|---|---|---|
| Measuring Points | |||||
| 1# | 161.666 | −132.227 | −60.987 | 369.657 | |
| 2# | 75.849 | −115.549 | −378.550 | 474.321 | |
| 3# | 78.161 | −101.818 | −477.033 | 608.969 | |
| 4# | 70.736 | −75.033 | −440.693 | 575.674 | |
| 5# | 100.995 | −71.499 | −285.726 | 387.764 | |
| 6# | 102.961 | −131.863 | −109.561 | 303.173 | |
| 7# | −58.234 | 59.018 | 54.177 | 151.497 | |
| 8# | −15.813 | 39.283 | 81.449 | 76.872 | |
| 9# | 21.333 | 71.828 | 87.594 | 47.624 | |
| 10# | 21.303 | 18.095 | 35.175 | 14.542 | |
| 11# | 7.542 | 6.307 | 20.541 | 13.117 | |
| Strain and Stress | ε1/10−6 | ε2/10−6 | ε2/10−6 | σ/MPa | |
|---|---|---|---|---|---|
| Measuring Points | |||||
| 1# | 23.919 | −97.578 | −152.341 | 195.148 | |
| 2# | 15.107 | −155.331 | −283.961 | 324.452 | |
| 3# | 26.326 | −206.429 | −391.872 | 431.596 | |
| 4# | −51.699 | −132.102 | −365.205 | 410.049 | |
| 5# | −100.039 | −96.584 | −279.449 | 305.745 | |
| 6# | 60.581 | −26.194 | −115.464 | 170.159 | |
| 7# | −16.241 | 54.402 | −69.058 | 61.440 | |
| 8# | −47.992 | 132.402 | −133.994 | 44.797 | |
| 9# | 76.052 | 49.032 | 65.042 | 13.977 | |
| 10# | 28.053 | 23.773 | 33.498 | 2.162 | |
| 11# | 14.556 | 21.381 | 18.224 | 3.542 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, H.; Lin, C.; Tian, Y.; Liu, Z.; Jiang, H.; Sun, D. Mechanical Properties Study of Fe-Mn-Si Shape Memory Alloys Welding Seam Formed by Laser Welding with Filler Powder. Materials 2018, 11, 1454. https://doi.org/10.3390/ma11081454
Ju H, Lin C, Tian Y, Liu Z, Jiang H, Sun D. Mechanical Properties Study of Fe-Mn-Si Shape Memory Alloys Welding Seam Formed by Laser Welding with Filler Powder. Materials. 2018; 11(8):1454. https://doi.org/10.3390/ma11081454
Chicago/Turabian StyleJu, Heng, Chengxin Lin, Yun Tian, Zhijie Liu, Huiling Jiang, and Deping Sun. 2018. "Mechanical Properties Study of Fe-Mn-Si Shape Memory Alloys Welding Seam Formed by Laser Welding with Filler Powder" Materials 11, no. 8: 1454. https://doi.org/10.3390/ma11081454
APA StyleJu, H., Lin, C., Tian, Y., Liu, Z., Jiang, H., & Sun, D. (2018). Mechanical Properties Study of Fe-Mn-Si Shape Memory Alloys Welding Seam Formed by Laser Welding with Filler Powder. Materials, 11(8), 1454. https://doi.org/10.3390/ma11081454




