Numerical Analysis and 1D/2D Sensitivity Study for Monolithic and Laminated Structural Glass Elements under Thermal Exposure
Abstract
:1. Introduction
2. Material Properties and Temperature Effects
2.1. Basic Properties
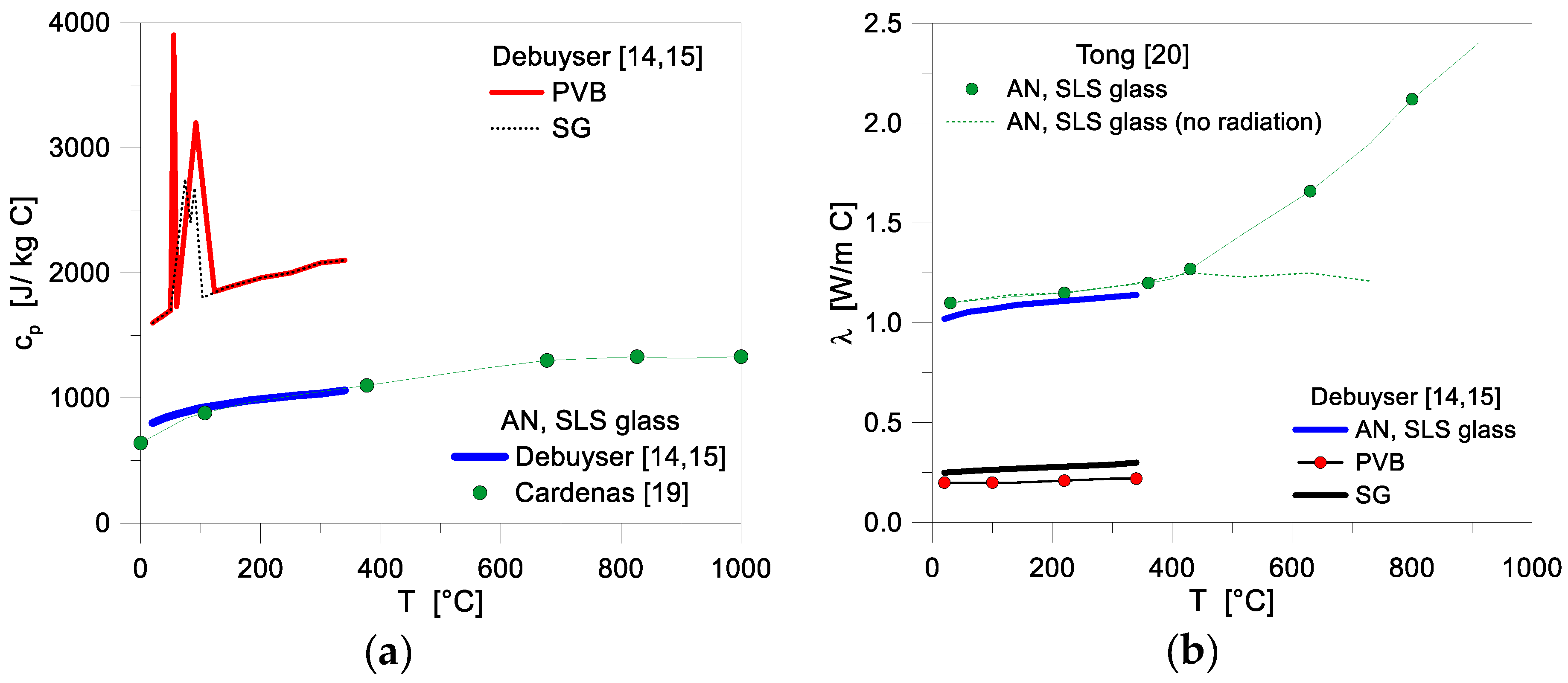
2.2. Specific Heat and Thermal Conductivity
2.3. Thermal Shock Performance
2.4. Temperature Dependence of Mechanical Properties of Glass Systems
3. Experimental and Numerical Studies
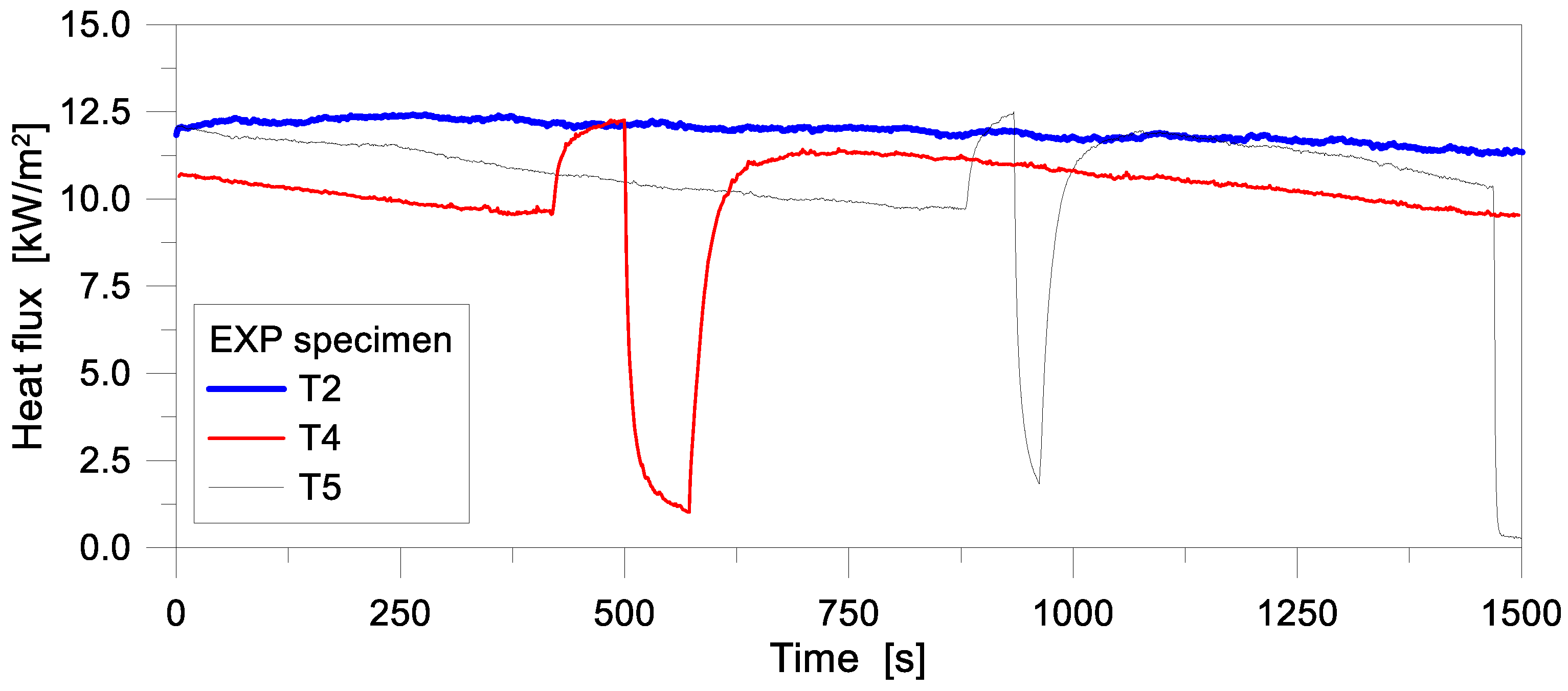
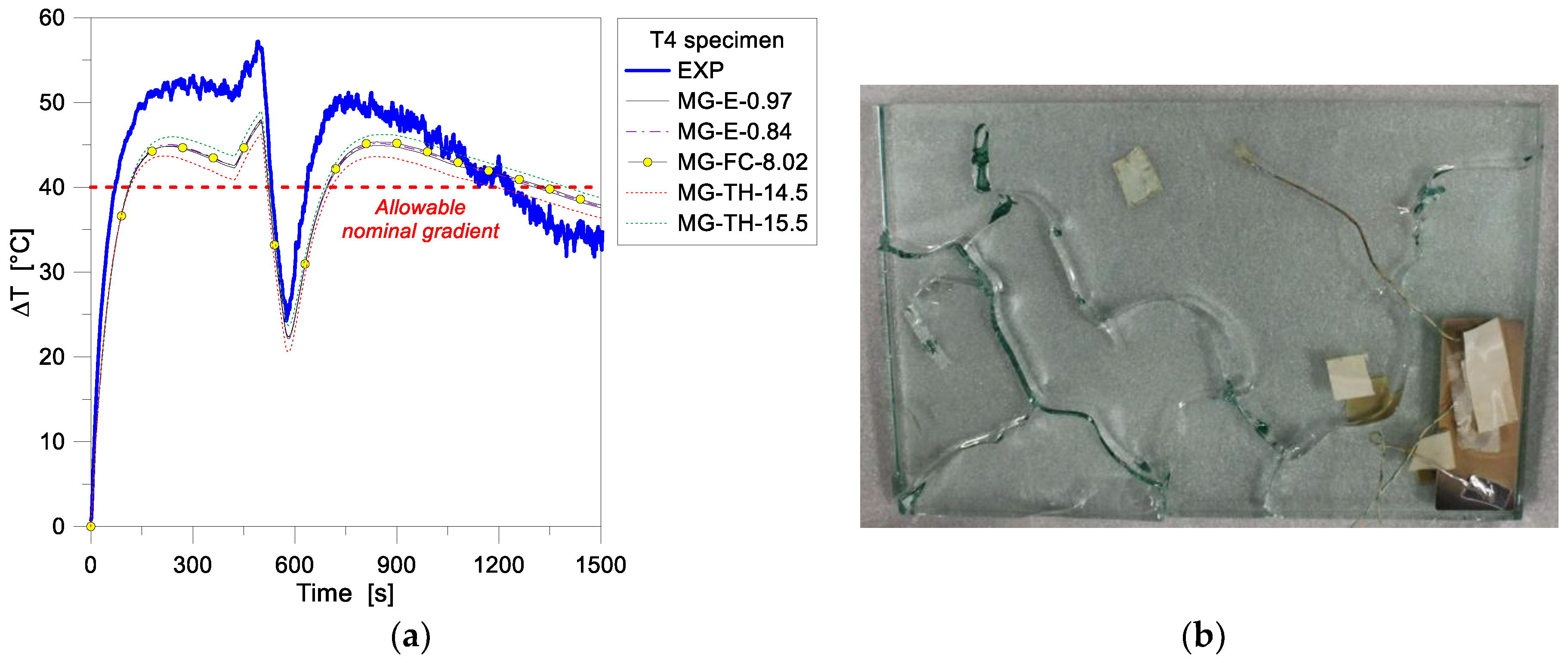
3.1. Reference Tests
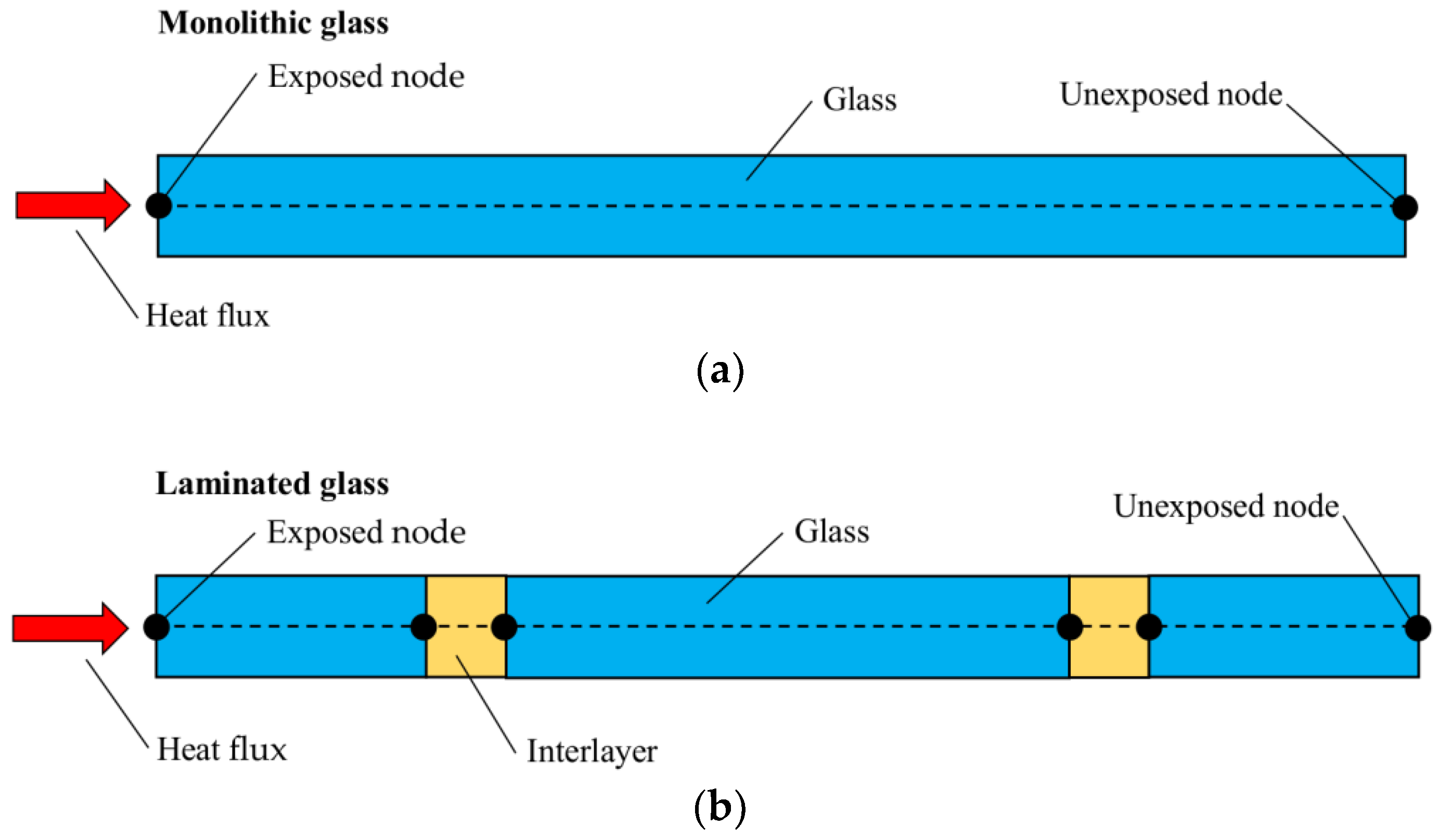
3.2. One-Dimensional (1D) Numerical Modlling
- -
- an emissivity coefficient for glass surface equal to ε = 0.97,
- -
- the Stefan–Boltzmann constant was set to σ = 5.67 × 10−8 W/m2K−4, with
- -
- an absolute zero temperature of −273.15 °C.
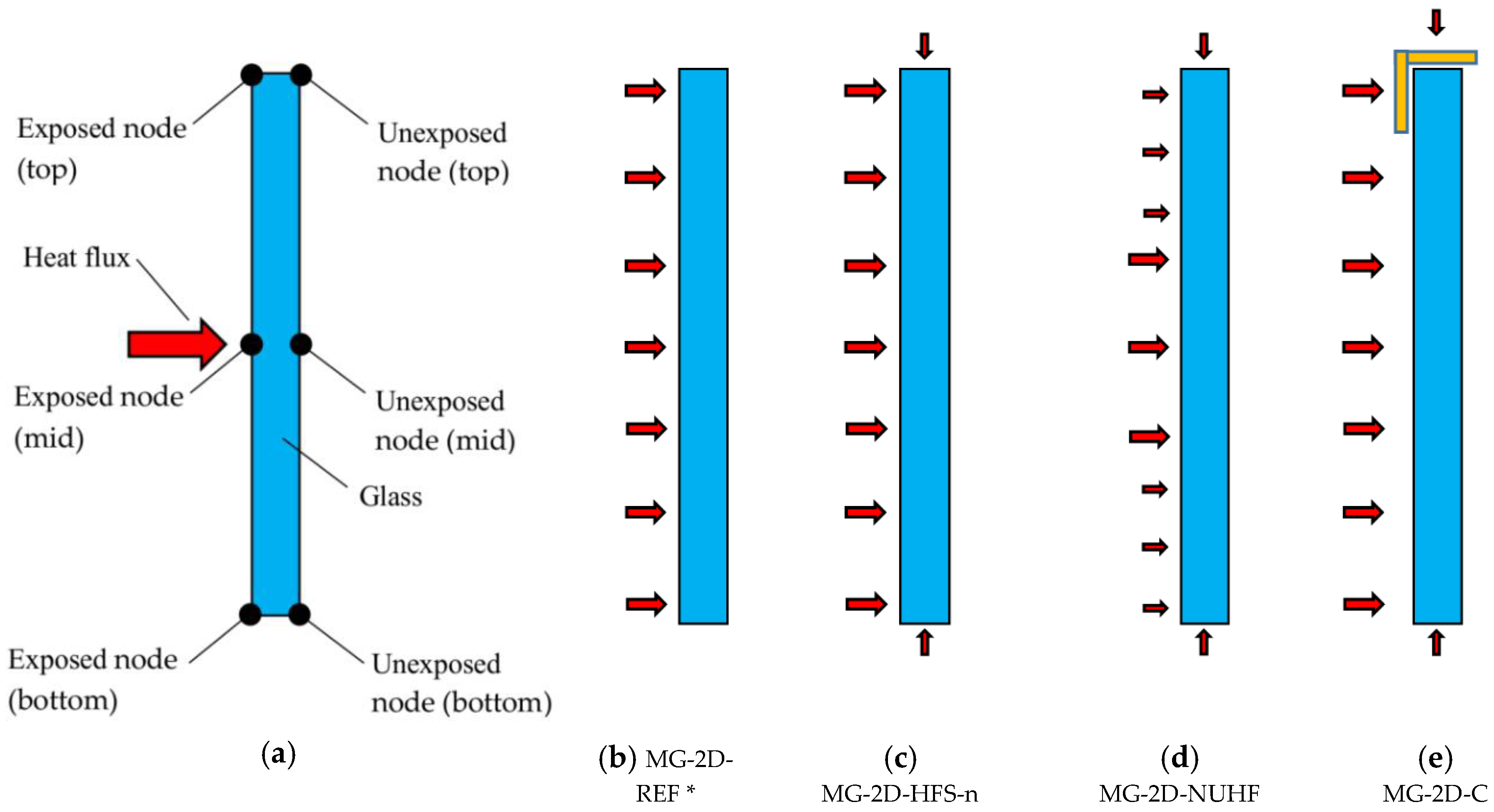
3.3. Two-Dimensional (2D) Numerical Modelling
4. Discussion of FE Numerical Results and Assessment towards the Past Experiments
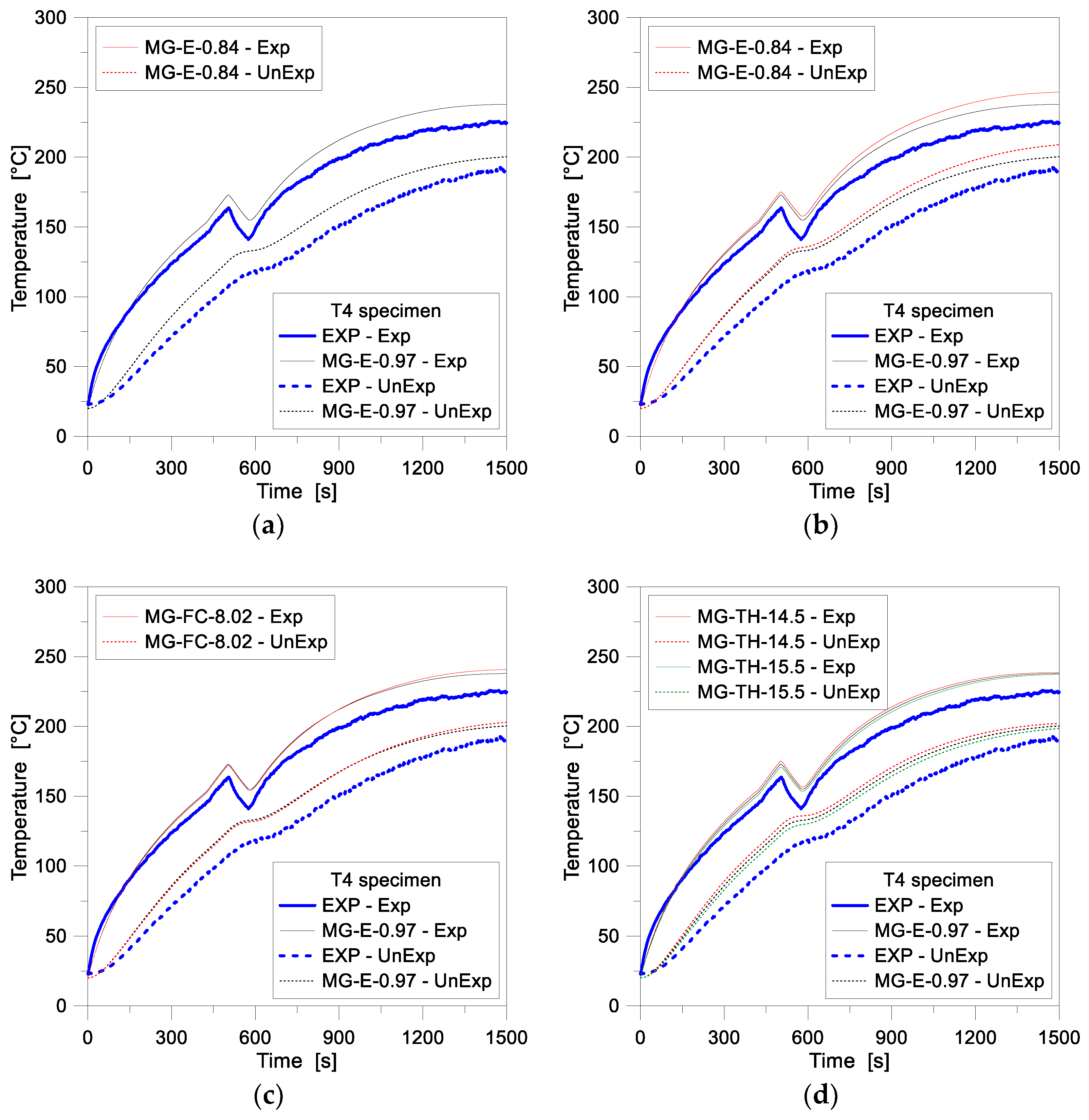
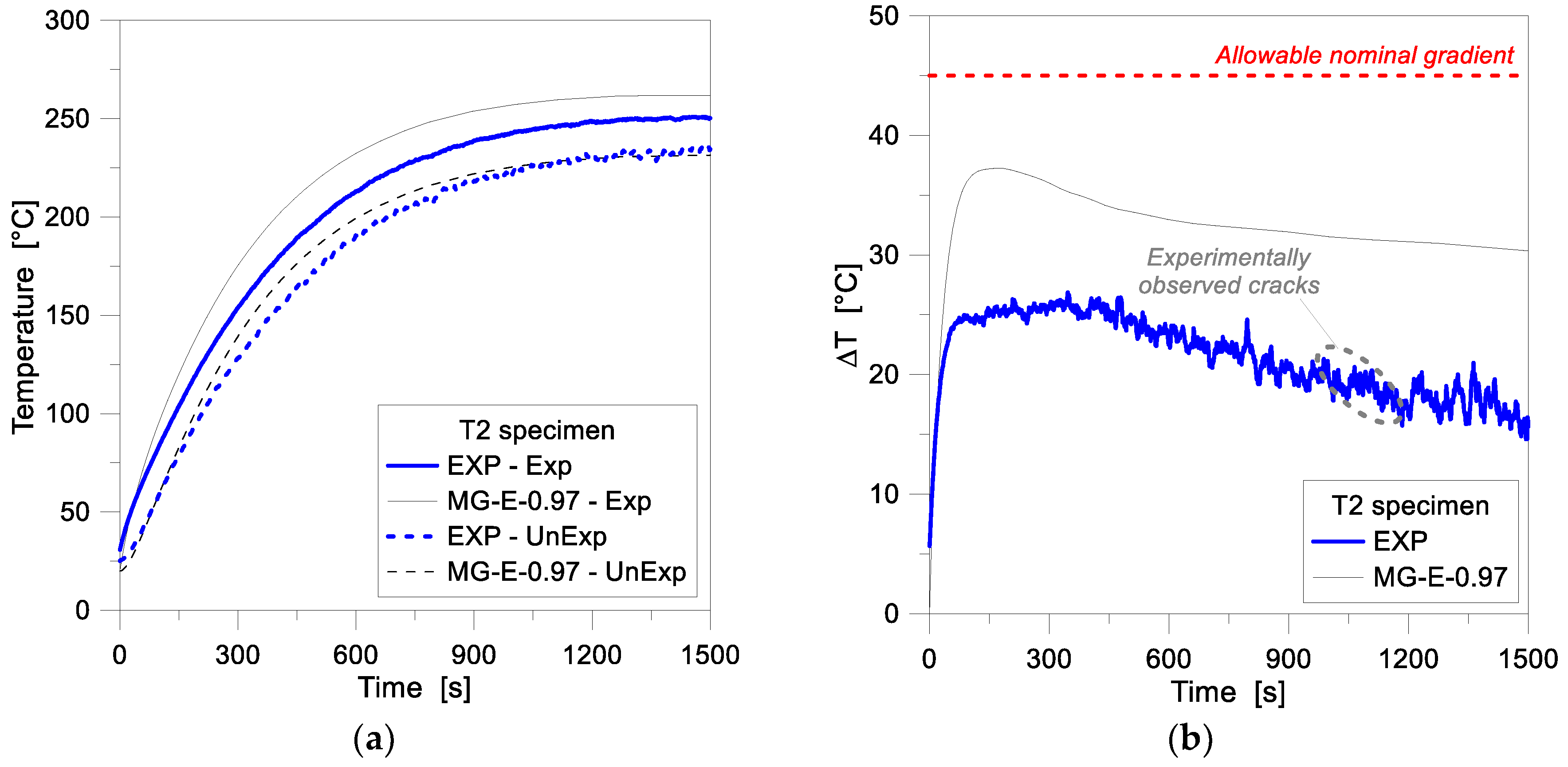
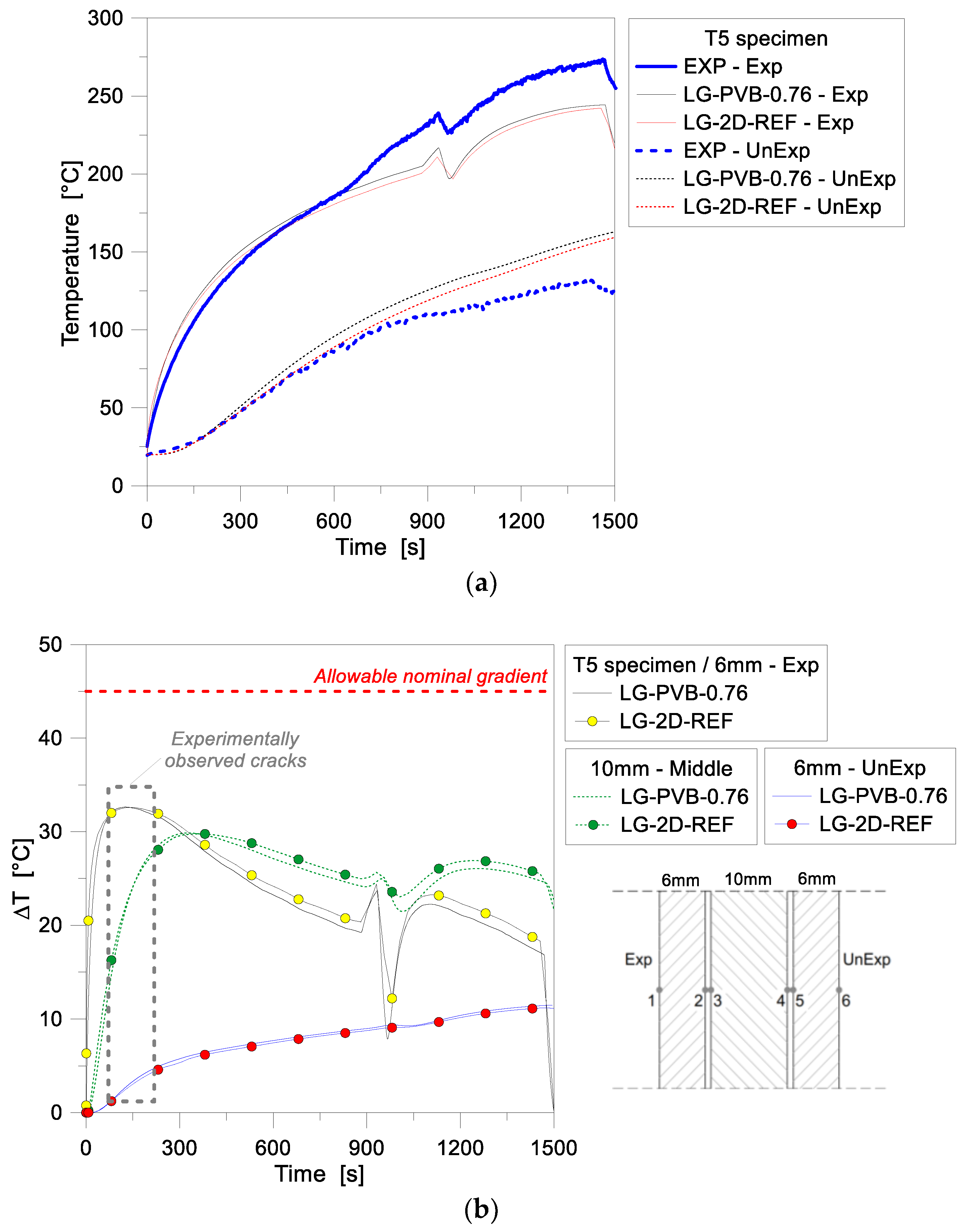
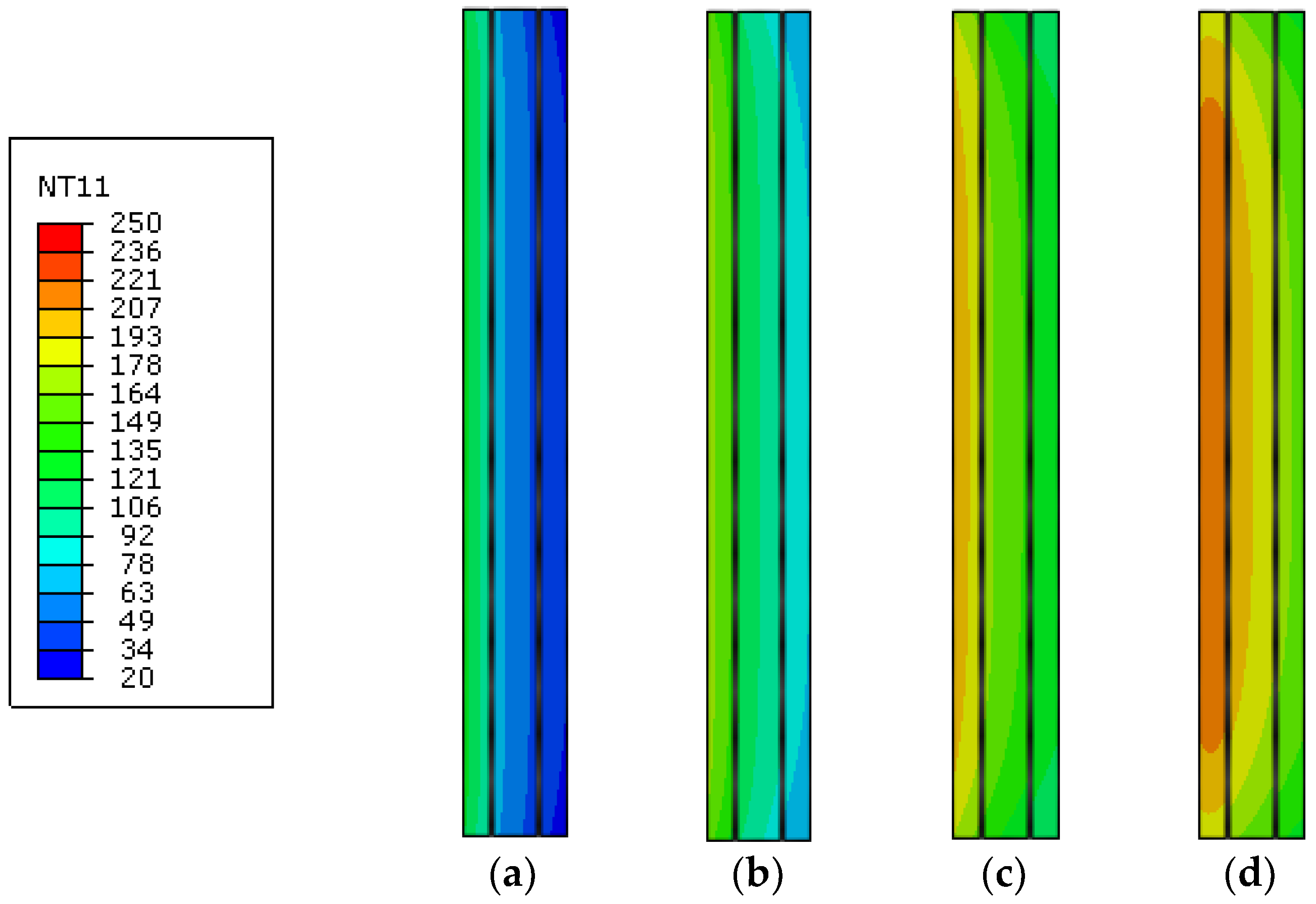
4.1. One-Dimensional (1D) Numerical Modelling
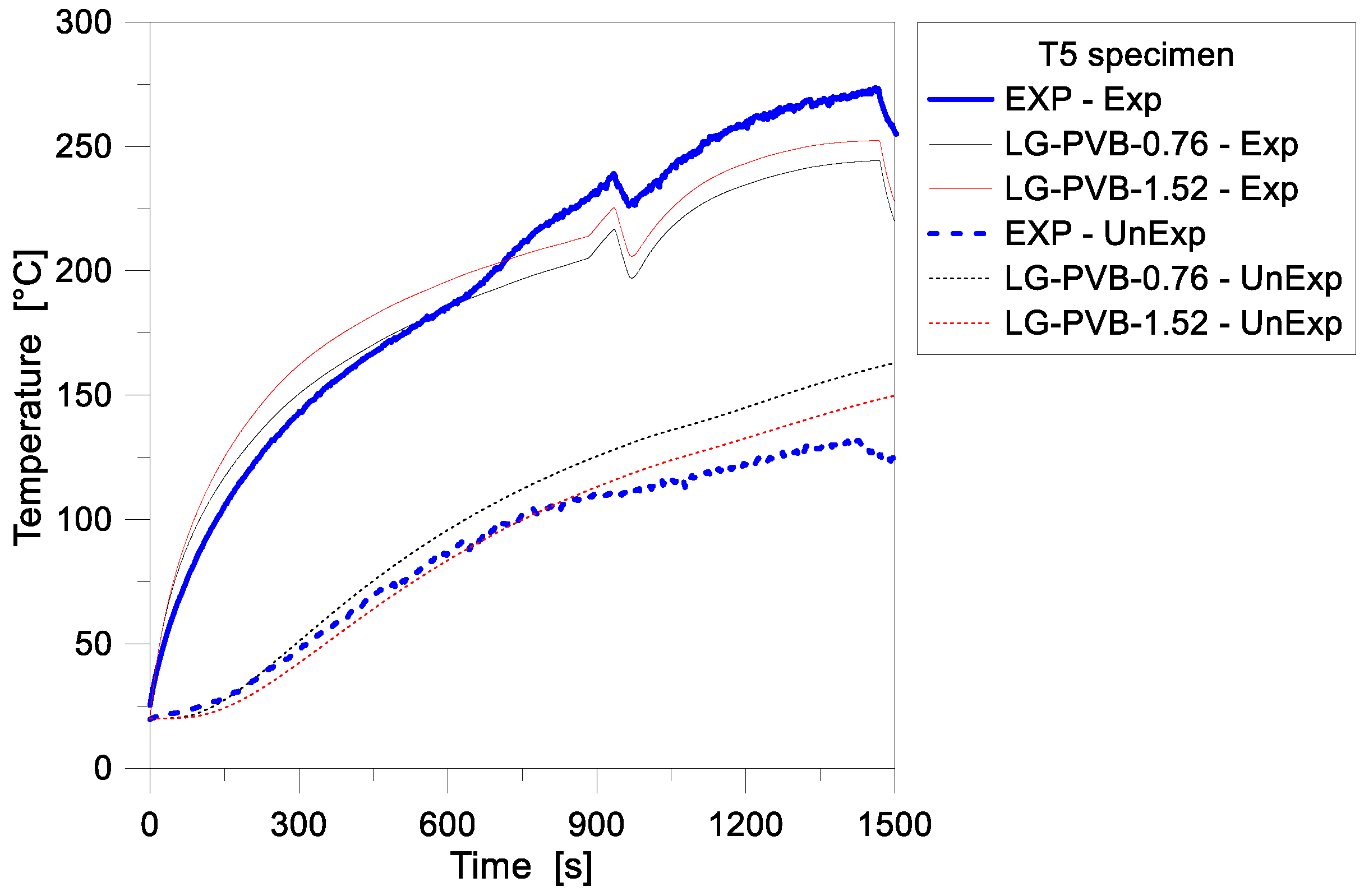
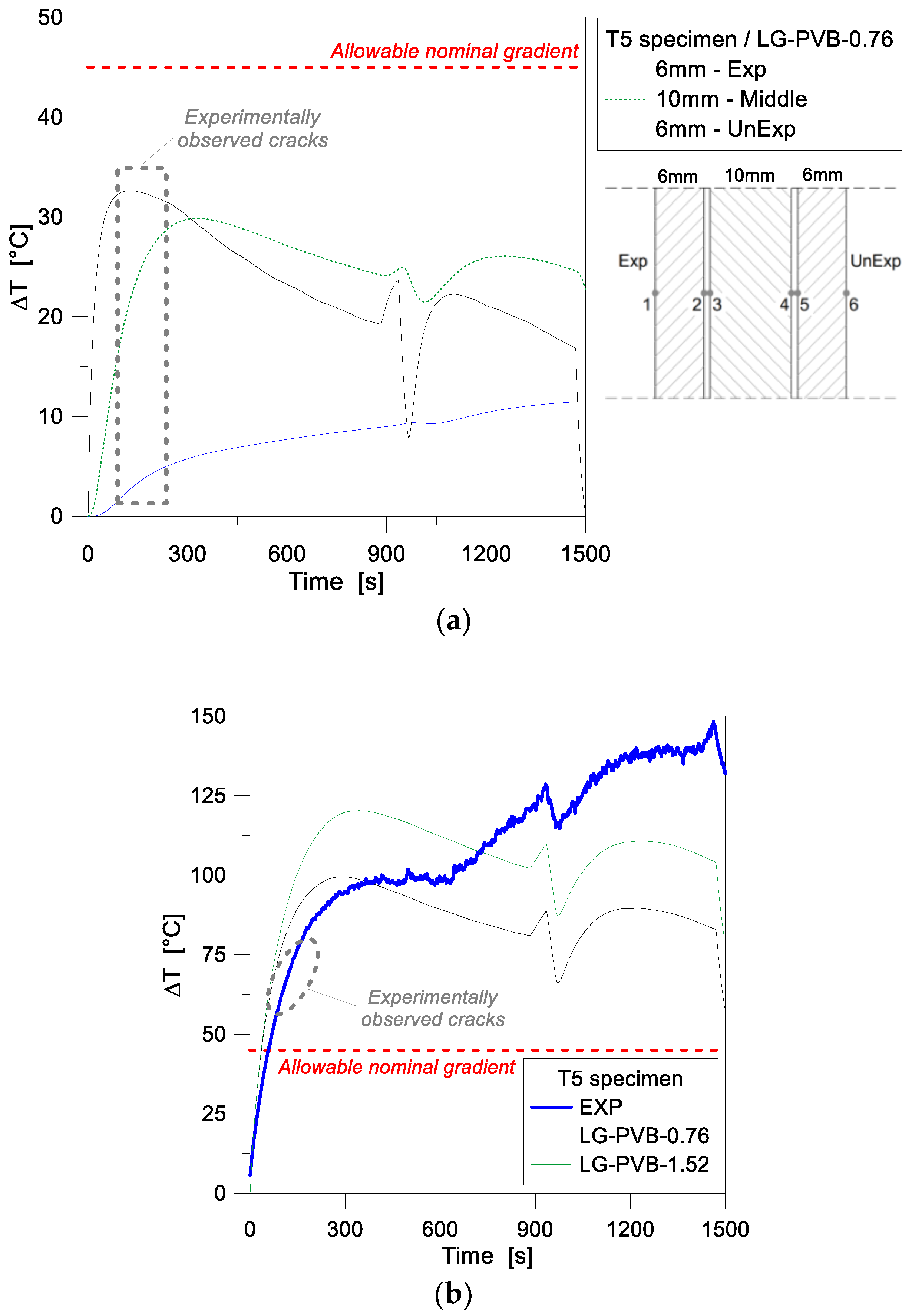
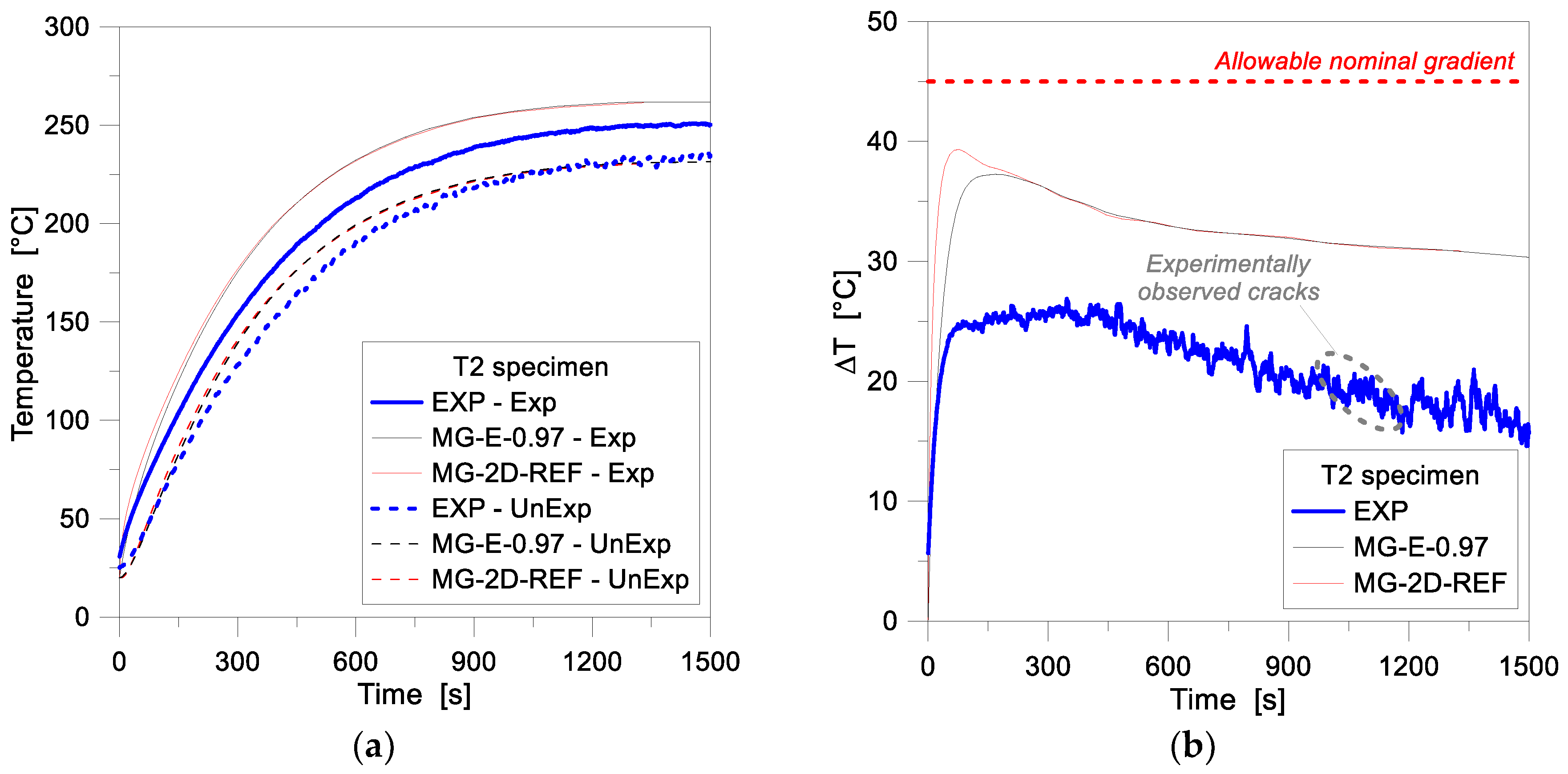
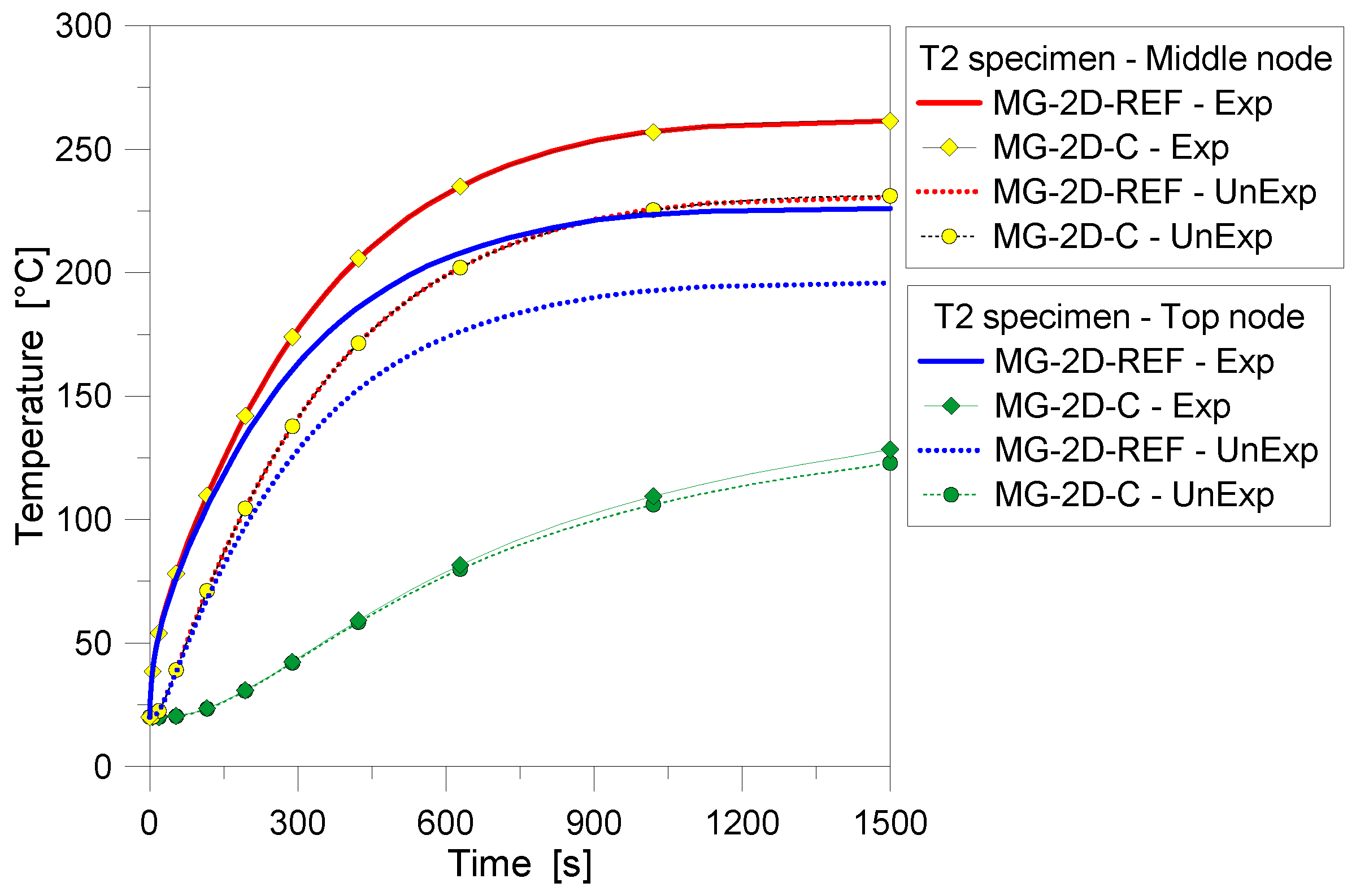
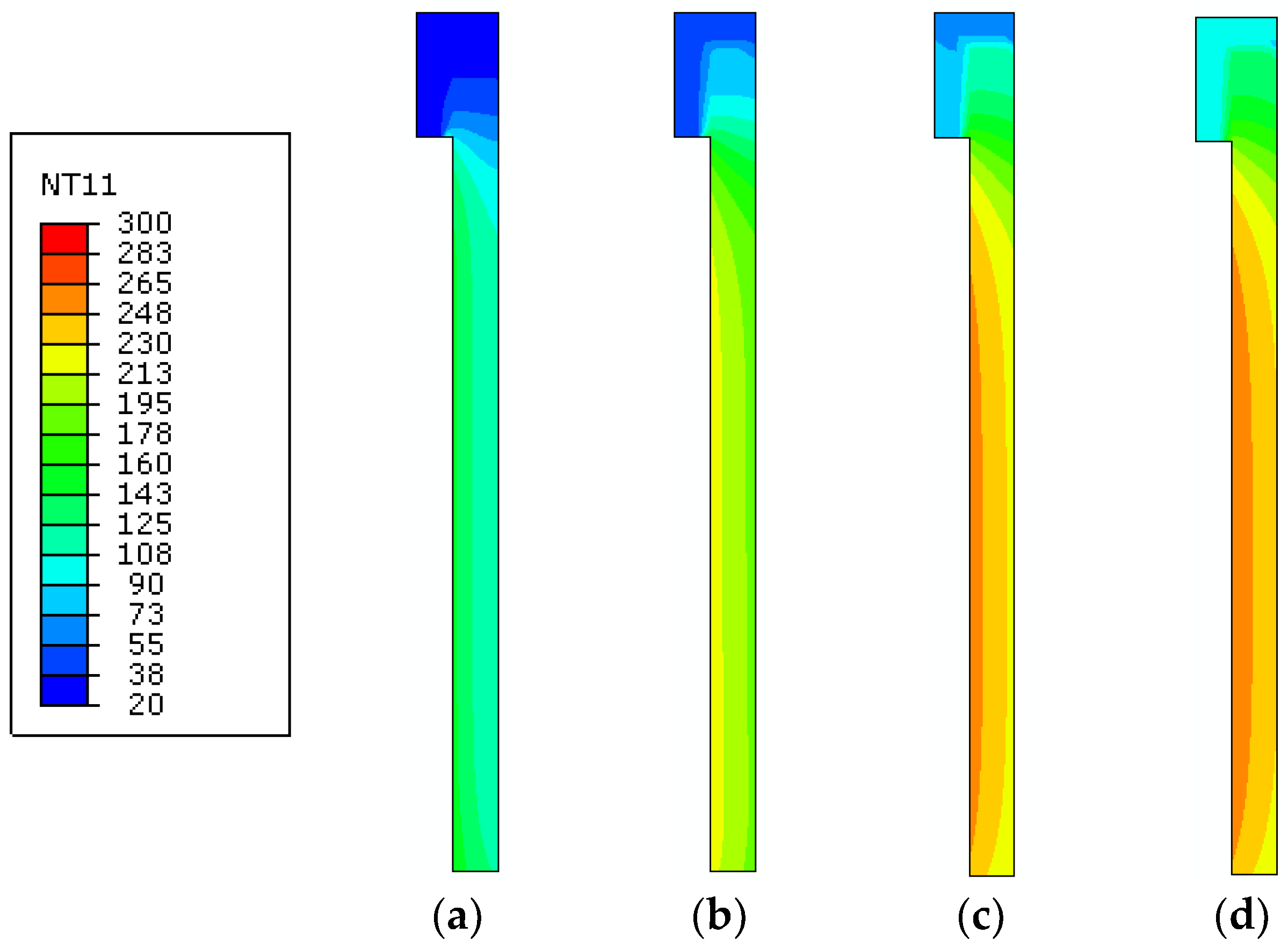
4.2. Two-Dimensional (2D) Numerical Modelling—Reference Configuration
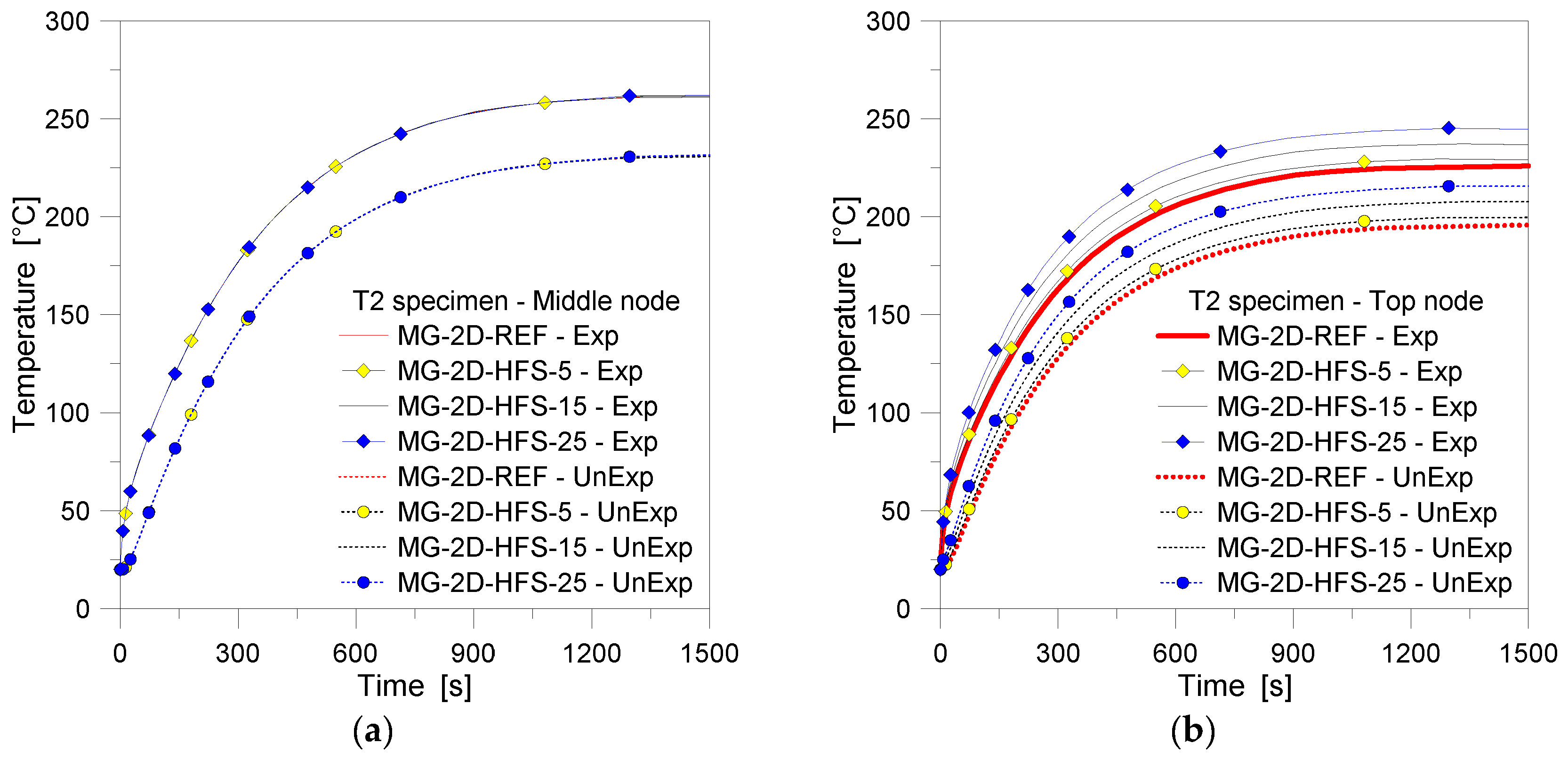
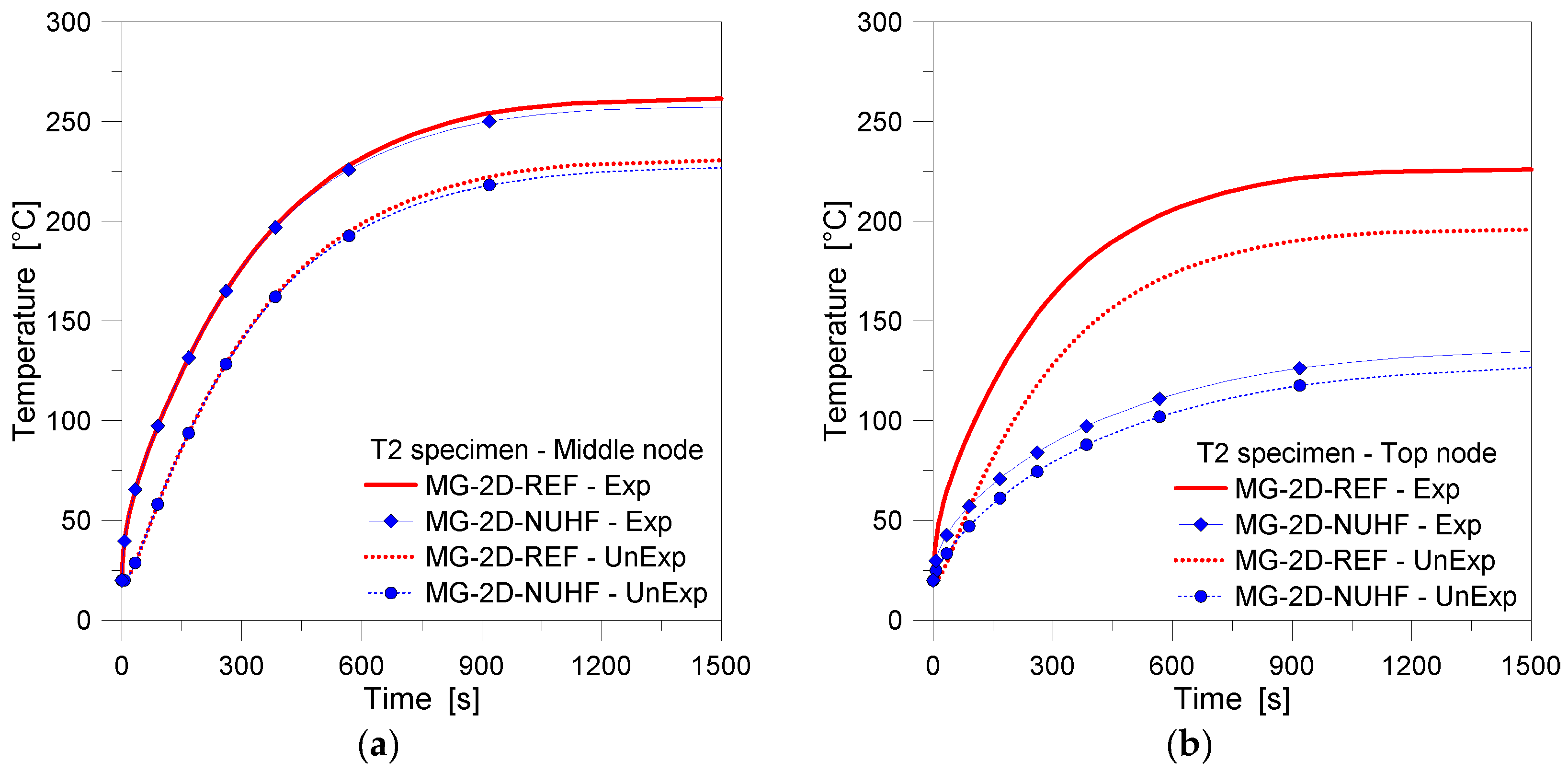
4.3. Two-Dimensional (2D) Numerical Modeling—Sensitivity Study
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Abbreviations
| AN | Annealed (glass) |
| CFD | Computational Fluid Dynamics |
| DOF | Degree Of Freedom |
| Exp | Exposed (node) |
| EXP | Experimental |
| EVA | Ethylene Vinyl Acetate |
| FE | Finite Element |
| FT | Fully Tempered (glass) |
| GFRP | Glass-Fiber-Reinforced Polymer |
| LG | Laminated glass |
| MG | Monolithic glass |
| MOE | Modulus of Elasticity |
| HS | Heat strengthened (glass) |
| PVB | PolyVinyl Butyral |
| SG | SentryGlas® |
| SLS | Soda-Lime-Silica (glass) |
| TC | Thermocouple |
| TPS | Transient Plane Source |
| UnExp | Unexposed (node) |
| 1D | one-dimensional |
| 2D | two-dimensional |
References
- Haldimann, M.; Luible, A.; Overend, M. Structural Use of Glass; IABSE: Zurich, Switzerland, 2008; ISBN 978-3-85748-119-2. [Google Scholar]
- Feldmann, M.; Kasper, R.; Abeln, B.; Cruz, P.; Belis, J. Guidance for European Structural Design of Glass Components—Support to the Implementation, Harmonization and Further Development of the Eurocodes; Dimova, P., Feldmann, D., Eds.; Report EUR 26439; Joint Research Centre–Institute for the Protection and Security of the Citizen: Ispra, Italy, 2014. [Google Scholar]
- Buildings Department. Code of Practice for Structural Use of Glass 2018. Available online: www.bd.gov.hk/english/documents/coee/SUG2018e.pdf (accessed on 24 April 2018).
- Sjögren, T. Laminated Safety Glass and Adhesives: A Literature Survey on Experimental Techniques and Experimental Data; SP Rapport: Borås, Sweden, 2012; ISBN 978-91-87017-40-7. [Google Scholar]
- Yang, N.; Wang, J.; Zhao, G.; Zhong, Y.; Wang, D. Experimental study of headform–PVB laminated windshield impact. Int. J. Crashworthiness 2016, 21, 521–531. [Google Scholar] [CrossRef]
- Bedon, C.; Zhang, X.; Santos, F.; Honfi, D.; Kozlowski, M.; Arrigoni, M.; Figuli, M.; Lange, D. Performance of structural glass facades under extreme loads—Design methods, existing research, current issues and trends. Constr. Build. Mater. 2018, 163, 921–937. [Google Scholar] [CrossRef]
- Bedon, C. Structural glass systems under fire: Overview of design issues, experimental research, and developments. Adv. Civ. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Campbell Window Film—How to Survive a Bomb Blast. Available online: https://www.youtube.com/watch?v=qKNVJb6Ls_E (accessed on 24 April 2018).
- Estero Shower Glass & Window—Hurricane Impact Windows. Available online: http://esteroglasscompany.com/windows/hurricane-impact-windows/ (accessed on 24 April 2018).
- Bedon, C.; Louter, C. Thermomechanical numerical modelling of structural glass under fire—Preliminary considerations and comparisons. In Proceedings of the Challenging Glass 6—Conference on Architectural and Structural Applications of Glass, Delft, The Netherlands, 6 May 2018. [Google Scholar]
- Fronsoe, C.; Krytenberg, T.; Vockler, K.; Swanson, J.; Carbary, L.; Barry, C.; Hoffman, S.; Torok, G.; Norville, S.; Blanchet, S. Silicone Spandrel Glass Coatings: Mitigating Glass Breakage Risk from Thermal and Other Stresses. In Proceedings of the Challenging Glass 6, Delft, The Netherlands, 6 May 2018. [Google Scholar] [CrossRef]
- Goosang, J.; Dongwoo, K.; Sanghoon, P.; Sojeong, P.; Myoungsouk, Y.; Kwangwoo, K. Downdraft Assessment of Glass Curtain Wall Buildings with Radiant Floor Heating System. Appl. Sci. 2017, 7, 1075. [Google Scholar] [CrossRef]
- Bedon, C.; Pascual Agullo, C.; Luna-Navarro, A.; Overend, M.; Favoino, F. Thermomechanical Investigation of Novel GFRP-glass Sandwich Facade Components. In Proceedings of the Challenging Glass Conference, Delft, The Netherlands, 6 May 2018; Volume 6, pp. 501–512. [Google Scholar] [CrossRef]
- Debuyser, M.; Sjöström, J.; Lange, D.; Honfi, D.; Sonck, D.; Belis, J. Behaviour of monolithic and laminated glass exposed to radiant heating. Constr. Build. Mater. 2017, 130, 212–229. [Google Scholar] [CrossRef]
- Debuyser, M. Exploratory Investigation of the Behaviour of Structural Glass in Fire. Master’s Thesis, Ghent University, Ghent, Belgium, 2015. [Google Scholar]
- Bedon, C.; Honfi, D.; Kozlowski, M. Numerical modelling of structural glass elements under thermal exposure. In Proceedings of the 3rd International Electronic Conference on Materials Sciences, 14–28 May 2018. [Google Scholar] [CrossRef]
- Simulia. ABAQUS v. 6.14; Computer Software and Online Documentation; Dassault Systems: Providence, RI, USA, 2018. [Google Scholar]
- EN 572-2:2004. Glass in Buildings—Basic Soda Lime Silicate Glass Products; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Cardenas, B.; Leon, N.; Pye, J.; Garcia, H.D. Design and modeling of high temperature solar thermal energy storage unit based on molten soda lime silica glass. Sol. Energy 2016, 126, 32–43. [Google Scholar] [CrossRef]
- Tong, T.W. Thermal Conductivity 22; Technomic Publishing Company, Ltd.: Lancaster, PA, USA, 1994; ISBN 1-56676-172-7. [Google Scholar]
- prEN thstr:2004. Glass in Buildings—Thermal Stress Capitulation Method; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Mognato, E.; Barbieri, A. The breakage of glass—Thermal shock and nickel sulfide inclusions. In COST Action TU0905 Mid-term Conference on Structural Glass; Belis, J., Louter, C., Mocibob, D., Eds.; CRC Press; Taylor& Francis Group: Boca Raton, Florida, FL, USA, 2013; ISBN 978-1-138-00044-5. [Google Scholar]
- Malou, Z.; Hamidouche, H.; Bouaouadja, N.; Chevalier, J.; Fantozzi, G. Thermal shock resistance of a soda lime glass. Ceramics-Silikáty 2013, 57, 39–44. [Google Scholar]
- Vandebroek, M. Thermal Fracture of Glass. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2015. Available online: https://biblio.ugent.be/publication/5757540/file/5757541 (accessed on 24 April 2018).
- Karlsson, S. Spontaneous fracture in thermally strengthened glass—A review and outlook. Ceramics-Silikáty 2017, 61, 188–201. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, H.; Wang, Y.; Sun, J. Thermal shock effect on the glass thermal stress response and crack propagation. Procedia Eng. 2013, 62, 717–724. [Google Scholar] [CrossRef]
- Drysdale, D. An Introduction to Fire Dynamics Dougal Drysdale; Wiley-Blackwell: Oxford, UK, 2011. [Google Scholar]
- Welty, J.R.; Wicks, C.E.; Wilson, R.E.; Rorrer, G. Fundamentals of Momentum, Heat and Mass Transfer, 5th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2008. [Google Scholar]
- Microelectronics Heat Transfer Laboratory—Fluid Properties Calculator. Available online: http://www.mhtl.uwaterloo.ca/old/onlinetools/airprop/airprop.html (accessed on 24 April 2018).
- Tolerances Handbook 06/2014, Saint-Gobain, 2014 ECKELT GLAS GmbH. Available online: http://www.eckelt.at/en/downloads/produkte/tolerances_handbook.pdf (accessed on 24 April 2018).


| Limit Values (°C) | |||
|---|---|---|---|
| Glass Type | As-Cut or Arrissed | Smooth Ground | Polished |
| float, or sheets ≤ 12-mm thick | 35 | 40 | 45 |
| float, 15 mm or 19-mm thick | 30 | 35 | 40 |
| float, 25-mm thick | 26 | 30 | 35 |
| patterned | 26 | ||
| wired patterned or polished wired glass | 22 | ||
| heat strengthened | 100 | ||
| tempered | 200 | ||
| laminated | smallest value of the component panes | ||
| Influencing Parameter | FE Model | Glass Thickness /Build-Up [mm] | Emissivity | Film Coefficient | Interlayer Thickness/Type |
|---|---|---|---|---|---|
| Emissivity & Film coefficient | MG-E-0.97 * | 15 | 0.97 | US | - |
| MG-E-0.84 | 15 | 0.84 | US | - | |
| MG-FC-8.02 | 15 | 0.84 | 8.02 | - | |
| Glass thickness | MG-TH-14.5 | 14.5 | 0.97 | US | - |
| MG-TH-15.5 | 15.5 | 0.97 | US | - | |
| Interlayer thickness | LG-PVB-0.76 | 6 + 10 + 6 | 0.97 | US | 0.76 mm/PVB |
| LG-PVB-1.52 | 6 + 10 + 6 | 0.97 | US | 1.52 mm/PVB |
| FE Model | Heat Flux ** | |||
|---|---|---|---|---|
| Exposed (Front) Surface | Top/Bottom Surface | Mechanical Restrains | Figure | |
| MG-2D-REF * | 100% | - | - | 6b |
| MG-2D-HFS-5 | 100% | 5% | - | 6c |
| MG-2D-HFS-15 | 100% | 15% | - | 6c |
| MG-2D-HFS-25 | 100% | 25% | - | 6c |
| MG-2D-NUHF | 100%/25% | 25% | - | 6d |
| MG-2D-C | 100% | 25% | Yes (steel clamp) | 6e |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozłowski, M.; Bedon, C.; Honfi, D. Numerical Analysis and 1D/2D Sensitivity Study for Monolithic and Laminated Structural Glass Elements under Thermal Exposure. Materials 2018, 11, 1447. https://doi.org/10.3390/ma11081447
Kozłowski M, Bedon C, Honfi D. Numerical Analysis and 1D/2D Sensitivity Study for Monolithic and Laminated Structural Glass Elements under Thermal Exposure. Materials. 2018; 11(8):1447. https://doi.org/10.3390/ma11081447
Chicago/Turabian StyleKozłowski, Marcin, Chiara Bedon, and Dániel Honfi. 2018. "Numerical Analysis and 1D/2D Sensitivity Study for Monolithic and Laminated Structural Glass Elements under Thermal Exposure" Materials 11, no. 8: 1447. https://doi.org/10.3390/ma11081447
APA StyleKozłowski, M., Bedon, C., & Honfi, D. (2018). Numerical Analysis and 1D/2D Sensitivity Study for Monolithic and Laminated Structural Glass Elements under Thermal Exposure. Materials, 11(8), 1447. https://doi.org/10.3390/ma11081447







