Abstract
The isothermal compression tests of the 2219 Al alloy were conducted at the temperature and the strain rate ranges of 623–773 K and 0.01–10 s−1, respectively, and the deformed microstructures were observed. The flow curves of the 2219 Al alloy obtained show that flow stress decreases with the increase in temperature and/or the decrease in strain rate. The physically based constitutive model is applied to describe the flow behavior during hot deformation. In this model, Young’s modulus and lattice diffusion coefficient are temperature-dependent, and the creep exponent is regarded as a variable. The predicted values calculated by the constitutive model are in good agreement with the experimental results. In addition, it is confirmed that the main softening mechanism of the 2219 Al alloy during hot deformation is dynamic recovery and incomplete continuous dynamic recrystallization (CDRX) by the analysis of electron backscattered diffraction (EBSD) micrographs. Moreover, CDRX can readily occur under the condition of high temperatures, low strain rates, and large strains. Meanwhile, the recrystallization grain size will also be larger.
1. Introduction
The 2219 Al alloy has long been used in the manufacture of various aerospace components (i.e., oxidizer and fuel tanks) due to its high strength, high fracture toughness, and reliable weldability [1]. During the formative process of the components, the hot working method is of great significance in obtaining the specific shapes and required properties [2]. Moreover, the characterization of flow behaviors in the hot working process largely determines the accuracy of the simulation by finite element method (FEM) [3]. It has been confirmed that the main softening mechanism in hot deformation process involves dynamic recrystallization (DRX) and dynamic recovery (DRV) [4], but the microstructural evolution is often very difficult to illustrate for its complexity [5,6,7]. Therefore, it is extremely important and necessary to investigate both of the flow behaviors and microstructural evolution on 2219 Al alloy during hot deformation [8,9,10].
Over the last decades, many efforts [11,12,13,14,15,16,17,18,19] have been made on the establishment of constitutive models to characterize flow behaviors accurately for various metals and alloys. A mathematical relationship between flow stress and deformation parameters (i.e., temperature, strain rate, strain) is usually used to represent the constitutive model [2]. Firstly, the constitutive model was constructed on the classical Hollomon equation [11] and Ludwik equation [12]. Later, Johnson and Cook [13] proposed the famous Johnson-Cook model, in which work hardening, strain rate, and temperature are taken into account. In addition, Sellars and McTegart [14] proposed another widely applied constitutive model by relating the temperature-compensated strain-rate parameter (i.e., Z parameter) to the flow stress. However, the constitutive model is obviously phenomenological and all the material parameters do not have obvious physical meaning. Recently, according to Mirzadeh et al. [15], a physically based constitutive model was proposed when the glide and climb of dislocations is the main deformation mechanism, in which only two material parameters remain and both of them have physical and metallurgical meaning. To characterize the whole flow curve under different strains, the material parameters are used to be expressed as functions of strain (i.e., strain compensation). This method has been successfully applied for steels [16,17], magnesium alloys [18], commercial-purity aluminum [9], and AA2030 aluminum alloy [19].
During the hot deformation process, DRX often takes place for most metals and alloys. Moreover, different kinds of thermomechanical processing (TMP) may lead to different DRX phenomena, such as discontinuous DRX (DDRX), continuous DRX (CDRX), and geometric DRX (GDRX) [20]. In order to recognize the differences of the three DRX types, many efforts [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] have been made on the observation and revelation of microstructural evolution during the hot forming process. DDRX usually occurs with new strain-free grains nucleation and the grains growth in low-stacking-fault energy (SFE) metals and alloys [21]. The investigation of DDRX behavior mainly focuses on the mechanism of nucleation and numerical models, which has been widely applied in different metals and alloys, such as 304 stainless steel [22,23], as-extruded 7075 aluminum alloy [24], and 3Cr2NiMnMo steel [25]. Recently, based on the published researches by Perdrix [26] and Montheillet et al. [27,28], CDRX occurs with high-angle grain boundaries (HAGBs) formed by the progressive lattice rotation of subgrains near grain boundaries during hot deformation. This mechanism has been verified in Mg alloys [29] and Al–Zn alloys [30]. Another transformation mechanism of low-angle grain boundaries (LAGBs) into HAGBs is by the progressive misorientation angles increases. This has also been reported in steel [31] and Al alloys [32]. Based on the mechanisms above, two numerical models of CDRX, the Gourdet-Montheillet model [33] and Toth et al. model [34], are proposed to characterize this process. Apart from DDRX and CDRX, GDRX is a field with less study, but is still observed in some metals and alloys during a large amount of hot deformation, such as commercial-purity Al [35] and Mg–Zn–Zr alloys [36,37]. However, the microstructural evolution with constitutive analysis for 2219 Al alloy under the hot deformation process is rarely reported.
In this study, the flow behavior of the 2219 Al alloy was studied by isothermal compression test, and an effective constitutive model based on physical mechanism was developed. The microstructure evolution during hot deformation was also investigated. Finally, the influence of different TMP conditions on CDRX behavior was discussed.
2. Materials and Methods
Isothermal-compression tests were conducted to investigate the flow behaviors and microstructural evolution of aluminum 2219 alloy during hot deformation. The chemical compositions (wt.%) of 2219 Al alloy used in this experiment are shown in Table 1.

Table 1.
The chemical compositions of 2219 Al alloy used in this test (wt.%).
The samples were cut from wrought billet and machined into a cylindrical shape with a diameter of 10 mm and height of 15 mm by a wire-cutting electrodischarge machine (WEDM, DK7745 by Zhengda (Zhengda Science and Technology Co., Limited, Taizhou, China)). Then, the samples were solution treated at 813 K for 2 h in an electric resistance furnace (SG-XS1200 by Sager (Sager Furnace Co., Limited, Shanghai, China)), followed by water quenching. Hot compression tests were conducted using a Gleeble-3500 thermosimulator (Dynamic Systems Inc., New York, NY, USA.). According to the traditionally used forming temperature for hot working and actual industrial processing, the deforming temperature: T = (0.7–0.85) Tm was adopted in this paper. Four different compression temperatures (773 K, 723 K, 673 K, 623 K) and four different strain rates (0.01 s−1, 0.1 s−1, 1 s−1, 10 s−1) were applied in the tests; the final true strain is up to 0.9. Each temperature was tested only once under four different strain rates, respectively. Tantalum foil and boron nitride were used to reduce the friction between anvils and the specimen. Each sample was heated to the specified forming temperature at a heating rate of 5 K/s, and then held for 3 min to eliminate the temperature gradient. The true stress-strain data were automatically collected from the computer system during the compression process. After the tests, all the samples were immediately water quenched to preserve the deformed microstructure. Then, the compressed samples were sectioned parallel to the compression axis for subsequent microstructural analysis by the electron backscattered diffraction (EBSD) technique. After the samples were grinded, they were then electropolished in a solution of 30% nitric acid and 70% methanol at 18 V for 50 s. HKL Channel5 software was used to analyze the EBSD data. In all the EBSD images, the LAGBs (orientation angle: 2°–15°) were marked by thin white lines, and the HAGBs (orientation angle: >15°) were marked by the thick black lines. Figure 1 shows the EBSD microstructure of 2219 Al alloy before compression. Coarse equiaxed recrystallized grains and deformed grains with many substructures were both detected.
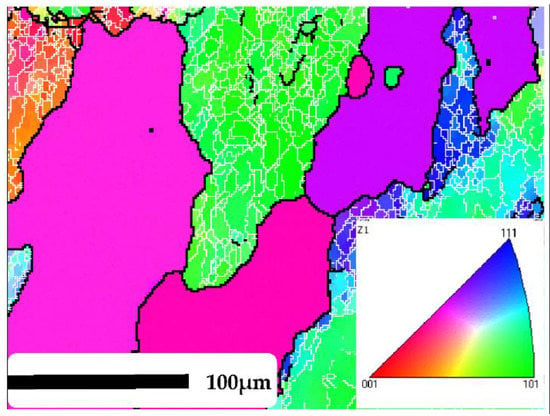
Figure 1.
The electron backscattered diffraction (EBSD) micrograph of 2219 Al alloy before deformation.
3. Results and Discussion
3.1. Flow Behaviors
The true stress-strain curves of the 2219 Al alloy at different temperatures and strain rates are illustrated in Figure 2. Although lubricants were used to reduce friction and isothermal conditions were controlled by the equipment itself, the temperature rise caused by deformation heat and small friction existed cannot be ignored. According to the friction correction criterion proposed by Roebuck [38], the range of B (i.e., barreling coefficient) obtained in this experiment was: , which means the measured stresses didn’t need to be corrected. In addition, the deformation heat produced as a result of a high strain rate would have a great influence on the flow stress [39], therefore the flow curves under the strain rates of 1 s−1 and 10 s−1 were modified by temperature compensation according to Humphreys F.J [40]. It can be clearly seen from Figure 2 that the flow stress increased rapidly to a peak value and then slightly fell to a relatively steady value, which shows an obvious characteristic of a single-peak type. Thus, each flow stress curve can be divided into three parts by strains: work-hardening part, softening part, and steady part [41,42]. The mechanism of each part is mainly controlled by the competition between work hardening and DRV and/or DRX during the hot deformation process [43]. For the work-hardening part, the rapid accumulation and proliferation of dislocations leads to obvious work hardening, but DRV develops too slowly. The synthesis result is the rapid increase of flow stress at this stage. For the softening part, high dislocation density largely promotes the development of DRV and the formation of DRX, which has exceeded the effect of work hardening. That is to say, the flow stress will slightly decrease. For the steady part, the multiplication and annihilation of dislocations approximately reached an offsetting state due to the effect of continuous deformation and DRV and/or DRX, respectively, thus, the flow stresses almost remained relatively stable values.
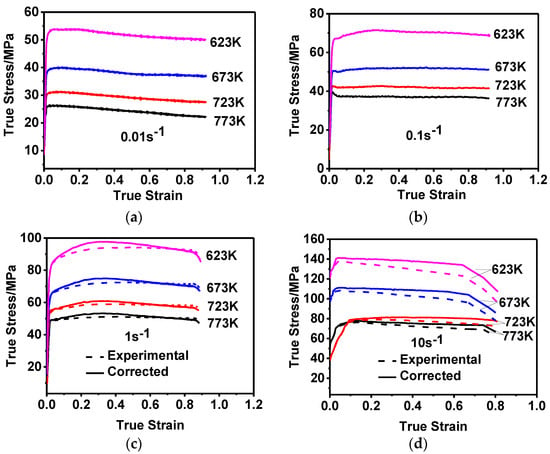
Figure 2.
The true strain-stress curves obtained at various strain rates and temperatures of (a) 0.01 s−1; (b) 0.1 s−1; (c) 1 s−1; (d) 10 s−1.
In addition, it is observed from Figure 2 that flow stress exhibited strong dependence on temperature and strain rate. Moreover, flow stress increased with the increase in strain rate and decrease in temperature. This phenomenon indicates that the effect of work hardening is more significant at low temperatures and/or high strain rates. Conversely, DRV and/or DRX developed readily at high temperatures and/or lower strain rates, such as 773 K/0.01 s−1, 773 K/0.1 s−1, 723 K/0.01 s−1. This is because hot compression is a thermal-activation process [5]. Therefore, there will be a larger driving force for the development of DRV and/or DRX due to the easier movement and migration of dislocation and grain boundary [44] at higher temperatures. On the other hand, it will develop more sufficiently to consume more dislocation density at lower strain rate. Thus, either of higher forming temperature and lower strain rate can promote the development of DRV and/or DRX, and finally result in the decrease of the flow stress.
3.2. Physically Based Constitutive Modeling
The activation energy means the energy required to overcome the barriers during the deformation process [45]. However, the value of activation energy on 2219 Al alloy (133 KJ/mol) calculated by Arrhenius model exhibits obvious deviation from that of the self-diffusion activation energy on Al alloy (142 KJ/mol) [46]. Some studies [15,46,47,48,49] indicate that the reason for the deviation may be the dependence of Young’s modulus and self-diffusion coefficient on temperature. Therefore, a physically constitutive model was proposed by considering Young’s modulus (E) and self-diffusion coefficient (D) as functions of temperature. Thus, the mathematical relationship is expressed as follows [47]:
where, (s−1) and (MPa) are the strain rate and the flow stress, respectively, B and are the material constants, and the index 5 represents the ideal value of the creep exponent. However, microstructural evolution (i.e., DRX) generally has a certain influence on the value of creep exponent, so it is reasonable to be considered as a variable (i.e., n) [39].
Therefore, Equation (1) can be rewritten as:
The relationships between self-diffusion activation energy and temperature, Young’s modulus and temperature can be expressed as [15,47,48,49]:
where D(T) is the lattice diffusion coefficient of aluminum alloy, and D0 is the pre-exponent coefficient of the lattice diffusion (1.7 × 10−4 m2/s), Qsd is the activation energy of lattice diffusion (142 KJ/mol), R is the universal gas constant (8.31 J·mol−1 K−1), and T is the forming temperature (K). is Poisson’s ratio (0.33), and G is the shear modulus; its relation with temperature can be expressed as [46]:
where G0 is the shear modulus at 300 K (2.54 × 104 MPa), TM is the melting temperature of 2219 Al alloy (916 K), and indicates the temperature dependence of shear modulus (–0.50). According to the parameters above, D(T) and E(T) can be expressed as follows:
In order to obtain the three unknown parameters () in Equation (2), the integrated physically based constitutive equations of the power, exponential and hyperbolic sine laws are summarized and expressed as follows [2]:
where B1, B2, n1 are material parameters and .
Based on the power and exponential functions of Equation (8), the material parameters n1 and can be obtained from the gradient of the graph of against and against . These plots are shown in Figure 3 (i.e., taking the strain of 0.5 as an example).
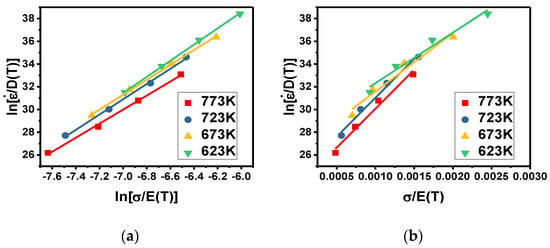
Figure 3.
Relationships between material parameters: (a) against ; (b) against .
Therefore, the parameter can be obtained by evaluating at different temperatures and strains; the values are shown in Figure 4a. It can be clearly seen that is dependent on both temperature and strain and increases with the increase in temperature and/or strain. So can be expressed as a function of temperature and strain, and its 3D nonlinear surface fitting (Parabola 2D Method) is shown in Figure 4b. Generally, the accuracy of the model’s fitting can be evaluated in terms of correlation coefficient (R2), which is expressed as follows [39]:
where Ei and Pi are the experimental and predicted values of each point, respectively, E and P are the average experimental and the predicted values, and N is the total number of the data sample used. According to the data analysis, has very good fitting with correlation coefficient R2 = 0.972; therefore, can be mathematically expressed as follows:
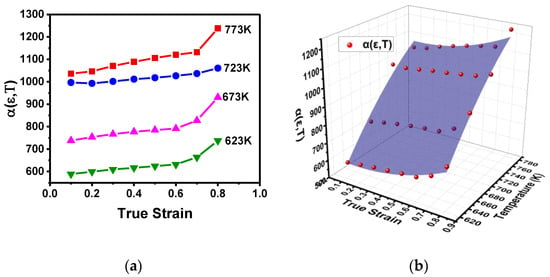
Figure 4.
The variation of : (a) at different strains and temperatures; (b) 3D illustration and its nonlinear surface fitting.
According to the hyperbolic sine function of Equation (8), the material parameters n and lnB can be obtained from the slope and intercept of the graph of against . The plot under the strain of 0.5 is shown in Figure 5. It can be clearly seen that the fitting lines at different temperatures have an approximate slope (n), but the intercepts are completely different. That means n is only a function of strain, while B is a function of temperature and strain.
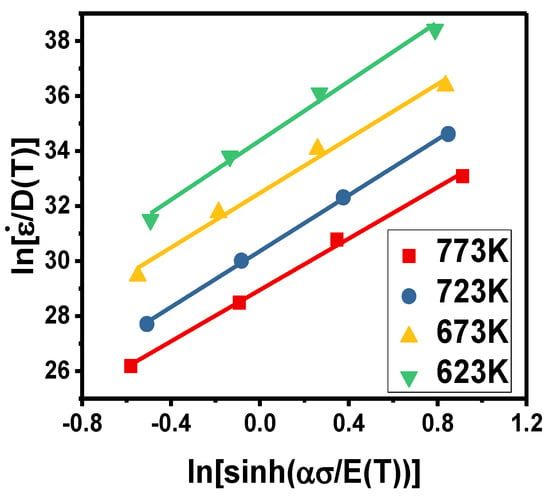
Figure 5.
Relationship between against for different parameters.
The variation of lnB under different temperatures and strains is represented in Figure 6a, and the 3D nonlinear surface fitting (Poly 2D) is shown in Figure 6b. According to the data analysis, the correlation coefficient of lnB is R2 = 0.992; therefore, lnB is expressed mathematically as follows:
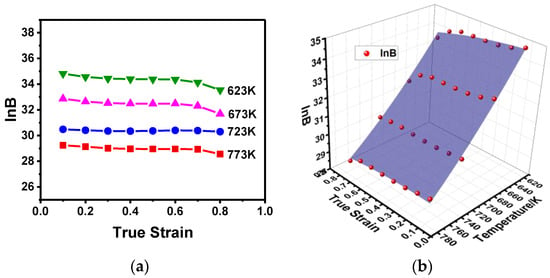
Figure 6.
The variation of lnB: (a) at different strains and temperatures; (b) 3D illustration and its nonlinear surface fitting.
The values of n at the different strains are plotted in Figure 7 and fitted by a 5th order polynomial. It can be seen that n is close to 5 and the slight deviation can be attributed to the microstructural evolution. As analyzed from the data, correlation coefficient of n is R2 = 0.999. Therefore, n is expressed mathematically as follows:
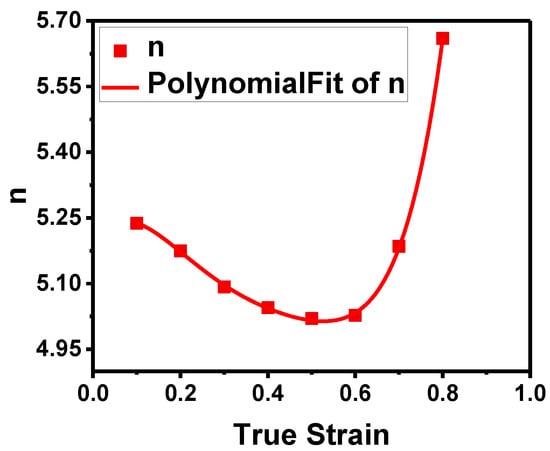
Figure 7.
Relationship between true strain and n by polynomial fitting.
The physically based constitutive model of 2219 Al alloy was established based on the governing equations above; from the integrated expression, shown in Equation (13), the flow stress of 2219 Al alloy in the temperature range of 623 K to 773 K, strain rate range of 0.01 s−1 to 10−1, and the strain range of 0~0.8 can be predicted.
3.3. Verification of the Model
In order to verify the physically based constitutive model, the experimental and predicted stresses under different deformation conditions are compared, as shown in Figure 8. It is obvious that the predicted flow stresses obtained from the physically based model are in good agreement with the experimental flow stresses for both modeling and prediction sets. To quantify the accuracy of the model, the correlation coefficient (R2) and average absolute relative error (AARE) were determined; the AARE is expressed as follows [39]:
where Ei and Pi are the experimental and predicted values of each point, and N is the total number of the data sample used.
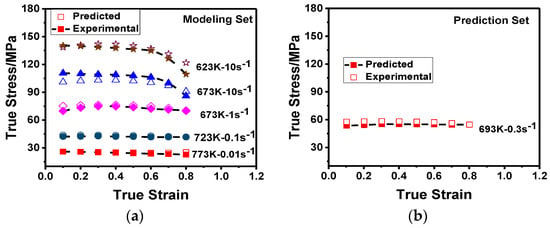
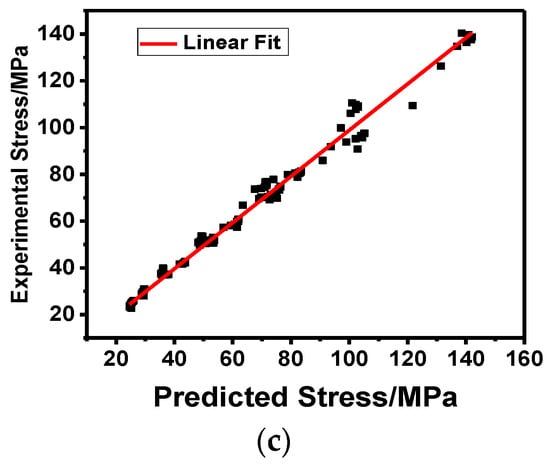
Figure 8.
Correlations between the experimental and predicted flow stresses of the physically based constitutive model: (a) under modeling set; (b) under prediction set; (c) by linear fit.
The correlation between the experimental and predicted flow stresses is R2 = 0.985 and the AARE = 3.88%. Conclusively, the physically based constitutive model can be used to predict the flow stress of 2219 Al alloy during hot deformation with high accuracy.
3.4. Microstructural Evolution
3.4.1. The Formation of CDRX
Microstructure observation was applied to investigate the formation and development of DRV and DRX during hot deformation [4]. Figure 9 shows the EBSD micrograph of the 2219 Al alloy after compression at a temperature of 673 K and strain rate of 10 s−1. Comparing with the samples before compression (Figure 1), it is observed that the grains were flattened in the direction of compression and a large amount of substructures with LAGBs were generated in the original grains. The deformed microstructure showed obvious characteristics of DRV. The SFE of the metals and alloys had a significant effect on the softening mechanisms (DRV and/or DRX). For a 2219 Al alloy with high SFE, it is more difficult to dissociate the perfect dislocation into two partials, but perfect dislocation glide, climb, and cross slip can occur easily. During hot deformation, rapid DRV takes place readily, and the stored energy is decreased by rearrangement and annihilation of dislocations, which generally retards the development of DDRX. However, it can be seen from Figure 9a that many fine grains with a size less than 10 μm appeared near the grain boundaries and a few incomplete fine grains (marked with black dotted circles) composed of HAGBs; partial LAGBs were also observed. It is reasonable to deduce that these incomplete fine grains will develop to whole recrystallized grains with continued deformation; that is to say, these partial LAGBs will transform into HAGBs [50]. Therefore, the special formation mechanism of new recrystallized grains is proved to be CDRX rather than the traditional DDRX on 2219 Al alloy during hot deformation [51,52].
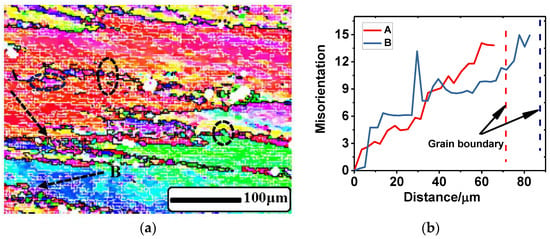
Figure 9.
EBSD measurement showing continuous dynamic recrystallization (CDRX) in 2219Al alloy. (a) Micrograph of the deformed sample under the condition of 673 K and 10 s−1; (b) the cumulative misorientation along the dotted line from A and B to the grain boundary.
Figure 9b exhibits the cumulative misorientation of the two dotted lines (shown in Figure 9a) from the interior of the grain (i.e., A and B) to the grain boundaries, respectively. An obvious increase of misorientation from the interior to the boundary was observed. Thus, as deformation continued, the misorientation of LAGBs near a grain boundary may gradually increase and the LAGBs will transform into HAGBs once the misorientation reached the critical value (15°) [53]. The development mechanism of substructures with LAGBs near the grain boundaries can be ascribed to the progressive lattice rotation [54]. Grain boundary sliding (GBS) was more likely to occur at specifically oriented boundaries, and then these grain boundaries got serrated due to the migration of the HAGBs as shown in Figure 9a. The small serrations on partial boundaries may be eliminated by GBS, but the large serrations or mantles may be gradually formed in the nonsliding boundaries. As GBS can still operate on the mantles, the remaining parts have to sustain the shear effects and distortion begins to occur. As a result, local lattices near the mantles have to rotate and asymmetric bulges are generated. Then, subgrains with intermediate grain boundaries are formed. New recrystallized grains will be formed as long as the partial LAGBs of these subgrains transform into HAGBs [55]. The results of the formation of CDRX are consistent with the study of Yin [50], Shimizu [52], and Beer [53].
3.4.2. The Influence of TMP on CDRX
The EBSD micrographs of the compressed samples under different deformed conditions are illustrated in Figure 10 to investigate the influence of TMP on CDRX. Among them, Figure 10a–c shows the microstructures under the conditions of 673 K, 10 s−1, and the strains of 0.2, 0.5, and 0.9, respectively. It can be seen clearly that, as the deformation continued, the original grains were gradually elongated, grain boundaries became more and more jagged, and the amount of small, recrystallized grains near the grain boundaries increased progressively. Thus, the increase in the strain can promote the formation of CDRX. However, the percentage of recrystallized grains is still very small; even at the strain of 0.9, the original grains and their internal substructures occupied the majority, which also proves that the predominant softening mechanism of the 2219 Al alloy during hot deformation was DRV.

Figure 10.
The EBSD micrographs of the deformed samples under conditions of: (a) 673 K and 0.1 s−1 with the strain of 0.2; (b) 673 K and 0.1 s−1 with the strain of 0.5; (c) 673 K and 0.1 s−1 with the strain of 0.9; (d) 623 K and 1 s−1 with the strain of 0.9; (e) 673 K and 1 s−1 with the strain of 0.9; (f) 773 K and 1 s−1 with the strain of 0.9; (g) 773 K and 0.1 s−1 with the strain of 0.9; (h) 773 K and 0.01 s−1 with the strain of 0.9.
In addition, Figure 10d–f shows the microstructures deformed at a strain rate of 1 s−1 and strain of 0.9 at different temperatures of 623 K, 673 K, and 773 K, respectively. It can be seen that, as the temperature increased, the amount of recrystallized grains near the grain boundaries gradually increased, and also the grain size gradually increased. This is due to the fact that the mobility of the grain boundaries will increase with the increase in temperature. Moreover, DRX is a thermal-activation process; therefore, there will be a greater driving force to promote the growth of the new grains at high temperature. So, the increase of forming temperature can promote the development of CDRX and growth of new grains. Finally, Figure 10f–h show the microstructures deformed at the temperature of 773 K, strain of 0.9, and different strain rates of 1 s−1, 0.1 s−1, and 0.01 s−1, respectively. It can also be observed that as the strain rate increased, the amount of recrystallized grains decreased, and the growth of new fine grains was greatly restricted. This is because the reduction of forming time restrains the growth of recrystallized grains at high strain rate. Therefore, the increase in strain rates limits the development of CDRX and the growth of its recrystallized grains. The results of the influence of TMP on CDRX obtained are consistent with the study of Wang [51] on AA7050 aluminum alloy.
4. Conclusions
In this study, the flow curves under different deformation conditions of 2219 Al alloy were obtained based on thermal-compression tests. The physically based constitutive model was established to describe its flow behavior. The microstructure evolution behavior of the 2219 Al alloy in thermal compression was also studied. The following conclusions can be drawn:
- The flow stress of the 2219 Al alloy is very sensitive to temperatures and strain rates, and its value decreases with the increase in temperatures and/or the decrease in strain rates.
- The physically based constitutive model of 2219 Al alloy established is proved to have good predictive performance, which can be used to accurately describe the flow behavior of the 2219 Al alloy in the temperature range of 623 K to 773 K, strain rate range of 0.01 s−1 to 10−1, and the strain range of 0~0.8.
- It has been proved that the main microstructure evolution of 2219 Al alloy under hot deformation is DRV and incomplete CDRX. Moreover, CDRX can occur readily at high temperatures, low strain rates and high strains; meanwhile, the recrystallized grains size will also be larger.
Author Contributions
Conceptualization, L.L.; methodology, Y.W. and H.G.; software, S.L.; validation, L.L. and S.L.; formal analysis, L.L. and H.G.; writing—original draft preparation, L.L.; writing—review and editing, Y.W. and A.S.A.
Funding
The research was funded by the National Natural Science Foundation of China (Grant Number: 51405520, U1637601 and 51327902), the Fundamental Research Funds for the Central Universities of Central South University (Grant Number: 502221801), and the Project of State Key Laboratory of High Performance Complex Manufacturing, Central South University (Grant Number: ZZYJKT2017-06).
Acknowledgments
The authors are very grateful for the experimental materials provided by the Collaborative Innovation Center of Nonferrous Metals, the thermal compression instruments provided by Suzhou Research Institute for Nonferrous Metal Co., Ltd, and the methodological guidance given by all colleagues in B405 office.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaibyshev, R.; Sitdikov, O.; Mazurina, I.; Lesuer, D.R. Deformation behavior of a 2219 Al alloy. Mater. Sci. Eng. A 2002, 334, 104–113. [Google Scholar] [CrossRef]
- Mirzadeh, H. Constitutive modeling and prediction of hot deformation flow stress under dynamic recrystallization conditions. Mech. Mater. 2015, 85, 66–79. [Google Scholar] [CrossRef]
- Toros, S.; Ozturk, F. Flow curve prediction of Al–Mg alloys under warm forming conditions at various strain rates by ANN. Appl. Soft Comput. 2011, 11, 1891–1898. [Google Scholar] [CrossRef]
- Huang, C.Q.; Jie, D.; Wang, S.X.; Liu, L.L. A physical-based constitutive model to describe the strain-hardening and dynamic recovery behaviors of 5754 aluminum alloy. Mater. Sci. Eng. A 2017, 699, 106–113. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Salehi, M.S.; Serajzadeh, S. A neural network model for prediction of static recrystallization kinetics under non-isothermal conditions. Comp. Mater. Sci. 2010, 49, 773–781. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, L.; Yang, H. Microstructure evolution of different loading zones during TA15 alloy multi-cycle isothermal local forging. Mater. Sci. Eng. A 2011, 528, 5112–5121. [Google Scholar] [CrossRef]
- Mcqueen, H.J.; Ryan, N.D. Constitutive analysis in hot working. Mater. Sci. Eng. A 2002, 322, 43–63. [Google Scholar] [CrossRef]
- Ashtiani, H.R.R.; Parsa, M.H.; Bisadi, H. Constitutive equations for elevated temperature flow behavior of commercial purity aluminum. Mater. Sci. Eng. A 2012, 545, 61–67. [Google Scholar] [CrossRef]
- Changizian, P.; Zarei-Hanzaki, A.; Roostaei, A.A. The high temperature flow behavior modeling of AZ81 magnesium alloy considering strain effects. Mater. Des. 2012, 39, 384–389. [Google Scholar] [CrossRef]
- Hollomon, J.H.; Member, J. Tensile Deformation. Met. Technol. 1945, 12, 268–290. [Google Scholar]
- Ludwig, P. Element der Technologischen Mechanik//Elemente der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. Eng. Fract. Mech. 1983, 21, 541–548. [Google Scholar]
- Sellars, C.M.; Mctegart, W.J. On the mechanism of hot deformation. Acta Metall. Mater. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Constitutive relationships for hot deformation of austenite. Acta Mater. 2011, 59, 6441–6448. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Cabrera, J.M.; Najafizadeh, A. Modeling and Prediction of Hot Deformation Flow Curves. Metall. Mater. Trans. A 2012, 43, 108–123. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comp. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Yu, D.H. Modeling high-temperature tensile deformation behavior of AZ31B magnesium alloy considering strain effects. Mater. Des. 2013, 51, 323–330. [Google Scholar] [CrossRef]
- Ashtiani, H.R.R.; Shahsavari, P. Strain-dependent constitutive equations to predict high temperature flow behavior of AA2030 aluminum alloy. Mech. Mater. 2016, 100, 209–218. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization phenomena in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Chen, F.; Cui, Z.; Chen, S. Recrystallization of 30Cr2Ni4MoV ultra-super-critical rotor steel during hot deformation. Part I: Dynamic recrystallization. Mater. Sci. Eng. A 2011, 528, 5073–5080. [Google Scholar] [CrossRef]
- Stewart, G.R.; Jonas, J.J.; Montheillet, F. Kinetics and Critical Conditions for the Initiation of Dynamic Recrystallization in 304 Stainless Steel. Iron Steel I Jpn. 2004, 44, 1581–1589. [Google Scholar] [CrossRef]
- Marchattiwar, A.; Sarkar, A.; Chakravartty, J.K.; Kashyap, B.P. Dynamic Recrystallization during Hot Deformation of 304 Austenitic Stainless Steel. J. Mater. Eng. Perform. 2013, 22, 2168–2175. [Google Scholar] [CrossRef]
- Quan, G.Z.; Mao, Y.P.; Li, G.S.; Lv, W.Q.; Wang, Y. A characterization for the dynamic recrystallization kinetics of as-extruded 7075 aluminum alloy based on true stress–strain curves. Comp. Mater. Sci. 2012, 55, 65–72. [Google Scholar] [CrossRef]
- Li, X.; Wu, X.C.; Zhang, X.X.; Li, M.Y. Dynamic Recrystallization of Hot Deformed 3Cr2NiMnMo Steel: Modeling and Numerical Simulation. J. Iron Steel Res. Int. 2013, 20, 98–104. [Google Scholar] [CrossRef]
- Perdrix, C.; Perrin, M.Y.; Montheillet, F. Mechanical behavior and structure development of aluminum during high amplitude hot deformation/comportment mecanique et evolution structural de l’aluminium au cours d’une deformation a chaud de grande amplitude. Metal 1981, 78, 309–320. [Google Scholar]
- Montheillet, F.; Gilormini, P.; Jonas, J.J. Relation between axial stresses and texture development during torsion testing: A simplified theory. Acta Metall. Mater. 1985, 33, 705–717. [Google Scholar] [CrossRef]
- Gourdet, S.; Montheillet, F. An experimental study of the recrystallization mechanism during hot deformation of aluminium. Mater. Sci. Eng. A 2000, 283, 274–288. [Google Scholar] [CrossRef]
- Ion, S.E.; Humphreys, F.J.; White, S.H. Dynamic recrystallisation and the development of microstructure during the high temperature deformation of magnesium. Acta Metall. Mater. 1982, 30, 1909–1919. [Google Scholar] [CrossRef]
- Gardner, K.J.; Grimes, R. Recrystallization during hot deformation of aluminium alloys. Met. Sci. 1979, 13, 216–222. [Google Scholar] [CrossRef]
- Yanushkevich, Z.; Belyakov, A.; Kaibyshev, R. Microstructural evolution of a 304-type austenitic stainless steel during rolling at temperatures of 773–1273 K. Acta Mater. 2015, 82, 244–254. [Google Scholar] [CrossRef]
- Kaibyshev, R.; Shipilova, K.; Musin, F.; Motohashi, Y. Continuous dynamic recrystallization in an Al–Li–Mg–Sc alloy during equal-channel angular extrusion. Mater. Sci. Eng. A 2005, 396, 341–351. [Google Scholar] [CrossRef]
- Gourdet, S.; Montheillet, F. A model of continuous dynamic recrystallization. Acta Mater. 2003, 51, 2685–2699. [Google Scholar] [CrossRef]
- Tóth, L.S.; Estrin, Y.; Lapovok, R.; Gu, C. A model of grain fragmentation based on lattice curvature. Acta Mater. 2010, 58, 1782–1794. [Google Scholar] [CrossRef]
- Finegan, B.A.; Mcfarlane, H.J. Evolution of flow stress in aluminium during ultra-high straining at elevated temperatures. Part II. Philos. Mag. A 1989, 60, 473–485. [Google Scholar]
- Mcqueen, H.J.; Myshlyaev, M.M.; Mwembela, A. Microstructural Evolution and Strength in Hot Working of ZK60 and other Mg Alloys. Can. Metall. Q. 2013, 42, 97–112. [Google Scholar] [CrossRef]
- Myshlyaev, M.M.; Mcqueen, H.J.; Mwembela, A.; Konopleva, E. Twinning, dynamic recovery and recrystallization in hot worked Mg–Al–Zn alloy. Mater. Sci. Eng. A 2002, 337, 121–133. [Google Scholar] [CrossRef]
- Roebuck, B.; Lord, J.D.; Brooks, M.; Loveday, M.S.; Sellars, C.M. Measurement of flow stress in hot axisymmetric compression tests. High Temp. Technol. 1997, 23, 59–83. [Google Scholar] [CrossRef]
- Wei, H.L.; Liu, G.Q.; Zhang, M.H. Physically based constitutive analysis to predict flow stress of medium carbon and vanadium microalloyed steels. Mater. Sci. Eng. A 2014, 602, 127–133. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena, 2nd ed.; Pergamon Press: Oxford, UK, 1995. [Google Scholar]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Prediction of 42CrMo steel flow stress at high temperature and strain rate. Mech. Res. Commun. 2008, 35, 142–150. [Google Scholar] [CrossRef]
- Wu, K.; Liu, G.Q.; Hu, B.F.; Wang, C.F.; Zhang, Y.W. Effect of processing parameters on hot compressive deformation behavior of a new Ni–Cr–Co based P/M superalloy. Mater. Sci. Eng. A 2011, 528, 4620–4629. [Google Scholar] [CrossRef]
- Solhjoo, S. Determination of critical strain for initiation of dynamic recrystallization. Mater. Des. 2010, 31, 1360–1364. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.S.; Zhong, J. Microstructural evolution in 42CrMo steel during compression at elevated temperatures. Mater. Lett. 2008, 62, 2132–2135. [Google Scholar] [CrossRef]
- Reyes-Calderón, F.; Mejía, I.; Cabrera, J.M. Hot deformation activation energy (QHW) of austenitic Fe–22Mn–1.5Al–1.5Si–0.4C TWIP steels microalloyed with Nb, V, and Ti. Mater. Sci. Eng. A 2013, 562, 46–52. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Cabrera, J.M.; Omar, A.A.; Prado, J.M.; Jonas, J.J. Modeling the flow behavior of a medium carbon microalloyed steel under hot working conditions. Metall. Mater. Trans. A 1997, 28, 2233–2244. [Google Scholar] [CrossRef]
- Cabrera, J.M.; Jonas, J.J.; Prado, J.M. Flow behaviour of medium carbon microalloyed steel under hot working conditions. Met. Sci. 2013, 12, 579–585. [Google Scholar] [CrossRef]
- Thomas, A.; El-Wahabi, M.; Cabrera, J.M.; Prado, J.M. High temperature deformation of Inconel 718. J. Mater. Process. Technol. 2006, 177, 469–472. [Google Scholar] [CrossRef]
- Yin, X.Q.; Park, C.H.; Li, Y.F.; Ye, W.J.; Zuo, Y.T. Mechanism of continuous dynamic recrystallization in a 50Ti-47Ni-3Fe shape memory alloy during hot compressive deformation. J. Alloy Compd. 2017, 693, 426–431. [Google Scholar] [CrossRef]
- Wang, S.; Luo, J.R.; Hou, L.G.; Zhang, J.S.; Zhuang, L.Z. Physically based constitutive analysis and microstructural evolution of AA7050 aluminum alloy during hot compression. Mater. Des. 2016, 107, 277–289. [Google Scholar] [CrossRef]
- Shimizu, I. Theories and applicability of grain size piezometers: The role of dynamic recrystallization mechanisms. J. Struct. Geol. 2008, 30, 899–917. [Google Scholar] [CrossRef]
- Beer, A.G.; Barnett, M.R. Microstructural Development during Hot Working of Mg-3Al-1Zn. Metall. Mater. Trans. A 2007, 38, 1856–1867. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wu, X.Y.; Chen, X.M.; Chen, J.; Wen, D.X. EBSD study of a hot deformed nickel-based superalloy. J. Alloy Compd. 2015, 640, 101–113. [Google Scholar] [CrossRef]
- Drury, M.R.; Humphreys, F.J. The development of microstructure in Al-5% Mg during high temperature deformation. Acta Metall. Mater. 1986, 34, 2259–2271. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).