Electro-Superplastic Solid State Welding of 40Cr/QCr0.5
Abstract
:1. Introduction
2. Experimental Materials and Procedures
2.1. Experimental Materials and Welding Samples
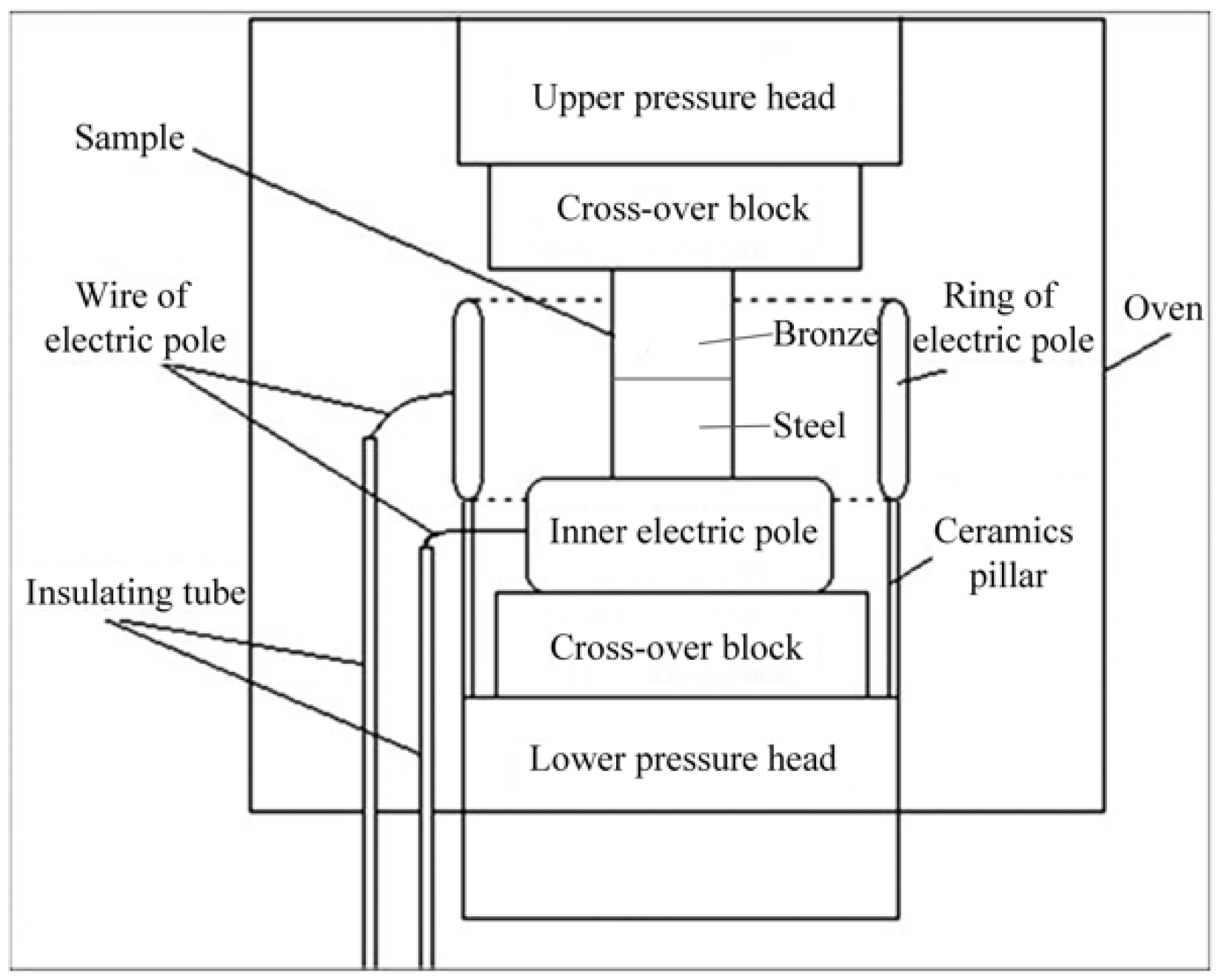
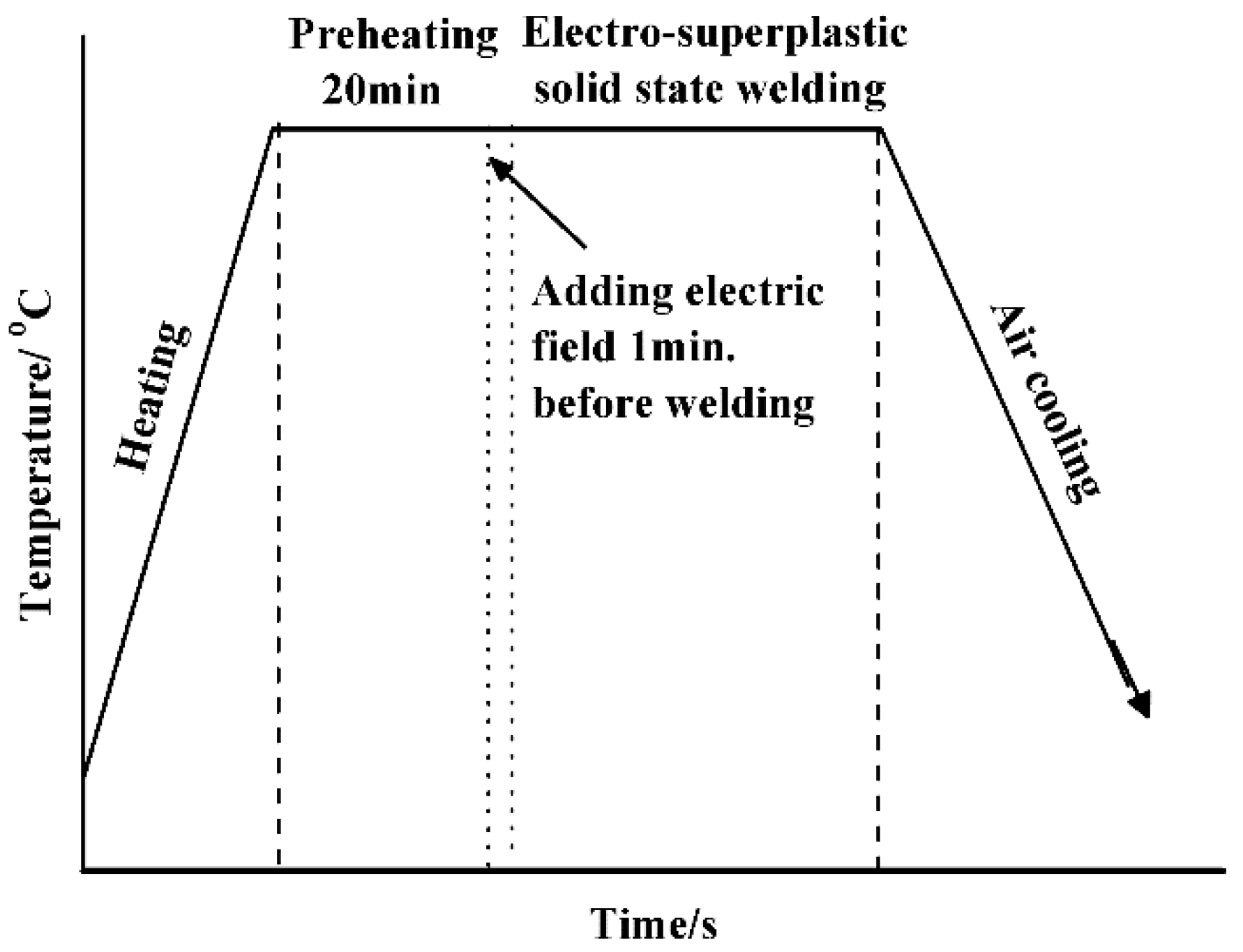
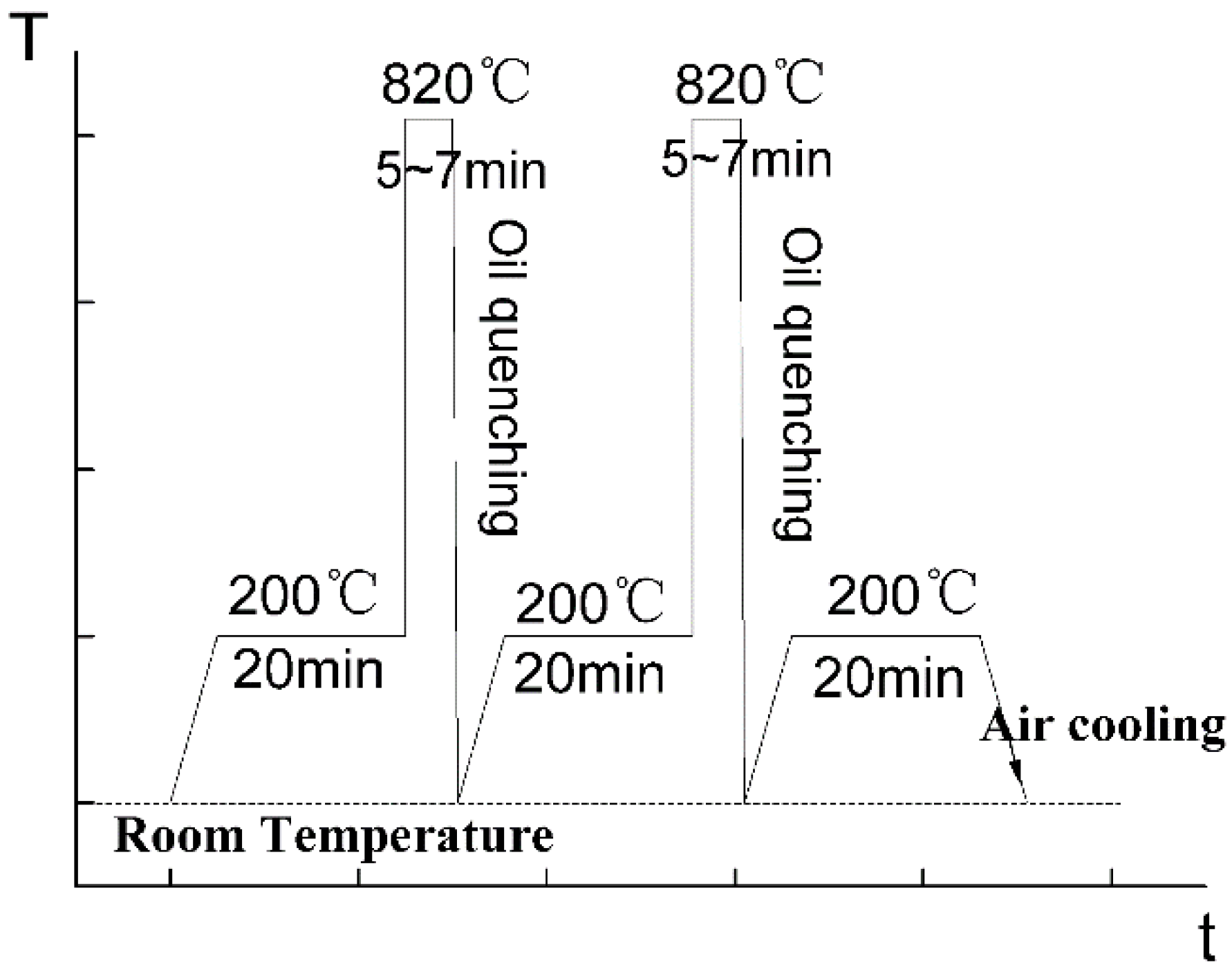
2.2. Electro-Superplastic Solid State Welding Tests
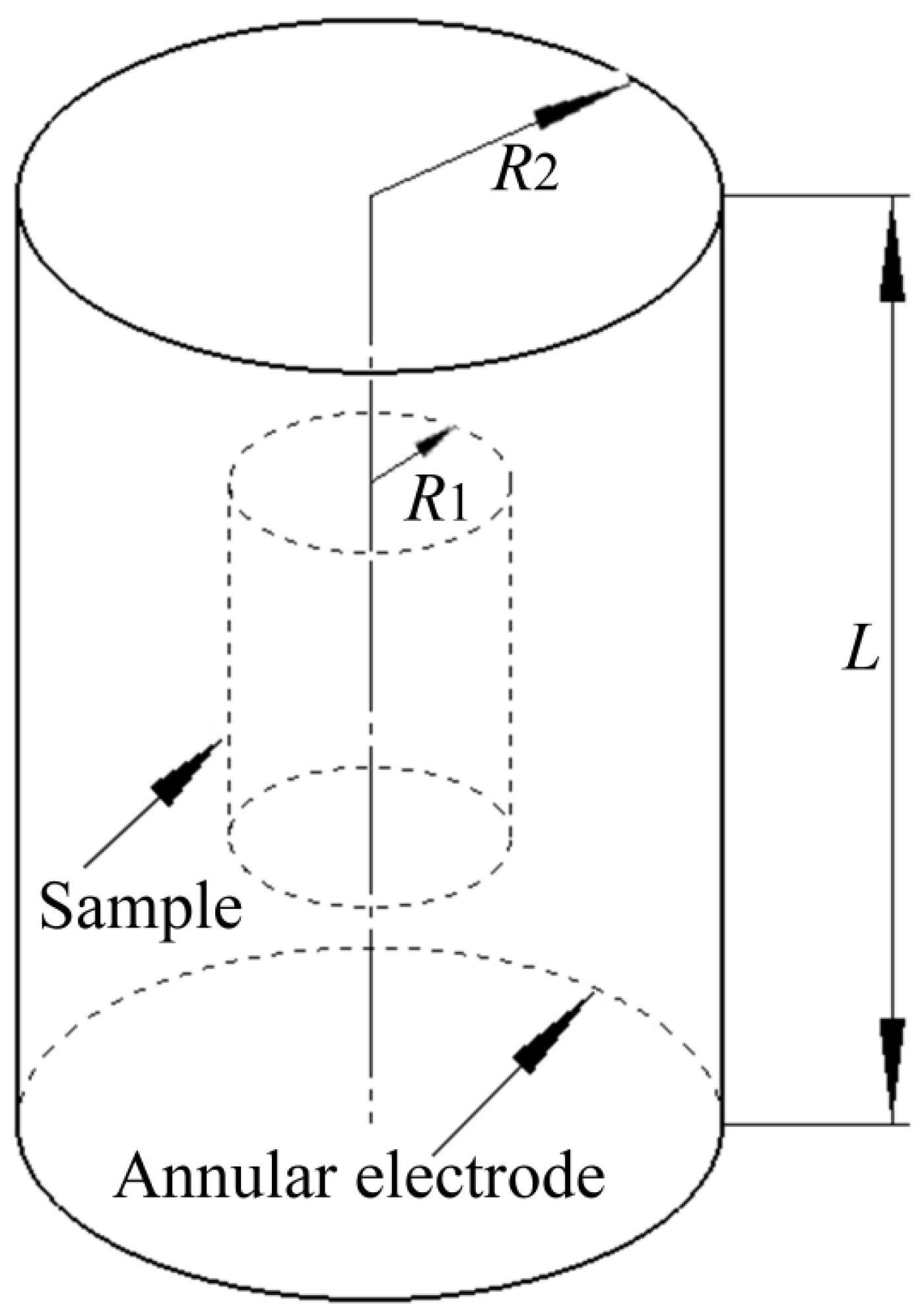
2.3. Calculation of Electrical Field Intensity
2.4. Welding Deformation Measurements and Tensile Tests
2.5. Investigation of Fracture Surfaces and Weld Interfaces
3. Results and Discussion
3.1. Material Treatment and Microstructure
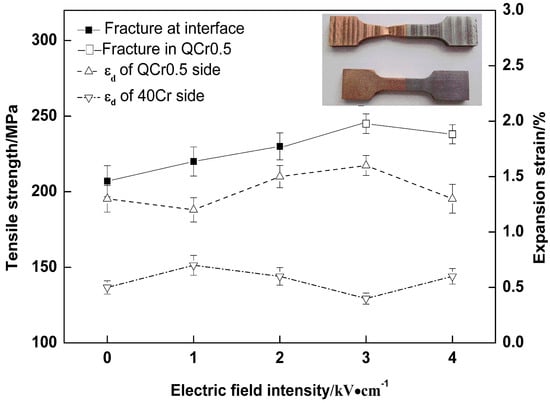
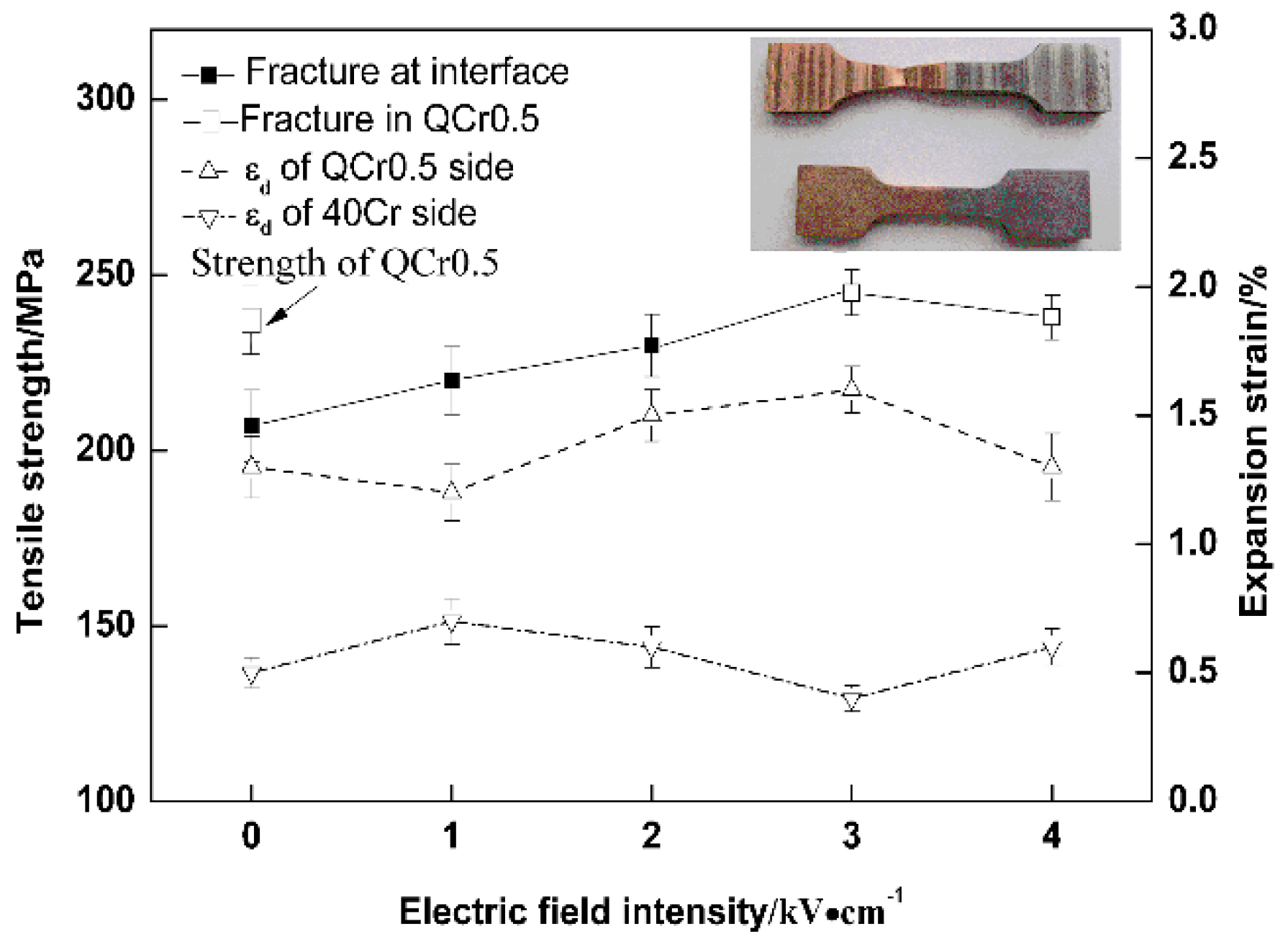
3.2. Effect of Electrical Field Intensity
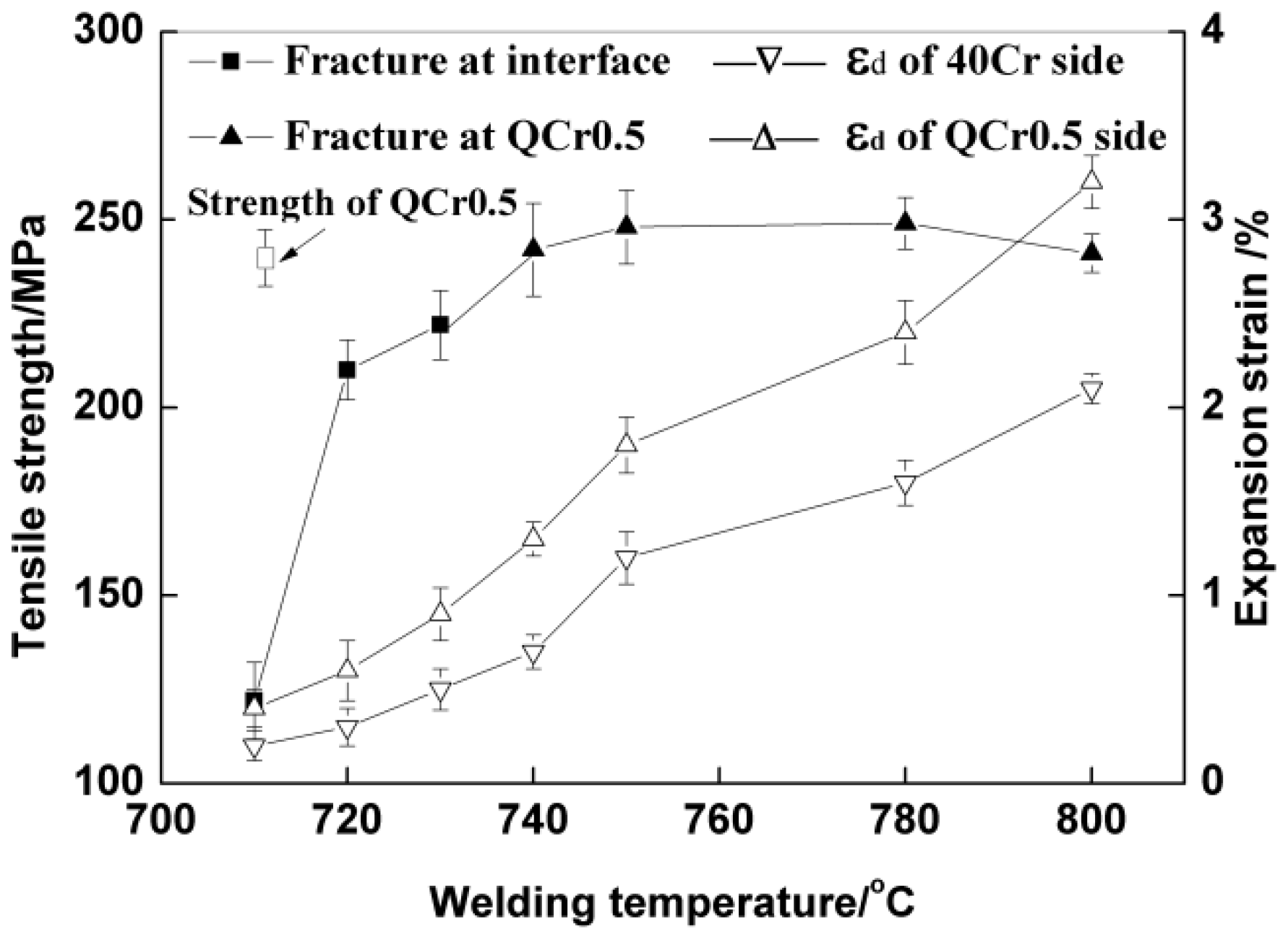
3.3. Effect of Welding Temperature
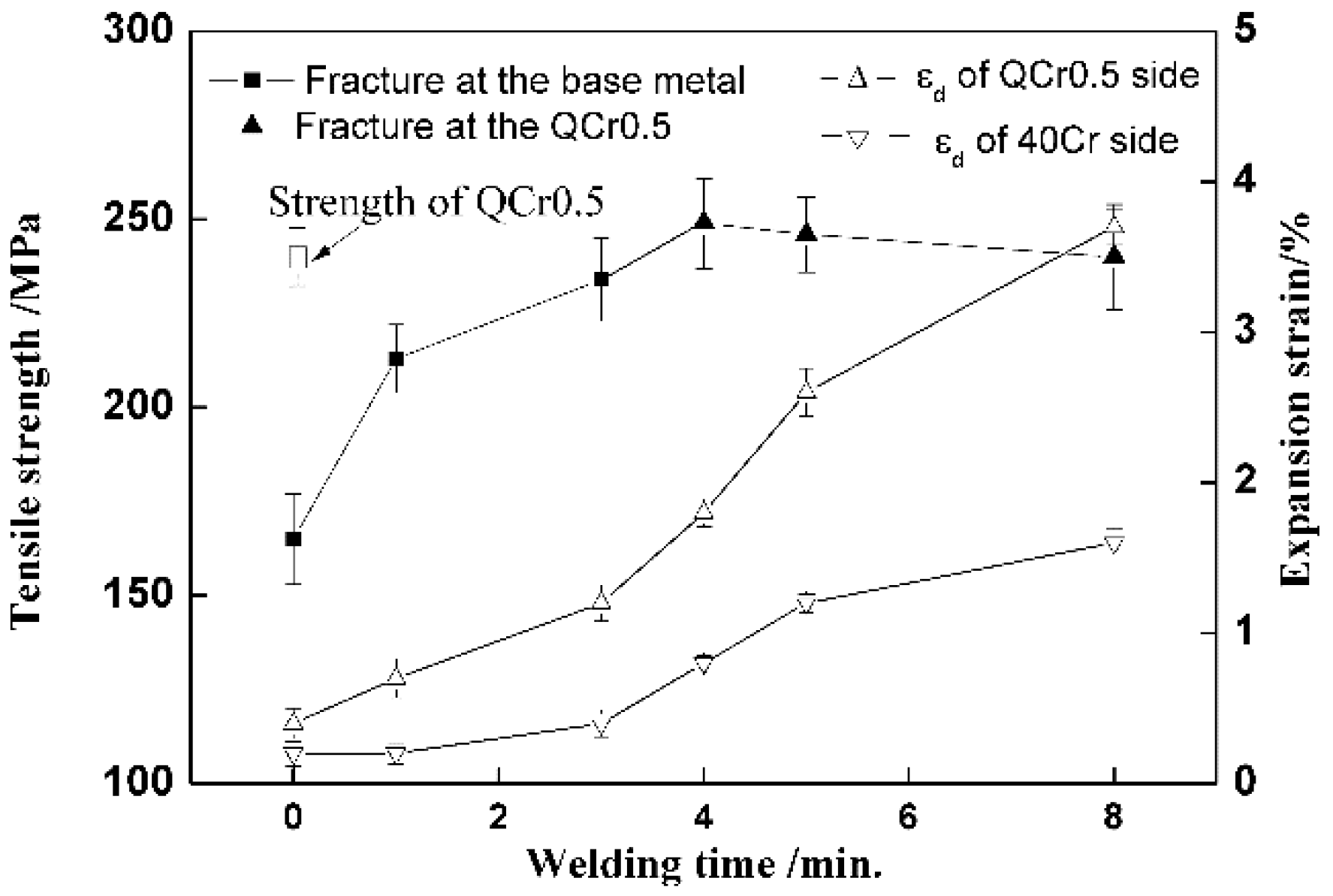
3.4. Effect of Welding Time
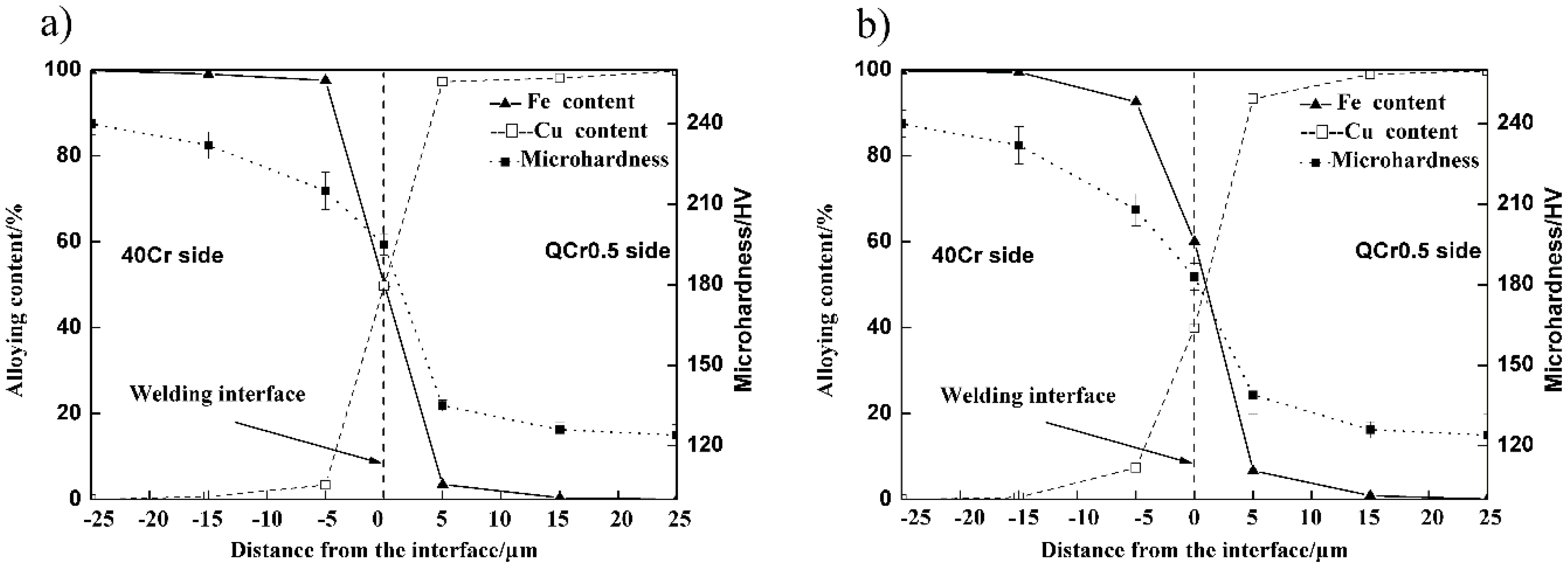
3.5. Observation of Fracture Surfaces and Weld Interfaces
3.6. Discussion
4. Conclusions
- Tensile strength of the 40Cr/QCr0.5 weld joint can be greatly increased by welding with an external electrical field. This can be attributed to better metallurgical bonding, achieved with an electrical field. Under optimal conditions, the tensile strength can be up to or exceeding that of the QCr0.5 base metal with a tensile fracture occurring in the QCr0.5 base metal. The parameters for the optimal condition include an external electrical field of E ≥ 3 kV/cm with no vacuum, no shield gas, a pre-pressure of 56.6 MPa, an initial strain rate of 1.5 × 10−4 s−1, a pressure welding temperature of 710–800 °C, and a pressure welding time of 0–8 min.
- The weld interface between 40Cr and QCr0.5 has achieved metallurgical bonding, and there are less micro-gaps, thicker transition regions, and more copper convexes and dimples on the fracture surface of the 40Cr side when applying an external electrical field of E = 3 kV/cm.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, J.; Sirois, D.; Li, S.; Sullivan, M.; Chin, B.A. Ballistic impact welding of copper to low carbon steel. J. Mater. Process. Technol. 2016, 232, 165–174. [Google Scholar] [CrossRef]
- Luo, C.; Ji, J.; Ling, F.; Li, D.; Yao, J. Effect of electric field on the dielectric properties of the Barium Strontium Titanate film. J. Alloy Compd. 2016, 687, 204–210. [Google Scholar] [CrossRef]
- Mishra, B.; Kumbhar, K.; Kumar, K.S.; Prasad, K.S.; Srinivas, M. Effect of copper addition on microstructure and mechanical properties of ultra-high strength NiSiCrCoMo steel. Mater. Sci. Eng. A 2016, 651, 177–183. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, Y.; Haghshenas, M.; Nguyen, T.; Galloway, J.; Gerlich, A.P. Interfacial microstructure and properties of copper clad steel produced using friction stir welding versus gas metal arc welding. Mater. Charact. 2015, 104, 1–9. [Google Scholar] [CrossRef]
- Zhang, K.; Yue, Y.; Ma, N.; Wu, Z.; Sun, J.; Yang, Y. Dynamic diffusion behavior of atoms in isothermal superplastic welding process of steel. Trans. China Weld. Inst. 2010, 31, 17–20. [Google Scholar]
- Conrad, H.; Yang, D. Effect of an electric field on the plastic deformation kinetics of electrodeposited Cu at low and intermediate temperatures. Acta Mater. 2002, 50, 2851–2866. [Google Scholar] [CrossRef]
- Baranov, Y.V. Effect of Electrostatic Fields on Mechanical Characteristics and Structure of Metals and Alloys. Mater. Sci. Eng. A 2000, 287, 288–300. [Google Scholar] [CrossRef]
- Fu, L.; Du, S.; Jie, W. External electric field effect on microstructure of friction welded joint of duralumin LY12. Acta Metall. Sin. 2002, 38, 433–437. [Google Scholar]
- Conrad, H.; Yang, D.; Becher, P. Effect of an applied electric field on the flow stress of ultrafine-grained 2.5Y-TZP at high temperatures. Mater. Sci. Eng. A 2008, 477, 358–365. [Google Scholar] [CrossRef]
- Yang, D.; Conrad, H. Influence of an electric field on the superplastic deformation of 3Y-TZP. Scr. Mater. 1997, 36, 1431–1435. [Google Scholar] [CrossRef]
- Conrad, H.; Yang, D. Effect of DC electric field on the tensile deformation of ultrafine-grained 3Y-TZP at 1450–1600 °C. Acta Mater. 2007, 55, 6789–6797. [Google Scholar] [CrossRef]
- Zheng, M.; Lu, X.P.; Conrad, H. Influence of an external electric field during quenching on the hardenability of steel. Scr. Mater. 2001, 44, 381–385. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, J.H.; Lee, C.H. Domain switching and creep behavior of a poled PZT wafer under through-thickness electric fields at high temperatures. Acta Mater. 2010, 58, 2237–2249. [Google Scholar] [CrossRef]
- Conrad, H. Space charge and the dependence of the flowstress of ceramics on an applied electric field. Scr. Mater. 2001, 44, 311–316. [Google Scholar] [CrossRef]
- Hall, D.A.; Evans, J.D.S.; Covey-Crump, S.J.; Holloway, R.F.; Oliver, E.C.; Mori, T.; Withers, P.J. Effects of superimposed electric field and porosity on the hydrostatic pressure-induced rhombohedral to orthorhombic martensitic phase transformation in PZT 95/5 ceramics. Acta Mater. 2010, 58, 6584–6591. [Google Scholar] [CrossRef]
- Conrad, H.; Yang, D.; Becher, P. Plastic deformation of ultrafine-grained 2.5Y-TZP exposed to a dc electric field with an air gap. Mater. Sci. Eng. A 2008, 496, 9–13. [Google Scholar] [CrossRef]
- Ran, S.; Biest, O.V.; Vleugels, J. In situ platelet-toughened TiB2-SiC composites prepared by reactive pulsed electric current sintering. Scr. Mater. 2011, 64, 1145–1148. [Google Scholar] [CrossRef]
- Matsusaka, S.; Watanabe, T. Improvement in laser micromachine ability of borosilicate glass by electric field assisted solid-state ion exchange. Scr. Mater. 2010, 62, 141–143. [Google Scholar] [CrossRef]
- Cao, W.D.; Lu, X.P.; Sprecher, A.E.; Conrad, H. Superplastic deformation behavior of 7475 Aluminum aloy in an electric field. Mater. Sci. Eng. A 1990, 129, 157–166. [Google Scholar] [CrossRef]
- Zhang, K.; Sun, J.; Wu, Z.; Ma, N.; Qiu, R.; Zhang, Z. Superplastic welding of 1.6%C-UHCS/40Cr steel in an electric field. Trans. China Weld. Inst. 2011, 32, 5–8. [Google Scholar]
- Miaoquan, L.; Shidun, W. Electric field modification during superplastic deformation of LY12CA duralumin. Acta Metall. Sin. 1995, 31, 272–276. [Google Scholar]
- Jiang, Z.; Du, H. Calculation of the Capacitance of the Cylindrical Capacitor with Arbitrary Dimensions. J. Electron. Meas. Inst. 2005, 19, 49–51. [Google Scholar]
- Ma, F.; Yang, Y.; W, C. Experiment of superplasticity of QCr0.5 under compression state. J. Luoyang Inst. Technol. 1999, 20, 14–17. [Google Scholar]
- Liu, Y.; Wang, L.; Ding, Y.; Cui, T.; Wang, Y. Effects of electric field treatment on microstructure and deformation behavior of GH4199 superalloy. Chin. J. Nonferrous Met. 2006, 16, 1749–1755. [Google Scholar]






| Mater. | Cu | Cr | Fe | Ni | C | Si | Mn | S | P |
|---|---|---|---|---|---|---|---|---|---|
| QCr0.5 | Rest | 0.4–1.1 | ≤0.1 | ≤0.05 | - | - | - | - | - |
| 40Cr | ≤0.03 | 0.8–1.1 | Rest | ≤0.30 | 0.37–0.44 | 0.17–0.37 | 0.50–0.80 | ≤0.035 | ≤0.035 |
| Materials | Hardness | Yield Strength | Tensile Strength | Melting Point |
|---|---|---|---|---|
| 40Cr | 240 HV200g | 510 MPa | 708 MPa | ≥1538 °C |
| QCr0.5 | 124 HV200g | 140 MPa | 238 MPa | 1080 °C |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, G.; Zhang, K. Electro-Superplastic Solid State Welding of 40Cr/QCr0.5. Materials 2018, 11, 1153. https://doi.org/10.3390/ma11071153
Wang Y, Wang G, Zhang K. Electro-Superplastic Solid State Welding of 40Cr/QCr0.5. Materials. 2018; 11(7):1153. https://doi.org/10.3390/ma11071153
Chicago/Turabian StyleWang, Yaoli, Guangxin Wang, and Keke Zhang. 2018. "Electro-Superplastic Solid State Welding of 40Cr/QCr0.5" Materials 11, no. 7: 1153. https://doi.org/10.3390/ma11071153
APA StyleWang, Y., Wang, G., & Zhang, K. (2018). Electro-Superplastic Solid State Welding of 40Cr/QCr0.5. Materials, 11(7), 1153. https://doi.org/10.3390/ma11071153