Combined Effects of Texture and Grain Size Distribution on the Tensile Behavior of α-Titanium
Abstract
1. Introduction
2. Materials and Methods
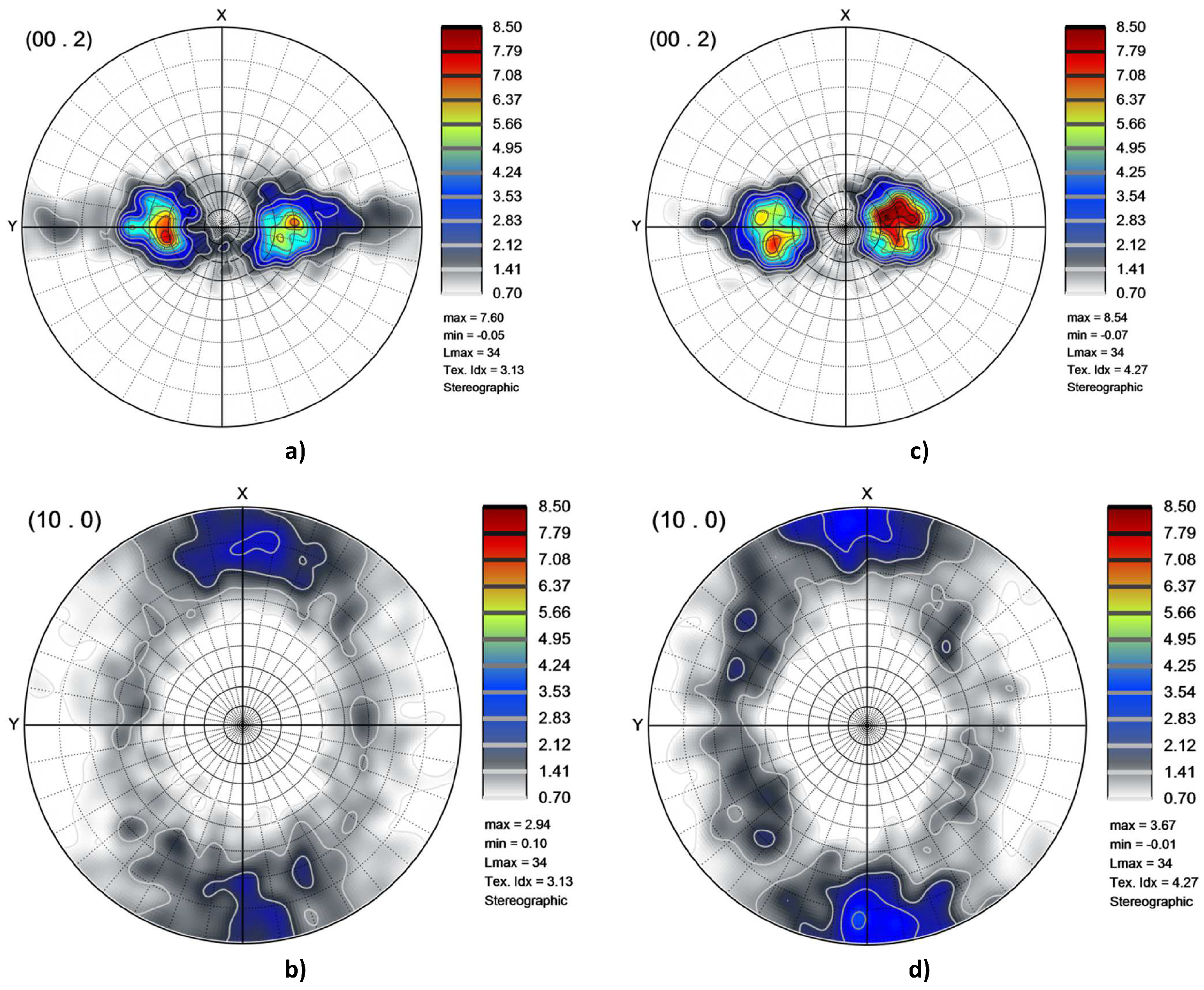
2.1. Preparation, Microstructural and Mechanical Characterization of the Specimens
2.2. Micromechanical Modeling Including Grain Size Effects
2.2.1. Micro-Macro Scale Transition
2.2.2. Single Crystal Constitutive Laws
2.2.3. Model Parameters
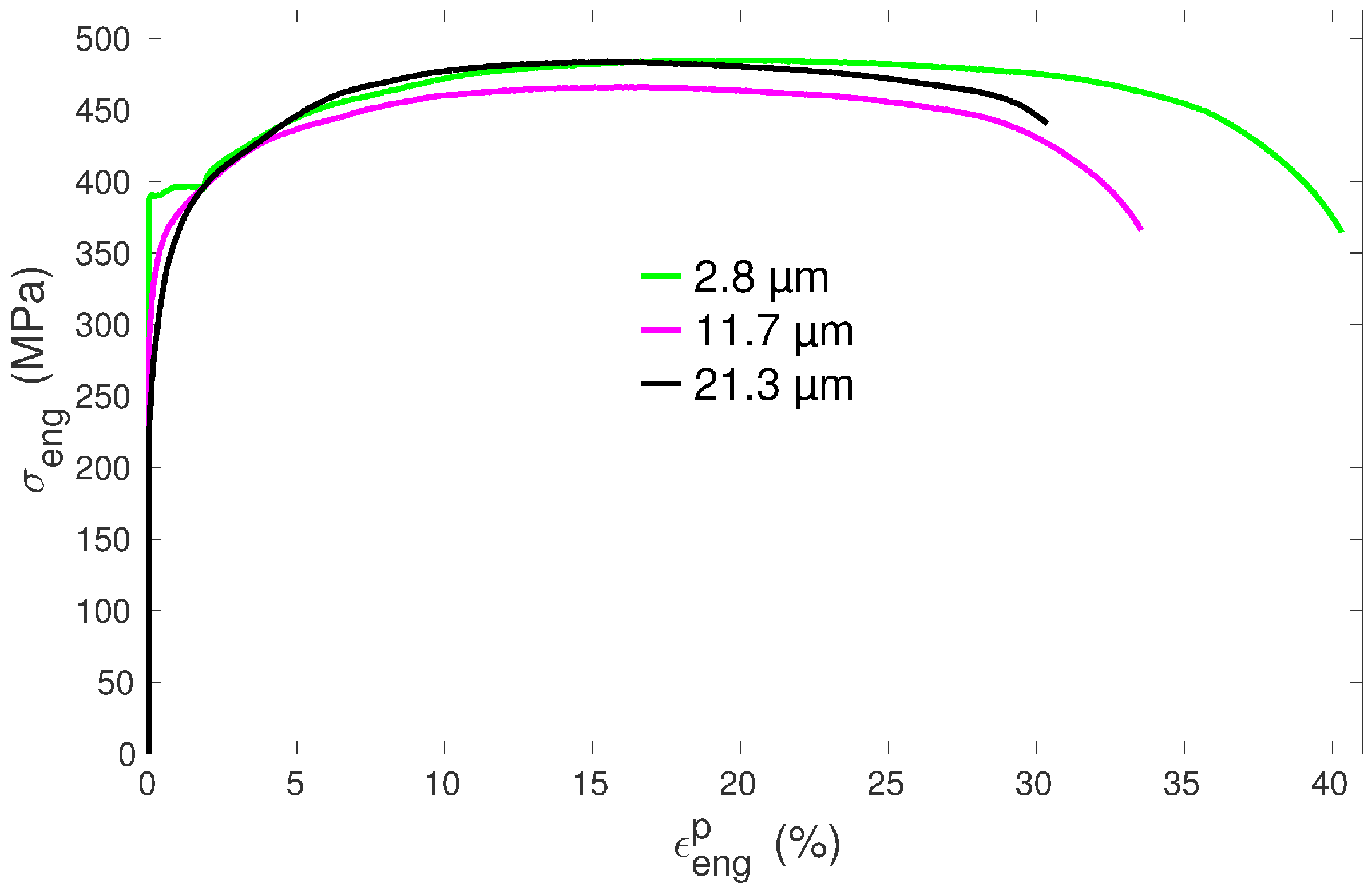
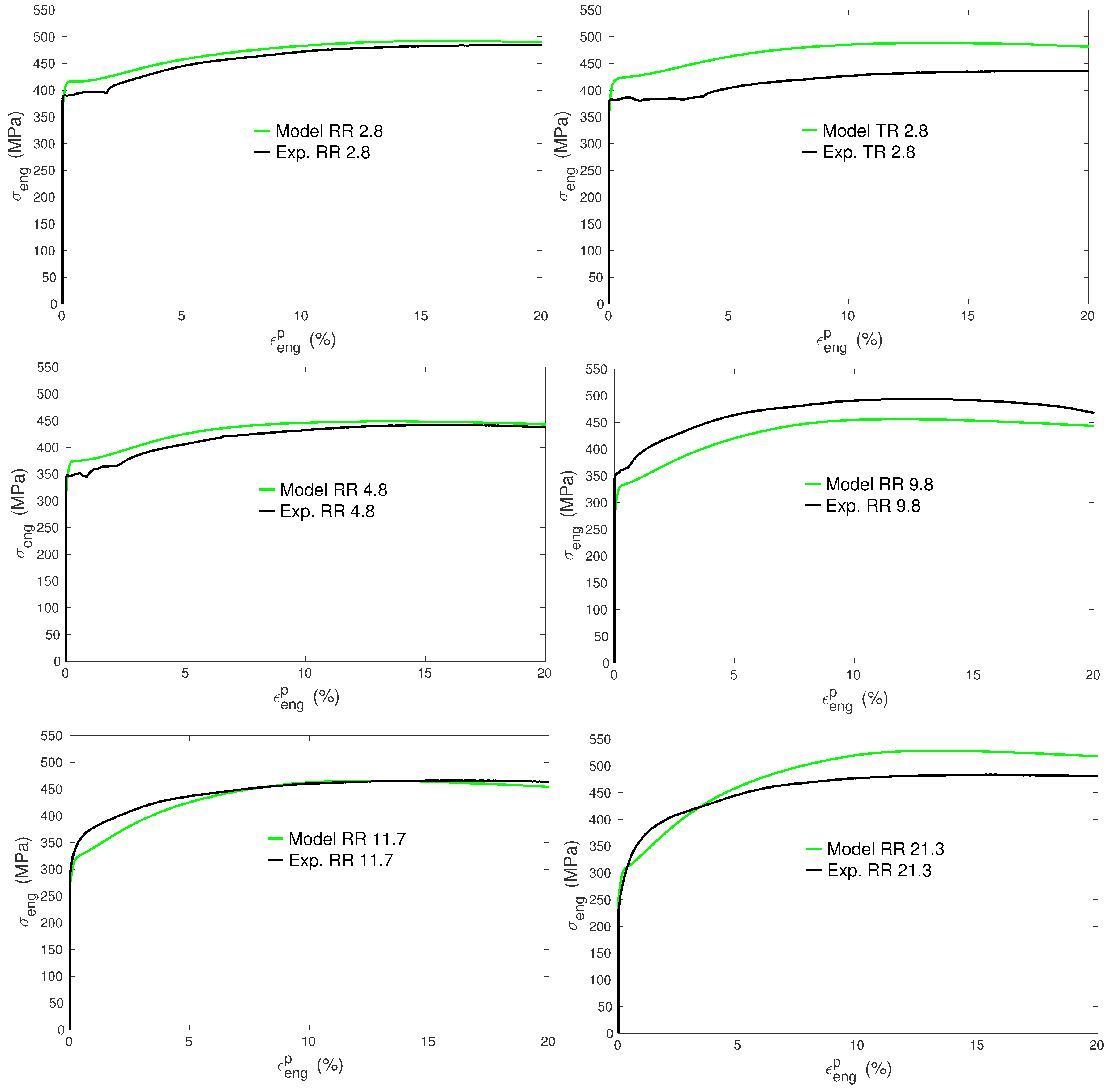
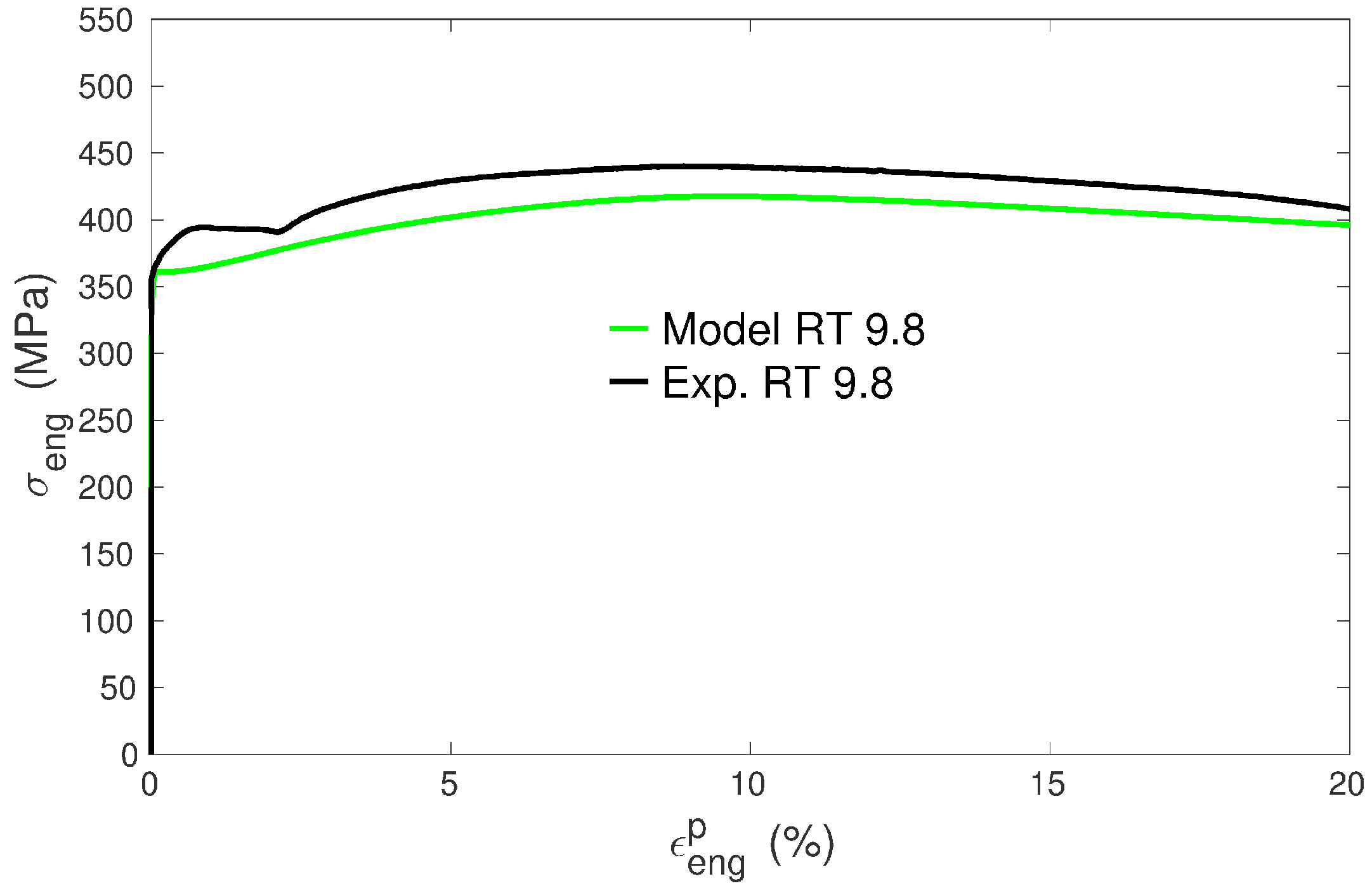
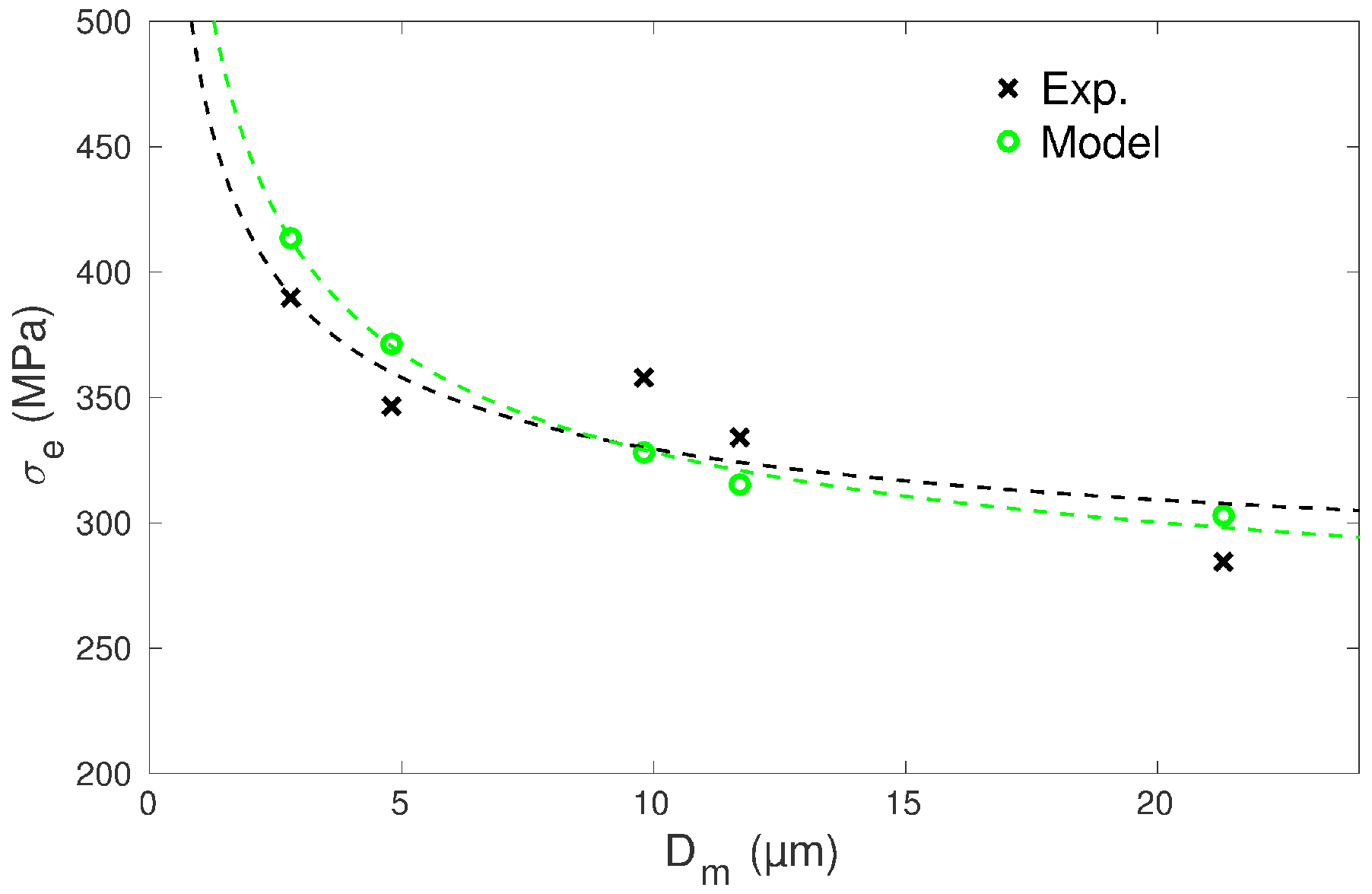
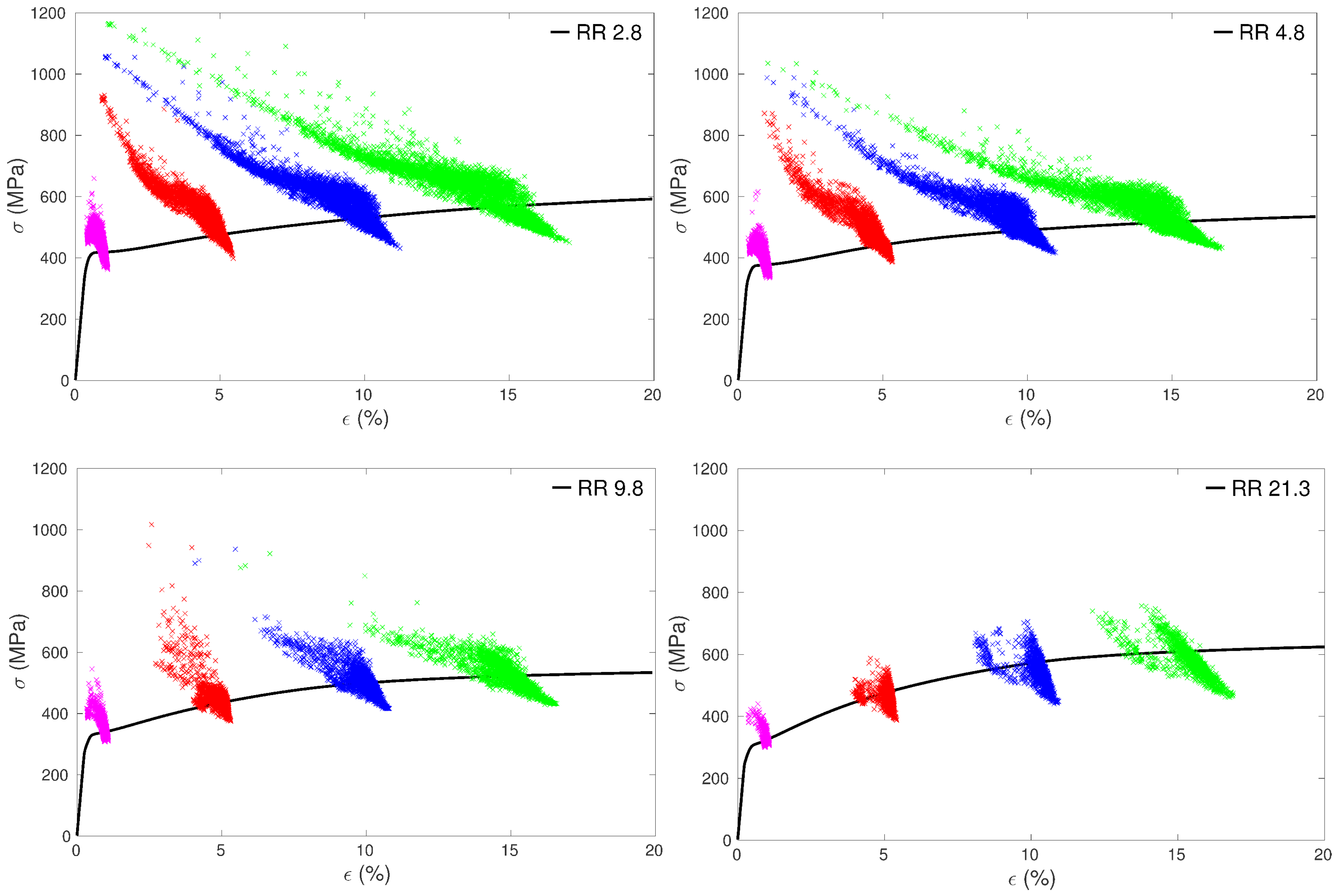
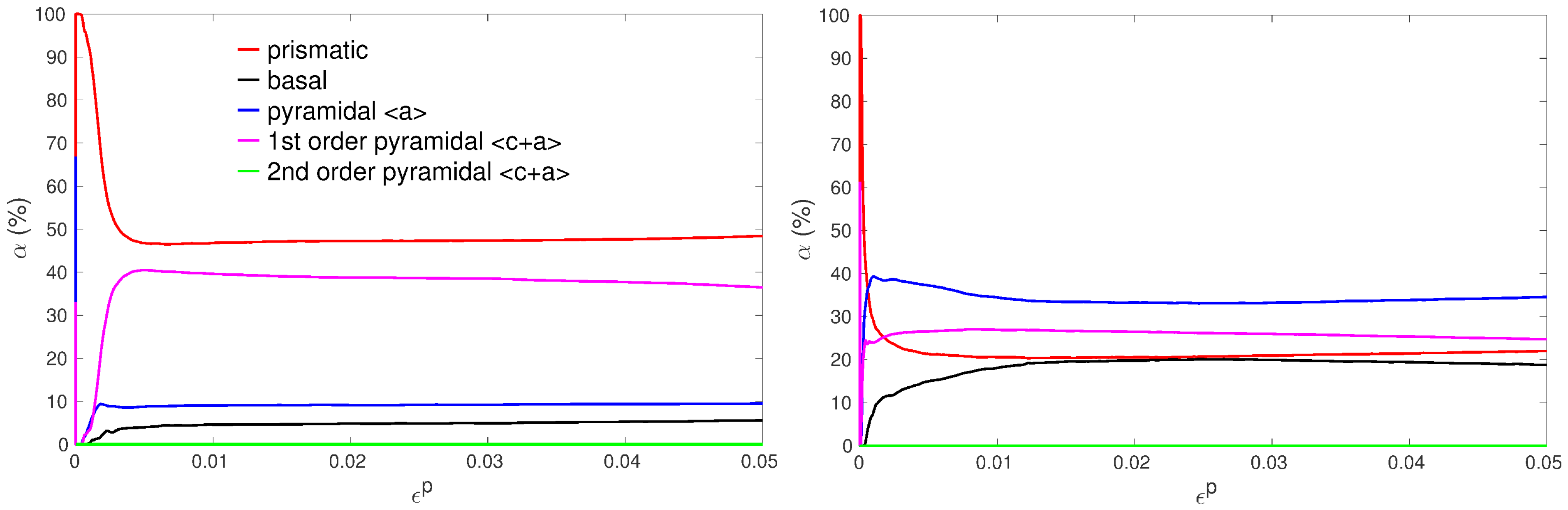
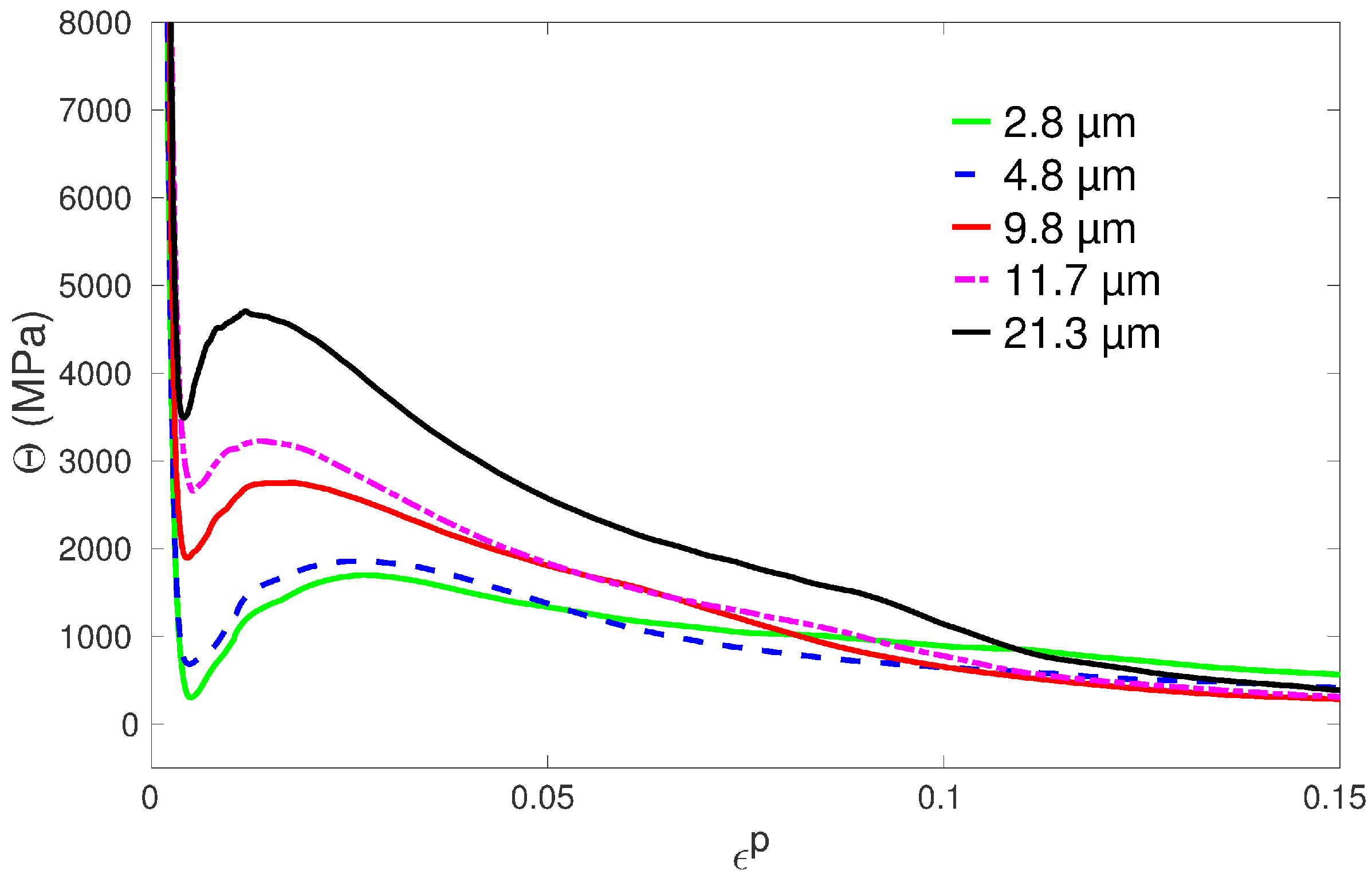
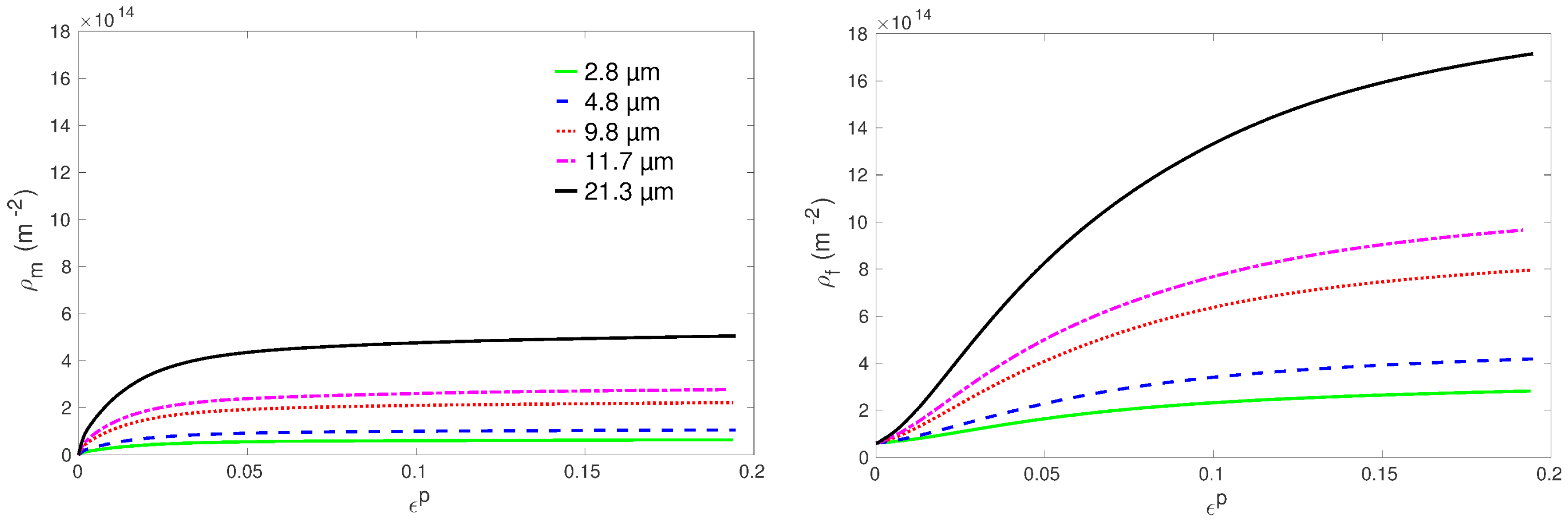
3. Results and Discussion
- the 0.2% yield stress: ,
- the maximal engineering stress: ,
- the corresponding engineering strain: ,
- the hardening amplitude: .
3.1. Yield Stress
3.2. Local Mechanical Fields
3.3. Slip Activity
3.4. Hardening Behavior
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Ti | titanium |
| cp | commercially pure |
| RD | rolling direction |
| TD | transverse direction |
| EBSD | electron backscatter diffraction |
| SEM | scanning electron microscopy |
| FEG | field emission gun |
| EVPSC | elasto-visco-plastic self-consistent |
| CRSS | critical resolved shear stress |
References
- Kocks, U.F.; Tomé, C.N.; Wenk, H.R. Texture and Anisotropy; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Berbenni, S.; Favier, V.; Berveiller, M. Impact of the grain size distribution on the behaviour of heterogeneous materials. Int. J. Plast. 2007, 23, 114–142. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Nicaise, N.; Berbenni, S.; Wagner, F.; Berveiller, M.; Lemoine, X. Coupled effects of grain size distributions and crystallographic textures on the plastic behaviour of IF steels. Int. J. Plast. 2011, 27, 232–249. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and aging of mild steel. Part III: discussion and results. Proc. Phys. Soc. Lond. 1951, 64, 747–753. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Hansen, N.; Ralph, B. The strain and grain size dependence of the flow stress of copper. Acta Metall. 1982, 30, 411–417. [Google Scholar] [CrossRef]
- Hansen, N. Polycrystalline strengthening. Metall. Trans. A 1985, 16A, 2167–2190. [Google Scholar] [CrossRef]
- Sinclair, C.W.; Poole, W.J.; Bréchet, Y. A model for the grain size dependent work hardening of copper. Scr. Mater. 2006, 55, 732–742. [Google Scholar] [CrossRef]
- Bunge, H.J.; Wagner, F.; Houtte, P.V. A new way to include the grain shape in texture simulations with the Taylor model. J. Phys. Lett. 1985, 46, L1109–L1113. [Google Scholar] [CrossRef]
- Raeisinia, B.; Sinclair, C.W.; Poole, W.J.; Tome, C.N. On the impact of grain size distribution on the plastic behaviour of polycrystalline metals. Model. Simul. Mater. Sci. Eng. 2008, 16, 025001. [Google Scholar] [CrossRef]
- Jain, A.; Duygulu, O.; Brown, D.W.; Tomé, C.N.; Agnew, S.R. Grain size effects on the tensile properties and deformation mechanisms of a magnesium alloy, AZ31B, sheet. Mater. Sci. Eng. A 2008, 486, 545–555. [Google Scholar] [CrossRef]
- Fromm, B.S.; Adams, B.L.; Ahmadi, S.; Knezevic, M. Grain size and orientation distributions: Application to yielding of α-titanium. Acta Mater. 2009, 57, 2339–2348. [Google Scholar] [CrossRef]
- Cordero, N.M.; Forest, S.; Busso, E.P.; Berbenni, S.; Cherkaoui, M. Grain size effects on plastic strain and dislocation density tensor fields in metal polycrystals. Comput. Mater. Sci. 2012, 52, 7–13. [Google Scholar] [CrossRef]
- Churchman, A.T. The slip modes of titanium and the effect of purity on their occurence during tensile deformation of single crystals. Proc. R. Soc. A 1954, 226, 216–226. [Google Scholar] [CrossRef]
- Levine, E.D. Deformation mechanisms in Titanium at low temperatures. Trans. Metall. Soc. AIME 1966, 236, 1558–1565. [Google Scholar]
- Roth, A.; Lebyodkin, M.A.; Lebedkina, T.A.; Lecomte, J.S.; Richeton, T.; Amouzou, K.E.K. Mechanisms of anisotropy of mechanical properties of α-titanium in tension conditions. Mater. Sci. Eng. A 2014, 596, 236–243. [Google Scholar] [CrossRef]
- Doquet, V.; Barkia, B. A micromechanical model of the viscoplastic behaviour of titanium accounting for its anisotropic and strain-rate dependent viscosity. Mech. Time-Depend. Mater. 2015, 19, 153–166. [Google Scholar] [CrossRef]
- Amouzou, K.E.K.; Richeton, T.; Roth, A.; Lebyodkin, M.A.; Lebedkina, T.A. Micromechanical modeling of hardening mechanisms in commercially pure α-titanium in tensile condition. Int. J. Plast. 2016, 80, 222–240. [Google Scholar] [CrossRef]
- Zhang, Z.; Jun, T.S.; Britton, T.B.; Dunne, F.P.E. Determination of Ti-6242 α and β slip properties using micro-pillar test and computational crystal plasticity. J. Mech. Phys. Solids 2016, 95, 393–410. [Google Scholar] [CrossRef]
- Zhang, Z.; Jun, T.S.; Britton, T.B.; Dunne, F.P.E. Intrinsic anisotropy of strain rate sensitivity in single crystal alpha titanium. Acta Mater. 2016, 118, 317–330. [Google Scholar] [CrossRef]
- Zhang, Z.; Dunne, F.P.E. Microstructure, Slip Accumulation and Load Shedding in Multiphase Alloys. Int. J. Fatigue 2018, 113, 324–334. [Google Scholar] [CrossRef]
- Mareau, C.; Berbenni, S. An affine formulation for the self-consistent modeling of elasto-viscoplastic heterogeneous materials based on the translated fields method. Int. J. Plast. 2015, 64, 134–150. [Google Scholar] [CrossRef]
- Lhadi, S.; Berbenni, S.; Gey, N.; Richeton, T.; Germain, L. Micromechanical modeling of the effect of elastic and plastic anisotropies on the mechanical behavior of β-Ti alloys. Int. J. Plast. 2018. [Google Scholar] [CrossRef]
- Beausir, B.; Fundenberger, J.J. ATEX-Software, Analysis Tools for Electron and X-ray Diffraction, Université de Lorraine. 2018. Available online: http://atex-software.eu/ (accessed on 17 May 2018).
- Wagner, F.; Bozzolo, N.; Landuyt, O.V.; Grosdidier, T. Evolution of recrystallisation texture and microstructure in low alloyed titanium sheets. Acta Mater. 2002, 50, 1245–1259. [Google Scholar] [CrossRef]
- Wang, Y.N.; Huang, J.C. Texture analysis in hexagonal materials. Mater. Chem. Phys. 2003, 81, 11–26. [Google Scholar] [CrossRef]
- Singh, A.K.; Schwarzer, R.A. Evolution of texture during thermomechanical processing of titanium and its alloys. Trans. Indian Inst. Met. 2008, 61, 371–387. [Google Scholar] [CrossRef]
- Becker, H.; Pantleon, W. Work-hardening stages and deformation mechanism maps during tensile deformation of commercially pure titanium. Comput. Mater. Sci. 2013, 76, 52–59. [Google Scholar] [CrossRef]
- Barkia, B.; Doquet, V.; Couzinié, J.P.; Guillot, I.; Héripré, E. In situ monitoring of the deformation mechanisms in titanium with different oxygen contents. Mater. Sci. Eng. A 2015, 636, 91–102. [Google Scholar] [CrossRef]
- Wagner, F.; Ouarem, A.; Richeton, T.; Toth, L.S. Improving Mechanical Properties of cp Titanium by Heat Treatment Optimization. Adv. Eng. Mater. 2018, 20, 1700237. [Google Scholar] [CrossRef]
- Masson, R.; Zaoui, A. Self-consistent estimates for the rate-dependentelastoplastic behaviour of polycrystalline materials. J. Mech. Phys. Solids 1999, 47, 1543–1568. [Google Scholar] [CrossRef]
- Conrad, H. Effect of interstitial solutes on the strength and ductility of titanium. Prog. Mater. Sci. 1981, 26, 123–403. [Google Scholar] [CrossRef]
- Naka, S. Etude des Mécanismes de Déformation Plastique à Basse Température de Monocristaux de Titane α. Ph.D. Thesis, Université de Paris Sud (Orsay), Orsay, France, 1983. [Google Scholar]
- Franciosi, P.; Berveiller, M.; Zaoui, A. Latent hardening in copper and aluminium single crystals. Acta Metall. 1980, 28, 273–283. [Google Scholar] [CrossRef]
- Messner, M.C.; Rhee, M.; Arsenlis, A.; Barton, N.R. A crystal plasticity model for slip in hexagonal close packed metals based on discrete dislocation simulations. Model. Simul. Mater. Sci. Eng. 2017, 25, 044001. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, Z.; Phuka, H.; Kenesei, P.; Park, J.S.; Lind, J.; Suter, R.M.; Bieler, T.R. Direct measurement of critical resolved shear stress of prismatic and basal slip in polycrystalline Ti using high energy X-ray diffraction microscopy. Acta Mater. 2017, 132, 598–610. [Google Scholar] [CrossRef]
- Pagan, D.C.; Shade, P.A.; Barton, N.R.; Park, J.S.; Kenesei, P.; Menasche, D.B.; Bernier, J.V. Modeling slip system strength evolution in Ti-7Al informed by in-situ grain stress measurements. Acta Mater. 2017, 128, 406–417. [Google Scholar] [CrossRef]
- Pagan, D.C.; Bernier, J.V.; Dale, D.D.; Ko, J.Y.P.; Turner, T.J.; Blank, B.; Shade, P.A. Measuring Ti-7Al slip system strengths at elevated temperature using high-energy X-ray diffraction. Scr. Mater. 2018, 142, 96–100. [Google Scholar] [CrossRef]
- Estrin, Y.; Kubin, L.P. Local strain hardening and nonuniformity of plastic deformation. Acta Metall. 1986, 34, 2455–2466. [Google Scholar] [CrossRef]
- Britton, T.B.; Wilkinson, A.J. Stress fields and geometrically necessarry dislocation density distributions near the head of a blocked slip band. Acta Mater. 2012, 60, 5773–5782. [Google Scholar] [CrossRef]
- Grabski, M.W.; Korski, R. Grain boundaries as sinks for dislocations. Philos. Mag. 1970, 22, 707–715. [Google Scholar] [CrossRef]
- Pond, R.C.; Smith, D.A. On the absorption of dislocations by grain boundaries. Philos. Mag. 1977, 36, 353–366. [Google Scholar] [CrossRef]
- Smith, D.A. Interaction of dislocations with grain boundaries. J. Phys. Colloq. 1982, 43, C6225–C6237. [Google Scholar] [CrossRef]
- Won, J.W.; Park, K.T.; Hong, S.G.; Lee, C.S. Anisotropic yielding behavior of rolling textured High purity titanium. Mater. Sci. Eng. A 2015, 637, 215–221. [Google Scholar] [CrossRef]
- Raabe, D.; Sachtleber, M.; Zhao, Z.; Roters, F.; Zaefferer, S. Micromechanical and macromechanical effects in grain scale polycrystal plasticity experimentation and simulation. Acta Mater. 2001, 49, 3433–3441. [Google Scholar] [CrossRef]
- Allain-Bonasso, N.; Wagner, F.; Berbenni, S.; Field, D.P. A study of plastic heterogeneity in IF steel by EBSD. Mater. Sci. Eng. A 2012, 548, 56–63. [Google Scholar] [CrossRef]
- Wagner, F.; Ouarem, A.; Gu, C.F.; Allain-Bonasso, N.; Toth, L.S. A new method to determine plastic deformation at the grain scale. Mater. Charact. 2014, 92, 106–117. [Google Scholar] [CrossRef]
- Grennerat, F.; Montagnat, M.; Castelnau, O.; Vacher, P.; Moulinec, H.; Suquet, P.; Duval, P. Experimental characterization of the intragranular strain field in columnar ice during transient creep. Acta Mater. 2012, 60, 3655–3666. [Google Scholar] [CrossRef]
- Ghaderi, A.; Barnett, M.R. Sensitivity of deformation twinning to grain size in titanium and magnesium. Acta Mater. 2011, 59, 7824–7839. [Google Scholar] [CrossRef]


| Specimen | Cold Rolling Reduction | Annealing Conditions | Number of Grains in the Data Set |
|---|---|---|---|
| RR 2.8 | 75% | 500 °C - 40 mn | 6254 |
| TR 2.8 | 75% | 500 °C - 40 mn | 7328 |
| RR 4.8 | 75% | 650 °C - 1 h | 8793 |
| RR 9.8 | 75% | 730 °C - 2 h | 3262 |
| RT 9.8 | 75% | 730 °C - 2 h | 3262 |
| RR 11.7 | 75% | 740 °C - 2 h | 4075 |
| RR 21.3 | 30% | 840 °C - 4 h | 1273 |
| P | B | ||||
|---|---|---|---|---|---|
| b (Å) | 2.95 | 2.95 | 2.95 | 5.53 | 5.53 |
| (GPa) | 35.0 | 37.1 | 46.5 | 47.7 | 49.2 |
| (MPa) | 50 | 90 | 120 | 75 | 150 |
| () | 80 | 15 | 15 | 15 | 15 |
| n | 65 | 32 | 32 | 32 | 32 |
| (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (MPa.m0.5) | ||
|---|---|---|---|---|---|---|---|
| 1.587 | 160 | 181 | 46.5 | 90 | 66 | 0.1 | |
| (ms−1) | (m−2) | (m−2) | |||||
| 75 | 80 | 0.7 | 0.1 | 10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richeton, T.; Wagner, F.; Chen, C.; Toth, L.S. Combined Effects of Texture and Grain Size Distribution on the Tensile Behavior of α-Titanium. Materials 2018, 11, 1088. https://doi.org/10.3390/ma11071088
Richeton T, Wagner F, Chen C, Toth LS. Combined Effects of Texture and Grain Size Distribution on the Tensile Behavior of α-Titanium. Materials. 2018; 11(7):1088. https://doi.org/10.3390/ma11071088
Chicago/Turabian StyleRicheton, Thiebaud, Francis Wagner, Cai Chen, and Laszlo S. Toth. 2018. "Combined Effects of Texture and Grain Size Distribution on the Tensile Behavior of α-Titanium" Materials 11, no. 7: 1088. https://doi.org/10.3390/ma11071088
APA StyleRicheton, T., Wagner, F., Chen, C., & Toth, L. S. (2018). Combined Effects of Texture and Grain Size Distribution on the Tensile Behavior of α-Titanium. Materials, 11(7), 1088. https://doi.org/10.3390/ma11071088







