Cononsolvency Transition of Polymer Brushes: A Combined Experimental and Theoretical Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Preperation of Polymer Brushes
2.2. VIS-Spectroscopic Ellipsometry Measurement
3. Results and Discussion
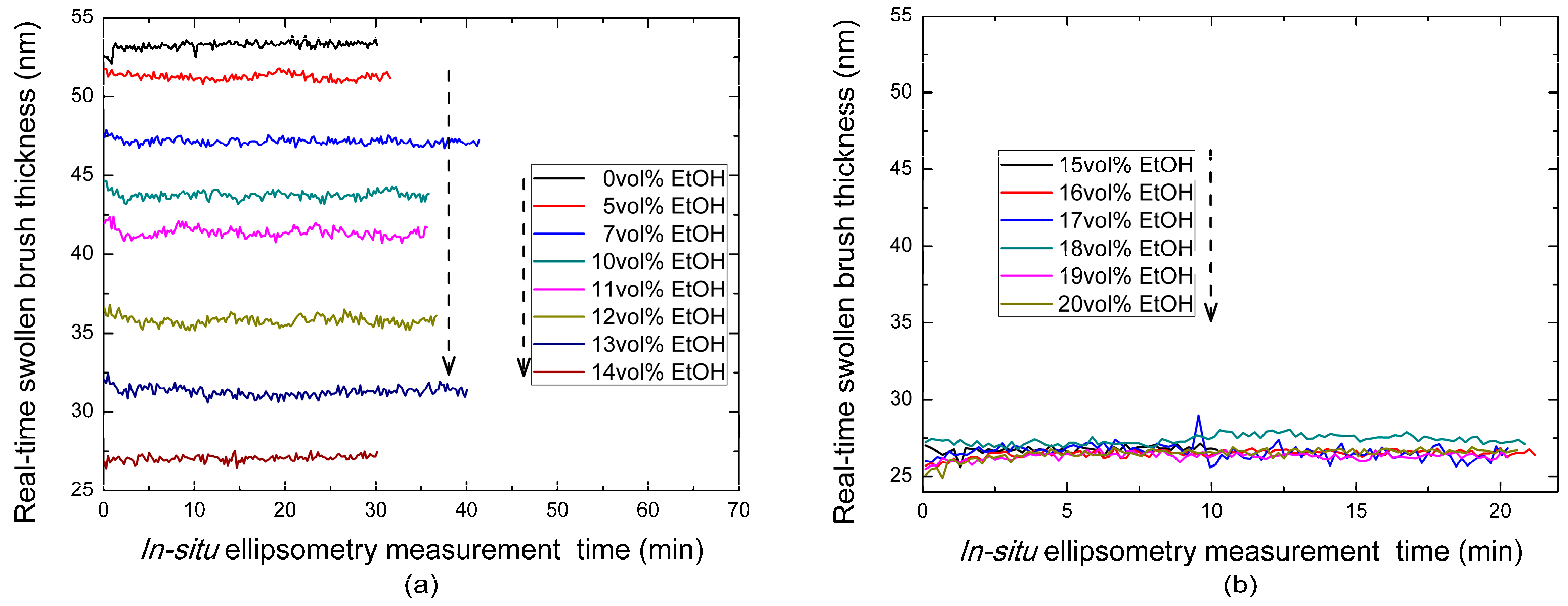
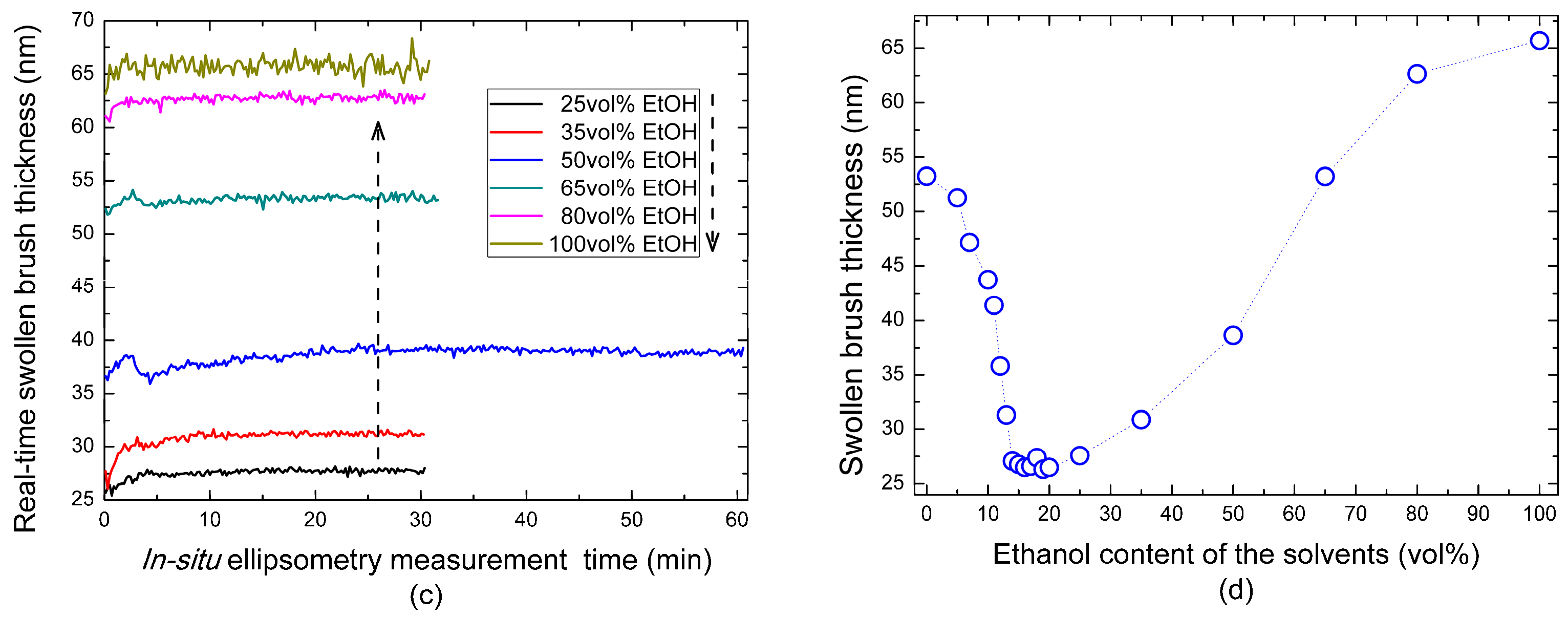
3.1. Ellipsometry Analysis of the Cononsolvency Transition in PNiPAAm Brushes
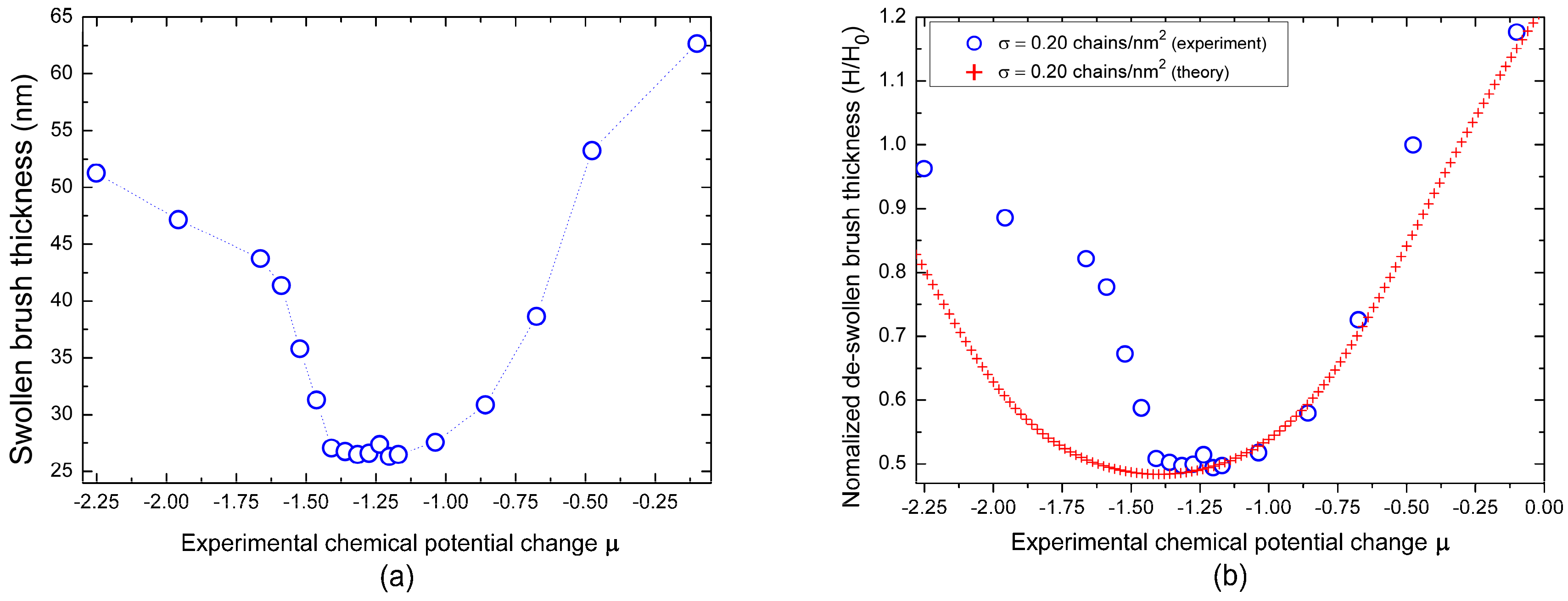
3.2. Application of the Adsorption-Attraction Model for Cononsolvency Transition in PNiPAAm Brushes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Raw Data of Swollen Thickness of PNiPAAm Brushes
| Ethanol Concentration | 0 vol % | 5 vol % | 7 vol % | 10 vol % | 11 vol % | 12 vol % | 13 vol % |
| Brush Thickness (nm) | 53.2 | 51.3 | 47.2 | 43.7 | 41.4 | 35.8 | 31.3 |
| Ethanol Concentration | 14 vol % | 15 vol % | 16 vol % | 17 vol % | 18 vol % | 19 vol % | 20 vol % |
| Brush Thickness (nm) | 27.1 | 26.8 | 26.5 | 26.6 | 27.4 | 26.3 | 26.5 |
| Ethanol Concentration | 25 vol % | 35 vol % | 50 vol % | 65 vol % | 80 vol % | 100 vol % |
| Brush Thickness (nm) | 27.6 | 30.9 | 38.6 | 53.2 | 62.6 | 65.7 |
Appendix A.2. The Role of Volume of Solvent Molecules in the Swelling of PNiPAAm Brushes
Appendix A.3. Definition of Chemical Potential Change
References and Note
- Zhang, Q.; Hoogenboom, R. Polymers with upper critical solution temperature behavior in alcohol/water solvent mixtures. Prog. Polym. Sci. 2015, 48, 122–142. [Google Scholar] [CrossRef]
- Scherzinger, C.; Schwarz, A.; Bardowb, A.; Leonhardb, K.; Richtering, W. Cononsolvency of poly-N-isopropyl acrylamide (PNIPAM): Microgels versus linear chains and macrogels. Curr. Opin. Colloid Interface Sci. 2014, 19, 84–94. [Google Scholar] [CrossRef]
- Winnik, F.M.; Ringsdorf, H.; Venzmer, J. Methanol-water as a co-nonsolvent system for poly(N-isopropylacrylamide). Macromolecules 1990, 23, 2415–2416. [Google Scholar] [CrossRef]
- Amiya, T.; Hirokawa, Y.; Hirose, Y.; Li, Y.; Tanaka, T. Reentrant phase transition of N-isopropylacrylamide gels in mixed solvents. J. Chem. Phys. 1987, 86, 2375. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; ISBN 978-0-8014-0134-3. [Google Scholar]
- Gennes, P.-G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979; ISBN 978-0-8014-1203-5. [Google Scholar]
- Zhulina, E.B.; Borisov, O.V.; Pryamitsyn, V.A.; Birshtein, T.M. Coil-globule type transitions in polymers. 1. Collapse of layers of grafted polymer chains. Macromolecules 1991, 24, 140–149. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Birshtein, T.M.; Borisov, O.V. Theory of ionizable polymer brushes. Macromolecules 1995, 28, 1491–1499. [Google Scholar] [CrossRef]
- Pryamitsyn, V.A.; Leermakers, F.A.M.; Fleer, G.J.; Zhulina, E.B. Theory of the collapse of the polyelectrolyte brush. Macromolecules 1996, 29, 8260–8270. [Google Scholar] [CrossRef]
- Birshtein, T.M.; Amoskov, V.M.; Mercurieva, A.A.; Pryamitsyn, V.A. Phase transitions in polymer brushes. Macromol. Symp. 1997, 113, 151–161. [Google Scholar] [CrossRef]
- Saphiannikova, M.G.; Pryamitsyn, V.A.; Cosgrove, T. Self-consistent brownian dynamics simulation of polymer brushes under shear. Macromolecules 1998, 31, 6662–6668. [Google Scholar] [CrossRef]
- John, J.; Keating, I.V.; Joseph, I.; Georges, B. Polymer brushes for membrane separations: A review. ACS Appl. Mater. Interfaces 2016, 8, 28383–28399. [Google Scholar]
- Chen, W.; Cordero, R.; Tran, H.; Ober, C.K. 50th anniversary perspective: Polymer brushes: Novel surfaces for future materials. Macromolecules 2017, 50, 4089–4113. [Google Scholar] [CrossRef]
- Nagase, K.; Okano, T.; Kanazawa, H. Poly(N-isopropylacrylamide) based thermoresponsive polymer brushes for bioseparation, cellular tissue fabrication, and nano actuators. Nano Struct. Nano Objects 2018, 16, 9–23. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, G. Reentrant behavior of poly(N-isopropylacrylamide) brushes in water−methanol mixtures investigated with a quartz crystal microbalance. Langmuir 2005, 21, 2086–2090. [Google Scholar] [CrossRef] [PubMed]
- Edmondson, S.; Nguyen, N.T.; Lewis, A.L.; Armes, S.P. Co-nonsolvency effects for surface-initiated poly(2-(methacryloyloxy)ethyl phosphorylcholine) brushes in alcohol/water mixtures. Langmuir 2010, 26, 7216–7226. [Google Scholar] [CrossRef] [PubMed]
- Sui, X.; Chen, Q.; Hempenius, M.A.; Vancso, G.J. Probing the collapse dynamics of poly(N-isopropylacrylamide) brushes by AFM: Effects of co-nonsolvency and grafting densities. Small 2011, 7, 1440–1447. [Google Scholar] [CrossRef] [PubMed]
- Espinosa-Marzal, R.M.; Nalam, P.C.; Bolisetty, S.; Spencer, N.D. Impact of solvation on equilibrium conformation of polymer brushes in solvent mixtures. Soft Matter 2013, 9, 4045–4057. [Google Scholar] [CrossRef]
- Yu, Y.; de la Cruz, R.A.L.; Kieviet, B.D.; Gojzewski, H.; Pons, A.C.; Vancso, J.; de Beer, S. Pick up, move and release of nanoparticles utilizing co-non-solvency of PNIPAM brushes. Nanoscale 2017, 9, 1670–1675. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Kooij, E.S.; Sui, X.; Padberg, C.J.; Hempenius, M.A.; Schöna, P.M.; Vancso, G.J. Collapse from the top: Brushes of poly(N-isopropylacrylamide) in co-nonsolvent mixtures. Soft Matter 2014, 10, 3134–3142. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Cirelli, M.; Kieviet, B.D.; Kooij, E.S.; Vancso, G.J.; de Beer, S. Tunable friction by employment of co-non-solvency of PNIPAM brushes. Polymer 2016, 102, 372–378. [Google Scholar] [CrossRef]
- Yu, Y.; Kieviet, B.D.; Kutnyanszky, E.; Vancso, G.J.; de Beer, S. Cosolvency-induced switching of the adhesion between poly(methyl methacrylate) brushes. ACS Macro Lett. 2015, 4, 75–79. [Google Scholar] [CrossRef]
- Nalam, P.C.; Daikhin, L.; Espinosa-Marzal, R.M.; Clasohm, J.; Urbakh, M.; Spencer, N.D. Two-fluid model for the interpretation of quartz crystal microbalance response: Tuning properties of polymer brushes with solvent mixtures. J. Phys. Chem. C 2013, 117, 4533–4543. [Google Scholar] [CrossRef]
- Wang, H.; Pemberton, J.E. Effect of solvent quality on laminar slip flow penetration of poly(N-isopropylacrylamide) films with an exploration of the mass transport mechanism. Langmuir 2017, 33, 7468–7478. [Google Scholar] [CrossRef] [PubMed]
- Mukherji, D.; Kremer, K. Coil–globule–coil transition of PNiPAm in aqueous methanol: Coupling all-atom simulations to semi-grand canonical coarse-grained reservoir. Macromolecules 2013, 46, 9158–9163. [Google Scholar] [CrossRef]
- Tanaka, F.; Koga, T. Temperature-responsive polymers in mixed solvents: Competitive hydrogen bonds cause cononsolvency. Phys. Rev. Lett. 2008, 101, 028302. [Google Scholar] [CrossRef] [PubMed]
- Mukherji, D.; Marques, C.M.; Kremer, K. Polymer collapse in miscible good solvents is a generic phenomenon driven by preferential adsorption. Nat. Commun. 2014, 5, 4882. [Google Scholar] [CrossRef] [PubMed]
- Jens-Uwe, S. Adsorption–attraction model for co-nonsolvency in polymer brushes. Macromolecules 2017, 50, 2219–2228. [Google Scholar]
- Jens-Uwe, S. Gluonic and regulatory solvents: A paradigm for tunable phase segregation in polymers. Macromolecules 2018, 51, 3066–3074. [Google Scholar]
- Chen, X.; Feng, W.; Han, X.; Liu, H. Possible way to study cononsolvency in confinement: A lattice density functional theory approach. Langmuir 2017, 33, 11446–11456. [Google Scholar] [CrossRef] [PubMed]
- Rauch, S.; Eichhorn, K.; Oertel, U.; Stamm, M.; Kuckling, D.; Uhlmann, P. Temperature responsive polymer brushes with clicked rhodamine B: Synthesis, characterization and swelling dynamics studied by spectroscopic ellipsometry. Soft Matter 2012, 8, 10260–10270. [Google Scholar] [CrossRef]
- Zdyrko, B.; Iyer, K.S.; Luzinov, I. Macromolecular anchoring layers for polymer grafting: Comparative study. Polymer 2006, 47, 272–279. [Google Scholar] [CrossRef]
- Werner, A.C.; Eichhorn, K.J.; Grundke, K.; Simon, F.; Grahlert, W.; Jacobasch, H.J. Insights on structural variations of protein adsorption layers on hydrophobic fluorohydrocarbon polymers gained by spectroscopic ellipsometry (part I). Colloids Surfaces A Physicochem. Eng. Asp. 1999, 156, 3–17. [Google Scholar] [CrossRef]
- Brittain, W.J.; Minko, S. A structural definition of polymer brushes. J. Polym. Sci. Part A Polym. Chem. 2007, 45, 3505–3512. [Google Scholar] [CrossRef]
- Kubota, K.; Fujishige, S.; Ando, I. Solution properties of poly(N-isopropylacrylamide) in water. Polym. J. 1990, 22, 15–20. [Google Scholar] [CrossRef]
- Xue, C.; Yonet-Tanyeri, N.; Brouette, N.; Sferrazza, M.; Braun, P.V.; Leckband, D.E. Protein adsorption on poly(N-isopropylacrylamide) brushes: Dependence on grafting density and chain collapse. Langmuir 2011, 27, 8810–8818. [Google Scholar] [CrossRef] [PubMed]
- Jentzsch, C.; Jens-Uwe, S. Polymer brushes in explicit poor solvents studied using a new variant of the bond fluctuation model. J. Chem. Phys. 2014, 141, 104908. [Google Scholar] [CrossRef] [PubMed]
- Dalgicdir, C.; Rodríguez-Ropero, F.; van der Vegt, N.F.A. Computational calorimetry of PNIPAM cononsolvency in water/methanol mixtures. J. Phys. Chem. B 2017, 121, 7741–7748. [Google Scholar] [CrossRef] [PubMed]
- Bentz, K.C.; Savin, D.A. Chain dispersity effects on brush properties of surface-grafted polycaprolactone-modified silica nanoparticles: Unique scaling behavior in the concentrated polymer brush regime. Macromolecules 2017, 50, 5565–5573. [Google Scholar] [CrossRef]
- Qi, S.; Klushin, L.I.; Skvortsov, A.M.; Schmid, F. Polydisperse polymer brushes: Internal structure, critical behavior, and interaction with flow. Macromolecules 2016, 49, 9665–9683. [Google Scholar] [CrossRef]
- De Vos, W.M.; Leermakers, F.A.M. Modeling the structure of a polydisperse polymer brush. Polymer 2009, 50, 305–316. [Google Scholar] [CrossRef]
- The volume of a polymer’s repeat unit can be estimated by using the formula of v = M0/(ρNA), where M0 is the molecular weight of repeat unit of the polymer, ρ is the polymer’s melt density and NA is the Avogadro’s number. Then the size of a repeat unit can be estimated as d = 2(3v/(4π))1/3.
- Job, G.; Rüffler, R. Physical Chemistry from a Different Angle; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3319156651. [Google Scholar]
- DDB Software Package, DDBST GmbH. Available online: http://www.ddbst.de/software-package.html (accessed on 10 June 2018).


| Polymer | Mn (g/mol) | h (nm) | σ (chains/nm2) | σ** (chains/nm2) | S (nm) | S/(2RG) | S/(2RP) |
|---|---|---|---|---|---|---|---|
| PGMA | 10–20,000 | 2.5 | - | - | - | - | - |
| PNiPAAm | 50,200 | 14.9 | 0.20 | 0.084 | 2.3 | 0.1 | 0.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yong, H.; Rauch, S.; Eichhorn, K.-J.; Uhlmann, P.; Fery, A.; Sommer, J.-U. Cononsolvency Transition of Polymer Brushes: A Combined Experimental and Theoretical Study. Materials 2018, 11, 991. https://doi.org/10.3390/ma11060991
Yong H, Rauch S, Eichhorn K-J, Uhlmann P, Fery A, Sommer J-U. Cononsolvency Transition of Polymer Brushes: A Combined Experimental and Theoretical Study. Materials. 2018; 11(6):991. https://doi.org/10.3390/ma11060991
Chicago/Turabian StyleYong, Huaisong, Sebastian Rauch, Klaus-Jochen Eichhorn, Petra Uhlmann, Andreas Fery, and Jens-Uwe Sommer. 2018. "Cononsolvency Transition of Polymer Brushes: A Combined Experimental and Theoretical Study" Materials 11, no. 6: 991. https://doi.org/10.3390/ma11060991
APA StyleYong, H., Rauch, S., Eichhorn, K.-J., Uhlmann, P., Fery, A., & Sommer, J.-U. (2018). Cononsolvency Transition of Polymer Brushes: A Combined Experimental and Theoretical Study. Materials, 11(6), 991. https://doi.org/10.3390/ma11060991







