Thermoresponsive Core-Shell Nanoparticles: Does Core Size Matter?
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results and Discussion
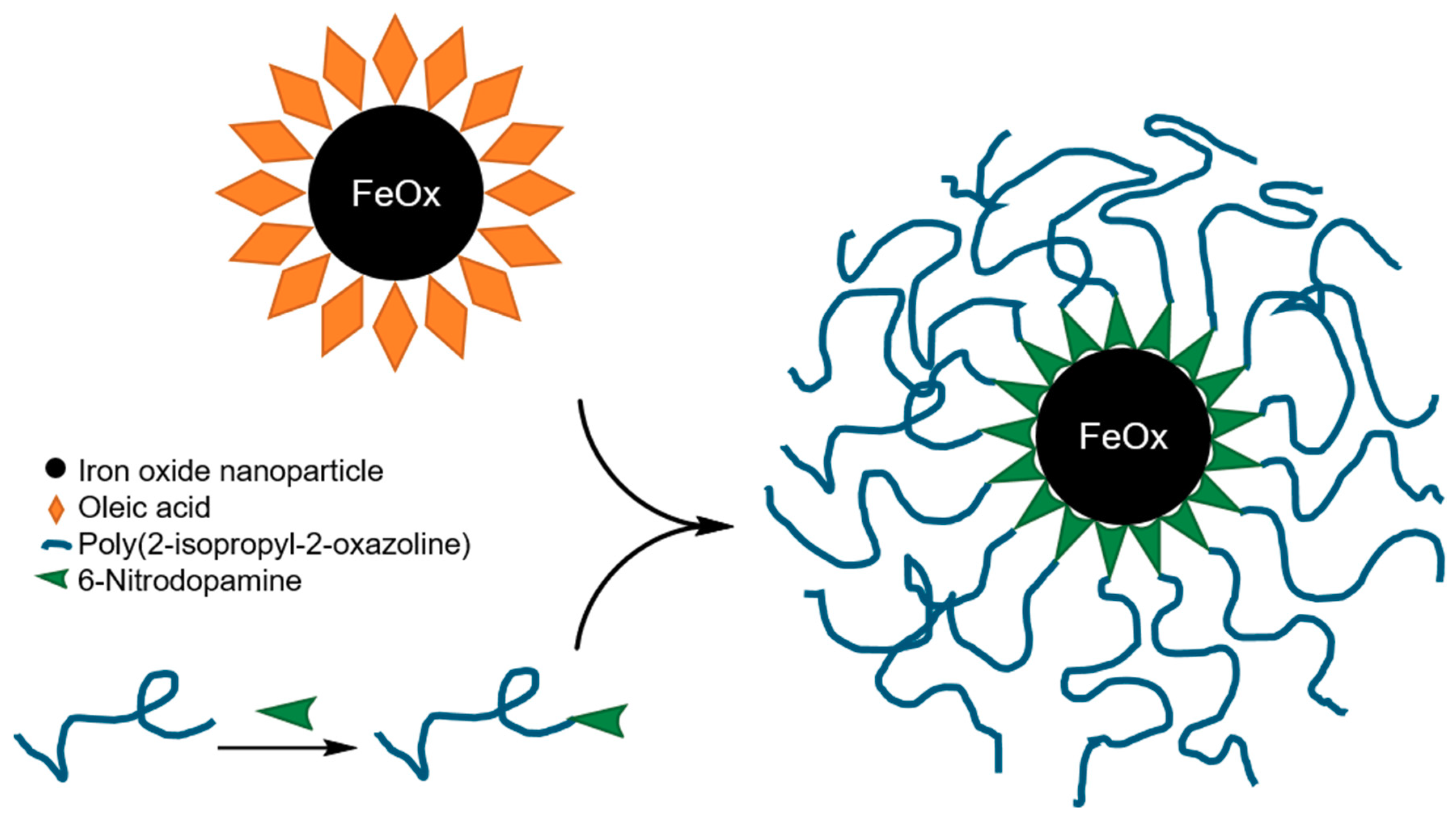
3.1. Preparation and Characterization of the Core-Shell Nanoparticles
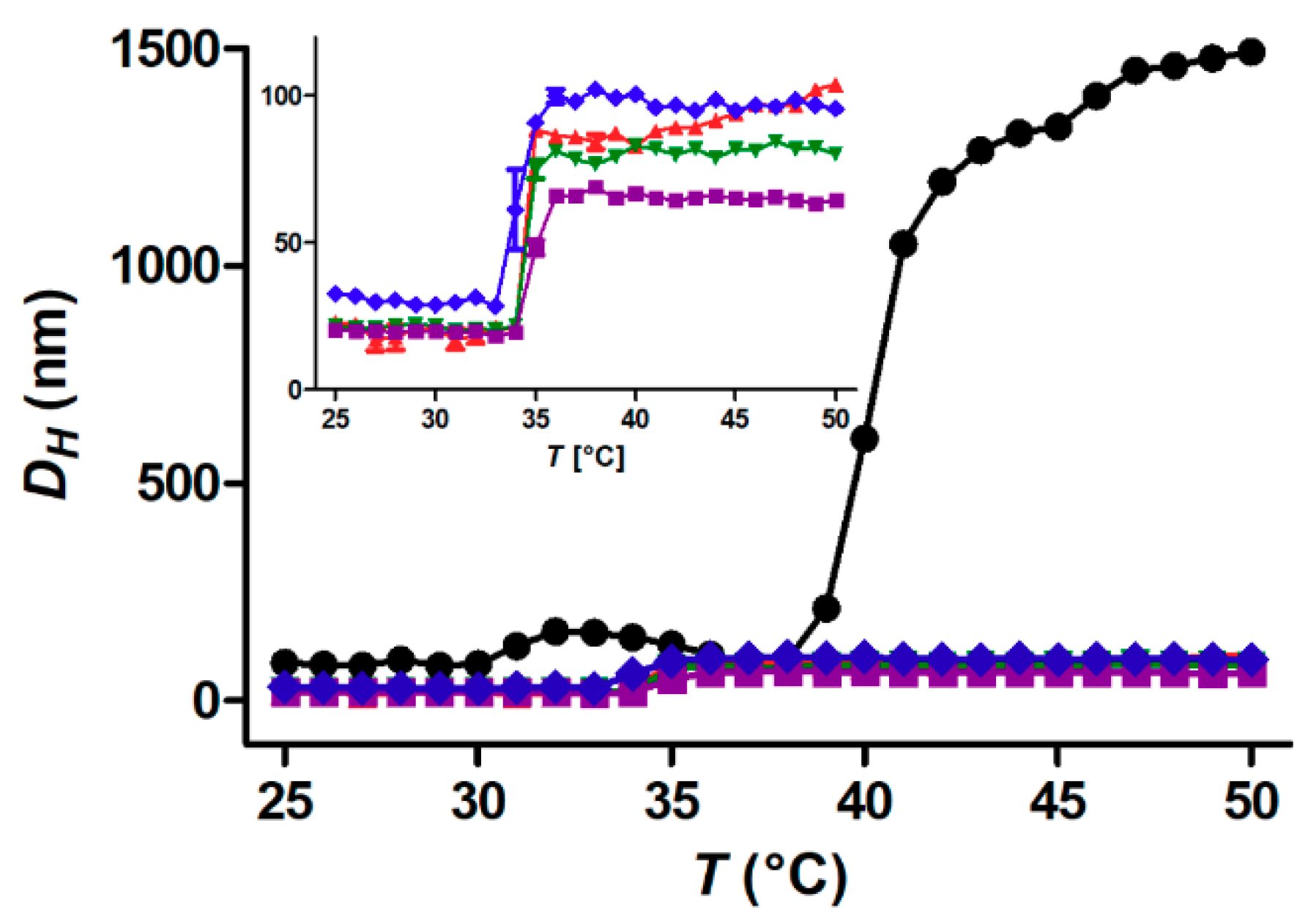
3.2. Temperature Dependence of Aggregation: Free Polymer versus Core-Shell Nanoparticles
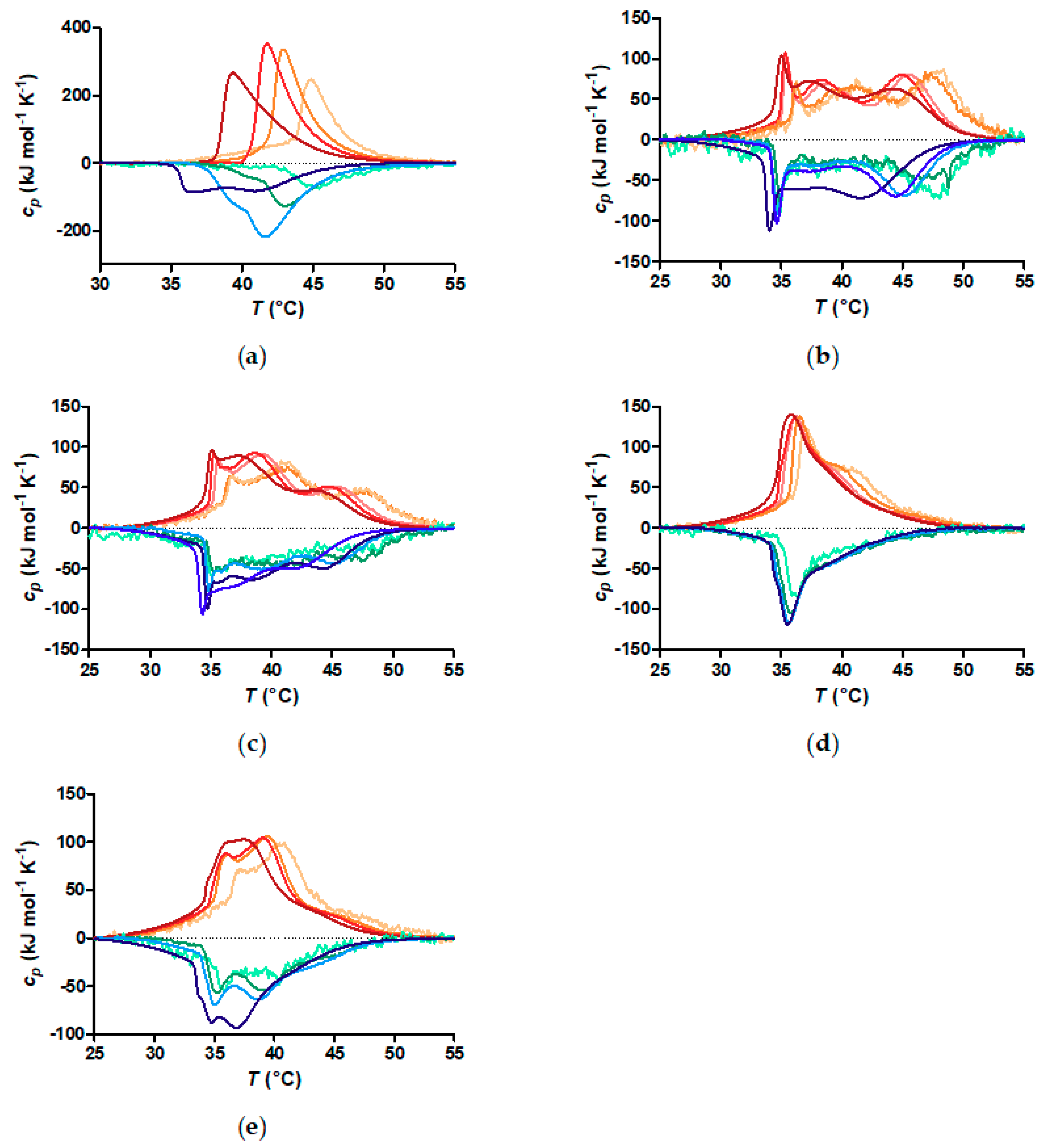
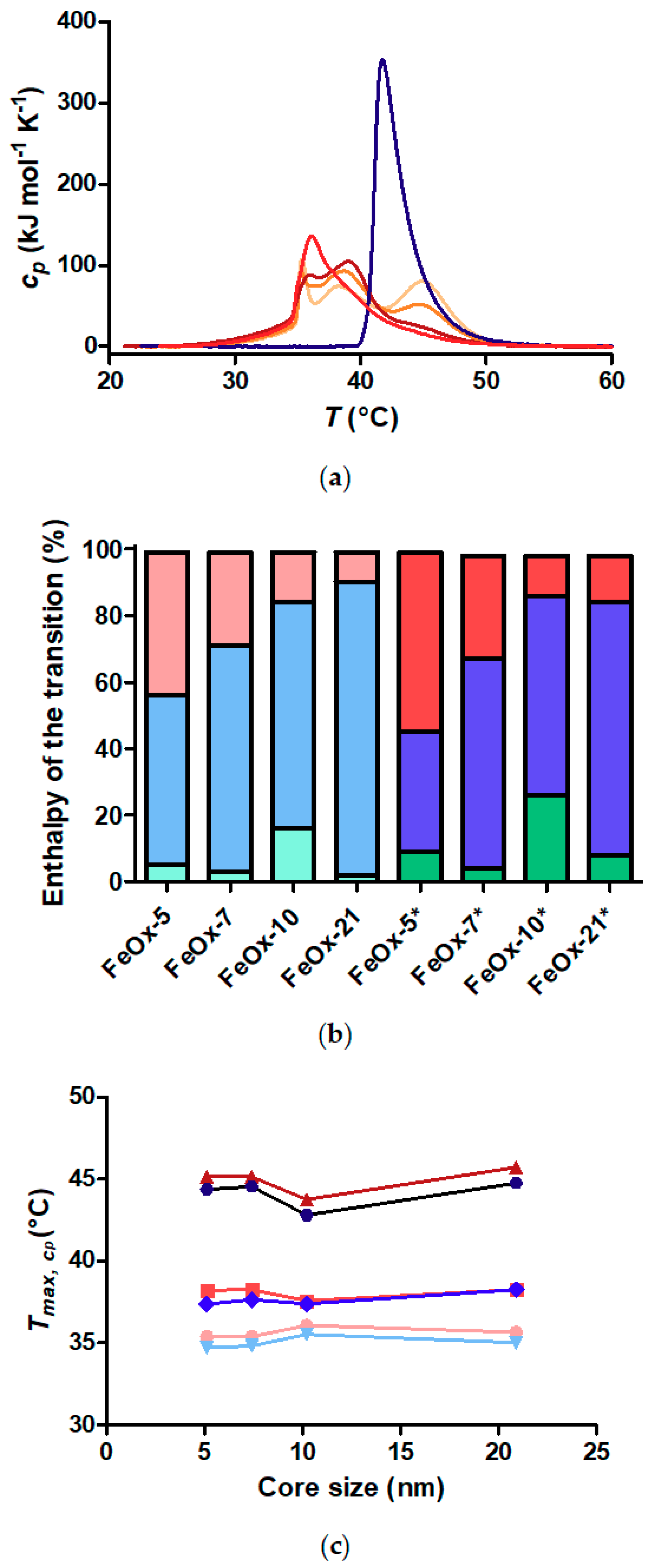
3.3. Critical Solution Temperature and Transition Enthalpies of Polymer Grafted to Nanoparticles
3.4. Is the Aggregation of the Thermoresponsive Core-Shell Nanoparticles Fully Reversible?
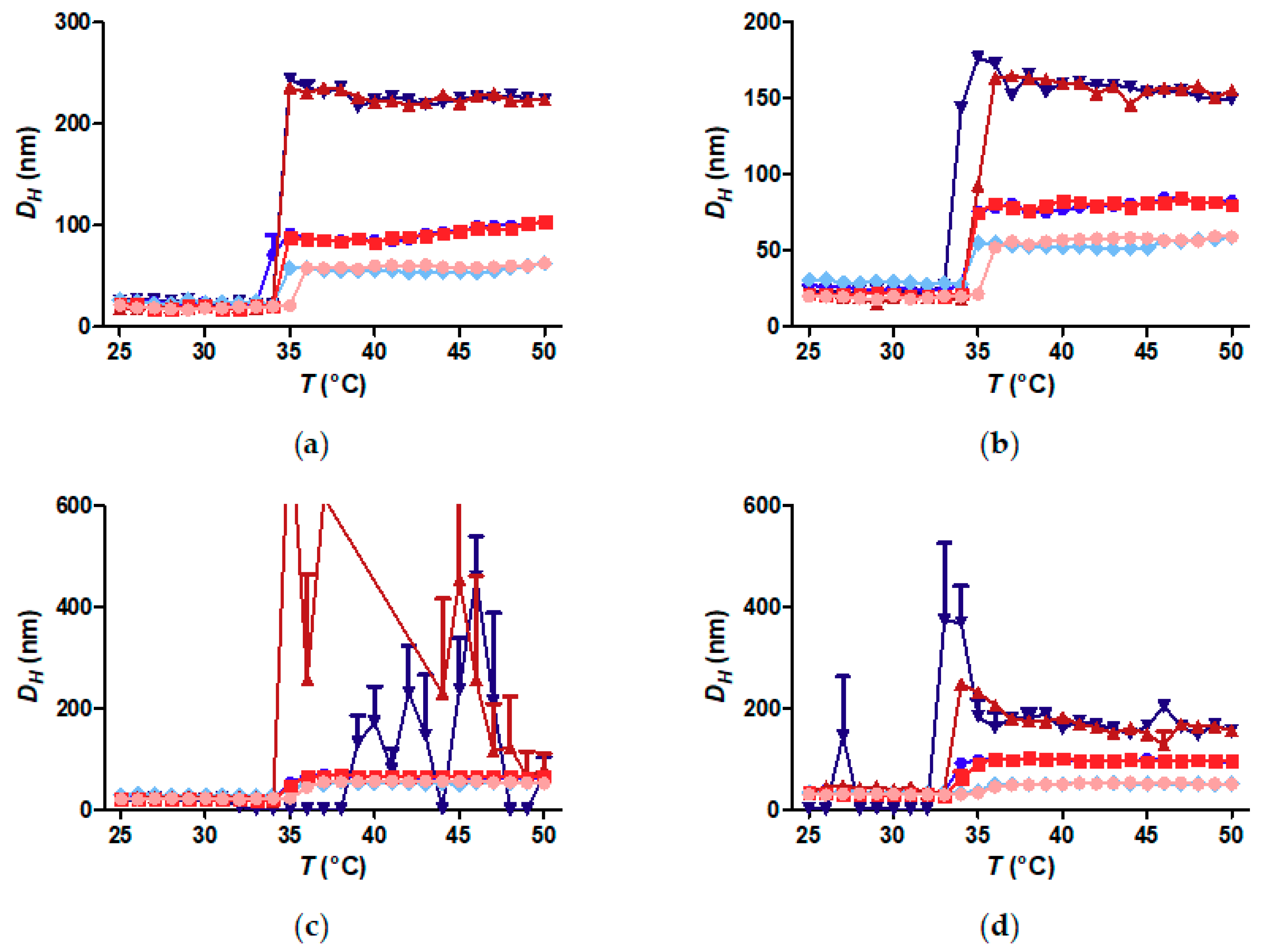
3.5. Does the Curvature Influence on Internal Brush Structure Affect the CST of the Polymer Shell?
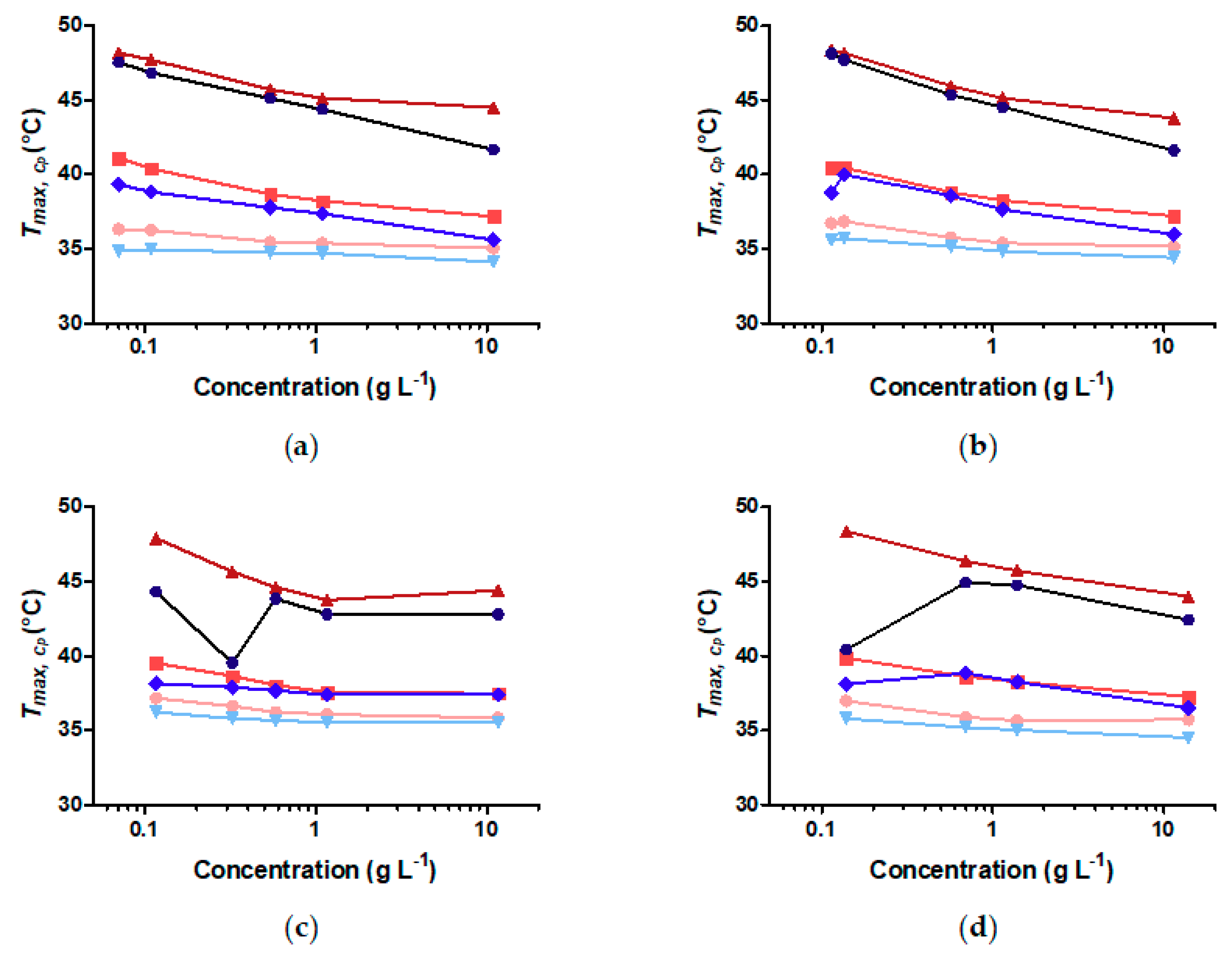
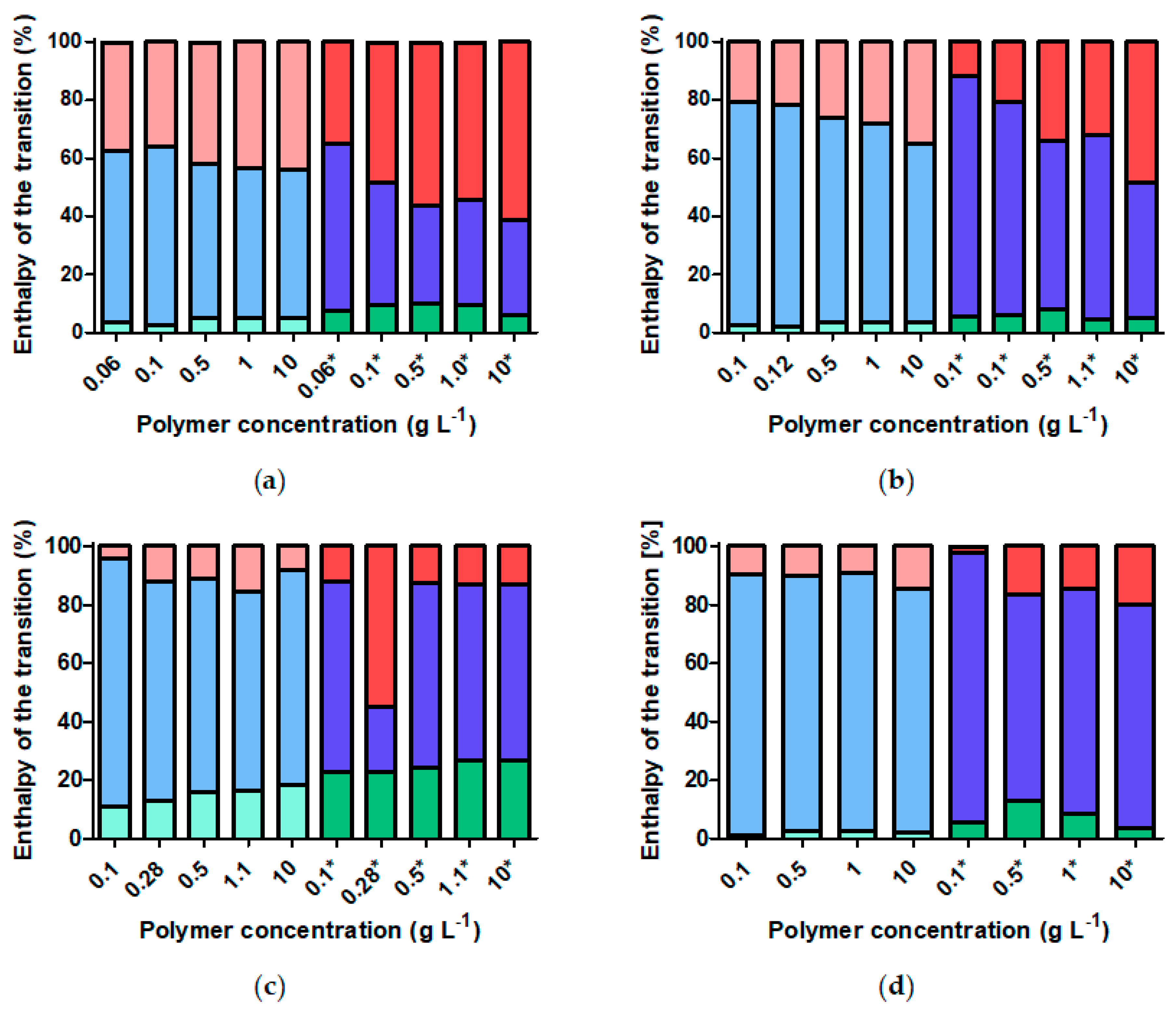
3.6. Does Nanoparticle Concentration Influence Brush CST and Thermally Induced Aggregation?
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Veiseh, O.; Gunn, J.W.; Zhang, M. Design and fabrication of magnetic nanoparticles for targeted drug delivery and imaging. Adv. Drug Deliv. Rev. 2010, 62, 284–304. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Ding, B.; Zhang, S.; Qi, X.; Wang, K.; Tian, J.; Yan, Y.; Ge, Y.; Wu, L. Near-infrared light-responsive nanoparticles with thermosensitive yolk-shell structure for multimodal imaging and chemo-photothermal therapy of tumor. Nanomed. Nanotechnol. Biol. Med. 2017, 13, 1607–1616. [Google Scholar] [CrossRef] [PubMed]
- Kakwere, H.; Leal, M.P.; Materia, M.E.; Curcio, A.; Guardia, P.; Niculaes, D.; Marotta, R.; Falqui, A.; Pellegrino, T. Functionalization of strongly interacting magnetic nanocubes with (thermo)responsive coating and their application in hyperthermia and heat-triggered drug delivery. ACS Appl. Mater. Interfaces 2015, 7, 10132–10145. [Google Scholar] [CrossRef] [PubMed]
- Hannecart, A.; Stanicki, D.; Vander Elst, L.; Muller, R.N.; Lecommandoux, S.; Thévenot, J.; Bonduelle, C.; Trotier, A.; Massot, P.; Miraux, S.; et al. Nano-thermometers with thermo-sensitive polymer grafted USPIOs behaving as positive contrast agents in low-field MRI. Nanoscale 2015, 7, 3754–3767. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Wang, D.; Zhou, F.; Liu, W. Electrostatic self-assembly of Au nanoparticles onto thermosensitive magnetic core-shell microgels for thermally tunable and magnetically recyclable catalysis. Small 2015, 11, 2807–2816. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Li, Y.; Li, F.; Zhang, M.; Zhang, Z.; Lin, H. Rational design of a thermalresponsive-polymer-switchable FRET system for enhancing the temperature sensitivity of upconversion nanophosphors. Nanoscale 2014, 6, 10179–10186. [Google Scholar] [CrossRef] [PubMed]
- Lü, T.; Zhang, S.; Qi, D.; Zhang, D.; Zhao, H. Thermosensitive poly(N-isopropylacrylamide)-grafted magnetic nanoparticles for efficient treatment of emulsified oily wastewater. J. Alloys Compd. 2016, 688, 513–520. [Google Scholar] [CrossRef]
- Schroffenegger, M.; Zirbs, R.; Kurzhals, S.; Reimhult, E. The role of chain molecular weight and hofmeister series ions in thermal aggregation of poly(2-isopropyl-2-oxazoline) grafted nanoparticles. Polymers 2018, 10, 451. [Google Scholar] [CrossRef]
- Shan, J.; Chen, J.; Nuopponen, M.; Tenhu, H. Two phase transitions of poly(N-isopropylacrylamide) brushes bound to gold nanoparticles. Langmuir 2004, 20, 4671–4676. [Google Scholar] [CrossRef] [PubMed]
- Kurzhals, S.; Gal, N.; Zirbs, R.; Reimhult, E. Controlled aggregation and cell uptake of thermoresponsive polyoxazoline-grafted superparamagnetic iron oxide nanoparticles. Nanoscale 2017, 9, 2793–2805. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Shan, J.; Van Assche, G.; Tenhu, H.; Van Mele, B. Demixing and remixing kinetics in aqueous dispersions of poly(N-isopropylacrylamide) (PNIPAM) brushes bound to gold nanoparticles studied by means of modulated temperature differential scanning calorimetry. Macromolecules 2009, 42, 5317–5327. [Google Scholar] [CrossRef]
- Shan, J.; Nuopponen, M.; Jiang, H.; Kauppinen, E.; Tenhu, H. Preparation of poly(N-isopropylacrylamide)-monolayer-protected gold clusters: Synthesis methods, core size, and thickness of monolayer. Macromolecules 2003, 36, 4526–4533. [Google Scholar] [CrossRef]
- Kurzhals, S.; Gal, N.; Zirbs, R.; Reimhult, E. Aggregation of thermoresponsive core-shell nanoparticles: Influence of particle concentration, dispersant molecular weight and grafting. J. Colloid Interface Sci. 2017, 500, 321–332. [Google Scholar] [CrossRef] [PubMed]
- Kurzhals, S.; Schroffenegger, M.; Gal, N.; Zirbs, R.; Reimhult, E. Influence of grafted block copolymer structure on thermoresponsiveness of superparamagnetic core–shell nanoparticles. Biomacromolecules 2017, 19, 1435–1444. [Google Scholar] [CrossRef] [PubMed]
- Amstad, E.; Gehring, A.U.; Fischer, H.H.; Nagaiyanallur, V.V.; Hähner, G.; Textor, M.; Reimhult, E.; Hähner, G.; Textor, M.; Reimhult, E. Influence of electronegative substituents on the binding affinity of catechol-derived anchors to Fe3O4 nanoparticles. J. Phys. Chem. 2011, 115, 683–691. [Google Scholar] [CrossRef]
- Yuen, A.K.L.; Hutton, G.A.; Masters, A.F.; Maschmeyer, T. The interplay of catechol ligands with nanoparticulate iron oxides. Dalton Trans. 2012, 41, 2545–2559. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Wei, Q.; Qu, S. Synthesis and characterization of uniform and crystalline magnetite nanoparticles via oxidation-precipitation and modified co-precipitation methods. Int. J. Electrochem. Sci. 2013, 8, 3786–3793. [Google Scholar] [CrossRef]
- Hyeon, T.; Lee, S.S.; Park, J.; Chung, Y.; Na, H.B. Synthesis of highly crystalline and monodisperse maghemite nanocrystallites without a size-selection process. J. Am. Chem. Soc. 2001, 123, 12798–12801. [Google Scholar] [CrossRef] [PubMed]
- Lassenberger, A.; Bixner, O.; Gruenewald, T.; Lichtenegger, H.; Zirbs, R.; Reimhult, E. Evaluation of high-yield purification methods on monodisperse peg-grafted iron oxide nanoparticles. Langmuir 2016, 32, 4259–4269. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; An, K.; Hwang, Y.; Park, J.G.; Noh, H.J.; Kim, J.Y.; Park, J.H.; Hwang, N.M.; Hyeon, T. Ultra-large-scale syntheses of monodisperse nanocrystals. Nat. Mater. 2004, 3, 891–895. [Google Scholar] [CrossRef] [PubMed]
- Lassenberger, A.; Scheberl, A.; Stadlbauer, A.; Stiglbauer, A.; Helbich, T.; Reimhult, E. Individually stabilized, superparamagnetic nanoparticles with controlled shell and size leading to exceptional stealth properties and high relaxivities. ACS Appl. Mater. Interfaces 2017, 9, 3343–3353. [Google Scholar] [CrossRef] [PubMed]
- Witte, H.; Seeliger, W. Cyclische imidsäureester aus nitrilen und aminoalkoholen. Justus Liebigs Ann. Chem. 1974, 1974, 996–1009. [Google Scholar] [CrossRef]
- Monnery, B.D.; Shaunak, S.; Thanou, M.; Steinke, J.H.G. Improved synthesis of linear poly(ethylenimine) via low-temperature polymerization of 2-isopropyl-2-oxazoline in chlorobenzene. Macromolecules 2015, 48, 3197–3206. [Google Scholar] [CrossRef]
- Mondini, S.; Ferretti, A.M.; Puglisi, A.; Ponti, A. Pebbles and PebbleJuggler: Software for accurate, unbiased, and fast measurement and analysis of nanoparticle morphology from transmission electron microscopy (TEM) micrographs. Nanoscale 2012, 4, 5356. [Google Scholar] [CrossRef] [PubMed]
- Amstad, E.; Textor, M.; Reimhult, E. Stabilization and functionalization of iron oxide nanoparticles for biomedical applications. Nanoscale 2011, 3, 2819. [Google Scholar] [CrossRef] [PubMed]
- Zirbs, R.; Lassenberger, A.; Vonderhaid, I.; Kurzhals, S.; Reimhult, E. Melt-grafting for the synthesis of core–shell nanoparticles with ultra-high dispersant density. Nanoscale 2015, 7, 11216–11225. [Google Scholar] [CrossRef] [PubMed]
- Aseyev, V.; Tenhu, H.; Winnik, F.M. Non-ionic thermoresponsive polymers in water. In Self Organized Nanostructures of Amphiphilic Block Copolymers II; Axel, H.E.M., Oleg, B., Eds.; Spriger: Berlin, Germany, 2010; Volume 54, pp. 29–89. ISBN 9783319248608. [Google Scholar]
- Zhao, J.; Hoogenboom, R.; Van Assche, G.; Van Mele, B. Demixing and remixing kinetics of poly(2-isopropyl-2-oxazoline) (PIPOZ) aqueous solutions studied by modulated temperature differential scanning calorimetry. Macromolecules 2010, 43, 6853–6860. [Google Scholar] [CrossRef]
- Katsumoto, Y.; Tsuchiizu, A.; Qiu, X.; Winnik, F.M. Dissecting the mechanism of the heat-induced phase separation and crystallization of poly(2-isopropyl-2-oxazoline) in water through vibrational spectroscopy and molecular orbital calculations. Macromolecules 2012, 45, 3531–3541. [Google Scholar] [CrossRef]
- Grünewald, T.A.; Lassenberger, A.; van Oostrum, P.D.J.; Rennhofer, H.; Zirbs, R.; Capone, B.; Vonderhaid, I.; Amenitsch, H.; Lichtenegger, H.C.; Reimhult, E. Core–shell structure of monodisperse poly(ethylene glycol)-grafted iron oxide nanoparticles studied by small-angle X-ray scattering. Chem. Mater. 2015, 27, 4763–4771. [Google Scholar] [CrossRef] [PubMed]
- Lo Verso, F.; Yelash, L.; Egorov, S.A.; Binder, K. Effect of the solvent quality on the structural rearrangement of spherical brushes: Coarse-grained models. Soft Matter 2012, 8, 4185. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Birshtein, T.M.; Borisov, O.V. Curved polymer and polyelectrolyte brushes beyond the daoud-cotton model. Eur. Phys. J. E 2006, 20, 243–256. [Google Scholar] [CrossRef] [PubMed]
- Daoud, M.; Cotton, J.P. Star shaped polymers: A model for the conformation and its concentration dependence. J. Phys. 1982, 43, 531–538. [Google Scholar] [CrossRef]
- Diab, C.; Akiyama, Y.; Kataoka, K.; Winnik, F.M. Microcalorimetric study of the temperature-induced phase separation in aqueous solutions of poly(2-isopropyl-2-oxazolines). Macromolecules 2004, 37, 2556–2562. [Google Scholar] [CrossRef]

| Sample | Core-shell Particle Concentration (g L−1) | Grafted Polymer Concentration (g L−1) | Particle Molarity (mol L−1) |
|---|---|---|---|
| FeOx-5 | 0.07 | 0.06 | 2.7 × 10−8 |
| FeOx-5 | 0.1088 | 0.1 | 4.0 × 10−9 |
| FeOx-5 | 0.54 | 0.5 | 2.0 × 10−7 |
| FeOx-5 | 1.088 | 1.0 | 4.0 × 10−7 |
| FeOx-5 | 10.88 | 10 | 4.0 × 10−6 |
| FeOx-7 | 0.114 | 0.1 | 2.2 × 10−8 |
| FeOx-7 | 0.135 | 1.12 | 2.7 × 10−8 |
| FeOx-7 | 0.57 | 0.5 | 1.1 × 10−7 |
| FeOx-7 | 1.14 | 1.0 | 2.2 × 10−7 |
| FeOx-7 | 11.4 | 10 | 2.2 × 10−6 |
| FeOx-10 | 0.116 | 0.1 | 9.3 × 10−9 |
| FeOx-10 | 0.324 | 0.28 | 2.7 × 10−9 |
| FeOx-10 | 0.58 | 0.5 | 4.7 × 10−8 |
| FeOx-10 | 1.16 | 1.0 | 9.3 × 10−8 |
| FeOx-10 | 11.6 | 10 | 9.3 × 10−7 |
| FeOx-21 | 0.139 | 0.1 | 2.7 × 10−9 |
| FeOx-21 | 0.695 | 0.5 | 1.3 × 10−8 |
| FeOx-21 | 1.39 | 1.0 | 2.7 × 10−8 |
| FeOx-21 | 13.9 | 10 | 2.7 × 10−7 |
| Sample | Core Diameter (nm) | TGA | |||
|---|---|---|---|---|---|
| Weight Loss (wt %) | Residue (wt %) | ||||
| FeOx-5 | 5.1 ± 0.6 | 91.9 | 8.1 | 1.2 | 19.7 ± 4.9 |
| FeOx-7 | 7.4 ± 0.5 | 87.3 | 12.7 | 1.0 | 21.4 ± 1.1 |
| FeOx-10 | 10.2 ± 0.7 | 86.1 | 13.9 | 1.3 | 21.6 ± 1.6 |
| FeOx-21 | 20.9 ± 1.3 | 72.1 | 27.9 | 1.1 | 30.5 ± 1.9 |
| Sample | CFT (°C) | ||
|---|---|---|---|
| Free Polymer | 108.7 ± 5.0 | 1340.9 ± 25.1 | 38 |
| FeOx-5 | 19.7 ± 1.0 | 91.7 ± 1.0 | 34 |
| FeOx-7 | 21.4 ± 0.7 | 80.9 ± 0.4 | 34 |
| FeOx-10 | 20.0 ± 0.3 | 65.5 ± 0.3 | 34 |
| FeOx-21 | 30.5 ± 0.4 | 97.7 ± 0.5 | 33 |
| Sample | Grafted Polymer Concentration (g L−1) | |||
|---|---|---|---|---|
| FeOx-5 | 0.06 | 3.85 | −3.16 | 82 |
| FeOx-5 | 0.1 | 4.13 | −2.29 | 55 |
| FeOx-5 | 0.5 | 3.86 | −2.65 | 69 |
| FeOx-5 | 1.0 | 3.97 | −2.88 | 72 |
| FeOx-5 | 10 | 4.05 | −3.71 | 92 |
| FeOx-5 mean | 3.97 ± 0.11 | −2.94 ± 0.48 | 74 | |
| FeOx-7 | 0.1 | 3.75 | −2.71 | 72 |
| FeOx-7 | 0.12 | 3.76 | −2.89 | 77 |
| FeOx-7 | 0.5 | 3.85 | −2.68 | 69 |
| FeOx-7 | 1.0 | 3.80 | −3.33 | 88 |
| FeOx-7 | 10 | 3.73 | −3.26 | 88 |
| FeOx-7 mean | 3.78 ± 0.05 | −2.97 ± 0.27 | 79 | |
| FeOx-10 | 0.1 | 3.47 | −1.66 | 48 |
| FeOx-10 | 0.28 | 3.40 | −2.35 | 69 |
| FeOx-10 | 0.5 | 3.30 | −2.37 | 72 |
| FeOx-10 | 1.0 | 3.33 | −2.37 | 71 |
| FeOx-10 | 10 | 3.53 | −3.08 | 87 |
| FeOx-10 mean | 3.41 ± 0.09 | −2.37 ± 0.45 | 69 | |
| FeOx-21 | 0.1 | 3.64 | −1.78 | 49 |
| FeOx-21 | 0.5 | 3.70 | −2.00 | 54 |
| FeOx-21 | 1.0 | 3.67 | −2.55 | 69 |
| FeOx-21 | 10 | 3.58 | −3.23 | 90 |
| FeOx-21 mean | 3.65 ± 0.04 | −2.39 ± 0.56 | 65 | |
| Free polymer | 0.1 | 4.46 | −1.75 | 39 |
| Free polymer | 0.5 | 4.76 | −2.66 | 56 |
| Free polymer | 1 | 4.85 | −5.06 | 104 |
| Free polymer | 10 | 4.81 | −3.04 | 63 |
| Free polymer mean | 4.72 ± 0.15 | −3.13 ± 1.21 | 66 |
| Sample | ||
|---|---|---|
| FeOx-5 | 19.7 ± 1.0 | 23.4 ± 0.7 |
| FeOx-7 | 21.4 ± 0.7 | 25.5 ± 0.5 |
| FeOx-10 | 20.0 ± 0.3 | 23.1 ± 0.6 |
| FeOx-21 | 30.5 ± 0.4 | 33.9 ± 0.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schroffenegger, M.; Reimhult, E. Thermoresponsive Core-Shell Nanoparticles: Does Core Size Matter? Materials 2018, 11, 1654. https://doi.org/10.3390/ma11091654
Schroffenegger M, Reimhult E. Thermoresponsive Core-Shell Nanoparticles: Does Core Size Matter? Materials. 2018; 11(9):1654. https://doi.org/10.3390/ma11091654
Chicago/Turabian StyleSchroffenegger, Martina, and Erik Reimhult. 2018. "Thermoresponsive Core-Shell Nanoparticles: Does Core Size Matter?" Materials 11, no. 9: 1654. https://doi.org/10.3390/ma11091654
APA StyleSchroffenegger, M., & Reimhult, E. (2018). Thermoresponsive Core-Shell Nanoparticles: Does Core Size Matter? Materials, 11(9), 1654. https://doi.org/10.3390/ma11091654







