Investigation of Groove Shape Variation during Steel Sheave Spinning
Abstract
:1. Introduction
2. Numerical and Experimental Models
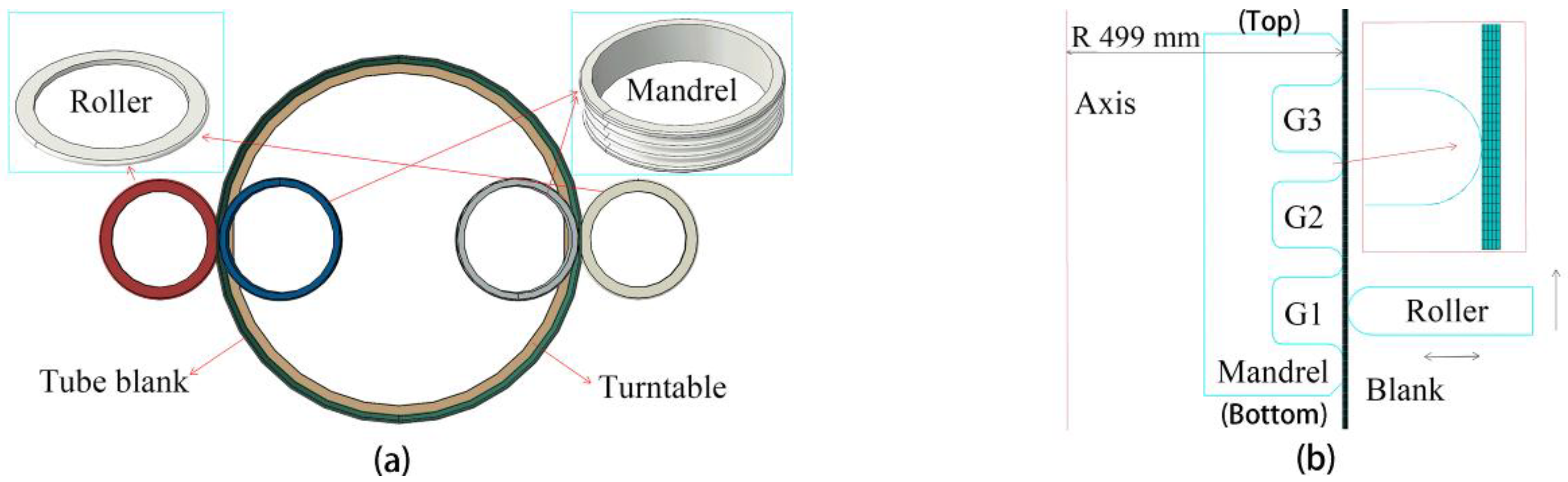
2.1. Research Methods
2.2. Numerical Model
2.3. Experiments
3. Results and Discussion
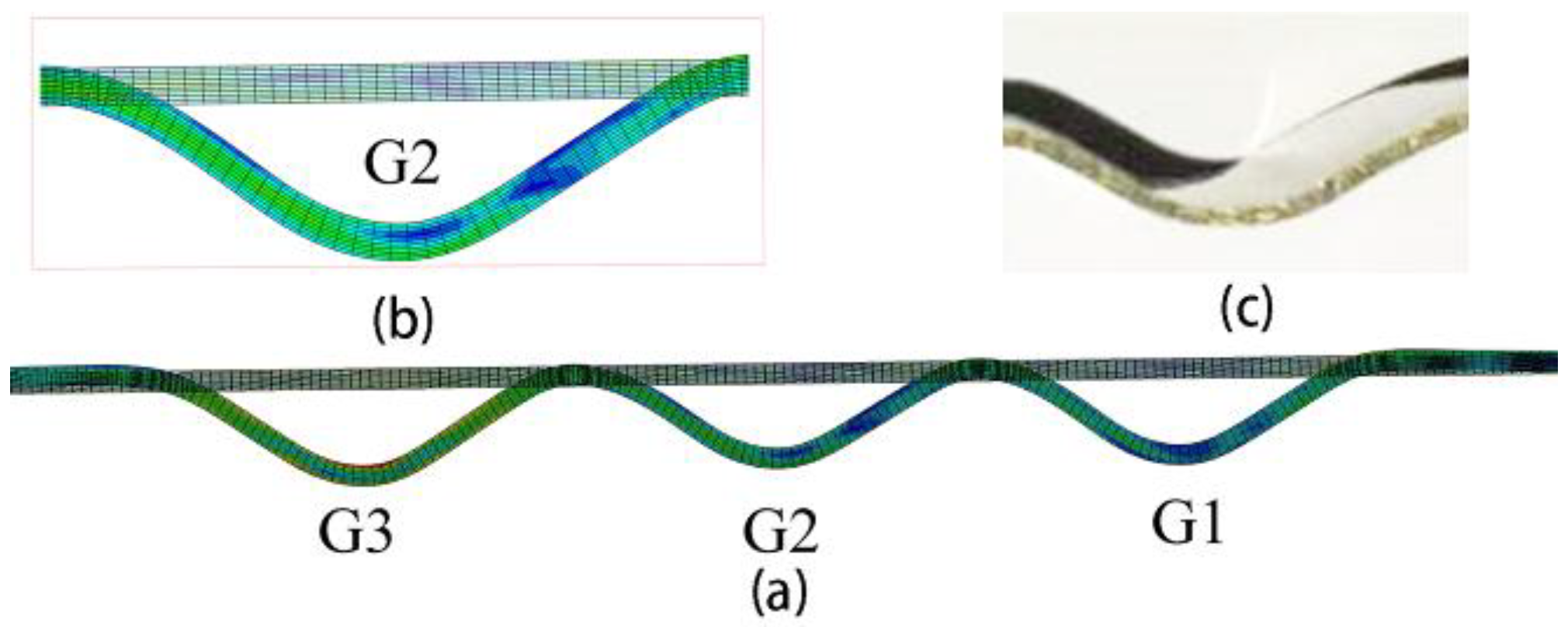
3.1. General Results
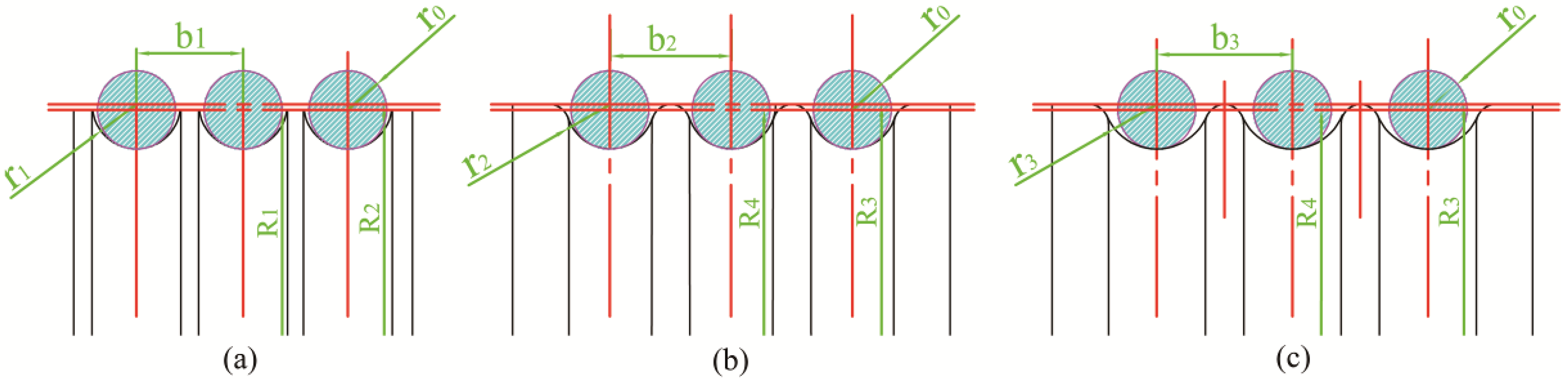
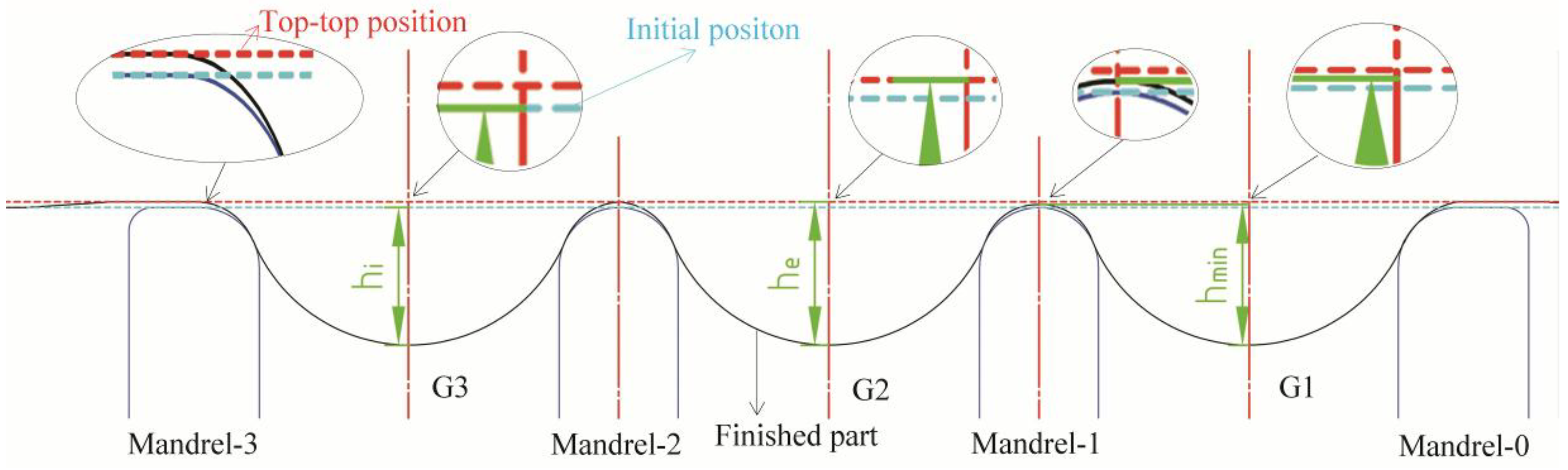
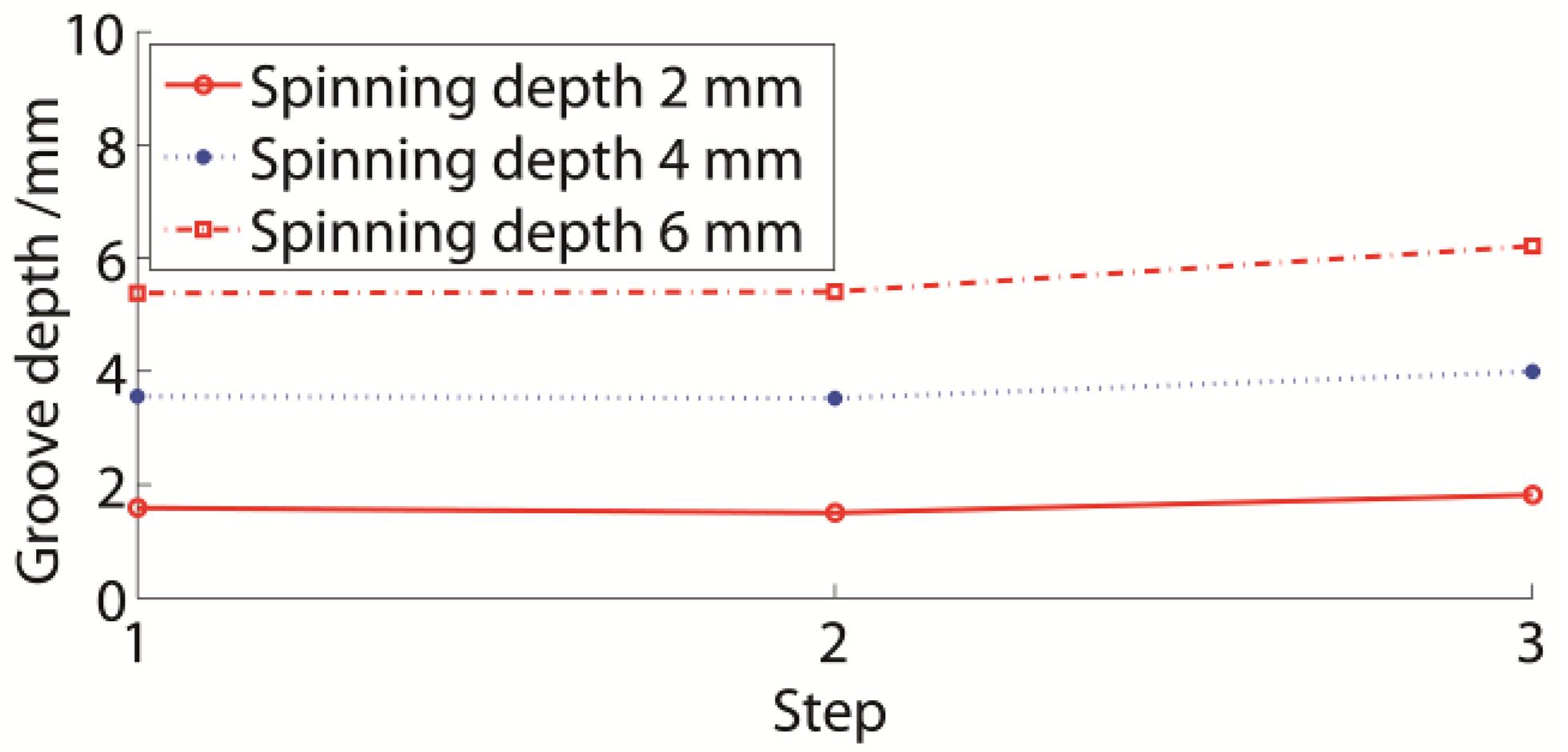
3.2. Depth Variation during Spinning
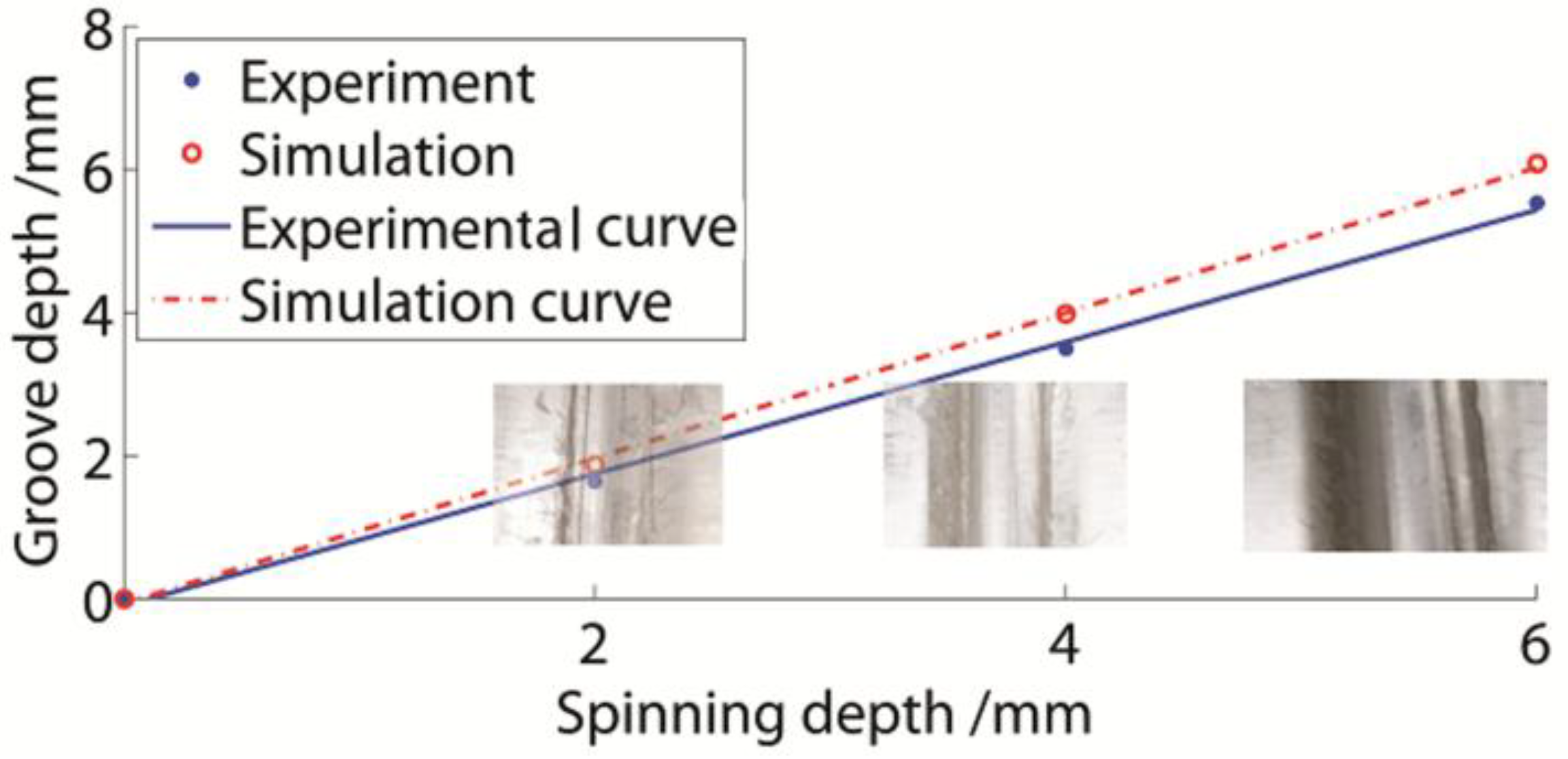
3.3. Relationship between Groove and Spinning Depths
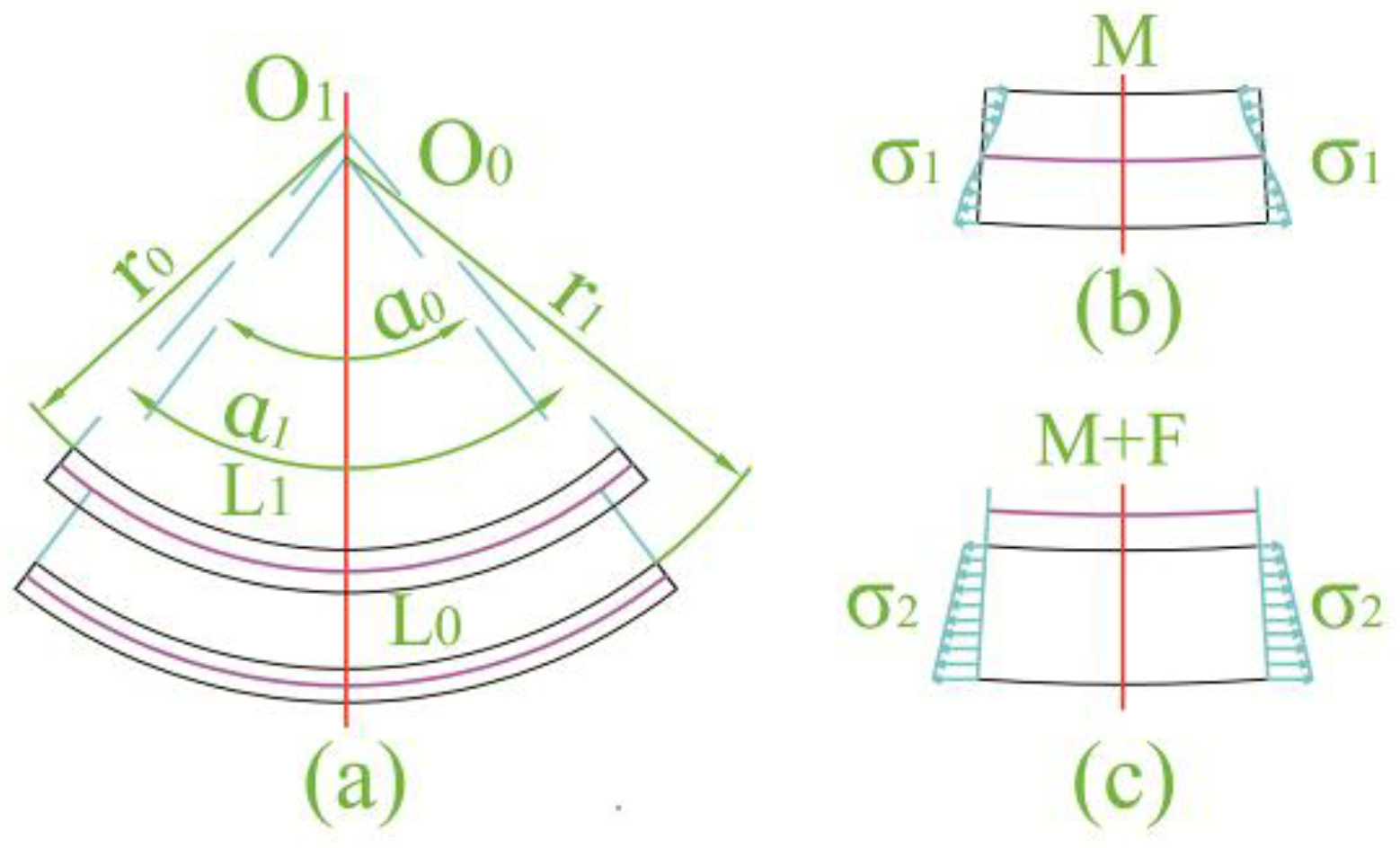
3.3.1. Spring-Back of Spinning Groove
3.3.2. Single-Groove Spinning
3.3.3. Three-Groove Spinning
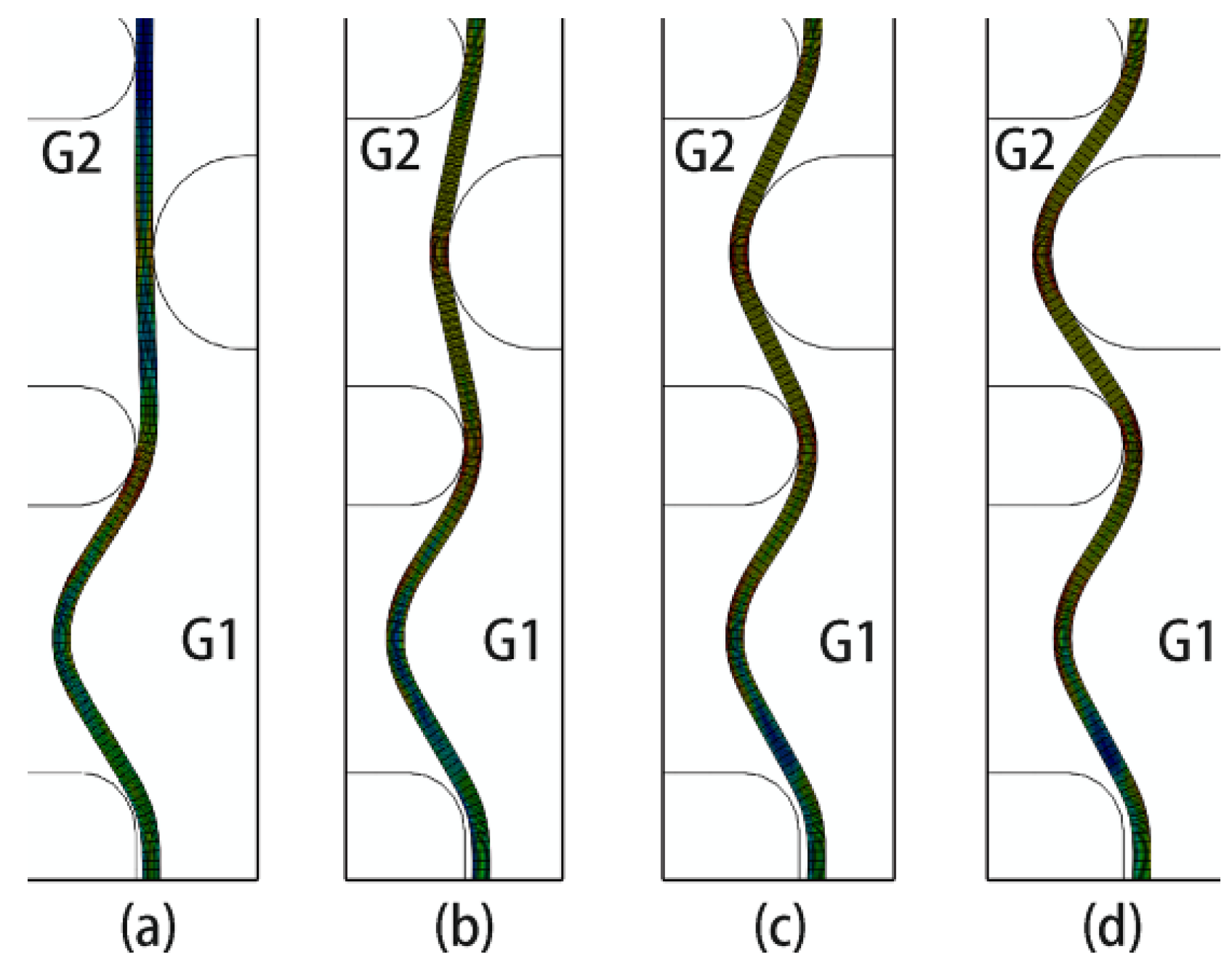
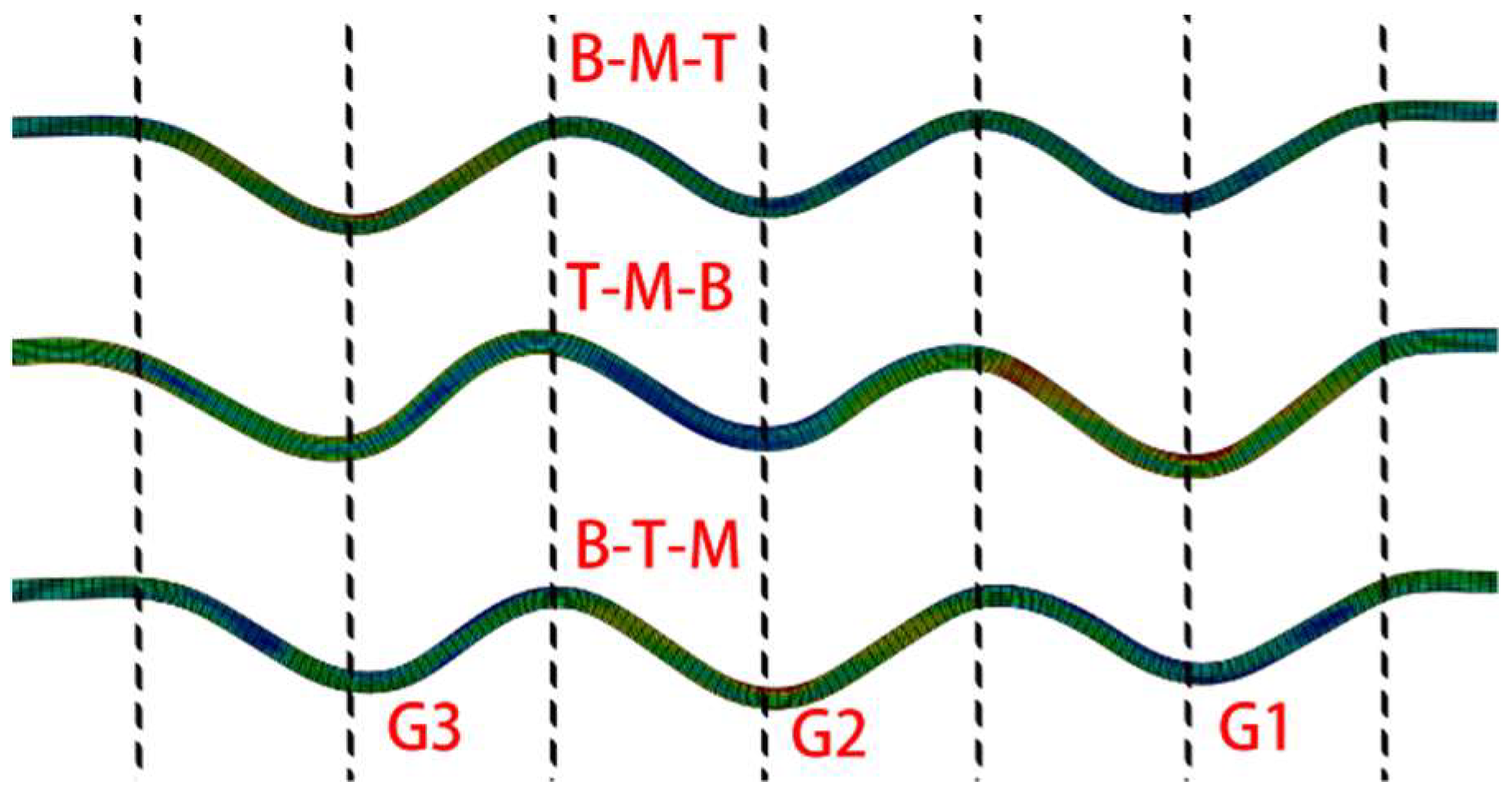
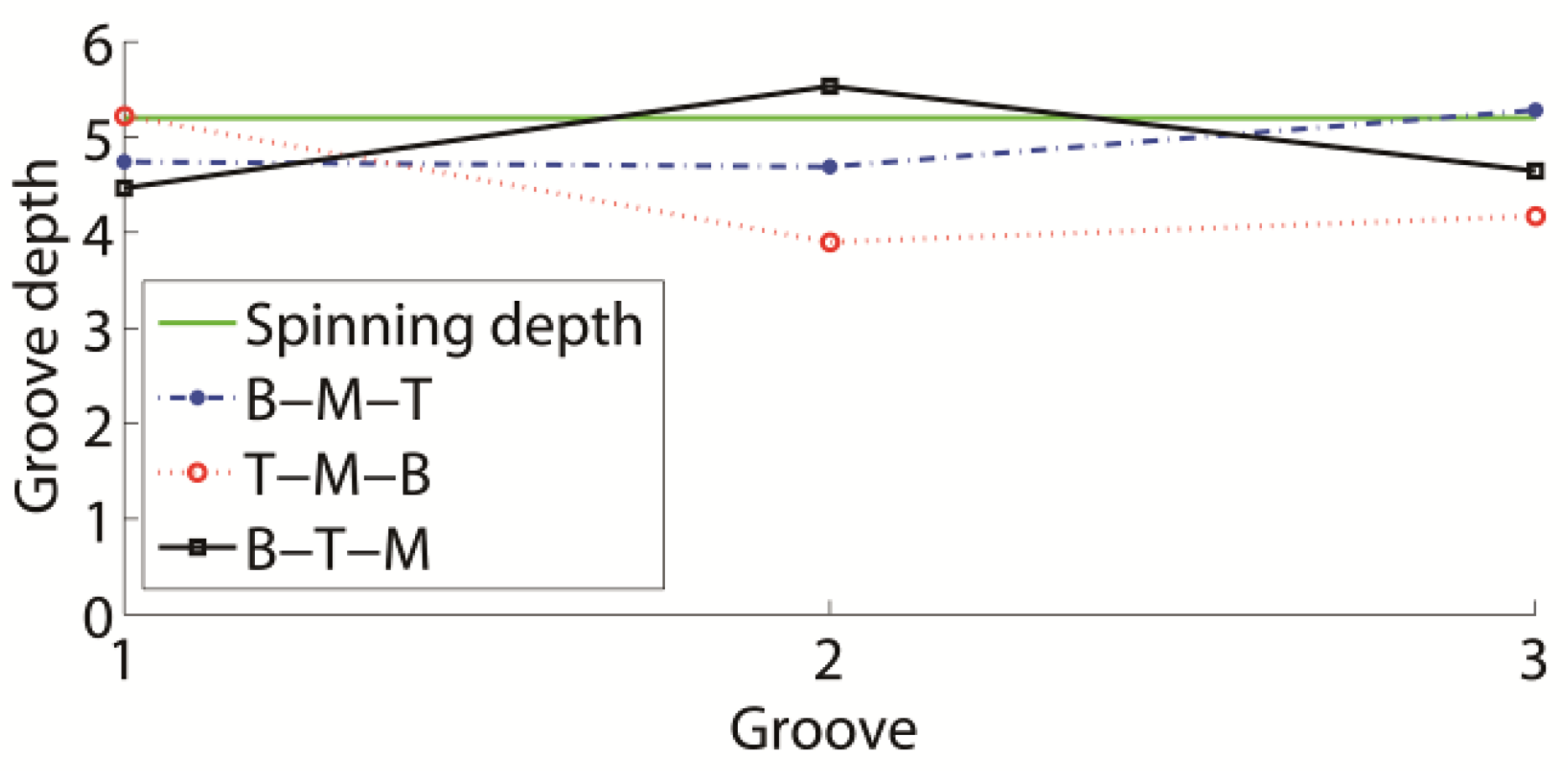
3.4. Effect of Groove Spinning Sequence
4. Conclusions
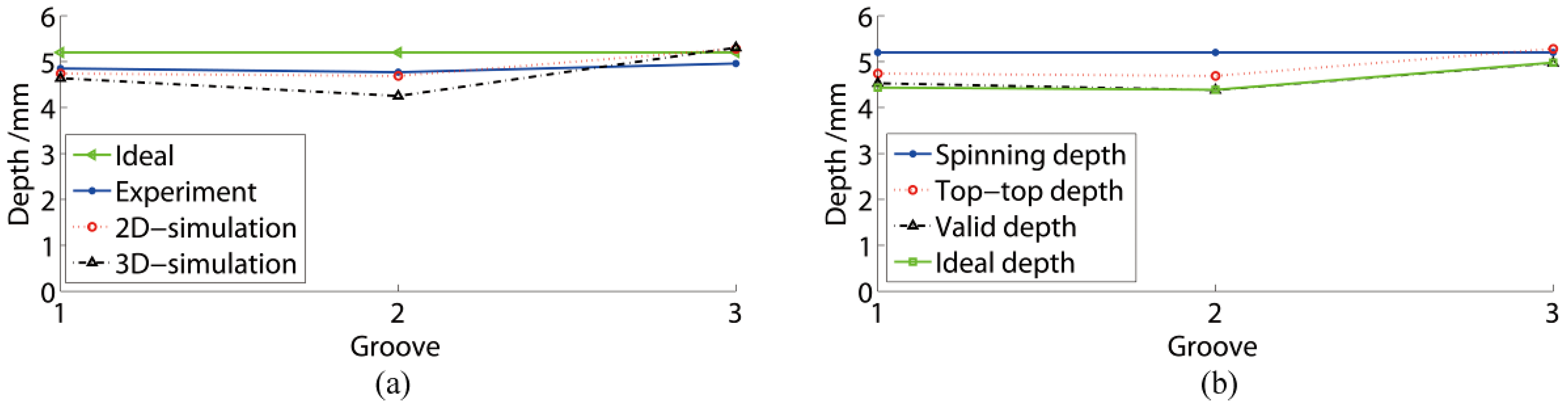
- The grooves of all 3D/ 2D numerical simulations and experiments were well formed. Also, the 2D numerical simulation, when the spring-back phenomenon was considered, matched the experimental results well. Therefore, the numerical method was efficient for the groove spinning study.
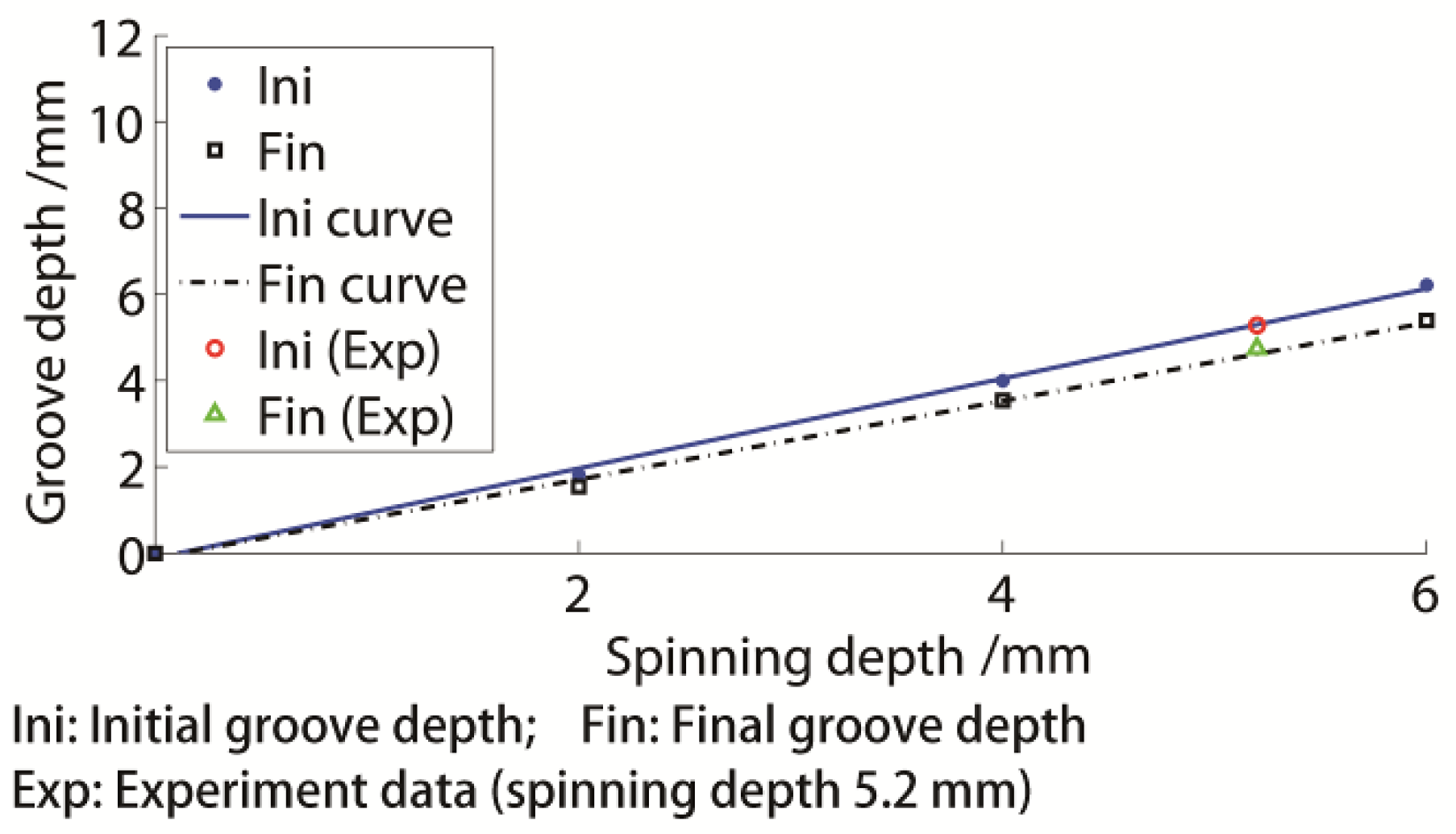
- The last formed groove was always the deepest of all grooves, while the former spun grooves had similar depths. When the spinning depth was 5.2 mm, the top–top groove depths of the last and former grooves were approximately 5.28 mm and 4.70 mm, respectively. Moreover, their valid groove depths were approximately 0.25 mm shallower than the top–top groove.
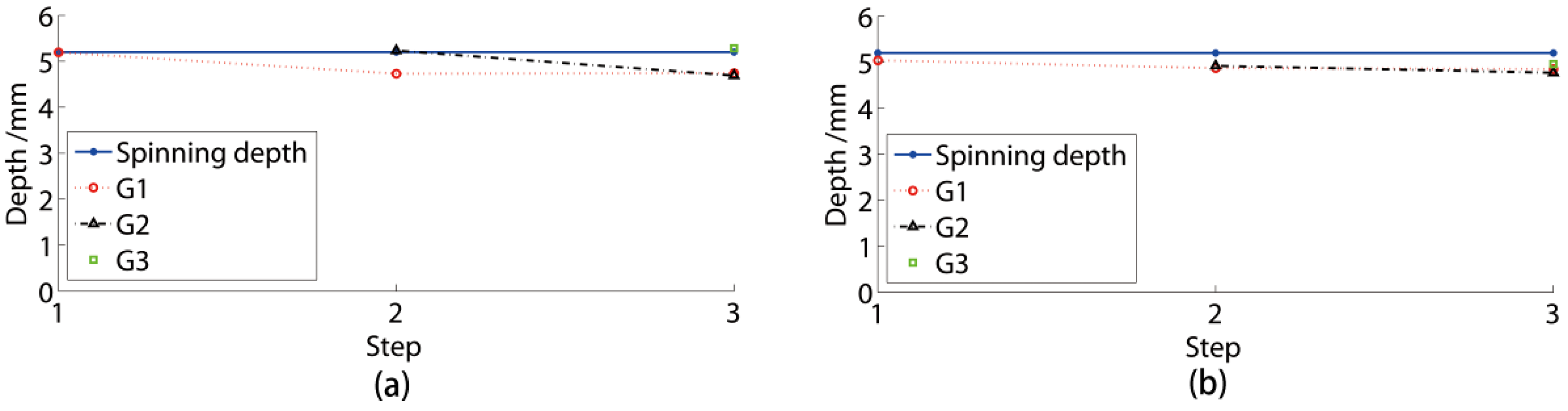
- The groove depth changed during spinning. The former groove depth was almost constant subsequent to the following spinning. The depth of Groove 1 was highly decreased during the second groove spinning, and changed slightly during the third groove spinning. The Groove 2 depth became lower, with a value equal to the final Groove 1 depth, following the third groove spinning. Therefore, the final groove depth of the spinning sheave could be regarded as the groove depth following the next groove spinning.
- The groove depth was nearly linearly dependent on the spinning depth. The groove depth of the single-groove spinning was slightly higher than the three-groove spinning. In addition, the single-groove depth could be used to calculate the multiple grooves’ depths. Equations for the relationship between the groove depth and the spinning depth as well as between the single and multiple groove depths were obtained. The groove processing could be designed with these equations.
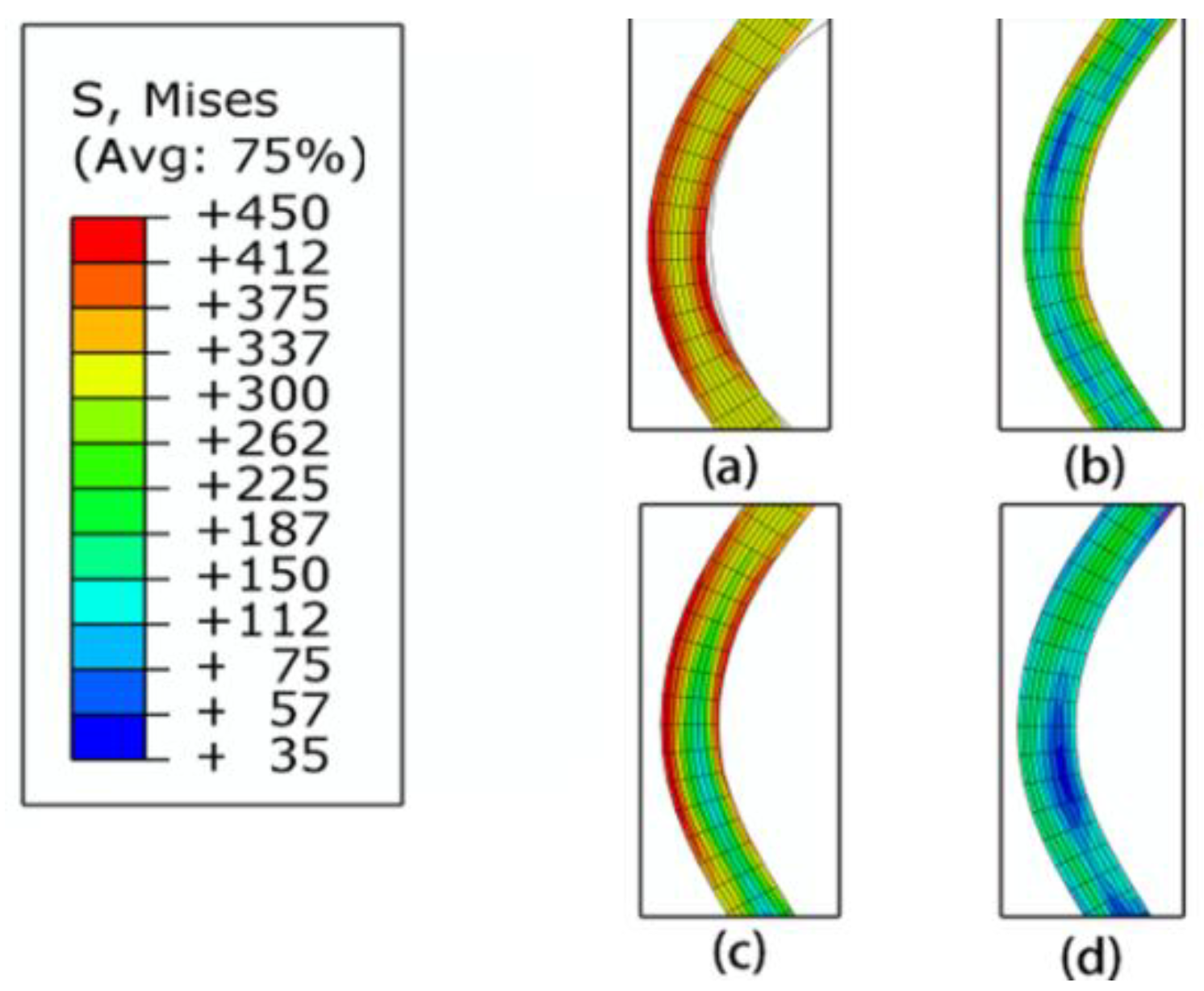
- The groove spinning sequences had an apparent effect on the spinning process. The B-M-T sequence was the most suitable for the sheave spinning. The B-M-T results were better groove shapes and higher groove depths than the other results. Also, the B-M-T result was a well-retained wall thickness, including similar stress and strain values to the other results. Therefore, B-M-T should be selected in the sheave spinning process.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Zhao, S.D.; Fan, S.Q.; Qian, D.Q. Sheet metal forming process of new crosshead sheave for elevator and its numerical simulation. Cailiao Kexue Yu Gongyi/Mater. Sci. Technol. 2010, 18, 176–181. [Google Scholar]
- Radtke, D.W. Novel manufacturing methods for tita-nium tanks and liners. Am. Inst-Itute Aero-Naut. Astronaut. 2006, 42, 9–12. [Google Scholar]
- Zhang, Q.; Zhang, C.; Zhang, M.J.; Zhu, C.C.; Fan, S.Q.; Zhao, S.D. Research of net-shape power spinning technology for Poly-V grooved aluminum pulley. Int. J. Adv. Manuf. Technol. 2015, 81, 1601–1618. [Google Scholar] [CrossRef]
- Childs, T.H.C.; Dalgarno, K.W.; Hojjati, M.H. The meshing of timing belt teeth in pulley grooves. J. Automob. Eng. 1997, 21, 205–218. [Google Scholar] [CrossRef]
- Zheng, S.M.; Cheng, L.D.; Liu, S.R. Model of the yarn twist propagation in compact spinning with a pneumatic groove. Fibres Text. East. Eur. 2011, 19, 84. [Google Scholar]
- Fan, X.; Zhao, S.; Jin, C.; Xiaolan, H. The experimental analysis of shear strength of round joints. J. Eng. Manuf. 2014, 228, 1280–1289. [Google Scholar] [CrossRef]
- El-Khabeery, M.M.; Fattouh, M.; El-Sheikh, M.N.; Hamed, O.A. On the conventional simple spinning of cylindrical aluminium cups. Int. J. Mach. Tools Manuf. 1991, 31, 203–219. [Google Scholar] [CrossRef]
- Jia, Z.; Han, Z.R.; Liu, B.M.; Fan, Z.J. Numerical simulation and experimental study on the non-axisymmetric die-less shear spinning. Int. J. Adv. Manuf. Technol. 2017, 92, 497–504. [Google Scholar] [CrossRef]
- Quigley, E.; Monaghan, J. Metal forming: An analysis of spinning processes. J. Mater. Process. Technol. 2000, 103, 114–119. [Google Scholar] [CrossRef]
- Huang, L.; Yang, H.; Zhan, M.; Hu, L. Forming characteristics of splitting spinning based on the behaviors of roller. Comput. Mater. Sci. 2009, 45, 449–461. [Google Scholar] [CrossRef]
- Huang, L.; Yang, H.; Zhan, M. 3D-FE modeling method of splitting spinning. Comput. Mater. Sci. 2008, 42, 643–652. [Google Scholar] [CrossRef]
- Long, H.; Hamilton, S. Simulation of effects of material deformation on thickness variation in conventional spinning. In Proceedings of the 9th International Conference on Technology of Plasticity (ICTP), Gyeongju, Korea, 7–11 September 2008; Hanrimwon Publishing Co.: Seoul, Korea, 2008; pp. 735–740. [Google Scholar]
- Wong, C.C.; Danno, A.; Tong, K.K.; Yong, M.S. Cold rotary forming of thin-wall component from flat-disc blank. J. Mater. Process. Technol. 2008, 208, 53–62. [Google Scholar] [CrossRef]
- Groche, P.; Fritsche, D. Application and modelling of flow forming manufacturing processes for internally geared wheels. Int. J. Mach. Tools Manuf. 2006, 46, 1261–1265. [Google Scholar] [CrossRef]
- Kawai, K.; Yang, L.-N.; Kudo, H. A flexible shear spinning of axi-symmetrical shells with a general-purpose mandrel. J. Mater. Process. Technol. 2007, 192–193, 13–17. [Google Scholar] [CrossRef]
- Nguyen, D.-T.; Dinh, D.-K.; Nguyen, H.-M.T.; Banh, T.-L.; Kim, Y.-S. Formability improvement and blank shape definition for deep drawing of cylindrical cup with complex curve profile from SPCC sheets using FEM. J. Cent. South Univ. 2014, 21, 27–34. [Google Scholar] [CrossRef]
- Chan, W.M.; Chew, H.I.; Lee, H.P.; Cheok, B.T. Finite element analysis of spring-back of V-bending sheet metal forming processes. J. Mater. Process. Technol. 2004, 148, 15–24. [Google Scholar] [CrossRef]
- Yilamu, K.; Hino, R.; Hamasaki, H.; Yoshida, F. Air bending and springback of stainless steel clad aluminum sheet. J. Mater. Process. Technol. 2010, 210, 272–278. [Google Scholar] [CrossRef]
- Hino, R.; Goto, Y.; Yoshida, F. Springback of sheet metal laminates in draw-bending. J. Mater. Process. Technol. 2003, 139, 341–347. [Google Scholar] [CrossRef]
- Mohebbi, M.S.; Akbarzadeh, A. Experimental study and FEM analysis of redundant strains in flow forming of tubes. J. Mater. Process. Technol. 2010, 210, 389–395. [Google Scholar] [CrossRef]
- Davoodi, B.; Zareh-Desari, B. Assessment of forming parameters influencing spring-back in multi-point forming process: A comprehensive experimental and numerical study. Mater. Des. 2014, 59, 103–114. [Google Scholar] [CrossRef]
- Wang, X. Stamping Handbook; Wang, X., Ed.; Machinery Industry Press: Beijing, China, 1990; pp. 123–147. ISBN 9787111023371. [Google Scholar]
- Pourboghrat, F.; Chu, E. Prediction of spring-back and side-wall curl in 2-D draw bending. J. Mater. Process. Technol. 1995, 50, 361–374. [Google Scholar] [CrossRef]
- Pourboghrat, F.; Chu, E. Springback in plane strain stretch/draw sheet forming. Int. J. Mech. Sci. 1995, 37, 327–341. [Google Scholar] [CrossRef]
- Zhao, J.; Yin, J.; Ma, R.; Ma, L. Springback equation of small curvature plane bending. Sci. China Technol. Sci. 2011, 54, 2386–2396. [Google Scholar] [CrossRef]
- Schuler GmbH. Metal Forming Handbook; Schuler GmbH, Ed.; Springer: Berlin, Germany; New York, NY, USA, 1998; ISBN 978-3-540-61185-1. [Google Scholar]



| Density/kg/m3 | Young’s Modulus/GPa | Poisson’s Ratio | Yield-Strength/MPa | Ultimate-Strength/MPa |
|---|---|---|---|---|
| 7219 | 200 | 0.3 | 310 | 607 |
| Items | B-M-T | T-M-B | B-T-M |
|---|---|---|---|
| Maximum-stress/MPa | 464.8 | 458.6 | 458.0 |
| Maximum-strain | 0.1246 | 0.1177 | 0.1172 |
| Minimum-thickness/mm | 0.9878 | 0.9752 | 0.9890 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Meng, D.; Zhao, S.; Li, S. Investigation of Groove Shape Variation during Steel Sheave Spinning. Materials 2018, 11, 960. https://doi.org/10.3390/ma11060960
Zhu C, Meng D, Zhao S, Li S. Investigation of Groove Shape Variation during Steel Sheave Spinning. Materials. 2018; 11(6):960. https://doi.org/10.3390/ma11060960
Chicago/Turabian StyleZhu, Chengcheng, Dean Meng, Shengdun Zhao, and Shuaipeng Li. 2018. "Investigation of Groove Shape Variation during Steel Sheave Spinning" Materials 11, no. 6: 960. https://doi.org/10.3390/ma11060960
APA StyleZhu, C., Meng, D., Zhao, S., & Li, S. (2018). Investigation of Groove Shape Variation during Steel Sheave Spinning. Materials, 11(6), 960. https://doi.org/10.3390/ma11060960






