Time-Resolved Spectroscopy of Ethanol Evaporation on Free-Standing Porous Silicon Photonic Microcavities
Abstract
1. Introduction
2. Materials and Methods
2.1. Porous Silicon Microcavity Fabrication
2.2. Porous Silicon Refractive Index
2.3. Porous Silicon Microcavity Ethanol Sensing
3. Results
3.1. Porous Silicon Microcavity Fabrication
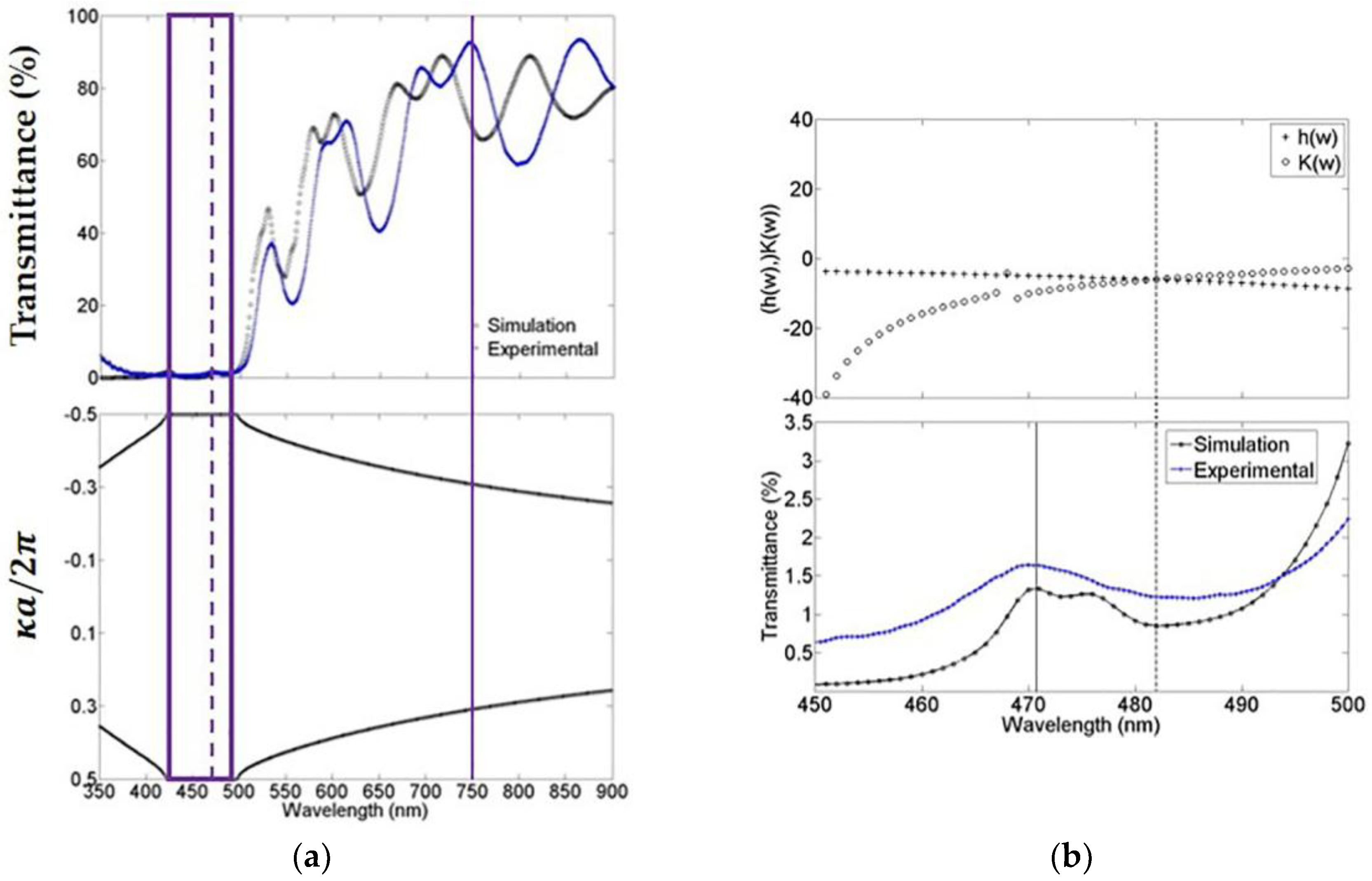
3.2. Porous Silicon Refractive Index
3.3. Porous Silicon Microcavity Bandgap Structure
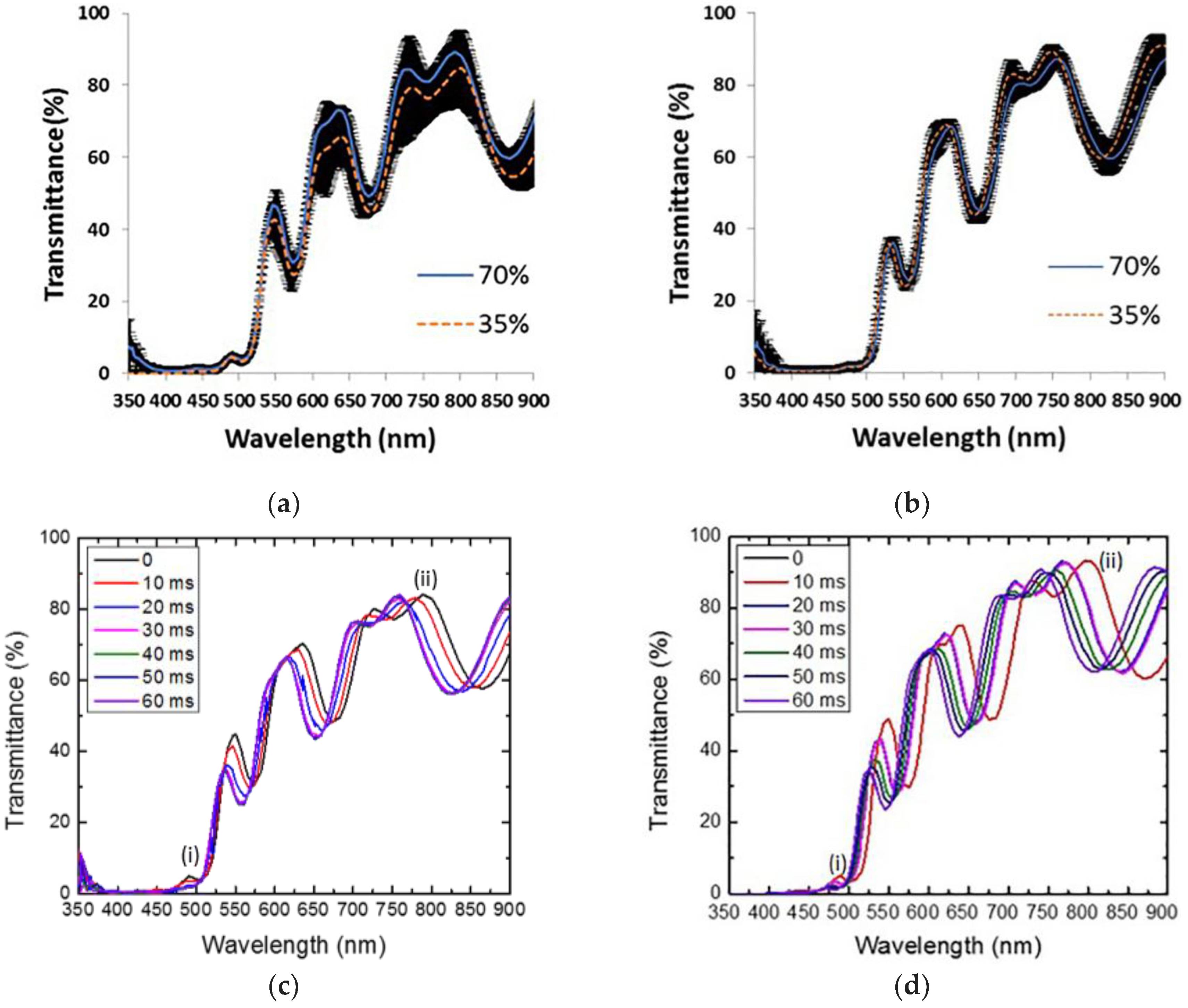
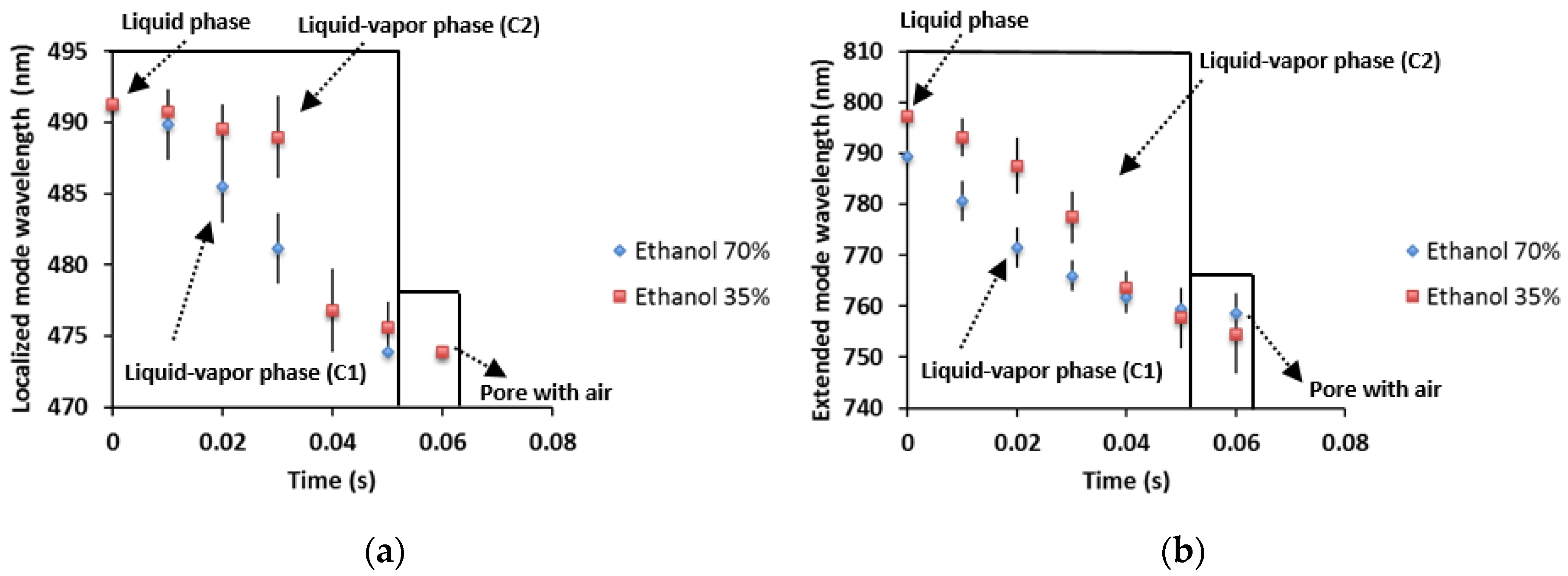
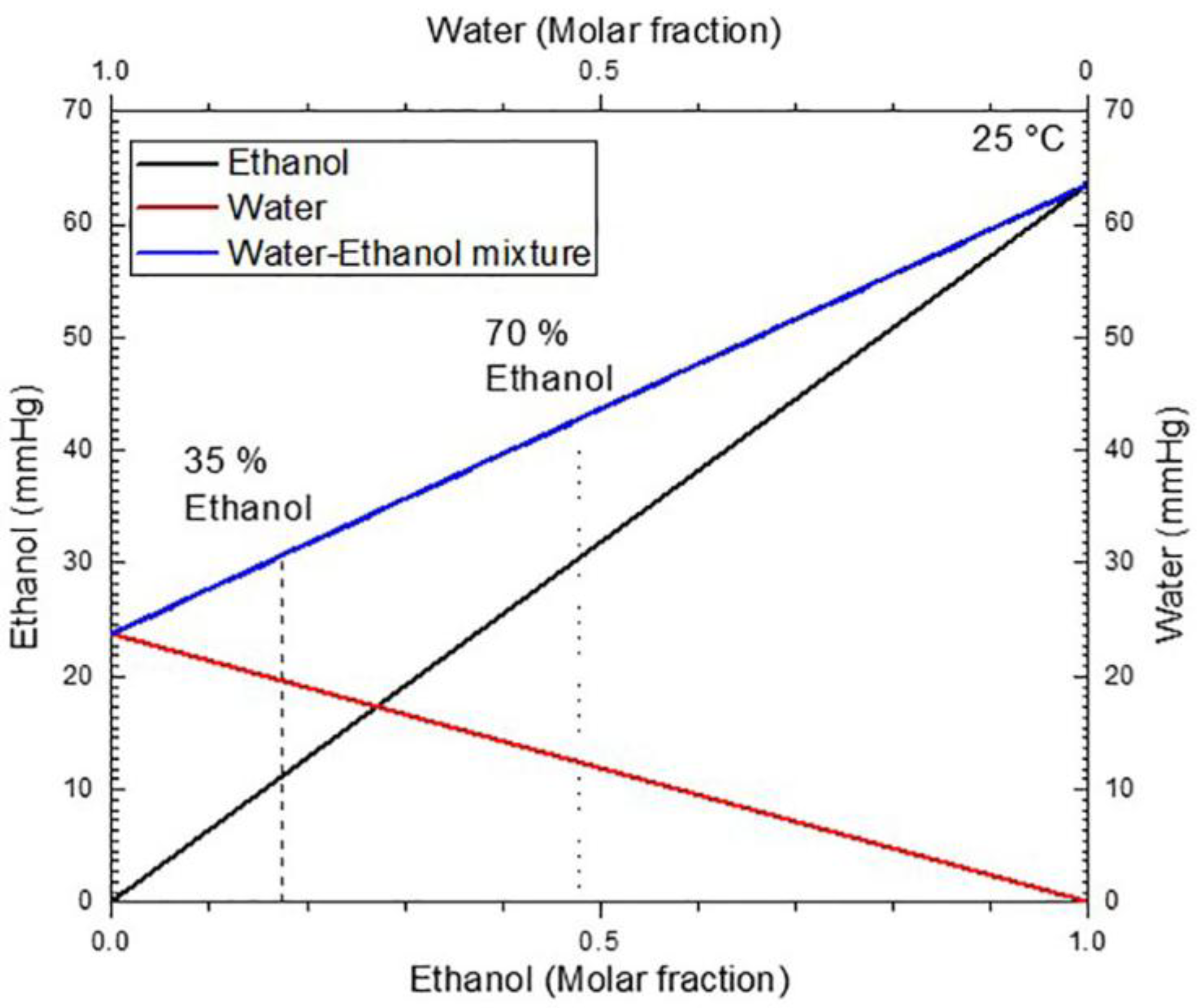
3.4. Porous Silicon Microcavity Ethanol Sensing
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Morales, F.; López, R.; García, G.; Rosendo, E.; Díaz, T.; Juárez, H. UV distributed Bragg reflectors build from porous silicon multilayers. J. Eur. Opt. Soc.-Rapid 2015, 10, 15016. [Google Scholar] [CrossRef]
- Lugo, J.E.; Lopez, H.A.; Chan, S.; Fauchet, P.M. Porous silicon multilayer structures: A photonic band gap analysis. AIP 2012, 91, 4966–4972. [Google Scholar] [CrossRef]
- Harraz, F.A. Porous silicon chemical sensor and biosensors: A review. Sens. Actuators B Chem. 2014, 202, 897–912. [Google Scholar] [CrossRef]
- Pacholski, C. Photonic Crystal Sensor Based on Porous Silicon. Sensors 2013, 13, 4694–4713. [Google Scholar] [CrossRef] [PubMed]
- Caroselli, R.; Martín, D.; Alcántara, S.P.; Quilez, F.P.; Morán, L.T.; García-Rupérez, J. Real-Time and In-Flow Sensing Using a High Sensitivy Porous Silicon Microcavity-Based Sensor. Sensors 2017, 17, 2813. [Google Scholar] [CrossRef] [PubMed]
- DeLouise, L.A.; Kou, P.M.; Miller, B.L. Cross-Correlation of Optical Microcavity Biosensor Response within Immobilized Enzyme Activy. Insights into Biosensor Sensitivy. Anal. Chem. 2005, 77, 3222–3230. [Google Scholar] [CrossRef] [PubMed]
- Kanaujia, P.K.; Bhatnagar, M.C.; Prakash, G.V. Effect of volatile solvent infiltration on optical and electrical characteristics of porous photonic structures. RSC Adv. 2014, 4, 21246–21253. [Google Scholar] [CrossRef]
- Vallance, C.; Trichet, A.A.P.; James, D.; Dolan, P.R.; Smith, J.M. Open-access microcavities for chemical sensing. Nanotechnology 2016, 27, 27. [Google Scholar] [CrossRef] [PubMed]
- Passaro, V.M.N.; Troia, B.; la Notte, M.; de Leonardls, F. Photonic resonant microcavities chemical and biochemical sensing. RSC Adv. 2013, 3, 25–44. [Google Scholar] [CrossRef]
- Li, P.; Jia, Z.; Lü, X.; Liu, Y.; Ning, X.; Mo, J.; Wang, J. Spectrometer-free biological detection method using porous silicon microcavity devices. OSA 2015, 23, 24626–24633. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Hu, M.; Zeng, P.; Ma, S.; Yan, W.; Qin, Y. Effect of etching current density on microstructure and NH3-sensing properties of porous silicon with intermediate-sized pores. Electrochim. Acta 2013, 108, 167–174. [Google Scholar] [CrossRef]
- Kim, H.-G.; Lee, K.-W. Electrostatic gas sensor with a porous silicon diaphragm. Sens. Actuators B Chem. 2015, 219, 10–16. [Google Scholar] [CrossRef]
- Levitsky, I.A. Porous silicon Structures as Optical Gas Sensors. Sensors 2015, 15, 19968–19991. [Google Scholar] [CrossRef] [PubMed]
- Rocchia, M.; Rosso, A.M.; Zeppa, G. Determination of ethanol content in wine through a porous silicon oxide microcavity. Sens. Actuators B Chem. 2007, 123, 89–93. [Google Scholar] [CrossRef]
- Volk, J.; le Grand, T.; Bársony, I.; GombkötÕ, J.; Ramsden, J.J. Porous silicon multilayer stack for sensitive refractive index determination of pure solvents. J. Phys. D Appl. Phys. 2005, 38, 1313–1317. [Google Scholar] [CrossRef]
- Dargaville, T.R.; Farrugia, B.L.; Broadbent, J.A.; Pace, S.; Upton, Z.; Voelcker, N.H. Sensor and imaging for wound healing: A review. Biosens. Bioelectron. 2013, 41, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Michelotti, F.; Sciacca, B.; Dominici, L.; Quaglio, M.; Descrovi, E.; Giorgis, F.; Geobaldo, F. Fast optical vapour sensing by Bloch surface waves on porous silicon membranes. Phys. Chem. Chem. Phys. 2010, 12, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Jia, Z.; Wu, X.R.; Li, P.; Wang, J. Influence of the permeable layer number of porous silicon microcavity on reflection spectrum. Optik 2015, 126, 599–602. [Google Scholar] [CrossRef]
- Sweetman, M.J.; Voelcker, N.H. Chemically patterned porous silicon photonic crystals towards internally referenced organic vapour sensors. RSC Adv. 2012, 2, 4620–4622. [Google Scholar] [CrossRef]
- Torres, V.; Martín, R.J.; Manotas, S.; Agulló, F.; MatínezDuart, J.M. Desarrollo de filtros interferenciales para emisores fotoluminiscentes basados en silicio poroso. Bol. Soc. Esp. Ceram. Vidr. 2004, 43, 506–509. [Google Scholar] [CrossRef]
- Theiβ, W. Optical Properties of porous silicon. Surf. Sci. Rep. 1997, 29, 91–93. [Google Scholar] [CrossRef]
- Klingdhirn, C. Semiconductor Optics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 79–88, 1439–2674. [Google Scholar]
- Van Groesen, E.; Sopaheluwakan, A.; Andonowati, A. Direct characterization of states and modes in defect grating structures. J. Nonlinear Opt. Phys. Mater. 2004, 13, 155–173. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 102–139. [Google Scholar]
- Bui, H.; van Nguyen, T.; Nguyen, T.A.; Pham, T.B.; Dang, Q.T.; Do, T.C.; Ngo, Q.M.; Coisson, R.; Pham, V.H. A Vapor Sensor Based on a Porous Silicon Microcavity for the Determination of solvent Solutions. J. Opt. Soc. Korea 2014, 18, 301–306. [Google Scholar] [CrossRef]

| Theoretical | Experimental | ||
|---|---|---|---|
| Porosity (%) | Refractive Index | Porosity (%) | Refractive Index |
| 50 | 2.06342 − 0.049064i | 39% | 3.4 |
| 66 | 1.9903 − 0.025293i | 74% | 1.62 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez Vivanco, M.D.R.; García, G.; Doti, R.; Faubert, J.; Lugo Arce, J.E. Time-Resolved Spectroscopy of Ethanol Evaporation on Free-Standing Porous Silicon Photonic Microcavities. Materials 2018, 11, 894. https://doi.org/10.3390/ma11060894
Jiménez Vivanco MDR, García G, Doti R, Faubert J, Lugo Arce JE. Time-Resolved Spectroscopy of Ethanol Evaporation on Free-Standing Porous Silicon Photonic Microcavities. Materials. 2018; 11(6):894. https://doi.org/10.3390/ma11060894
Chicago/Turabian StyleJiménez Vivanco, María Del Rayo, Godofredo García, Rafael Doti, Jocelyn Faubert, and Jesus Eduardo Lugo Arce. 2018. "Time-Resolved Spectroscopy of Ethanol Evaporation on Free-Standing Porous Silicon Photonic Microcavities" Materials 11, no. 6: 894. https://doi.org/10.3390/ma11060894
APA StyleJiménez Vivanco, M. D. R., García, G., Doti, R., Faubert, J., & Lugo Arce, J. E. (2018). Time-Resolved Spectroscopy of Ethanol Evaporation on Free-Standing Porous Silicon Photonic Microcavities. Materials, 11(6), 894. https://doi.org/10.3390/ma11060894




