One-Dimensional and Two-Dimensional Analytical Solutions for Functionally Graded Beams with Different Moduli in Tension and Compression
Abstract
:1. Introduction
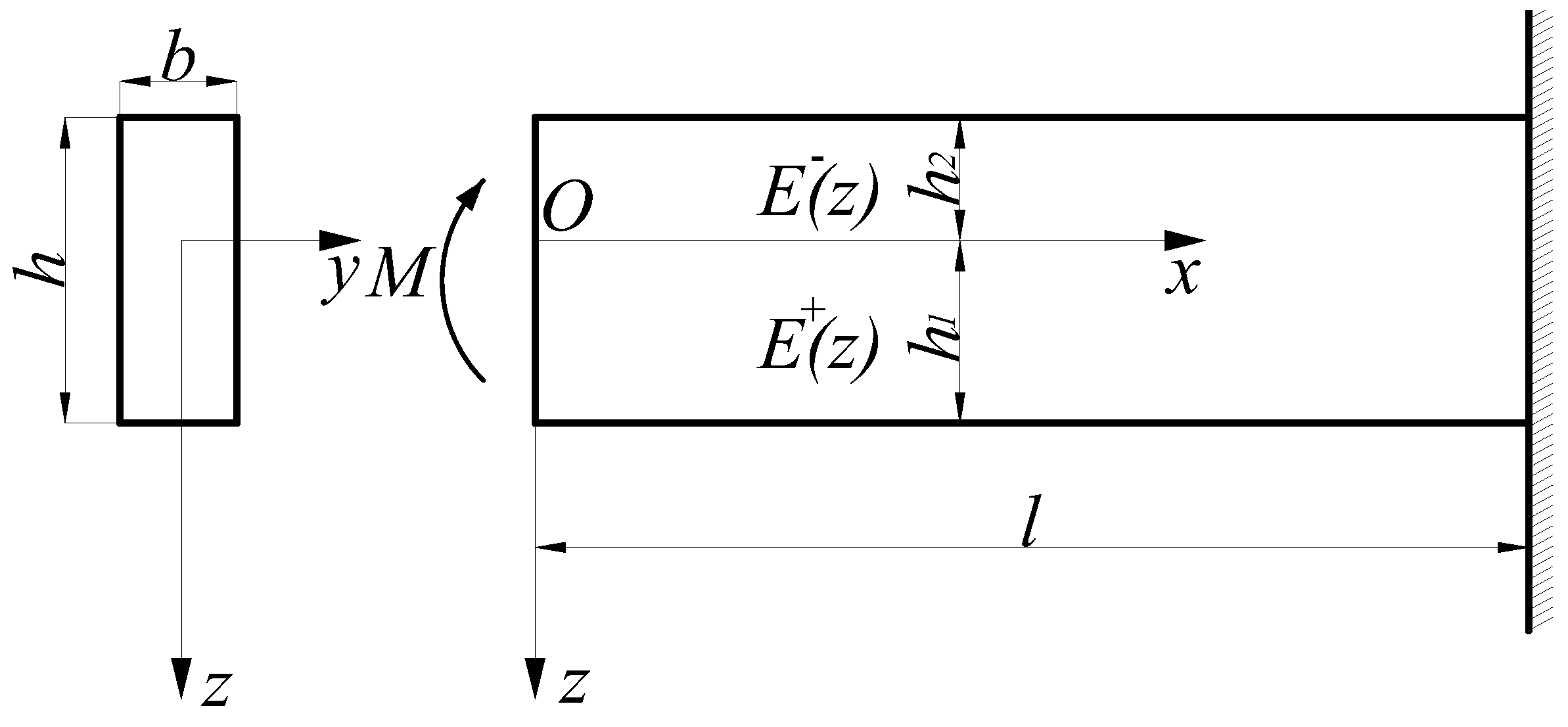
2. Functionally Graded Beams under Pure Bending
2.1. One-Dimensional Solution
2.1.1. Bending Stress
2.1.2. Deflection Curve
2.1.3. Determination of the Neutral Layer
2.2. Two-Dimensional Solution
2.2.1. Stress
2.2.2. Displacement
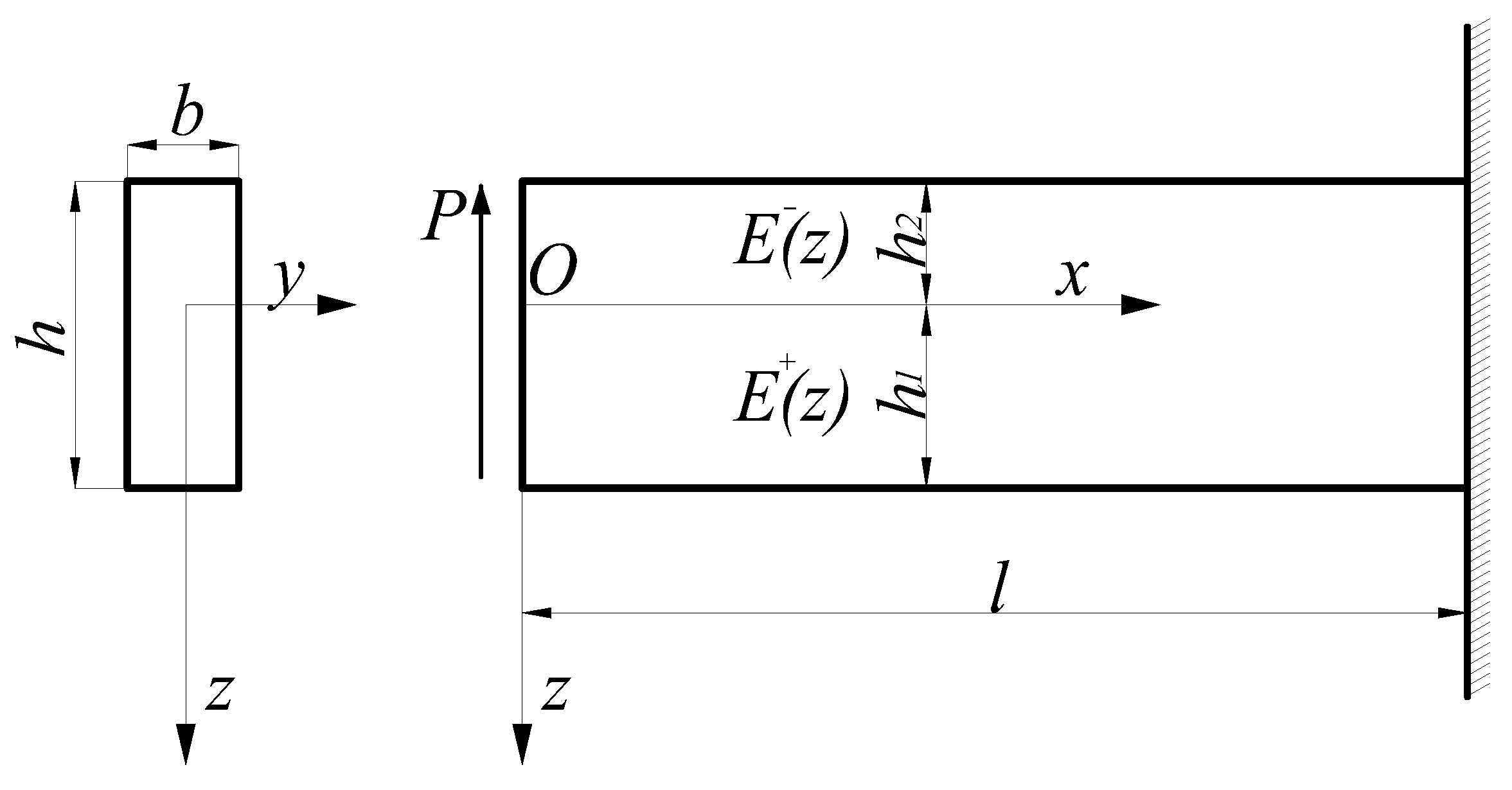
3. Bimodular Functionally Graded Beams under Latera-Force Bending
4. Results and Discussions
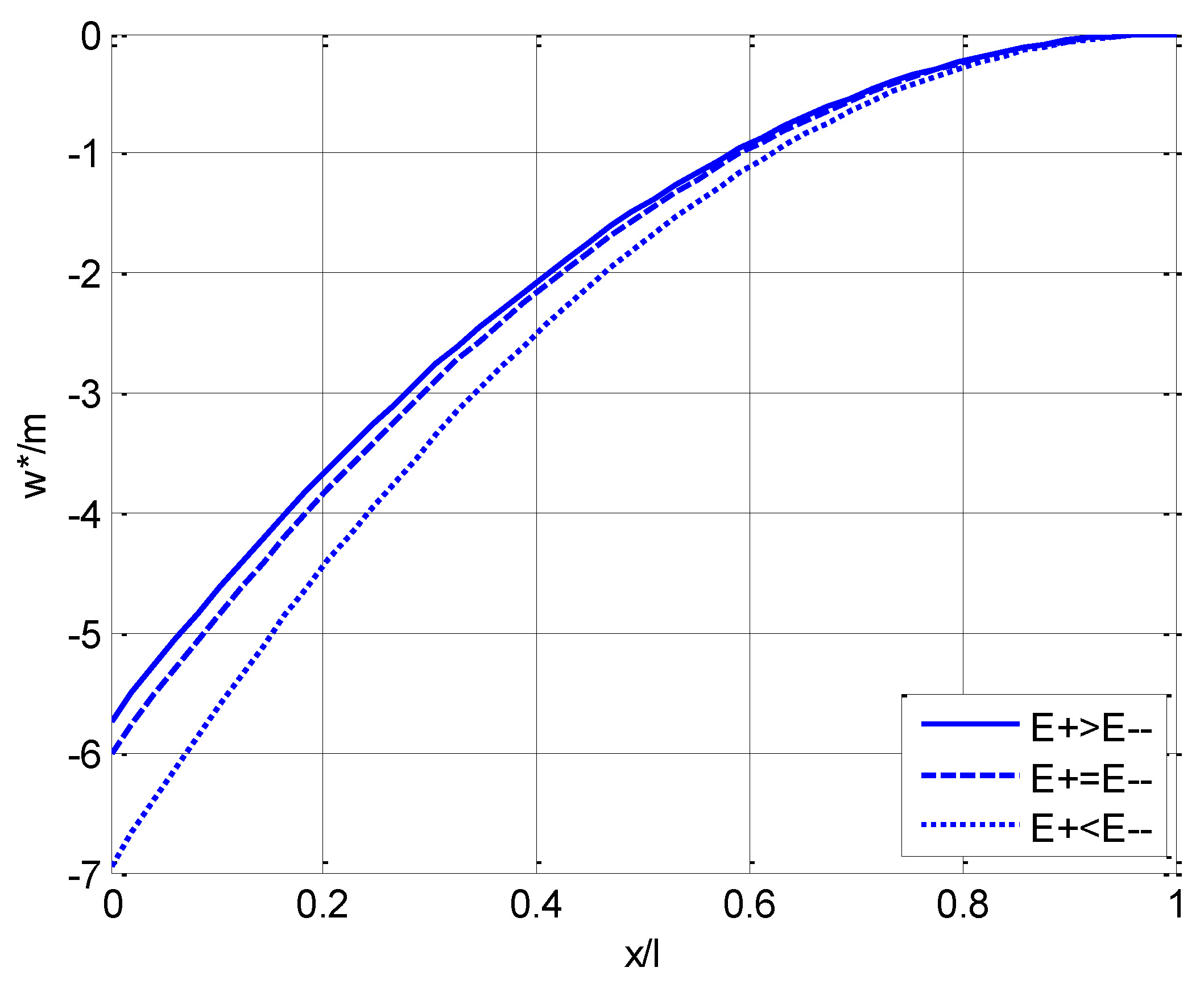
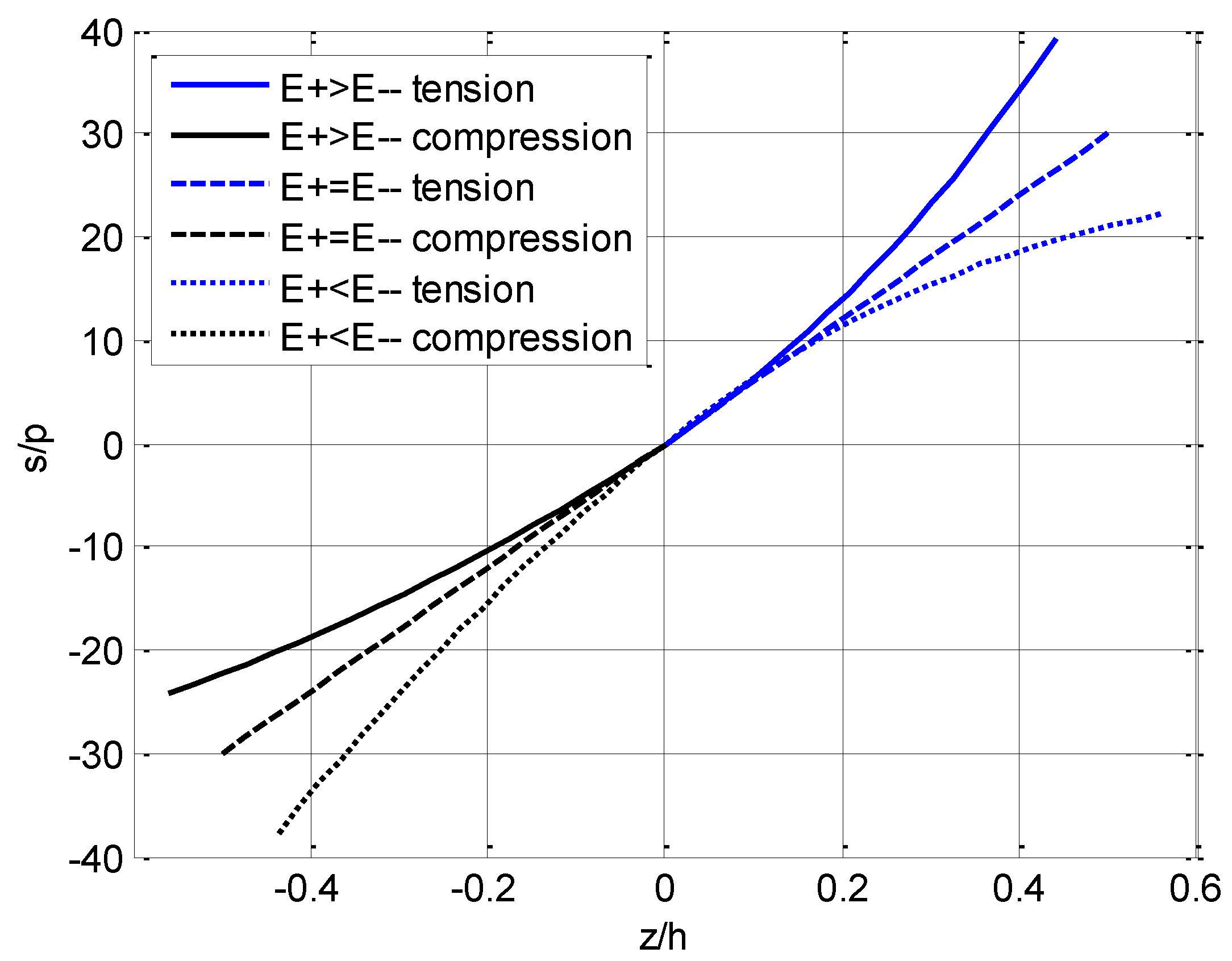
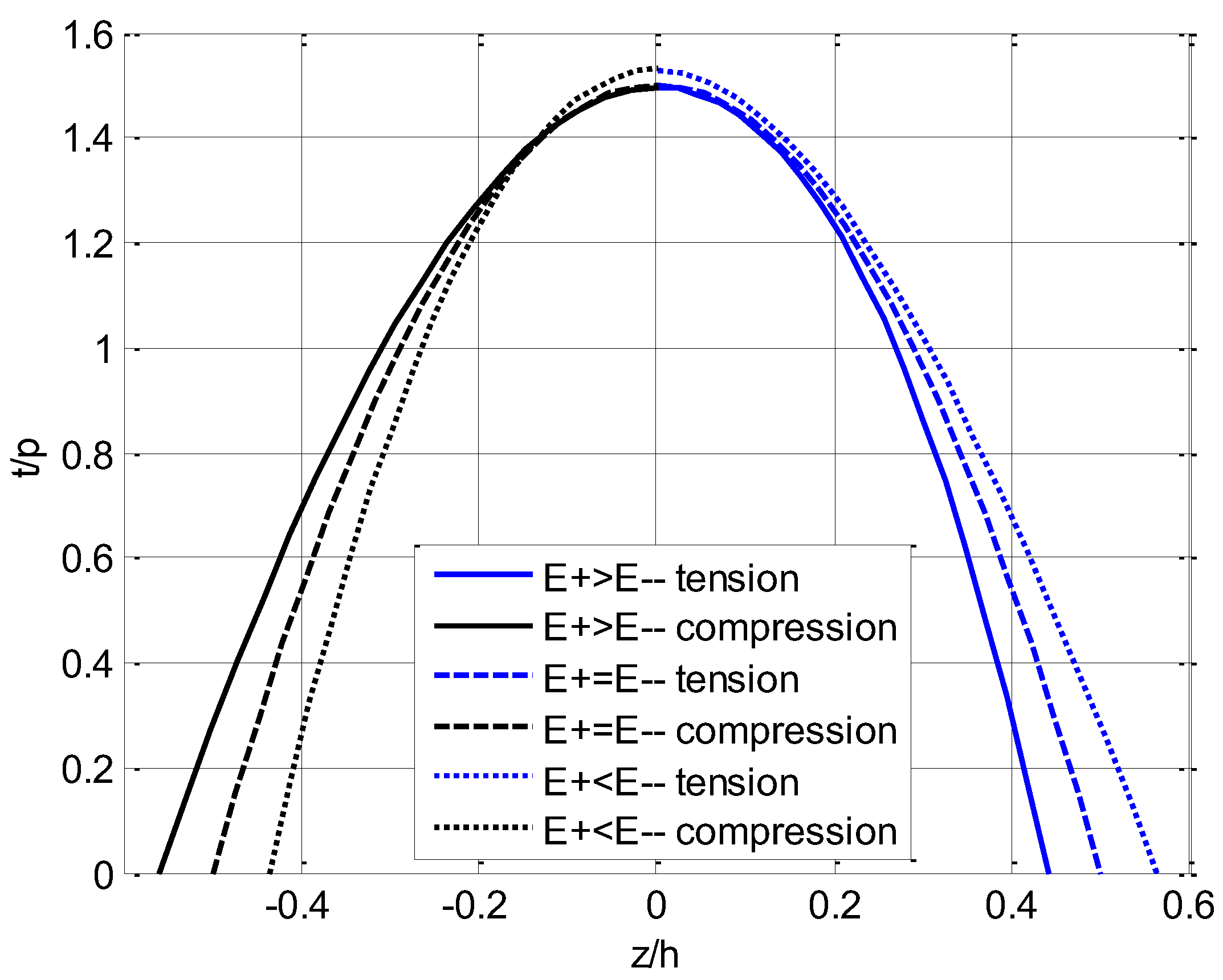
4.1. Comparision among Three Types of Beam
4.2. Plane Section Assumption
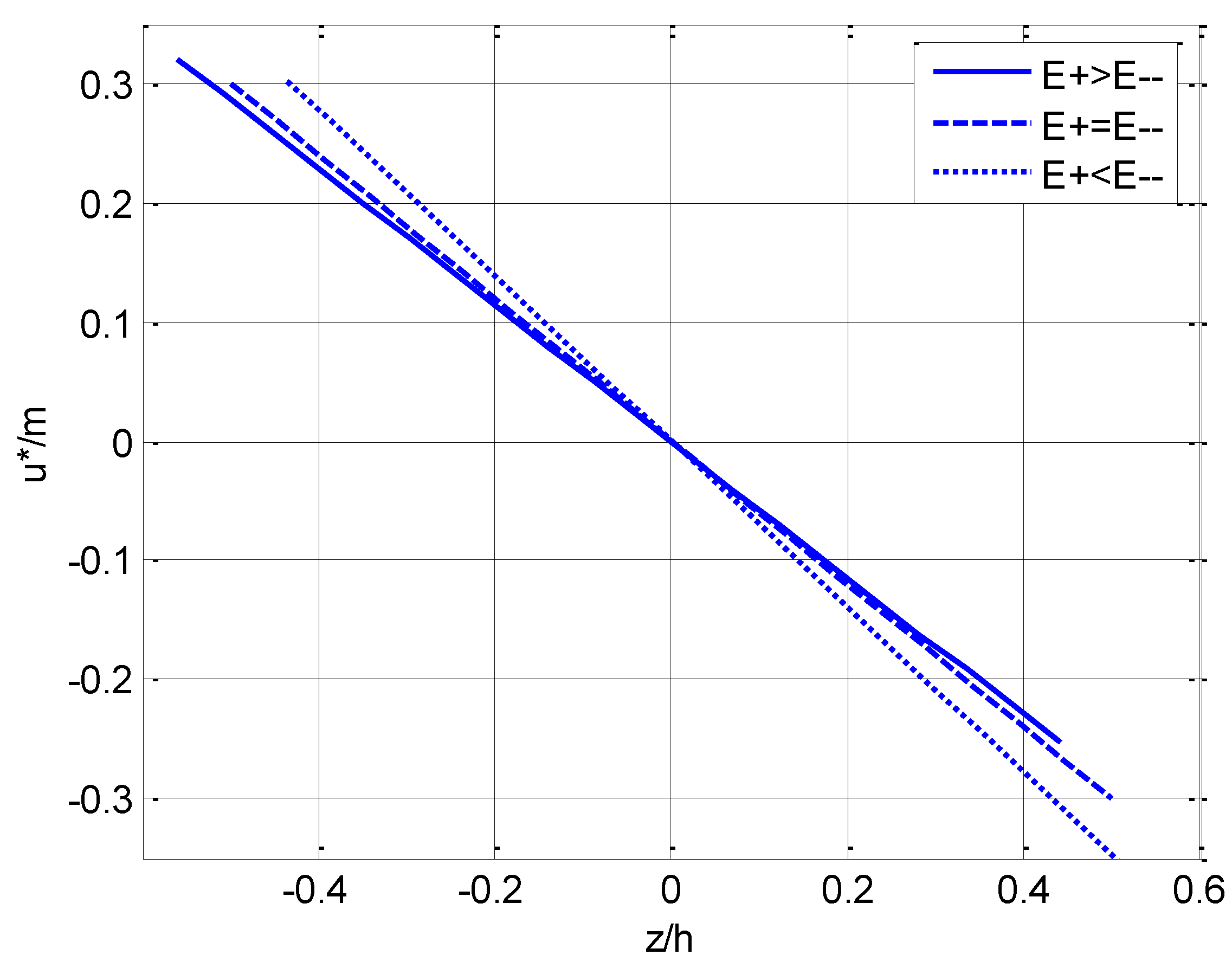
4.3. Bimodular Effect on Stress and Displacement
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Jones, R.M. Stress-strain relations for materials with different moduli in tension and compression. AIAA J. 1977, 15, 16–23. [Google Scholar] [CrossRef]
- Bertoldi, K.; Bigoni, D.; Drugan, W.J. Nacre: An orthotropic and bimodular elastic material. Compos. Sci. Technol. 2008, 68, 1363–1375. [Google Scholar] [CrossRef]
- Tran, A.D.; Bert, C.W. Bending of thick beams of bimodulus materials. Compos. Struct. 1982, 15, 627–642. [Google Scholar] [CrossRef]
- Reddy, J.N. Transient response of laminated, bimodular-material, composite rectangular plates. J. Compos. Mater. 1982, 16, 139–152. [Google Scholar] [CrossRef]
- Bert, C.W.; Gordaninejad, F. Transverse shear effects in bimodular composite laminates. J. Compos. Mater. 1983, 17, 282–298. [Google Scholar] [CrossRef]
- Ramana Murthy, P.V.; Rao, K.P. Analysis of curved laminated beams of bimodulus composite materials. J. Compos. Mater. 1983, 17, 435–438. [Google Scholar] [CrossRef]
- Bruno, D.; Lato, S.; Zinno, R. Nonlinear analysis of doubly curved composite shells of bimodular material. Compos. Part B 1993, 3, 419–435. [Google Scholar] [CrossRef]
- Zinno, R.; Greco, F. Damage evolution in bimodular laminated composites under cyclic loading. Compos. Struct. 2001, 53, 381–402. [Google Scholar] [CrossRef]
- Ambartsumyan, S.A. Basic equations and relations in the theory of anisotropic bodies with different moduli in tension and compression. Inzh. Zhur. MTT (Proc. Acad. Sci. USSR Eng. J. Mech. Solids) 1969, 3, 51–61. [Google Scholar]
- Liu, X.B.; Zhang, Y.Z. Modulus of elasticity in shear and accelerate convergence of different extension-compression elastic modulus finite element method. J. Dalian Univ. Technol. 2000, 40, 527–530. [Google Scholar]
- Ye, Z.M.; Chen, T.; Yao, W.J. Progresses in elasticity theory with different modulus in tension and compression and related FEM. Chin. J. Mech. Eng. 2004, 26, 9–14. [Google Scholar]
- Zhao, H.L.; Ye, Z.M. Analytic elasticity solution of bi-modulus beams under combined loads. Appl. Math. Mech. (Engl. Ed.) 2015, 36, 427–438. [Google Scholar] [CrossRef]
- Du, Z.L.; Zhang, Y.P.; Zhang, W.S.; Guo, X. A new computational framework for materials with different mechanical responses in tension and compression and its applications. Int. J. Solids Struct. 2016, 100–101, 54–73. [Google Scholar] [CrossRef]
- Sun, J.Y.; Zhu, H.Q.; Qin, S.H.; Yang, D.L.; He, X.T. A review on the research of mechanical problems with different moduli in tension and compression. J. Mech. Sci. Technol. 2010, 24, 1845–1854. [Google Scholar] [CrossRef]
- Sankar, B.V. An elasticity solution for functionally graded beams. Compos. Sci. Technol. 2001, 61, 689–696. [Google Scholar] [CrossRef]
- Sankar, B.V.; Tzeng, J.T. Thermal stresses in functionally graded beams. AIAA J. 2002, 40, 1228–1232. [Google Scholar] [CrossRef]
- Venkataraman, S.; Sankar, B.V. Elasticity solution for stresses in a sandwich beam with functionally graded core. AIAA J. 2003, 41, 2501–2505. [Google Scholar] [CrossRef]
- Zhu, H.; Sankar, B.V. A combined Fourier series-Galerkin method for the analysis of functionally graded beams. ASME J. Appl. Mech. 2004, 71, 421–424. [Google Scholar] [CrossRef]
- Zhong, Z.; Yu, T. Analytical solution of a cantilever functionally graded beam. Compos. Sci. Technol. 2007, 67, 481–488. [Google Scholar] [CrossRef]
- Nie, G.J.; Zhong, Z.; Chen, S. Analytical solution for a functionally graded beam with arbitrary graded material properties. Compos. Part B 2013, 44, 274–282. [Google Scholar] [CrossRef]
- Daouadji, T.H.; Henni, A.H.; Tounsi, A.; Abbes, A.B. Elasticity solution of a cantilever functionally graded beam. Appl. Compos. Mater. 2013, 20, 1–15. [Google Scholar] [CrossRef]
- Yao, W.J.; Ye, Z.M. Analytical solution for bending beam subject to lateral force with different modulus. Appl. Math. Mech. (Engl. Ed.) 2004, 25, 1107–1117. [Google Scholar]
- He, X.T.; Chen, S.L.; Sun, J.Y. Elasticity solution of simple beams with different modulus under uniformly distributed load. Chin. J. Eng. Mech. 2007, 24, 51–56. [Google Scholar]
- He, X.T.; Xu, P.; Sun, J.Y.; Zheng, Z.L. Analytical solutions for bending curved beams with different moduli in tension and compression. Mech. Adv. Mater. Struct. 2015, 22, 325–337. [Google Scholar] [CrossRef]
- He, X.T.; Chen, Q.; Sun, J.Y.; Zheng, Z.L.; Chen, S.L. Application of the Kirchhoff hypothesis to bending thin plates with different moduli in tension and compression. J. Mech. Mater. Struct. 2010, 5, 755–769. [Google Scholar] [CrossRef]
- He, X.T.; Li, W.M.; Sun, J.Y.; Wang, Z.X. An elasticity solution of functionally graded beams with different moduli in tension and compression. J. Mech. Mater. Struct. 2018, 25, 143–154. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Bui, T.Q. Vibration analysis of third-order shear deformable FGM beams with elastic support by Chebyshev collocation method. Int. J. Struct. Stab. Dyn. 2018, 18, 1850071. [Google Scholar] [CrossRef]
- Fu, Y.; Yao, J.; Wan, Z.; Zhao, G. Free vibration analysis of moderately thick orthotropic functionally graded plates with general boundary restraints. Materials 2018, 11, 273. [Google Scholar] [CrossRef] [PubMed]
- Nguyen Dinh, D.; Nguyen, P.D. The dynamic response and vibration of functionally graded carbon nanotube-reinforced composite (FG-CNTRC) truncated conical shells resting on elastic foundations. Materials 2017, 10, 1194. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Pañeda, E.; Gallego, R. Numerical analysis of quasi-static fracture in functionally graded materials. Int. J. Mech. Mater. Des. 2015, 11, 405–424. [Google Scholar] [CrossRef]
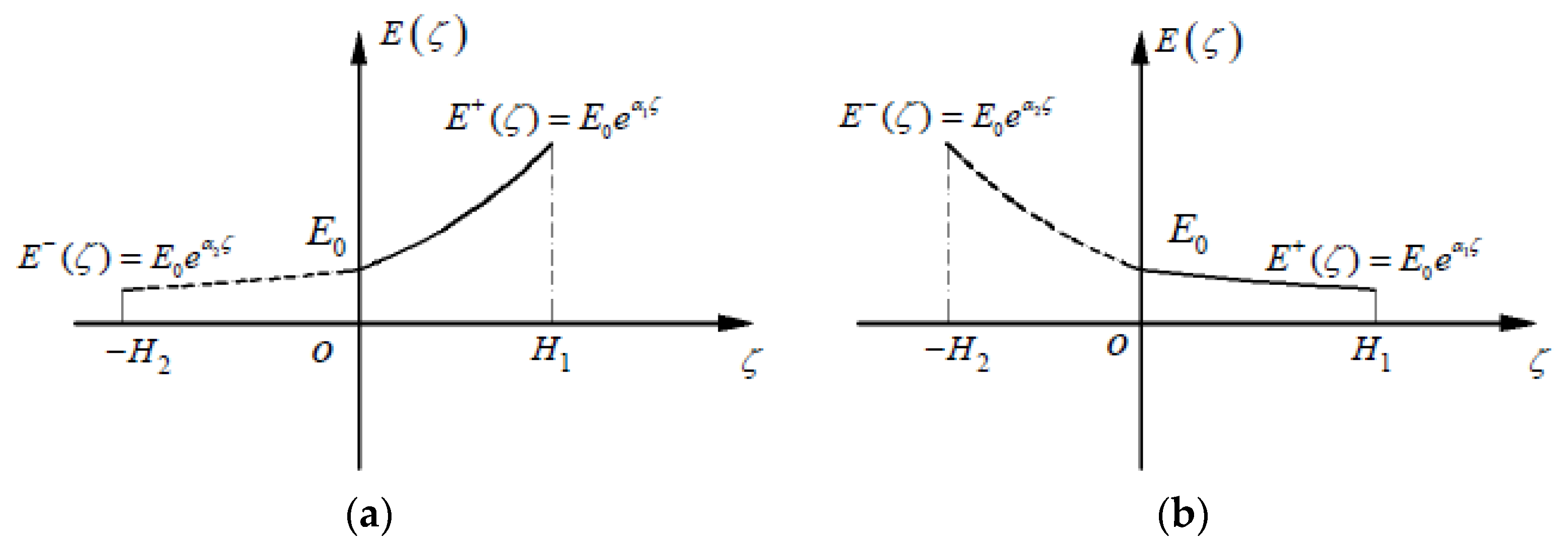
| Quantities | A Classical Beam | A FGM Beam | A Bimodular FGM Beam |
|---|---|---|---|
| Modulus of elasticity | |||
| Moment of inertia | |||
| Bending stiffness | |||
| Curvature | |||
| Bending stress | |||
| Static moment when computing shearing stress | |||
| Shearing stress | |||
| Cases | Groups | |||||
|---|---|---|---|---|---|---|
| (a) | 1.0 | 2.0 | 0.3725 | 0.6275 | 0.0560 | |
| (b) | 2.0 | 1.0 | 0.3859 | 0.6141 | 0.0836 | |
| (c) | 1.0 | 1.0 | 0.4180 | 0.5820 | 0.0762 | |
| (d) | 1.0 | 0.5 | 0.4399 | 0.5601 | 0.0872 | |
| (e) | 0.5 | 0.5 | 0.4585 | 0.5415 | 0.0815 | |
| (f) | 0 | 0 | 1/2 | 1/2 | 1/12 | |
| (g) | −2.0 | −1.0 | 0.6275 | 0.3725 | 0.0560 | |
| (h) | −1.0 | −2.0 | 0.6141 | 0.3859 | 0.0836 | |
| (i) | −1.0 | −1.0 | 0.5820 | 0.4180 | 0.0762 | |
| (j) | −1.0 | −0.5 | 0.5638 | 0.4362 | 0.0720 | |
| (k) | −0.5 | −0.5 | 0.5415 | 0.4585 | 0.0815 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Sun, J.-y.; Dong, J.; He, X.-t. One-Dimensional and Two-Dimensional Analytical Solutions for Functionally Graded Beams with Different Moduli in Tension and Compression. Materials 2018, 11, 830. https://doi.org/10.3390/ma11050830
Li X, Sun J-y, Dong J, He X-t. One-Dimensional and Two-Dimensional Analytical Solutions for Functionally Graded Beams with Different Moduli in Tension and Compression. Materials. 2018; 11(5):830. https://doi.org/10.3390/ma11050830
Chicago/Turabian StyleLi, Xue, Jun-yi Sun, Jiao Dong, and Xiao-ting He. 2018. "One-Dimensional and Two-Dimensional Analytical Solutions for Functionally Graded Beams with Different Moduli in Tension and Compression" Materials 11, no. 5: 830. https://doi.org/10.3390/ma11050830
APA StyleLi, X., Sun, J.-y., Dong, J., & He, X.-t. (2018). One-Dimensional and Two-Dimensional Analytical Solutions for Functionally Graded Beams with Different Moduli in Tension and Compression. Materials, 11(5), 830. https://doi.org/10.3390/ma11050830





