Band Structures and Transport Properties of High-Performance Half-Heusler Thermoelectric Materials by First Principles
Abstract
:1. Introduction
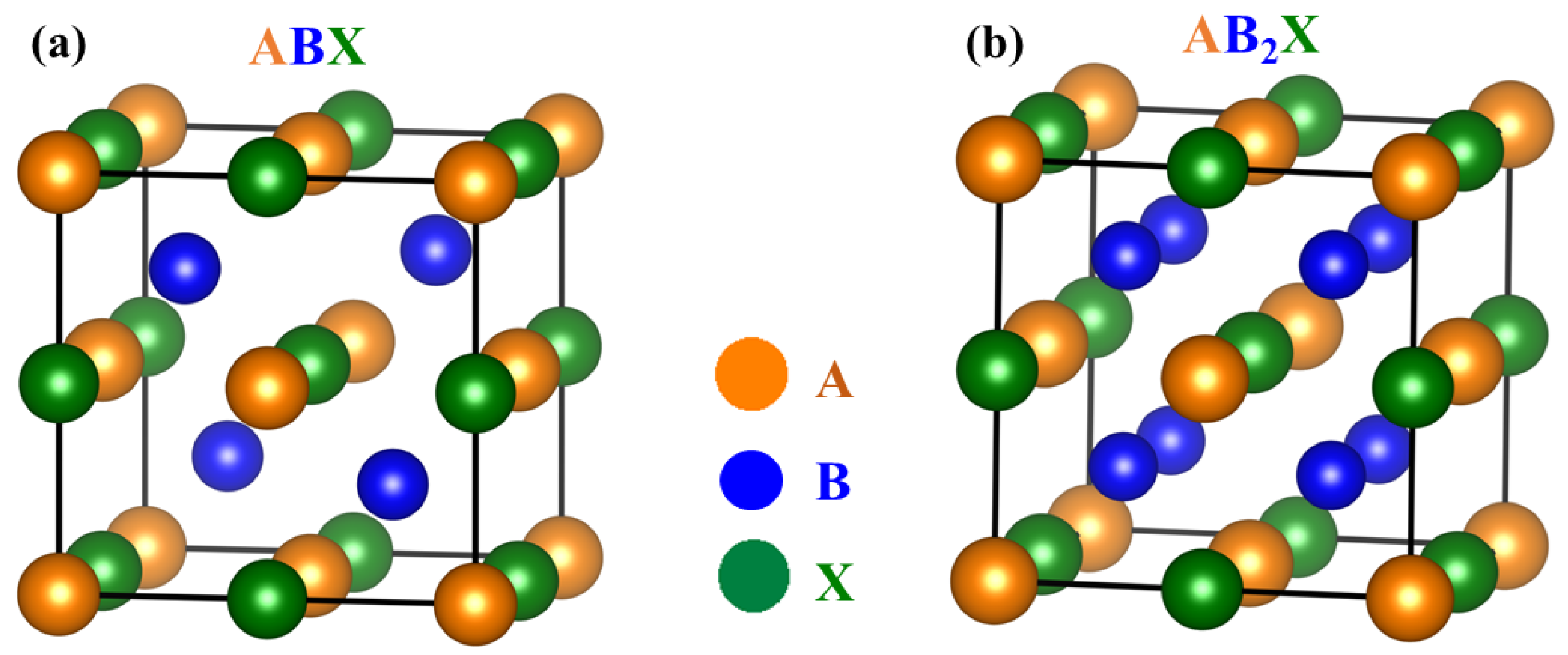
2. Manipulating the Band Structures of HH Compounds
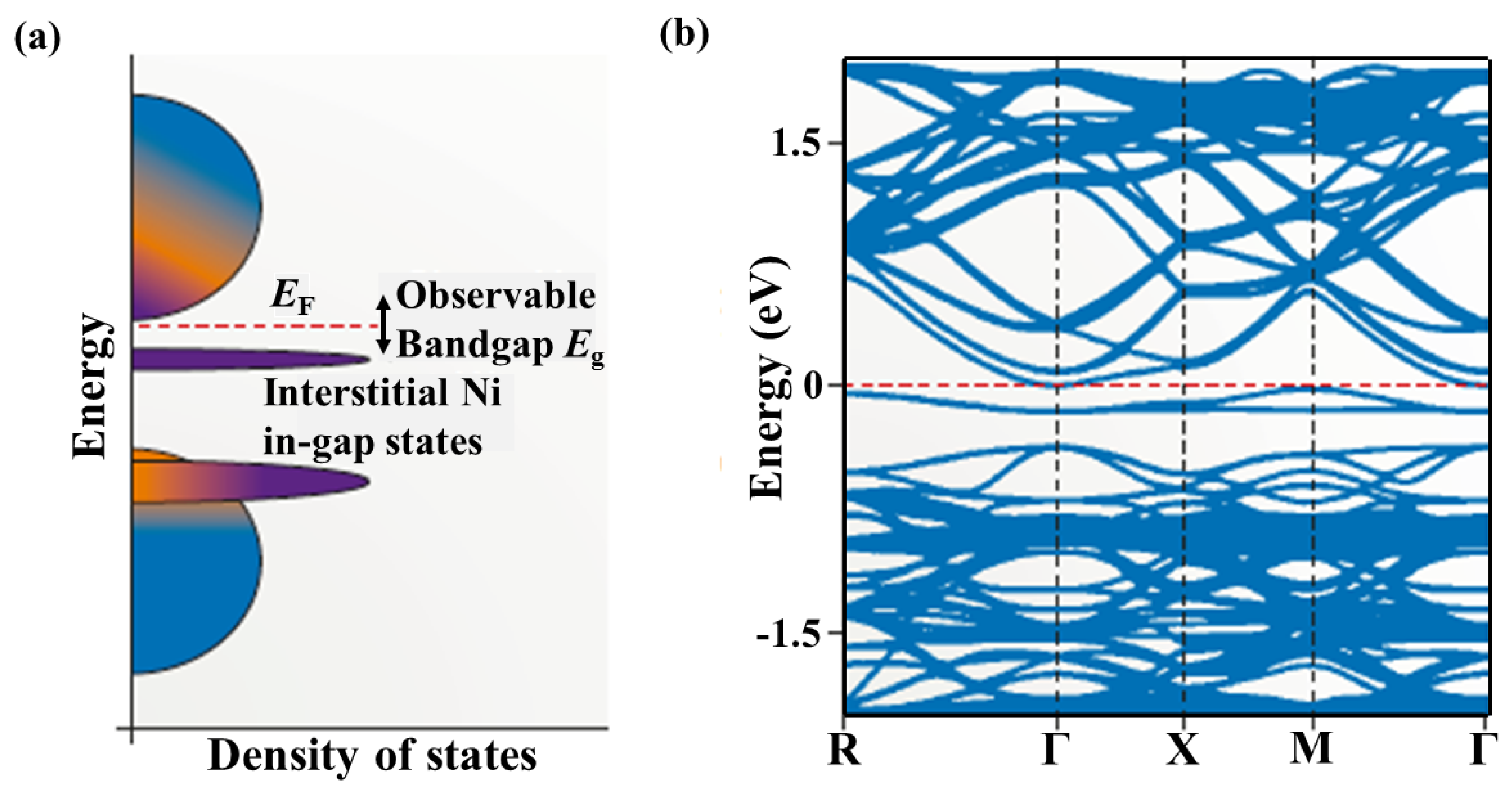
2.1. Band Structures and Atomic Disorders in N-Type MNiSn
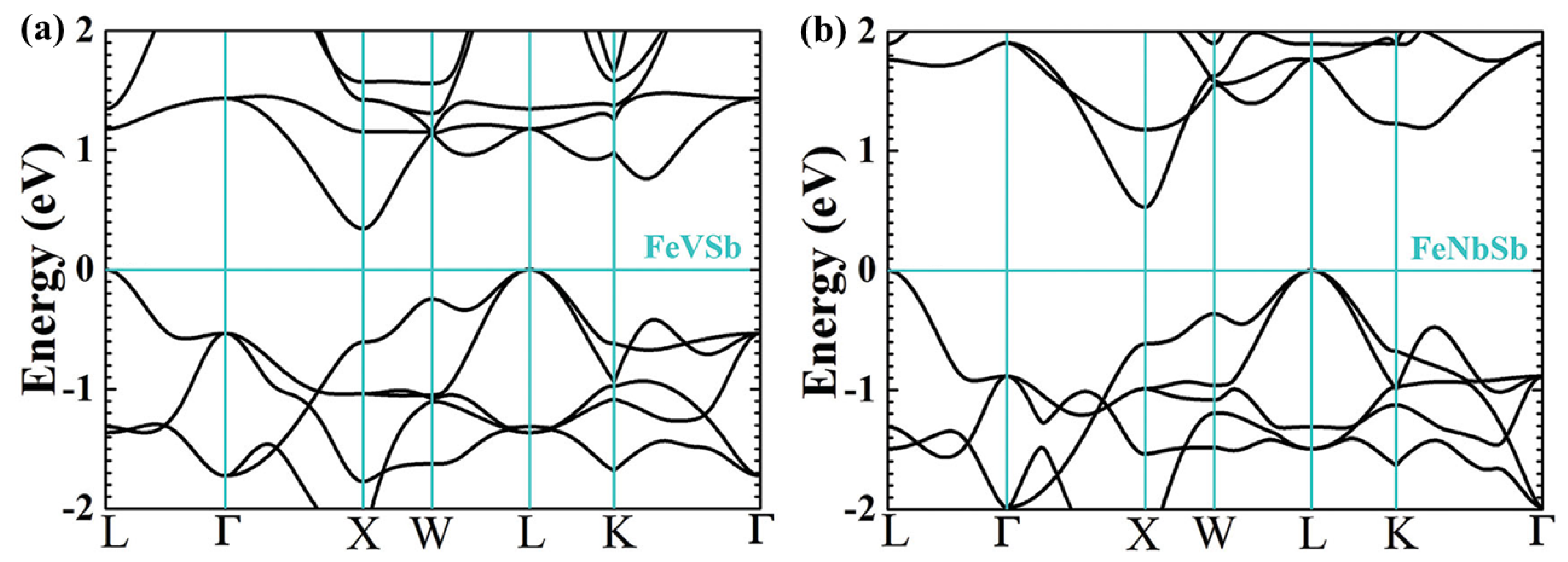
2.2. Performance Optimization of P-Type Heavy-Band HH Using Band Engineering
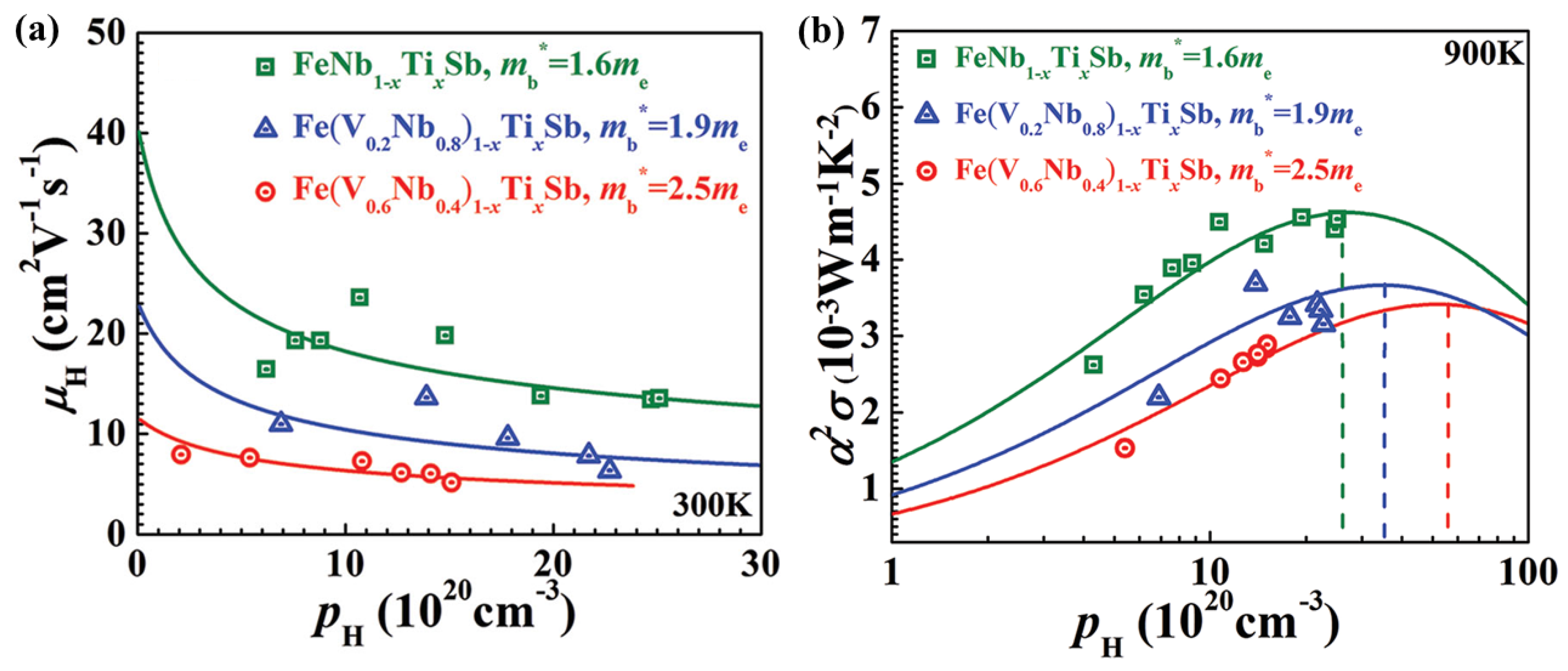
3. Electronic Transport Properties of HH Compounds
3.1. Constant Relaxation Time Approximation
3.2. Constant Mean Free Path Approximation
3.3. Calculations of Relaxation Times
4. Lattice Thermal Conductivities of HH Compounds
5. Conclusions and Outlook
Funding
Acknowledgments
Conflicts of Interest
References
- He, J.; Tritt, T.M. Advances in thermoelectric materials research: Looking back and moving forward. Science 2017, 357, eaak9997. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; Shi, X.; LaLonde, A.; Wang, H.; Chen, L.; Snyder, G.J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Page, A.; Poudeu, P.F.P.; Uher, C. A first-principles approach to half-heusler thermoelectrics: Accelerated prediction and understanding of material properties. J. Materiomics 2016, 2, 104–113. [Google Scholar] [CrossRef]
- Yang, J.; Xi, L.; Qiu, W.; Wu, L.; Shi, X.; Chen, L.; Yang, J.; Zhang, W.; Uher, C.; Singh, D.J. On the tuning of electrical and thermal transport in thermoelectrics: An integrated theory-experiment perspective. NPJ Comput. Mater. 2016, 2, 114–130. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Fu, C.; Xie, H.; Liu, Y.; Zhao, X. High efficiency half-heusler thermoelectric materials for energy harvesting. Adv. Energy Mater. 2015, 5, 1500588. [Google Scholar] [CrossRef]
- Xin, J.; Tang, Y.; Liu, Y.; Zhao, X.; Pan, H.; Zhu, T. Valleytronics in thermoelectric materials. NPJ Quantum Mater. 2018, 3, 9. [Google Scholar] [CrossRef]
- Zaitsev, V.K.; Fedorov, M.I.; Gurieva, E.A.; Eremin, I.S.; Konstantinov, P.P.; Samunin, A.Y.; Vedernikov, M.V. Highly effective Mg2Si1−xSnx thermoelectrics. Phys. Rev. B 2006, 74, 045207. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, R.; Cheng, N.; Zhang, Y.; Yang, J.; Uher, C.; Shi, X.; Chen, L.; Zhang, W. High-performance pseudocubic thermoelectric materials from non-cubic chalcopyrite compounds. Adv. Mater. 2014, 26, 3848–3853. [Google Scholar] [CrossRef] [PubMed]
- Murphy-Armando, F.; Fahy, S. First-principles calculation of carrier-phonon scattering in n-type Si1−xGex alloys. Phys. Rev. B 2008, 78, 035202. [Google Scholar] [CrossRef]
- Zhu, T.; Liu, Y.; Fu, C.; Heremans, J.P.; Snyder, J.G.; Zhao, X. Compromise and synergy in high-efficiency thermoelectric materials. Adv. Mater. 2017, 29, 1605884. [Google Scholar] [CrossRef] [PubMed]
- Morelli, D.T.; Jovovic, V.; Heremans, J.P. Intrinsically minimal thermal conductivity in cubic I−V−VI2 semiconductors. Phys. Rev. Lett. 2008, 101, 035901. [Google Scholar] [CrossRef] [PubMed]
- Jana, M.K.; Pal, K.; Waghmare, U.V.; Biswas, K. The origin of ultralow thermal conductivity in InTe: Lone-pair-induced anharmonic rattling. Angew. Chem. Int. Ed. 2016, 55, 7792–7796. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Li, W.; Li, S.; Zhang, X.; Chen, Z.; Xu, Y.; Chen, Y.; Pei, Y. High thermoelectric performance of Ag9GaSe6 enabled by low cutoff frequency of acoustic phonons. Joule 2017, 1, 816–830. [Google Scholar] [CrossRef]
- Shi, X.; Chen, L.; Uher, C. Recent advances in high-performance bulk thermoelectric materials. Int. Mater. Rev. 2016, 61, 379–415. [Google Scholar] [CrossRef]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.D.; Ozolins, V.; Heremans, J.P. Lone pair electrons minimize lattice thermal conductivity. Energy Environ. Sci. 2013, 6, 570–578. [Google Scholar] [CrossRef]
- Kurosaki, K.; Kosuga, A.; Muta, H.; Uno, M.; Yamanaka, S. Ag9TlTe5: A high-performance thermoelectric bulk material with extremely low thermal conductivity. Appl. Phys. Lett. 2005, 87, 061919. [Google Scholar] [CrossRef]
- Yu, J.; Xia, K.; Zhao, X.; Zhu, T. High performance p-type half-Heusler thermoelectric materials. J. Phys. D Appl. Phys. 2018, 51, 113001. [Google Scholar] [CrossRef]
- Xie, W.; Weidenkaff, A.; Tang, X.; Zhang, Q.; Poon, J.; Tritt, T.M. Recent advances in nanostructured thermoelectric half-heusler compounds. Nanomaterials 2012, 2, 379–412. [Google Scholar] [CrossRef] [PubMed]
- Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Kimura, Y.; Tanoguchi, T.; Kita, T. Vacancy site occupation by Co and Ir in half-Heusler ZrNiSn and conversion of the thermoelectric properties from n-type to p-type. Acta Mater. 2010, 58, 4354–4361. [Google Scholar] [CrossRef]
- Aliev, F.G.; Brandt, N.B.; Kozyr’Kov, V.V.; Moshchalkov, V.V.; Skolozdra, R.V.; Stadnyk, Y.V. Metal-insulator transition of RNiSn (R = Zr, Hf, Ti) intermetallic vacancy systems. JETP Lett. 1987, 45, 684–687. [Google Scholar]
- Aliev, F.G.; Brandt, N.B.; Moshchalkov, V.V.; Kozyrkov, V.V.; Skolozdra, R.V.; Belogorokhov, A.I. Gap at the fermi level in the intermetallic vacancy system RniSn (R = Ti, Zr, Hf). Z. Phys. B 1989, 75, 167–171. [Google Scholar] [CrossRef]
- Qiu, P.; Yang, J.; Huang, X.; Chen, X.; Chen, L. Effect of antisite defects on band structure and thermoelectric performance of ZrNiSn half-heusler alloys. Appl. Phys. Lett. 2010, 96, 152105. [Google Scholar] [CrossRef]
- Xie, H.H.; Mi, J.L.; Hu, L.P.; Lock, N.; Chirstensen, M.; Fu, C.G.; Iversen, B.B.; Zhao, X.B.; Zhu, T.J. Interrelation between atomic switching disorder and thermoelectric properties of ZrNiSn half-Heusler compounds. CrystEngComm 2012, 14, 4467–4471. [Google Scholar] [CrossRef]
- Do, D.T.; Mahanti, S.D.; Pulikkoti, J.J. Electronic structure of Zr-Ni-Sn systems: Role of clustering and nanostructures in half-Heusler and Heusler limits. J. Phys. Condens. Matter 2014, 26, 275501. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Zhu, T.; Pei, Y.; Xie, H.; Wang, H.; Snyder, G.J.; Liu, Y.; Liu, Y.; Zhao, X. High band degeneracy contributes to high thermoelectric performance in p-type half-Heusler compounds. Adv. Energy Mater. 2014, 4, 1400600. [Google Scholar] [CrossRef]
- Fu, C.; Zhu, T.; Liu, Y.; Xie, H.; Zhao, X. Band engineering of high performance p-ype FeNbSb based half-Heusler thermoelectric materials for figure of merit zT > 1. Energy Environ. Sci. 2015, 8, 216–220. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, H.; Fu, C.; Snyder, G.J.; Zhao, X.; Zhu, T. Demonstration of a phonon-glass electron-crystal strategy in (Hf,Zr)NiSn half-Heusler thermoelectric materials by alloying. J. Mater. Chem A 2015, 3, 22716–22722. [Google Scholar] [CrossRef]
- Schwall, M.; Balke, B. Phase separation as a key to a thermoelectric high efficiency. Phys. Chem. Chem. Phys. 2013, 15, 1868–1872. [Google Scholar] [CrossRef] [PubMed]
- Schwall, M.; Balke, B. On the phase separation in n-type thermoelectric half-Heusler materials. Materials 2018, 11, 649. [Google Scholar] [CrossRef] [PubMed]
- Ouardi, S.; Fecher, G.H.; Balke, B.; Schwall, M.; Kozina, X.; Stryganyuk, G.; Felser, C.; Ikenaga, E.; Yamashita, Y.; Ueda, S.; et al. Thermoelectric properties and electronic structure of substituted heusler compounds: NiTi0.3−xScxZr0.35Hf0.35Sn. Appl. Phys. Lett. 2010, 97, 8616. [Google Scholar] [CrossRef]
- Xie, H.; Wang, H.; Pei, Y.; Fu, C.; Liu, X.; Snyder, G.J.; Zhao, X.; Zhu, T. Beneficial contribution of alloy disorder to electron and phonon transport in half-heusler thermoelectric materials. Adv. Funct. Mater. 2013, 23, 5123–5130. [Google Scholar] [CrossRef]
- Mao, J.; Zhou, J.; Zhu, H.; Liu, Z.; Zhang, H.; He, R.; Chen, G.; Ren, Z. Thermoelectric properties of n-type ZrNiPb-based half-Heuslers. Chem. Mater. 2017, 29, 867–872. [Google Scholar] [CrossRef]
- Toboła, J.; Jodin, L.; Pecheur, P.; Scherrer, H.; Venturini, G.; Malaman, B.; Kaprzyk, S. Composition-induced metal-semiconductor-metal crossover in half-Heusler Fe1−xNixTiSb. Phys. Rev. B 2001, 64, 155103. [Google Scholar] [CrossRef]
- Inorganic Crystal Structure Database (ICSD). Available online: http://icsd.ill.eu/icsd/ (accessed on 8 May 2018).
- Yang, J.; Li, H.; Wu, T.; Zhang, W.; Chen, L.; Yang, J. Evaluation of half-Heusler compounds as thermoelectric materials based on the calculated electrical transport properties. Adv. Funct. Mater. 2008, 18, 2880–2888. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Öğüt, S.; Rabe, K.M. Band gap and stability in the ternary intermetallic compounds NiSnM(M = Ti,Zr,Hf): A first-principles study. Phys. Rev. B 1995, 51, 10443–10453. [Google Scholar] [CrossRef]
- Larson, P.; Mahanti, S.D.; Kanatzidis, M.G. Structural stability of Ni-containing half-Heusler compounds. Phys. Rev. B 2000, 62, 12754–12762. [Google Scholar] [CrossRef]
- Miyamoto, K.; Kimura, A.; Sakamoto, K.; Ye, M.; Cui, Y.; Shimada, K.; Namatame, H.; Taniguchi, M.; Fujimori, S.-I.; Saitoh, Y.; et al. In-gap Electronic states responsible for the excellent thermoelectric properties of Ni-based half-Heusler alloys. Appl. Phys. Express 2008, 1, 081901. [Google Scholar] [CrossRef]
- Hazama, H.; Matsubara, M.; Asahi, R.; Takeuchi, T. Improvement of thermoelectric properties for half-Heusler TiNiSn by interstitial Ni defects. J. Appl. Phys. 2011, 110, 063710. [Google Scholar] [CrossRef]
- Douglas, J.E.; Chater, P.A.; Brown, C.M.; Pollock, T.M.; Seshadri, R. Nanoscale structural heterogeneity in Ni-rich half-Heusler TiNiSn. J. Appl. Phys. 2014, 116, 163514. [Google Scholar] [CrossRef]
- Zeier, W.G.; Schmitt, J.; Hautier, G.; Aydemir, U.; Gibbs, Z.M.; Felser, C.; Snyder, G.J. Engineering half-Heusler thermoelectric materials using Zintl chemistry. Nat. Rev. Mater. 2016, 1, 16032. [Google Scholar] [CrossRef]
- Zahedifar, M.; Kratzer, P. Band structure and thermoelectric properties of half-Heusler semiconductors from many-body perturbation theory. Phys. Rev. B 2018, 97, 035204. [Google Scholar] [CrossRef]
- Fu, C.; Xie, H.; Liu, Y.; Zhu, T.J.; Xie, J.; Zhao, X.B. Thermoelectric properties of FeVSb half-Heusler compounds by levitation melting and spark plasma sintering. Intermetallics 2013, 32, 39–43. [Google Scholar] [CrossRef]
- Fu, C.; Xie, H.; Zhu, T.J.; Xie, J.; Zhao, X.B. Enhanced phonon scattering by mass and strain field fluctuations in Nb substituted FeVSb half-Heusler thermoelectric materials. J. Appl. Phys. 2012, 112, 124915. [Google Scholar] [CrossRef]
- Fu, C.; Liu, Y.; Xie, H.; Liu, X.; Zhao, X.; Jeffrey Snyder, G.; Xie, J.; Zhu, T. Electron and phonon transport in Co-doped FeV0.6Nb0.4Sb half-Heusler thermoelectric materials. J. Appl. Phys. 2013, 114, 134905. [Google Scholar] [CrossRef]
- Zou, M.; Li, J.F.; Guo, P.; Kita, T. Synthesis and thermoelectric properties of fine-grained FeVSb system half-Heusler compound polycrystals with high phase purity. J. Phys. D Appl. Phys. 2010, 43, 415403. [Google Scholar] [CrossRef]
- Jodin, L.; Tobola, J.; Pecheur, P.; Scherrer, H.; Kaprzyk, S. Effect of substitutions and defects in half-Heusler FeVSb studied by electron transport measurements and KKR-CPA electronic structure calculations. Phys. Rev. B 2004, 70, 184207. [Google Scholar] [CrossRef]
- Fang, T.; Zheng, S.; Chen, H.; Cheng, H.; Wang, L.; Zhang, P. Electronic structure and thermoelectric properties of p-type half-Heusler compound NbFeSb: A first-principles study. RSC Adv. 2016, 6, 10507–10512. [Google Scholar] [CrossRef]
- Pei, Y.; LaLonde, A.D.; Wang, H.; Snyder, G.J. Low effective mass leading to high thermoelectric performance. Energy Environ. Sci. 2012, 5, 7963–7969. [Google Scholar] [CrossRef]
- Hu, L.P.; Zhu, T.J.; Wang, Y.G.; Xie, H.H.; Xu, Z.J.; Zhao, X.B. Shifting up the optimum figure of merit of p-type bismuth telluride-based thermoelectric materials for power generation by suppressing intrinsic conduction. NPG Asia Mater. 2014, 6, e88. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, P.; Liu, R.; Xi, L.; Zheng, S.; Zhang, W.; Chen, L.; Singh, D.J.; Yang, J. Trends in electrical transport of p-type skutterudites RFe4Sb12 (R = Na, K, Ca, Sr, Ba, La, Ce, Pr, Yb) from first-principles calculations and Boltzmann transport theory. Phys. Rev. B 2011, 84, 235205. [Google Scholar] [CrossRef]
- Yang, J.; Liu, R.; Chen, Z.; Xi, L.; Yang, J.; Zhang, W.; Chen, L. Power factor enhancement in light valence band p-type skutterudites. Appl. Phys. Lett. 2012, 101, 022101. [Google Scholar] [CrossRef]
- Fang, T.; Zheng, S.; Zhou, T.; Yan, L.; Zhang, P. Computational prediction of high thermoelectric performance in p-type half-Heusler compounds with low band effective mass. Phys. Chem. Chem. Phys. 2017, 19, 4411–4417. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.; Bai, S.; Liu, Y.; Tang, Y.; Chen, L.; Zhao, X.; Zhu, T. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 2015, 6, 8144. [Google Scholar] [CrossRef] [PubMed]
- Askerov, B.M. Electron Transport Phenomena in Semiconductors; World Scientific Press: Singapore, 1994. [Google Scholar]
- Mahan, G.D.; Sofo, J.O. The best thermoelectric. Proc. Natl. Acad. Sci. USA 1996, 93, 7436–7439. [Google Scholar] [CrossRef] [PubMed]
- Gorai, P.; Stevanović, V.; Toberer, E.S. Computationally guided discovery of thermoelectric materials. Nat. Rev. Mater. 2017, 2, 201753. [Google Scholar] [CrossRef]
- Scheidemantel, T.J.; Ambrosch-Draxl, C.; Thonhauser, T.; Badding, J.V.; Sofo, J.O. Transport coefficients from first-principles calculations. Phys. Rev. B 2003, 68, 125210. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.; Setyawan, W.; Mingo, N.; Curtarolo, S. Assessing the thermoelectric properties of sintered compounds via high-throughput ab-initio calculations. Phys. Rev. X 2011, 1, 021012. [Google Scholar] [CrossRef]
- Carrete, J.; Mingo, N.; Wang, S.; Curtarolo, S. Nanograined half-Heusler semiconductors as advanced thermoelectrics: An ab initio high-throughput statistical study. Adv. Funct. Mater. 2014, 24, 7427–7432. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and measurement of association between two things. Int. J. Epidemiol. 2010, 39, 1137–1150. [Google Scholar] [CrossRef] [PubMed]
- Kandpal, H.C.; Felser, C.; Seshadri, R. Covalent bonding and the nature of band gaps in some half-eusler compounds. J. Phys. D Appl. Phys. 2006, 39, 776–785. [Google Scholar] [CrossRef]
- Pettifor, D.G. A chemical scale for crystal-structure maps. Solid State Commun. 1984, 51, 31–34. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Madsen, G.K.H. High-throughput exploration of alloying as design strategy for thermoelectrics. Phys. Rev. B 2015, 92, 085205. [Google Scholar] [CrossRef]
- Zou, D.F.; Xie, S.H.; Liu, Y.Y.; Lin, J.G.; Li, J.Y. Electronic structure and thermoelectric properties of half-Heusler Zr0.5Hf0.5NiSn by first-principles calculations. J. Appl. Phys. 2013, 113, 193705. [Google Scholar] [CrossRef]
- Hong, A.J.; Li, L.; He, R.; Gong, J.J.; Yan, Z.B.; Wang, K.F.; Liu, J.M.; Ren, Z.F. Full-scale computation for all the thermoelectric property parameters of half-Heusler compounds. Sci. Rep. 2016, 6, 22778. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Fu, C.; Liu, Y.; Xia, K.; Aydemir, U.; Chasapis, T.C.; Snyder, G.J.; Zhao, X.; Zhu, T. Unique Role of Refractory Ta Alloying in Enhancing the Figure of Merit of NbFeSb Thermoelectric Materials. Adv. Energy Mater. 2018, 8, 1701313. [Google Scholar] [CrossRef]
- Morelli, D.T.; Heremans, J.P.; Slack, G.A. Estimation of the isotope effect on the lattice thermal conductivity of group IV and group III-V semiconductors. Phys. Rev. B 2002, 66, 195304. [Google Scholar] [CrossRef]
- Miller, S.A.; Gorai, P.; Ortiz, B.R.; Goyal, A.; Gao, D.; Barnett, S.A.; Mason, T.O.; Snyder, G.J.; Lv, Q.; Stevanović, V.; Toberer, E.S. Capturing anharmonicity in a lattice thermal conductivity model for high-throughput predictions. Chem. Mater. 2017, 29, 2494–2501. [Google Scholar] [CrossRef]
- Andrea, L.; Hug, G.; Chaput, L. Ab initio phonon properties of half-Heusler NiTiSn, NiZrSn and NiHfSn. J. Phys. Condens. Mat. 2015, 27, 425401. [Google Scholar] [CrossRef] [PubMed]
- Katre, A.; Carrete, J.; Mingo, N. Unraveling the dominant phonon scattering mechanism in the thermoelectric compound ZrNiSn. J. Mater. Chem. A 2016, 4, 15940–15944. [Google Scholar] [CrossRef]
- Carrete, J.; Li, W.; Mingo, N.; Wang, S.; Curtarolo, S. Finding unprecedentedly low-thermal-conductivity half-Heusler semiconductors via high-throughput materials modeling. Phys. Rev. X 2014, 4, 011019. [Google Scholar] [CrossRef]
- Giannozzi, P.; de Gironcoli, S.; Pavone, P.; Baroni, S. Ab initio calculation of phonon dispersions in semiconductors. Phys. Rev. B 1991, 43, 7231–7242. [Google Scholar] [CrossRef]
- Toher, C.; Plata, J.J.; Levy, O.; de Jong, M.; Asta, M.; Nardelli, M.B.; Curtarolo, S. High-throughput computational screening of thermal conductivity, Debye temperature, and Grüneisen parameter using a quasiharmonic Debye model. Phys. Rev. B 2014, 90, 174107. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Madsen, G.K.H. A novel p-type half-Heusler from high-throughput transport and defect calculations. J. Mater. Chem C 2016, 4, 11261–11268. [Google Scholar] [CrossRef]
- Yu, Y.G.; Zhang, X.; Zunger, A. Natural off-stoichiometry causes carrier doping in half-Heusler filled tetrahedral structures. Phys. Rev. B 2017, 95, 085201. [Google Scholar] [CrossRef]
- Gautier, R.; Zhang, X.; Hu, L.; Yu, L.; Lin, Y.; Sunde, T.O.L.; Chon, D.; Poeppelmeier, K.R.; Zunger, A. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat. Chem. 2015, 7, 308–316. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; He, R.; Chen, S.; Zhang, H.; Dahal, K.; Zhou, H.; Wang, H.; Zhang, Q.; Ren, Z. A new n-type half-Heusler thermoelectric material NbCoSb. Mater. Res. Bull. 2015, 70, 773–778. [Google Scholar] [CrossRef]
- Zeier, W.G.; Anand, S.; Huang, L.; He, R.; Zhang, H.; Ren, Z.; Wolverton, C.; Snyder, G.J. Using the 18-electron rule to understand the nominal 19-electron half-Heusler NbCoSb with Nb vacancies. Chem. Mater. 2017, 29, 1210–1217. [Google Scholar] [CrossRef]
- Xia, K.; Liu, Y.; Anand, S.; Snyder, G.J.; Xin, J.; Yu, J.; Zhao, X.; Zhu, T. Enhanced thermoelectric performance in 18-electron Nb0.8CoSb half-Heusler compound with intrinsic Nb vacancies. Adv. Funct. Mater. 2018, 28, 1705845. [Google Scholar] [CrossRef]
- Anand, S.; Xia, K.; Hegde, V.I.; Aydemir, U.; Kocevski, V.; Zhu, T.; Wolvertona, C.; Snyder, G.J. A valence balanced rule for discovery of 18-electron half-Heuslers with defects. Energy Environ. Sci. 2018. [Google Scholar] [CrossRef]
- Tang, Y.; Li, X.; Martin, L.H.J.; Cuervoreyes, E.; Ivas, T.; Leinenbach, C.; Anand, S.; Peters, M.; Snyder, G.J.; Battaglia, C. Impact of ni content on the thermoelectric properties of half-Heusler TiNiSn. Energy Environ. Sci. 2018, 11, 311–320. [Google Scholar] [CrossRef]
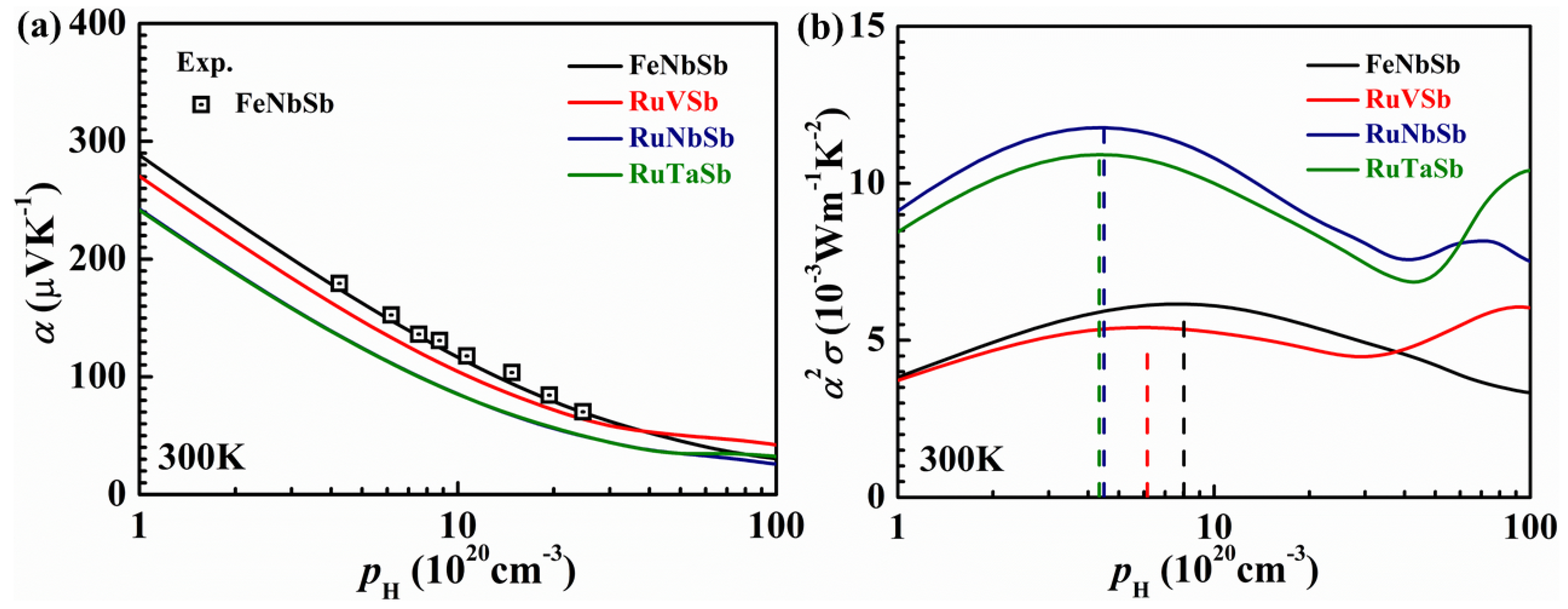
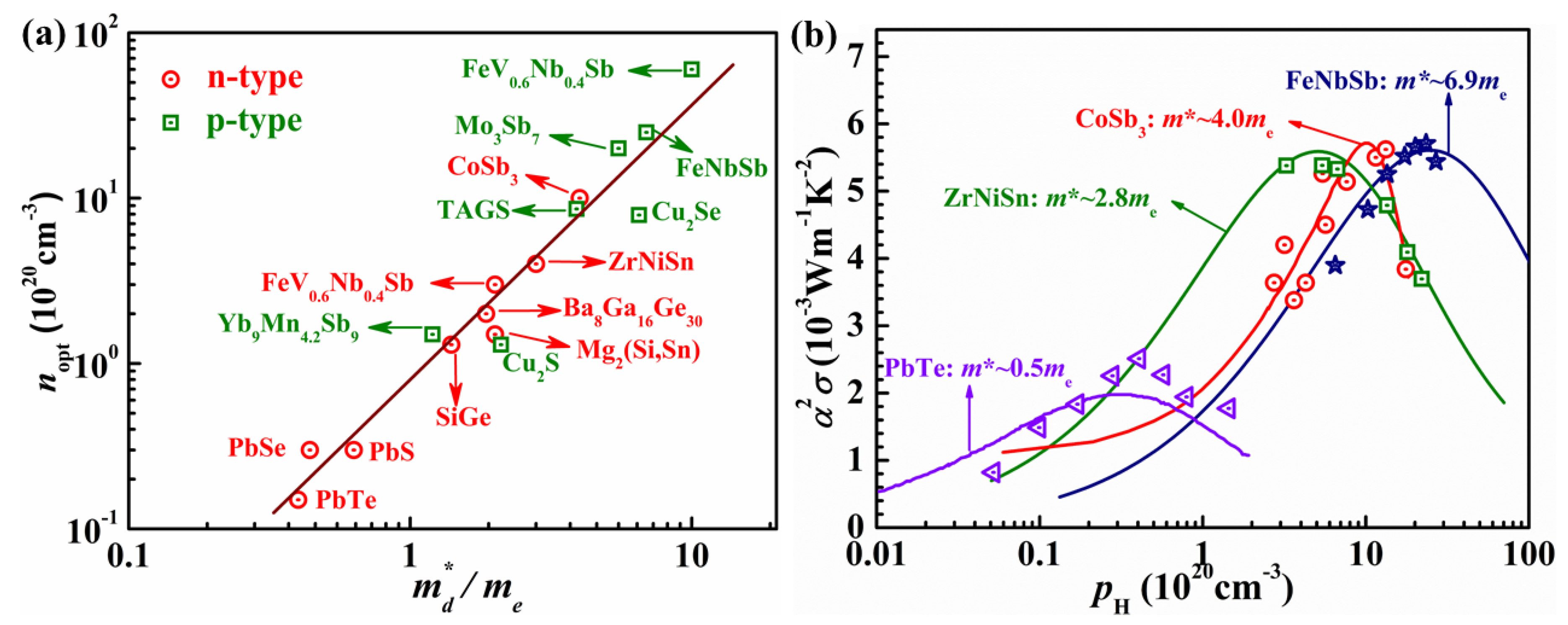
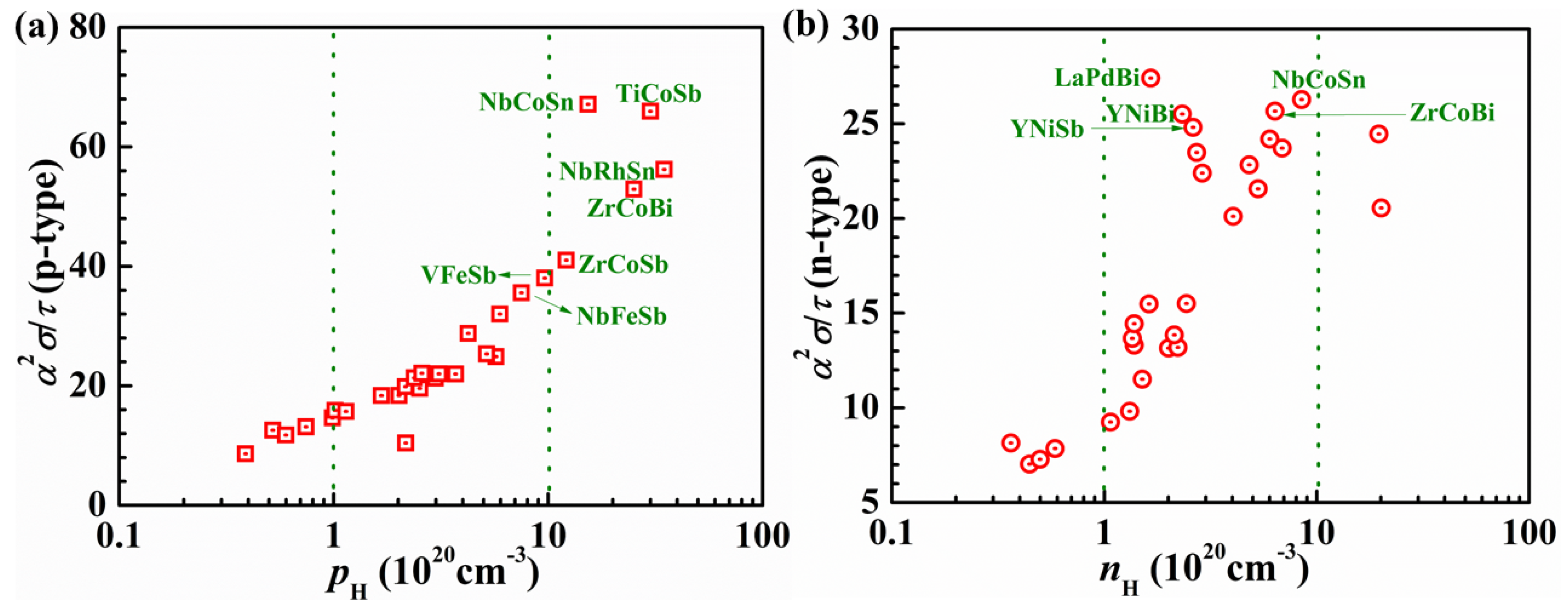
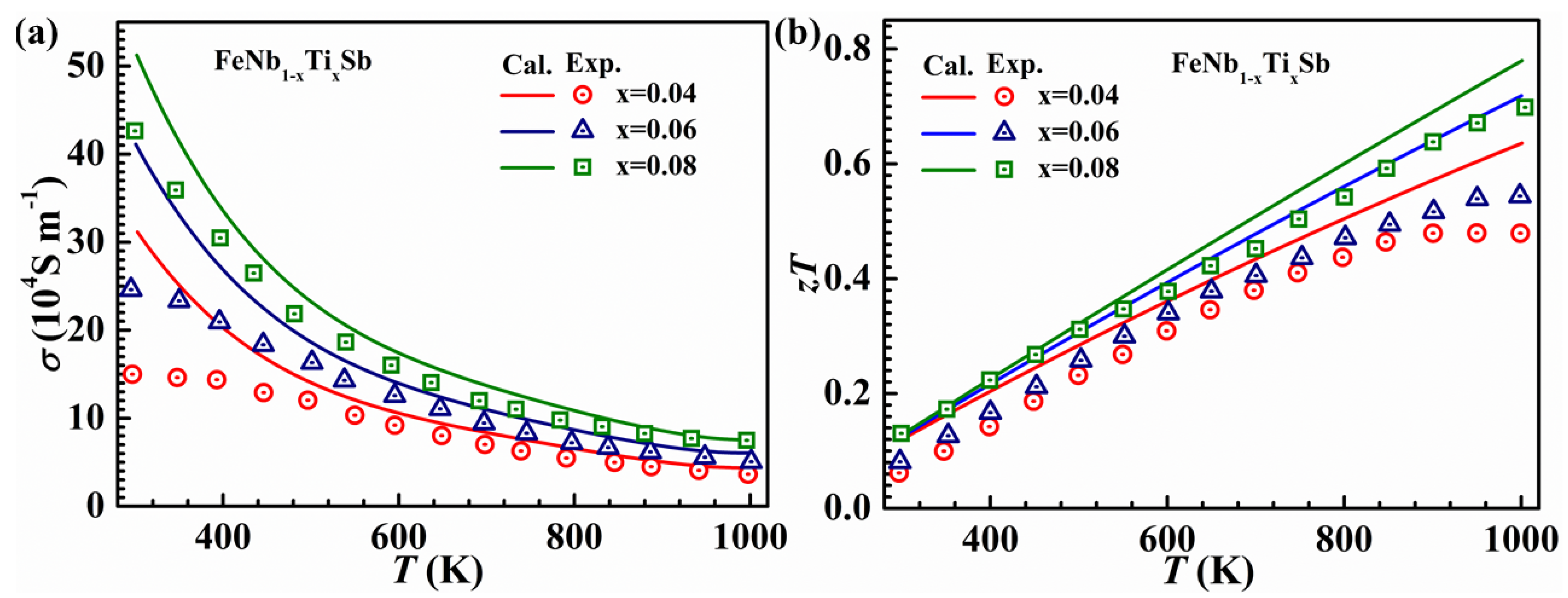
| Materials | κω | κtransf | κforest | κanh | κL |
|---|---|---|---|---|---|
| TiNiSn | 17.9 | 57.1 | 20.3 | 16.8 | 15.4 |
| ZrNiSn | 19.6 | 73.3 | 20.7 | 17.5 | 13.3 |
| HfNiSn | - | 75.4 | 22.1 | 19.5 | 15.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, T.; Zhao, X.; Zhu, T. Band Structures and Transport Properties of High-Performance Half-Heusler Thermoelectric Materials by First Principles. Materials 2018, 11, 847. https://doi.org/10.3390/ma11050847
Fang T, Zhao X, Zhu T. Band Structures and Transport Properties of High-Performance Half-Heusler Thermoelectric Materials by First Principles. Materials. 2018; 11(5):847. https://doi.org/10.3390/ma11050847
Chicago/Turabian StyleFang, Teng, Xinbing Zhao, and Tiejun Zhu. 2018. "Band Structures and Transport Properties of High-Performance Half-Heusler Thermoelectric Materials by First Principles" Materials 11, no. 5: 847. https://doi.org/10.3390/ma11050847
APA StyleFang, T., Zhao, X., & Zhu, T. (2018). Band Structures and Transport Properties of High-Performance Half-Heusler Thermoelectric Materials by First Principles. Materials, 11(5), 847. https://doi.org/10.3390/ma11050847






