Magnetoresistance Effect and the Applications for Organic Spin Valves Using Molecular Spacers
Abstract
1. Introduction
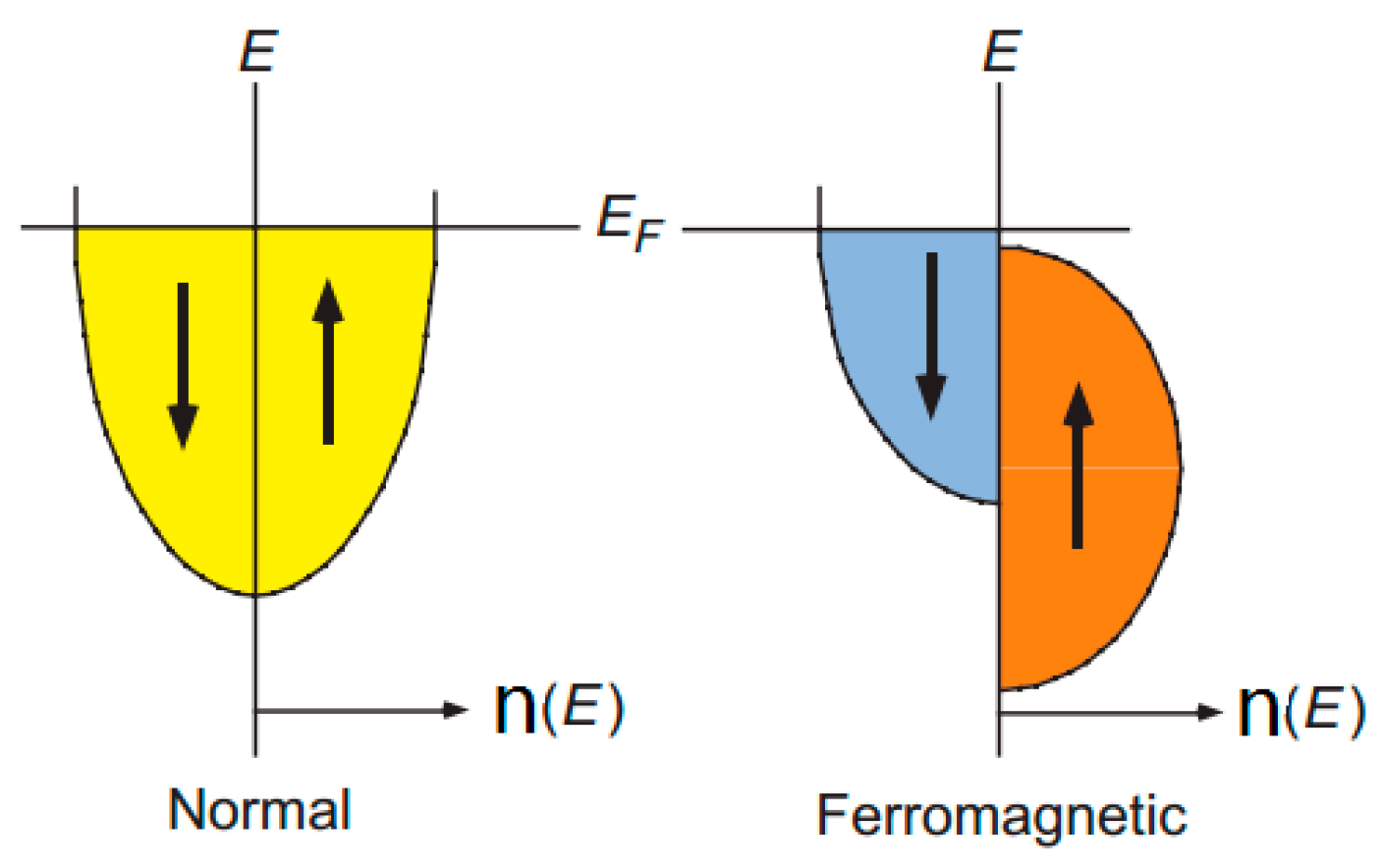
2. Spin Polarization of Ferromagnetic Electrode
3. Traditional Organic Spin Valves
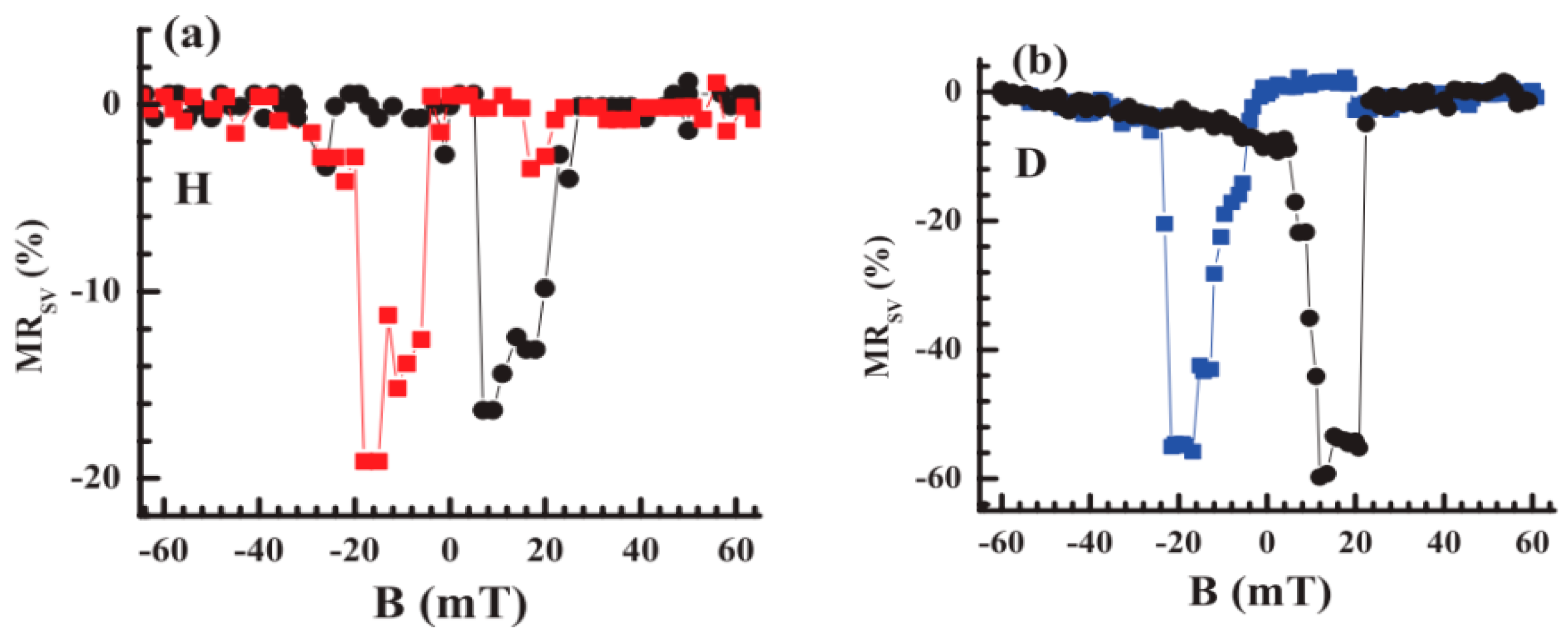
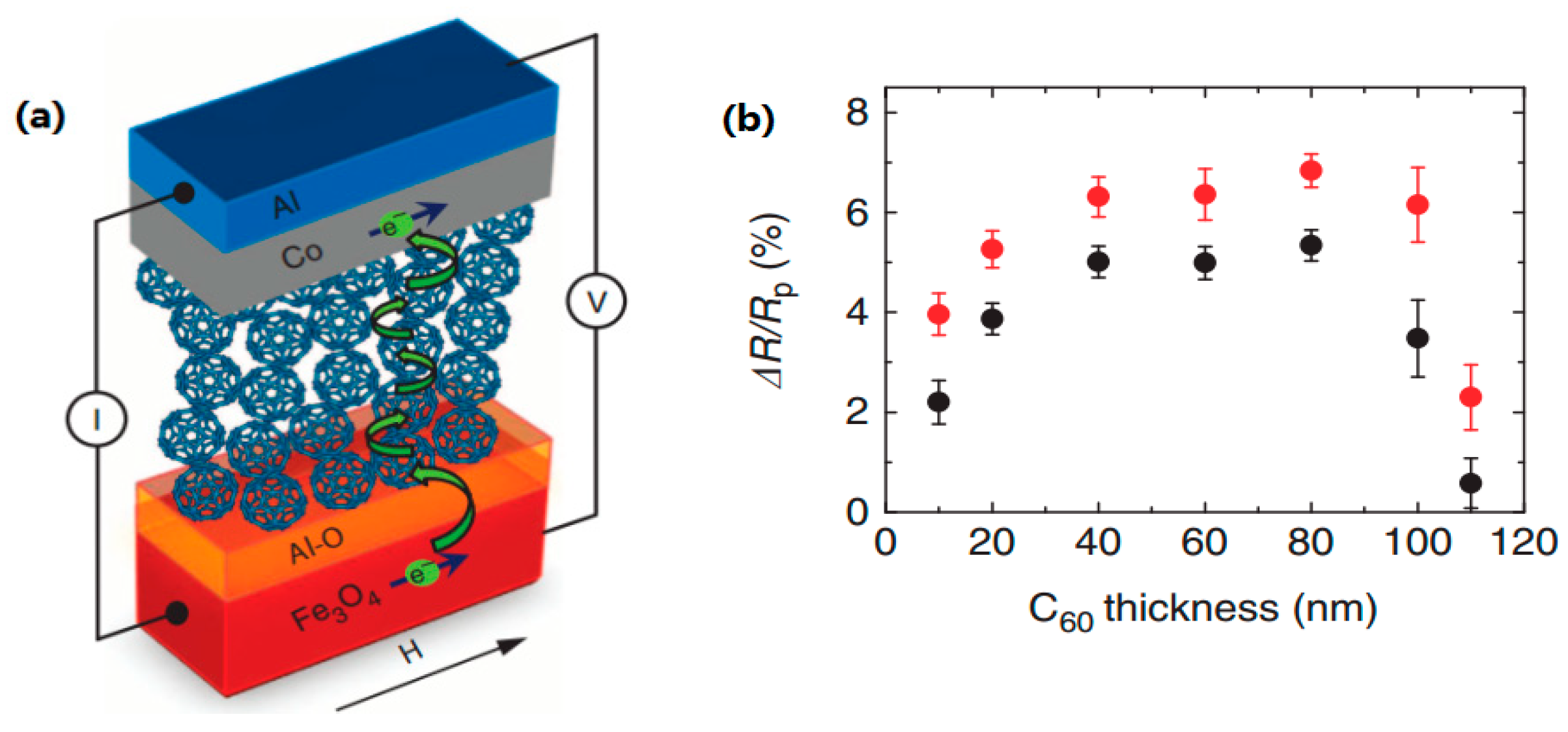
3.1. GMR and TMR Effects in Molecule Spin Valves
3.2. Effects of Spin Orbit Coupling and Hyperfine Interaction
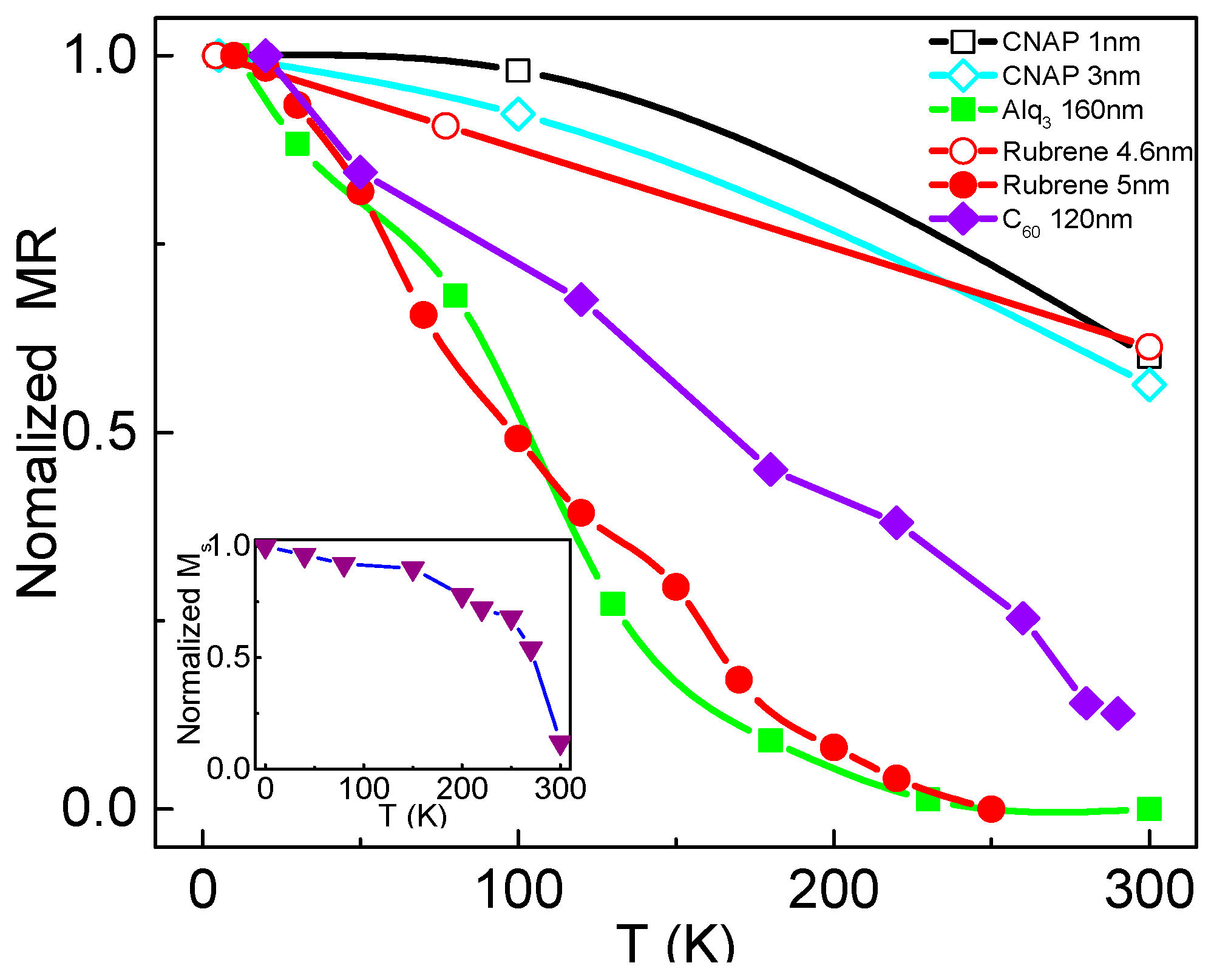
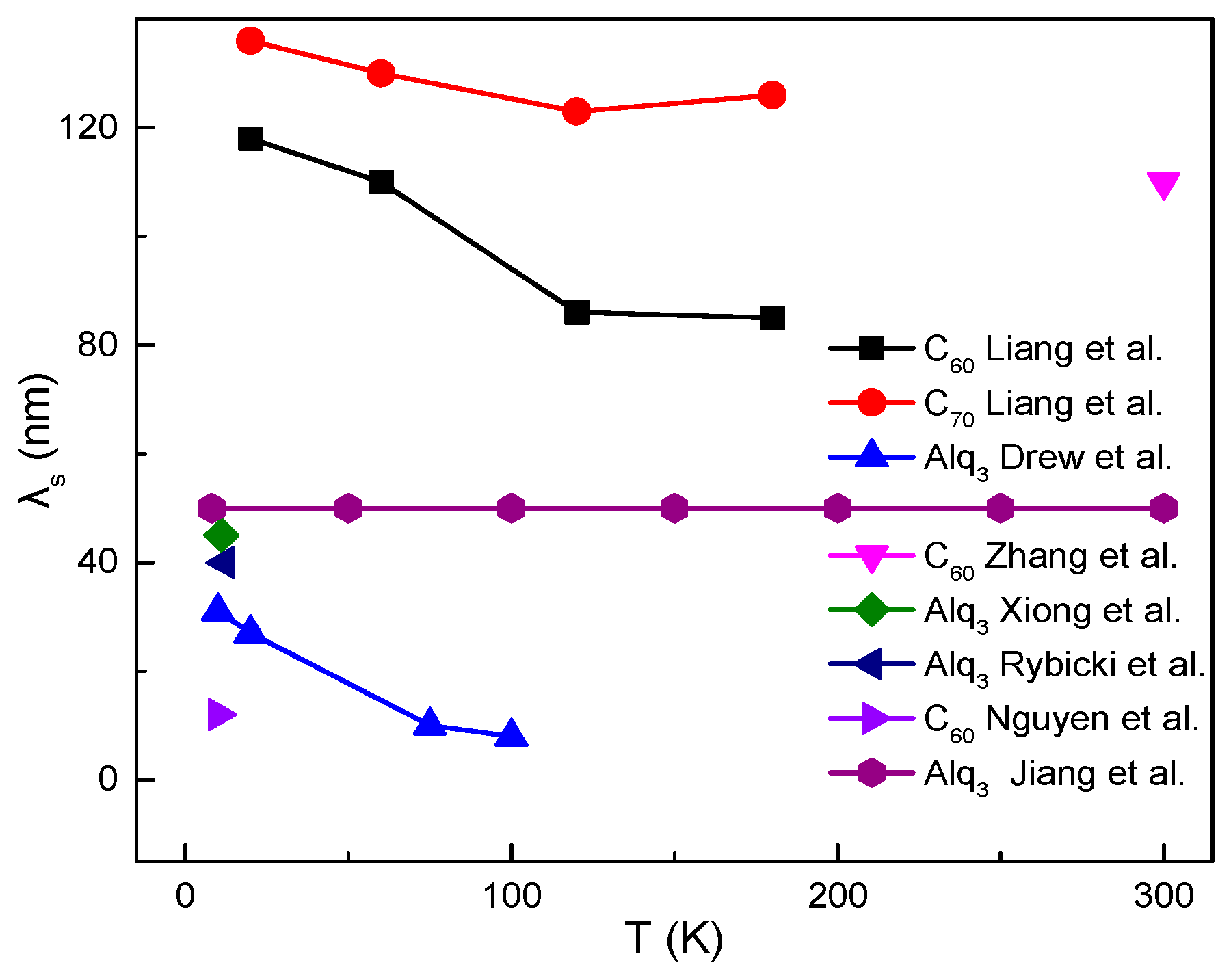
3.3. Dependence of MR on Measurement Temperature
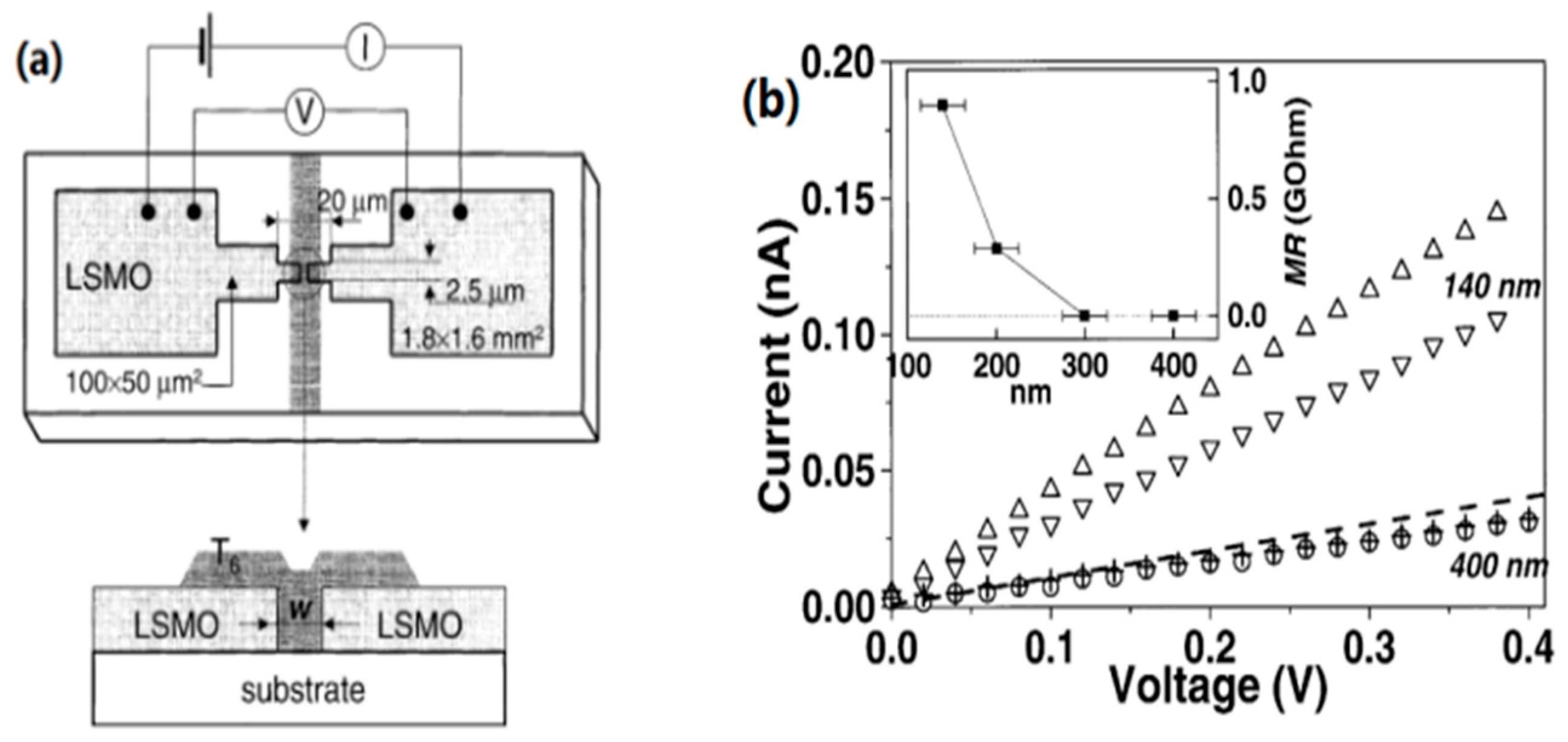
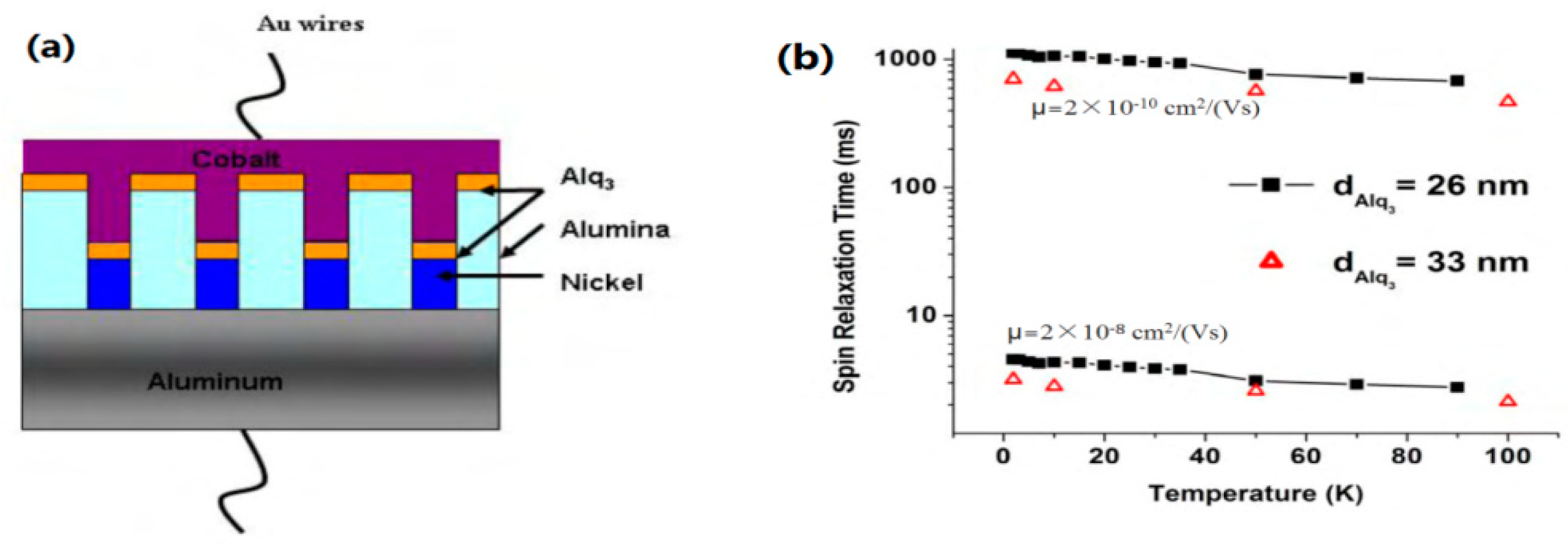
3.4. Nanowire Spin Valve
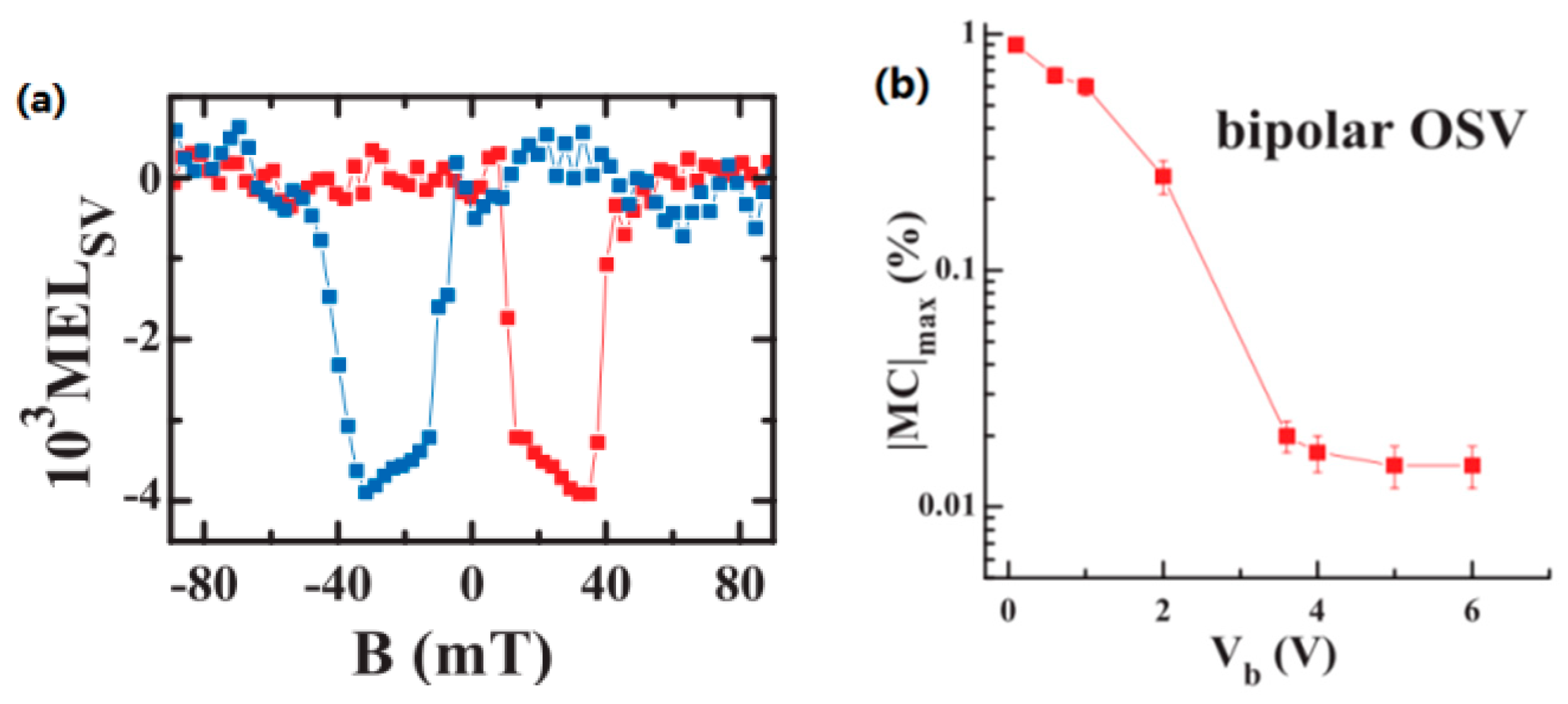
3.5. Hanle Effect in OSVs
4. Other Spin Devices
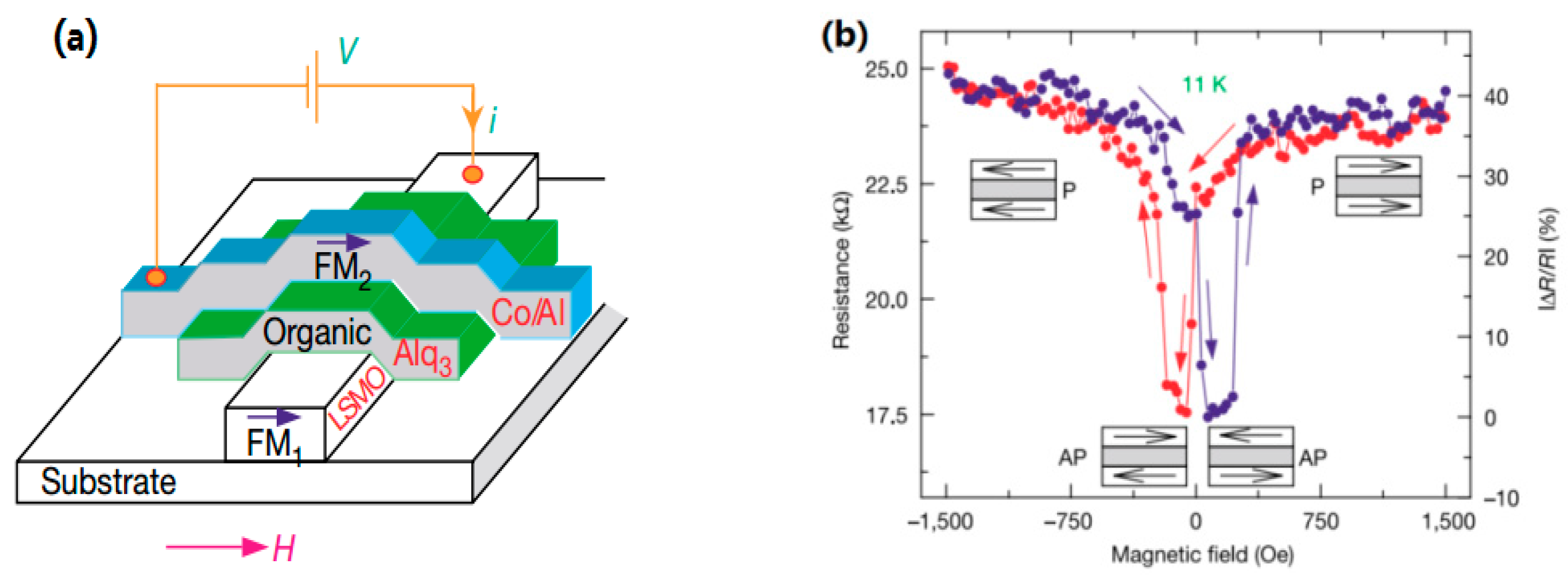
4.1. Spin-OLED
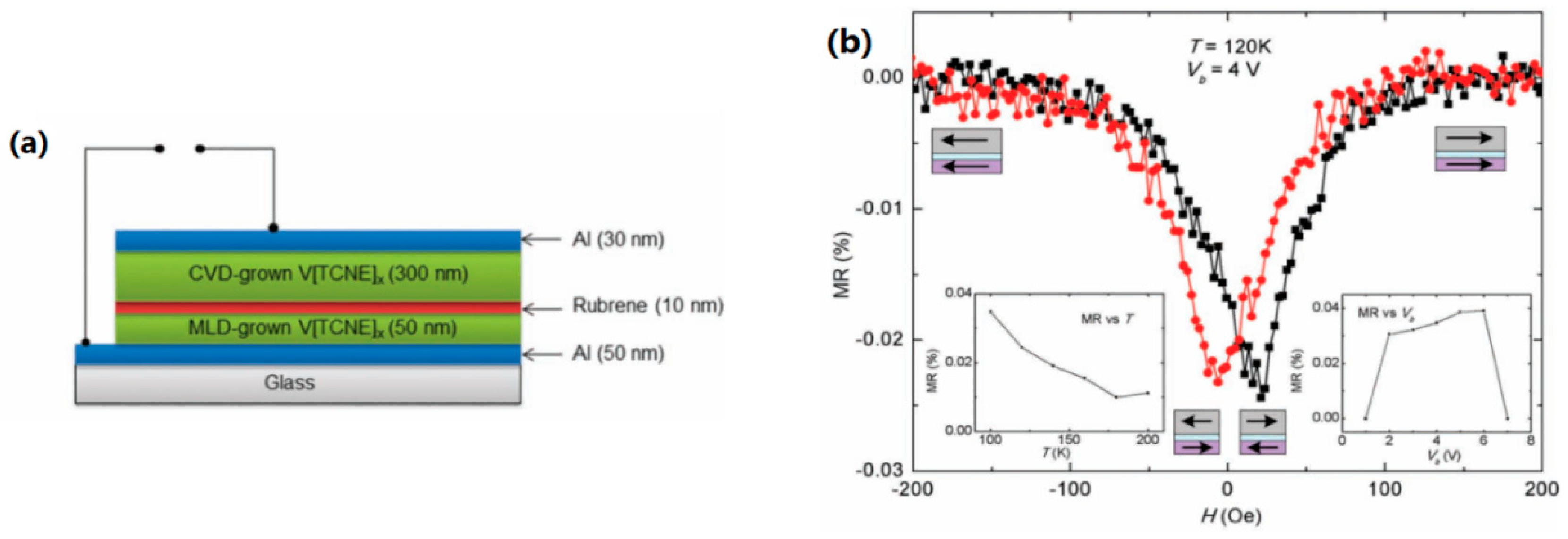
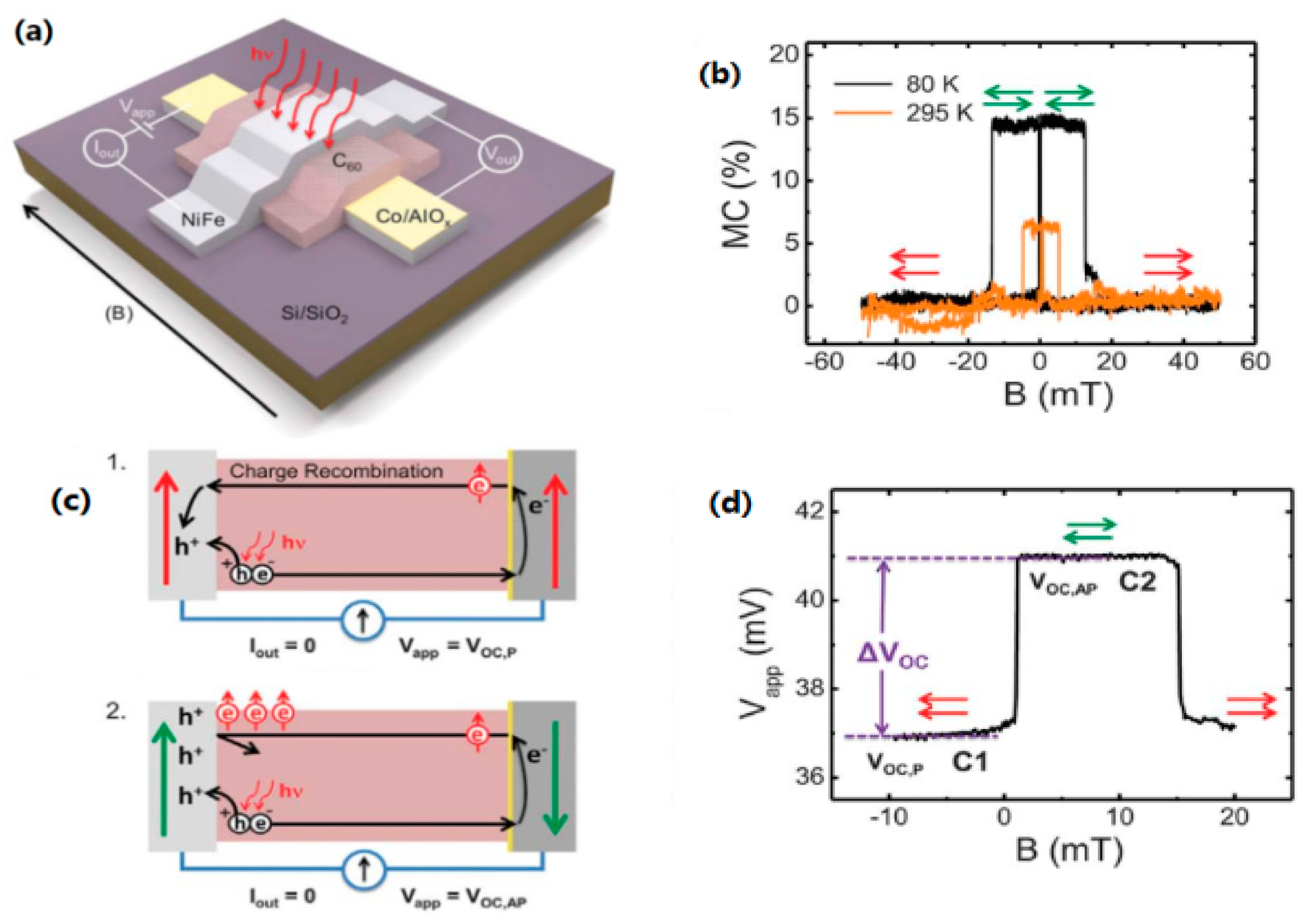
4.2. Spin-Photovoltaic Devices
5. Concluding Remarks
Funding
Conflicts of Interest
References
- Xiong, Z.H.; Di, W.; Vardeny, Z.V.; Jing, S. Giant magnetoresistance in organic spin-valves. Nature 2004, 427, 821. [Google Scholar] [CrossRef] [PubMed]
- Dediu, V.; Murakami, M.; Matacotta, F.C.; Taliani, C.; Barbanera, S. Room temperature spin polarized injection in organic semiconductors. Solid State Commun. 2002, 122, 181–184. [Google Scholar] [CrossRef]
- Prinz, G.A. Magnetoelectronics. Science 1998, 282, 1660–1663. [Google Scholar] [CrossRef] [PubMed]
- Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnar, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef] [PubMed]
- Boehme, C.; Lupton, J.M. Challenges for organic spintronics. Nat. Nanotech. 2013, 8, 612–615. [Google Scholar] [CrossRef] [PubMed]
- Sanvito, S. Molecular spintronics. Chem. Soc. Rev. 2011, 40, 3336–3355. [Google Scholar] [CrossRef] [PubMed]
- Awschalom, D.D.; Flatte, M.E. Challenges for semiconductor spintronics. Nat. Phys. 2007, 3, 153–159. [Google Scholar] [CrossRef]
- Zhang, X.; Tong, J.; Zhu, H.; Wang, Z.; Zhou, L.; Wang, S.; Miyashita, T.; Mitsuishi, M.; Qin, G. Room temperature magnetoresistance effects in ferroelectric poly(vinylidene fluoride) spin valves. J. Mater. Chem. C 2017, 5, 5055–5062. [Google Scholar] [CrossRef]
- Majumdar, S.; Majumdar, H.S.; Laiho, R.; Österbacka, R. Comparing small molecules and polymer for future organic spin-valves. J. Alloys Compd. 2006, 423, 169–171. [Google Scholar] [CrossRef]
- Majumdar, S.; Majumdar, H.S. On the origin of decay of spin current with temperature in organic spintronic devices. Org. Electron. 2012, 13, 2653–2658. [Google Scholar] [CrossRef]
- Szulczewski, G.; Tokuc, H.; Oguz, K.; Coey, J.M.D. Magnetoresistance in magnetic tunnel junctions with an organic barrier and an MgO spin filter. Appl. Phys. Lett. 2009, 95, 202506. [Google Scholar] [CrossRef]
- Wang, T.X.; Wei, H.X.; Zeng, Z.M.; Han, X.F.; Hong, Z.M.; Shi, G.Q. Magnetic/nonmagnetic/magnetic tunnel junction based on hybrid organic Langmuir-Blodgett-films. Appl. Phys. Lett. 2006, 88, 242505. [Google Scholar] [CrossRef]
- Yu, Z.G. Impurity-band transport in organic spin valves. Nat. Commun. 2014, 5, 4842. [Google Scholar] [CrossRef] [PubMed]
- Vardeny, Z.V. A new face for organics. Interview by Fabio Pulizzi. Nat. Mater. 2009, 8, 696–697. [Google Scholar] [PubMed]
- Szulczewski, G.; Sanvito, S.; Coey, M.A. Spin of their own. Nat. Mater. 2009, 8, 693–695. [Google Scholar] [CrossRef] [PubMed]
- Dediu, V.A.; Hueso, L.E.; Bergenti, I.; Taliani, C. Spin routes in organic semiconductors. Nat. Mater. 2009, 8, 707–716. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Wudl, F. Organic spin transporting materials: Present and future. J. Mater. Chem. A 2014, 2, 48–57. [Google Scholar] [CrossRef]
- Gu, H.; Zhang, X.; Wei, H.; Huang, Y.; Wei, S.; Guo, Z. An overview of the magnetoresistance phenomenon in molecular systems. Chem. Soc. Rev. 2013, 42, 5907–5943. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Ehrenfreund, E.; Vardeny, Z.V. The first decade of organic spintronics research. Chem. Commun. 2014, 50, 1781–1793. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Mizukami, S.; Ma, Q.; Kubota, T.; Oogane, M.; Naganuma, H.; Ando, Y.; Miyazaki, T. Spin-dependent transport behavior in C60 and Alq3 based spin valves with a magnetite electrode (invited). J. Appl. Phys. 2014, 115, 172608. [Google Scholar] [CrossRef]
- Zhang, X.; Mizukami, S.; Kubota, T.; Oogane, M.; Naganuma, H.; Ando, Y.; Miyazaki, T. Interface effects on perpendicular magnetic anisotropy for molecular-capped cobalt ultrathin films. Appl. Phys. Lett. 2011, 99, 162509. [Google Scholar] [CrossRef]
- Wagemans, W.; Koopmans, B. Spin transport and magnetoresistance in organic semiconductors. Phys. Status Solidi B 2011, 248, 1029–1041. [Google Scholar] [CrossRef]
- Shim, J.H.; Raman, K.V.; Park, Y.J.; Santos, T.S.; Miao, G.X.; Satpati, B.; Moodera, J.S. Large spin diffusion length in an amorphous organic semiconductor. Phys. Rev. Lett. 2008, 100, 226603. [Google Scholar] [CrossRef] [PubMed]
- Bobbert, P.A.; Wagemans, W.; van Oost, F.W.; Koopmans, B.; Wohlgenannt, M. Theory for spin diffusion in disordered organic semiconductors. Phys. Rev. Lett. 2009, 102, 156604. [Google Scholar] [CrossRef] [PubMed]
- Santos, T.S.; Lee, J.S.; Migdal, P.; Lekshmi, I.C.; Satpati, B.; Moodera, J.S. Room-temperature tunnel magnetoresistance and spin-polarized tunneling through an organic semiconductor barrier. Phys. Rev. Lett. 2007, 98, 016601. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Yin, L.; Sun, C.; Guo, H.; Gai, Z.; Zhang, X.G.; Ward, T.Z.; Cheng, Z.; Shen, J. Giant magnetoresistance in organic spin valves. Phys. Rev. Lett. 2010, 104, 236602. [Google Scholar] [CrossRef] [PubMed]
- Dediu, V.; Hueso, L.E.; Bergenti, I.; Riminucci, A.; Borgatti, F.; Graziosi, P.; Newby, C.; Casoli, F.; De Jong, M.P.; Taliani, C.; et al. Room-temperature spintronic effects inAlq3-based hybrid devices. Phys. Rev. B 2008, 78, 115203. [Google Scholar] [CrossRef]
- Zhang, X.; Mizukami, S.; Kubota, T.; Ma, Q.; Oogane, M.; Naganuma, H.; Ando, Y.; Miyazaki, T. Observation of a large spin-dependent transport length in organic spin valves at room temperature. Nat. Commun. 2013, 4, 1392. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ma, Q.; Suzuki, K.; Sugihara, A.; Qin, G.; Miyazaki, T.; Mizukami, S. Magnetoresistance effect in rubrene-based spin valves at room temperature. ACS Appl. Mater. Interfaces 2015, 7, 4685–4692. [Google Scholar] [CrossRef] [PubMed]
- Binasch, G.; Grünberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 1989, 39, 4828–4830. [Google Scholar] [CrossRef]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Nguyen Van Dau, F.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. [Google Scholar] [CrossRef] [PubMed]
- Miyazaki, T.; Tezuka, N. Giant magnetic tunneling effect in Fe/Al2O3/Fe junction. J. Magn. Magn. Mater. 1995, 139, L231–L234. [Google Scholar] [CrossRef]
- Moodera, J.S.; Kinder, L.R.; Wong, T.M.; Meservey, R. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions. Phys. Rev. Lett. 1995, 74, 3273–3276. [Google Scholar] [CrossRef] [PubMed]
- Pramanik, S.; Stefanita, C.G.; Patibandla, S.; Bandyopadhyay, S.; Garre, K.; Harth, N.; Cahay, M. Observation of extremely long spin relaxation times in an organic nanowire spin valve. Nat. Nanotech. 2007, 2, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Ehrenfreund, E.; Vardeny, Z.V. Spin-Polarized Light-Emitting Diode Based on an Organic Biplar Spin Valve. Science 2012, 337, 204–209. [Google Scholar] [CrossRef] [PubMed]
- Arisi, E.; Bergenti, I.; Dediu, V.; Loi, M.A.; Muccini, M.; Murgia, M.; Ruani, G.; Taliani, C.; Zamboni, R. Organic light emitting diodes with spin polarized electrodes. J. Appl. Phys. 2003, 93, 7682–7683. [Google Scholar] [CrossRef]
- Ding, B.; Song, Q.; Alameh, K. Room-temperature spin-polarized organic light-emitting diodes with a single ferromagnetic electrode. Appl. Phys. Lett. 2014, 104, 203302. [Google Scholar] [CrossRef]
- Bergenti, I.; Dediu, V.; Arisi, E.; Mertelj, T.; Murgia, M.; Riminucci, A.; Ruani, G.; Solzi, M.; Taliani, C. Spin polarised electrodes for organic light emitting diodes. Org. Electron. 2004, 5, 309–314. [Google Scholar] [CrossRef]
- Zhang, Y.; Basel, T.P.; Gautam, B.R.; Yang, X.; Mascaro, D.J.; Liu, F.; Vardeny, Z.V. Spin-enhanced organic bulk heterojunction photovoltaic solar cells. Nat. Commun. 2012, 3, 1043. [Google Scholar] [CrossRef] [PubMed]
- Tajima, H.; Miyakawa, M.; Isozaki, H.; Yasui, M.; Suzuki, N.; Matsuda, M. Magnetophotocurrent effect in organic photovoltaic cells at low temperatures. Synth. Met. 2010, 160, 256–261. [Google Scholar] [CrossRef]
- Kanchibotla, B.; Pramanik, S.; Bandyopadhyay, S.; Cahay, M. Transverse spin relaxation time in organicmolecules: A possible platform for fault tolerant room temperature quantum computing. Phys. Rev. B 2008, 78, 10–19. [Google Scholar]
- Parkin, S.; Jiang, X.; Kaiser, C.; Panchula, A.; Roche, K.; Samant, M. Magnetically Engineered Spintronic Sensors and Memory. Proc. IEEE 2003, 91, 661–680. [Google Scholar] [CrossRef]
- Suzuki, K.Z.; Izumi, T.; Zhang, X.; Sugihara, A.; Pham, S.-T.; Taka, H.; Sato, S.; Isobe, H.; Mizukami, S. Room temperature magnetoresistance in an organic spin valve with an aromatic hydrocarbon macrocycle. APL Mater. 2017, 5, 046101. [Google Scholar] [CrossRef]
- Julliere, M. Tunneling between ferromagnetic films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Sun, M.F.; Wang, X.C.; Chen, G.F.; Mi, W.B. Geometric distortion and spin-dependent electronic structure of C6H6-adsorbed Fe3O4(001): A first-principles study. J. Appl. Phys. 2017, 121, 015306. [Google Scholar] [CrossRef]
- Zhang, Q.; Yin, L.; Mi, W.; Wang, X. Large Spatial Spin Polarization at Benzene/La2/3Sr1/3MnO3 Spinterface: Toward Organic Spintronic Devices. J. Phys. Chem. C 2016, 120, 6156–6164. [Google Scholar] [CrossRef]
- Moodera, J.S.; Mathon, G. Spin polarized tunneling in ferromagnetic junctions. J. Magn. Magn. Mater. 1999, 200, 248–273. [Google Scholar] [CrossRef]
- Velasco, S.; Román, F.L. Determining the Curie Temperature of Iron and Nickel. Phys. Teach. 2007, 45, 387–389. [Google Scholar] [CrossRef]
- Schneider, C.M.; Bressler, P.; Schuster, P.; Kirschner, J.; de Miguel, J.J.; Miranda, R. Curie temperature of ultrathin films of fcc-cobalt epitaxially grown on atomically flat Cu(100) surfaces. Phys. Rev. Lett. 1990, 64, 1059–1062. [Google Scholar] [CrossRef] [PubMed]
- Monsma, D.J.; Parkin, S.S.P. Spin polarization of tunneling current from ferromagnet/Al2O3 interfaces using copper-doped aluminum superconducting films. Appl. Phys. Lett. 2000, 77, 720–722. [Google Scholar] [CrossRef]
- Nadgorny, B.; Mazin, I.I.; Osofsky, M.; Soulen, R.J.; Broussard, P.; Stroud, R.M.; Singh, D.J.; Harris, V.G.; Arsenov, A.; Mukovskii, Y. Origin of high transport spin polarization inLa0.7Sr0.3MnO3:Direct evidence for minority spin states. Phys. Rev. B 2001, 63, 184433. [Google Scholar] [CrossRef]
- Haghiri-Gosnet, A.M.; Wolfman, J.; Mercey, B.; Simon, C.; Lecoeur, P.; Korzenski, M.; Hervieu, M.; Desfeux, R.; Baldinozzi, G. Microstructure and magnetic properties of strained La0.7Sr0.3MnO3 thin films. J. Appl. Phys. 2000, 88, 4257. [Google Scholar] [CrossRef]
- Zhang, Z.; Satpathy, S. Electron states, magnetism, and the Verwey transition in magnetite. Phys. Rev. B 1991, 44, 13319–13331. [Google Scholar] [CrossRef]
- Pradhan, K.; Kampf, A.P. Electronic and magnetic reconstructions in manganite superlattices. Phys. Rev. B 2013, 87, 155152. [Google Scholar] [CrossRef]
- Lofwander, T.; Grein, R.; Eschrig, M. Is CrO2 fully spin polarized? Analysis of Andreev spectra and excess current. Phys. Rev. Lett. 2010, 105, 207001. [Google Scholar] [CrossRef] [PubMed]
- Kämper, K.P.; Schmitt, W.; Güntherodt, G.; Gambino, R.J.; Ruf, R. CrO2-A New Half-Metallic Ferromagnet? Phys. Rev. Lett. 1987, 105, 2788–2791. [Google Scholar] [CrossRef] [PubMed]
- Coey, J.M.D.; Venkatesan, M. Half-metallic ferromagnetism: Example of CrO2 (invited). J. Appl. Phys. 2002, 91, 8345–8350. [Google Scholar] [CrossRef]
- Kawasugi, Y.; Ujino, T.; Tada, H. Room-temperature magnetoresistance in organic spin-valves based on a Co2MnSi Heusler alloy. Org. Electron. 2013, 14, 3186–3189. [Google Scholar] [CrossRef]
- Ikegami, T.; Kawayama, I.; Tonouchi, M.; Nakao, S.; Yamashita, Y.; Tada, H. Planar-type spin valves based on low-molecular-weight organic materials with La0.67Sr0.33MnO3 electrodes. Appl. Phys. Lett. 2008, 9, 153304. [Google Scholar] [CrossRef]
- Liang, S.; Geng, R.; Yang, B.; Zhao, W.; Chandra Subedi, R.; Li, X.; Han, X.; Nguyen, T.D. Curvature-enhanced Spin-orbit Coupling and Spinterface Effect in Fullerene-based Spin Valves. Sci. Rep. 2016, 6, 19461. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Li, T.; Chen, F.; Zhang, F. Excellent spin transport in spin valves based on the conjugated polymer with high carrier mobility. Sci. Rep. 2015, 5, 9355. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Belmonte, G.; Munar, A.; Barea, E.M.; Bisquert, J.; Ugarte, I.; Pacios, R. Charge carrier mobility and lifetime of organic bulk heterojunctions analyzed by impedance spectroscopy. Org. Electron. 2008, 9, 847–851. [Google Scholar] [CrossRef]
- Horowitz, G.; Garnier, F.; Yassar, A.; Hajlaoui, R.; Kouki, F. Field-effect transistor made with a sexithiophene single crystal. Adv. Mater. 1996, 8, 52–54. [Google Scholar] [CrossRef]
- Park, H.; Shin, D.S.; Yu, H.S.; Chae, H.B. Electron mobility in tris(8-hydroxyquinoline)aluminum (Alq3) films by transient electroluminescence from single layer organic light emitting diodes. Appl. Phys. Lett. 2007, 90, 202103. [Google Scholar] [CrossRef]
- Takeya, J.; Yamagishi, M.; Tominari, Y.; Hirahara, R.; Nakazawa, Y.; Nishikawa, T.; Kawase, T.; Shimoda, T.; Ogawa, S. Very high-mobility organic single-crystal transistors with in-crystal conduction channels. Appl. Phys. Lett. 2007, 90, 102120. [Google Scholar] [CrossRef]
- Su, Y.R.; Xie, W.G.; Li, Y.; Shi, Y.; Zhao, N.; Xu, J.B. A low-temperature, solution-processed high-kdielectric for low-voltage, high-performance organic field-effect transistors (OFETs). J. Phys. D Appl. Phys. 2013, 46, 095105. [Google Scholar] [CrossRef]
- Hosokawa, C.; Tokailin, H.; Higashi, H.; Kusumoto, T. Transient electroluminescence from hole transporting emitting layer in nanosecond region. Appl. Phys. Lett. 1993, 63, 1322–1324. [Google Scholar] [CrossRef]
- Lee, C.B.; Uddin, A.; Andersson, T.G. Investigation of charge carrier mobility in 5,6,11,12-tetraphenylnapthacene (rubrene) and coumarin 6 doped Alq3 films. Solid State Commun. 2007, 142, 206–211. [Google Scholar] [CrossRef]
- Ishihara, S.; Hase, H.; Okachi, T.; Naito, H. Determination of charge carrier mobility in tris(8-hydroxy-quinolinato) aluminum by means of impedance spectroscopy measurements. Org. Electron. 2011, 12, 1364–1369. [Google Scholar] [CrossRef]
- Marumoto, K.; Arai, N.; Goto, H.; Kijima, M.; Murakami, K.; Tominari, Y.; Takeya, J.; Shimoi, Y.; Tanaka, H.; Kuroda, S.-I.; et al. Microscopic mechanisms behind the high mobility in rubrene single-crystal transistors as revealed by field-induced electron spin resonance. Phys. Rev. B 2011, 83, 075302. [Google Scholar] [CrossRef]
- Burke, F.; Stamenov, P.; Coey, J.M.D. Charge injection, transport and localization in rubrene. Synth. Met. 2011, 161, 563–569. [Google Scholar] [CrossRef]
- Rashba, E.I. Theory of electrical spin injection Tunnel contacts as a solution of the conductivity mismatch problem. Phys. Rev. B Condens. Matter 2000, 62, R16267–R16270. [Google Scholar] [CrossRef]
- Li, B.; Kao, C.Y.; Yoo, J.W.; Prigodin, V.N.; Epstein, A.J. Magnetoresistance in an all-organic-based spin valve. Adv. Mater. 2011, 23, 3382–3386. [Google Scholar] [CrossRef] [PubMed]
- Schmaus, S.; Bagrets, A.; Nahas, Y.; Yamada, T.K.; Bork, A.; Bowen, M.; Beaurepaire, E.; Evers, F.; Wulfhekel, W. Giant magnetoresistance through a single molecule. Nat. Nanotech. 2011, 6, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.L.A.; Le, T.Q.; Sanderink, J.G.M.; van der Wiel, W.G.; de Jong, M.P. The Multistep Tunneling Analogue of Conductivity Mismatch in Organic Spin Valves. Adv. Funct. Mater. 2012, 22, 1180–1189. [Google Scholar] [CrossRef]
- Barraud, C.; Seneor, P.; Mattana, R.; Fusil, S.; Bouzehouane, K.; Deranlot, C.; Graziosi, P.; Hueso, L.; Bergenti, I.; Dediu, V.; et al. Unravelling the role of the interface for spin injection into organic semiconductors. Nat. Phys. 2010, 6, 615–620. [Google Scholar] [CrossRef]
- Gobbi, M.; Golmar, F.; Llopis, R.; Casanova, F.; Hueso, L.E. Room-temperature spin transport in C60-based spin valves. Adv. Mater. 2011, 23, 1609–1613. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ai, X.; Zhang, R.; Ma, Q.; Wang, Z.; Qin, G.; Wang, J.; Wang, S.; Suzuki, K.; Miyazaki, T.; et al. Spin conserved electron transport behaviors in fullerenes (C60 and C70) spin valves. Carbon 2016, 106, 202–207. [Google Scholar] [CrossRef]
- Jiang, S.W.; Wang, P.; Chen, B.B.; Zhou, Y.; Ding, H.F.; Wu, D. Tuning carrier mobility without spin transport degrading in copper-phthalocyanine. Appl. Phys. Lett. 2015, 107, 042407. [Google Scholar] [CrossRef]
- Sun, X.; Bedoya-Pinto, A.; Mao, Z.; Gobbi, M.; Yan, W.; Guo, Y.; Atxabal, A.; Llopis, R.; Yu, G.; Liu, Y.; et al. Active Morphology Control for Concomitant Long Distance Spin Transport and Photoresponse in a Single Organic Device. Adv. Mater. 2016, 28, 2609–2615. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.W.; Wang, P.; Jiang, S.C.; Chen, B.B.; Wang, M.; Jiang, Z.S.; Wu, D. Fabrication of lateral organic spin valves based on La0.7Sr0.3MnO3 electrodes. Spin 2014, 4, 1440008. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, T.; Katz, H.E.; Reich, D.H. Effects of carrier mobility and morphology in organic semiconductor spin valves. J. Appl. Phys. 2009, 105, 07C708. [Google Scholar] [CrossRef]
- Hong, J.Y.; Ou Yang, K.H.; Wang, B.Y.; Li, K.S.; Shiu, H.W.; Chen, C.H.; Chan, Y.L.; Wei, D.H.; Chang, F.H.; Lin, H.J.; et al. Interfacial spectroscopic characterization of organic/ferromagnet hetero-junction of 3,4,9,10-perylene-teracarboxylic dianhydride-based organic spin valves. Appl. Phys. Lett. 2014, 104, 083301. [Google Scholar] [CrossRef]
- Wang, F.J.; Yang, C.G.; Vardeny, Z.V.; Li, X.G. Spin response in organic spin valves based onLa2/3Sr1/3MnO3 electrodes. Phys. Rev. B 2007, 75, 245324. [Google Scholar] [CrossRef]
- Palosse, M.; Séguy, I.; Bedel-Pereira, É.; Villeneuve-Faure, C.; Mallet, C.; Frère, P.; Warot-Fonrose, B.; Biziere, N.; Bobo, J.-F. Spin transport in benzofurane bithiophene based organic spin valves. AIP Adv. 2014, 4, 017117. [Google Scholar] [CrossRef]
- Sun, X.; Gobbi, M.; Bedoya-Pinto, A.; Txoperena, O.; Golmar, F.; Llopis, R.; Chuvilin, A.; Casanova, F.; Hueso, L.E. Room-temperature air-stable spin transport in bathocuproine-based spin valves. Nat. Commun. 2013, 4, 2794. [Google Scholar] [CrossRef]
- Yu, Z.G. Spin-orbit coupling and its effects in organic solids. Phys. Rev. B Condens. Mater. 2012, 85, 1262–1275. [Google Scholar] [CrossRef]
- Devkota, J.; Geng, R.; Subedi, R.C.; Nguyen, T.D. Organic Spin Valves: A Review. Adv. Funct. Mater. 2016, 26, 3881–3898. [Google Scholar] [CrossRef]
- Yu, Z.G. Spin-orbit coupling, spin relaxation, and spin diffusion in organic solids. Phys. Rev. Lett. 2011, 106, 106602. [Google Scholar] [CrossRef] [PubMed]
- Niu, L.B.; Chen, L.J.; Chen, P.; Cui, Y.T.; Zhang, Y.; Shao, M.; Guan, Y.X. Hyperfine interaction vs. spin–orbit coupling in organic semiconductors. RSC Adv. 2016, 6, 111421–111426. [Google Scholar] [CrossRef]
- Drew, A.J.; Hoppler, J.; Schulz, L.; Pratt, F.L.; Desai, P.; Shakya, P.; Kreouzis, T.; Gillin, W.P.; Suter, A.; Morley, N.A.; et al. Direct measurement of the electronic spin diffusion length in a fully functional organic spin valve by low-energy muon spin rotation. Nat. Mater. 2009, 8, 109–114. [Google Scholar] [CrossRef] [PubMed]
- Cinchetti, M.; Heimer, K.; Wustenberg, J.P.; Andreyev, O.; Bauer, M.; Lach, S.; Ziegler, C.; Gao, Y.; Aeschlimann, M. Determination of spin injection and transport in a ferromagnet/organic semiconductor heterojunction by two-photon photoemission. Nat. Mater. 2009, 8, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Siegert, B.; Donarini, A.; Grifoni, M. Effects of spin-orbit coupling and many-body correlations in STM transport through copper phthalocyanine. Beilstein J. Nanotech. 2015, 6, 2452–2462. [Google Scholar] [CrossRef] [PubMed]
- Pramanik, S.; Bandyopadhyay, S.; Garre, K.; Cahay, M. Normal and inverse spin-valve effect in organic semiconductor nanowires and the background monotonic magnetoresistance. Phys. Rev. B 2006, 74, 235329. [Google Scholar] [CrossRef]
- Nuccio, L.; Willis, M.; Schulz, L.; Fratini, S.; Messina, F.; D’Amico, M.; Pratt, F.L.; Lord, J.S.; McKenzie, I.; Loth, M.; et al. Importance of spin-orbit interaction for the electron spin relaxation in organic semiconductors. Phys. Rev. Lett. 2013, 110, 216602. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Zhang, G.; Meng, R.; Gao, K.; Xie, S. Trap effect of triplet excitons on magnetoresistance in organic devices. Org. Electron. 2015, 25, 12–15. [Google Scholar] [CrossRef]
- Li, X.X.; Dong, X.F.; Lei, J.; Xie, S.J.; Saxena, A. Theoretical investigation of organic magnetoresistance based on hyperfine interaction. Appl. Phys. Lett. 2012, 100, 142408. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Basel, T.P.; Pu, Y.J.; Li, X.G.; Ehrenfreund, E.; Vardeny, Z.V. Isotope effect in the spin response of aluminum tris(8-hydroxyquinoline) based devices. Phys. Rev. B 2012, 85, 245437. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Hukic-Markosian, G.; Wang, F.; Wojcik, L.; Li, X.G.; Ehrenfreund, E.; Vardeny, Z.V. Isotope effect in spin response of pi-conjugated polymer films and devices. Nat. Mater. 2010, 9, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Li, T.; Guo, X. Vertical graphene spin valves based on La2/3Sr1/3MnO3 electrodes. ACS Appl. Mater. Interfaces 2014, 6, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Rybicki, J.; Lin, R.; Wang, F.; Wohlgenannt, M.; He, C.; Sanders, T.; Suzuki, Y. Tuning the performance of organic spintronic devices using X-ray generated traps. Phys. Rev. Lett. 2012, 109, 076603. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Wang, F.; Li, X.-G.; Ehrenfreund, E.; Vardeny, Z.V. Spin diffusion in fullerene-based devices: Morphology effect. Phys. Rev. B 2013, 87, 075205. [Google Scholar] [CrossRef]
- Yoo, J.-W.; Jang, H.W.; Prigodin, V.N.; Kao, C.; Eom, C.B.; Epstein, A.J. Tunneling vs. giant magnetoresistance in organic spin valve. Synth. Met. 2010, 160, 216–222. [Google Scholar] [CrossRef]
- Yoo, J.-W.; Jang, H.W.; Prigodin, V.N.; Kao, C.; Eom, C.B.; Epstein, A.J. Giant magnetoresistance in ferromagnet/organic semiconductor/ferromagnet heterojunctions. Phys. Rev. B 2009, 80, 205207. [Google Scholar] [CrossRef]
- Cinchetti, M.; Dediu, V.A.; Hueso, L.E. Activating the molecular spinterface. Nat. Mater. 2017, 16, 507–515. [Google Scholar] [CrossRef] [PubMed]
- Bergenti, I.; Borgatti, F.; Calbucci, M.; Riminucci, A.; Cecchini, R.; Graziosi, P.; MacLaren, D.A.; Giglia, A.; Rueff, J.P.; Ceolin, D.; et al. Oxygen Impurities Link Bistability and Magnetoresistance in Organic Spin Valves. ACS Appl. Mater. Interfaces 2018, 10, 8132–8140. [Google Scholar] [CrossRef] [PubMed]
- Barraud, C.; Bouzehouane, K.; Deranlot, C.; Fusil, S.; Jabbar, H.; Arabski, J.; Rakshit, R.; Kim, D.J.; Kieber, C.; Boukari, S.; et al. Unidirectional Spin-Dependent Molecule-Ferromagnet Hybridized States Anisotropy in Cobalt Phthalocyanine Based Magnetic Tunnel Junctions. Phys. Rev. Lett. 2015, 114, 206603. [Google Scholar] [CrossRef] [PubMed]
- Baadji, N.; Sanvito, S. Giant resistance change across the phase transition in spin-crossover molecules. Phys. Rev. Lett. 2012, 108, 217201. [Google Scholar] [CrossRef] [PubMed]
- Djeghloul, F.; Ibrahim, F.; Cantoni, M.; Bowen, M.; Joly, L.; Boukari, S.; Ohresser, P.; Bertran, F.; Le Fevre, P.; Thakur, P.; et al. Direct observation of a highly spin-polarized organic spinterface at room temperature. Sci. Rep. 2013, 3, 1272. [Google Scholar] [CrossRef] [PubMed]
- Baadji, N.; Piacenza, M.; Tugsuz, T.; Sala, F.D.; Maruccio, G.; Sanvito, S. Electrostatic spin crossover effect in polar magnetic molecules. Nat. Mater. 2009, 8, 813–817. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Cui, B.; Li, F.; Zhou, X.; Pan, F. Recent progress in voltage control of magnetism: Materials, mechanisms, and performance. Prog. Mater. Sci. 2017, 87, 33–82. [Google Scholar] [CrossRef]
- Jiang, S.W.; Liu, S.; Wang, P.; Luan, Z.Z.; Tao, X.D.; Ding, H.F.; Wu, D. Exchange-Dominated Pure Spin Current Transport in Alq3 Molecules. Phys. Rev. Lett. 2015, 115, 086601. [Google Scholar] [CrossRef] [PubMed]
- Riminucci, A.; Prezioso, M.; Pernechele, C.; Graziosi, P.; Bergenti, I.; Cecchini, R.; Calbucci, M.; Solzi, M.; Alek Dediu, V. Hanle effect missing in a prototypical organic spintronic device. Appl. Phys. Lett. 2013, 102, 092407. [Google Scholar] [CrossRef]
- Watanabe, S.; Ando, K.; Kang, K.; Mooser, S.; Vaynzof, Y.; Kurebayashi, H.; Saitoh, E.; Sirringhaus, H. Polaron spin current transport in organic semiconductors. Nat. Phys. 2014, 10, 308–313. [Google Scholar] [CrossRef]
- Wohlgenannt, M.; Tandon, K.; Mazumdar, S.; Ramasesha, S.; Vardeny, Z.V. Formation cross-sections of singlet and triplet excitions in π-conjugated polymers. Nature 2001, 409, 494. [Google Scholar] [CrossRef] [PubMed]
- Salis, G.; Alvarado, S.; Tschudy, M.; Brunschwiler, T.; Allenspach, R. Hysteretic electroluminescence in organic light-emitting diodes for spin injection. Phys. Rev. B 2004, 70, 08203. [Google Scholar] [CrossRef]
- Sun, X.; Vélez, S.; Atxabal, A.; Bedoya-Pinto, A.; Parui, S.; Zhu, X.; Llopis, R.; Casanova, F.; Hueso, L.E. A molecular spin-photovoltaic device. Science 2017, 357, 677–680. [Google Scholar] [CrossRef] [PubMed]
| Electrode | Spin Polarization P (%) | Curie Temperature TC (K) |
|---|---|---|
| Fe | 44 [47] | 1043 [48] |
| Co | 34 [47] | 1388 [49] |
| Ni | 31 [50] | 631 [48] |
| LSMO | 100 [51] | 369 [52] |
| Fe3O4 | ∼100 [53] | 851 [54] |
| CrO2 | 100 [55,56] | 392 [57] |
| Co2MnSi | 100 [58] | 900 [58] |
| Organic Materials | Chemical Structure | FM Electrodes | MR @ Temperature |
|---|---|---|---|
| T6 |  | LSMO/LSMO [2] | 30%@ RT [2] |
| Alq3 | 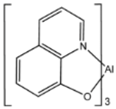 | LSMO/Co [1] Co/Al2O3/Py [25] LSMO/Co [26,76] | −40%@11 K [1] 6.0@300 K [25] 300%@2 K [76] @10 K [26] |
| Rubrene | 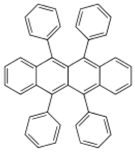 | Fe3O4/AlOx/Co [29] Fe/Al2O3/Co [23] | 6%@ RT [29] 16%@4.2 K 6%@295 K [23] |
| C60 | 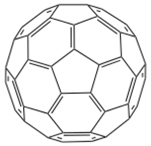 | Fe3O4/AlOx/Co [28] Co/AlOx/Py [77] | 5.3%@ RT [28] (5–10)%@ RT [77] |
| C70 |  | Fe3O4/AlOx/Co [78] LSMO/Co [60] | 2.5%@150 K 0.3%@300 K [78] 6%@20 K 0.7%@290 K [60] |
| CuPc |  | LSMO/Co [79] Co/AlOx/Ni80Fe20 [80] | 6%@ 10 K 0.84%@ RT [79] >4%@ RT (F16CuPc) [80] |
| pentacene | 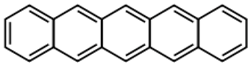 | LSMO/LSMO [59,81] | 2%@9 K [59] 5.5%@5.3 K [81] |
| PTCDA |  | Fe/Co [82] NiFe/Co/AlOx/AlOx/Co [83] | 0.4%@9 K [82] 13.5%@ RT [83] |
| α-NPD | 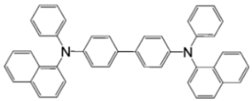 | LSMO/Co [84] | 14 ± 4%@14 K [84] |
| CVB |  | LSMO/Co [84] | 18 ± 3%@14 K [84] |
| CNAP | 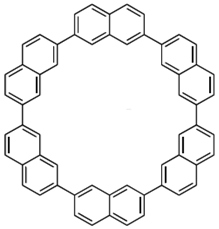 | Co/AlOx/Ni80Fe20 [43] | 4–6%@5 K 1–2%@300 K [43] |
| benzofurane bithiophene (BF3) | 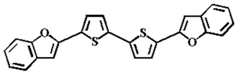 | NiFe/AlOx/Co [85] | 3%@40 K [85] |
| BCP | 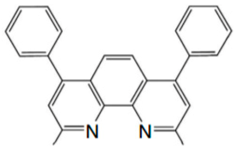 | Co/AlOx/NiFe [86] | >4%@ RT [86] |
| TPD | 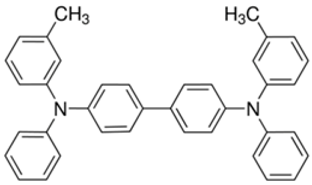 | Co2MnSi/Co [58] LSMO/Co [58] | 10.7%@5 K 7.8%@ RT [58] 19%@5 K [58] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Duan, Q.; Tong, J.; Chang, Y.; Zhou, L.; Qin, G.; Zhang, X. Magnetoresistance Effect and the Applications for Organic Spin Valves Using Molecular Spacers. Materials 2018, 11, 721. https://doi.org/10.3390/ma11050721
Yao X, Duan Q, Tong J, Chang Y, Zhou L, Qin G, Zhang X. Magnetoresistance Effect and the Applications for Organic Spin Valves Using Molecular Spacers. Materials. 2018; 11(5):721. https://doi.org/10.3390/ma11050721
Chicago/Turabian StyleYao, Xiannian, Qingqing Duan, Junwei Tong, Yufang Chang, Lianqun Zhou, Gaowu Qin, and Xianmin Zhang. 2018. "Magnetoresistance Effect and the Applications for Organic Spin Valves Using Molecular Spacers" Materials 11, no. 5: 721. https://doi.org/10.3390/ma11050721
APA StyleYao, X., Duan, Q., Tong, J., Chang, Y., Zhou, L., Qin, G., & Zhang, X. (2018). Magnetoresistance Effect and the Applications for Organic Spin Valves Using Molecular Spacers. Materials, 11(5), 721. https://doi.org/10.3390/ma11050721





