Near-Infrared Spectroscopic Method for Monitoring Water Content in Epoxy Resins and Fiber-Reinforced Composites
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.2. Methods
3. Results and Discussion
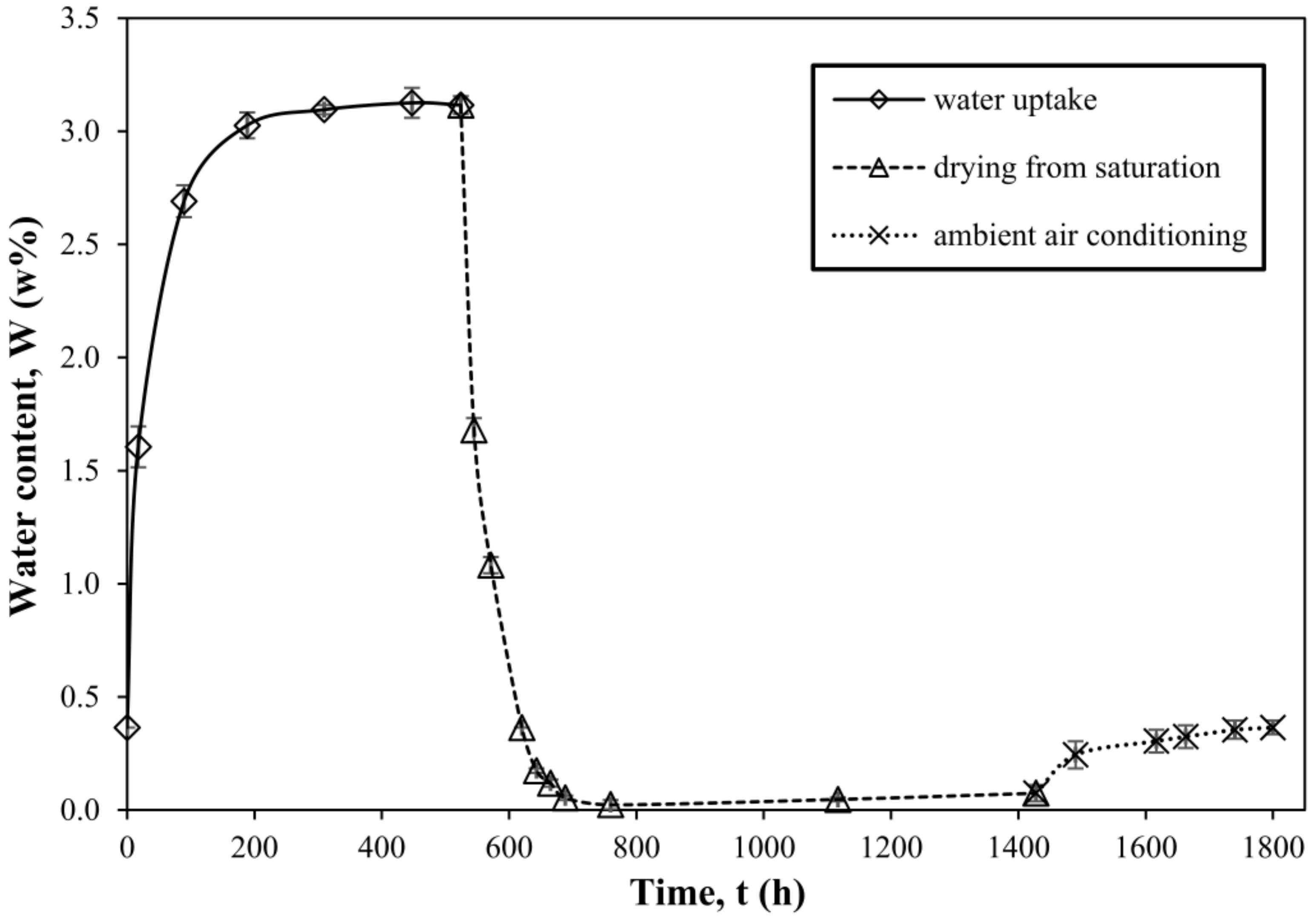
3.1. Water Uptake, Drying and Conditioning in Air Experiments of Neat Resin
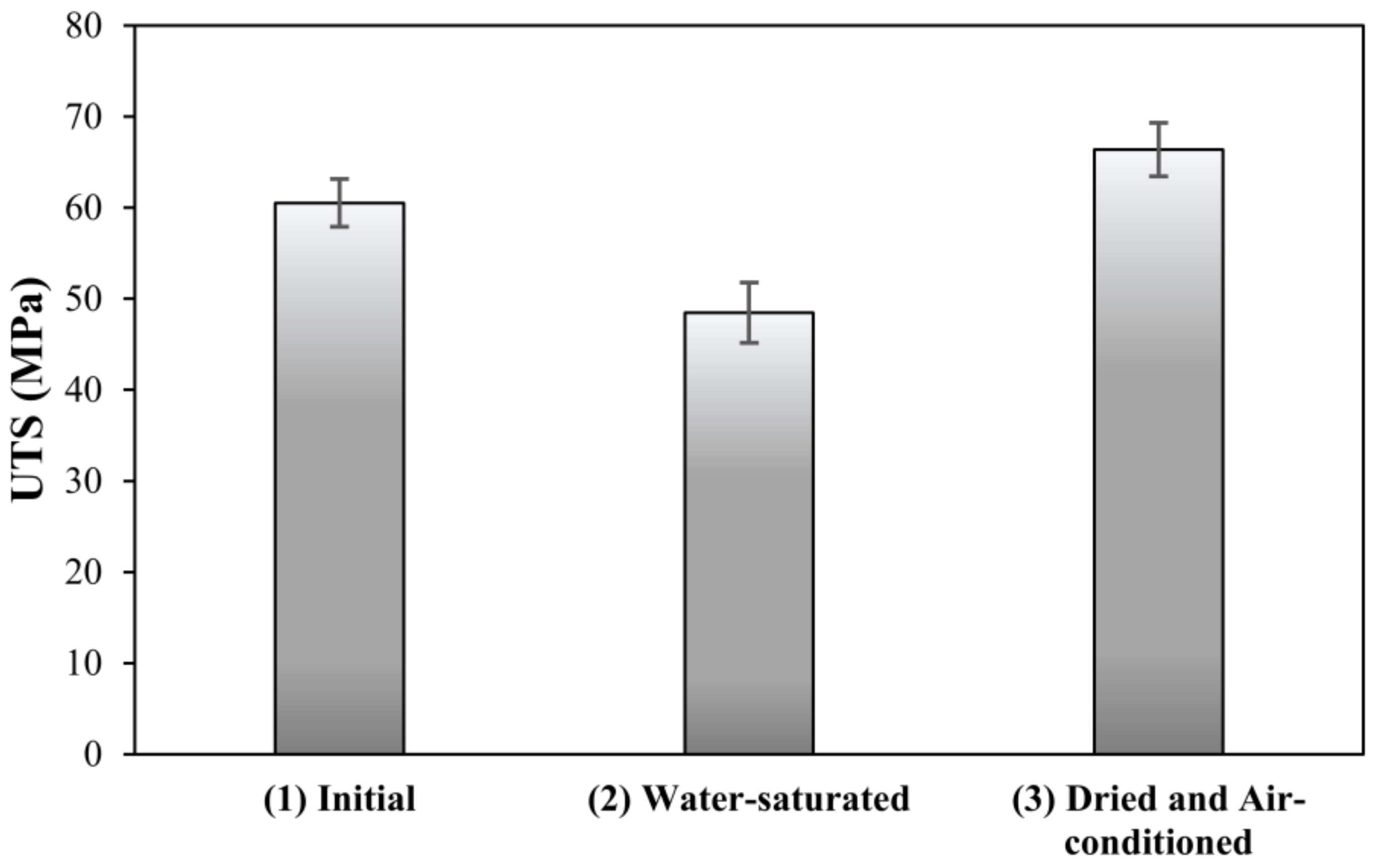
3.2. Reversible Drop in Ultimate Tensile Strength of Neat Resin with Water Content
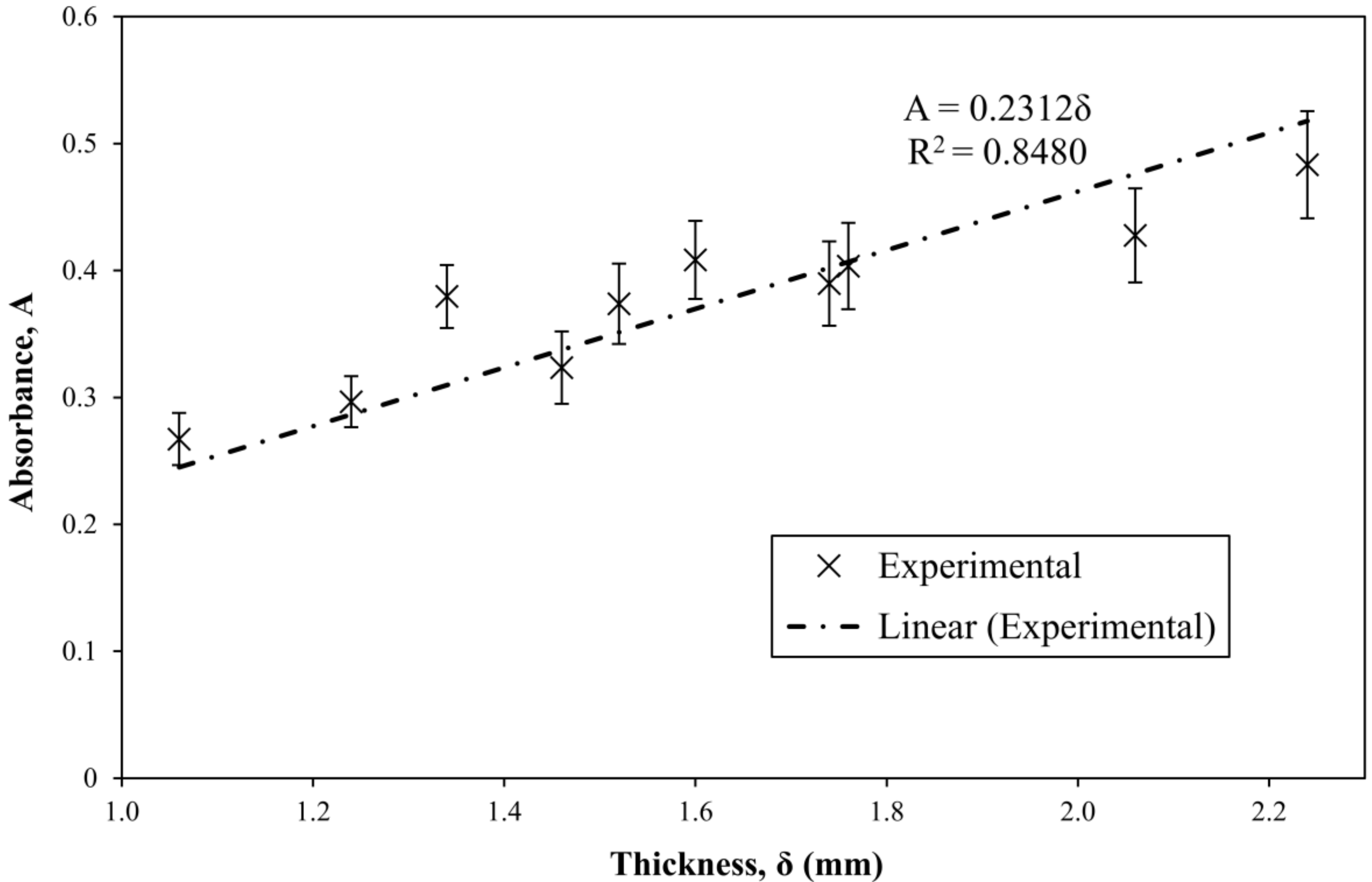
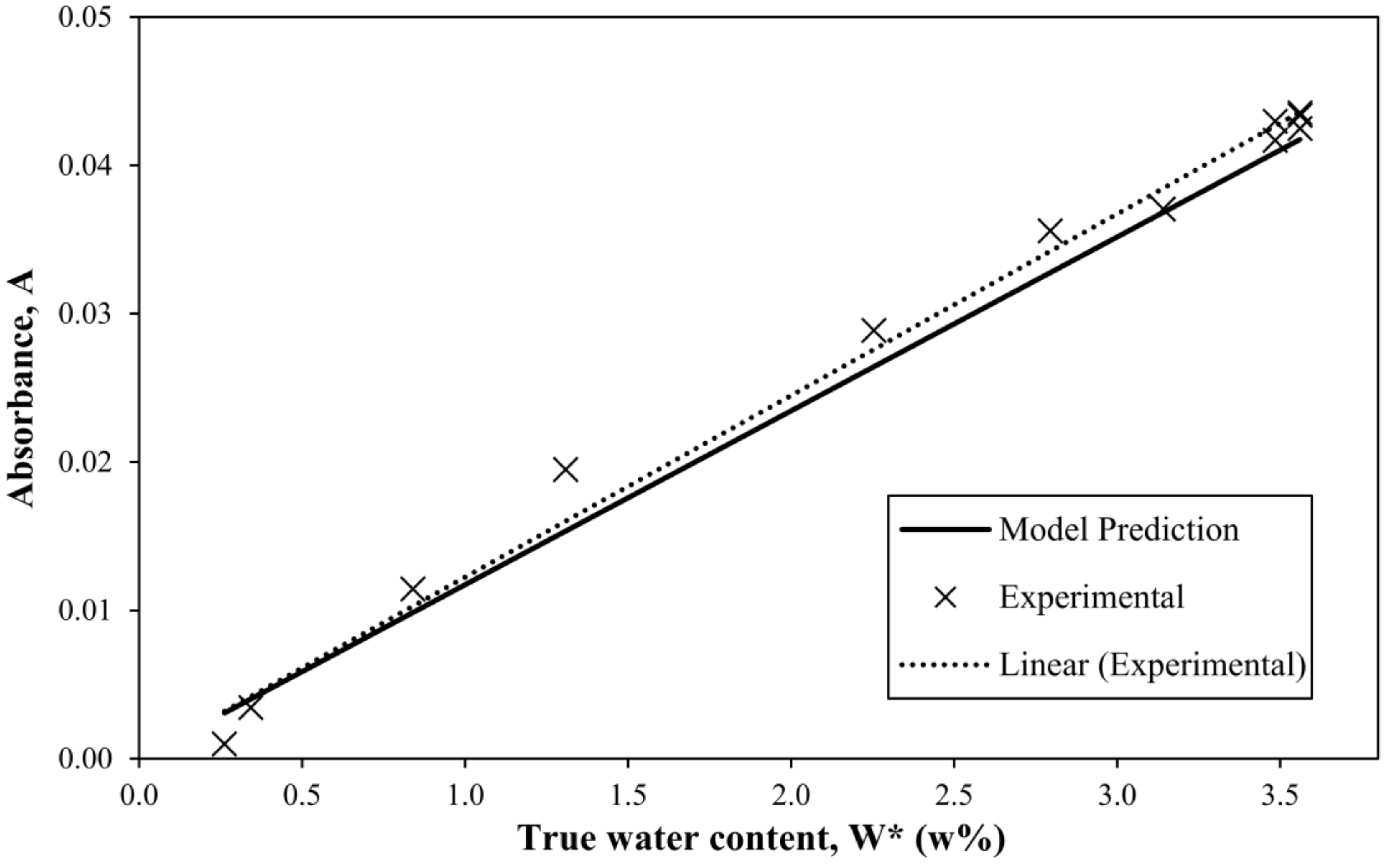
3.3. The Method for Monitoring Water Content in Neat Resin
3.4. Extension of the Method to Samples of Varying Thickness
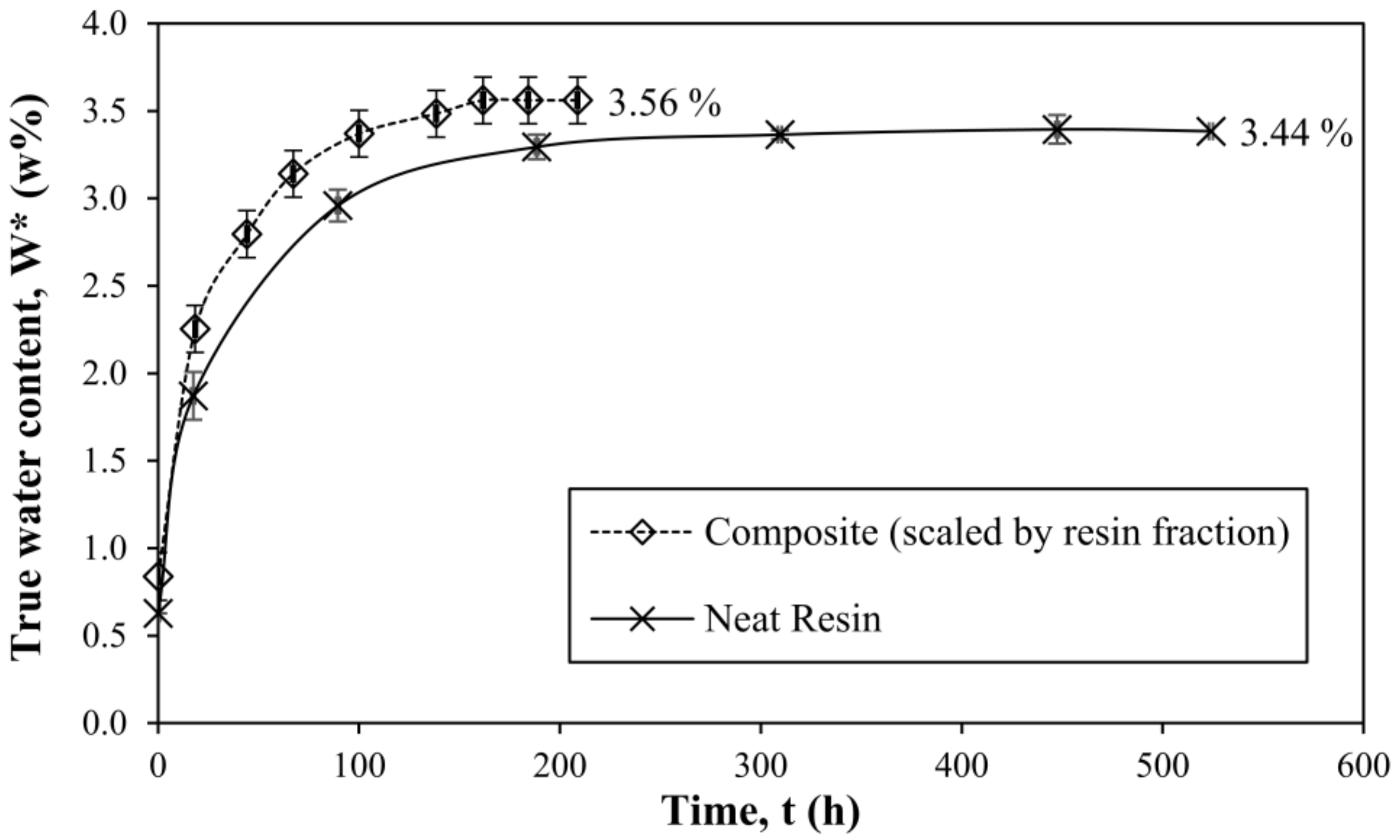
3.5. Extension of the Method to Composite Systems
3.6. Final Remarks on the Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, L.; Yu, Y.; Wu, Q.; Zhan, G.; Li, S. Effect of Chemical Structure on the Water Sorption of Amine-Cured Epoxy Resins. Corros. Sci. 2009, 51, 3000. [Google Scholar] [CrossRef]
- Lee, M.C.; Peppas, N.A. Water Transport in Epoxy-Resins. Prog. Polym. Sci. 1993, 18, 947. [Google Scholar]
- Wang, J.; Gong, J.; Gong, Z.; Yan, X.; Wang, B.; Wu, Q.; Li, S. Effect of Curing Agent Polarity on Water Absorption and Free Volume in Epoxy Resin Studied by PALS. Nucl. Instrum. Methods Phys. Res. B 2010, 268, 2355. [Google Scholar] [CrossRef]
- Morel, E.; Bellenger, V.; Verdu, J. Structure-Water Absorption Relationships for Amine-Cured Epoxy Resins. Polymer 1985, 26, 1719. [Google Scholar] [CrossRef]
- Echtermeyer, A.T. Integrating Durability in Marine Composite Certification. In Durability of Composites in a Marine Environment; Davies, P., Rajapakse, Y.D.S., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 179–194. [Google Scholar]
- Weitsman, Y. Coupled Damage and Moisture-Transport in Fiber-Reinforced, Polymeric Composites. Int. J. Solids Struct. 1987, 23, 1003. [Google Scholar] [CrossRef]
- Weitsman, Y.J.; Elahi, M. Effects of Fluids on the Deformation, Strength and Durability of Polymeric Composites—An Overview. Mech. Time-Depend. Mater. 2000, 4, 107. [Google Scholar] [CrossRef]
- Roy, S. Moisture-Induced Degradation in Long-Term Durability of Polymeric Matrix Composites; Pochiraju, V.K., Tandon, P.G., Schoeppner, A.G., Eds.; Springer: Boston, MA, USA, 2012; pp. 181–236. [Google Scholar]
- Apicella, A.; Nicolais, L. Effect of Water on the Properties of Epoxy Matrix and Composite. Adv. Polym. Sci. 1985, 72, 69. [Google Scholar]
- Lefebvre, D.R.; Elliker, P.R.; Takahashi, K.M.; Raju, V.R.; Kaplan, M.L. The Critical Humidity Effect in the Adhesion of Epoxy to Glass: Role of Hydrogen Bonding. J. Adhes. Sci. Technol. 2000, 14, 925. [Google Scholar] [CrossRef]
- Guermazi, N.; Elleuch, K.; Ayedi, H.F. The Effect of Time and Aging Temperature on Structural and Mechanical Properties of Pipeline Coating. Mater. Des. 2009, 30, 2006. [Google Scholar] [CrossRef]
- Wu, C.F.; Xu, W.J. Atomistic Simulation Study of Absorbed Water Influence on Structure and Properties of Crosslinked Epoxy Resin. Polymer 2007, 48, 5440. [Google Scholar] [CrossRef]
- Bertolino, V.; Cavallaro, G.; Lazzara, G.; Merli, M.; Milioto, S.; Parisi, F.; Sciascia, L. Effect of the Biopolymer Charge and the Nanoclay Morphology on Nanocomposite Materials. Ind. Eng. Chem. Res. 2016, 55, 7373. [Google Scholar] [CrossRef]
- Ciprioti, S.V.; Tuffi, R.; Dell’Era, A.; Poggetto, F.D.; Bollino, F. Thermal Behavior and Structural Study of SiO2/Poly(ε-caprolactone) Hybrids Synthesized via Sol-Gel Method. Materials 2018, 11, 275. [Google Scholar] [CrossRef]
- Mijović, J.; Zhang, H. Local Dynamics and Molecular Origin of Polymer Network−Water Interactions as Studied by Broadband Dielectric Relaxation Spectroscopy, FTIR, and Molecular Simulations. Macromolecules 2003, 36, 1279. [Google Scholar] [CrossRef]
- Philippe, L.V.S.; Lyon, S.B.; Sammon, C.; Yarwood, J. Validation of Electrochemical Impedance Measurements for Water Sorption into Epoxy Coatings Using Gravimetry and Infra-Red Spectroscopy. Corros. Sci. 2008, 50, 887. [Google Scholar] [CrossRef]
- Cotugno, S.; Mensitieri, G.; Musto, P.; Sanguigno, L. Molecular Interactions in and Transport Properties of Densely Crosslinked Networks: A Time-Resolved FT-IR Spectroscopy Investigation of the Epoxy/H2O System. Macromolecules 2005, 38, 801. [Google Scholar] [CrossRef]
- Weir, M.D.; Bastide, C.; Sung, C.S.P. Characterization of Interaction of Water in Epoxy by UV Reflection Spectroscopy. Macromolecules 2001, 34, 4923. [Google Scholar] [CrossRef]
- Mijović, J.; Zhang, H. Molecular Dynamics Simulation Study of Motions and Interactions of Water in a Polymer Network. J. Phys. Chem. B 2004, 108, 2557. [Google Scholar] [CrossRef]
- MacQueen, R.C.; Granata, R.D. A Positron Annihilation Lifetime Spectroscopic Study of the Corrosion Protective Properties of Epoxy Coatings. Prog. Org. Coat. 1996, 28, 97. [Google Scholar] [CrossRef]
- Muroga, S.; Hikima, Y.; Ohshima, M. Near-Infrared Spectroscopic Evaluation of the Water Content of Molded Polylactide under the Effect of Crystallization. Appl. Spectrosc. 2017, 71, 1300. [Google Scholar] [CrossRef] [PubMed]
- Genkawa, T.; Watari, M.; Nishii, T.; Ozaki, Y. Development of a Near-Infrared/Mid-Infrared Dual-Region Spectrometer for Online Process Analysis. Appl. Spectrosc. 2012, 66, 773. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, Y. Near-Infrared Spectroscopy—Its Versatility in Analytical Chemistry. Anal. Sci. 2012, 28, 545. [Google Scholar] [CrossRef] [PubMed]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Hygrothermal Aging of Amine Epoxy: Reversible Static and Fatigue Properties. Polym. Test. 2018, submitted. [Google Scholar]
- Rocha, I.B.C.M.; Raijmaekers, S.; Nijssen, R.P.L.; van der Meer, F.P.; Sluys, L.J. Hygrothermal ageing behaviour of a glass/epoxy composite used in wind turbine blades. Compos. Struct. 2017, 174, 110. [Google Scholar] [CrossRef]
- Camacho, W.; Valles-Lluch, A.; Ribes-Greus, A.; Karksson, S. Determination of Moisture Content in Nylon 6,6 by Near-Infrared Spectroscopy and Chemometrics. J. Appl. Polym. Sci. 2003, 87, 2165. [Google Scholar] [CrossRef]
- Kuda-Malwathumullage, C.P.S.; Small, G.W. Determination of Moisture Content of Polyamide 66 Directly from Combination Region Near-Infrared Spectra. J. Appl. Polym. Sci. 2014, 131, 40645. [Google Scholar] [CrossRef]
- Zhou, G.X.; Ge, Z.; Dorwart, J.; Izzo, B.; Kukura, J.; Bicker, G.; Wyvratt, J. Determination and Differentiation of Surface and Bound Water in Drug Substances by Near Infrared Spectroscopy. J. Pharm. Sci. 2003, 92, 1058. [Google Scholar] [CrossRef] [PubMed]
- Cavallaro, G.; Lazzara, G.; Konnova, S.; Fakhrullin, R.; Lvov, Y. Composite films of natural clay nanotubes with cellulose and chitosan. Green Mater. 2014, 2, 232. [Google Scholar] [CrossRef]
- De Rodriguez, N.G.; Thielemans, W.; Dufresne, A. Sisal cellulose whiskers reinforced polyvinyl acetate nanocomposites. Cellulose 2006, 13, 261. [Google Scholar] [CrossRef]
- Musto, P.; Ragosta, G.; Mascia, L. Vibrational Spectroscopy Evidence for the Dual Nature of Water Sorbed into Epoxy Resins. Chem. Mater. 2000, 12, 1331. [Google Scholar] [CrossRef]
- Moy, P.; Karasz, F.E. Epoxy-Water Interactions. Polym. Eng. Sci. 1980, 20, 315. [Google Scholar] [CrossRef]
- Zhou, J.M.; Lucas, J.P. Hygrothermal Effects of Epoxy Resin. Part I: The Nature of Water in Epoxy. Polymer 1999, 40, 5505. [Google Scholar] [CrossRef]
- Barrie, J.A.; Sagoo, P.S.; Johncock, P. The Sorption and Diffusion of Water in Epoxy Resins. J. Membr. Sci. 1984, 18, 197. [Google Scholar] [CrossRef]
- Falk, M.; Ford, T.A. Infrared Spectrum and Structure of Liquid Water. Can. J. Chem. 1966, 44, 1699. [Google Scholar] [CrossRef]
- Wiedemair, V.; Mayr, S.; Wimmer, D.S.; Köck, E.M.; Penner, S.; Kerstan, A.; Steinmassl, P.-A.; Dumfahrt, H.; Huck, C.W. Novel Molecular Spectroscopic Multimethod Approach for Monitoring Water Absorption/Desorption Kinetics of CAD/CAM Poly(Methyl Methacrylate) Prosthodontics. Appl. Spectrosc. 2017, 71, 1600. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, F.A.; Carlsson, L.A.; Acha, B.A. Evaluation of Water Degradation of Vinylester and Epoxy Matrix Composites by Single Fiber and Composite Tests. J. Mater. Sci. 2008, 43, 5230. [Google Scholar] [CrossRef]

| True Water Content, W* (%) | Wavenumber (cm−1) |
|---|---|
| 0.26 | 5230 |
| 0.61 | 5225 |
| 1.68 | 5219 |
| 1.88 | 5214 |
| 2.84 | 5214 |
| 2.94 | 5208 |
| 3.34 | 5208 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Near-Infrared Spectroscopic Method for Monitoring Water Content in Epoxy Resins and Fiber-Reinforced Composites. Materials 2018, 11, 586. https://doi.org/10.3390/ma11040586
Krauklis AE, Gagani AI, Echtermeyer AT. Near-Infrared Spectroscopic Method for Monitoring Water Content in Epoxy Resins and Fiber-Reinforced Composites. Materials. 2018; 11(4):586. https://doi.org/10.3390/ma11040586
Chicago/Turabian StyleKrauklis, Andrey E., Abedin I. Gagani, and Andreas T. Echtermeyer. 2018. "Near-Infrared Spectroscopic Method for Monitoring Water Content in Epoxy Resins and Fiber-Reinforced Composites" Materials 11, no. 4: 586. https://doi.org/10.3390/ma11040586
APA StyleKrauklis, A. E., Gagani, A. I., & Echtermeyer, A. T. (2018). Near-Infrared Spectroscopic Method for Monitoring Water Content in Epoxy Resins and Fiber-Reinforced Composites. Materials, 11(4), 586. https://doi.org/10.3390/ma11040586







