Mesoscopic Constitutive Model for Predicting Failure of Bulk Metallic Glass Composites Based on the Free-Volume Model
Abstract
:1. Introduction
2. Analytical Model of BMGCs
2.1. Constitutive Model of BMGs
2.2. Constitutive Model of Ductile Phases
2.3. Homogenization Method for BMGCs
2.4. Failure of the BMG Matrix
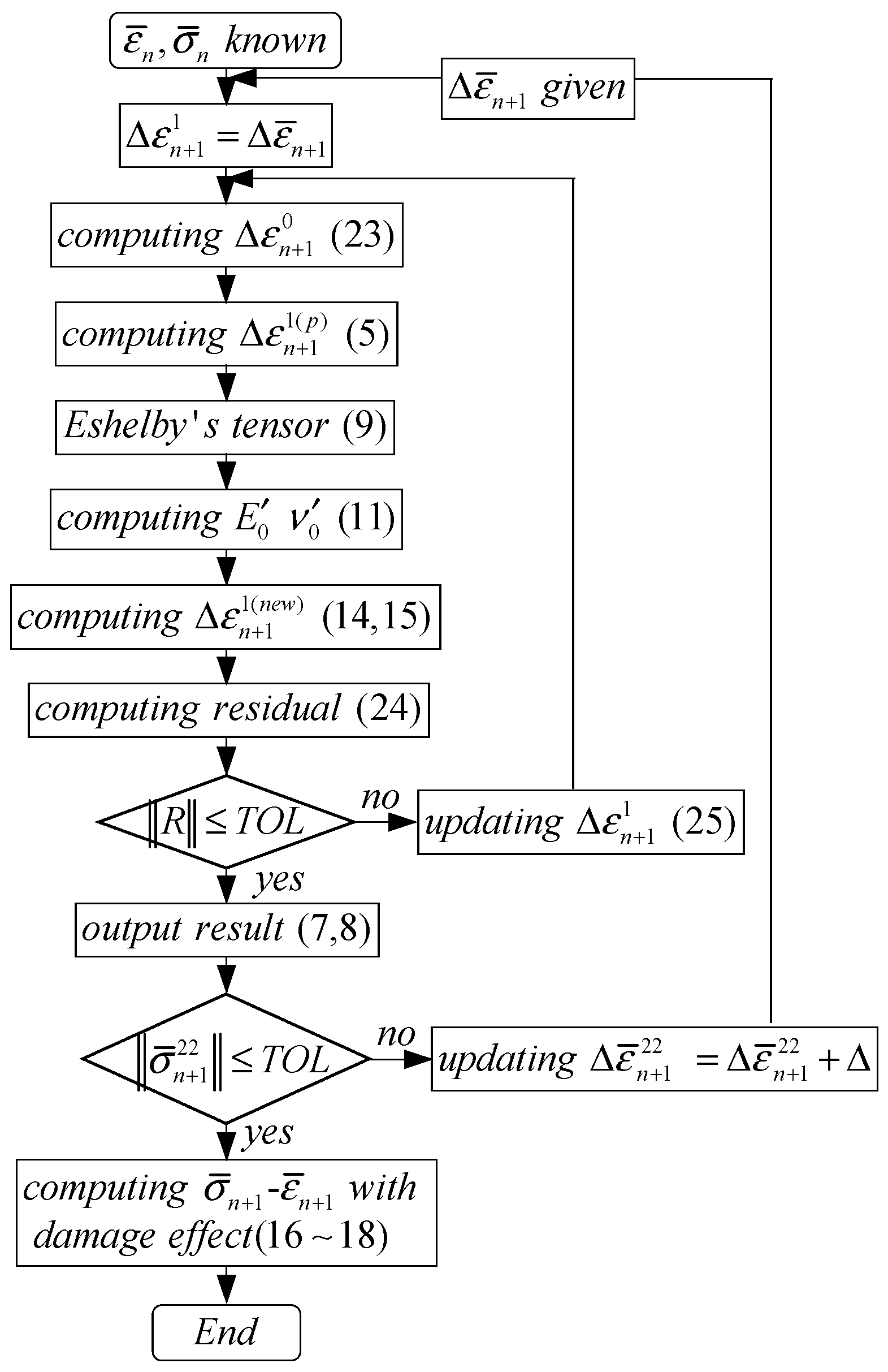
3. Numerical Implementation
4. Results and Discussion
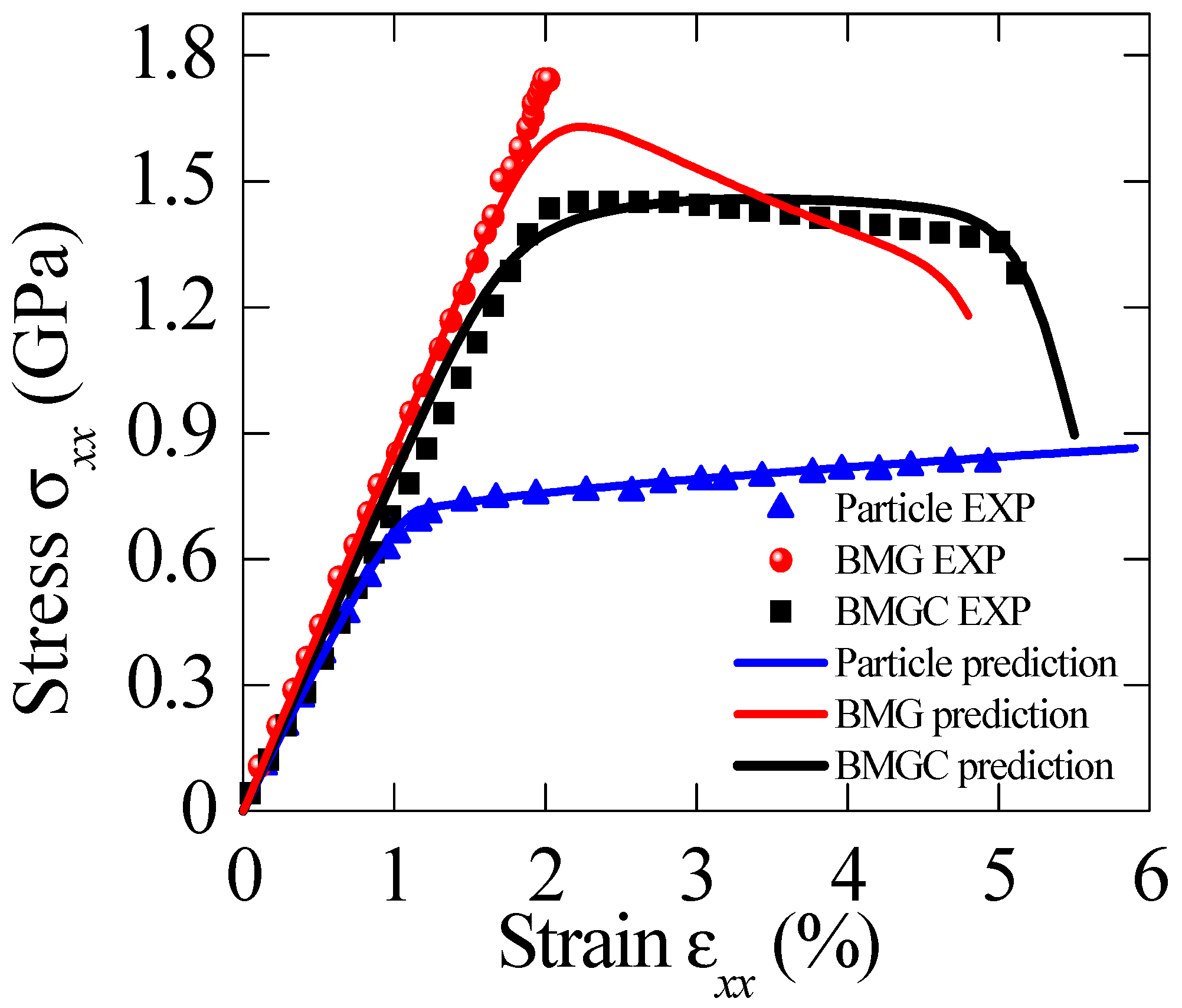
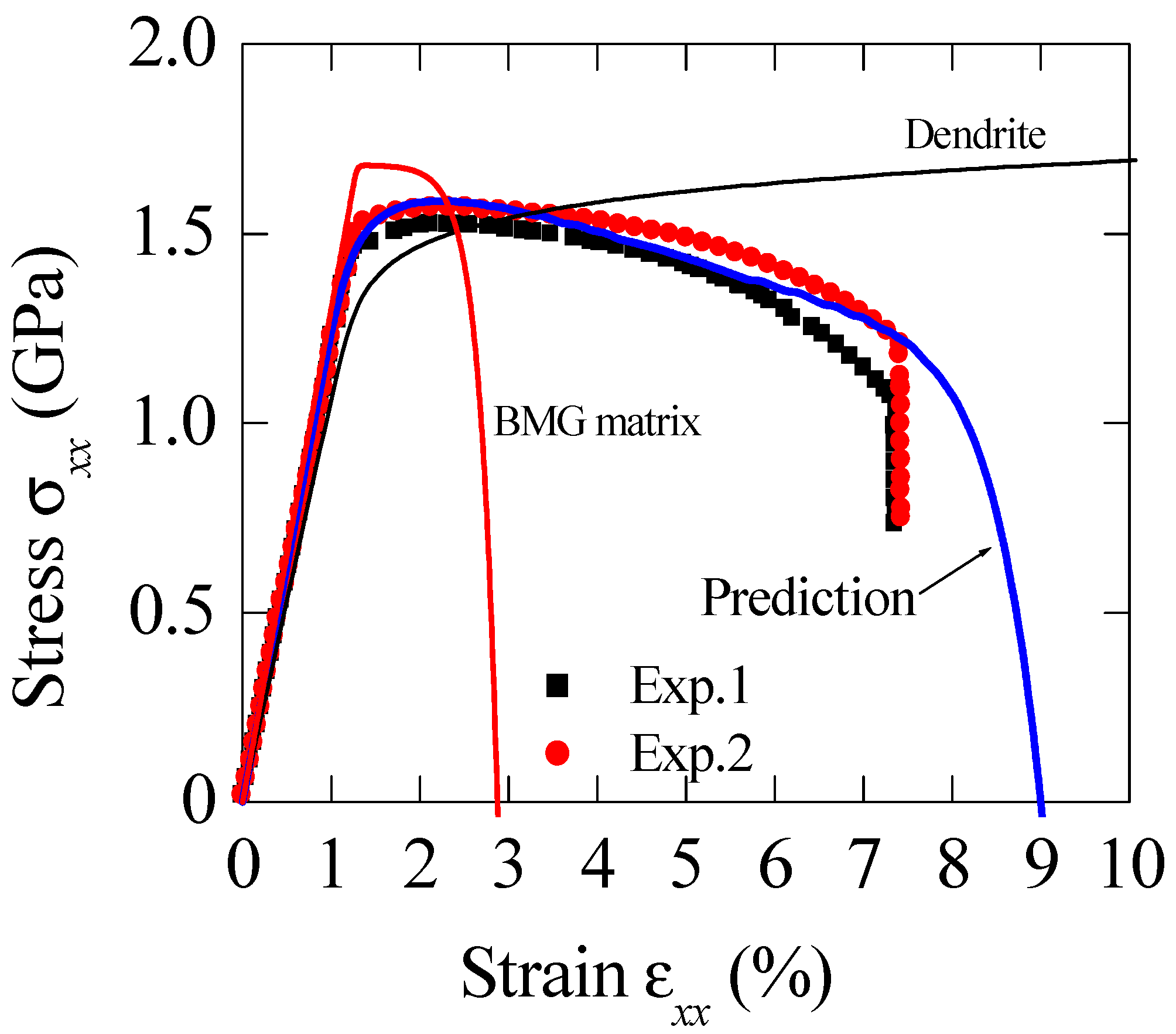
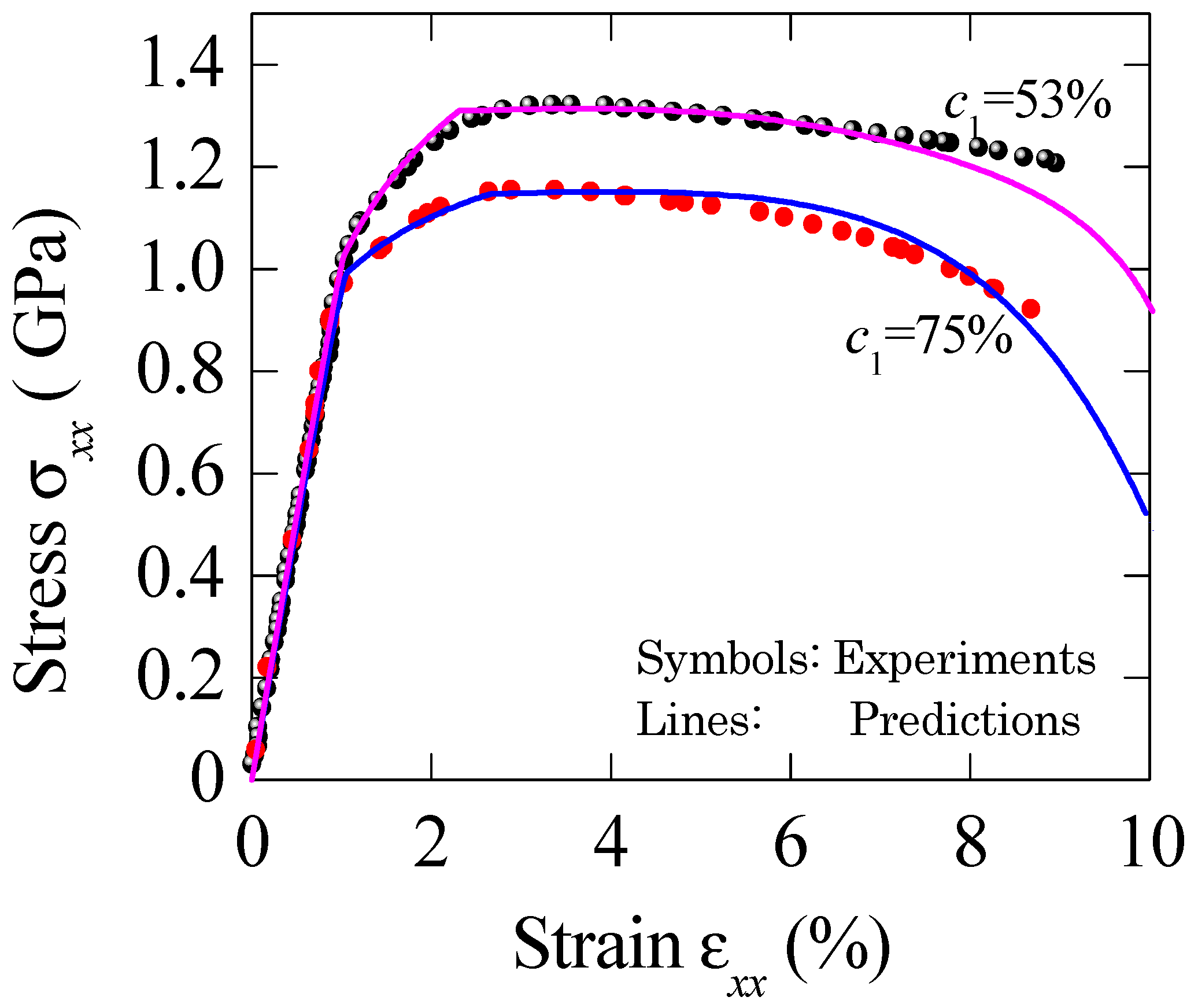
4.1. Comparisons with the Experiments
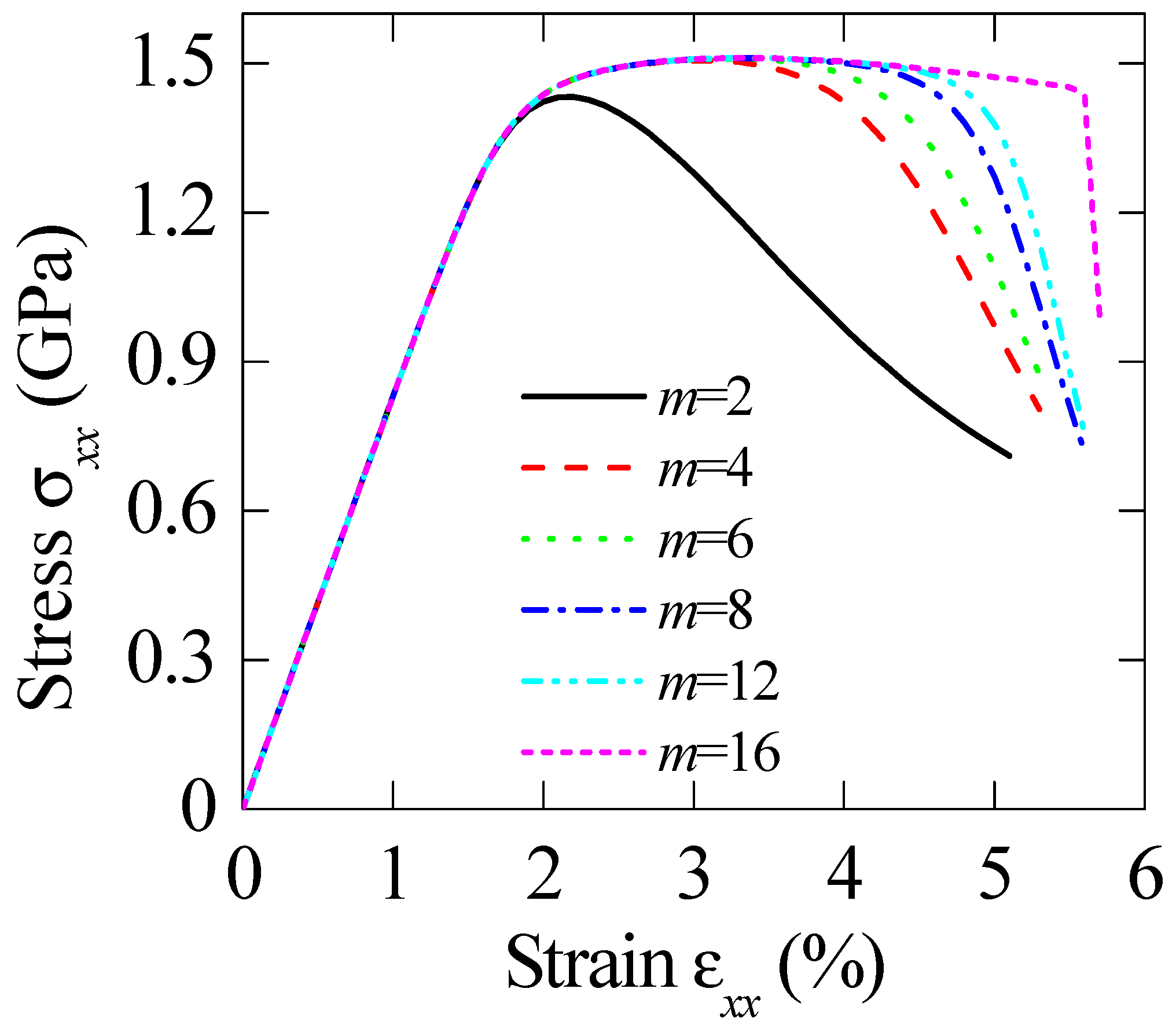
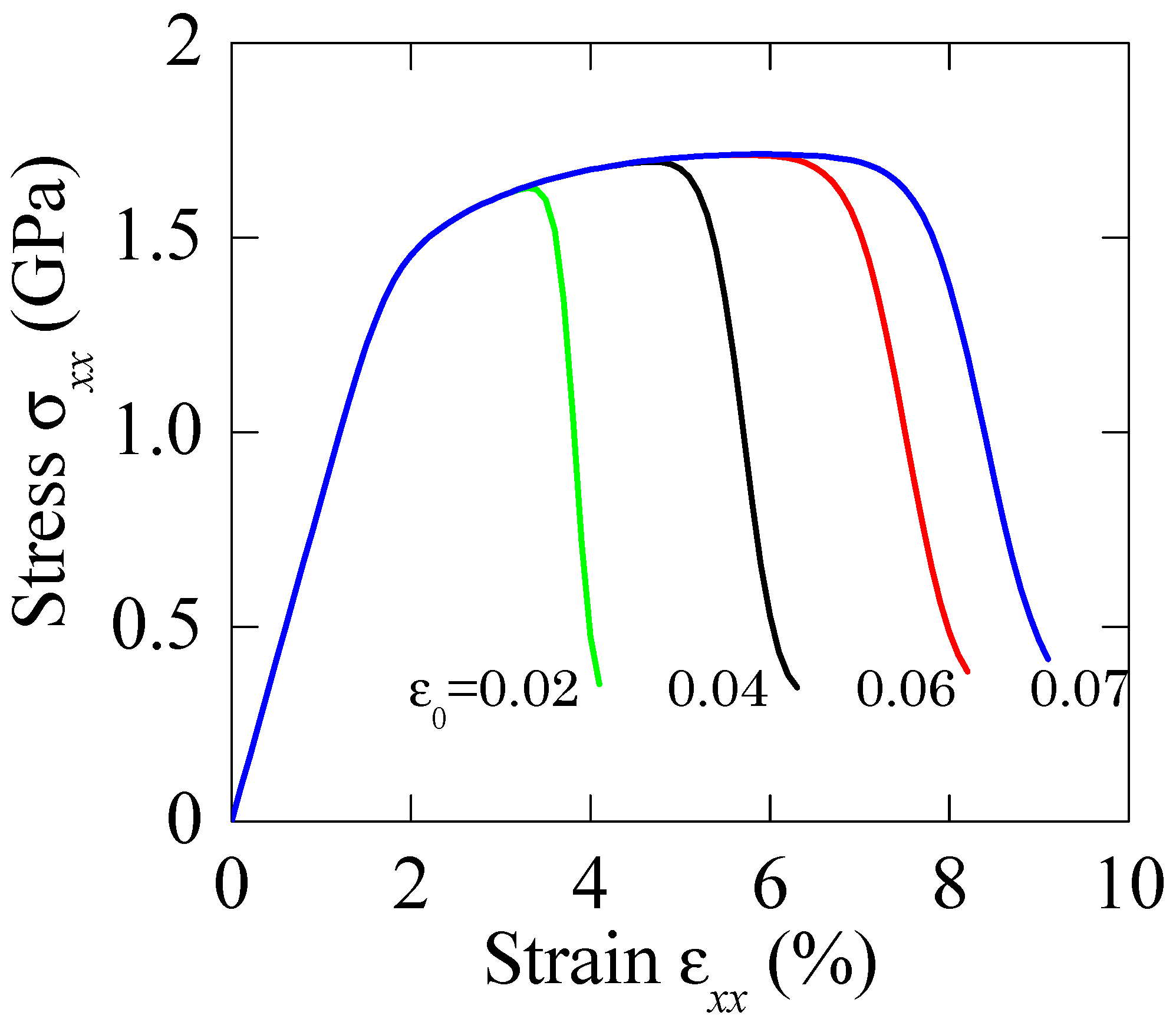
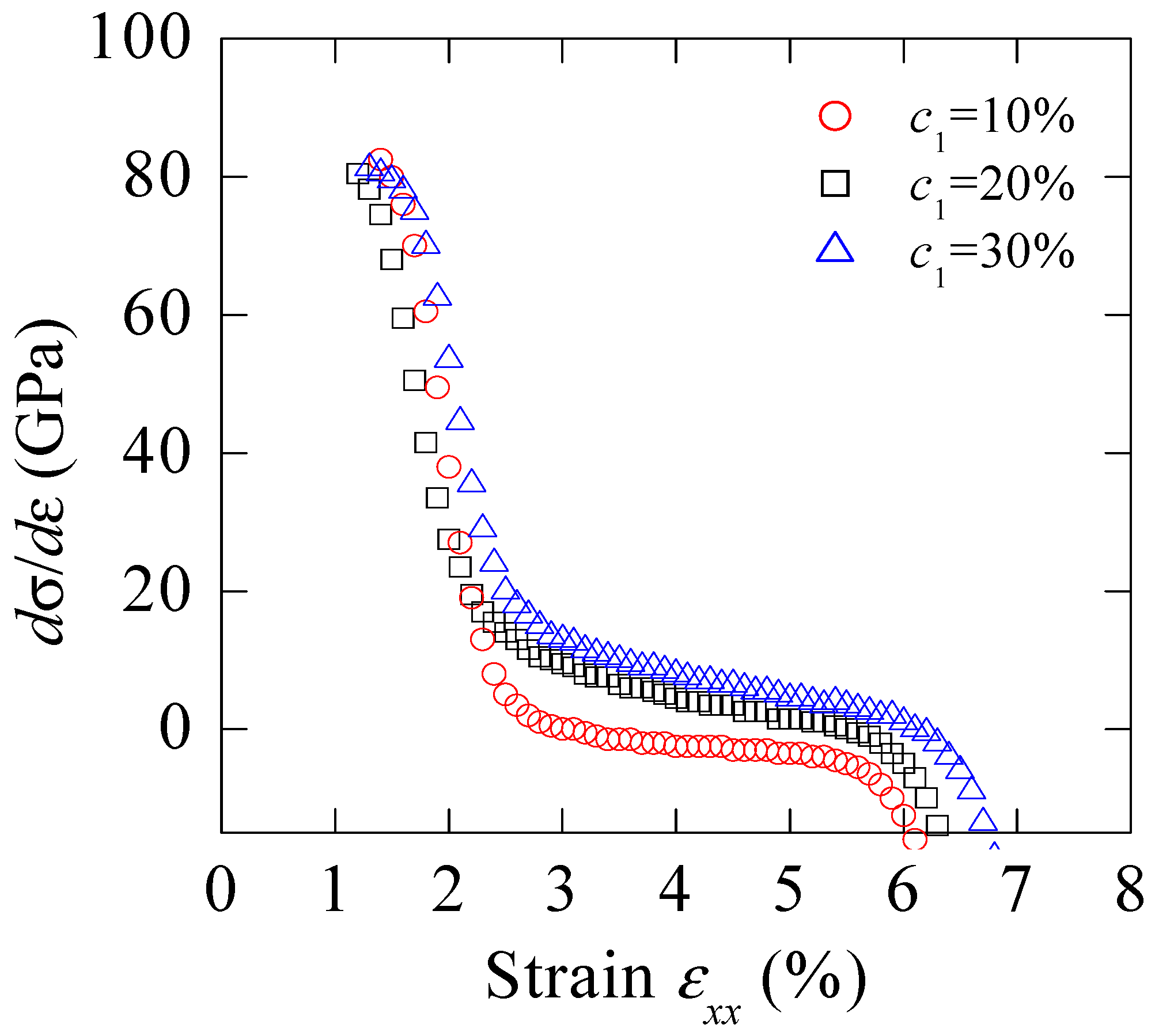
4.2. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Marandi, K.; Shim, V.P.W. A finite-deformation constitutive model for bulk metallic glass composites. Contin. Mech. Thermodyn. 2014, 26, 321–341. [Google Scholar] [CrossRef]
- Marandi, K.; Thamburaja, P.; Shim, V.P.W. Constitutive description of Bulk Metallic Glass composites at high homologous temperatures. Mech. Mater. 2014, 75, 151–164. [Google Scholar] [CrossRef]
- Qiao, J.W.; Zhang, T.; Yang, F.Q.; Liaw, P.K.; Pauly, S.; Xu, B.S. A tensile deformation model for in-situ dendrite/metallic glass matrix composites. Sci. Rep. 2013, 3, 2816. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Mota, A.; Ortiz, M. A finite-deformation constitutive model of bulk metallic glass plasticity. Comput. Mech. 2006, 37, 194–204. [Google Scholar] [CrossRef]
- Sun, X.H.; Qiao, J.W.; Jiao, Z.M.; Wang, Z.H.; Yang, H.J.; Xu, B.S. An improved tensile deformation model for in-situ dendrite/metallic glass matrix composites. Sci. Rep. 2015, 5, 13964. [Google Scholar] [CrossRef] [PubMed]
- Rao, W.; Zhang, J.; Jiang, H.; Kang, G.Z. Meso-mechanical constitutive model of bulk metallic glass matrix composites. Mech. Mater. 2016, 103, 68–77. [Google Scholar] [CrossRef]
- Jiang, Y.P.; Tohgo, K.; Shimamura, Y. A micromechanics-based incremental damage theory of bulk metallic glass (BMG) composites. Int. J. Damage Mech. 2016, 25, 358–376. [Google Scholar] [CrossRef]
- Jiang, Y.P.; Shi, X.P.; Qiu, K. Micromechanical modeling the plastic deformation of particle reinforced bulk metallic glass composites. Metall. Mater. Trans. A 2015, 46, 2015–3705. [Google Scholar] [CrossRef]
- Jiang, Y.P. An analytical model for particulate reinforced composites (PRCs) taking account of particle debonding and matrix cracking. Mater. Res. Express 2016, 3, 106501. [Google Scholar] [CrossRef]
- Jiang, Y.P. Micromechanics constitutive model for predicting the stress–strain relations of particle toughened bulk metallic glass matrix composites. Intermetallics 2017, 90, 147–151. [Google Scholar] [CrossRef]
- Weng, G.J. The overall elastoplastic stress-strain relations of dual-phase metals. J. Mech. Phys. Solids 1990, 38, 419–441. [Google Scholar] [CrossRef]
- Zhu, L.L.; Lu, J. Modelling the plastic deformation of nanostructured metals with bimodal grain size distribution. Int. J. Plast. 2012, 30, 166–184. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Steif, P.S.; Spaepen, F.; Hutchinson, J.W. Strain localization in amorphous metals. Acta Metall. 1982, 30, 447–455. [Google Scholar] [CrossRef]
- Conner, R.D.; Johnson, W.L.; Paton, N.E.; Nix, W.D. Shear bands and cracking of metallic glass plates in bending. J. Appl. Phys. 2003, 94, 904–911. [Google Scholar] [CrossRef]
- Yamamoto, H. Conditions for shear localization in the ductile fracture of void-containing materials. Int. J. Fract. 1978, 14, 347–365. [Google Scholar] [CrossRef]
- Kachanov, M. Elastic solids with many cracks and related problems. Adv. Appl. Mech. 1994, 30, 259–445. [Google Scholar]
- Szuecs, F.; Kim, C.P.; Johnson, W.L. Mechanical properties of Zr56.2Ti13.8Nb5.0Cu6.9Ni5.6Be12.5ductile phase reinforced bulk metallic glass composite. Acta Mater. 2001, 49, 1507–1513. [Google Scholar]
- Qiao, J.W.; Sun, A.C.; Huang, E.W.; Zhang, Y.; Liaw, P.K.; Chuang, C.P. Tensile deformation micromechanisms for bulk metallic glass matrix composites: From work-hardening to softening. Acta Mater. 2011, 59, 4126–4137. [Google Scholar] [CrossRef]
- Narayan, R.L.; Singh, P.S.; Hofmann, D.C.; Hutchinson, N.; Flores, K.M.; Ramamurty, U. On the microstructure–tensile property correlations in bulk metallic glass matrix composites with crystalline dendrites. Acta Mater. 2012, 60, 5089–5100. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y. Mesoscopic Constitutive Model for Predicting Failure of Bulk Metallic Glass Composites Based on the Free-Volume Model. Materials 2018, 11, 327. https://doi.org/10.3390/ma11020327
Jiang Y. Mesoscopic Constitutive Model for Predicting Failure of Bulk Metallic Glass Composites Based on the Free-Volume Model. Materials. 2018; 11(2):327. https://doi.org/10.3390/ma11020327
Chicago/Turabian StyleJiang, Yunpeng. 2018. "Mesoscopic Constitutive Model for Predicting Failure of Bulk Metallic Glass Composites Based on the Free-Volume Model" Materials 11, no. 2: 327. https://doi.org/10.3390/ma11020327
APA StyleJiang, Y. (2018). Mesoscopic Constitutive Model for Predicting Failure of Bulk Metallic Glass Composites Based on the Free-Volume Model. Materials, 11(2), 327. https://doi.org/10.3390/ma11020327




