Progress and Challenges of Ultrasonic Testing for Stress in Remanufacturing Laser Cladding Coating
Abstract
:1. Introduction
2. Basic Theory of Ultrasonic Testing for Stress
2.1. Acoustoelasticity Theory
- (1)
- The direction of longitudinal wave propagation is parallel to the stress direction:
- (2)
- The direction of longitudinal wave propagation is perpendicular to the stress direction:
- (3)
- The direction of transverse wave propagation and the direction of polarization are parallel and perpendicular to the stress direction, respectively:
- (4)
- The direction of transverse wave propagation and the direction of polarization are perpendicular to the stress direction:
- (5)
- The direction of transverse wave propagation and the direction of polarization are perpendicular and parallel to the stress direction, respectively:
- (6)
- Longitudinal wave under static pressure:
- (7)
- Transverse wave under static pressure:
2.2. Nonlinear Acoustoelasticity Theory
3. Ultrasonic Testing for Stress in Laser Cladding Coating
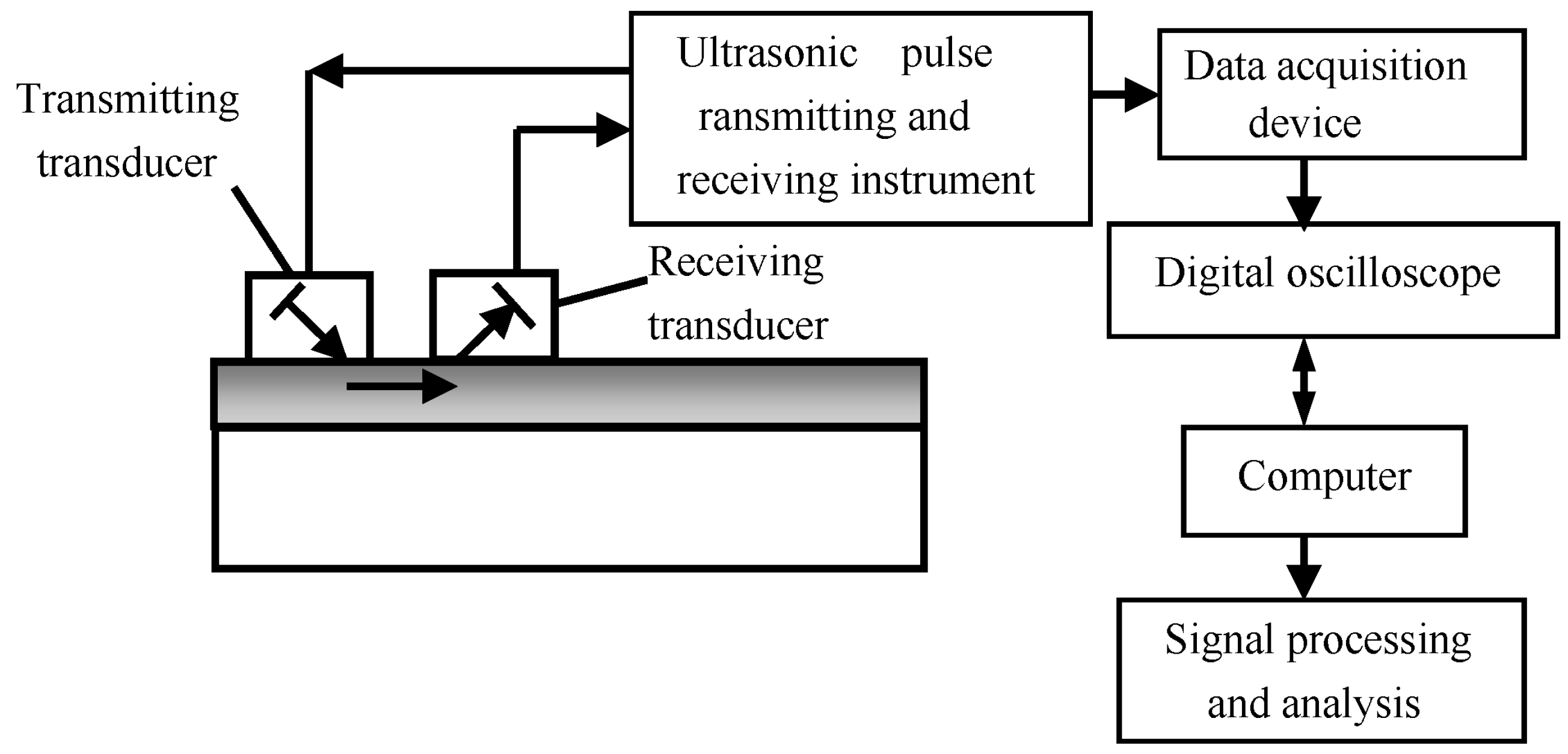
3.1. Ultrasonic Testing Methods for Stress
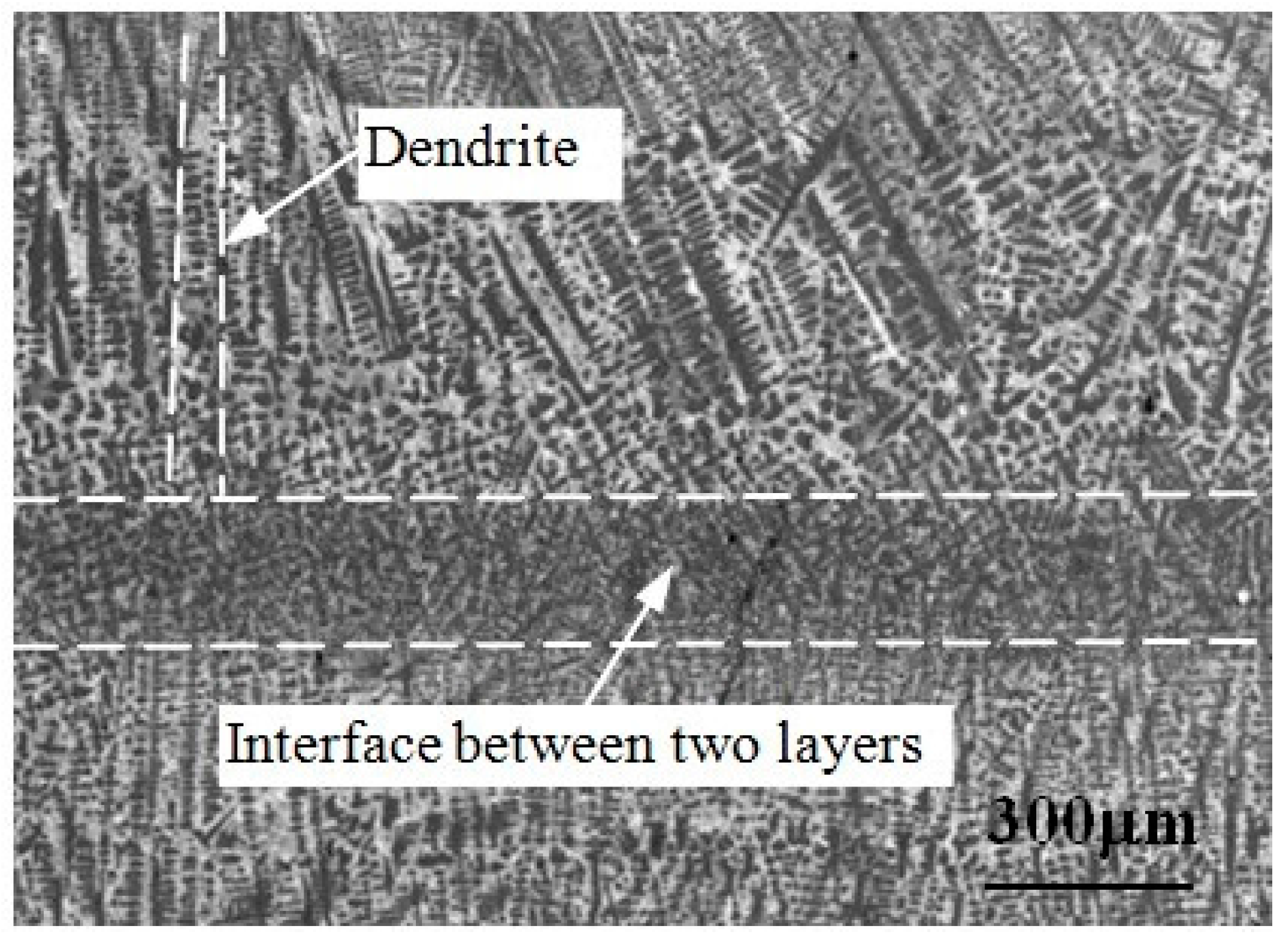
3.2. The Influence Mechanism of Micro Factors on Ultrasonic Testing for Stress
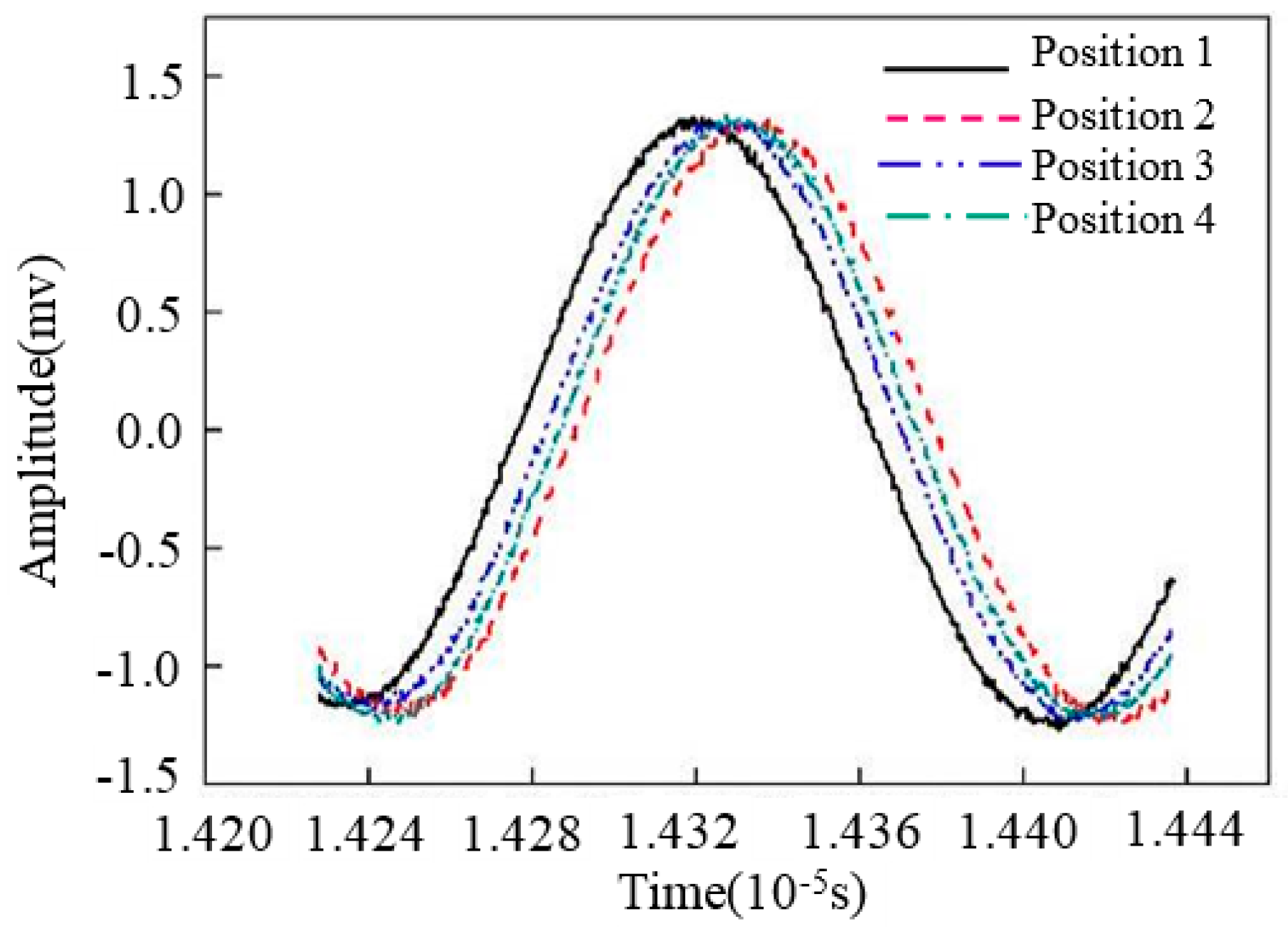
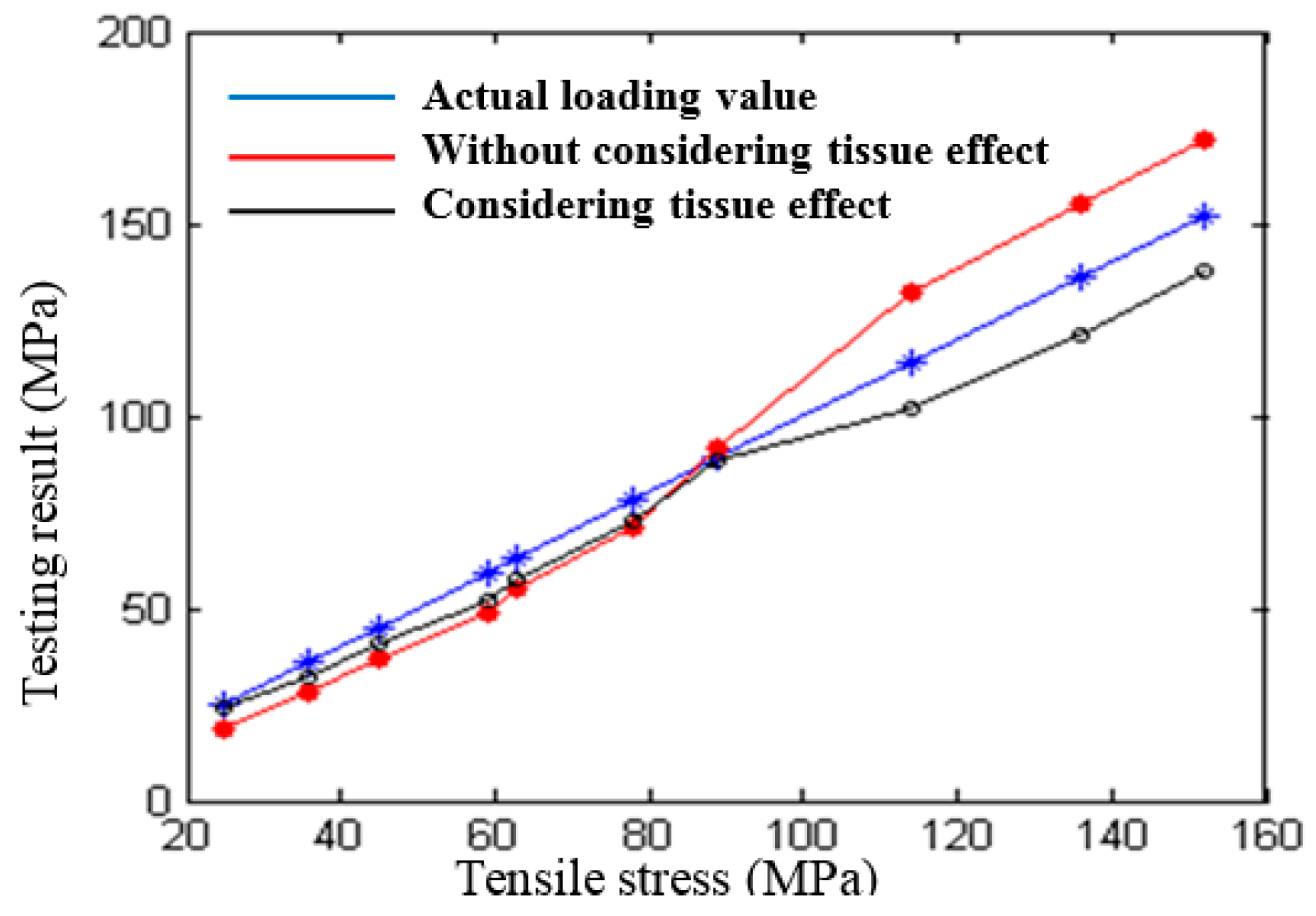
3.3. The Influence Mechanism of Macro Factors on Ultrasonic Testing for Stress
4. Strategies for Solving Related Problems
4.1. Obtain Full-Effective Acoustic Field Information
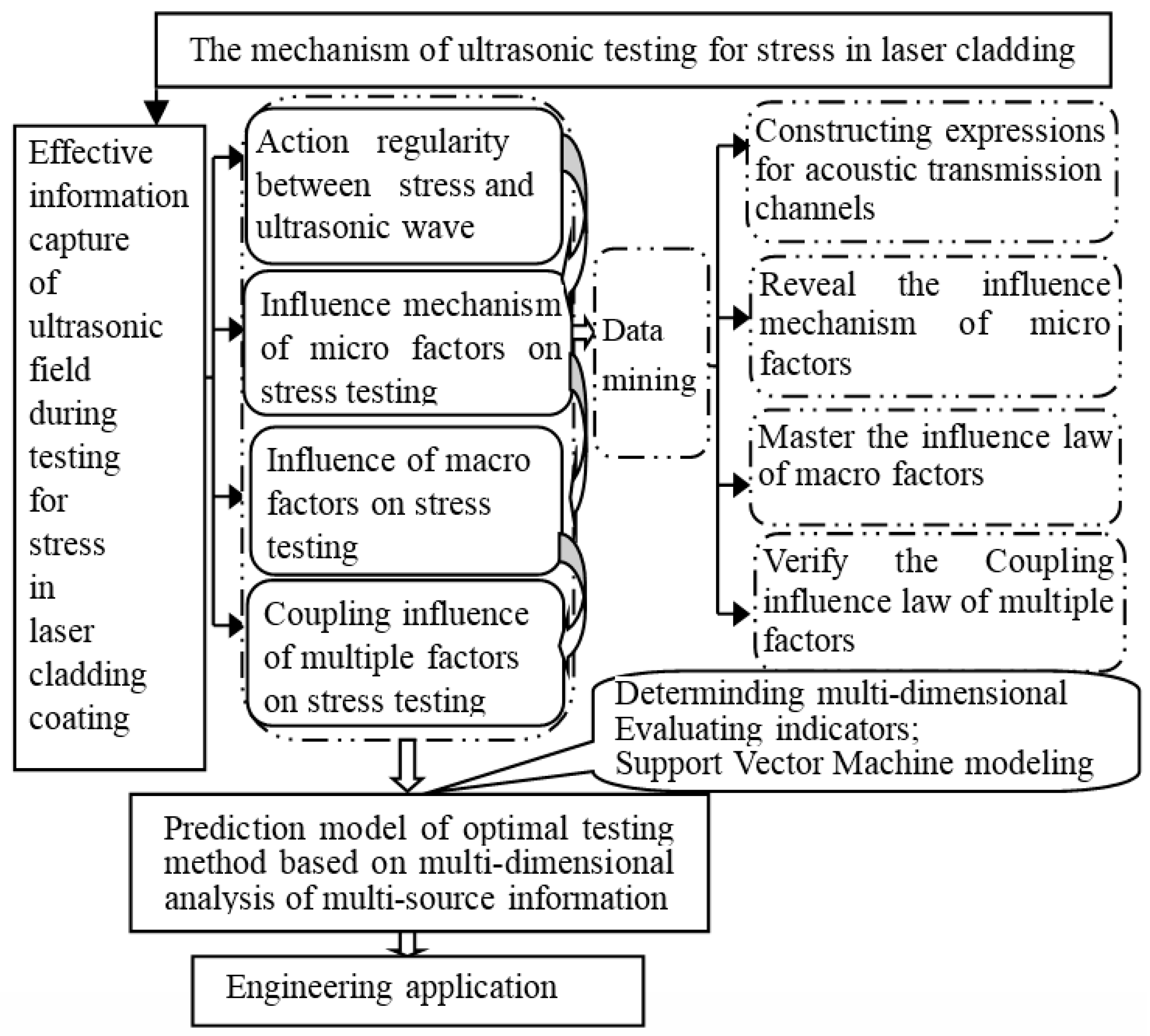
4.2. Technology Roadmap
5. Conclusions and Future Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- He, X.; Kong, D.J.; Song, R.G. Microstructures and properties of laser cladding Al-TiC-CeO2 composite coatings. Materials 2018, 11, 198. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.X.; Dong, S.Y.; Xu, B.S.; Wang, Y.J.; Ren, W.B.; Fang, J.X. Effect of molten pool convection on pores and elements distribution in the process of laser cladding. Infrared Laser Eng. 2014, 43, 2832–2839. [Google Scholar]
- United States International Trade Commission. Remanufactured Goods: An Overview of the USA and Global Industries, Markets, and Trade; USITC Publication: Washington, DC, USA, 2012.
- Xu, B.S. Green remanufacturing engineering and its development strategy in china. Front. Eng. Manag. 2016, 2, 102–106. [Google Scholar] [CrossRef]
- Fang, J.X.; Dong, S.Y.; Wang, Y.J.; Xu, B.S.; Zhang, Z.H.; Xia, D.; He, P. The effects of solid-state phase transformation upon stress evolution in laser metal powder deposition. Mater. Des. 2015, 87, 807–814. [Google Scholar] [CrossRef]
- Kattire, P.; Paul, S.; Singh, R.; Yan, W. Experimental characterization of laser cladding of CPM 9V on H13 tool steel for die repair applications. J. Manuf. Processes 2015, 20, 492–499. [Google Scholar] [CrossRef]
- Rong, Y.M.; Huang, Y.; Xu, J.J.; Zheng, H.J.; Zhang, G.J. Numerical simulation and experiment analysis of angular distortion and residual stress in hybrid laser-magnetic welding. J. Mater. Process. Technol. 2017, 245, 270–277. [Google Scholar] [CrossRef]
- Krzyzanowski, M.; Bajda, S.; Liu, Y.; Triantaphyllou, A.; Mark Rainforth, W.; Glendenning, M. 3D analysis of thermal and stress evolution during laser cladding of bioactive glass coatings. J. Mech. Behav. Biomed. Mater. 2016, 59, 404–417. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.I. Estimation of residual stress by instrumented indentation: A review. J. Ceram. Process. Res. 2009, 10, 391–400. [Google Scholar]
- Steinzig, M.; Upshaw, D.; Rasty, J. Influence of drilling parameters on the accuracy of hole-drilling residual stress measurements. Exp. Mech. 2014, 54, 1537–1543. [Google Scholar] [CrossRef]
- Sanderson, T. On the evaluation of residual stresses in bi-layer materials using the bent strip method. Surf. Coat. Technol. 2008, 202, 1493–1501. [Google Scholar] [CrossRef]
- Giri, A.; Mahapatra, M.M. On the measurement of sub-surface residual stresses in SS 304L welds by dry ring core technique. Measurement 2017, 106, 152–160. [Google Scholar] [CrossRef]
- Lin, J.; Ma, N.; Lei, Y.P.; Murakawa, H. Measurement of residual stress in arc welded lap joints by cosα X-ray diffraction method. J. Mater. Process. Technol. 2017, 243, 387–394. [Google Scholar] [CrossRef]
- Ren, S.K.; Ren, X.Z. Studies on laws of stress-magnetization based on magnetic memory testing technique. J. Magn. Magn. Mater. 2018, 449, 165–171. [Google Scholar] [CrossRef]
- Li, H.B.; Zhang, P.C.; Li, G.; Lu, J.B.; Wu, Q.W.; Gu, Y.J. Stress measurement for nonstoichiometric ceria films based on Raman spectroscopy. J. Alloys Compd. 2016, 682, 132–137. [Google Scholar] [CrossRef]
- Liu, B.; Dong, S.Y.; Xu, B.S.; He, P. Coating thickness affects surface stress measurement of brush electro-plating nickel coating using Rayleigh wave approach. Ultrasonics 2012, 52, 861–865. [Google Scholar] [CrossRef] [PubMed]
- Junge, M.; Qu, J.; Jacobs, L.J. Relationship between Rayleigh wave polarization and state of stress. Ultrasonics 2006, 44, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Lalik, K.; Dominik, I.; Ćwiąkała, P.; Kwaśniewski, J. Integrated stress measurement system in tower crane mast. Measurement 2017, 102, 47–56. [Google Scholar] [CrossRef]
- Tanuma, K.; Man, C.S.; Chen, Y. Dispersion of Rayleigh waves in weakly anisotropic media with vertically-inhomogeneous initial stress. Int. J. Eng. Sci. 2015, 92, 63–66. [Google Scholar] [CrossRef]
- Pamnani, R.; Sharma, G.K.; Mahadevan, S.; Jayakumar, T.; Vasudevan, M.; Rao, B.P.C. Residual stress studies on arc welding joints of naval steel (DMR-249A). J. Manuf. Processes 2015, 20, 104–111. [Google Scholar] [CrossRef]
- De Marchi, L.; Marzani, A.; Miniaci, M. A dispersion compensation procedure to extend pulse-echo defects location to irregular waveguides. NDT E Int. 2013, 54, 115–122. [Google Scholar] [CrossRef]
- Ocelík, V.; Eekma, M.; Hemmati, I.; Hosson, J.T.M.D. Elimination of Start/Stop defects in laser cladding. Surf. Coat. Technol. 2012, 206, 2403–2409. [Google Scholar] [CrossRef]
- Jendrzejewski, R.; Śliwiński, G.; Krawczuk, M.; Ostachowicz, W. Temperature and stress during laser cladding of double-layer coatings. Surf. Coat. Technol. 2006, 201, 3328–3334. [Google Scholar] [CrossRef]
- Muwala, G.; Karmakar, D.P.; Nath, A.K. In-process detection of microstructural changes in laser cladding of in-situ Inconel 718/TiC metal matrix composite coating. J. Alloys Compd. 2018, 740, 545–558. [Google Scholar]
- Florez-Ospina, J.F.; Benitez, H.D. From local to global analysis of defect detectability in infrared non-destructive testing. Infrared Phys. Technol. 2014, 63, 211–221. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Naugolnykh, K.; Ostrovsky, L. Nonlinear Wave Processes in Acoustics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Miniaci, M.; Gliozzi, A.S.; Morvan, B.; Krushynska, A.; Bosia, F.; Scalerandi, M.; Pugno, N.M. Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Phys. Rev. Lett. 2017, 118, 214301. [Google Scholar] [CrossRef] [PubMed]
- Hughes, D.S. Ultrasonic velocity in an elastic solid. J. Appl. Phys. 1950, 21, 294–301. [Google Scholar] [CrossRef]
- Hughes, D.S.; Kelly, J.L. Second-order elastic deformation of solids. Phys. Rev. 1953, 92, 1145. [Google Scholar] [CrossRef]
- Toupin, R.A.; Bernstein, B. Sound waves in deformed perfectly elastic materials acoustoelastic effect. J. Acoust. Soc. Am. 1961, 33, 216–225. [Google Scholar] [CrossRef]
- Brugger, K.; Thurston, R.N. Sound velocity in stressed crystals and third-order elastic coefficients. J. Acoust. Soc. Am. 1964, 36, 1041. [Google Scholar] [CrossRef]
- Mason, W.P. Physical Acoustics: Principles and Methods; Academic Press: New York, NY, USA; London, UK, 1964. [Google Scholar]
- Johson, G.C. Acoustoelastic theory for elastic-plastic materials. J. Acoust. Soc. Am. 1981, 70, 591–595. [Google Scholar] [CrossRef]
- Johson, G.C. The effect of plastic deformation on the acoustoelastic response of metals. J. Appl. Mech. 1983, 50, 689–691. [Google Scholar] [CrossRef]
- Okada, K. Acoustoelastic determination of stress in slightly orthotropic materials. Exp. Mech. 1981, 21, 461–466. [Google Scholar] [CrossRef]
- Pao, Y.H.; Gamer, U. Acoustoelastic waves in orthotropic media. J. Acoust. Soc. Am. 1985, 77, 806–812. [Google Scholar] [CrossRef]
- Bjørnø, L. Forty years of nonlinear ultrasound. Ultrasonics 2002, 40, 11–17. [Google Scholar] [CrossRef]
- Hikata, A.; Chick, B.B.; Elbaum, C. Effect of dislocations on finite amplitude ultrasonic waves in aluminum. Appl. Phys. Lett. 1963, 3, 195–197. [Google Scholar] [CrossRef]
- Rudenko, O.V.; Soluyan, S.I. Theoretical Foundations of Nonlinear Acoustics; Springer: New York, NY, USA, 1977. [Google Scholar]
- Abeele, E.A.V.D.; Sutin, A.; Carmeliet, J.; Johnson, P.A. Micro-damage diagnostics using nonlinear elastic wave spectroscopy (NEWS). NDT E Int. 2001, 34, 239–248. [Google Scholar]
- Kim, J.Y.; Jacobs, L.J.; Qu, J.; Littles, J.W. Experimental characterization of fatigue damage in a nickel-base superalloy using nonlinear ultrasonic waves. J. Acoust. Soc. Am. 2006, 120, 1266–1273. [Google Scholar] [CrossRef]
- Yan, H.J.; Xu, C.G.; Lin, Q.; Cai, H.C. Metal suface fatigue detection using nonlinear ultrasonic. Appl. Mech. Mater. 2014, 510, 156–162. [Google Scholar] [CrossRef]
- Bompan, K.F.; Haach, V.G. Ultrasonic tests in the evaluation of the stress level in concrete prisms based on the acoustoelasticity. Constr. Build. Mater. 2018, 162, 740–750. [Google Scholar] [CrossRef]
- Song, H.; Popovics, J.S. Characterization of steel-concrete interface bonding conditions using attenuation characteristics of guided waves. Cem. Concr. Compos. 2017, 83, 111–124. [Google Scholar] [CrossRef]
- Zhang, S.Z.; Li, X.B.; Jeong, H. Measurement of rayleigh wave beams using angle beam wedge transducers as the transmitter and receiver with consideration of beam spreading. Sensors 2017, 17, 1449. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.H.; Post, M.A.; Xu, P.C. Stress evaluation using ultrasonic interference spectrum of leaky lamb waves. Exp. Mech. 2011, 51, 971–980. [Google Scholar] [CrossRef]
- Chimenti, D.E.; Zhang, J.; Zeroug, S.; Felsen, L.B. Interaction of acoustic beams with fluid-loaded elastic structures. J. Acoust. Soc. Am. 1994, 95, 45–59. [Google Scholar] [CrossRef]
- Liu, B.; Dong, S.Y. Stress evaluation of laser cladding coating with critically refracted longitudinal wave based on cross correlation function. Appl. Acoust. 2016, 101, 98–103. [Google Scholar] [CrossRef]
- Allen, D.R.; Sayeres, C.M. The measurement of residual stress in textured steel using an ultrasonic velocity combinations technique. Ultrasonics 1984, 22, 179–188. [Google Scholar] [CrossRef]
- Dong, S.Y.; Yan, X.L.; Xu, B.S. Influence of microstructure and residual stress on surface stress measurement of laser cladding layer by Rayleigh wave. J. Mech. Eng. 2015, 51, 50–56. (In Chinese) [Google Scholar] [CrossRef]
- Chaki, S.; Bourse, G. Guided ultrasonic waves for non-destructive monitoring of the stress levels in prestressed steel strands. Ultrasonics 2009, 49, 162–171. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Kim, J.Y.; Jacobs, L.; Qu, J. Experimental study of nonlinear Rayleigh wave propagation in shot-peened aluminum plates-feasibility of measuring residual stress. NDT E Int. 2011, 44, 67–74. [Google Scholar] [CrossRef]
- King, R.B.; Fortunko, C.M. Acoustoelastic evaluation of arbitrary plane residual stress states in nonhomogeneous anisotropic plates. Ultrasonics 1983, 21, 256–258. [Google Scholar] [CrossRef]
- Thompson, R.B.; Smith, J.F.; Lee, S.S. Microstructure-independent acoustoelastic measurement of stress. Appl. Phys. Lett. 1984, 44, 296–298. [Google Scholar] [CrossRef]
- Rokhlin, S.I.; Wang, W. Double through-transmission bulk wave method for ultrasonic phase velocity measurement and determination of elastic constants of composite materials. J. Acoust. Soc. Am. 1992, 91, 3303–3312. [Google Scholar] [CrossRef]
- Walaszek, H.; Hoblos, J.; Bourse, G.; Robin, C. Effect of microstructure on ultrasonic measurement of residual stress in welded joints. Mater. Sci. Forum 2002, 404, 875–880. [Google Scholar] [CrossRef]
- Du, H.; Turner, J.A. Dependence of diffuse ultrasonic backscatter on residual stress in 1080 steel. Ultrasonics 2016, 67, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.C.; Wu, B.; Qin, F.; He, C.F.; Han, Q. Observation of ultrasonic guided wave propagation behaviors in pre-stressed multi-wire structures. Ultrasonics 2017, 73, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Kim, G.J.; Kwak, H.G. Characterization of stress-dependent ultrasonic nonlinearity variation in concrete under cyclic loading using nonlinear resonant ultrasonic method. Constr. Mater. 2017, 145, 272–282. [Google Scholar] [CrossRef]
- Pedram, S.K.; Haig, A.; Lowe, P.S.; Thornicroft, K.; Gan, L.; Mudge, P. Split-spectrum signal signal processing for reduction of the effect of dispersive wave modes in long-range ultrasonic testing. Phys. Procedia 2015, 70, 388–392. [Google Scholar] [CrossRef]
- Li, H.G.; Zhou, Z.G. Air-coupled ultrasonic signal processing method for detection Stomata defects in materials. NDT E Int. 2017, 92, 167–176. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Kudela, P.; Krawczuk, M.; Zak, A. Guided Waves in Structures for SHM: The Time—Domain Spectral Element Method; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Rezaei, A.; Dadouche, A.; Wickramasinghe, V.; Dmochowski, W. A Comparison study between acoustic sensors for bearing fault detection under different speed and load using a variety of signal processing techniques. Tribol. Trans. 2011, 54, 179–186. [Google Scholar] [CrossRef]
- Fateri, S.; Boulgouris, N.V.; Wilkinson, A.; Balachandran, W.; Gan, T.H. Frequency-sweep examination for wave mode identification in multimodal ultrasonic guided wave signal. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1515–1524. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.L.; Dong, S.Y.; Xu, B.S.; Liu, B.; Wang, W.L. Cepstrum analysis method in surface acoustic wave signals time delay estimation. Vib. Shock 2013, 32, 159–162. (In Chinese) [Google Scholar]
- Das, R. Support Vector Machines for Odiya Handwritten Numeral Recognition. Int. J. Adv. Res. Comput. Sci. 2013, 4, 139–143. [Google Scholar]
- Xu, N.; Zhou, Z.G. Numerical simulation and experiment for inspection of corner-shaped components using ultrasonic phased array. NDT E Int. 2014, 63, 283–284. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Gang, T. Nonparaxial multi-Gaussian beam models and measurement models for phased array transducers. Ultrasonics 2009, 49, 126–130. [Google Scholar] [CrossRef] [PubMed]
- Siegler, J.; Leifsson, L.; Grandin, R.; Koziel, S.; Bekasiewicz, A. Surrogate modeling of ultrasonic nondestructive evaluation simulations. Procedia Comput. Sci. 2016, 80, 1114–1124. [Google Scholar] [CrossRef]
- Comot, P.; Bocher, P.; Belanger, P. Ultrasonic guided wave inspection of Inconel 625 brazed lap joints: Simulation and experimentation. NDT E Int. 2017, 91, 717–718. [Google Scholar] [CrossRef]
- Shi, L.; Wu, C.S.; Padhy, G.K.; Gao, S. Numerical simulation of ultrasonic field and its acoustoplastic influence on friction stir welding. Mater. Des. 2016, 104, 102–115. [Google Scholar] [CrossRef]
- Pamel, A.V.; Huthwaite, P.; Brett, C.R.; Lowe, M.J.S. Numerical simulations of ultrasonic array imaging of highly scattering materials. NDT E Int. 2016, 81, 9–19. [Google Scholar] [CrossRef]
- Nakahata, K.; Sugahara, H.; Barth, M.; Köhler, B.; Schubert, F. Three dimensional image-based simulation of ultrasonic wave propagation in polycrystalline metal using phase-field modeling. Ultrasonics 2016, 67, 18–29. [Google Scholar] [CrossRef] [PubMed]
- Luan, T.N.; Modrak, R.T. Ultrasonic wavefield inversion and migration in complex heterogeneous structures: 2D numerical imaging and nondestructive testing experiments. Ultrasonics 2018, 82, 357–370. [Google Scholar]
- Dhatt, G.; Touzot, G.; Lefrançois, E. Finite Element Method; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Yan, X.L.; Dong, S.Y.; Xue, N. Numerical simulation of ultrasonic propagation and defect testing in laser cladding remanufacturing parts. Chin. Sci. Bull. 2016, 61, 45–51. (In Chinese) [Google Scholar]
- Kim, D.; Kim, J.; Sheen, D. Absorbing boundary conditions for wave propagation in viscoelastic media. J. Comput. Appl. Math. 1996, 76, 301–314. [Google Scholar] [CrossRef]
- Wu, Z.J.; Fan, L.F. The numerical manifold method for elastic wave propagation in rock with time-dependent absorbing boundary conditions. Eng. Anal. Bound. Elem. 2014, 46, 41–50. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: A Introduction to Cluster Analysis; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Taouali, O.; Jaffel, I.; Lahdhiri, H.; Harkat, M.F.; Messaoud, H. New fault detection method based on reduced kernel principal component analysis (RKPCA). Int. J. Adv. Manuf. Technol. 2016, 85, 1547–1552. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.-L.; Dong, S.-Y.; Xu, B.-S.; Cao, Y. Progress and Challenges of Ultrasonic Testing for Stress in Remanufacturing Laser Cladding Coating. Materials 2018, 11, 293. https://doi.org/10.3390/ma11020293
Yan X-L, Dong S-Y, Xu B-S, Cao Y. Progress and Challenges of Ultrasonic Testing for Stress in Remanufacturing Laser Cladding Coating. Materials. 2018; 11(2):293. https://doi.org/10.3390/ma11020293
Chicago/Turabian StyleYan, Xiao-Ling, Shi-Yun Dong, Bin-Shi Xu, and Yong Cao. 2018. "Progress and Challenges of Ultrasonic Testing for Stress in Remanufacturing Laser Cladding Coating" Materials 11, no. 2: 293. https://doi.org/10.3390/ma11020293
APA StyleYan, X.-L., Dong, S.-Y., Xu, B.-S., & Cao, Y. (2018). Progress and Challenges of Ultrasonic Testing for Stress in Remanufacturing Laser Cladding Coating. Materials, 11(2), 293. https://doi.org/10.3390/ma11020293




