Physics of Discrete Impurities under the Framework of Device Simulations for Nanostructure Devices
Abstract
1. Introduction
2. Theoretical Foundations of Drift-Diffusion Device Simulations
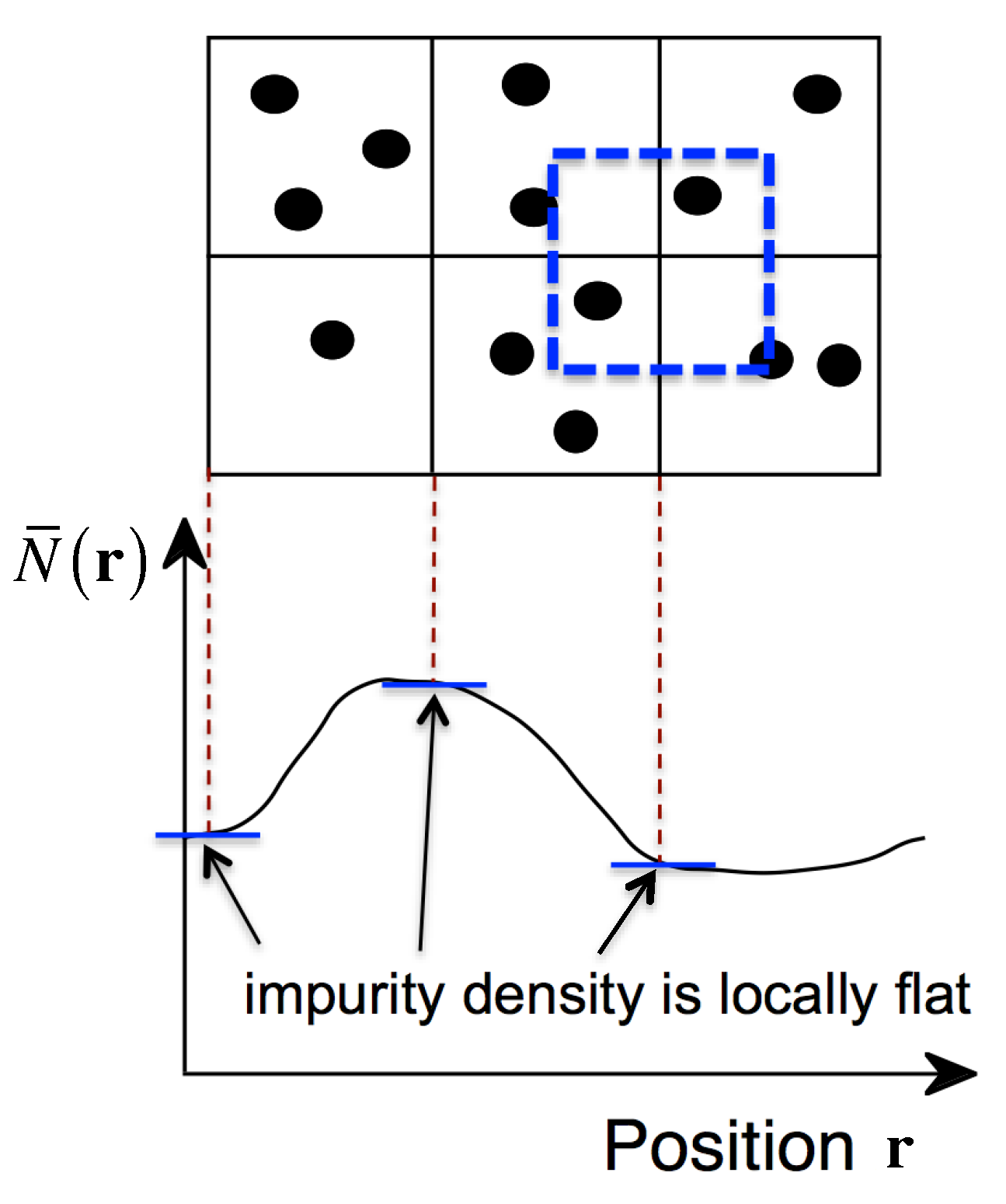
2.1. Meaning of the Long-Wavelength Limit in Drift-Diffusion Simulations
2.2. Incomplete Screening of the Long-Range Part of the Coulomb Potential
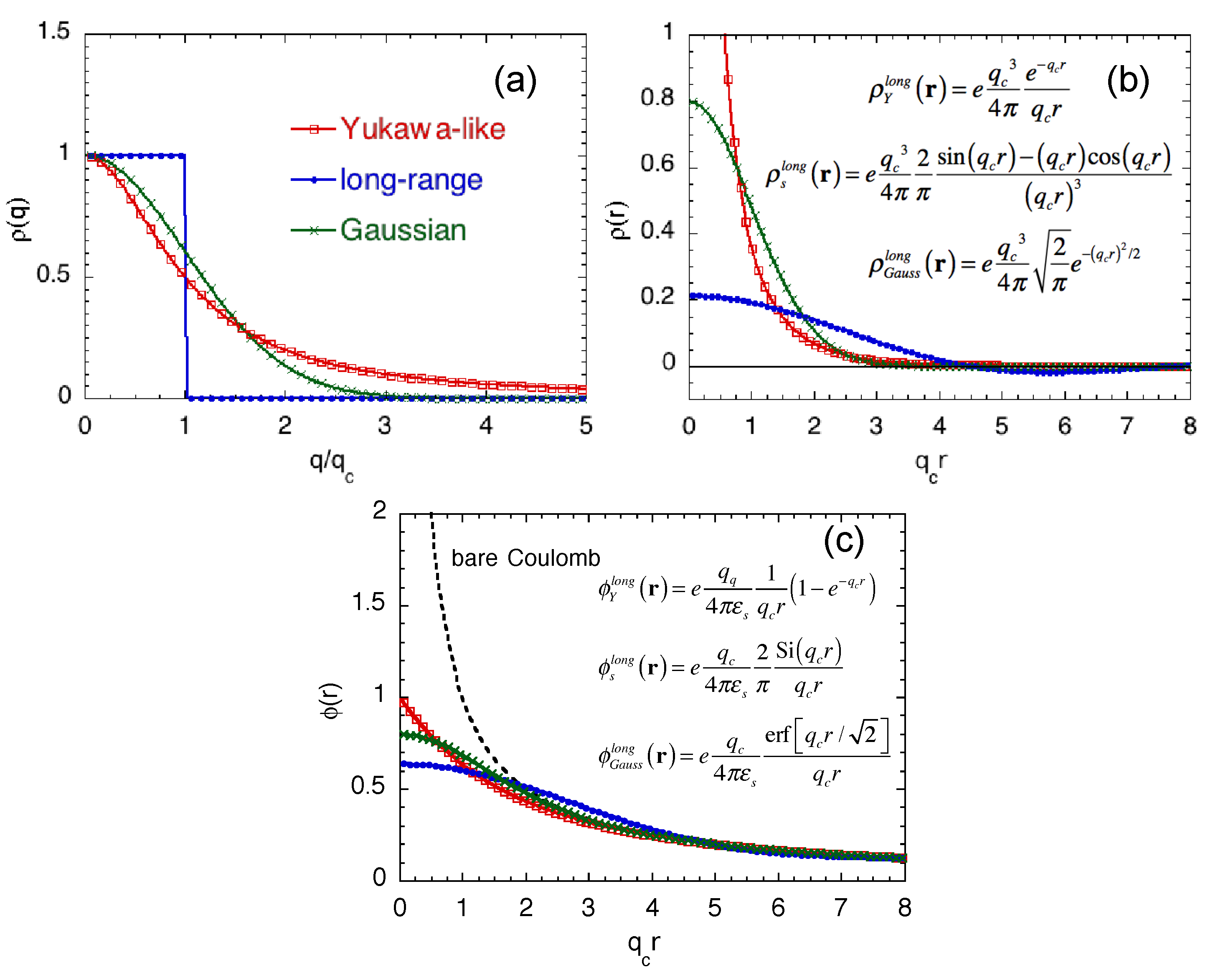
3. Discrete Impurity Models for Drift-Diffusion Simulation
3.1. Discrete Impurity in the Bulk Structure
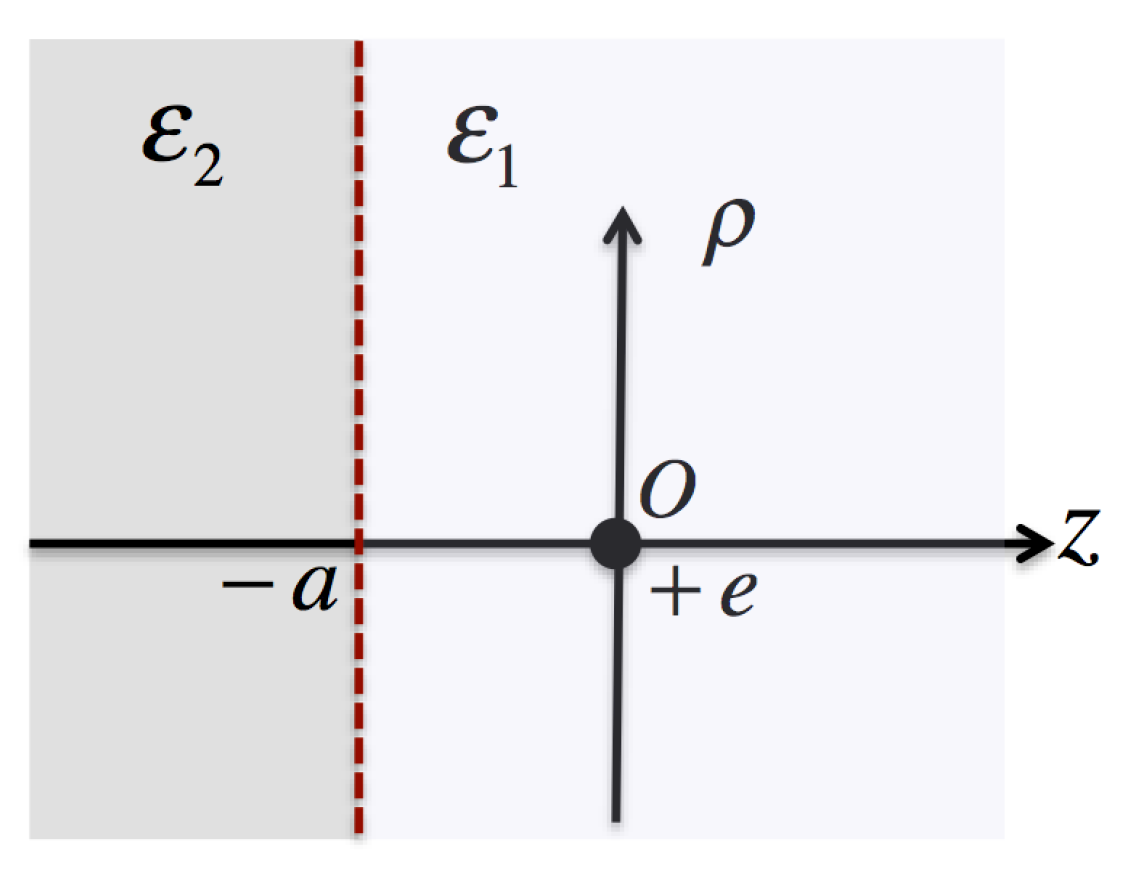
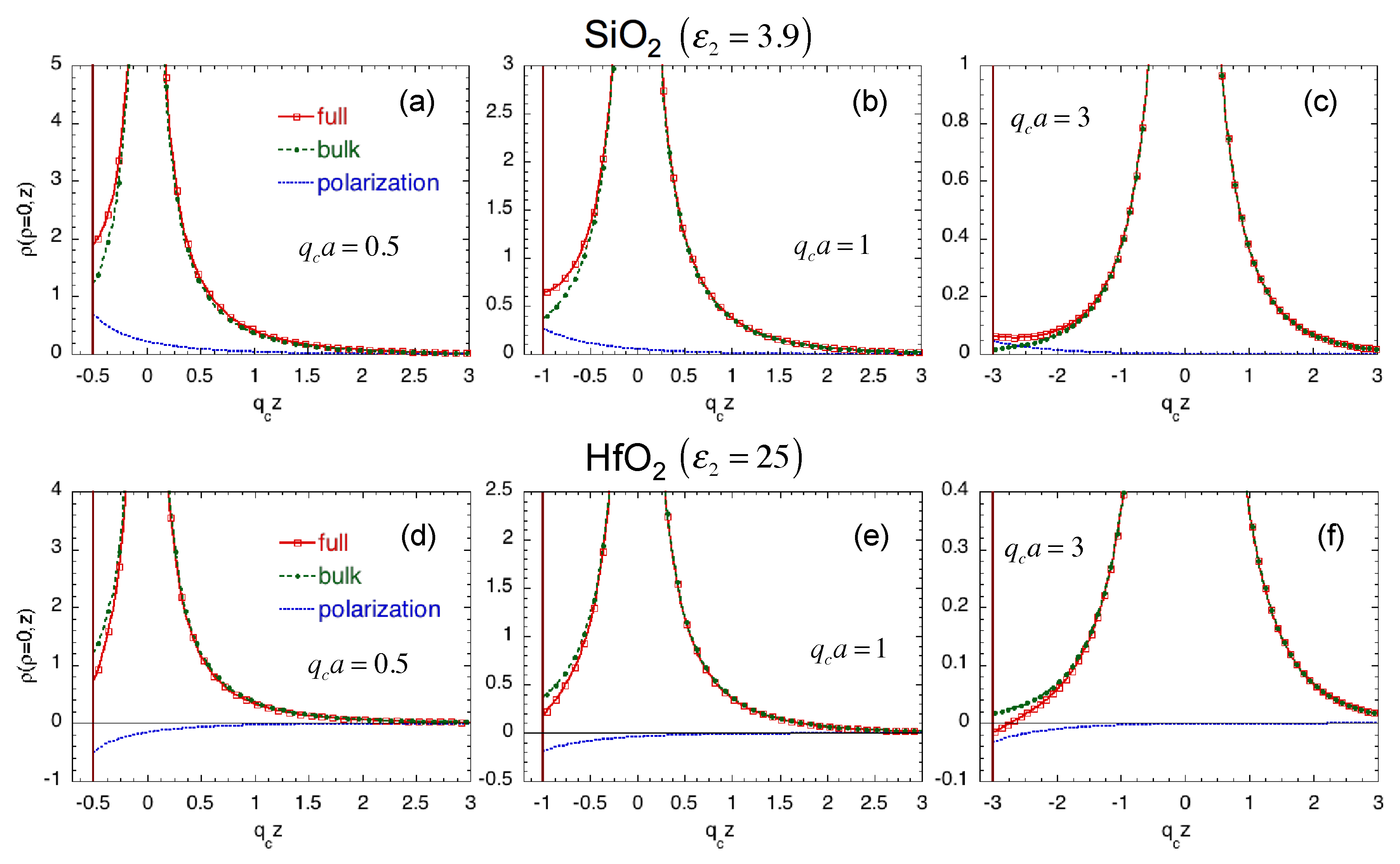
3.2. Discrete Impurity Including the Effects of Interface
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fiori, G.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerjee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768–779. [Google Scholar] [CrossRef] [PubMed]
- Zographos, N.; Zechner, C.; Martin-Bragado, I.; Lee, K.; Oh, Y.S. Multiscale modeling of doping processes in advanced semiconductor devices. Mater. Sci. Semicond. Process. 2017, 62, 49–61. [Google Scholar] [CrossRef]
- Tsunomura, T.; Nishida, A.; Hiramoto, T. Verification of Threshold Voltage Variation of Scaled Transistors with Ultralarge-Scale Device Matrix Array Test Element Group. Jpn. J. Appl. Phys. 2009, 48, 124505. [Google Scholar] [CrossRef]
- Nishinohara, K.; Shigyo, N.; Wada, T. Effects of microscopic fluctuations in dopant distributions on MOSFET threshold voltage. IEEE Trans. Electron Dev. 1992, 39, 634–639. [Google Scholar] [CrossRef]
- Wong, H.S.; Taur, Y. Three-dimensional “atomistic” simulation of discrete random dopant distribution effects in sub-0.1 μm MOSFET’s. In Proceedings of the IEEE International Electron Devices Meeting, Technical Digest, Washington, DC, USA, 5–8 December 1993; pp. 705–708. [Google Scholar]
- Stolk, P.A.; Klaassen, D.B.M. The effect of statistical dopant fluctuations on MOS device performance. In Proceedings of the International Electron Devices Meeting, Technical Digest, San Francisco, CA, USA, 8–11 December 1996; pp. 627–630. [Google Scholar]
- Sano, N.; Matsuzawa, K.; Mukai, M.; Nakayama, N. Role of long-range and short-range Coulomb potentials in threshold characteristics under discrete dopants in sub-0.1 μm Si-MOSFETs. In Proceedings of the International Electron Devices Meeting, Technical Digest, San Francisco, CA, USA, 11–13 December 2000; pp. 275–278. [Google Scholar]
- Sano, N.; Tomizawa, M. Random dopant model for three-dimensional drift-diffusion simulations in metal-oxide-semiconductor field-effect-transistors. Appl. Phys. Lett. 2001, 79, 2267–2269. [Google Scholar] [CrossRef]
- Sano, N.; Matsuzawa, K.; Mukai, M.; Nakayama, N. On discrete random dopant modeling in drift-diffusion simulations: physical meaning of ‘atomistic’ dopants. Microelectron. Reliab. 2002, 42, 189–199. [Google Scholar] [CrossRef]
- Asenov, A.; Brown, A.R.; Davies, J.H.; Kaya, S.; Slavcheva, G. Simulation of intrinsic parameter fluctuations in decananometer and nanometer-scale MOSFETs. IEEE Trans. Electron Dev. 2003, 50, 1837–1852. [Google Scholar] [CrossRef]
- Damrongplasit, N.; Shin, C.; Kim, S.H.; Vega, R.A.; Liu, T.K. Study of Random Dopant Fluctuation Effects in Germanium-Source Tunnel FETs. IEEE Trans. Electron Dev. 2011, 58, 3541–3548. [Google Scholar] [CrossRef]
- Damrongplasit, N.; Kim, S.H.; Liu, T.K. Study of Random Dopant Fluctuation Induced Variability in the Raised-Ge-Source TFET. IEEE Electron Dev. Lett. 2013, 34, 184–186. [Google Scholar] [CrossRef]
- Li, Y.; Chang, H.; Lai, C.; Chao, P.; Chen, C. Process variation effect, metal-gate work-function fluctuation and random dopant fluctuation of 10-nm gate-all-around silicon nanowire MOSFET devices. In Proceedings of the International Electron Devices Meeting, Technical Digest, Washington, DC, USA, 7–9 December 2015; pp. 34.4.1–34.4.4. [Google Scholar]
- Yoon, J.S.; Rim, T.; Kim, J.; Kim, K.; Baek, C.K.; Jeong, Y.H. Statistical variability study of random dopant fluctuation on gate-all-around inversion-mode silicon nanowire field-effect transistors. Appl. Phys. Lett. 2015, 106, 103507. [Google Scholar] [CrossRef]
- Chen, C.Y.; Lin, J.T.; Chiang, M.H. Threshold-voltage variability analysis and modeling for junctionless double-gate transistors. Microelectron. Reliab. 2017, 74, 22–26. [Google Scholar] [CrossRef]
- Yu, H.; Kim, D.; Rhee, S.; Choi, S.; Park, Y.J. A Mobility Model for Random Discrete Dopants and Application to the Current Drivability of DRAM Cell. IEEE Trans. Electron Dev. 2017, 64, 4246–4251. [Google Scholar] [CrossRef]
- Yoon, J.; Baek, R. Study on Random Dopant Fluctuation in Core Shell Tunneling Field-Effect Transistors. IEEE Trans. Electron Dev. 2018, 65, 3131–3135. [Google Scholar] [CrossRef]
- Dollfus, P.; Bournel, A.; Galdin, S.; Barraud, S.; Hesto, P. Effect of discrete impurities on electron transport in ultrashort MOSFET using 3D MC simulation. IEEE Trans. Electron Dev. 2004, 51, 749–756. [Google Scholar] [CrossRef]
- Alexander, C.; Roy, G.; Asenov, A. Random-Dopant-Induced Drain Current Variation in Nano-MOSFETs: A Three-Dimensional Self-Consistent Monte Carlo Simulation Study Using “Ab Initio” Ionized Impurity Scattering. IEEE Trans. Electron Dev. 2008, 55, 3251–3258. [Google Scholar] [CrossRef]
- Martinez, A.; Aldegunde, M.; Seoane, N.; Brown, A.; Barker, J.; Asenov, A. Quantum-Transport Study on the Impact of Channel Length and Cross Sections on Variability Induced by Random Discrete Dopants in Narrow Gate-All-Around Silicon Nanowire Transistors. IEEE Trans. Electron Dev. 2011, 58, 2209–2217. [Google Scholar] [CrossRef]
- Georgiev, V.P.; Towie, E.A.; Asenov, A. Impact of Precisely Positioned Dopants on the Performance of an Ultimate Silicon Nanowire Transistor: A Full Three-Dimensional NEGF Simulation Study. IEEE Trans. Electron Dev. 2013, 60, 965–971. [Google Scholar] [CrossRef]
- Sellier, J.; Dimov, I. The Wigner-Boltzmann Monte Carlo method applied to electron transport in the presence of a single dopant. Compt. Phys. Commun. 2014, 185, 2427–2435. [Google Scholar] [CrossRef]
- Carrillo-Nuñez, H.; Lee, J.; Berrada, S.; Medina-Bailón, C.; Adamu-Lema, F.; Luisier, M.; Asenov, A.; Georgiev, V.P. Random Dopant-Induced Variability in Si-InAs Nanowire Tunnel FETs: A Quantum Transport Simulation Study. IEEE Electron Dev. Lett. 2018, 39, 1473–1476. [Google Scholar] [CrossRef]
- Sano, N. Physical issues in device modeling: Length-scale, disorder, and phase interference. In Proceedings of the International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Kamakura, Japan, 7–9 September 2017; pp. 1–4. [Google Scholar]
- Karasawa, T.; Nakanishi, K.; Sano, N. Discrete impurity and mobility in drift-diffusion simulations for device characteristics variability. In Proceedings of the International Semiconductor Device Research Symposium, College Park, MD, USA, 9–11 December 2009; pp. 1–2. [Google Scholar]
- Sano, N. Impurity-limited resistance and phase interference of localized impurities under quasi-one dimensional nano-structures. J. Appl. Phys. 2015, 118, 244302. [Google Scholar] [CrossRef]
- Sano, N. Variability and self-average of impurity-limited resistance in quasi-one dimensional nanowires. Solid-State Electron. 2017, 128, 25–30. [Google Scholar] [CrossRef]
- Kittel, C. Quantum Theory of Solids, 2nd Rev. ed.; John-Wiley & Sons: Hoboken, NJ, USA, 1987; p. 101. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sano, N.; Yoshida, K.; Yao, C.-W.; Watanabe, H. Physics of Discrete Impurities under the Framework of Device Simulations for Nanostructure Devices. Materials 2018, 11, 2559. https://doi.org/10.3390/ma11122559
Sano N, Yoshida K, Yao C-W, Watanabe H. Physics of Discrete Impurities under the Framework of Device Simulations for Nanostructure Devices. Materials. 2018; 11(12):2559. https://doi.org/10.3390/ma11122559
Chicago/Turabian StyleSano, Nobuyuki, Katsuhisa Yoshida, Chih-Wei Yao, and Hiroshi Watanabe. 2018. "Physics of Discrete Impurities under the Framework of Device Simulations for Nanostructure Devices" Materials 11, no. 12: 2559. https://doi.org/10.3390/ma11122559
APA StyleSano, N., Yoshida, K., Yao, C.-W., & Watanabe, H. (2018). Physics of Discrete Impurities under the Framework of Device Simulations for Nanostructure Devices. Materials, 11(12), 2559. https://doi.org/10.3390/ma11122559




