Estimation of Notched Composite Plates Fatigue Life Using Residual Strength Model Calibrated by Step-Wise Tests
Abstract
:1. Introduction
2. Fatigue Life Model
3. Material Characterization
4. Fatigue Model Calibration
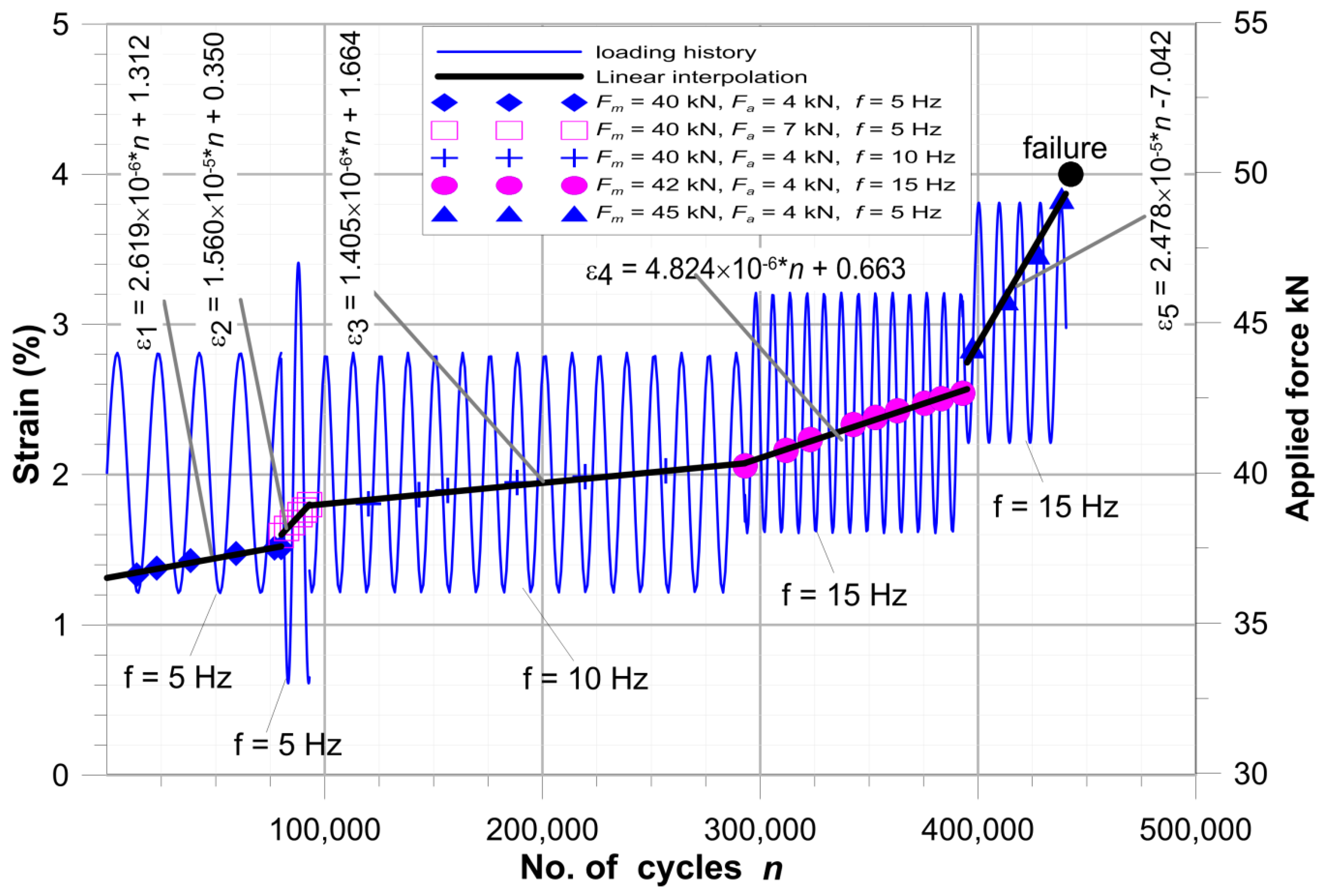
- The fatigue failure occurs at the critical strain ε1max = 3.94%,
- The increase of strain under cyclic load with constant loading condition is linear,
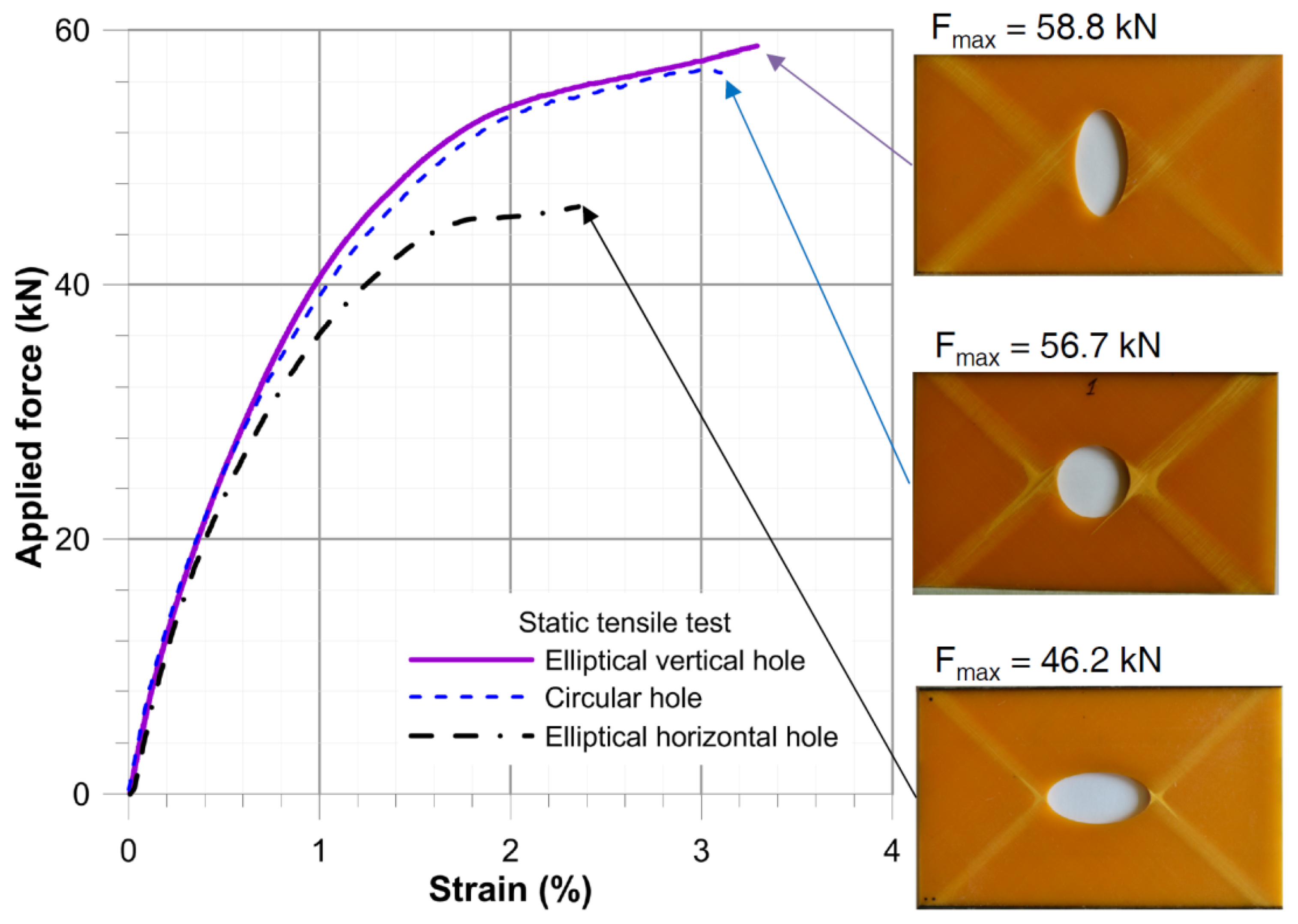
- Fatigue life prognosis was made using the strain after the static tensile test (Figure 7—as the initial strain under the maximal fatigue stress) and using the slope of the strain growth line under cyclic load tg(a) (Figure 8, Table 2—for determination of the duration of material degradation until the critical strain is achieved ε1max).
5. Fatigue Tests
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| tg(a) | slope of strain growth line |
| DF | damage parameter |
| Ei | Young’s modulus in the i direction |
| f | loading frequency |
| Fm, Fa | mean value and amplitude of loading, respectively |
| R | stress ratio |
| n | number of loading cycles |
| Nf | number of cycles to failure |
| predicted number of cycles to failure | |
| expected number of cycles to failure | |
| α and β | material constants |
| δ | relative error |
| δ1 | relative difference |
| ε1max | critical strain in loading direction |
| σmin and σmax | minimal and maximal applied fatigue stress in loading direction, respectively |
| σu | ultimate stress of material in loading direction |
| ν12 | Poisson’s ratio |
| θ | smallest angle of fibres between the loading direction and fibre direction |
Appendix A
- Determination of the ultimate stress of material in loading direction σu for investigated laminate,
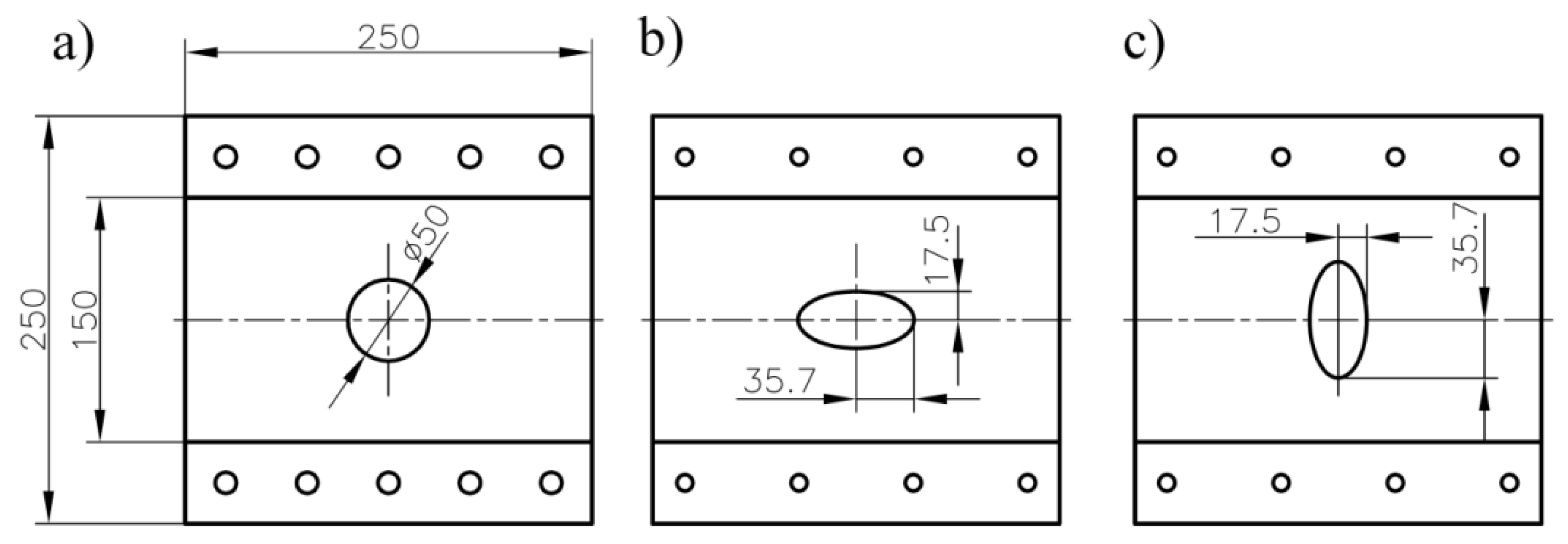
- Determination of F–ε curves (static tension) for investigated notched composite structure, F-is applied force,
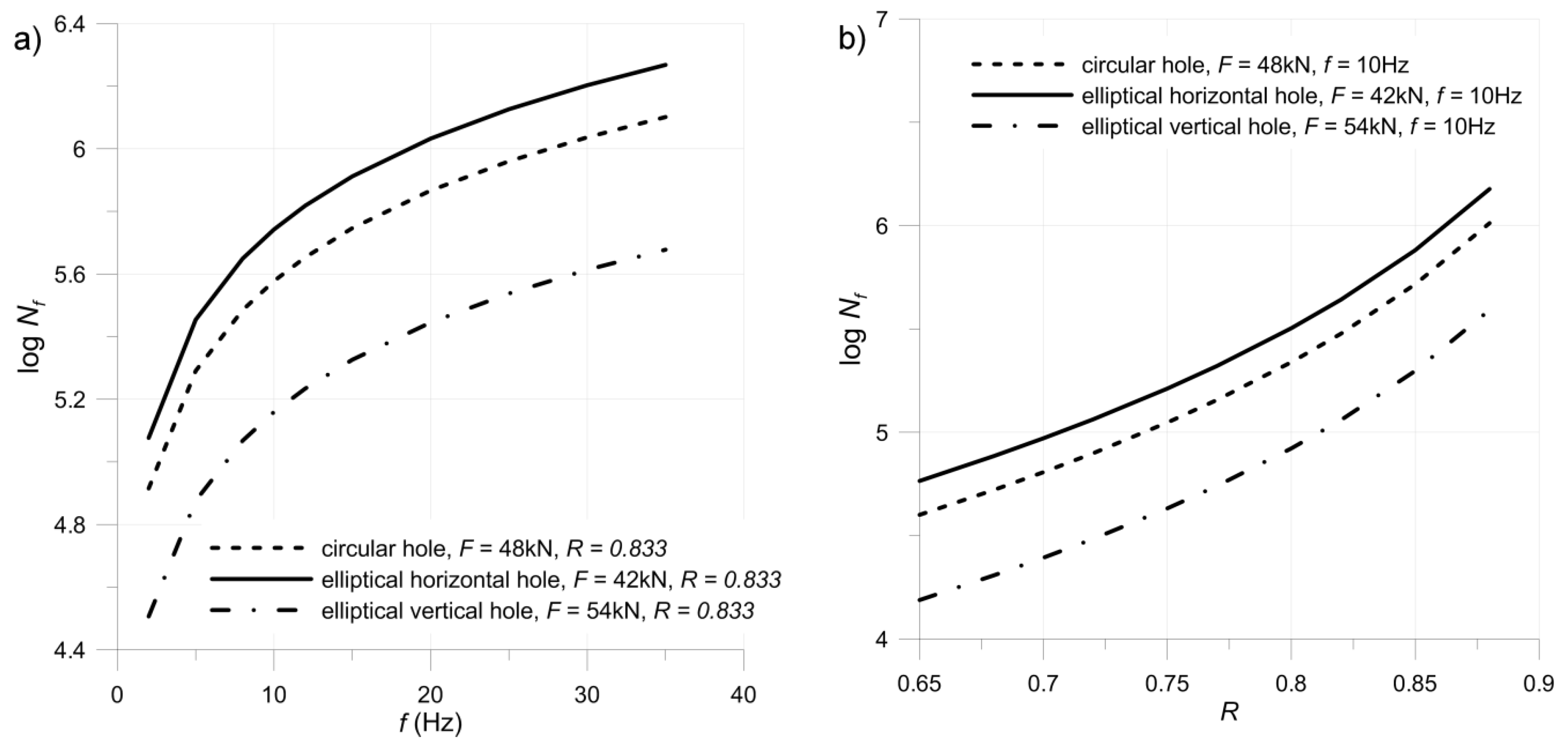
- Determination of ranges of the loading parameters (the stress ratio R, frequency f, the maximal tensile load-σmax),
- Step-wise fatigue tests,
- Determination of the critical strain ε1max for investigated structure,
- Calculation of the slopes of strain growth lines tg(a),
- Estimations of the using the strain after the static tensile test, tg(a) and ε1max,
- Determination of the material constants α and β for the obtained data.
References
- Nikbakt, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures Part I: Laminated composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- Muc, A.; Romanowicz, P. Effect of notch on static and fatigue performance of multilayered composite structures under tensile loads. Compos. Struct. 2017, 178, 27–36. [Google Scholar] [CrossRef]
- Hosoi, A.; Kawada, H. Fatigue Life Prediction for Transverse Crack Initiation of CFRP Cross-Ply and Quasi-Isotropic Laminates. Materials 2018, 11, 1182. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Waisman, H. Progressive delamination analysis of composite materials using XFEM and a discrete damage zone model. Comput. Mech. 2015, 55, 1–26. [Google Scholar] [CrossRef]
- Ouyang, X.; Pan, Z.; Qian, Z.; Ma, Y.; Ye, G.; van Breugel, K. Numerical Modelling of the Effect of Filler/Matrix Interfacial Strength on the Fracture of Cementitious Composites. Materials 2018, 11, 1362. [Google Scholar] [CrossRef] [PubMed]
- Ukadgaonker, V.G.; Rao, D.K.N. A general solution for stresses around holes in symmetric laminates under inplane loading. Compos. Struct. 2000, 49, 339–354. [Google Scholar] [CrossRef]
- Toubal, L.; Moussa Karama, M.; Lorrain, B. Stress concentration in a circular hole in composite plate. Compos. Struct. 2005, 68, 3–36. [Google Scholar] [CrossRef]
- Beyene, A.T.; Belingardi, G.; Koricho, E.G. Effect of notch on quasi-static and fatigue flexural performance of Twill E-Glass/Epoxy composite. Compos. Struct. 2016, 153, 825–842. [Google Scholar] [CrossRef]
- Hochard, C.; Miot, S.; Thollon, Y. Fatigue of laminated composite structures with stress concentrations. Compos. Part B Eng. 2014, 65, 11–16. [Google Scholar] [CrossRef]
- Gamdani, F.; Boukhili, R.; Vadean, A. Tensile strength of open-hole, pin-loaded and multi-bolted single-lap joints in woven composite plates. Mater. Des. 2015, 88, 702–712. [Google Scholar] [CrossRef]
- Green, B.G.; Wisnom, M.R.; Hallett, S.R. An experimental investigation into the tensile strength scaling of notched composites. Compos. Part A Appl. Sci. 2007, 38, 867–878. [Google Scholar] [CrossRef]
- Broughton, W.R.; Gower, M.R.L.; Lodeiro, M.J.; Pilkington, G.D.; Shaw, R.M. An experimental assessment of open-hole tension–tension fatigue behaviour of a GFRP laminate. Compos. Part A 2011, 42, 1310–1320. [Google Scholar] [CrossRef]
- Francis, P.H.; Walrath, D.E.; Sims, D.F.; Weed, D.N. Biaxial fatigue loading of notched composites. J. Compos. Mater. 1997, 11, 488–501. [Google Scholar] [CrossRef]
- Hirschfeld, D.A.; Herakovich, C.T. Failure Analysis of Notched Unidirectional Graphite/Epoxy Tubes under Combined Loading. In Composite Materials: Fatigue and Fracture (4th Volume); Stinchcomb, W.W., Ashbaugh, N.E., Eds.; STP 1156; ASTM International: Philadelphia, PA, USA, 1993; pp. 72–85. [Google Scholar]
- Shen, G.; Glinka, G.; Plumtree, A. Fatigue life prediction of notched composite components. Fatigue Fract. Eng. Mater. Struct. 1994, 17, 77–91. [Google Scholar] [CrossRef]
- Fujii, T.; Shiina, T.; Okubo, K. Fatigue notch sensitivity of glass woven fabric composites having a circular hole under tension/torsion biaxial loading. J. Compos. Mater. 1994, 28, 234–251. [Google Scholar] [CrossRef]
- Quaresimin, M.; Susmel, L. Multiaxial fatigue behaviour of composite laminates. Key Eng. Mater. 2002, 221–222, 71–80. [Google Scholar] [CrossRef]
- Satapathy, M.R.; Vinayak, B.G.; Jayaprakash, K.; Naik, N.K. Fatigue behavior of laminated composites with a circular hole under in-plane multiaxial loading. Mater. Des. 2013, 51, 347–356. [Google Scholar] [CrossRef]
- Hertzberg, R.W.; Manson, J.A. Fatigue of Engineering Plastics; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Scharpery, R.A. Deformation and Failure Analysis of Viscoelastic Composite Materials; AMD-vol. 13; ASME: New York, NY, USA, 1975. [Google Scholar]
- Sauer, J.A.; Richardson, G.C. Fatigue of polymer. Int. J. Fract. 1980, 16, 499–532. [Google Scholar] [CrossRef]
- Radon, J.C. Fatigue crack growth in polymers. Int. J. Fract. 1980, 16, 533–552. [Google Scholar] [CrossRef]
- Reifsnider, K.L. Fatigue behavior of composite materials. Int. J. Fract. 1980, 16, 563–583. [Google Scholar] [CrossRef]
- Reifsnider, K.L. Damage and damage mechanics. In Fatigue of Composite Materials; Reifsnider, K.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Dillard, D.A. Viscoelastic behavior of laminated composite materials. In Fatigue of Composite Materials; Reifsnider, K.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Mandell, J.F. Fatigue behavior of short fibre composite materials. In Fatigue of Composite Materials; Reifsnider, K.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Quaresimin, M.; Susmel, L.; Talreja, R. Fatigue behaviour and life assessment of composite laminates under multiaxial loadings. Int. J. Fatigue 2010, 32, 2–16. [Google Scholar] [CrossRef]
- De Smet, B.J.; Bach, P.W. Database FACT, Fatigue of Composites for Wind Turbines; Energy research Centre of the Netherlands report: ECN-C-94-045; ECN: Petten, The Netherlands, 1994. [Google Scholar]
- Roundi, W.; El Mahi, A.; El Gharad, A.; Rebiere, J.L. Experimental and numerical investigation of the effects of stacking sequence and stress ratio on fatigue damage of glass/epoxy composites. Compos. Part B 2017, 109, 64–71. [Google Scholar] [CrossRef]
- Mandell, J.F.; Meier, U. Effect of stress ratio, frequency and loading time on the tensile fatigue of glass-reinforced epoxy. In Long-Term Behavior of Composites; ASTM International: West Conshohocken, PA, USA, 1983; Volume 813, pp. 55–77. [Google Scholar]
- Elyn, F.; El-Kadi, H. Effect of stress ratio on the fatigue of unidirectional glass fibre/epoxy composite laminae. Composites 1994, 25, 917–924. [Google Scholar]
- Mohammadi, B.; Fazlali, B. Off-axis fatigue behaviour of unidirectional laminates based on a microscale fatigue damage model under different stress ratios. Int. J. Fatigue 2018, 106, 11–23. [Google Scholar] [CrossRef]
- Saff, C.R. Effect of load frequency and lay-up on fatigue life of composites. In Long-Term Behavior of Composites; O’Brien, T.K., Ed.; ASTM International: West Conshohocken, PA, USA, 1983; Volume 813, pp. 78–91. [Google Scholar]
- Sun, C.T.; Chan, W.S. Frequency effect on the fatigue life of a laminated composites. In Proceedings of the Fifth Conference on Composite Materials: Testing and Design, New Orleans, LA, USA, 20–22 March 1978; ASTM International: West Conshohocken, PA, USA, 1979; Volume 674, pp. 418–430. [Google Scholar]
- Llobet, J.; Maimi, P.; Mayugo, J.A.; Essa, Y.; Martin de la Escalera, F. A fatigue damage and residual strength model for unidirectional carbon/epoxy composites under on-axis tension-tension loadings. Int. J. Fatigue 2017, 103, 508–515. [Google Scholar] [CrossRef]
- Van Paepegem, W. Fatigue damage modelling of composite materials with the phenomenological residual stiffness approach. In Fatigue Life Prediction of Composites and Composite Structures; Vassilopoulos, A.P., Ed.; Woodhead Publishing: Cambridge, UK, 2010; pp. 102–138. [Google Scholar]
- D’Amore, A.; Grassia, L. Phenomenological approach to the study of hierarchical damage mechanisms in composite materials subjected to fatigue loadings. Compos. Struct. 2017, 175, 1–6. [Google Scholar] [CrossRef]
- DOT/FAA/AR-10/6. Determining the Fatigue Life of Composites Aircraft Structures Using Life and Load-Enhancement Factors. 2011. Available online: http://www.tc.faa.gov/its/worldpac/techrpt/ar10-6.pdf (accessed on 10 June 2018).
- Haftchenari, H.; Varvani-Farahani, A. Microcracking response of CFRP composites at different temperatures. In Fatigue Damage of Materials: Experiment and Analysis Book Series: Advances in Damage Mechanics; WIT Press: Southampton, UK, 2003; Volume 5, pp. 389–398. [Google Scholar]
- Kennedy, C.R.; Brádaigh, C.M.; Leen, S.B. A multiaxial fatigue damage model for fibre reinforced polymer composites. Compos. Struct. 2013, 106, 201–210. [Google Scholar] [CrossRef] [Green Version]
- Barski, M.; Kędziora, P.; Muc, A.; Romanowicz, P. Structural Health Monitoring (SHM) methods in machine design and operation. Arch. Mech. Eng. 2014, 61, 653–677. [Google Scholar] [CrossRef]
- Romanowicz, P. Numerical assessment of fatigue load capacity of cylindrical crane wheel using multiaxial high-cycle fatigue criteria. Arch. Appl. Mech. 2017, 87, 1707–1726. [Google Scholar] [CrossRef]
- Sendeckyj, G.P. Life prediction for resin matrix composite materials. In Fatigue of Composite Materials; Reifsnider, K.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Degrieck, J.; Van Paepegem, W. Fatigue damage modeling of fibre-reinforced composite materials: Review. Appl. Mech. Rev. 2001, 54, 279–300. [Google Scholar] [CrossRef]
- Vinayak, B.G.; Jayaprakash, K.; Naik, N.K. Fatigue behavior of laminated composites with a circular hole under in-plane uniaxial random loading. Mater. Des. 2012, 40, 245–256. [Google Scholar] [CrossRef]
- Fatemi, A.; Yang, L. Cumulative fatigue damage and life prediction theories: A survey of the state of the art for homogeneous materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Mortazavuan, S.; Fatemi, A. Fatigue behavior and modeling of short fiber reinforced polymer composites: A literature review. Int. J. Fatigue 2015, 70, 297–321. [Google Scholar] [CrossRef]
- Ueda, T.; Asakura, K. Rapid Method for Determining the Fatigue Limit of Hard Drawn Steel Wire by Means of Stepwise Load Increase Test. J. Soc. Mater. Sci. 1964, 127, 264–269. [Google Scholar] [CrossRef]
- Skibicki, D. Applying a Stepwise Load for Calculation of the S-N Curve for Trabecular Bone Based on the Linear Hypothesis for Fatigue Damage Accumulation. Mater. Sci. Forum 2012, 726, 39–42. [Google Scholar]
- Dengel, D.; Harig, H. Estimation of the fatigue limit by progressively-increasing load tests. Fatigue Fract. Eng. Mater. Struct. 1980, 3, 113–128. [Google Scholar] [CrossRef]
- Colombo, C.; Libonati, F.; Pezzani, F.; Salerno, A.; Vergani, L. Fatigue behaviour of a GFRP laminate by thermographic measurements. Procedia Eng. 2011, 10, 3518–3527. [Google Scholar] [CrossRef]
- Harizi, W.; Chaki, S.; Bourse, G.; Ourak, M. Mechanical damage assessment of Glass Fiber-Reinforced Polymer composites using passive infrared thermography. Compos. Part B 2014, 59, 74–79. [Google Scholar] [CrossRef]
- Huang, J.; Pastor, M.L.; Garnier, C.; Gong, X. Rapid evaluation of fatigue limit on thermographic data analysis. Int. J. Fatigue 2017, 104, 293–301. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, Z.; Zhang, B.; Zhao, S. A phenomenological fatigue life prediction model of glass fiber reinforced polymer composites. Mater. Des. 2015, 66, 77–81. [Google Scholar] [CrossRef]
- Muc, A.; Barski, M.; Chwał, M.; Romanowicz, P.; Stawiarski, A. Fatigue damage growth monitoring for composite structures with holes. Compos. Struct. 2018, 189, 117–126. [Google Scholar] [CrossRef]
- Stawiarski, A.; Miarka, S.; Barski, M.; Romanowicz, P. Fatigue damage detection in composite plate with a circular hole by elastic wave propagation method. Compos. Theory Pract. 2016, 16, 20–24. [Google Scholar]
- Wu, F.; Yao, W. A fatigue damage model of composite materials. Int. J. Fatigue 2010, 32, 134–138. [Google Scholar] [CrossRef]
- Mejlej, V.G.; Osorio, D.; Vietor, T. An improved fatigue failure model for multidirectional fiber-reinforced composite laminates under any stress ratios of cyclic loading. Procedia CIRP 2017, 66, 27–32. [Google Scholar] [CrossRef]
- Stojković, N.; Folić, R.; Pasternak, H. Mathematical model for the prediction of strength degradation of composites subjected to constant amplitude fatigue. Int. J. Fatigue 2017, 103, 478–487. [Google Scholar] [CrossRef]
- Epaarachchi, J.A.; Clausen, P.D. A new approach to a fatigue damage model for glass-fibre reinforced plastic composites. In Proceedings of the Seventh International Conference on Composites Engineering (ICCE/7), Denver, CO, USA, 2–8 July 2000; pp. 211–212. [Google Scholar]
- Epaarachchi, J.A.; Clausen, P.D. An empirical model for fatigue behavior prediction of glass fibre-reinforced plastic composites for various stress ratios and test frequencies. Compos. Part A 2003, 34, 313–326. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L.; Ceparano, A. correlations between damage accumulation and strength degradation of fiber reinforced composites subjected to cyclic loading. Procedia Eng. 2016, 167, 97–102. [Google Scholar] [CrossRef]
- D’Amore, A.; Caprino, G.; Stupak, P.; Zhou, J.; Nicolais, L. Effect of stress ratio on the flexural fatigue behaviour of continuous strand mat reinforced plastics. Sci. Eng. Compos. Mater. 1996, 5, 1–8. [Google Scholar] [CrossRef]
- Caprino, G.; D’Amore, A. Flexural fatigue behavior of random continuous-fibre-reinforced thermoplastic. Compos. Sci. Technol. 1998, 58, 957–965. [Google Scholar] [CrossRef]
- Toumi, R.B.; Renard, J.; Monin, M.; Nimdum, P. Fatigue damage modelling of continuous E-glass fibre/epoxy composite. Procedia Eng. 2013, 66, 723–736. [Google Scholar] [CrossRef]
- ASTM-D3039/D3039M-14. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- D’Amore, A.; Grassia, L. Constitutive law describing the strength degradation kinetics of fibre-reinforced composites subjected to constant amplitude cyclic loading. Mech. Time-Depend. Mater. 2016, 20, 1–12. [Google Scholar] [CrossRef]
- Movahedi-Rad, V.; Keller, T.; Vasilopoulos, A.P. Fatigue damage in angle-ply GFRP laminates under tension-tension fatigue. Int. J. Fatigue 2018, 109, 60–69. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Iwashita, K.; Sasaki, T.; Hamaguchi, Y. Tensile fatigue behaviour of FRP and hybrid FRP sheets. Compos. Part B 2010, 41, 396–402. [Google Scholar] [CrossRef]
- Yang, J.N.; Lee, L.J.; Sheu, D.Y. Modulus reduction and fatigue damage of matrix dominated composite laminates. Compos. Struct. 1992, 21, 91–100. [Google Scholar] [CrossRef]
- Muc, A.; Chwał, M.; Romanowicz, P.; Stawiarski, A. Fatigue-damage evolution of notched composite multilayered structures under tensile loads. J. Compos. Sci. 2018, 2, 27. [Google Scholar] [CrossRef]
- Romanowicz, P. Experimental and numerical estimation of the damage level in multilayered composite plates. Mater. Werkst. 2018, 49, 591–605. [Google Scholar] [CrossRef]
- D’Amore, A.; Giorgio, M.; Grassia, L. Modeling the residual strength of carbon fiber reinforced composites subjected to cyclic loading. Int. J. Fatigue 2015, 78, 31–37. [Google Scholar] [CrossRef]
- Kędziora, P.; Romanowicz, P.; Muc, A. Fuzzy sets—Fatigue tests. Compos. Theory Pract. 2016, 16, 90–95. [Google Scholar]
- Muc, A. A fuzzy set approach to interlaminar cracks simulation problem. Int. J. Fatigue 2002, 24, 419–427. [Google Scholar] [CrossRef]

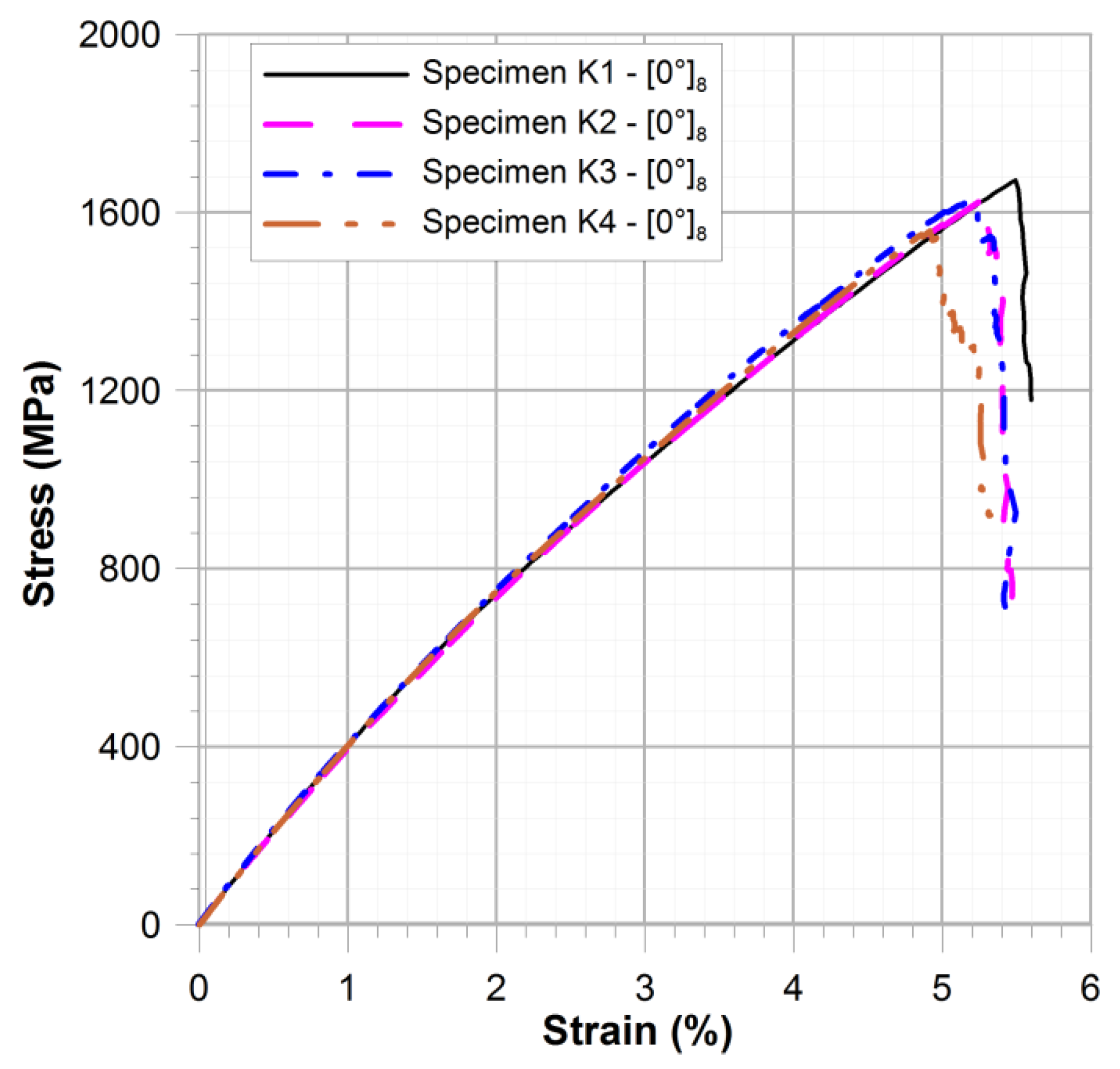
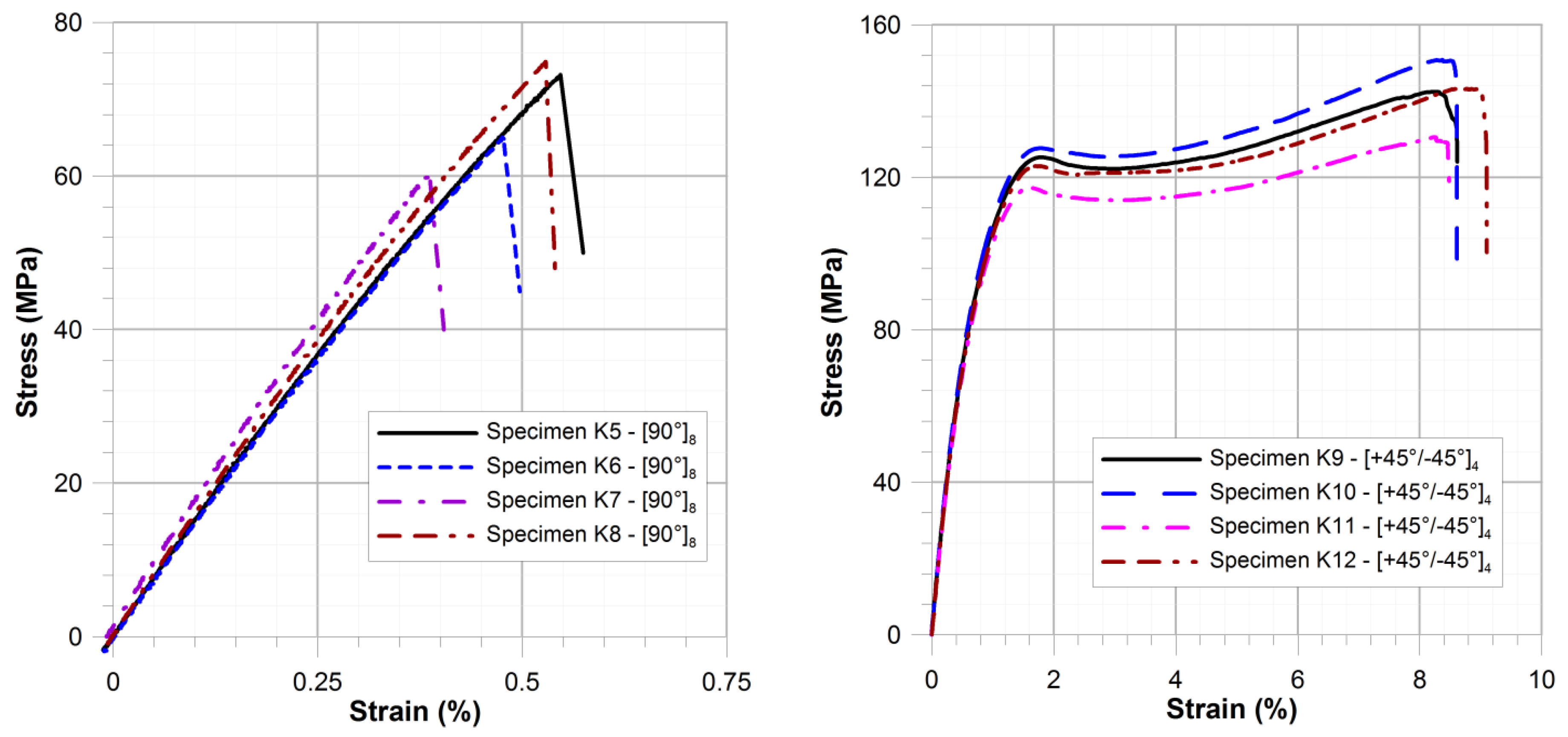
| E1 [GPa] | E2 [GPa] | ν12 | Tensile Strength [MPa] | ε1max [%] | ||||
|---|---|---|---|---|---|---|---|---|
| [0°]8 | [45°/−45°]4 | [90°]8 | [0°]8 | [45°/−45°]4 | [90°]8 | |||
| 46.4 | 14.9 | 0.27 | 1601 | 141.8 | 68.7 | 5.59 | 8.41 | 0.5 |
| No. | Loading Parameters | Number of Executed Cycles | Increase of Strains in (%) Per 50 k Cycles | Tg(a)-Slope of Strain Growth Line | Expected |
|---|---|---|---|---|---|
| 1 | Fm = 40 kN, Fa = 4 kN, R = 0.818, f = 5 Hz, | N = 0–80,000 | 0.131 | 2.619 × 10−6 | 1.045 × 106 |
| 2 | Fm = 40 kN, Fa = 7 kN, R = 0.702, f = 5 Hz, | N = 80,000–93,000 | 0.78 | 1.560 × 10−5 | 1.635 × 105 |
| 3 | Fm = 40 kN, Fa = 4 kN, R = 0.818, f = 10 Hz, | N = 93,000–293,000 | 0.07 | 1.405 × 10−6 | 1.95 × 106 |
| 4 | Fm = 42 kN, Fa = 4 kN, R = 0.826, f = 15 Hz, | N = 293,000–393,000 | 0.241 | 4.824 × 10−6 | 5.432 × 105 |
| 5 | Fm = 45 kN, Fa = 4 kN, R = 0.837, f = 15 Hz | N = 393,000–440,460 | 1.239 | 2.478 × 10−5 | 0.973 × 105 |
| No. | Expected (Details in Table 2) | Calculated Using Model (6)—, α = 0.123351, β = 0.244873 | Difference δ1 (7) |
|---|---|---|---|
| 1 | 6.02 | 5.81 | 1.2 × 10−3 |
| 2 | 5.21 | 4.71 | 9.5 × 10−3 |
| 3 | 6.29 | 6.10 | 9.2 × 10−4 |
| 4 | 5.73 | 6.02 | 2.5 × 10−3 |
| 5 | 4.99 | 5.59 | 14.8 × 10−3 |
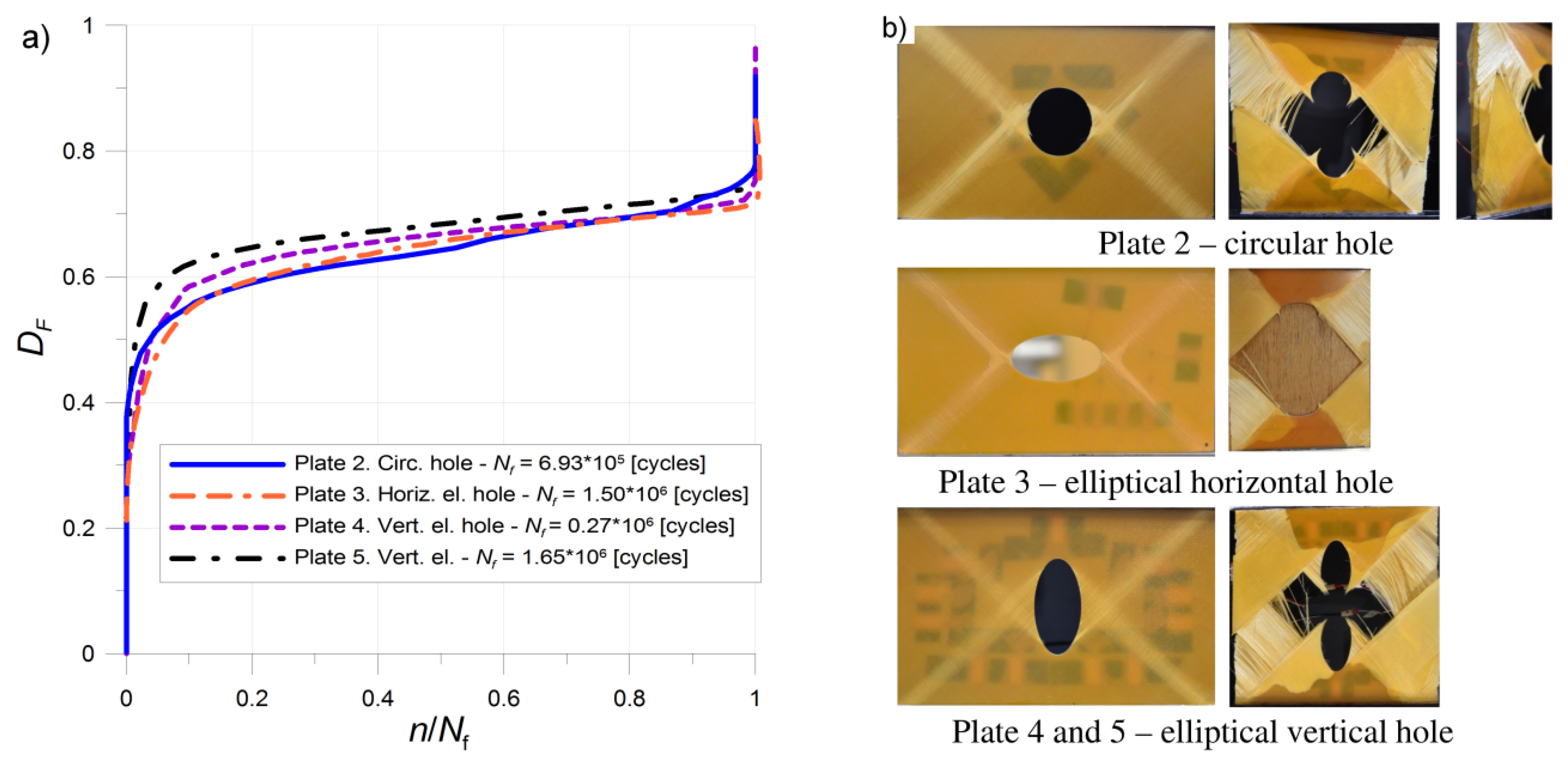
| No. | Hole | Loading Parameters | Log (Nf) Experiment | Log (Nf) Predicted | Error δ (8) |
|---|---|---|---|---|---|
| 2 | Circular | Fm = 44 kN, Fa = 4 kN, f = 15 Hz | 5.84 | 5.75 | 2.54 × 10−4 |
| 3 | Elliptical horizontal | Fm = 38 kN, Fa = 4 kN, f = 30 Hz, | 6.18 | 6.04 | 4.86 × 10−4 |
| 4 | Elliptical vertical | Fm = 50 kN, Fa = 5 kN, f = 30 Hz | 5.43 | 5.30 | 5.64 × 10−4 |
| 5 | Elliptical vertical | Fm = 50 kN, Fa = 4 kN, f = 30 Hz, | 6.21 | 5.77 | 5.18 × 10−3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanowicz, P.; Muc, A. Estimation of Notched Composite Plates Fatigue Life Using Residual Strength Model Calibrated by Step-Wise Tests. Materials 2018, 11, 2180. https://doi.org/10.3390/ma11112180
Romanowicz P, Muc A. Estimation of Notched Composite Plates Fatigue Life Using Residual Strength Model Calibrated by Step-Wise Tests. Materials. 2018; 11(11):2180. https://doi.org/10.3390/ma11112180
Chicago/Turabian StyleRomanowicz, Paweł, and Aleksander Muc. 2018. "Estimation of Notched Composite Plates Fatigue Life Using Residual Strength Model Calibrated by Step-Wise Tests" Materials 11, no. 11: 2180. https://doi.org/10.3390/ma11112180
APA StyleRomanowicz, P., & Muc, A. (2018). Estimation of Notched Composite Plates Fatigue Life Using Residual Strength Model Calibrated by Step-Wise Tests. Materials, 11(11), 2180. https://doi.org/10.3390/ma11112180






