A Numerical Method to Model Non-linear Damping Behaviour of Martensitic Shape Memory Alloys
Abstract
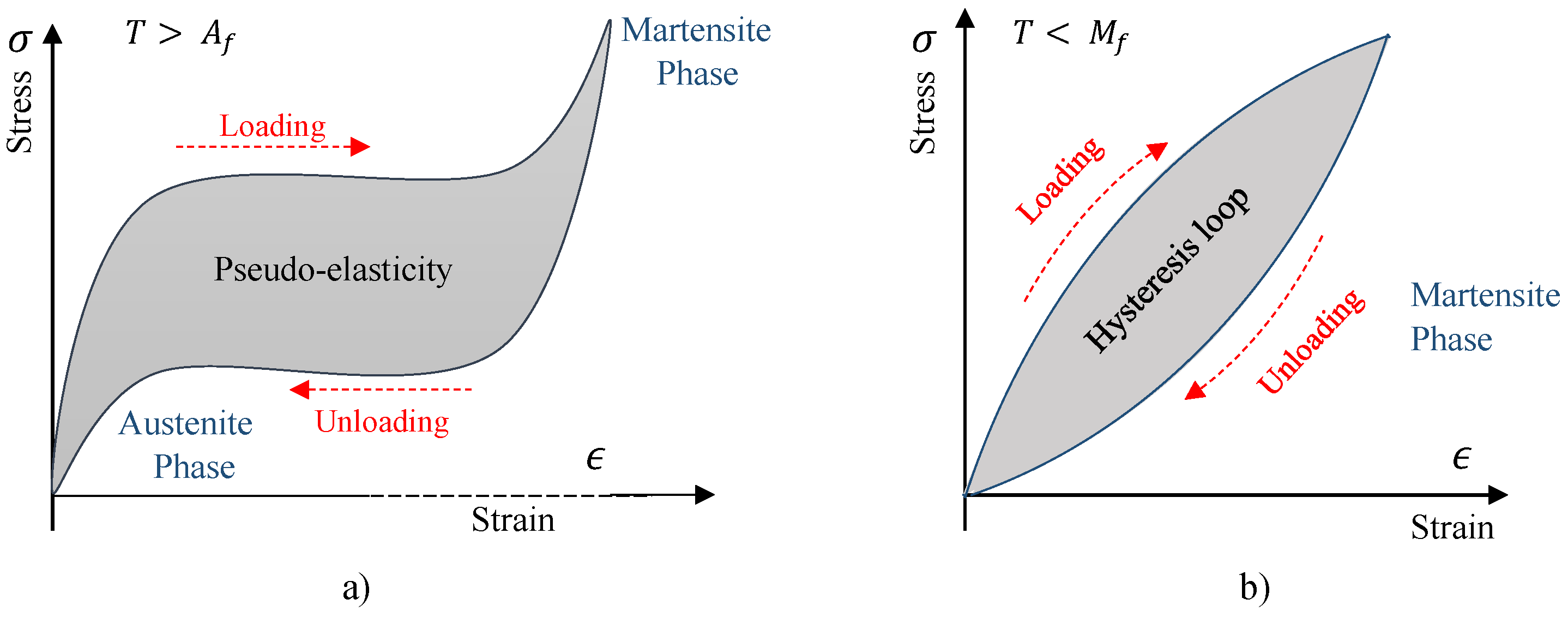
1. Introduction
2. Materials
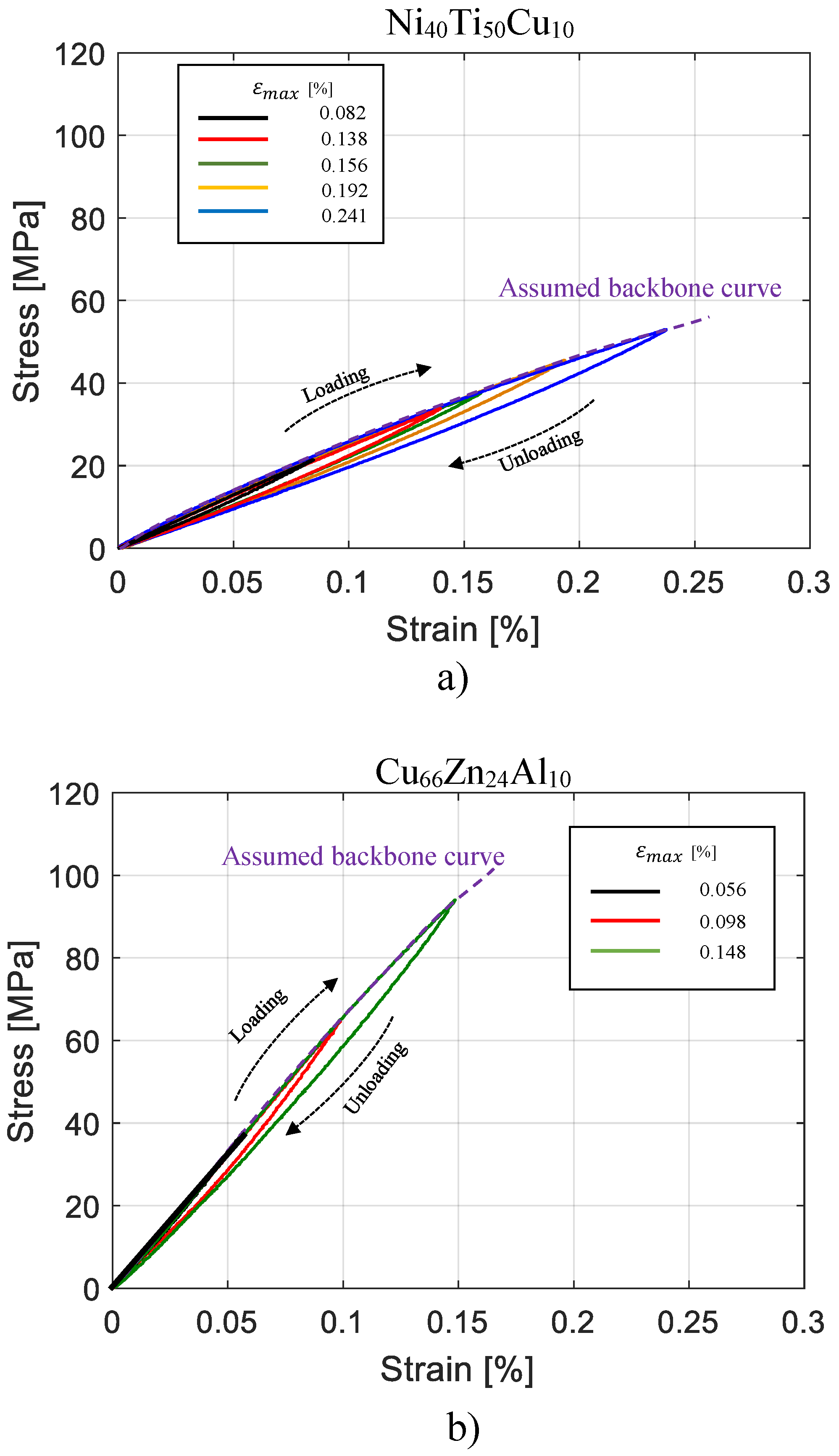
- at each maximum strain level the cycle is fully reversible and reproducible at each maximum strain level;
- the cyclic loading path always follows the backbone curve;
- each new series of cycles at a given maximum strain is not affected by a previous series of cycles at different maximum strain levels.
3. Model of the Nonlinear Damping Behaviour
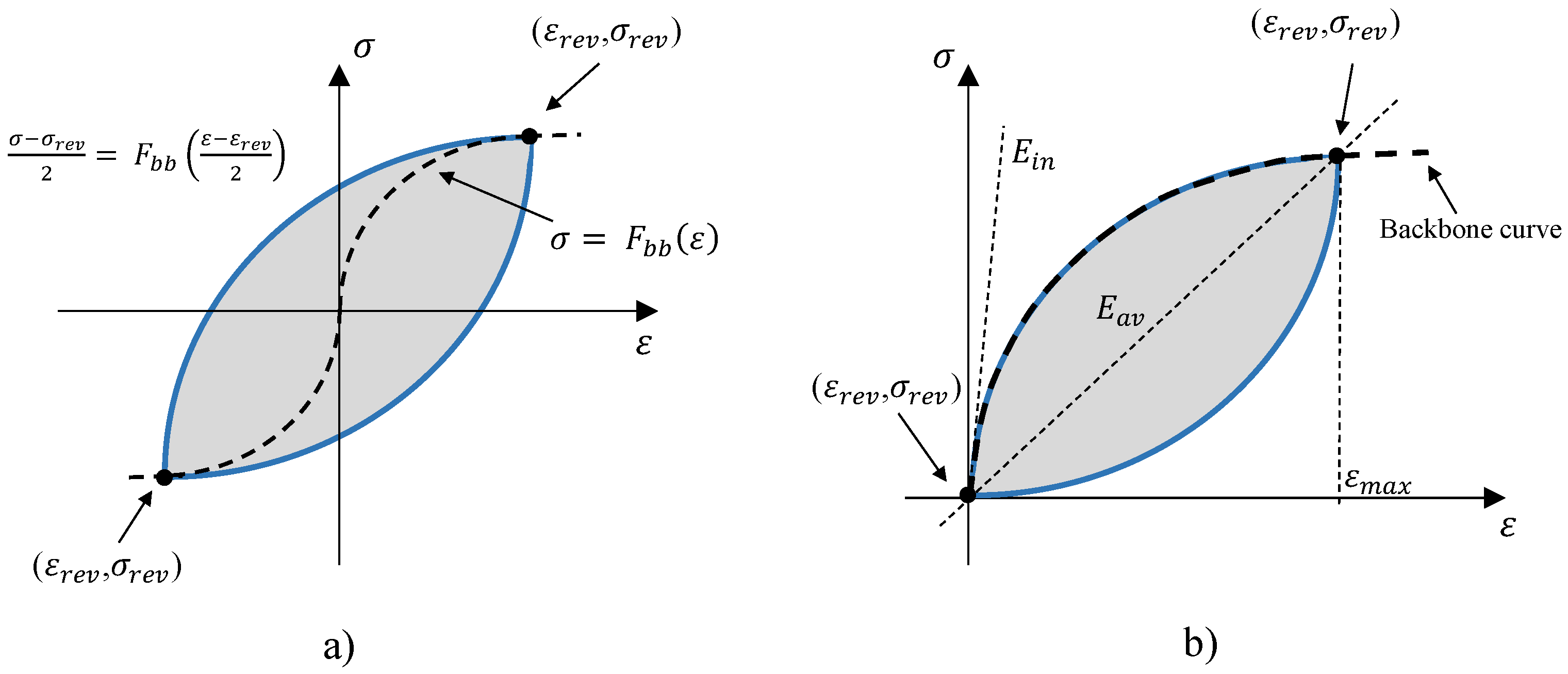
- For an initial loading in a cyclic test, the stress strain path follows the backbone curves:where is called backbone function.
- If a stress reversal occurs at a point defined by (, ), the stress strain path will be given by:
- If the loading curve intersects the backbone curve, it follows the backbone curve until the following stress reversal.
- If an unloading or reloading curve crosses an unloading or reloading curve from the previous cycle, the stress–strain curve follows that of the previous cycle.
- The actual elastic properties for each strain increment, were calculated according to Equation (5), based on the principal strain with highest absolute value () and the last reversal strain (). The actual principal strain is calculated from the strain values in standard direction () at the beginning of the increment.
- Reversal points were detected from the sign change of the actual and previous principal strain and principal strain increments. In both cases the principal strain with highest absolute value is considered. Taking this into consideration results in the symmetrical behaviour of the model with respect to the origin of the axes.
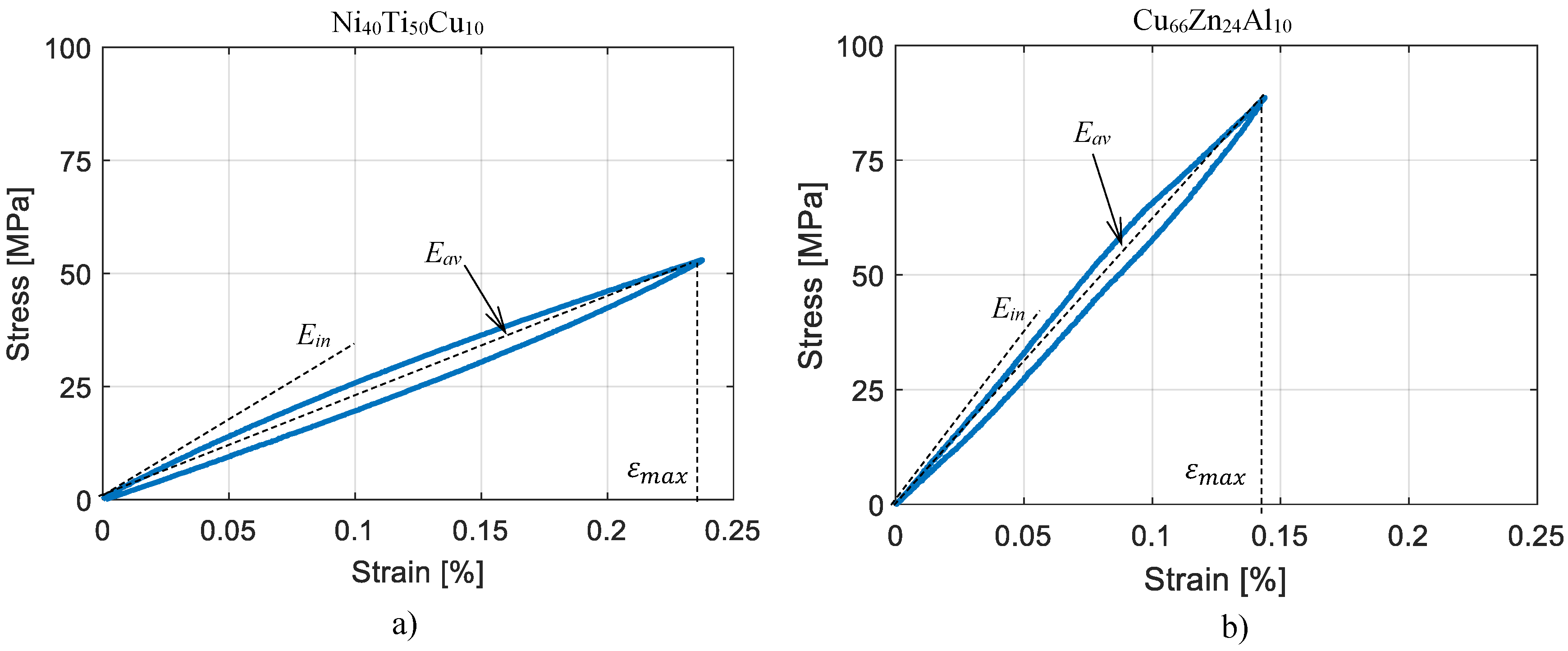
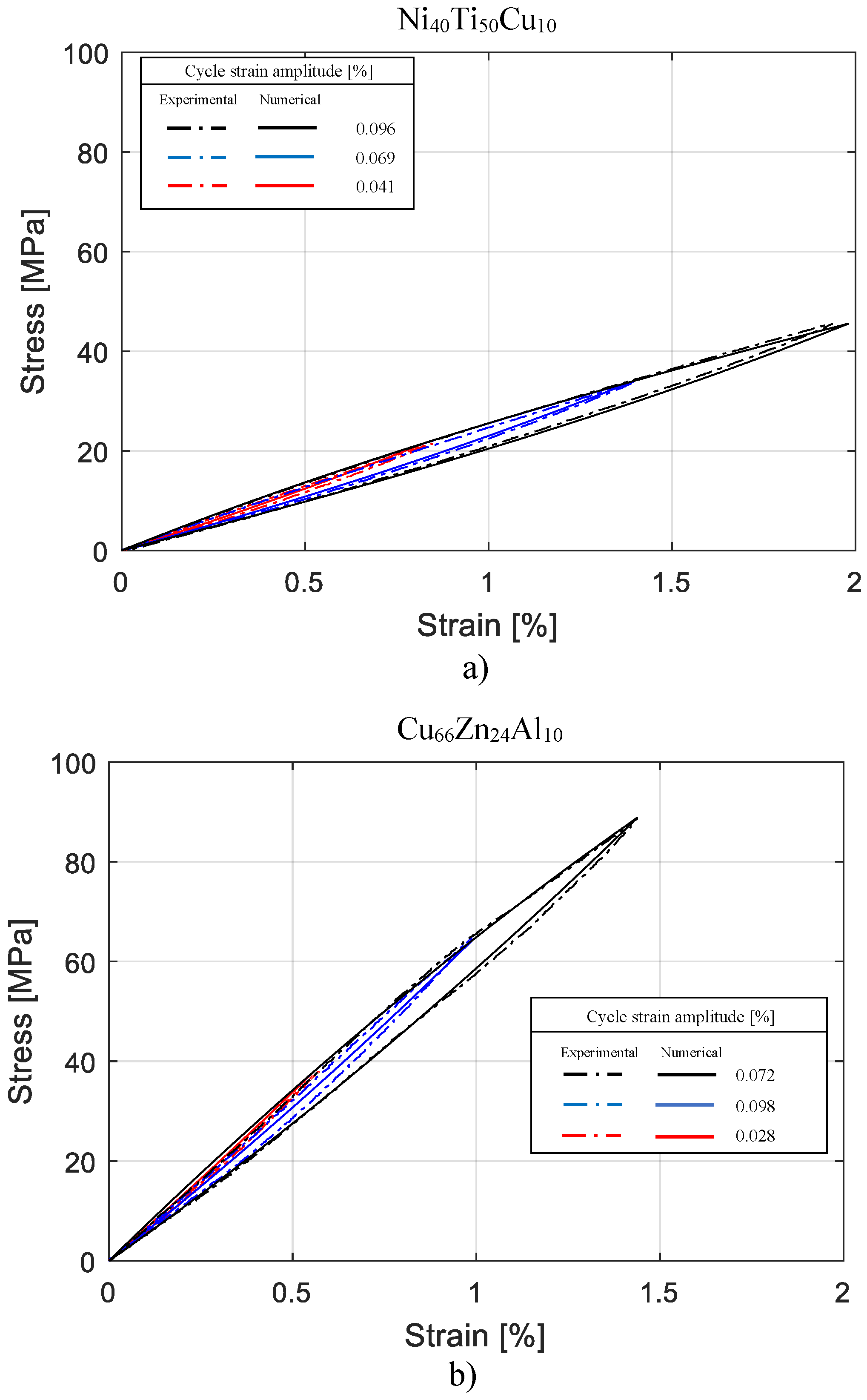
4. Validation of the Material Model
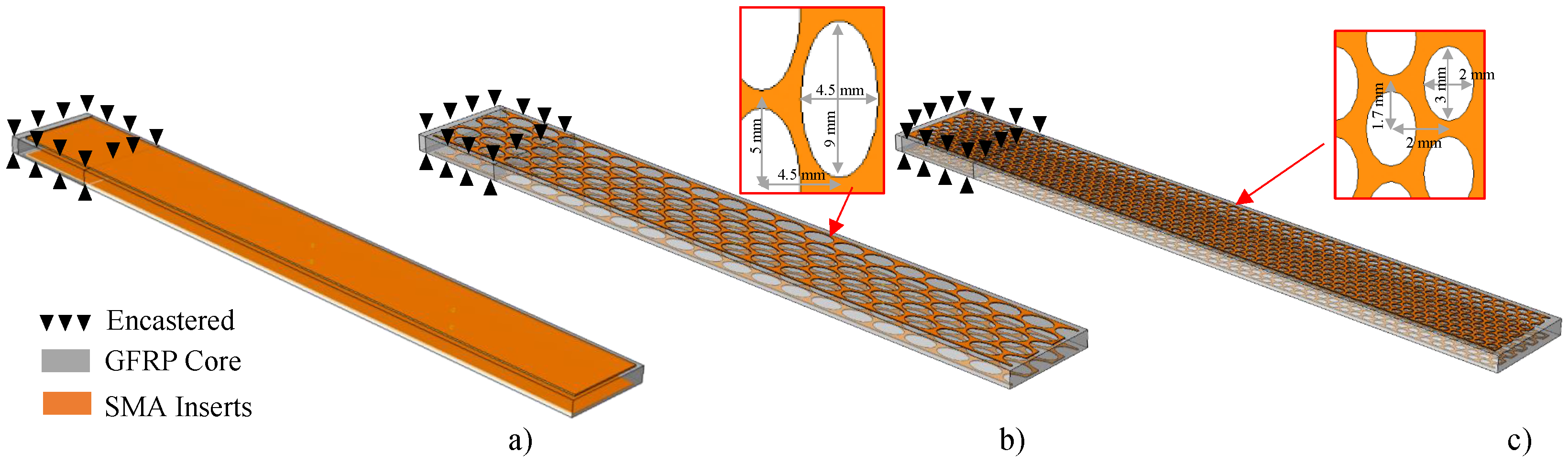
5. Application to Hybrid Structures
5.1. Finite Element Model
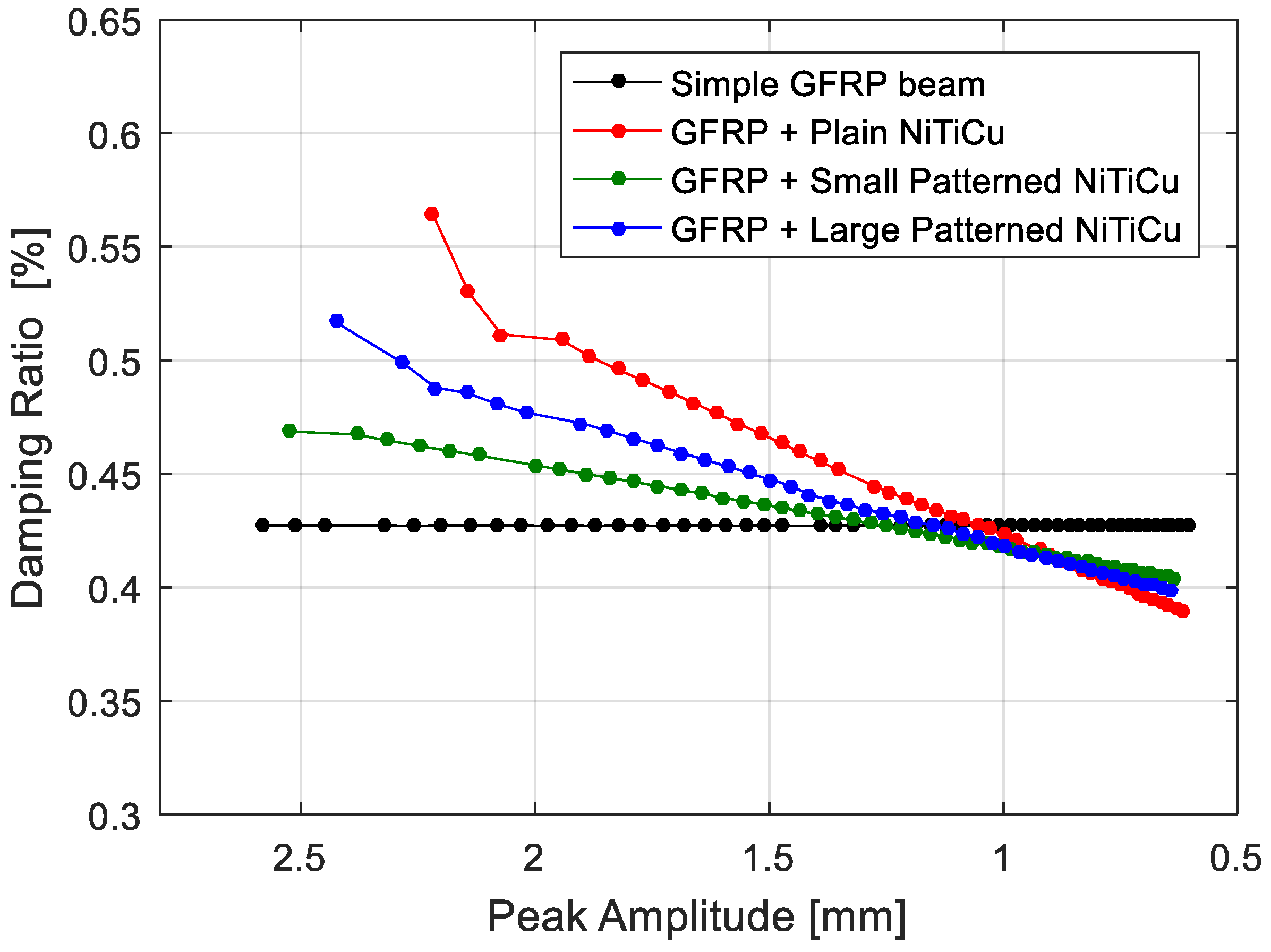
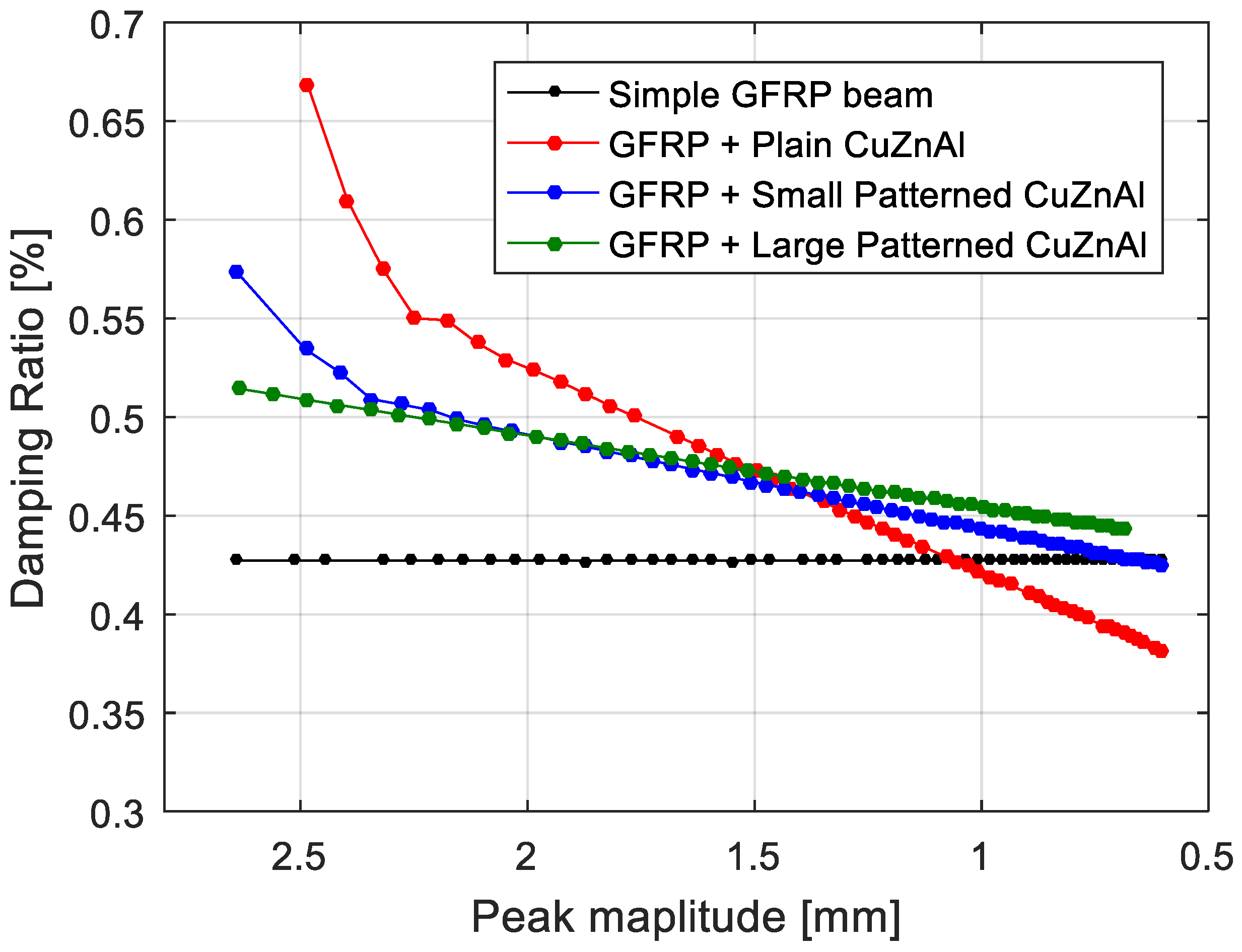
5.2. Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oliveira, J.P.; Miranda, R.M.; Fernandes, F.M.B. Welding and Joining of NiTi Shape Memory Alloys: A Review. Prog. Mater. Sci. 2017, 88, 412–466. [Google Scholar] [CrossRef]
- Oliveira, J.P.; Zeng, Z.; Omori, T.; Zhou, N.; Miranda, R.M.; Fernandes, F.M.B. Improvement of damping properties in laser processed superelastic Cu-Al-Mn shape memory alloys. Mater. Des. 2016, 98, 280–284. [Google Scholar] [CrossRef]
- Lester, B.T.; Baxevanis, T.; Chemisky, Y.; Lagoudas, D.C. Review and perspectives: Shape memory alloy composite systems. Acta Mech. 2015, 226, 3907–3960. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Manfredi, L.; Huan, Y.; Cuschieri, A. Low power consumption mini rotary actuator with SMA wires. Smart Mater. Struct. 2017, 26, 115003. [Google Scholar] [CrossRef]
- Song, S.H.; Lee, J.Y.; Rodrigue, H.; Choi, I.S.; Kang, Y.J.; Ahn, S.H. 35 Hz shape memory alloy actuator with bending-twisting mode. Sci. Rep. 2016, 6, 21118. [Google Scholar] [CrossRef] [PubMed]
- Van Humbeeck, J.; Kustov, S. Active and passive damping of noise and vibrations through shape memory alloys: Applications and mechanisms. Smart Mater. Struct. 2005, 14, S171–S185. [Google Scholar] [CrossRef]
- Birman, V. Properties and response of composite material with spheroidal superelastic shape memory alloy inclusions subject to three-dimensional stress state. J. Phys. D Appl. Phys. 2010, 43, 225402. [Google Scholar] [CrossRef]
- Balapgol, B.S.; Bajoria, K.M.; Kulkarni, S.A. Natural frequencies of a multilayer SMA laminated composite cantilever plate. Smart Mater. Struct. 2006, 15, 1021–1032. [Google Scholar] [CrossRef]
- Van Humbeeck, J. Damping capacity of thermoelastic martensite in shape memory alloys. J. Alloys Compd. 2003, 355, 58–64. [Google Scholar] [CrossRef]
- Biffi, C.A.; Bassani, P.; Tuissi, A.; Carnevale, M.; Lecis, N.; LoConte, A.; Previtali, B. Numerical and Experimental Characterizations of Damping Properties of SMAs Composite for Vibration Control Systems. J. Mater. Eng. Perform. 2012, 21, 2713–2718. [Google Scholar] [CrossRef]
- Bassani, P.; Biffi, C.A.; Carnevale, M.; Lecis, N.; Previtali, B.; Lo Conte, A. Passive damping of slender and light structures. Mater. Des. 2013, 45, 88–95. [Google Scholar] [CrossRef]
- Haghdoust, P.; Cinquemani, S.; Lo Conte, A.; Lecis, N. Optimal design of damping layers in SMA/GFRP laminated hybrid composites. Smart Mater. Struct. 2017, 26, 105015. [Google Scholar] [CrossRef]
- Haghdoust, P.; Conte, A.L.; Cinquemani, S.; Lecis, N. Simulation of strain-dependent damping in SMA embedded hybrid beams. Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2018, 10598, 105983I. [Google Scholar] [CrossRef]
- Treviso, A.; Van Genechten, B.; Mundo, D.; Tournour, M. Damping in composite materials: Properties and models. Compos. Part B Eng. 2015, 78, 144–152. [Google Scholar] [CrossRef]
- Lazan, B. Damping of Materials and Members in Structural Mechanics; Pergamon Press: Oxford, UK, 1968. [Google Scholar]
- Mielczarek, A.; Riehemann, W.; Vogelgesang, S.; Zak, H.; Tonn, B. Amplitude-dependent internal friction of CuAlMn shape memory alloys. High Damp. Mater. II 2006, 319, 45–51. [Google Scholar] [CrossRef]
- Auricchio, F.; Fugazza, D.; DesRoches, R. Numerical and experimental evaluation of the damping properties of shape-memory alloys. J. Eng. Mater. Technol. Trans. ASME 2006, 128, 312–319. [Google Scholar] [CrossRef]
- Birman, V. Review of constitutive equations for shape memory alloys. In Proceedings of the Engineering Mechanics, Fort Lauderdale, FL, USA, 20–22 Janarary 1996; pp. 792–795. [Google Scholar]
- Oberaigner, E.R.; Tanaka, K.; Fischer, F.D. Investigation of the damping behavior of a vibrating shape memory alloy rod using a micromechanical model. Smart Mater. Struct. 1996, 5, 456–463. [Google Scholar] [CrossRef]
- Wang, L.X.; Melnik, R.V.N. Numerical model for vibration damping resulting from the first-order phase transformations. Appl. Math. Model. 2007, 31, 2008–2018. [Google Scholar] [CrossRef]
- Gholampour, A.A.; Ghassemieh, M.; Kiani, J. State of the art in nonlinear dynamic analysis of smart structures with SMA members. Int. J. Eng. Sci. 2014, 75, 108–117. [Google Scholar] [CrossRef]
- Haghdoust, P.; Conte, A.L.; Cinquemani, S.; Lecis, N. Investigation of shape memory alloy embedded wind turbine blades for the passive control of vibrations. Smart Mater. Struct. 2018, 27, 105012. [Google Scholar] [CrossRef]
- Adams, R.; Bacon, D.G.C. Effect of Fibre Orientation and Laminate Geometry on the Dynamic Properties of CFRP. J. Compos. Mater. 1973, 7, 402–428. [Google Scholar] [CrossRef]
- El Mahi, A.; Assarar, M.; Sefrani, Y.; Berthelot, J.M. Damping analysis of orthotropic composite materials and laminates. Compos. Part B Eng. 2008, 39, 1069–1076. [Google Scholar] [CrossRef]
- Berthelot, J.M.; Assarar, M.; Sefrani, Y.; El Mahi, A. Damping analysis of composite materials and structures. Compos. Struct. 2008, 85, 189–204. [Google Scholar] [CrossRef]
- Youzera, H.; Meftah, S.A.; Challamel, N.; Tounsi, A. Nonlinear damping and forced vibration analysis of laminated composite beams. Compos. Part B Eng. 2012, 43, 1147–1154. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Ferrari, G.; Amabili, M. Identification of the viscoelastic response and nonlinear damping of a rubber plate in nonlinear vibration regime. Mech. Syst. Signal Process. 2018, 111, 376–398. [Google Scholar] [CrossRef]
- Puzrin, A. Constitutive Modelling in Geomechanics; Springer: Berlin, Germany, 2012. [Google Scholar]
- Zhou, A.G.; Basu, S.; Friedman, G.; Finkel, P.; Yeheskel, O.; Barsoum, M.W. Hysteresis in kinking nonlinear elastic solids and the Preisach-Mayergoyz model. Phys. Rev. B 2010, 82, 094105. [Google Scholar] [CrossRef]
- Barsoum, M.W.; Radovic, M.; Zhen, T.; Finkel, P.; Kalidindi, S.R. Dynamic elastic hysteretic solids and dislocations. Phys. Rev. Lett. 2005, 94, 085501. [Google Scholar] [CrossRef] [PubMed]
- Muravskii, G.B. On frequency independent damping. J. Sound Vib. 2004, 274, 653–668. [Google Scholar] [CrossRef]
- Gottlieb, O.; Habib, G. Non-linear model-based estimation of quadratic and cubic damping mechanisms governing the dynamics of a chaotic spherical pendulum. J. Vib. Control 2012, 18, 536–547. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear damping in large-amplitude vibrations: modelling and experiments. Nonlinear Dyn 2018, 93, 5–18. [Google Scholar] [CrossRef]
- Masing, G. Eigenspannungen und Verfestigung beim Messing. In Proceedings of the 2nd International Congress on Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 332–335. [Google Scholar]
- Kramer, S. Geothechnical Earthquake Engineering; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Muravskii, G. On description of hysteretic behaviour of materials. Int. J. Solids Struct. 2005, 42, 2625–2644. [Google Scholar] [CrossRef]
- Chiang, D.Y. The generalized Masing models for deteriorating hysteresis and cyclic plasticity. Appl. Math. Model. 1999, 23, 847–863. [Google Scholar] [CrossRef]
- Puzrin, A.; Burland, J. Logarithmic stress–strain function for rocks and soils. Geotechnique 1996, 46, 157–164. [Google Scholar] [CrossRef]
- Pyke, R. Nonlinear Soil Models for Irregular Cyclic Loading. J. Geotech. Eng. Div. 1979, 157, 715–726. [Google Scholar]
- Lo Conte, A.; Biffi, C.; Tuissi, A.; Ali, A. Computational model for delamination growth at SMA–GFRP interface of hybrid composite. Procedia Struct. Integr. 2016, 2, 1538–1545. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II; Springer: Berlin, Germany, 1991. [Google Scholar]



| Material | (°C) | (°C) | (°C) | (°C) |
|---|---|---|---|---|
| Ni40Ti50Cu10 | 32 | 49 | 52 | 61 |
| Cu66Zn24Al10 | 50 | 63 | 60 | 68 |
| Material | (GPa) | (GPa) | (%) |
|---|---|---|---|
| Ni40Ti50Cu10 | 28.6 | 22.26 | 0.241 |
| Cu66Zn24Al10 | 66.7 | 56.9 | 0.1486 |
| Cycle Strain Amplitude (%) | Loss Factor | Elastic Modulus | ||||
|---|---|---|---|---|---|---|
| Numerical (-) | Experimental (-) | Error (%) | Numerical (GPa) | Experimental (GPa) | Error (%) | |
| 0.041 | 0.051 | 0.049 | 4.08 | 26.06 | 25.24 | 3.24 |
| 0.054 | 0.064 | 0.055 | 16.36 | 25.20 | 24.20 | 4.13 |
| 0.069 | 0.077 | 0.068 | 13.23 | 24.34 | 24.21 | 0.53 |
| 0.078 | 0.084 | 0.082 | 2.43 | 23.88 | 23.87 | 0.04 |
| 0.089 | 0.091 | 0.082 | 10.97 | 23.38 | 24.05 | 2.78 |
| 0.096 | 0.096 | 0.091 | 5.49 | 22.98 | 23.41 | 1.83 |
| 0.12 | 0.104 | 0.106 | 1.88 | 22.26 | 22.29 | 0.13 |
| Cycle Strain Amplitude (%) | Loss Factor | Elastic Modulus | ||||
|---|---|---|---|---|---|---|
| Numerical (-) | Experimental (-) | Error (%) | Numerical (GPa) | Experimental (GPa) | Error (%) | |
| 0.028 | 0.025 | 0.015 | 66.66 | 68.06 | 65.81 | 3.41 |
| 0.049 | 0.046 | 0.045 | 2.22 | 64.95 | 65.16 | 0.32 |
| 0.072 | 0.070 | 0.072 | 2.77 | 61.76 | 61.57 | 0.31 |
| 0.074 | 0.073 | 0.062 | 17.74 | 61.43 | 63.28 | 2.92 |
| Layup No. | SMA Insert | Pattern |
|---|---|---|
| Ref Layup | – | |
| Hyb Layup 1 | Ni40Ti50Cu10 | – |
| Hyb Layup 2 | Large | |
| Hyb Layup 3 | Small | |
| Hyb Layup 4 | Cu66Zn24Al10 | – |
| Hyb Layup 5 | Large | |
| Hyb Layup 6 | Small |
| Material | Elastic Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) |
|---|---|---|---|
| GFRP | 17 | 0.27 | 1880 |
| Ni40Ti50Cu10 | Hysteresis model | 7400 | |
| Cu66Zn24Al10 | Hysteresis model | 6600 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haghdoust, P.; Lo Conte, A.; Cinquemani, S.; Lecis, N. A Numerical Method to Model Non-linear Damping Behaviour of Martensitic Shape Memory Alloys. Materials 2018, 11, 2178. https://doi.org/10.3390/ma11112178
Haghdoust P, Lo Conte A, Cinquemani S, Lecis N. A Numerical Method to Model Non-linear Damping Behaviour of Martensitic Shape Memory Alloys. Materials. 2018; 11(11):2178. https://doi.org/10.3390/ma11112178
Chicago/Turabian StyleHaghdoust, Pouya, Antonietta Lo Conte, Simone Cinquemani, and Nora Lecis. 2018. "A Numerical Method to Model Non-linear Damping Behaviour of Martensitic Shape Memory Alloys" Materials 11, no. 11: 2178. https://doi.org/10.3390/ma11112178
APA StyleHaghdoust, P., Lo Conte, A., Cinquemani, S., & Lecis, N. (2018). A Numerical Method to Model Non-linear Damping Behaviour of Martensitic Shape Memory Alloys. Materials, 11(11), 2178. https://doi.org/10.3390/ma11112178







