Experimental and Numerical Study of Nonlinear Lamb Waves of a Low-Frequency S0 Mode in Plates with Quadratic Nonlinearity
Abstract
1. Introduction
2. Nonlinear Lamb Waves
3. Numerical Simulation
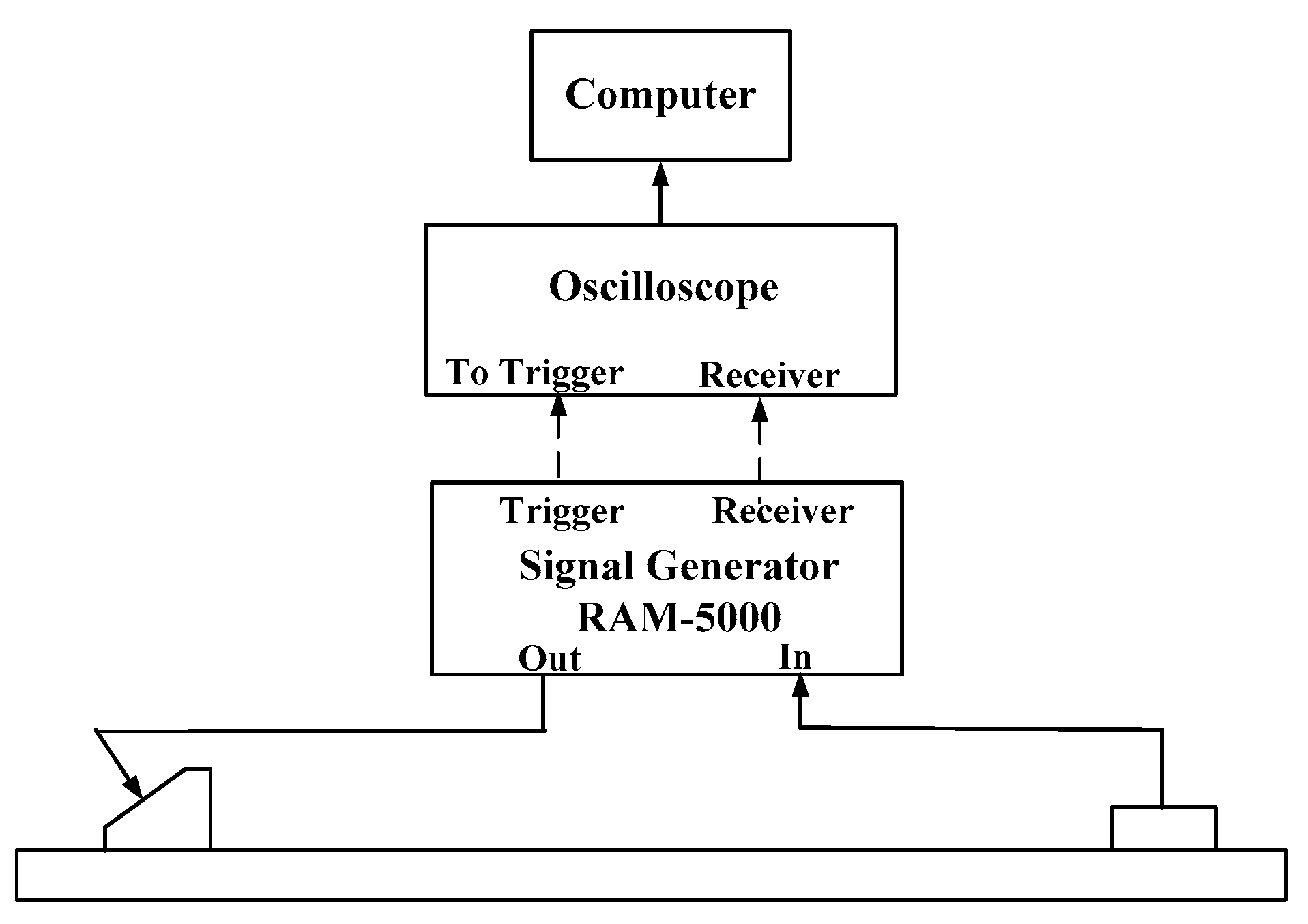
4. Experimental Measurement
5. Result Discussion
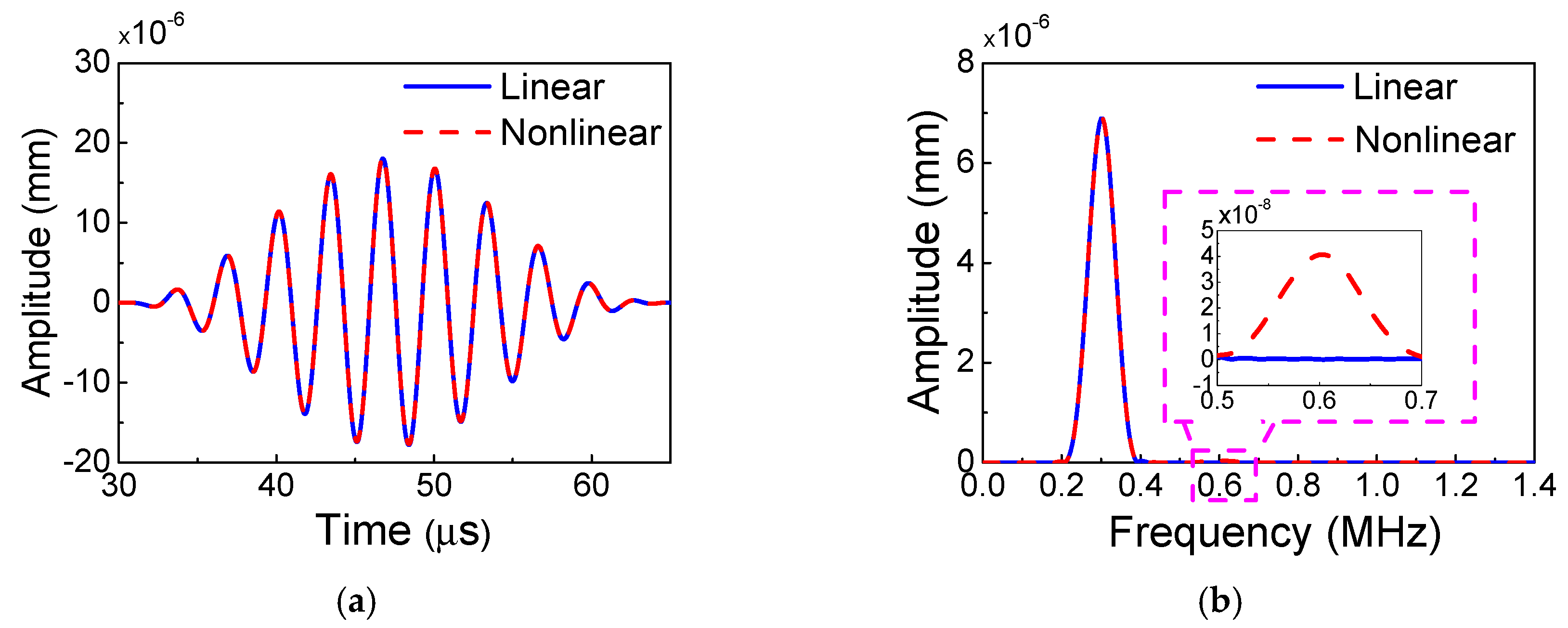
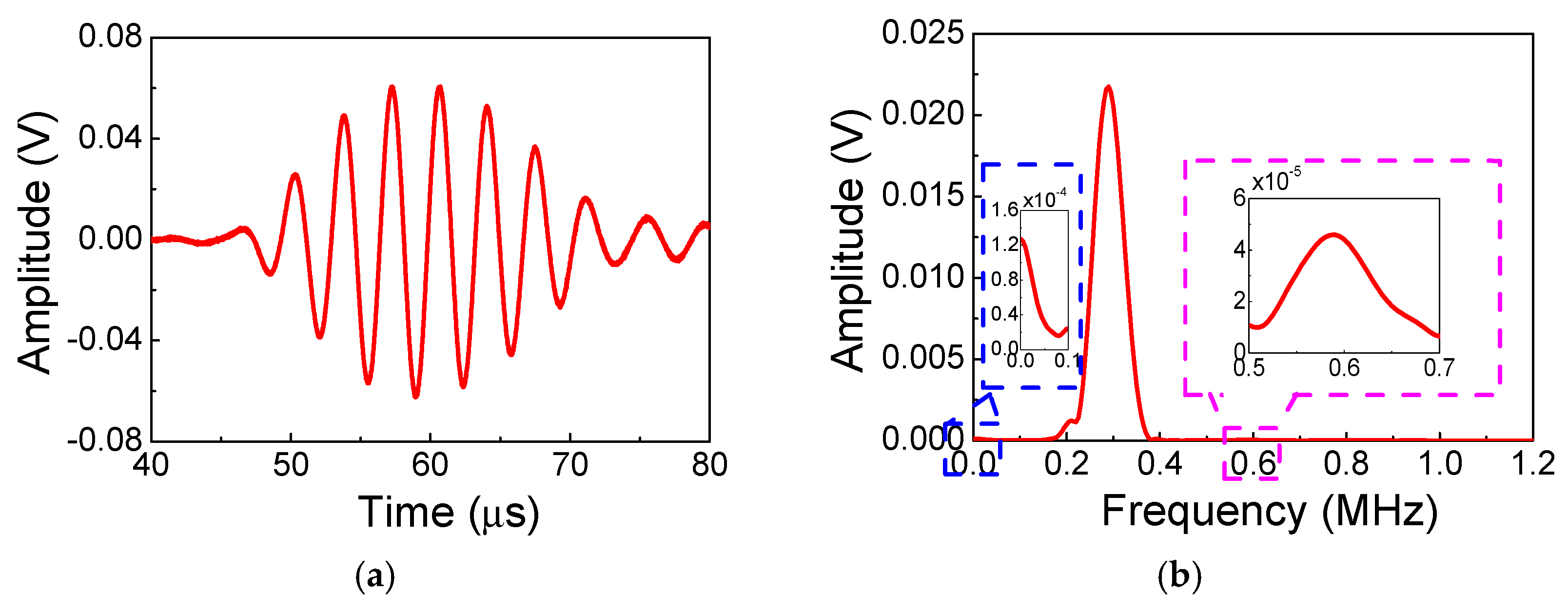
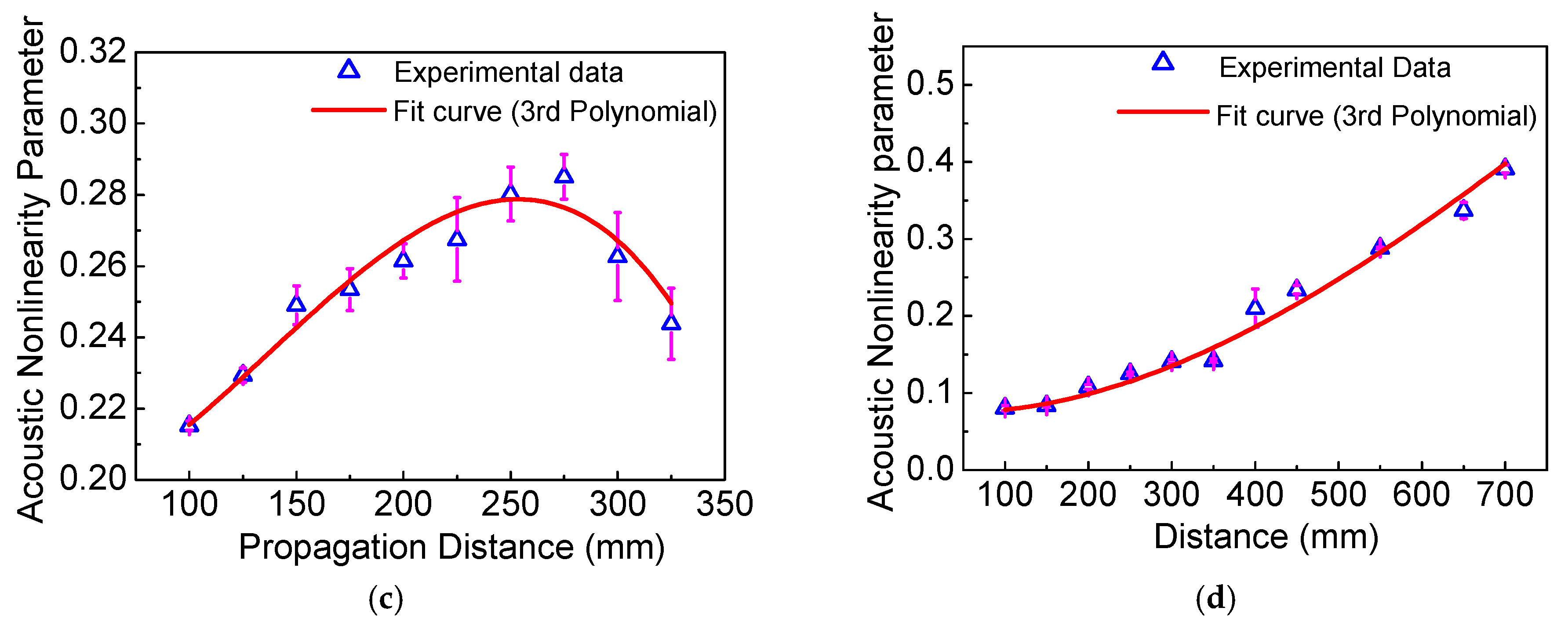
5.1. Fundamental Waves and Second Harmonics
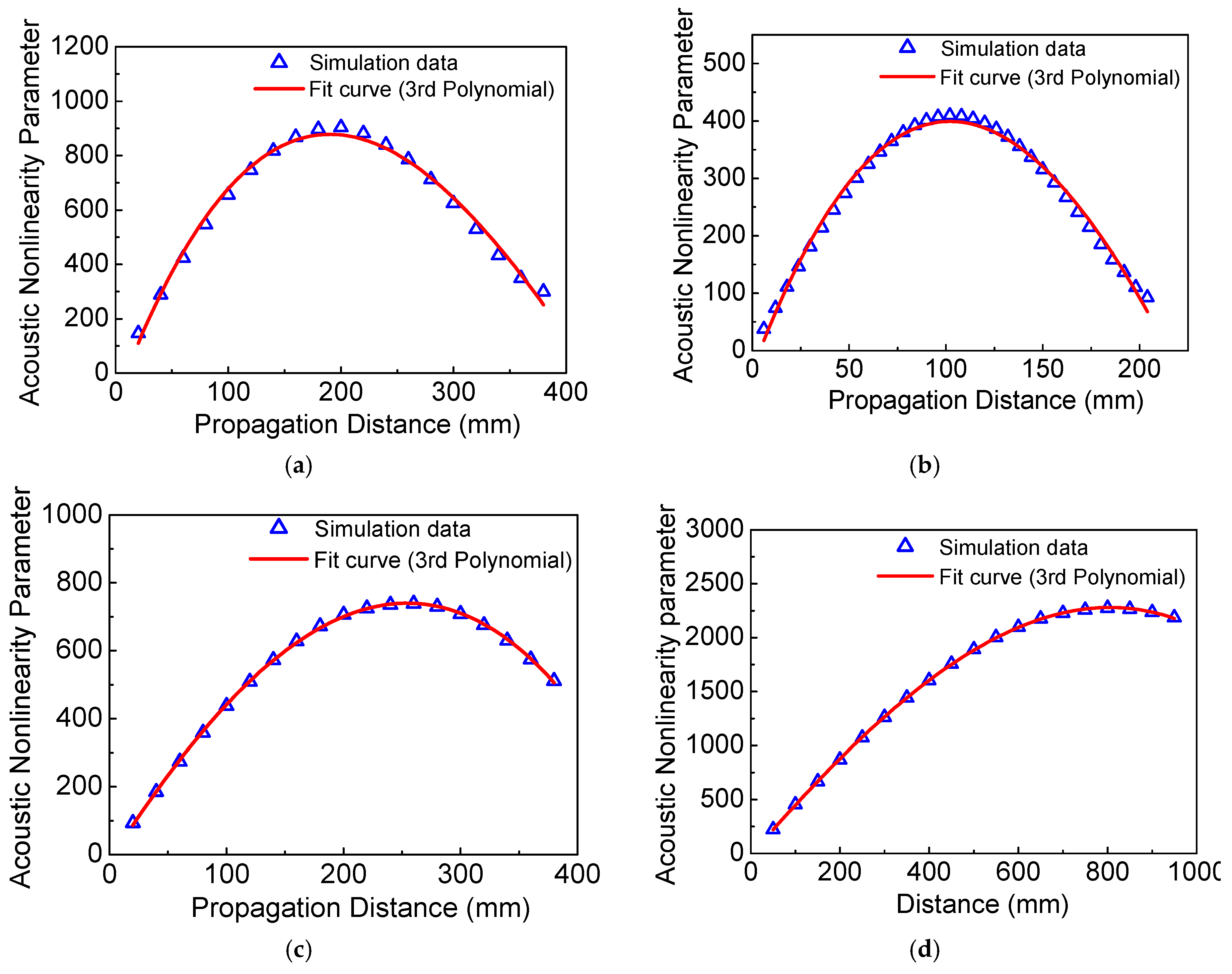
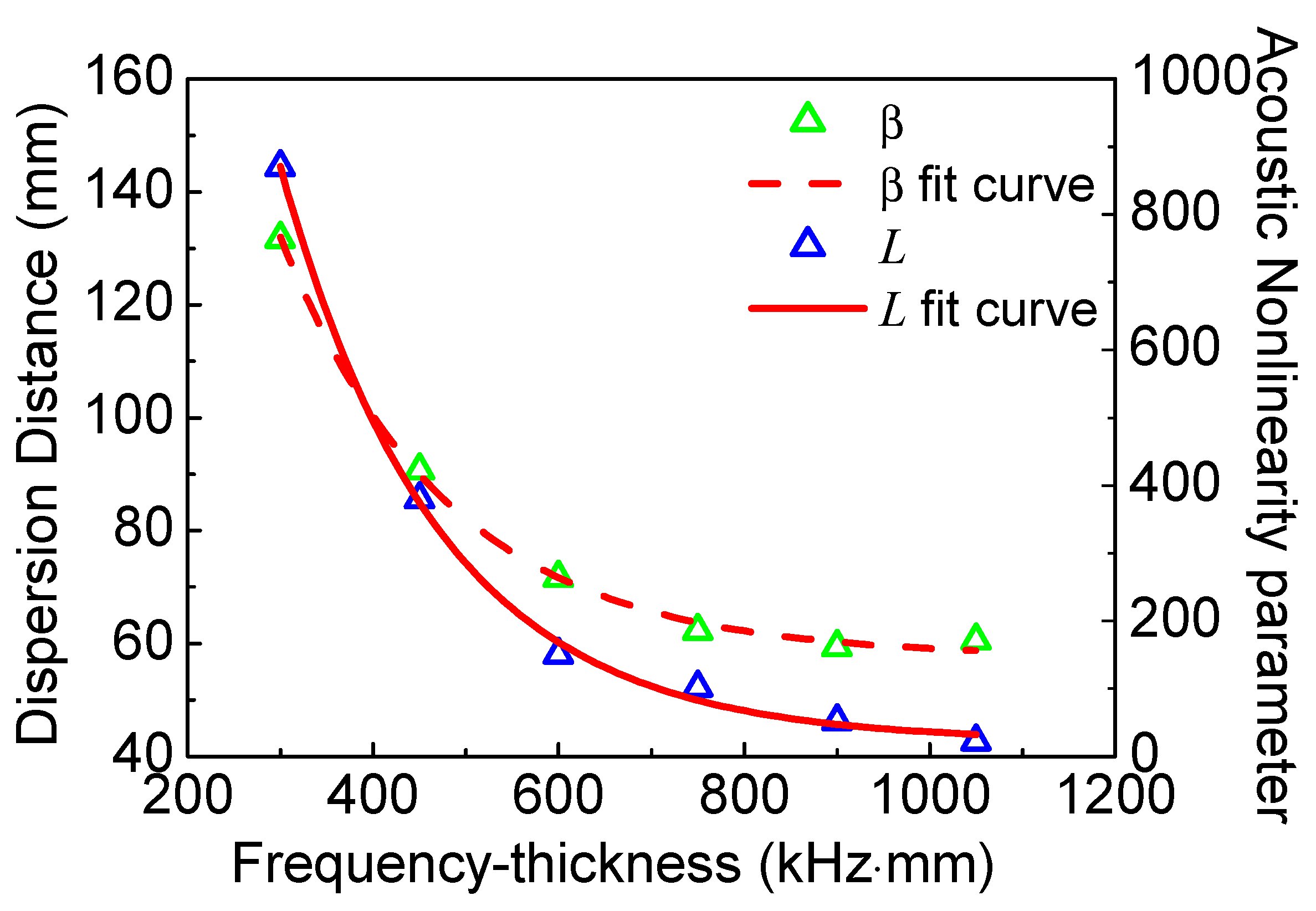
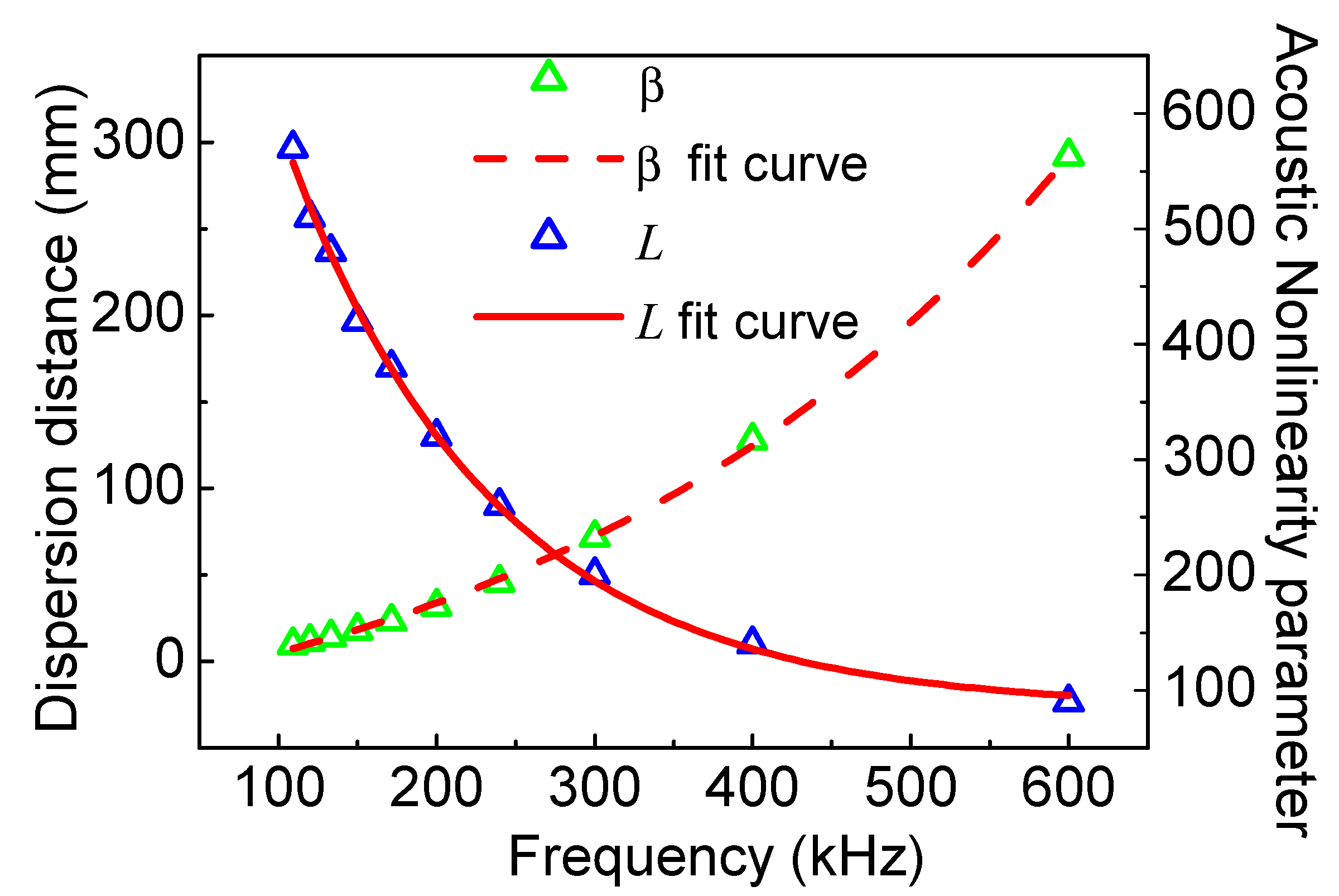
5.2. The Influence of Frequency-Thickness
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Szilard, J. Ultrasonic Testing: Nonconventional Testing Techniques; John Wiley & Sons Ltd.: New York, NY, USA, 1982. [Google Scholar]
- Blitz, J.; Simpson, G. Ultrasonic Methods of Non-Destructive Testing; Springer Nature: Berlin, Germany, 1995. [Google Scholar]
- Drinkwater, B.W.; Wilcox, P.D. Ultrasonic arrays for non-destructive evaluation: A review. NDT E Int. 2006, 39, 525–541. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Ogi, H.; Hirao, M.; Aoki, S. Noncontact monitoring of surface-wave nonlinearity for predicting the remaining life of fatigued steels. J. Appl. Phys. 2001, 90, 438–442. [Google Scholar] [CrossRef]
- Nagy, P.B. Fatigue damage assessment by nonlinear ultrasonic materials characterization. Ultrasonics 1998, 36, 375–381. [Google Scholar] [CrossRef]
- Donskoy, D.; Zagrai, A.; Chudnovsky, A.; Golovin, E.; Agarwala, V.S. Assessment of incipient material damage and remaining life prediction with nonlinear acoustics. J. Acoust. Soc. Am. 2006, 119, 3293. [Google Scholar] [CrossRef]
- Li, W.; Cho, Y.; Achenbach, J.D. Detection of thermal fatigue in composites by second harmonic Lamb waves. Smart Mater. Struct. 2012, 21, 85–93. [Google Scholar] [CrossRef]
- Biwa, S.; Nakajima, S.; Ohno, N. On the acoustic nonlinearity of solid-solid contact with pressure-dependent interface stiffness. J. Appl. Mech. 2004, 71, 508–515. [Google Scholar] [CrossRef]
- Cantrell, J.H. Fundamentals and applications of nonlinear ultrasonic nondestructive evaluation. In Ultrasonic Nondestructive Evaluation; CRC Press: Boca Raton, FL, USA, 2004; pp. 363–434. [Google Scholar]
- Chillara, V.K.; Lissenden, C.J. Nonlinear guided waves in plates: A numerical perspective. Ultrasonics 2014, 54, 1553–1558. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Giurgiutiu, V. WaveFormRevealer: An analytical framework and predictive tool for the simulation of multi-modal guided wave propagation and interaction with damage. Struct. Health Monit. 2014, 13, 491–511. [Google Scholar] [CrossRef]
- Shen, Y.; Giurgiutiu, V. Predictive modeling of nonlinear wave propagation for structural health monitoring with piezoelectric wafer active sensors. J. Intell. Mater. Syst. Struct. 2014, 25, 506–520. [Google Scholar] [CrossRef]
- Solodov, I.Y.; Krohn, N.; Busse, G. CAN: An example of nonclassical acoustic nonlinearity in solids. Ultrasonics 2002, 40, 621–625. [Google Scholar] [CrossRef]
- Lu, Y.; Ye, L.; Su, Z.; Yang, C. Quantitative assessment of through-thickness crack size based on Lamb wave scattering in aluminium plates. NDT E Int. 2008, 41, 59–68. [Google Scholar] [CrossRef]
- Shen, Y.; Cesnik, C.E.S. Modeling of nonlinear interactions between guided waves and fatigue cracks using local interaction simulation approach. Ultrasonics 2016, 74, 106–123. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.-X.; Yang, J. Characterization of elastic anisotropy of a solid plate using nonlinear Lamb wave approach. J. Sound Vib. 2007, 308, 201–211. [Google Scholar] [CrossRef]
- Deng, M.; Xiang, Y.; Liu, L. Time-domain analysis and experimental examination of cumulative second-harmonic generation by primary Lamb wave propagation. J. Appl. Phys. 2011, 109, 113525. [Google Scholar] [CrossRef]
- Matsuda, N.; Biwa, S. Phase and group velocity matching for cumulative harmonic generation in Lamb waves. J. Appl. Phys. 2011, 109, 094903. [Google Scholar] [CrossRef]
- Li, M.; Deng, M.; Gao, G.; Xiang, Y. Mode pair selection of circumferential guided waves for cumulative second-harmonic generation in a circular tube. Ultrasonics 2018, 82, 171–177. [Google Scholar] [CrossRef] [PubMed]
- Matlack, K.H.; Kim, J.-Y.; Jacobs, L.J.; Qu, J. Experimental characterization of efficient second harmonic generation of Lamb wave modes in a nonlinear elastic isotropic plate. J. Appl. Phys. 2011, 109, 014905. [Google Scholar] [CrossRef]
- Li, M.; Deng, M.; Gao, G.; Xiang, Y. Modeling of second-harmonic generation of circumferential guided wave propagation in a composite circular tube. J. Sound Vib. 2018, 421, 234–245. [Google Scholar] [CrossRef]
- Bermes, C.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Experimental characterization of material nonlinearity using Lamb waves. Appl. Phys. Lett. 2007, 90, 021901. [Google Scholar] [CrossRef]
- Bermes, C.; Kim, J.-Y.; Qu, J.; Jacobs, L.J. Nonlinear Lamb waves for the detection of material nonlinearity. Mech. Syst. Signal Process. 2008, 22, 638–646. [Google Scholar] [CrossRef]
- Müller, M.F.; Kim, J.-Y.; Qu, J.; Jacobs, L.J. Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates. J. Acoust. Soc. Am. 2010, 127, 2141–2152. [Google Scholar] [CrossRef] [PubMed]
- Matlack, K.H.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Review of second harmonic generation measurement techniques for material state determination in metals. J. Nondestruct. Eval. 2015, 34, 273. [Google Scholar] [CrossRef]
- Wan, X.; Tse, P.W.; Xu, G.H.; Tao, T.F.; Zhang, Q. Analytical and numerical studies of approximate phase velocity matching based nonlinear S0 mode Lamb waves for the detection of evenly distributed microstructural changes. Smart Mater. Struct. 2016, 25, 045023. [Google Scholar] [CrossRef]
- Zuo, P.; Zhou, Y.; Fan, Z. Numerical and experimental investigation of nonlinear ultrasonic Lamb waves at low frequency. Appl. Phys. Lett. 2016, 109, 021902. [Google Scholar] [CrossRef]
- Castaings, M.; Le Clezio, E.; Hosten, B. Modal decomposition method for modeling the interaction of Lamb waves with cracks. J. Acoust. Soc. Am. 2002, 112, 2567–2582. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.F.; Bo, L.; Liu, Y.L.; Zhao, Y.X.; Zhang, J.; Hu, N.; Fu, S.Y.; Deng, M.X. Detection of micro-cracks using nonlinear lamb waves based on the Duffing-Holmes system. J. Sound Vib. 2017, 405, 175–186. [Google Scholar] [CrossRef]
- Jiao, J.; Meng, X.; He, C.; Wu, B. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates. NDT E Int. 2016, 85, 63–71. [Google Scholar]
- Ishii, Y.; Biwa, S.; Adachi, T. Non-collinear interaction of guided elastic waves in an isotropic plate. J. Sound Vib. 2018, 419, 390–404. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y.; Cao, P.; Hu, N. Mixing of ultrasonic Lamb waves in thin plates with quadratic nonlinearity. Ultrasonics 2018, 87, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Xiang, Y.; Liu, C.-J.; Deng, M.; Ma, C.; Xuan, F.-Z. Fatigue damage evaluation using nonlinear Lamb Waves with Quasi phase-velocity matching at low frequency. Materials 2018, 11, 1920. [Google Scholar] [CrossRef] [PubMed]
- Hasanian, M.; Lissenden, C.J. Second order harmonic guided wave mutual interactions in plate: Vector analysis, numerical simulation, and experimental results. J. Appl. Phys. 2017, 122, 084901. [Google Scholar] [CrossRef]
- Liu, X.; Bo, L.; Liu, Y.; Zhao, Y.; Zhang, J.; Deng, M.; Hu, N. Location identification of closed crack based on Duffing oscillator transient transition. Mech. Syst. Signal Process. 2018, 100, 384–397. [Google Scholar] [CrossRef]
- Radecki, R.; Su, Z.; Cheng, L.; Packo, P.; Staszewski, W.J. Modelling nonlinearity of guided ultrasonic waves in fatigued materials using a nonlinear local interaction simulation approach and a spring model. Ultrasonics 2018, 84, 272–289. [Google Scholar] [CrossRef]
- Liu, Y.; Kim, J.-Y.; Jacobs, L.J.; Qu, J.; Li, Z. Experimental investigation of symmetry properties of second harmonic Lamb waves. J. Appl. Phys. 2012, 111, 053511. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.; Cao, P.; Qiu, Y. Experiment and FEM study of one-way mixing of elastic waves with quadratic nonlinearity. NDT E Int. 2015, 72, 33–40. [Google Scholar] [CrossRef]
- Lima, W.J.N.D.; Hamilton, M.F. Finite-amplitude waves in isotropic elastic plates. J. Sound Vib. 2003, 265, 819–839. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Li, F.L.; Cao, P.; Liu, Y.L.; Zhang, J.Y.; Fu, S.Y.; Zhang, J.; Hu, N. Generation mechanism of nonlinear ultrasonic Lamb waves in thin plates with randomly distributed micro-cracks. Ultrasonics 2017, 79, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Ding, X.; Li, F.; Zhou, S.; Liu, Y.; Hu, N.; Su, Z.; Zhao, Y.; Zhang, J.; Deng, M. Interaction of Lamb wave modes with weak material nonlinearity: Generation of symmetric zero-frequency mode. Sensors 2018, 18, 2451. [Google Scholar] [CrossRef] [PubMed]





| ρ (kg/m3) | λ (MPa) | μ (MPa) | l (MPa) | m (MPa) | n (MPa) |
|---|---|---|---|---|---|
| 2704 | 5.11 × 104 | 2.63 × 104 | −2.82 × 105 | −3.39 × 105 | −4.16 × 105 |
| Case | L/mm (Numerical Simulations) | L/mm (Experiments) | Error |
|---|---|---|---|
| f = 300 kHz, h = 2.0 mm | 180 | 175 | 2.8% |
| f = 300 kHz, h = 2.5 mm | 100 | 125 | 25% |
| f =240 kHz, h = 2.5 mm | 240 | 250 | 4.2% |
| f = 200 kHz, h = 2.0 mm | 800 | 700 | 12.5% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Zhao, Y.; Hu, N.; Liu, Y.; Zhang, J.; Deng, M. Experimental and Numerical Study of Nonlinear Lamb Waves of a Low-Frequency S0 Mode in Plates with Quadratic Nonlinearity. Materials 2018, 11, 2096. https://doi.org/10.3390/ma11112096
Ding X, Zhao Y, Hu N, Liu Y, Zhang J, Deng M. Experimental and Numerical Study of Nonlinear Lamb Waves of a Low-Frequency S0 Mode in Plates with Quadratic Nonlinearity. Materials. 2018; 11(11):2096. https://doi.org/10.3390/ma11112096
Chicago/Turabian StyleDing, Xiangyan, Youxuan Zhao, Ning Hu, Yaolu Liu, Jun Zhang, and Mingxi Deng. 2018. "Experimental and Numerical Study of Nonlinear Lamb Waves of a Low-Frequency S0 Mode in Plates with Quadratic Nonlinearity" Materials 11, no. 11: 2096. https://doi.org/10.3390/ma11112096
APA StyleDing, X., Zhao, Y., Hu, N., Liu, Y., Zhang, J., & Deng, M. (2018). Experimental and Numerical Study of Nonlinear Lamb Waves of a Low-Frequency S0 Mode in Plates with Quadratic Nonlinearity. Materials, 11(11), 2096. https://doi.org/10.3390/ma11112096






