Strain Conditions for the Inverse Heusler Type Fully Compensated Spin-Gapless Semiconductor Ti2MnAl: A First-Principles Study
Abstract
:1. Introduction
2. Computational Details
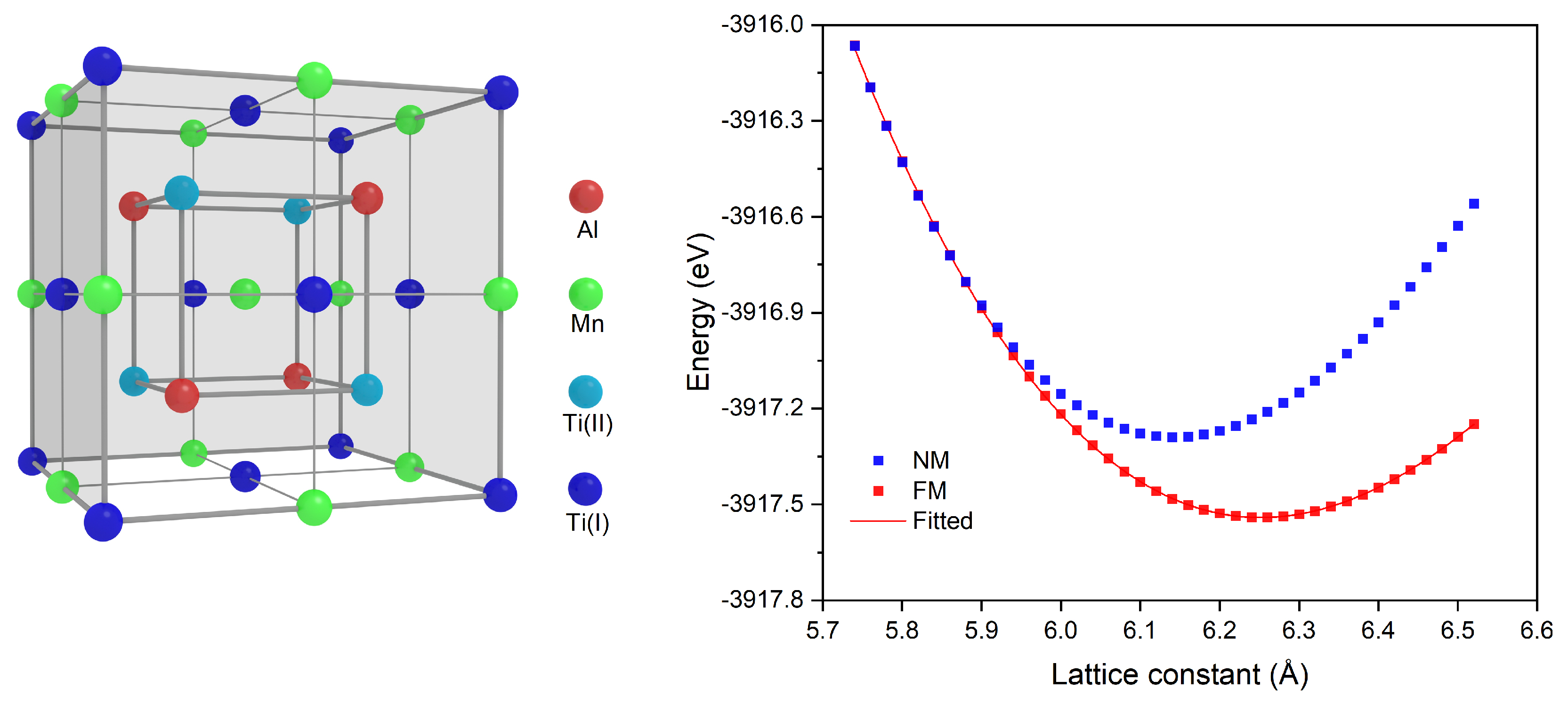
2.1. Crystal Structure and Equilibrium Lattice
2.2. Electronic and Magnetic Properties
2.3. Mechanical Properties
2.4. Thermodynamic Properties
3. Results and Discussion
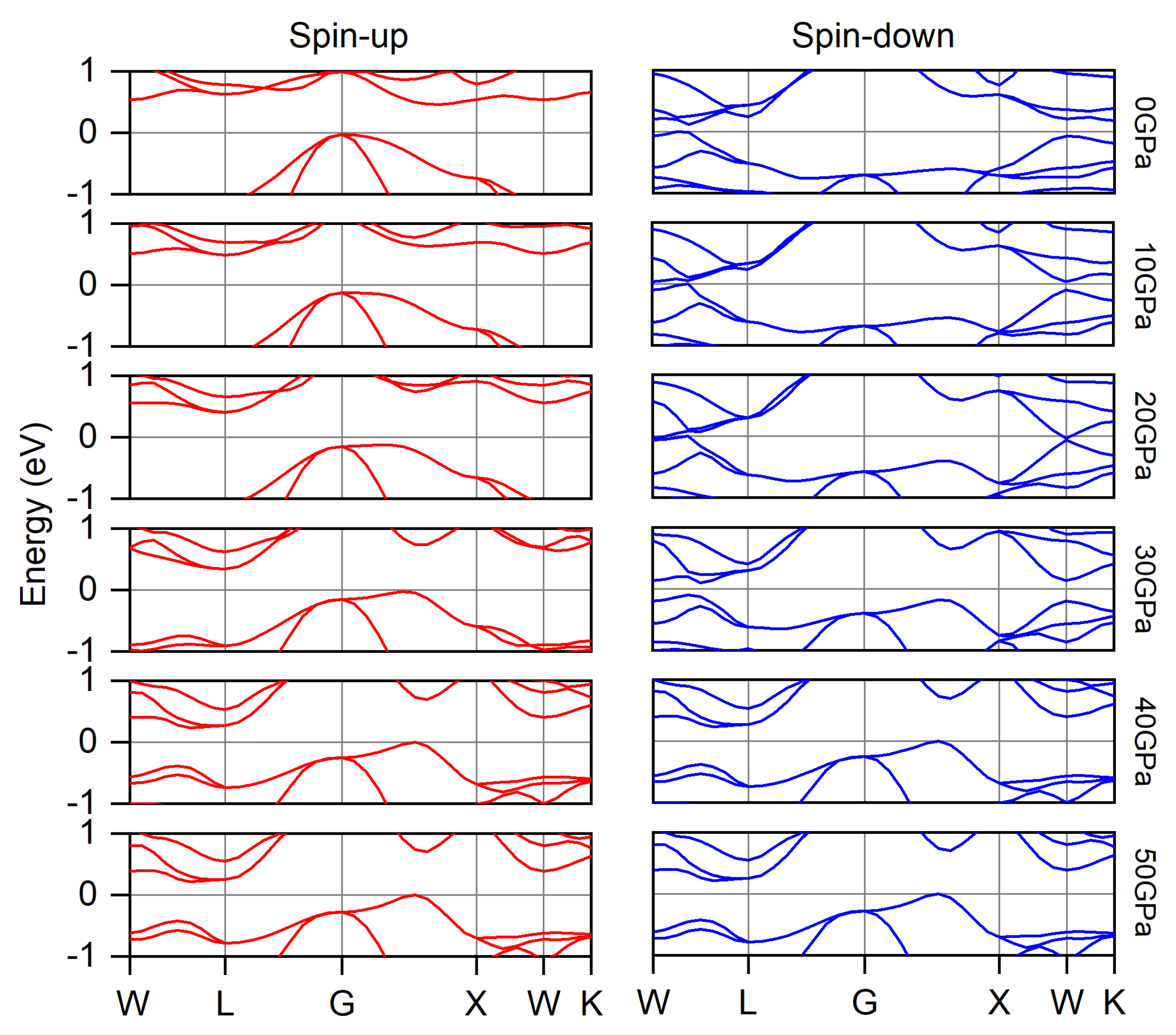
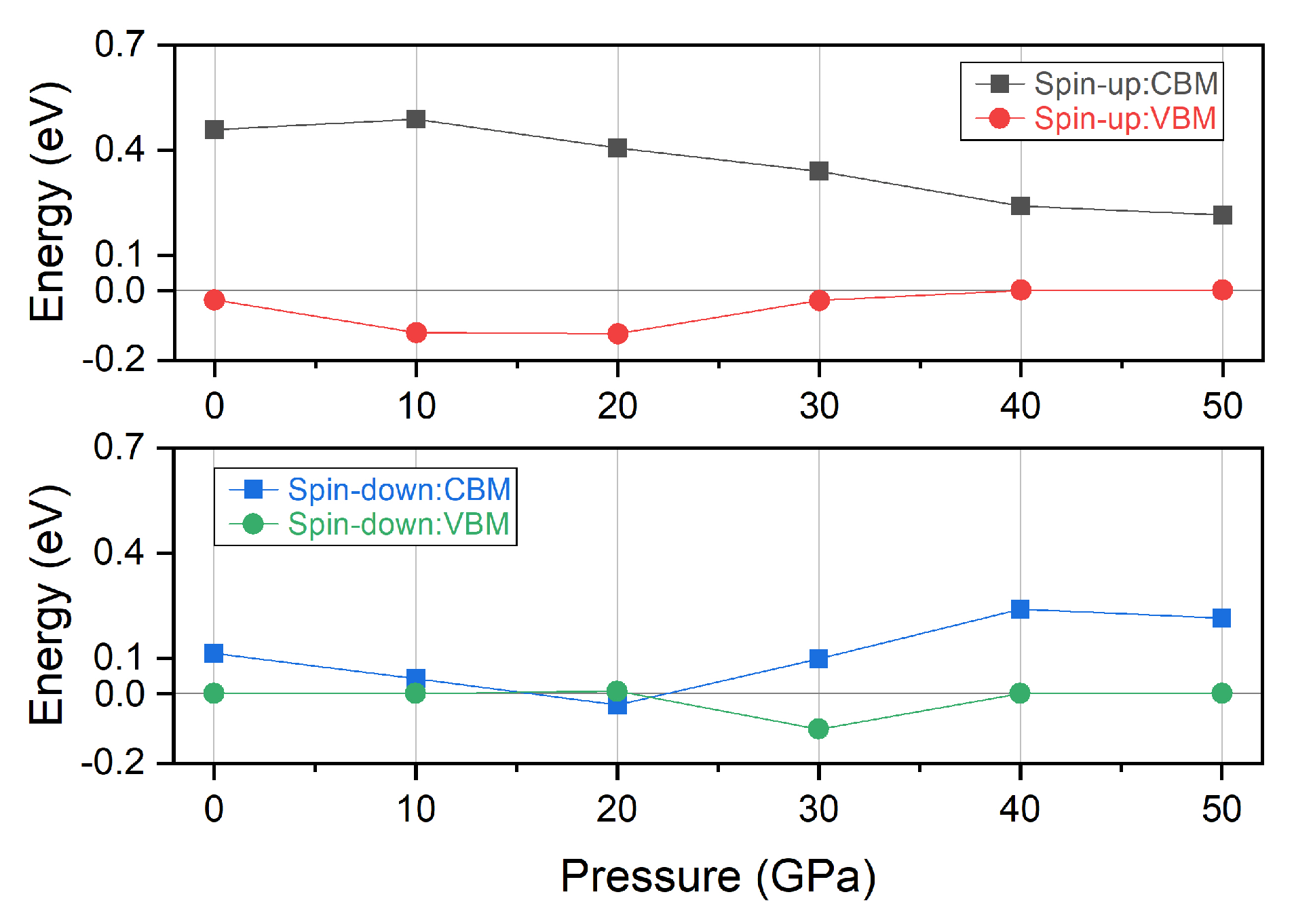
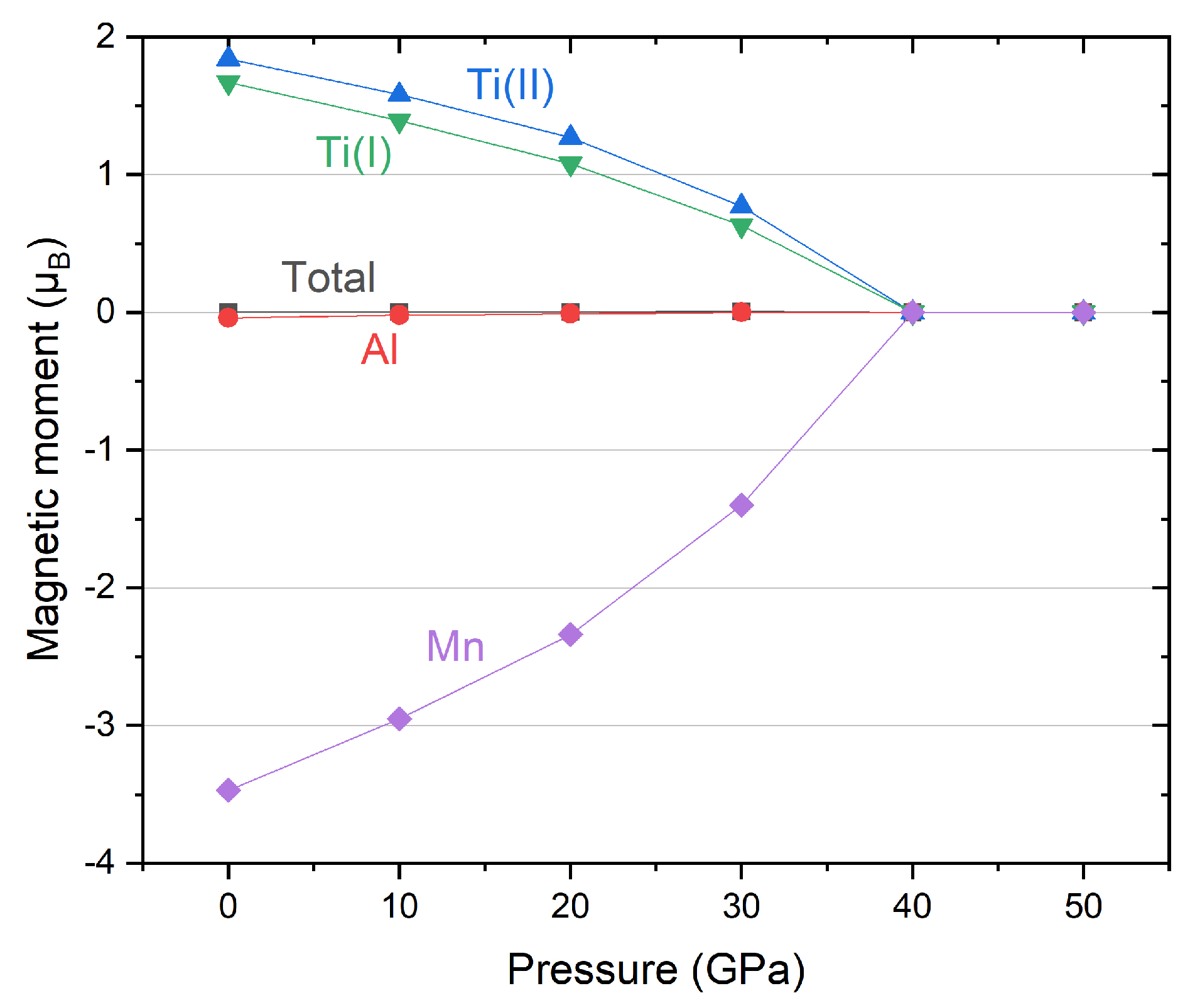
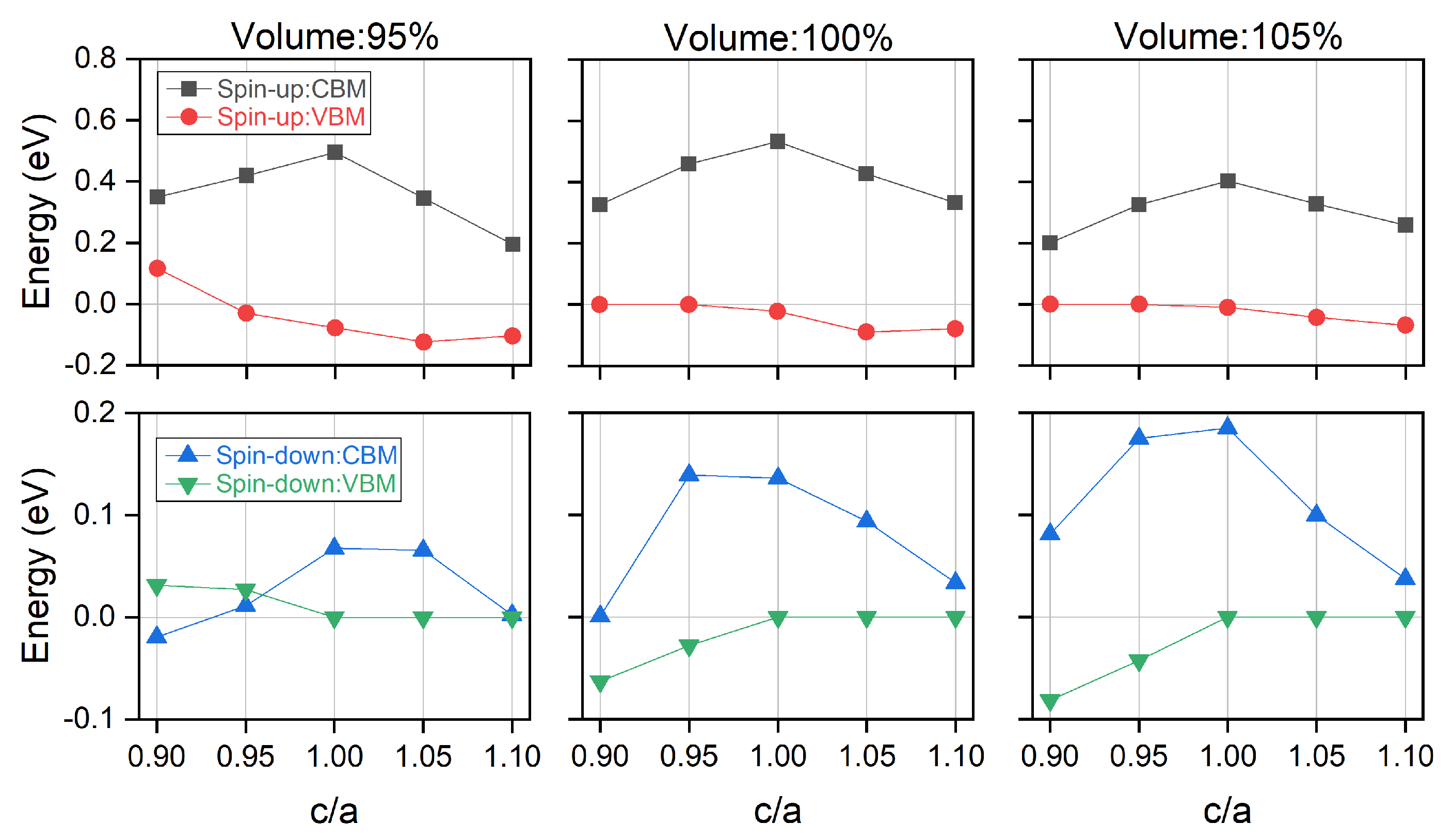
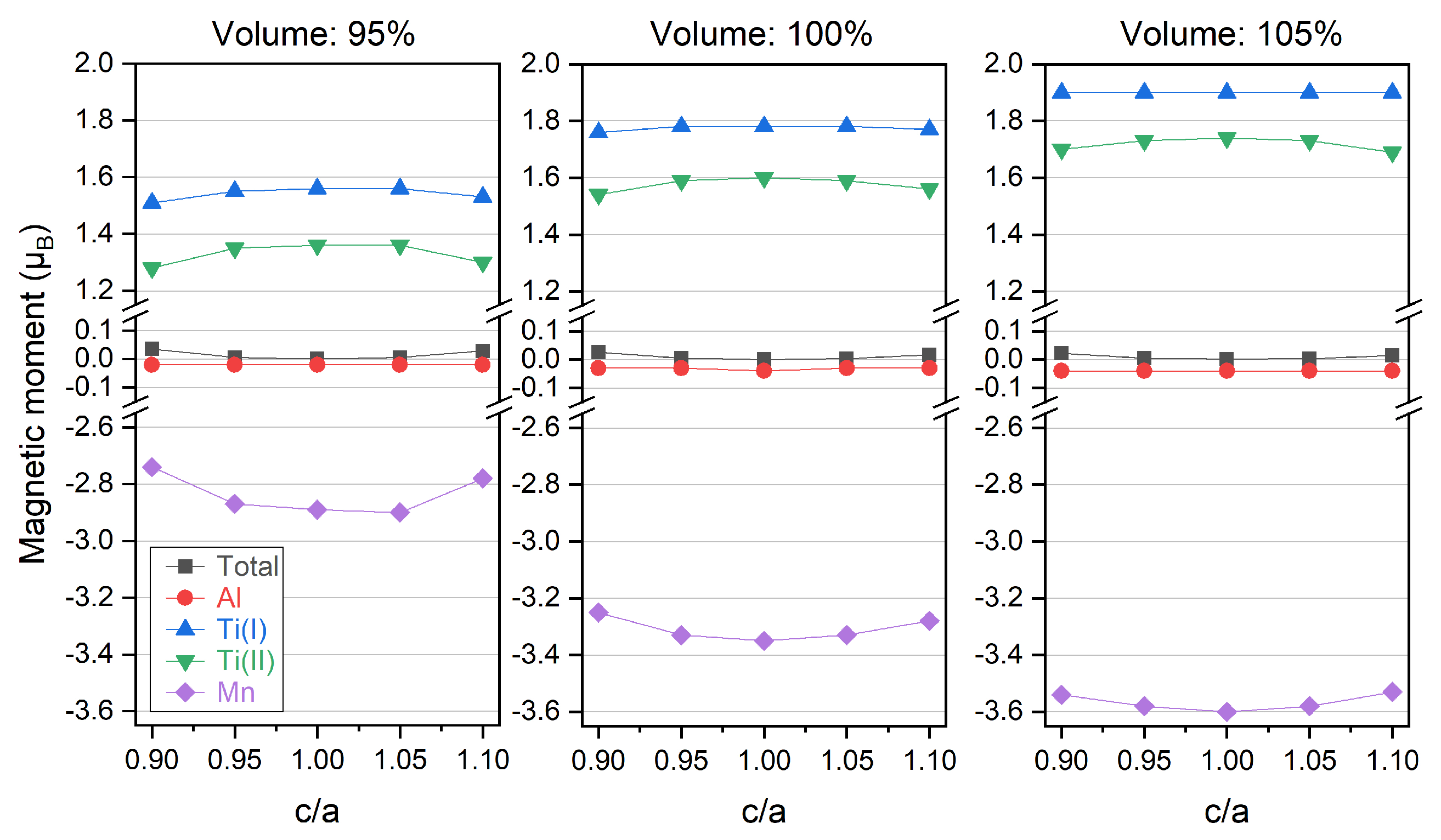
3.1. Electronic, Magnetic and Spin-Gapless Behaviors
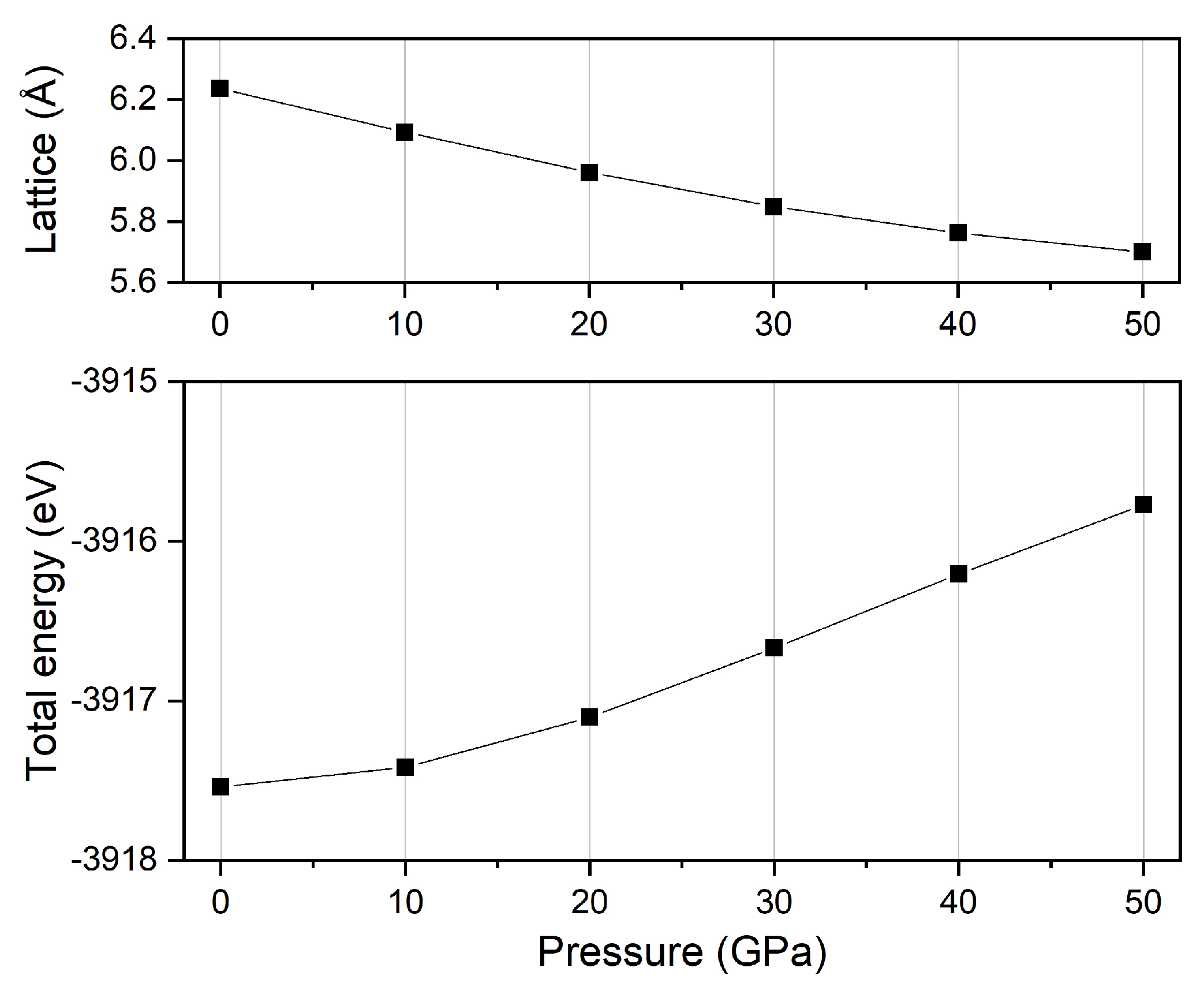
3.2. Mechanic Property and Dynamic Stability
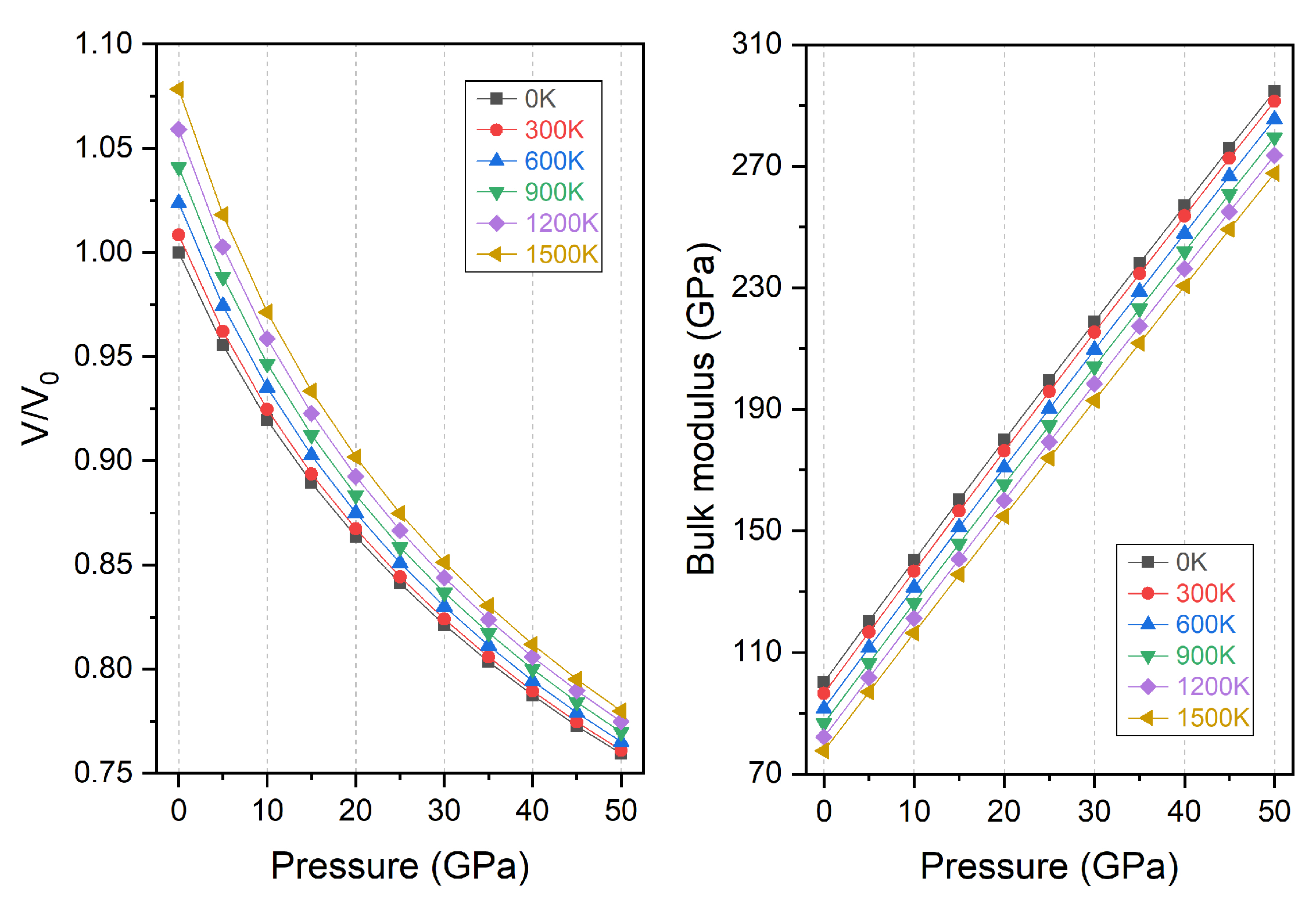
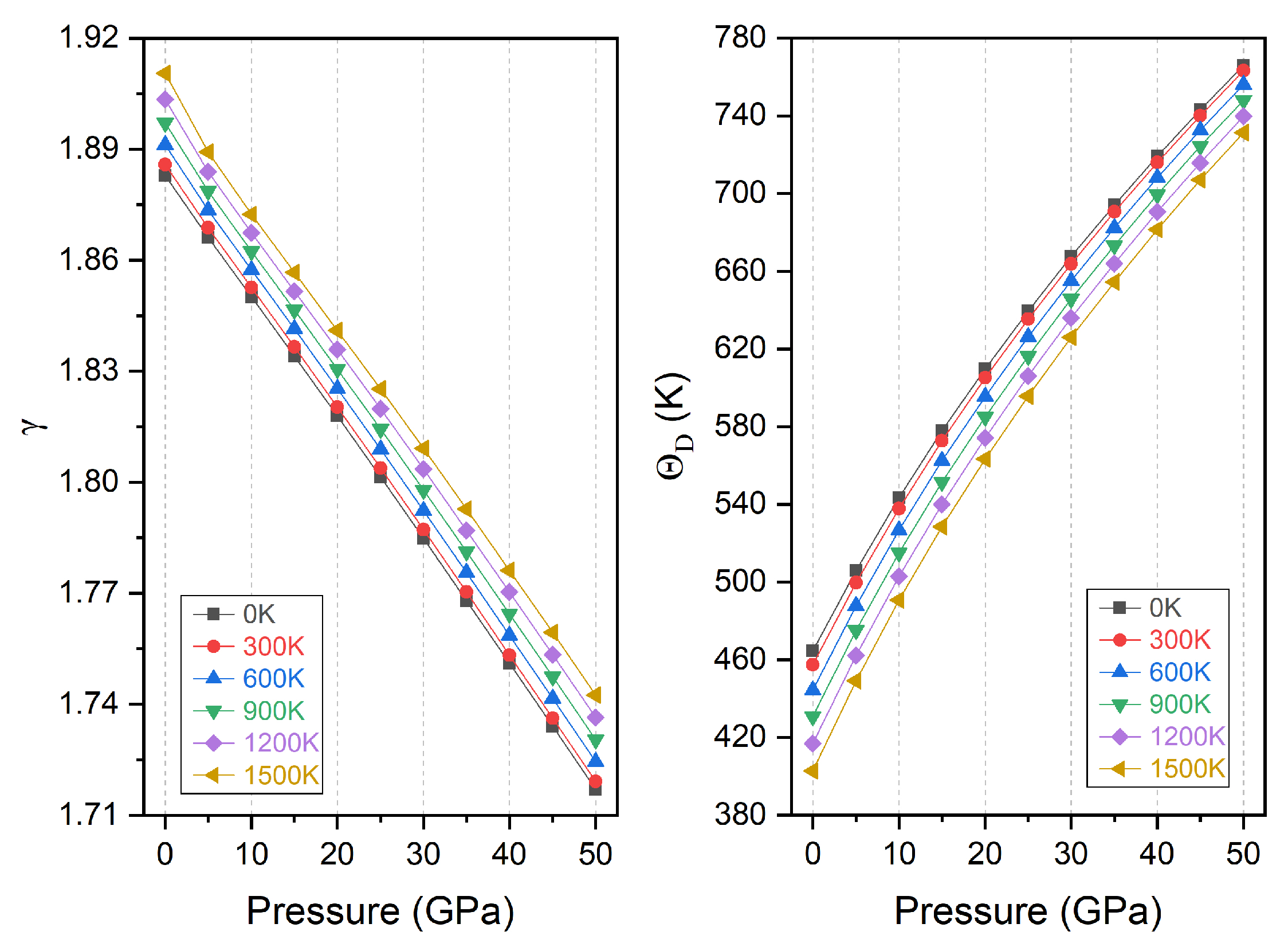
3.3. Thermodynamic Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Žutić, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef] [Green Version]
- de Groot, R.A.; Mueller, F.M.; Van Engen, P.G.; Buschow, K.H.J. New Class of Materials: Half-Metallic Ferromagnets. Phys. Rev. Lett. 1983, 50, 2024–2027. [Google Scholar] [CrossRef] [Green Version]
- van Leuken, H.; de Groot, R.A. Half-Metallic Antiferromagnets. Phys. Rev. Lett. 1995, 74, 1171–1173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, G.Y.; Hu, L.; Yao, K.L.; Luo, B.; Liu, N. Large half-metallic gaps in the quaternary Heusler alloys CoFeCrZ (Z=Al, Si, Ga, Ge): A first-principles study. J. Alloys Compd. 2013, 551, 539–543. [Google Scholar] [CrossRef]
- Han, Y.; Wu, Y.; Li, T.; Khenata, R.; Yang, T.; Wang, X. Electronic, Magnetic, Half-Metallic, and Mechanical Properties of a New Equiatomic Quaternary Heusler Compound YRhTiGe: A First-Principles Study. Materials 2018, 11, 797. [Google Scholar] [CrossRef] [PubMed]
- Alijani, V.; Ouardi, S.; Fecher, G.H.; Winterlik, J.; Naghavi, S.S.; Kozina, X.; Stryganyuk, G.; Felser, C.; Ikenaga, E.; Yamashita, Y.; Ueda, S.; Kobayashi, K. Electronic, structural, and magnetic properties of the half-metallic ferromagnetic quaternary Heusler compounds CoFeMnZ (Z = Al, Ga, Si, Ge). Phys. Rev. B 2011, 84, 224416. [Google Scholar] [CrossRef]
- Bainsla, L.; Suresh, K.G. Equiatomic quaternary Heusler alloys: A material perspective for spintronic applications. Appl. Phys. Rev. 2016, 3, 031101. [Google Scholar] [CrossRef] [Green Version]
- Bainsla, L.; Mallick, A.I.; Coelho, A.A.; Nigam, A.K.; Varaprasad, B.S.D.C.S.; Takahashi, Y.K.; Alam, A.; Suresh, K.G.; Hono, K. High spin polarization and spin splitting in equiatomic quaternary CoFeCrAl Heusler alloy. J. Magn. Magn. Mater. 2015, 394, 82–86. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Chen, X.; Zhou, T.; Yuan, H.; Chen, H. Structural stability, half-metallicity and magnetism of the CoFeMnSi/GaAs(001) interface. Appl. Surf. Sci. 2015, 346, 1–10. [Google Scholar] [CrossRef]
- Bainsla, L.; Mallick, A.I.; Raja, M.M.; Nigam, A.K.; Varaprasad, B.S.D.C.S.; Takahashi, Y.K.; Alam, A.; Suresh, K.G.; Hono, K. Spin gapless semiconducting behavior in equiatomic quaternary CoFeMnSi Heusler alloy. Phys. Rev. B 2015, 91, 104408. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Khachai, H.; Khenata, R.; Yuan, H.; Wang, L.; Wang, W.; Bouhemadou, A.; Hao, L.; Dai, X.; Guo, R.; Liu, G.; Cheng, Z. Structural, electronic, magnetic, half-metallic, mechanical, and thermodynamic properties of the quaternary Heusler compound FeCrRuSi: A first-principles study. Sci. Rep. 2017, 7, 16183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.L. Proposal for a New Class of Materials: Spin Gapless Semiconductors. Phys. Rev. Lett. 2008, 100, 156404. [Google Scholar] [CrossRef] [PubMed]
- Lukashev, P.; Kharel, P.; Gilbert, S.; Staten, B.; Hurley, N.; Fuglsby, R.; Huh, Y.; Valloppilly, S.; Zhang, W.; Yang, K.; et al. Investigation of spin-gapless semiconductivity and half-metallicity in Ti2MnAl-based compounds. Appl. Phys. Lett. 2016, 108, 141901. [Google Scholar] [CrossRef]
- Skaftouros, S.; Özdoğan, K.; Şaşıoğlu, E.; Galanakis, I. Search for spin gapless semiconductors: The case of inverse Heusler compounds. Appl. Phys. Lett. 2013, 102, 022402. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Jin, Y. A spin-gapless semiconductor of inverse Heusler Ti2CrSi alloy: First-principles prediction. J. Magn. Magn. Mater. 2015, 385, 55–59. [Google Scholar] [CrossRef]
- Xu, G.Z.; Liu, E.K.; Du, Y.; Li, G.J.; Liu, G.D.; Wang, W.H.; Wu, G.H. A new spin gapless semiconductors family: Quaternary Heusler compounds. EPL (Europhys. Lett.) 2013, 102, 17007. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.T.; Cheng, Z.X.; Wang, J.L.; Rozale, H.; Wang, L.Y.; Yu, Z.Y.; Yang, J.T.; Liu, G.D. Strain-induced diverse transitions in physical nature in the newly designed inverse Heusler alloy Zr2MnAl. J. Alloys Compd. 2016, 686, 549–555. [Google Scholar] [CrossRef]
- Zheng, N.; Jin, Y. Band-gap and Slater–Pauling rule in half-metallic Ti2-based Heusler alloys: A first-principles study. J. Magn. Magn. Mater. 2012, 324, 3099–3104. [Google Scholar] [CrossRef]
- Faleev, S.V.; Ferrante, Y.; Jeong, J.; Samant, M.G.; Jones, B.; Parkin, S.S.P. Unified explanation of chemical ordering, the Slater-Pauling rule, and half-metallicity in full Heusler compounds. Phys. Rev. B 2017, 95, 045140. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.H.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef]
- Skaftouros, S.; Özdoğan, K.; Şaşıoğlu, E.; Galanakis, I. Generalized Slater-Pauling rule for the inverse Heusler compounds. Phys. Rev. B 2013, 87, 024420. [Google Scholar] [CrossRef]
- Fang, Q.L.; Zhao, X.M.; Zhang, J.M.; Xu, K.W. Magnetic properties and half-metallic in bulk and (001) surface of Ti2MnAl Heusler alloy with Hg2CuTi-type structure. Thin Solid Films 2014, 558, 241–246. [Google Scholar] [CrossRef]
- Jakobsson, A.; Mavropoulos, P.; Şaşıoğlu, E.; Blügel, S.; Ležaić, M.; Sanyal, B.; Galanakis, I. First-principles calculations of exchange interactions, spin waves, and temperature dependence of magnetization in inverse-Heusler-based spin gapless semiconductors. Phys. Rev. B 2015, 91, 174439. [Google Scholar] [CrossRef]
- Feng, W.; Fu, X.; Wan, C.; Yuan, Z.; Han, X.; Quang, N.V.; Cho, S. Spin gapless semiconductor like Ti2MnAl film as a new candidate for spintronics application. Phys. Status Solidi (RRL)—Rapid Res. Lett. 2015, 9, 641–645. [Google Scholar] [CrossRef]
- Singh, M.; Kashyap, M.K.; Saini, H.S. Corroborating the Spin Gapless Character of Ti2Mnal Inverse Heusler Alloy: A study of Strains Effect. Mater. Today Proc. 2018, 5, 15421–15425. [Google Scholar] [CrossRef]
- Han, J.; Gao, G. Large tunnel magnetoresistance and temperature-driven spin filtering effect based on the compensated ferrimagnetic spin gapless semiconductor Ti2MnAl. Appl. Phys. Lett. 2018, 113, 102402. [Google Scholar] [CrossRef]
- Shi, W.; Muechler, L.; Manna, K.; Zhang, Y.; Koepernik, K.; Car, R.; van den Brink, J.; Felser, C.; Sun, Y. Prediction of a magnetic Weyl semimetal without spin-orbit coupling and strong anomalous Hall effect in the Heusler compensated ferrimagnet Ti2MnAl. Phys. Rev. B 2018, 97, 060406. [Google Scholar] [CrossRef]
- Noky, J.; Gayles, J.; Felser, C.; Sun, Y. Strong anomalous Nernst effect in collinear magnetic Weyl semimetals without net magnetic moments. Phys. Rev. B 2018, 97, 220405. [Google Scholar] [CrossRef] [Green Version]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
- Segall, M.D.; Philip, J.D.L.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.P.; Zhang, Y.L.; Sun, X.W.; Song, T.; Guo, P. The electronic and magnetic properties of defects on half-metallic Ti2NiIn alloy. J. Solid State Chem. 2016, 233, 221–228. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, J.; Yip, S.; Phillpot, S.; Wolf, D. Mechanical instabilities of homogeneous crystals. Phys. Rev. B 1995, 52, 12627–12635. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Cherid, S.; Benstaali, W.; Abbad, A.; Bentata, S.; Lantri, T.; Abbar, B. Theoretical prediction of half metallic ferromagnetic full-Heusler alloys Cs2CrGe. Solid State Commun. 2017, 260, 14–18. [Google Scholar] [CrossRef]
- Blanco, M.A.; Francisco, E.; Luaña, V. GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model. Comput. Phys. Commun. 2004, 158, 57–72. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Abbasi-Pérez, D.; Luaña, V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Otero-de-la Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Jia, H.Y.; Dai, X.F.; Wang, L.Y.; Liu, R.; Wang, X.T.; Li, P.P.; Cui, Y.T.; Liu, G.D. Ti2MnZ (Z=Al, Ga, In) compounds: Nearly spin gapless semiconductors. AIP Adv. 2014, 4, 047113. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.P.; Deng, J.B.; Mao, G.Y.; Chu, S.B.; Hu, X.R. Half-metallic properties for the Ti2YZ (Y = Fe, Co, Ni, Z = Al, Ga, In) Heusler alloys: A first-principles study. Intermetallics 2012, 29, 86–91. [Google Scholar] [CrossRef]
- Galanakis, I.; Özdoğan, K.; Şaşıoğlu, E.; Aktaş, B. Doping of Mn2VAl and Mn2VSi Heusler alloys as a route to half-metallic antiferromagnetism. Phys. Rev. B 2007, 75, 092407. [Google Scholar] [CrossRef]
- Yip, S.; Li, J.; Tang, M.; Wang, J. Mechanistic aspects and atomic-level consequences of elastic instabilities in homogeneous crystals. Mater. Sci. Eng. A 2001, 317, 236–240. [Google Scholar] [CrossRef] [Green Version]
- Sin’ko, G.V.; Smirnov, N.A. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure. J. Phys. Condens. Matter 2002, 14, 6989. [Google Scholar]

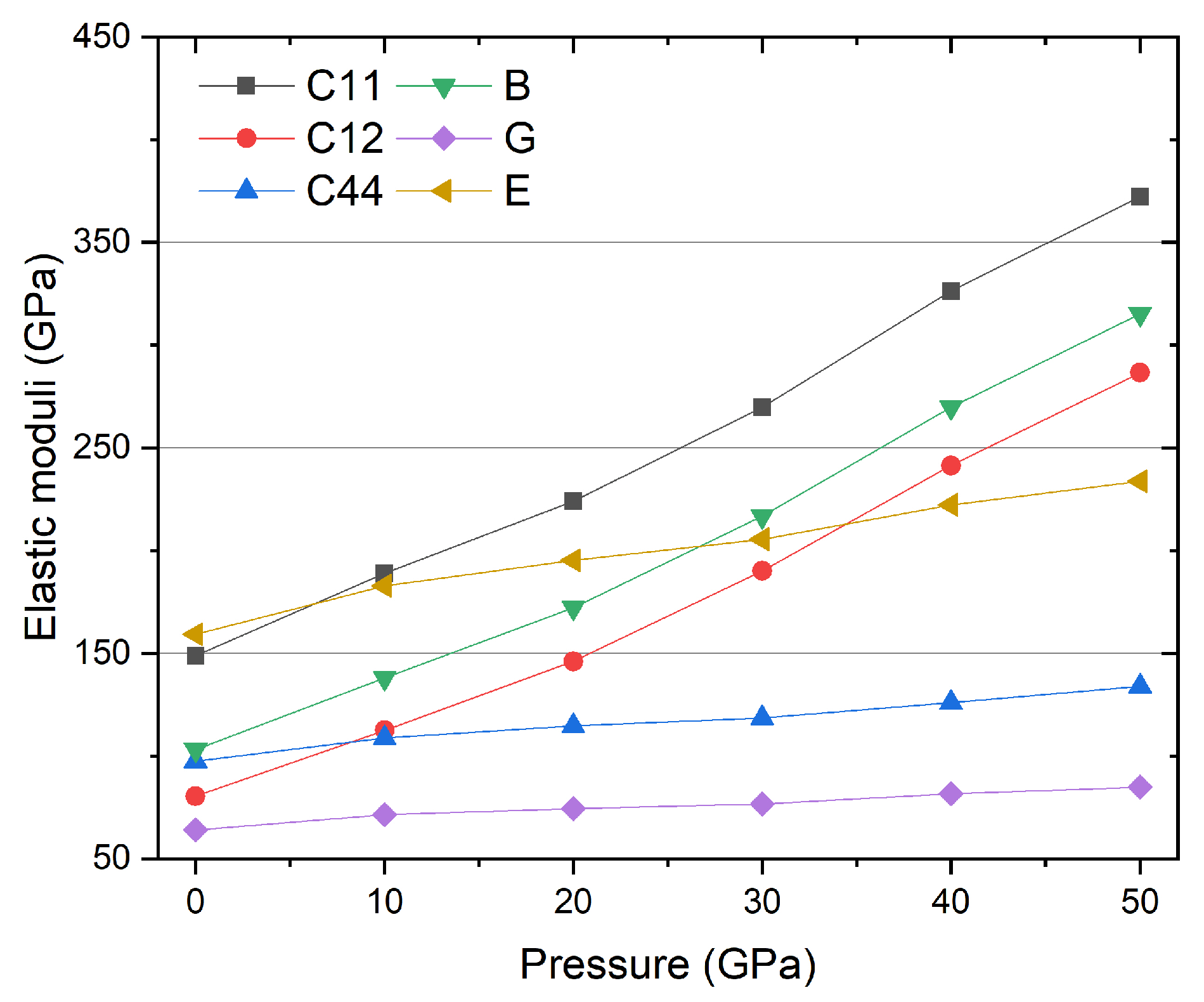


| P | C11 | C12 | C44 | B | G | E | B/G |
|---|---|---|---|---|---|---|---|
| (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | |
| 0 | 148.79 | 80.46 | 97.49 | 103.23 | 64.07 | 159.27 | 1.61 |
| 10 | 188.84 | 112.49 | 108.70 | 137.94 | 71.50 | 182.90 | 1.93 |
| 20 | 224.07 | 146.10 | 114.62 | 172.09 | 74.45 | 195.21 | 2.31 |
| 30 | 269.74 | 190.16 | 118.48 | 216.69 | 76.57 | 205.51 | 2.83 |
| 40 | 326.34 | 241.45 | 126.10 | 269.75 | 81.57 | 222.31 | 3.31 |
| 50 | 372.21 | 286.61 | 133.91 | 315.14 | 84.90 | 233.71 | 3.71 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Hao, L.; Khenata, R.; Wang, X. Strain Conditions for the Inverse Heusler Type Fully Compensated Spin-Gapless Semiconductor Ti2MnAl: A First-Principles Study. Materials 2018, 11, 2091. https://doi.org/10.3390/ma11112091
Yang T, Hao L, Khenata R, Wang X. Strain Conditions for the Inverse Heusler Type Fully Compensated Spin-Gapless Semiconductor Ti2MnAl: A First-Principles Study. Materials. 2018; 11(11):2091. https://doi.org/10.3390/ma11112091
Chicago/Turabian StyleYang, Tie, Liyu Hao, Rabah Khenata, and Xiaotian Wang. 2018. "Strain Conditions for the Inverse Heusler Type Fully Compensated Spin-Gapless Semiconductor Ti2MnAl: A First-Principles Study" Materials 11, no. 11: 2091. https://doi.org/10.3390/ma11112091
APA StyleYang, T., Hao, L., Khenata, R., & Wang, X. (2018). Strain Conditions for the Inverse Heusler Type Fully Compensated Spin-Gapless Semiconductor Ti2MnAl: A First-Principles Study. Materials, 11(11), 2091. https://doi.org/10.3390/ma11112091







