Fast Analytic Simulation for Multi-Laser Heating of Sheet Metal in GPU
Abstract
:1. Introduction
2. Literature Review
2.1. Multi-Beam Single Trajectory vs. Multiple-Trajectory Simultaneous Laser Heating
2.2. Thermal Simulation for Sheet Metal Laser Heating
2.3. Conclusions of the Literature Review
3. Methodology
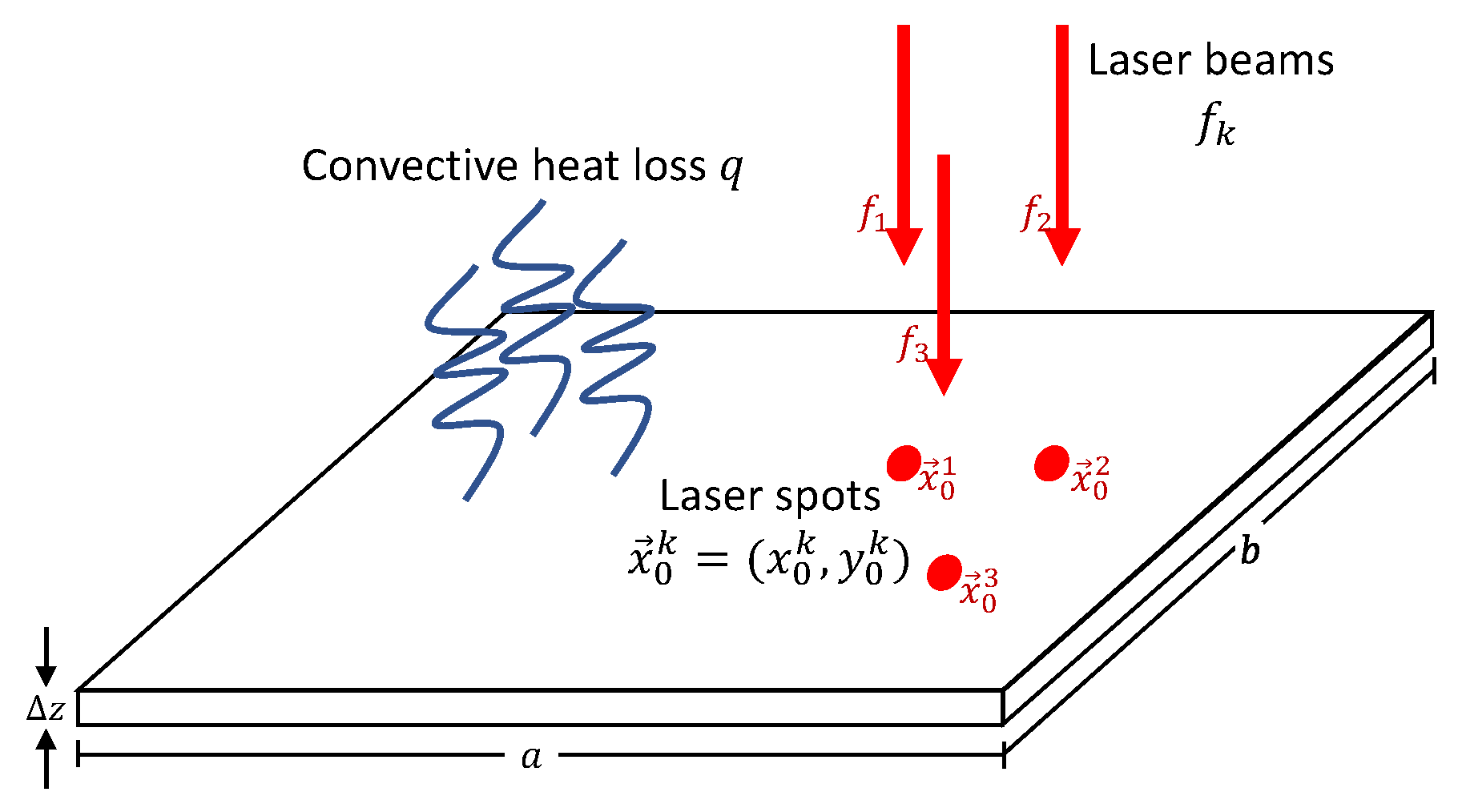
3.1. Heat Transfer Equation for Multi-Beam Laser Heating
3.2. Analytic Solution
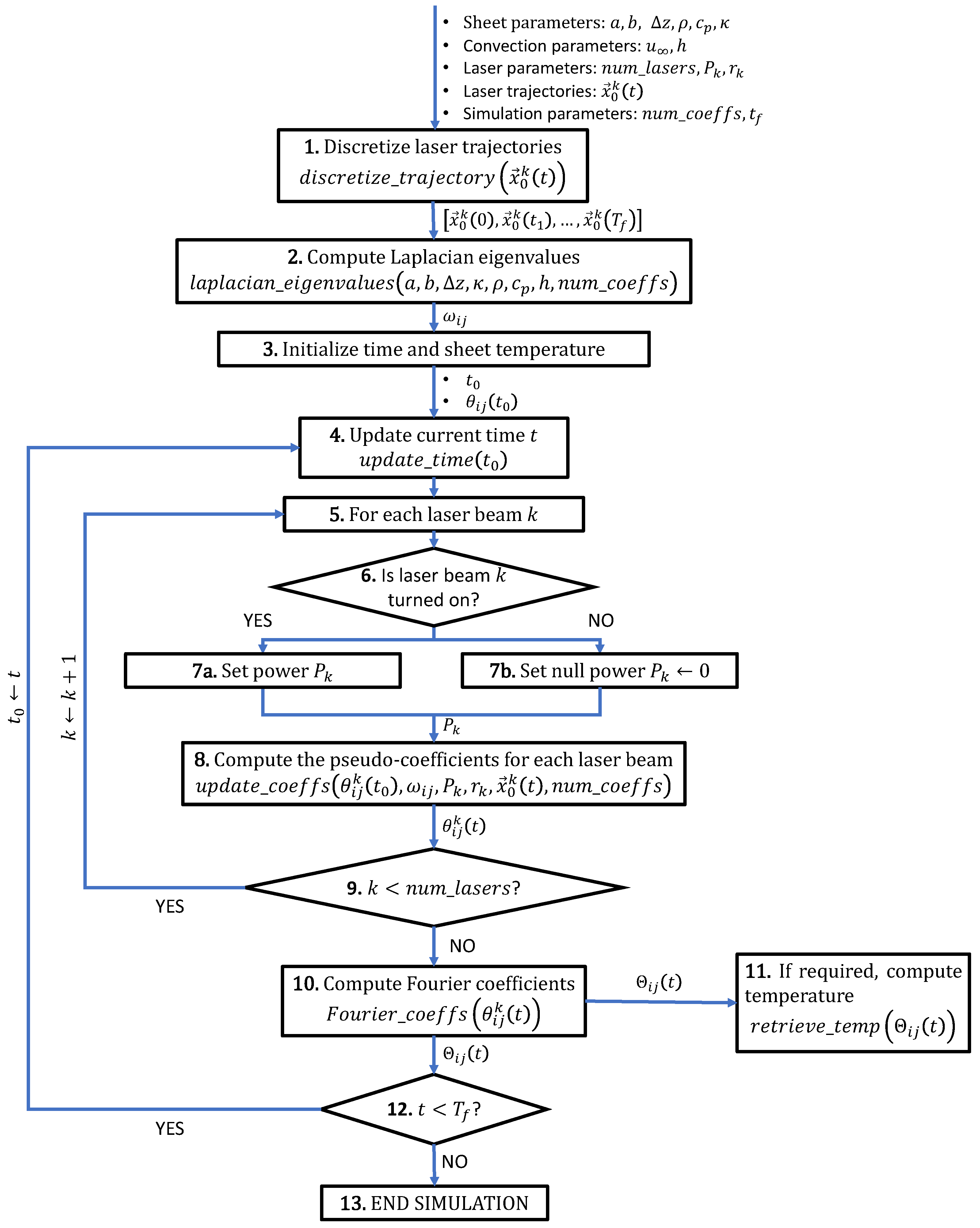
3.3. Algorithm
- Discretize laser trajectories: As discussed in Section 3.2, the laser beam trajectories are discretized as sequences of piecewise linear trajectories , as described in [31]. The only requirement for this discretization is the fact that all laser beam trajectories must share the same time discretization, i.e., are the same for all trajectories .
- Compute the Laplacian eigenvalues: The Laplacian eigenvalues of the sheet are computed as per Equation (8). Since the eigenvalues are time-independent, this step is performed before the simulation loop starts.
- Initialize time and sheet temperature: The simulation time is initialized to . In order to satisfy the initial temperature condition , the pseudo coefficients are initialized as (see Equation (4)).
- Update current time t: The current simulation time is updated according to the previous time , in concordance with the discretization of trajectories from step 1.
- For each laser beam k: This inner loop computes the pseudo-coefficients for each laser beam ().
- Question: Is laser beam k turned on?: This step allows for simulating asynchronous laser beams by asking at the current time t if the laser is turned on/off. Therefore, each laser beam might have its own internal time frame , different from the simulation time frame .
- Set power /Set null power : In the previous step, the program checks the state (on/off) of the current laser beam k. The laser is turned on by the simulation by setting its corresponding power input . In the case of the laser being turned off, the simulation simply sets its power to 0.
- Question: ?: Check if the pseudo-coefficients have been computed for all the laser beams.
- If required, compute temperature: The temperature field is computed on a set of discrete points sampled on the sheet as per Equation (4). The number of coefficients used to compute the solution is truncated to . This step is optional since the result may be stored in the frequency domain (). Therefore, the temperature is made available only when requested by the user, allowing for skipping iterations of no interest and allowing non-monotonic access to the transient temperature history, improving the performance in the process.
- ?: Check if the simulation has reached the final step.
- END SIMULATION
- In step 1 of the previous algorithm, the curved laser beam trajectories are discretized as piecewise linear ones , which inherently produces the time discretization . This time discretization does not affect the numerical accuracy of the temperature solution. Therefore, as opposed to FEA (Finite Element Analysis), the time step size of our algorithm can be arbitrarily large.
- Step 6 allows turning on/off any laser beam at any point of the simulation, allowing complete asynchronicity between the multiple laser beams. In addition, the algorithm allows to change any laser parameters at will, resulting in time-dependent parameters (laser power) and (spot radius). For simplicity, this manuscript uses constant parameters.
- The complete information of the solution is stored in the frequency domain (step 10) and temperature data is computed only when requested. Therefore, the user requests the temperature only at specific times and in specific zones (i.e., at the middle or the end of the simulation). This frequency-based approach has the advantage of providing non-monotonic access to the temperature history, allowing arbitrary simulation time-location requests. Furthermore, since the space discretization does not affect the solution, any sheet sampling can be used to render the temperature (rectangular grid, triangular mesh, a curve or a single point in the sheet).
- In step 10, each pseudo-coefficient is independent from the rest of the pseudo-coefficients (Equation (6)). Similarly, in step 11, the temperature value u at a given point is independent from the temperature on the rest of the sheet (Equation (4)). Therefore, the computation in both of these steps is parallelized.
4. Results
4.1. Comparison with FEA
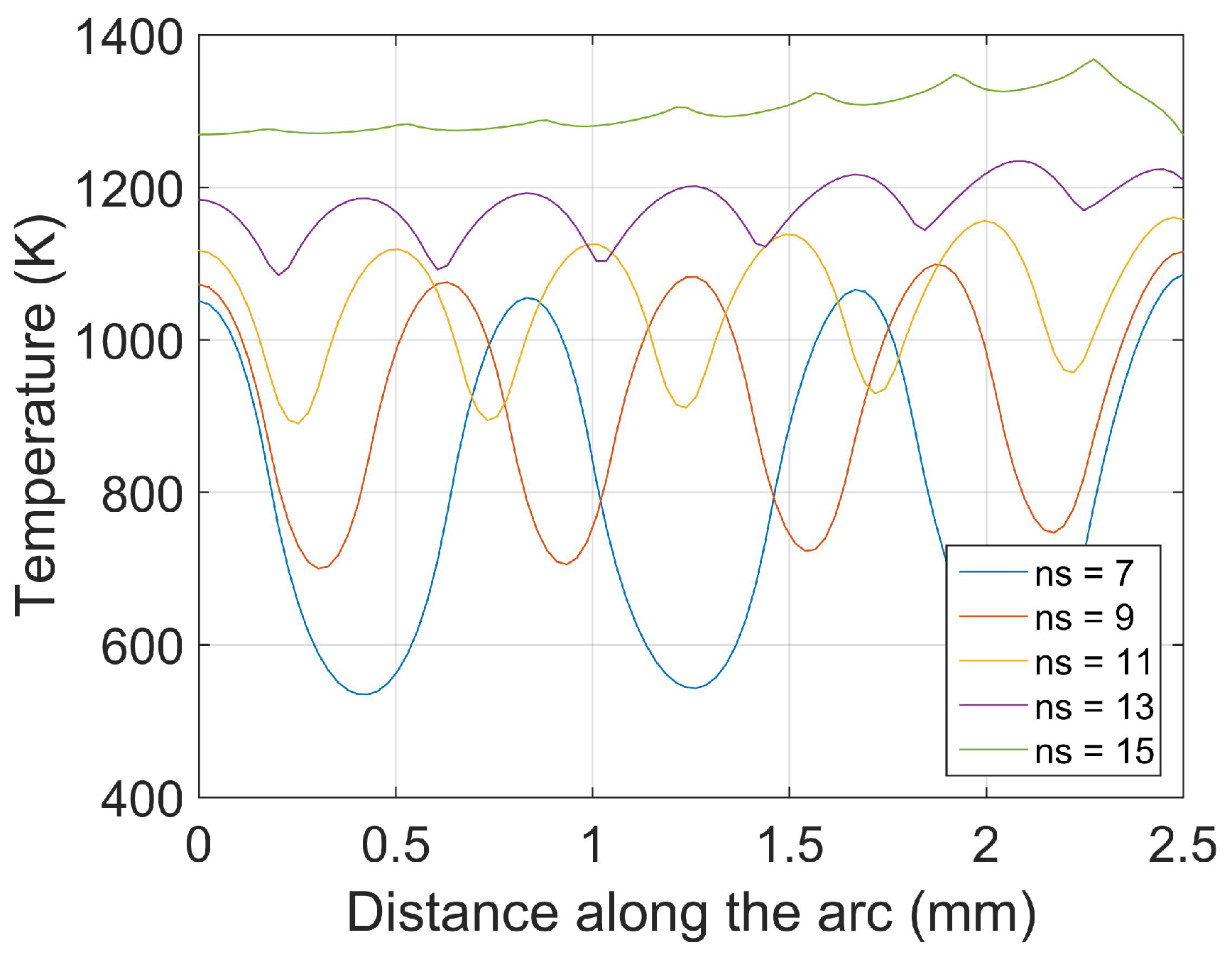
4.2. Multiple Laser Beams
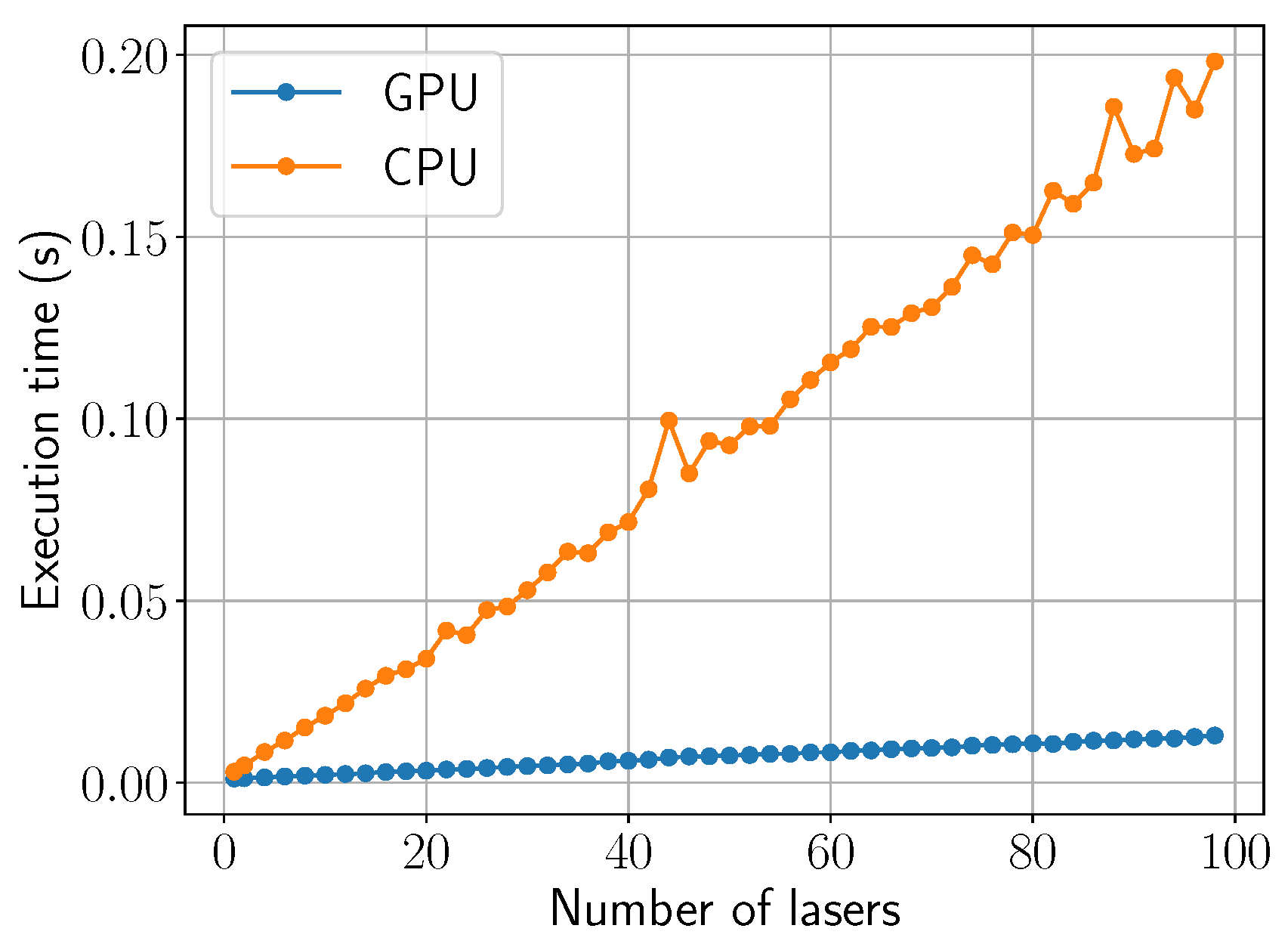
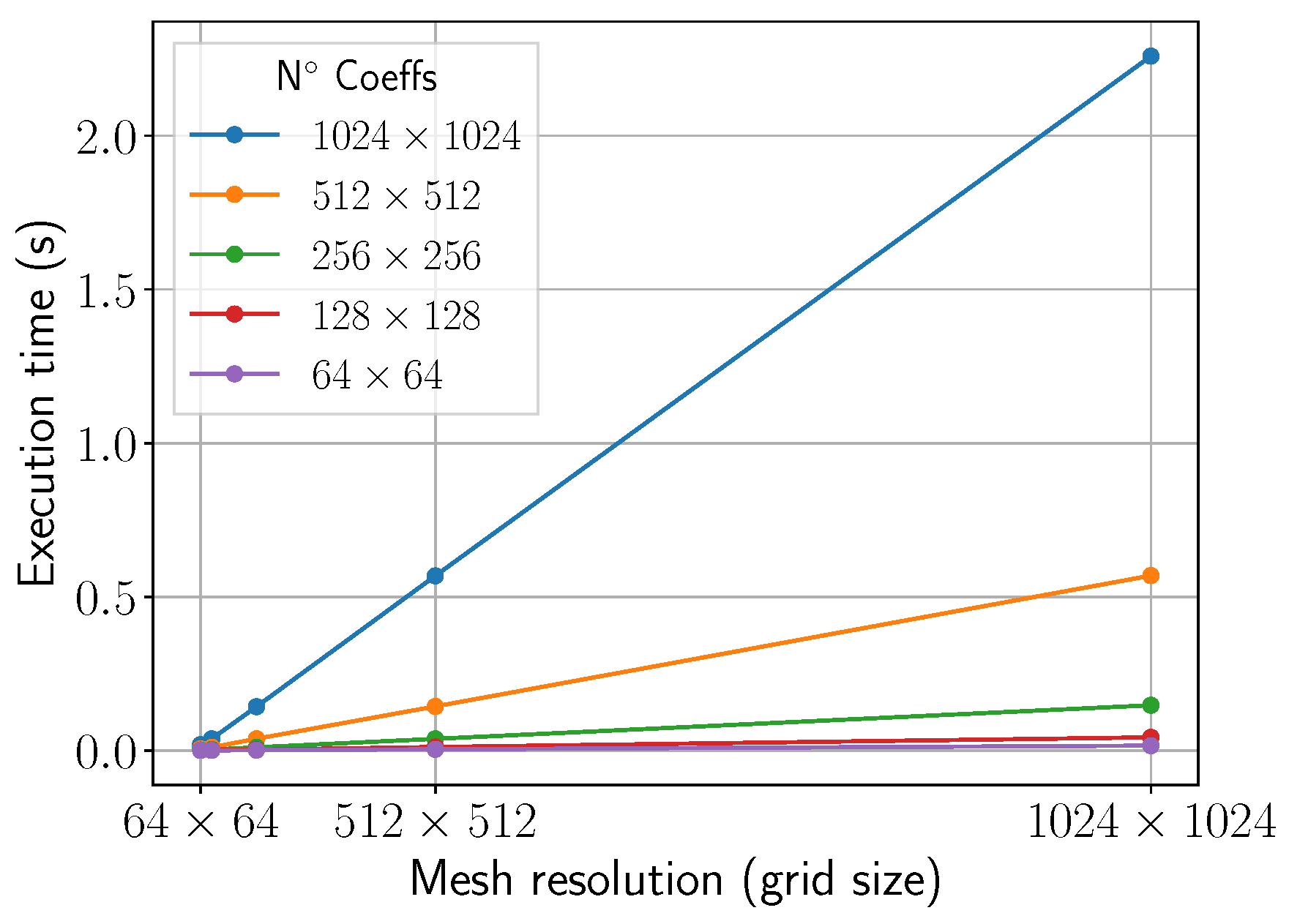
4.3. Performance Assessment
4.4. Integration within an Interactive Laser Cutting Simulation Environment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FEA/FEM | Finite Element Analysis/Finite Element Method. |
| GPU | Graphics Processing Unit. |
| Width, height and thickness of the sheet (m). | |
| Spatial and temporal (s) coordinates for the simulation. | |
| Temperature distribution along the sheet at any given time (K). | |
| Sheet density (kg/m). | |
| Sheet specific heat (J/(kg K)). | |
| Sheet thermal conductivity (W/(m K)). | |
| R | Sheet reflectivity (). |
| Temperature-dependent heat convection on the sheet surface (W/m). | |
| Ambient temperature K. | |
| h | Natural convection coefficient (W/(m K)). |
| Heat input from laser beam k (W/m). . | |
| Power of laser beam k (W). | |
| Radius of laser spot k (m). | |
| Laser spot center for laser beam k at time t. | |
| Simulation time frame in which the laser beam k remains turned on. . | |
| Scan speed of laser beam k (m/s). | |
| Sum of all laser beam heat sources (W/m). | |
| Fourier basis function associated to the x coordinate. . | |
| Fourier basis function associated to the y coordinate. . | |
| Fourier coefficient associated to basis functions and . | |
| Pseudo-Fourier-coefficient associated to the k-th laser beam source. | |
| ij-th eigenvalue of the heat operator (Laplacian) on the rectangular sheet. |
References
- Wiesner, A.; Schwarze, D. Multi-Laser Selective Laser Melting. In Proceedings of the 8th International Conference on Photonic Technologies LANE 2014, Fürth, Germany, 8–11 September 2014; pp. 1–3. [Google Scholar]
- Shuja, S.; Yilbas, B. Laser multi-beam heating of moving steel sheet: Thermal stress analysis. Opt. Lasers Eng. 2013, 51, 446–452. [Google Scholar] [CrossRef]
- Mejia, D.; Moreno, A.; Ruiz-Salguero, O.; Barandiaran, I. Appraisal of open software for finite element simulation of 2D metal sheet laser cut. Int. J. Interact. Des. Manuf. 2017, 11, 547–558. [Google Scholar] [CrossRef]
- Abe, F.; Osakada, K.; Shiomi, M.; Uematsu, K.; Matsumoto, M. The manufacturing of hard tools from metallic powders by selective laser melting. International symposium on advanced forming and die manufacturing technology. J. Mater. Process. Technol. 2001, 111, 210–213. [Google Scholar] [CrossRef]
- Kaakkunen, J.J.J.; Laakso, P.; Kujanpää, V. Adaptive multibeam laser cutting of thin steel sheets with fiber laser using spatial light modulator. J. Laser Appl. 2014, 26, 032008. [Google Scholar] [CrossRef]
- Heeling, T.; Zimmermann, L.; Wegener, K. Multi-Beam Strategies for the Optimization of the Selective Laser Melting Process. In Solid Freeform Fabrication 2016, Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016; The University of Texas Press: Austin, TX, USA, 2016; pp. 1428–1438. [Google Scholar] [CrossRef]
- Olsen, F.O.; Hansen, K.S.; Nielsen, J.S. Multibeam fiber laser cutting. J. Laser Appl. 2009, 21, 133–138. [Google Scholar] [CrossRef]
- Modest, M. Three-dimensional, Transient model for laser machining of ablating/decomposing materials. Int. J. Heat Mass Transf. 1996, 39, 221–234. [Google Scholar] [CrossRef]
- Modest, M. Laser through-cutting and drilling models for ablating/decomposing materials. J. Laser Appl. 1997, 9, 137–145. [Google Scholar] [CrossRef]
- Han, G.; Na, S. A study on torch path planning in laser cutting processes part 1: Calculation of heat flow in contour laser beam cutting. J. Manuf. Syst. 1999, 18, 54–61. [Google Scholar] [CrossRef]
- Xu, W.; Fang, J.; Wang, X.; Wang, T.; Liu, F.; Zhao, Z. A numerical simulation of temperature field in plasma-arc forming of sheet metal. J. Mater. Process. Tech. 2005, 164–165, 1644–1649. [Google Scholar] [CrossRef]
- Kim, M. Transient evaporative laser-cutting with boundary element method. Appl. Math. Model. 2000, 25, 25–39. [Google Scholar] [CrossRef]
- Kim, M. Transient evaporative laser cutting with moving laser by boundary element method. Appl. Math. Model. 2004, 28, 891–910. [Google Scholar] [CrossRef]
- Yilbas, B.S.; Arif, A.F.M.; Abdul Aleem, B.J. Laser cutting of rectangular blanks in thick sheet steel: Effect of cutting speed on thermal stresses. J. Mater. Eng. Perform. 2010, 19, 177–184. [Google Scholar] [CrossRef]
- Akhtar, S. Laser cutting of thick-section circular blanks: Thermal stress prediction and microstructural analysis. Int. J. Adv. Manuf. Technol. 2014, 71, 1345–1358. [Google Scholar] [CrossRef]
- Akhtar, S.; Kardas, O.; Keles, O.; Yilbas, B. Laser cutting of rectangular geometry into aluminum alloy: Effect of cut sizes on thermal stress field. Opt. Laser Eng. 2014, 61, 57–66. [Google Scholar] [CrossRef]
- Yilbas, B.; Akhtar, S.; Karatas, C. Laser cutting of rectangular geometry into alumina tiles. Opt. Laser Eng. 2014, 55, 35–43. [Google Scholar] [CrossRef]
- Yilbas, B.; Akhtar, S.; Keles, O. Laser cutting of triangular blanks from thick aluminum foam plate: Thermal stress analysis and morphology. Appl. Therm. Eng. 2014, 62, 28–36. [Google Scholar] [CrossRef]
- Roberts, I.; Wang, C.; Esterlein, R.; Stanford, M.; Mynors, D. A three-dimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. Int. J. Mach. Tool. Manuf. 2009, 49, 916–923. [Google Scholar] [CrossRef]
- Shi, B.; Attia, H. Integrated process of laser-assisted machining and laser surface heat treatment. J. Manuf. Sci. Eng. 2013, 135. [Google Scholar] [CrossRef]
- Akarapu, R.; Li, B.; Segall, A. A thermal stress and failure model for laser cutting and forming operations. J. Fail. Anal. Prev. 2004, 4, 51–62. [Google Scholar] [CrossRef]
- Nyon, K.; Nyeoh, C.; Mokhtar, M.; Abdul-Rahman, R. Finite element analysis of laser inert gas cutting on Inconel 718. Int. J. Adv. Manuf. Technol. 2012, 60, 995–1007. [Google Scholar] [CrossRef]
- Fu, C.; Sealy, M.; Guo, Y.; Wei, X. Finite element simulation and experimental validation of pulsed laser cutting of nitinol. J. Manuf. Process. 2015, 19, 81–86. [Google Scholar] [CrossRef]
- Yilbas, B.; Akhtar, S.; Keles, O. Laser cutting of aluminum foam: Experimental and model studies. J. Manuf. Sci. Eng. 2013, 135. [Google Scholar] [CrossRef]
- Kheloufi, K.; Hachemi, A.; Benzaoui, A. Numerical simulation of Transient three-dimensional temperature and kerf formation in laser fusion cutting. J. Heat Transf. ASME 2015, 137. [Google Scholar] [CrossRef]
- Yuan, P.; Gu, D. Molten pool behaviour and its physical mechanism during selective laser melting of TiC/AlSi10Mg nanocomposites: Simulation and experiments. J. Phys. D Appl. Phys. 2015, 48, 035303. [Google Scholar] [CrossRef]
- Modest, M.; Abakians, H. Evaporative Cutting of a Semi-infinite Body With a Moving CW laser. J. Heat Transf. ASME 1986, 108, 602–607. [Google Scholar] [CrossRef]
- Zimmer, K. Analytical solution of the laser-induced temperature distribution across internal material interfaces. Int. J. Heat Mass Transf. 2009, 52, 497–503. [Google Scholar] [CrossRef]
- Jiang, H.J.; Dai, H.L. Effect of laser processing on three dimensional thermodynamic analysis for HSLA rectangular steel plates. Int. J. Heat Mass Transf. 2015, 82, 98–108. [Google Scholar] [CrossRef]
- Winczek, J. Analytical solution to Transient temperature field in a half-infinite body caused by moving volumetric heat source. Int. J. Heat Mass Transf. 2010, 53, 5774–5781. [Google Scholar] [CrossRef]
- Mejia, D.; Moreno, A.; Arbelaiz, A.; Posada, J.; Ruiz-Salguero, O.; Chopitea, R. Accelerated thermal simulation for three-dimensional interactive optimization of computer numeric control sheet metal laser cutting. J. Manuf. Sci. Eng. 2017, 140. [Google Scholar] [CrossRef]
- Heeling, T.; Wegener, K. Computational investigation of synchronized multibeam strategies for the selective laser melting process. Phys. Procedia 2016, 83, 899–908. [Google Scholar] [CrossRef]
- Shuja, S.Z.; Yilbas, B.S. Multi-beam laser heating of steel: Temperature and thermal stress analysis. Trans. Can. Soc. Mech. Eng. 2012, 36, 373–381. [Google Scholar] [CrossRef]
- Petzet, V.; Büskens, C.; Pesch, H.J.; Karkhin, V.; Makhutin, M.; Prikhodovsky, A.; Ploshikhin, V. OPTILAS: Numerical Optimization as a Key Tool for the Improvement of Advanced Multi-Beam Laser Welding Techniques. In High Performance Computing in Science and Engineering, Garching 2004; Bode, A., Durst, F., Eds.; Springer: Berlin, Germany, 2005; pp. 153–166. [Google Scholar]
- Yilbas, B.; Akhtar, S. Laser bending of metal sheet and thermal stress analysis. Opt. Laser Technol. 2014, 61, 34–44. [Google Scholar] [CrossRef]
- Moreno, A.; Segura, Á.; Arregui, H.; Posada, J.; Ruíz de Infante, Á.; Canto, N. Geometry and Algebra. In Future Vision and Trends on Shapes, Geometry and Algebra; Springer: London, UK, 2014; pp. 135–149. [Google Scholar]
- Velez, G.; Moreno, A.; Infante, A.R.D.; Chopitea, R. Real-time part detection in a virtually machined sheet metal defined as a set of disjoint regions. Int. J. Comput. Integr. Manuf. 2016, 29, 1089–1104. [Google Scholar] [CrossRef]

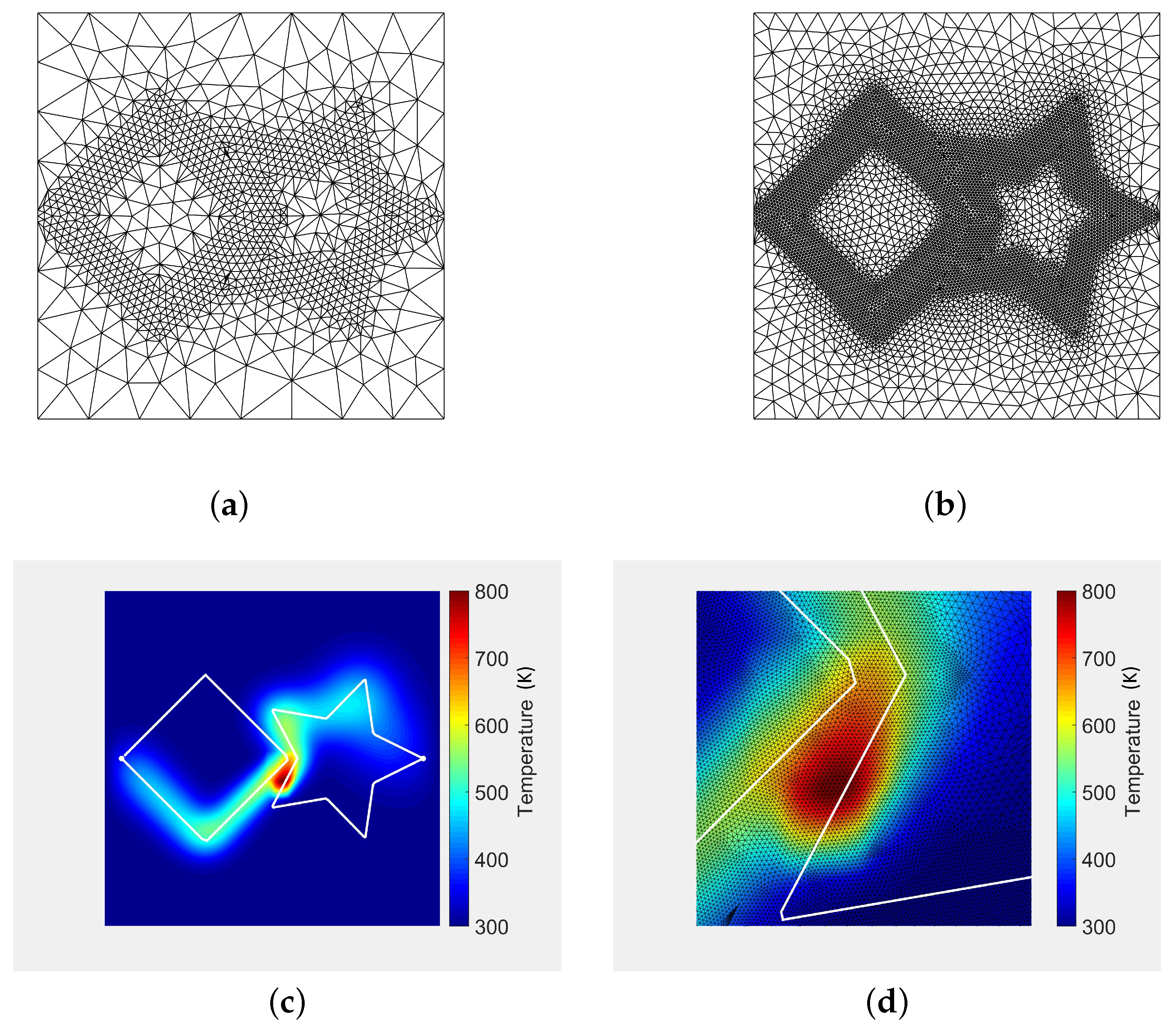
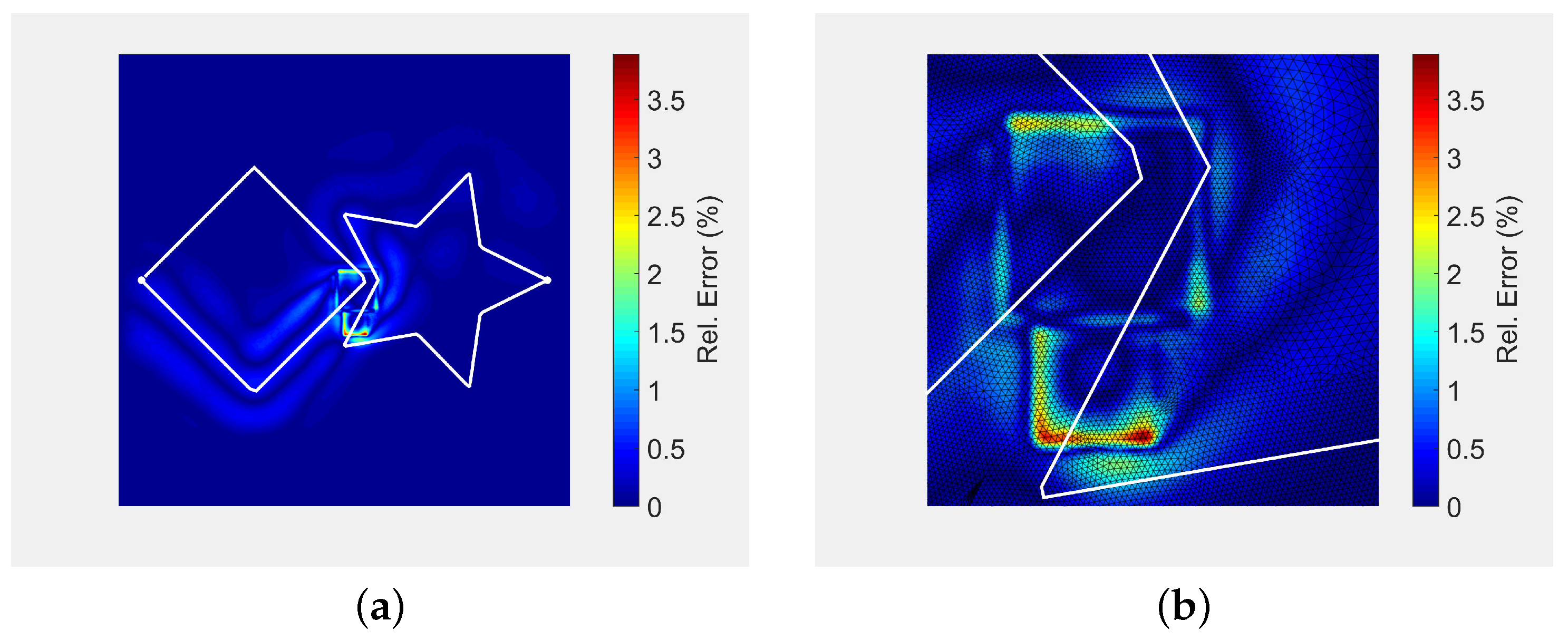



| Parameter | Description | Value |
|---|---|---|
| Geometry | ||
| a | width | 0.01 m |
| b | height | 0.01 m |
| thickness | 0.001 m | |
| Material | AISI 304 Steel | |
| density | 8030 | |
| specific heat | ||
| thermal conductivity | ||
| R | reflectivity | 0 |
| Convection Type | Natural | |
| h | convection coefficient | |
| ambient temperature |
| Parameter | Description | Star Trajectory | Square Trajectory |
|---|---|---|---|
| start time of trajectory | 0.00 s | 0.06 s | |
| end time of trajectory | 0.16 s | 0.13 s | |
| power | 100 W | 200 W | |
| spot radius | 0.0003 m | 0.0005 m | |
| trajectory speed | 0.1 m/s | 0.2 m/s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mejia-Parra, D.; Montoya-Zapata, D.; Arbelaiz, A.; Moreno, A.; Posada, J.; Ruiz-Salguero, O. Fast Analytic Simulation for Multi-Laser Heating of Sheet Metal in GPU. Materials 2018, 11, 2078. https://doi.org/10.3390/ma11112078
Mejia-Parra D, Montoya-Zapata D, Arbelaiz A, Moreno A, Posada J, Ruiz-Salguero O. Fast Analytic Simulation for Multi-Laser Heating of Sheet Metal in GPU. Materials. 2018; 11(11):2078. https://doi.org/10.3390/ma11112078
Chicago/Turabian StyleMejia-Parra, Daniel, Diego Montoya-Zapata, Ander Arbelaiz, Aitor Moreno, Jorge Posada, and Oscar Ruiz-Salguero. 2018. "Fast Analytic Simulation for Multi-Laser Heating of Sheet Metal in GPU" Materials 11, no. 11: 2078. https://doi.org/10.3390/ma11112078
APA StyleMejia-Parra, D., Montoya-Zapata, D., Arbelaiz, A., Moreno, A., Posada, J., & Ruiz-Salguero, O. (2018). Fast Analytic Simulation for Multi-Laser Heating of Sheet Metal in GPU. Materials, 11(11), 2078. https://doi.org/10.3390/ma11112078






