Understanding Graphene Response to Neutral and Charged Lead Species: Theory and Experiment
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis and Characterization of the Epitaxial Graphene
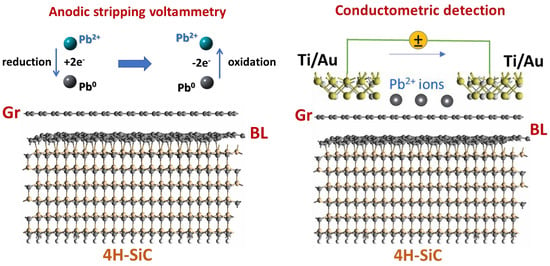
2.2 Electrochemical Measurements
2.3. Conductometric Measurements
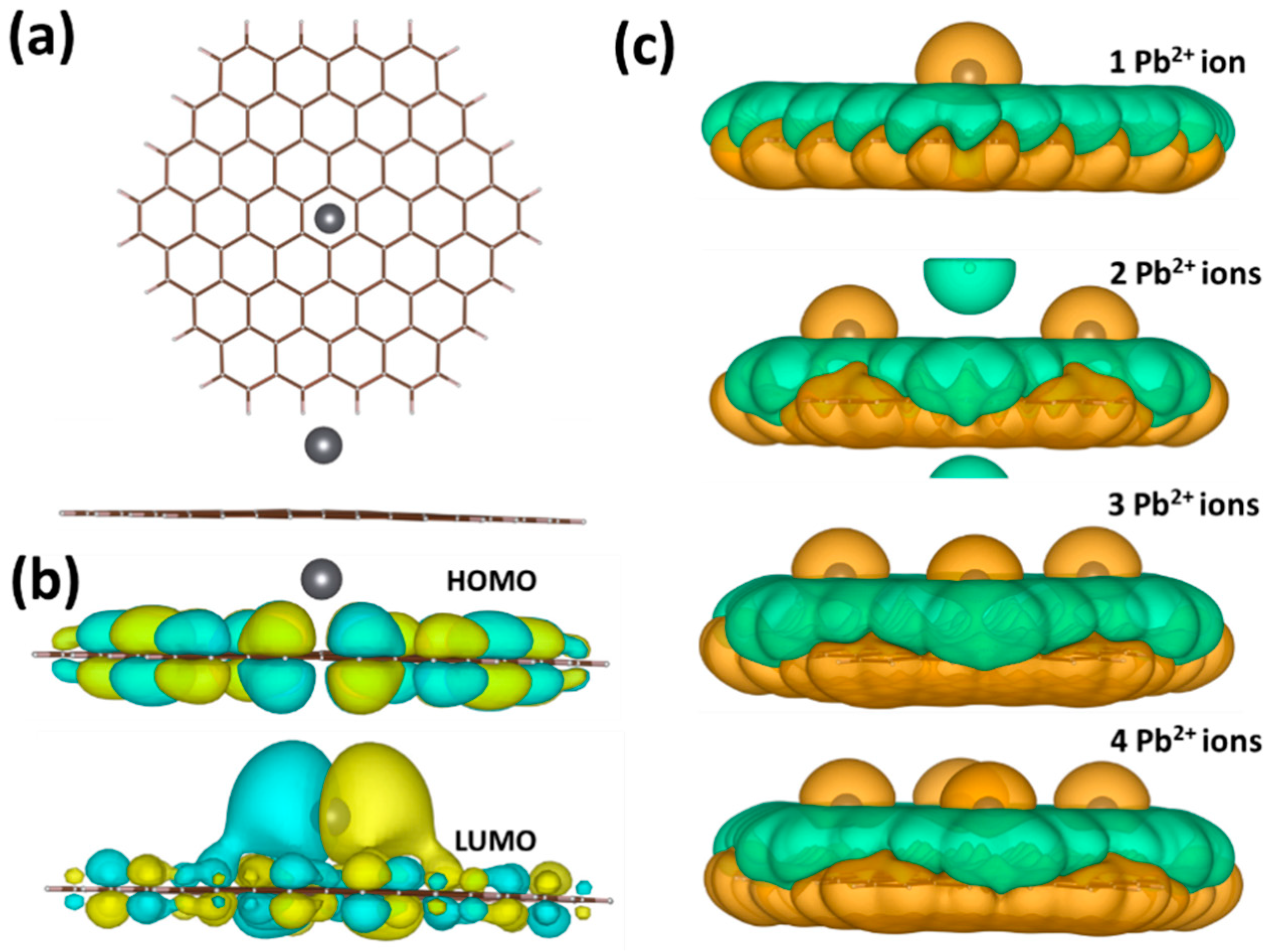
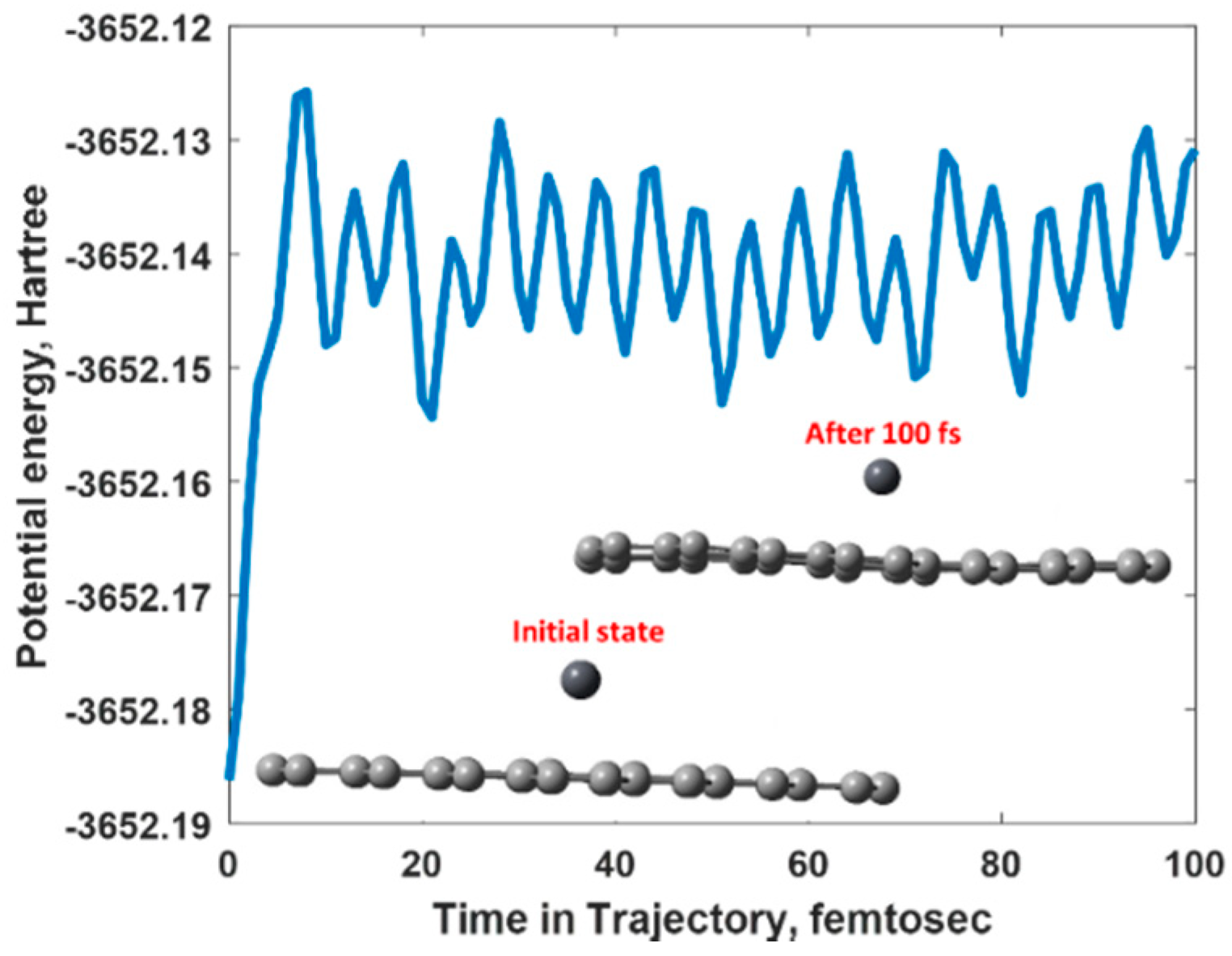
2.4. Density Functional Theory (DFT) Calculations
3. Results
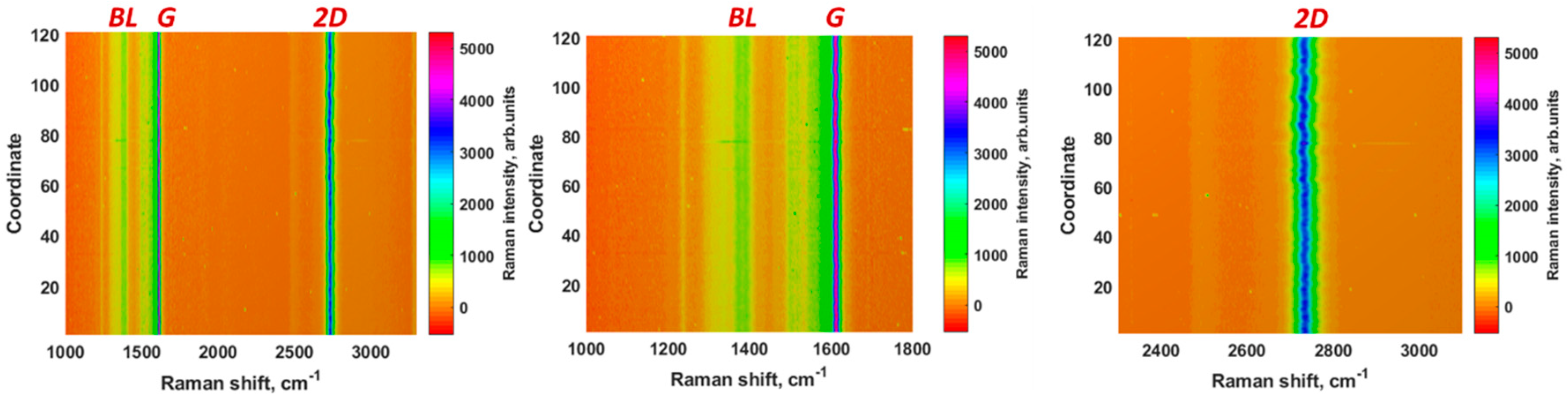
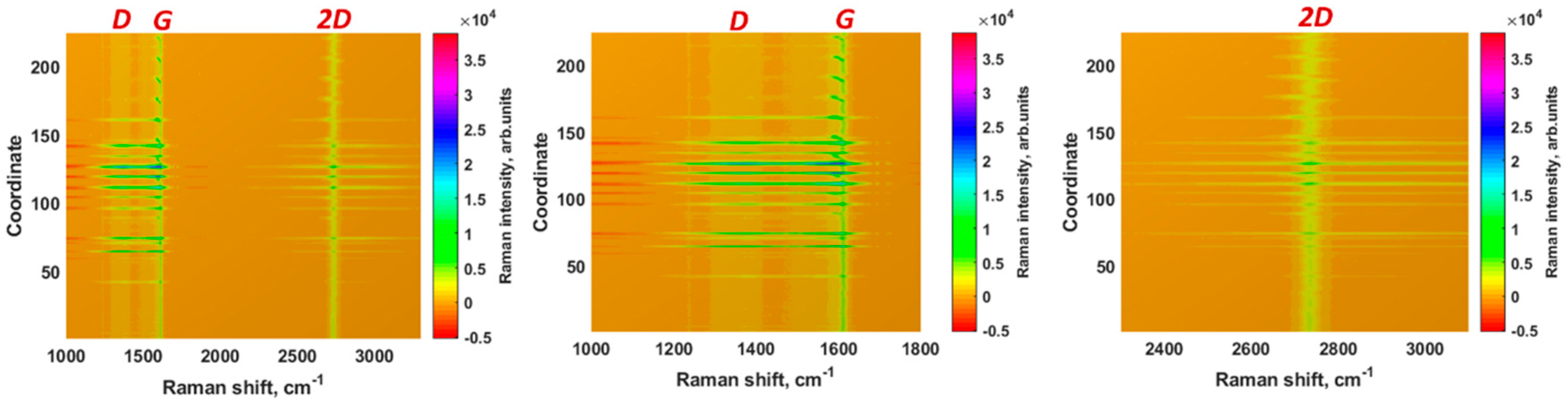
3.1. Properties of the Epitaxial Graphene Electrode
3.2. Electrochemical Activity of Epitaxial Graphene towards Lead
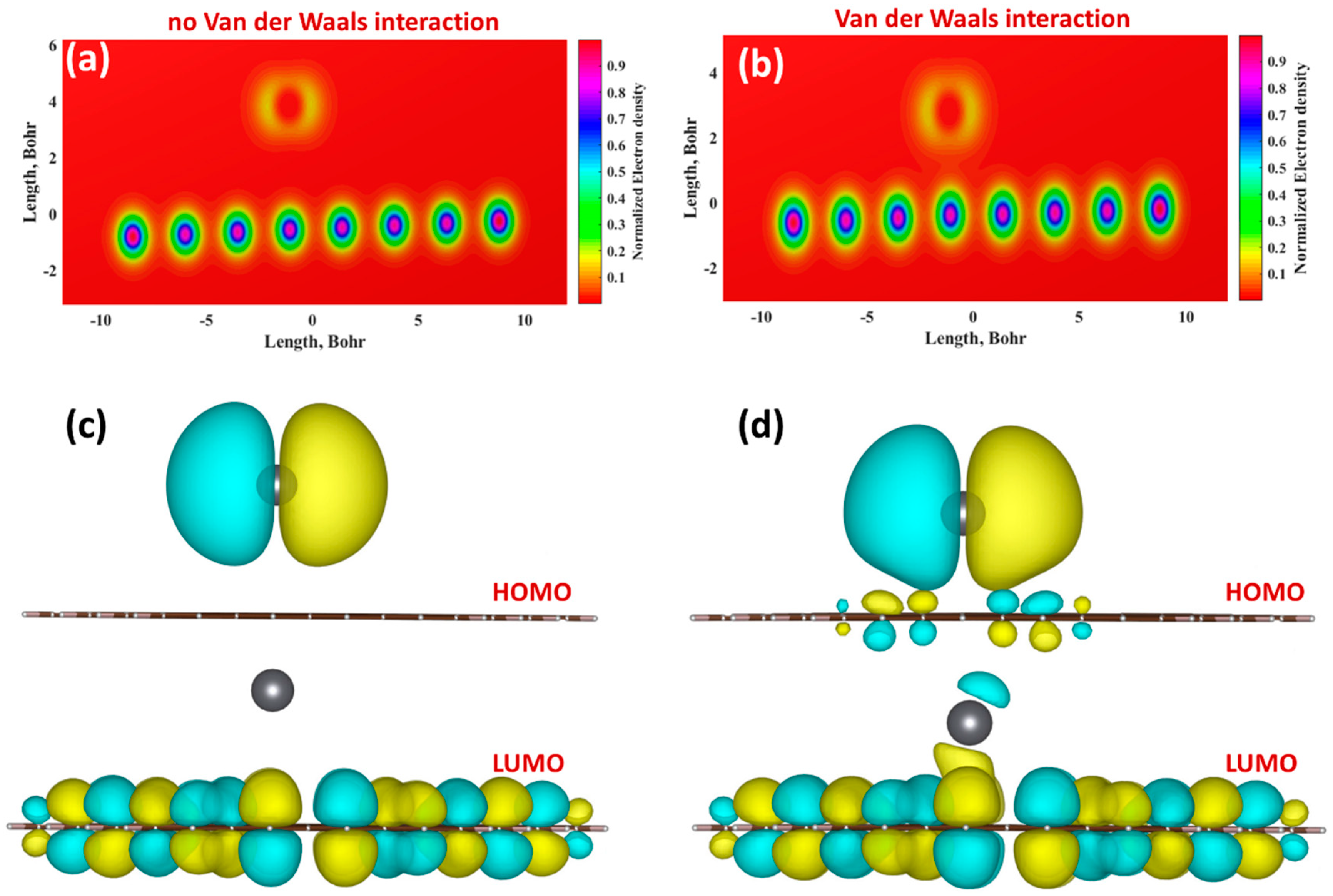
3.3. Mechanism of the Electrochemical Response of Epitaxial Graphene towards Lead
3.4. Conductometric Response of Epitaxial Graphene towards Pb
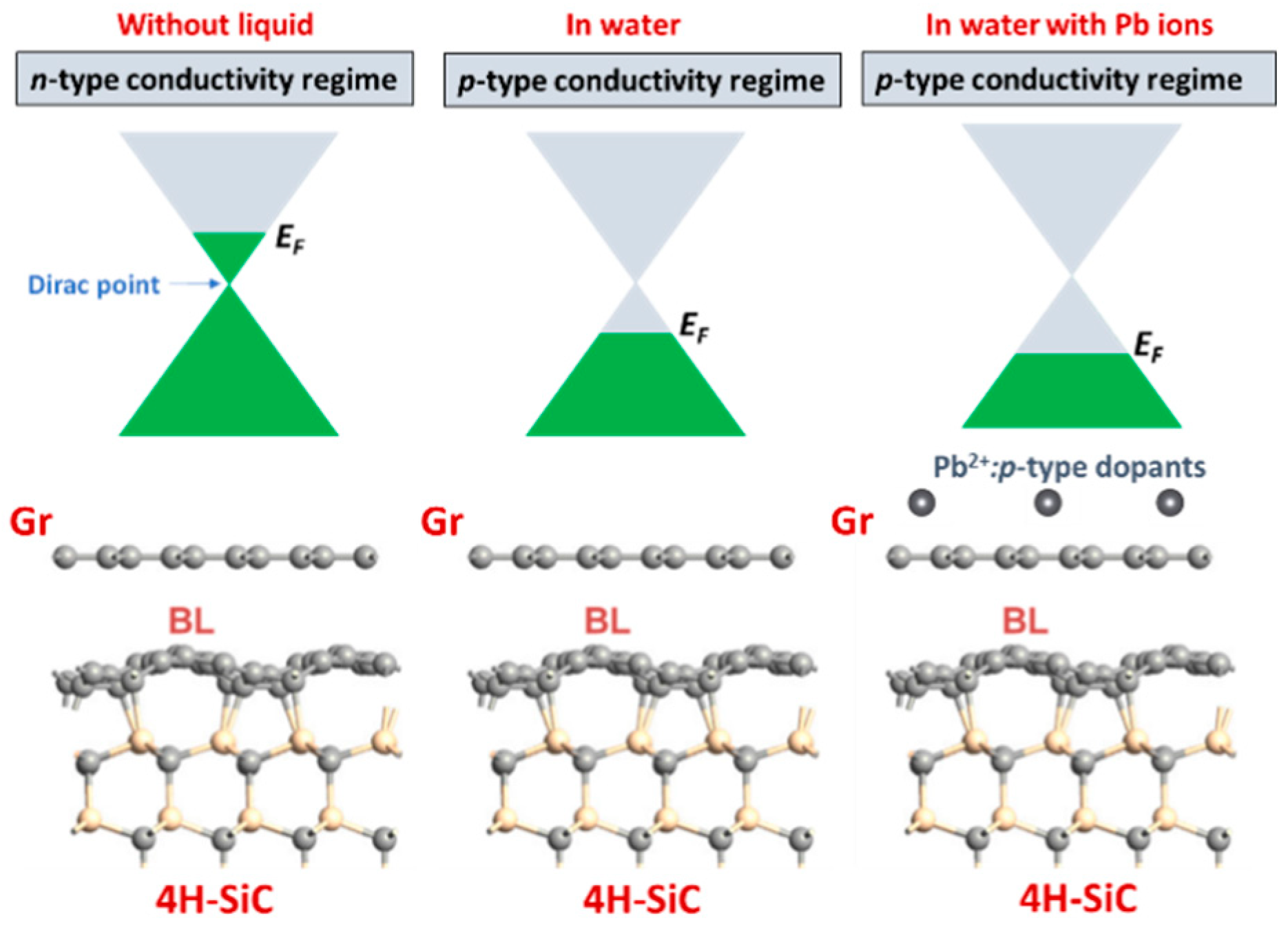
3.5. Mechanism of Conductometric Response of Epitaxial Graphene towards Lead
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lidsky, T.I.; Schneider, J.S. Lead neurotoxicity in children: Basic mechanisms and clinical correlates. Brain 2003, 126, 5–19. [Google Scholar] [CrossRef] [PubMed]
- Ahyayauch, H.; García-Arribas, A.B.; Sot, J.; González-Ramírez, E.J.; Busto, J.V.; Monasterio, B.G.; Jiménez-Rojo, N.; Contreras, F.X.; Rendón-Ramírez, A.; Martin, C.; et al. Pb(II) Induces Scramblase Activation and Ceramide-Domain Generation in Red Blood Cells. Sci. Rep. 2018, 8, 7456. [Google Scholar] [CrossRef] [PubMed]
- Schanne, F.A.X.; Moskal, J.R.; Gupta, R.K. Effect of lead on intracellular free calcium ion concentration in a presynaptic neuronal model: 19F-NMR study of NG108-15 cells. Brain Res. 1989, 503, 308–311. [Google Scholar] [CrossRef]
- Toscano, C.D.; Guilarte, T.R. Lead neurotoxicity: From exposure to molecular effects. Brain Res. Rev. 2005, 49, 529–554. [Google Scholar] [CrossRef] [PubMed]
- Adonaylo, V.N.; Oteiza, P.I. Pb2+ promotes lipid oxidation and alterations in membrane physical properties. Toxicology 1999, 132, 19–32. [Google Scholar] [CrossRef]
- Wani, A.L.; Ara, A.; Usmani, J.A. Lead toxicity: A review. Interdiscipl. Toxicol. 2015, 8, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Liu, X.; Chen, Z.; Xu, H.; Ding, X. Bioaccumulation of Lead and the Effects of Lead on Catalase Activity, Glutathione Levels, and Chlorophyll Content in the Leaves of Wheat. Commun. Soil Sci. Plant Anal. 2010, 41, 935–944. [Google Scholar] [CrossRef]
- Hou, S.; Yuan, L.; Jin, P.; Ding, B.; Qin, N.; Li, L.; Liu, X.; Wu, Z.; Zhao, G.; Deng, Y. A clinical study of the effects of lead poisoning on the intelligence and neurobehavioral abilities of children. Theor. Biol. Med. Model. 2013, 10, 13. [Google Scholar] [CrossRef] [PubMed]
- Lanphear, B.P.; Rauch, S.; Auinger, P.; Allen, R.W.; Hornung, R.W. Low-level lead exposure and mortality in US adults: A population-based cohort study. Lancet Public Health 2018, 3, e177–e184. [Google Scholar] [CrossRef]
- Skerfving, S.; Bergdahl, I.A. Lead. In Handbook on the Toxicology of Metals, 3rd ed.; Nordberg, G.F., Fowler, B.A., Nordberg, M., Friberg, L.T., Eds.; Elsevier B.V.: Amsterdam, The Netherlands, 2007; pp. 599–635. ISBN 978-0-12-369413-3. [Google Scholar]
- Tsuchiya, K.; Iwao, S. Interrelationships among zinc, copper, lead, and cadmium in food, feces, and organs of humans. Environ. Health Perspect. 1978, 25, 119–124. [Google Scholar] [CrossRef] [PubMed]
- Payne, J.C.; ter Horst, M.A.; Godwin, H.A. Lead fingers: Pb2+ binding to structural zinc-binding domains determined directly by monitoring lead-thiolate charge-transfer bands. J. Am. Chem. Soc. 1999, 121, 6850–6855. [Google Scholar] [CrossRef]
- Kirberger, M.; Yang, J.J. Structural Differences between Pb2+- and Ca2+-binding Sites in Proteins: Implications with Respect to Toxicity. J. Inorg. Biochem. 2008, 102, 1901–1909. [Google Scholar] [CrossRef] [PubMed]
- Kirberger, M.; Wong, H.C.; Jiang, J.; Yang, J.J. Metal toxicity and opportunistic binding of Pb2+ in proteins. J. Inorg. Biochem. 2013, 125, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Needleman, H.L.; Gunnoe, C.; Leviton, A.; Reed, R.; Peresie, H.; Maher, C.; Barrett, P. Deficit in psychologic and classroom performance of children with elevated dentine lead levels. N. Engl. J. Med. 1979, 300, 689–695. [Google Scholar] [CrossRef] [PubMed]
- Wedeen, R.P. Bone lead, hypertension, and lead nephropathy. Environ. Health Perspect. 1988, 78, 57–60. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.C.; Butrimovitz, G.P.; Purdy, W.C. Direct Measurement of Zinc in Plasma by Atomic Absorption Spectroscopy. Clin. Chem. 1979, 25, 1487–1491. [Google Scholar] [PubMed]
- Jenner, G.; Longerich, H.; Jackson, S.; Fryer, B. ICP-MS—A powerful tool for high-precision trace-element analysis in Earth sciences: Evidence from analysis of selected U.S.G.S. reference samples. Chem. Geol. 1990, 83, 133–148. [Google Scholar] [CrossRef]
- Allen, H.E.; Matson, W.R.; Mancy, K.H. Trace Metal Characterization in Aquatic Environments by Anodic Stripping Voltammetry. J. Water Pollut. Control Fed. 1970, 42, 573–581. [Google Scholar]
- Gardiner, J.; Stiff, M.J. The determination of cadmium, lead, copper and zinc in ground water, estuarine water, sewage and sewage effluent by anodic stripping voltammetry. Water Res. 1975, 9, 517–523. [Google Scholar] [CrossRef]
- Beneš, P.; Koc, J.; Stulík, K. The use of anodic stripping voltammetry for determination of the concentration and forms of existence of lead in natural waters. Water Res. 1979, 13, 967–975. [Google Scholar] [CrossRef]
- Bansod, B.; Kumar, T.; Thakur, R.; Rana, S.; Singh, I. A review on various electrochemical techniques for heavy metal ions detection with different sensing platforms. Biosens. Bioelectron. 2017, 94, 443–455. [Google Scholar] [CrossRef] [PubMed]
- March, G.; Nguyen, T.D.; Piro, B. Modified Electrodes Used for Electrochemical Detection of Metal Ions in Environmental Analysis. Biosensors 2015, 5, 241–275. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, C.; Wang, S.; Liu, Q.; Feng, H.; Ma, X.; Guo, J. Electrochemical microfluidics techniques for heavy metal ion detection. Analyst 2018, 143, 4230–4246. [Google Scholar] [CrossRef] [PubMed]
- Hauser, P.C.; Zhang, Z.P. Flow-injection determination of lead by hydride generation and conductometric detection. Fresenius J. Anal. Chem. 1996, 355, 141–143. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ji, B.; Zhang, W.; Lin, B.; Wang, Q.; Ding, J. Developing Modified Graphene Oxide Based Sensor for Lead Ions Detection in Water. ChemistrySelect 2016, 1, 1751–1755. [Google Scholar] [CrossRef]
- Zhou, G.; Chang, J.; Cui, S.; Pu, H.; Wen, Z.; Chen, J. Real-Time, Selective Detection of Pb2+ in Water Using a Reduced Graphene Oxide/Gold Nanoparticle Field-Effect Transistor Device. ACS Appl. Mater. Interfaces 2014, 6, 19235–19241. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Guidelines for Drinking-Water Quality, 4th ed.; WHO Press: Geneva, Switzerland, 2011; pp. 383–384. ISBN 978-92-4-154815-1. [Google Scholar]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Nie, J.; He, B.; Cheng, Y.; Yin, W.; Hou, C.; Huo, D.; Qian, L.; Qin, Y.; Fa, H. Design of L-cysteine functionalized Au@SiO2@Fe3O4/nitrogen-doped graphene nanocomposite and its application in electrochemical detection of Pb2+. Chem. Res. Chin. Univ. 2017, 33, 951–957. [Google Scholar] [CrossRef]
- Magerusan, L.; Socaci, C.; Coros, M.; Pogacean, F.; Rosu, M.C.; Gergely, S.; Pruneanu, S.; Leostean, C.; Pana, I.O. Electrochemical platform based on nitrogen-doped graphene/chitosan nanocomposite for selective Pb2+ detection. Nanotechnology 2017, 28, 114001. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Li, Z.; Liu, C.; Chang, Y.; Wen, J.; Zhao, H.; Cao, H.; Zhang, Y.; Liu, D. Amino-modification and successive electrochemical reduction of graphene oxide for highly sensitive electrochemical detection of trace Pb2+. Carbon 2016, 109, 479–486. [Google Scholar] [CrossRef]
- Yuan, G.; Chen, H.; Xia, C.; Gao, L.; Yu, C. Ultrasensitive electrochemical detection of secretoneurin based on Pb2+-decorated reduced graphene oxide-tetraethylene pentamine as a label. Biosens. Bioelectron. 2015, 69, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zeng, G.-M.; Zhang, Y.; Tang, L.; Chen, J.; Cheng, M.; Zhang, L.-H.; He, L.; Guo, Y.; He, X.-X.; et al. Highly sensitive electrochemical sensor using a MWCNTs/GNPs-modified electrode for lead (II) detection based on Pb2+-induced G-rich DNA conformation. Analyst 2014, 139, 5014–5020. [Google Scholar] [CrossRef] [PubMed]
- Priya, T.; Dhanalakshmi, N.; Thennarasu, S.; Thinakarana, N. A novel voltammetric sensor for the simultaneous detection of Cd2+ and Pb2+ using graphene oxide/κ-carrageenan/l-cysteine nanocomposite. Carbohydr. Polym. 2018, 182, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Palisoc, S.T.; Estioko, L.C.D.; Natividad, M.T. Voltammetric determination of lead and cadmium in vegetables by graphene paste electrode modified with activated carbon from coconut husk. Mater. Res. Express 2018, 5, 085035. [Google Scholar] [CrossRef]
- Liu, S.; Wu, T.; Li, F.; Zhang, Q.; Dong, X.; Niu, L. Disposable graphene sensor with an internal reference electrode for stripping analysis of heavy metals. Anal. Methods 2018, 10, 1986–1992. [Google Scholar] [CrossRef]
- Li, L.; Liu, D.; Shi, A.; You, T. Simultaneous stripping determination of cadmium and lead ions based on the N-doped carbon quantum dots-graphene oxide hybrid. Sens. Actuators B 2018, 255, 1762–1770. [Google Scholar] [CrossRef]
- Ren, W.; Zhang, Y.; Li, M. Sensitive determination of Zn2+, Cd2+ and Pb2+ at electrochemically reduced nanoporous graphene oxide/bismuth film electrode. Int. J. Electrochem. Sci. 2018, 13, 1331–1342. [Google Scholar] [CrossRef]
- Muralikrishna, S.; Nagaraju, D.H.; Balakrishna, R.G.; Surareungchai, W.; Ramakrishnappa, T.; Shivanandareddy, A.B. Hydrogels of polyaniline with graphene oxide for highly sensitive electrochemical determination of lead ions. Anal. Chim. Acta 2017, 990, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Palisoc, S.T.; Valeza, N.C.; Natividad, M.T. Fabrication of an effective gold nanoparticle/graphene/Nafion® modified glassy carbon electrode for high sensitive detection of trace Cd2+, Pb2+ and Cu2+ in tobacco and tobacco products. Int. J. Electrochem. Sci. 2017, 12, 3859–3872. [Google Scholar] [CrossRef]
- Wei, X.; Wang, C.; Dou, P.; Zheng, J.; Cao, Z.; Xu, X. Synthesis of NiCo2O4 nanoneedle@polypyrrole arrays supported on 3D graphene electrode for high-performance detection of trace Pb2+. J. Mater. Sci. 2017, 52, 3893–3905. [Google Scholar] [CrossRef]
- Rong, R.; Zhao, H.; Gan, X.; Chen, S.; Quan, X. An electrochemical sensor based on graphene-polypyrrole nanocomposite for the specific detection of Pb (II). Nano 2017, 12, 1750008. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Q.; Yang, B.; Xu, Q.; Xu, Q.; Hu, X. Electrochemical sensor construction based on Nafion/calcium lignosulphonate functionalized porous graphene nanocomposite and its application for simultaneous detection of trace Pb2+ and Cd2+. Sens. Actuators B 2018, 259, 540–551. [Google Scholar] [CrossRef]
- Seabra, A.B.; Paula, A.J.; de Lima, R.; Alves, O.L.; Durań, N. Nanotoxicity of Graphene and Graphene Oxide. Chem. Res. Toxicol. 2014, 27, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Shtepliuk, I.; Khranovskyy, V.; Yakimova, R. Combining graphene with silicon carbide: Synthesis and properties—A review. Semicond. Sci. Technol. 2016, 31, 113004. [Google Scholar] [CrossRef]
- Virojanadara, C.; Syväjarvi, M.; Yakimova, R.; Johansson, L.; Zakharov, A.; Balasubramanian, T. Homogeneous large-area graphene layer growth on 6H-SiC(0001). Phys. Rev. B 2008, 78, 245403. [Google Scholar] [CrossRef]
- Yazdi, G.R.; Iakimov, T.; Yakimova, R. Epitaxial Graphene on SiC: A Review of Growth and Characterization. Crystals 2016, 6, 53. [Google Scholar] [CrossRef]
- Shtepliuk, I.; Vagin, M.; Ivanov, I.G.; Iakimov, T.; Reza Yazdi, G.; Yakimova, R. Lead (Pb) interfacing with epitaxial graphene. Phys. Chem. Chem. Phys. 2018, 20, 17105–17116. [Google Scholar] [CrossRef] [PubMed]
- Oliveros, A.; Coletti, C.; Frewin, C.L.; Locke, C.; Starke, U.; Saddow, S.E. Cellular Interactions on Epitaxial Graphene on SiC (0001) Substrates. Mater. Sci. Forum 2011, 679–680, 831–834. [Google Scholar] [CrossRef]
- Yager, T.; Webb, M.J.; Grennberg, H.; Yakimova, R.; Lara-Avila, S.; Kubatkin, S. High mobility epitaxial graphene devices via aqueous-ozone processing. Appl. Phys. Lett. 2015, 106, 063503. [Google Scholar] [CrossRef]
- Vagin, M.Y.; Sekretaryova, A.N.; Ivanov, I.G.; Håkansson, A.; Iakimov, T.; Syväjärvi, M.; Yakimova, R.; Lundström, I.; Eriksson, M. Monitoring of epitaxial graphene anodization. Electrochim. Acta 2017, 238, 91–98. [Google Scholar] [CrossRef]
- Shtepliuk, I.; Khranovskyy, V.; Yakimova, R. Insights into the origin of the excited transitions in graphene quantum dots interacting with heavy metals in different media. Phys. Chem. Chem. Phys. 2017, 19, 30445–30463. [Google Scholar] [CrossRef] [PubMed]
- Yakimova, R.; Iakimov, T.; Syväjärvi, M. Process for Growth of Graphene. U.S. Patent US9150417B2, 6 October 2015. [Google Scholar]
- Ivanov, I.G.; Hassan, J.; Iakimov, T.; Zakharov, A.A.; Yakimova, R.; Janzén, E. Layer-number determination in graphene on SiC by reflectance mapping. Carbon 2014, 77, 492–500. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nomura, M.; Wakita, H.; Ohtaki, H. An extended X-ray absorption fine structure study of aqueous rare earth perchlorate solutions in liquid and glassy states. J. Chem. Phys. 1988, 89, 5153–5159. [Google Scholar] [CrossRef]
- Sémon, L.; Boehme, C.; Billard, I.; Hennig, C.; Lützenkirchen, K.; Reich, T.; Roßberg, A.; Rossini, I.; Wipff, G. Do Perchlorate and Triflate Anions Bind to the Uranyl Cation in an Acidic Aqueous Medium? A Combined EXAFS and Quantum Mechanical Investigation. ChemPhysChem 2001, 2, 591–598. [Google Scholar] [CrossRef]
- Binnemans, K. Applications of tetravalent cerium compounds. In Handbook on the Physics and Chemistry of Rare Earths, 1st ed.; Gschneidner, K.A., Jr., Bünzli, J.-C.G., Pecharsky, V.K., Eds.; Elsevier Science Publisher B.V.: Amsterdam, The Netherlands, 2006; Volume 3, pp. 306–307. ISBN 9780080466729. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision D. 01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.M.L.; Sundermann, A. Correlation consistent valence basis sets for use with the Stuttgart–Dresden–Bonn relativistic effective core potentials: The atoms Ga–Kr and In–Xe. J. Chem. Phys. 2001, 114, 3408–3420. [Google Scholar] [CrossRef]
- Shtepliuk, I.; Caffrey, N.M.; Iakimov, T.; Khranovskyy, V.; Abrikosov, I.A.; Yakimova, R. On the interaction of toxic Heavy Metals (Cd, Hg, Pb) with graphene quantum dots and infinite graphene. Sci. Rep. 2017, 7, 3934. [Google Scholar] [CrossRef] [PubMed]
- Shtepliuk, I.; Yakimova, R. Interband Absorption in Few-Layer Graphene Quantum Dots: Effect of Heavy Metals. Materials 2018, 11, 1217. [Google Scholar] [CrossRef] [PubMed]
- Shtepliuk, I.; Yakimova, R. Interband transitions in closed-shell vacancy containing graphene quantum dots complexed with heavy metals. Phys. Chem. Chem. Phys. 2018, 20, 21528–21543. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Available online: https://pubchem.ncbi.nlm.nih.gov/compound/25137955 (accessed on 27 September 2018).
- Cossi, M.; Barone, V. Time-dependent density functional theory for molecules in liquid solutions. J. Chem. Phys. 2001, 115, 4708. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions I. J. Chem. Phys. 1955, 23, 1833. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Schlegel, H.B.; Millam, J.M.; Iyengar, S.S.; Voth, G.A.; Daniels, A.D.; Scuseria, G.E.; Frisch, M.J. Ab initio molecular dynamics: Propagating the density matrix with Gaussian orbitals. J. Chem. Phys. 2001, 114, 9758–9763. [Google Scholar] [CrossRef]
- Brownson, D.A.C.; Banks, C.E. The Handbook of Graphene Electrochemistry; Springer: London, UK, 2014; Chapter 2; pp. 23–77. ISBN 978-1-4471-6427-2. [Google Scholar]
- Zanello, P. Inorganic Electrochemistry: Theory, Practice and Application; The Royal Society of Chemistry: Cambridge, UK, 2003; pp. 117–118. ISBN 0-85404-661-5. [Google Scholar]
- Klingler, R.J.; Kochi, J.K. Electron-transfer kinetics from cyclic voltammetry. Quantitative description of electrochemical reversibility. J. Phys. Chem. 1981, 85, 1731–1741. [Google Scholar] [CrossRef]
- Hardcastle, P.; Seabourne, C.R.; Zan, R.; Brydson, R.M.D.; Bangert, U.; Ramasse, Q.M.; Novoselov, K.S.; Scott, A.J. Mobile metal adatoms on single layer, bilayer, and trilayer graphene: An ab initio DFT study with van der Waals corrections correlated with electron microscopy data. Phys. Rev. B 2013, 87, 195430. [Google Scholar] [CrossRef]
- Wilhite, P.; Vyas, A.A.; Tan, J.; Tan, J.; Yamada, T.; Wang, P.; Park, J.; Yang, C.Y. Metal–nanocarbon contacts. Semicond. Sci. Technol. 2014, 29, 054006. [Google Scholar] [CrossRef]
- Peng, S.; Cho, K.; Qi, P.; Dai, H. Ab initio study of CNT NO2 gas sensor. Chem. Phys. Lett. 2004, 387, 271. [Google Scholar] [CrossRef]
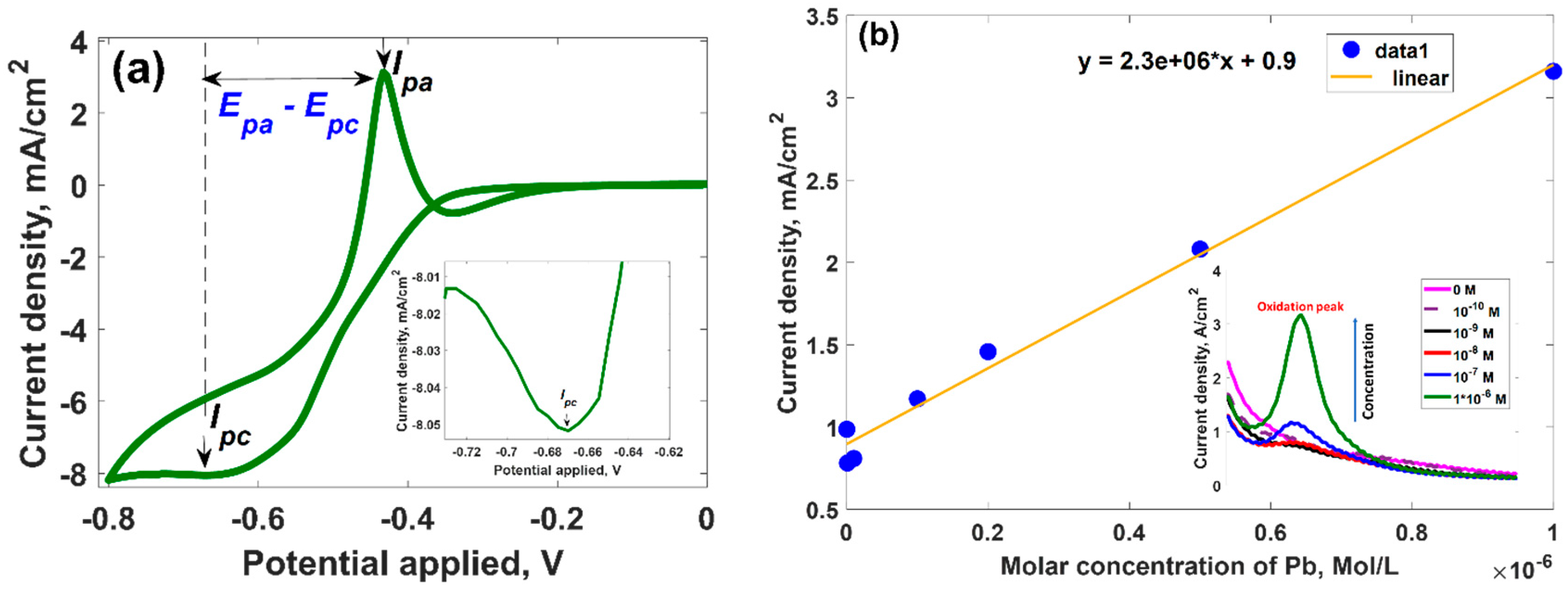

| Parameter | Anodic Process Pb0 − 2e→Pb2+ | Cathodic Process Pb2+ + 2e→Pb0 |
|---|---|---|
| Current density, mA/cm2 | 3.129 | −0.852 |
| Potential, V | −0.433 | −0.669 |
| Diffusion coefficient, 10−3 × cm2∙s−1 | 87.1 | 6.5 |
| Electron transfer rate constant, 10−2 × cm∙s−1 | 0.57 | 1.46 |
| Method | Interaction Energy, eV | Adsorption Energy, eV | Deformation Energy, eV | Distance, Å | Charge on Pb Atom | Dipole Moments, a.u. | |||
|---|---|---|---|---|---|---|---|---|---|
| Mulliken | Hirshfeld | Dx | Dy | Dz | |||||
| No vdW | −0.0049 | −0.0069 | 0.0020 | 4.36 | −0.00795 | −0.01466 | −0.00120 | 0.0000 | 0.055689 |
| With vdW | 0.3244 | 0.3163 | 0.0081 | 3.18 | −0.04861 | −0.14125 | −0.00659 | 0.0000 | 0.382385 |
| Number of Pb Ions | Interaction Energy per Ion, eV | Adsorption Energy per Ion, eV | Deformation Energy, eV | Average Distance, Å | Charge on Pb2+ Ion | Dipole Moments, a.u. | |||
|---|---|---|---|---|---|---|---|---|---|
| Mulliken | Hirshfeld | Dx | Dy | Dz | |||||
| 1 | −1.6244 | −1.6586 | 0.0342 | 2.45 | 1.3753 | 0.9826 | −0.0021 | −0.0012 | 1.375 |
| −0.5749 * | −0.6168 * | 0.0418 * | 2.44 * | 1.5854 * | 1.2984 * | −0.004 * | −0.001 * | 1.284 * | |
| 2 | −0.5759 | −0.6254 | 0.0990 | 2.47 | 1.3732 | 0.9957 | −0.0000 | −0.0009 | 2.864 |
| 3 | −0.3868 | −0.4221 | 0.1059 | 2.51 | 1.4294 | 1.0497 | −0.0006 | −0.3469 | 4.228 |
| 4 | −0.3221 | −0.3496 | 0.1059 | 2.53 | 1.4723 | 1.1357 | −0.0002 | −0.0011 | 5.566 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shtepliuk, I.; Santangelo, M.F.; Vagin, M.; Ivanov, I.G.; Khranovskyy, V.; Iakimov, T.; Eriksson, J.; Yakimova, R. Understanding Graphene Response to Neutral and Charged Lead Species: Theory and Experiment. Materials 2018, 11, 2059. https://doi.org/10.3390/ma11102059
Shtepliuk I, Santangelo MF, Vagin M, Ivanov IG, Khranovskyy V, Iakimov T, Eriksson J, Yakimova R. Understanding Graphene Response to Neutral and Charged Lead Species: Theory and Experiment. Materials. 2018; 11(10):2059. https://doi.org/10.3390/ma11102059
Chicago/Turabian StyleShtepliuk, Ivan, Maria Francesca Santangelo, Mikhail Vagin, Ivan G. Ivanov, Volodymyr Khranovskyy, Tihomir Iakimov, Jens Eriksson, and Rositsa Yakimova. 2018. "Understanding Graphene Response to Neutral and Charged Lead Species: Theory and Experiment" Materials 11, no. 10: 2059. https://doi.org/10.3390/ma11102059
APA StyleShtepliuk, I., Santangelo, M. F., Vagin, M., Ivanov, I. G., Khranovskyy, V., Iakimov, T., Eriksson, J., & Yakimova, R. (2018). Understanding Graphene Response to Neutral and Charged Lead Species: Theory and Experiment. Materials, 11(10), 2059. https://doi.org/10.3390/ma11102059