First-Principles Calculations on Structural Property and Anisotropic Elasticity of γ1-Ti4Nb3Al9 under Pressure
Abstract
1. Introduction
2. Materials and Methods
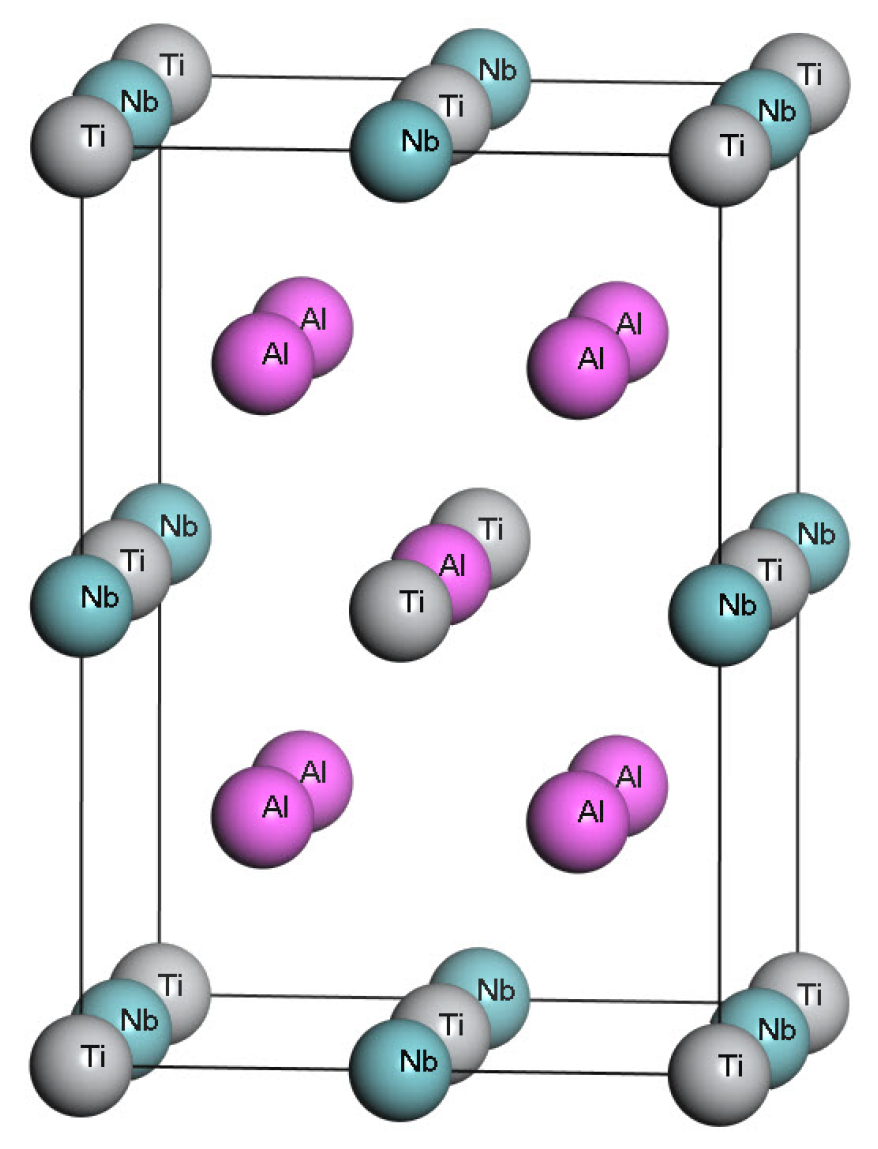
2.1. Crystal Structure of -TiNbAl Phase
2.2. Computational Details
2.3. Calculations of Elastic Constants and Related Properties
3. Results and Discussion
3.1. Bulk Properties at Zero Pressure
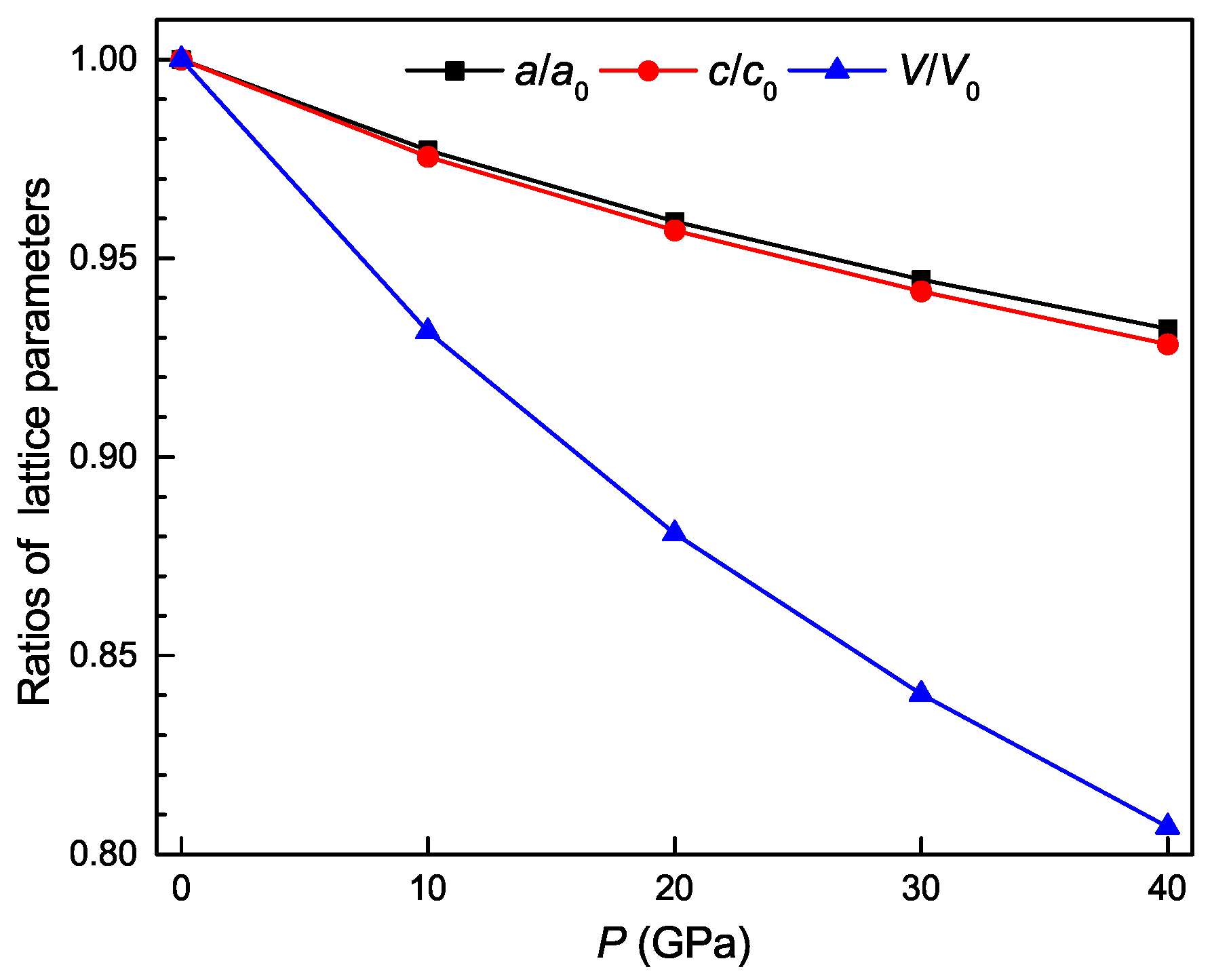
3.2. Pressure Dependence of Structural Property
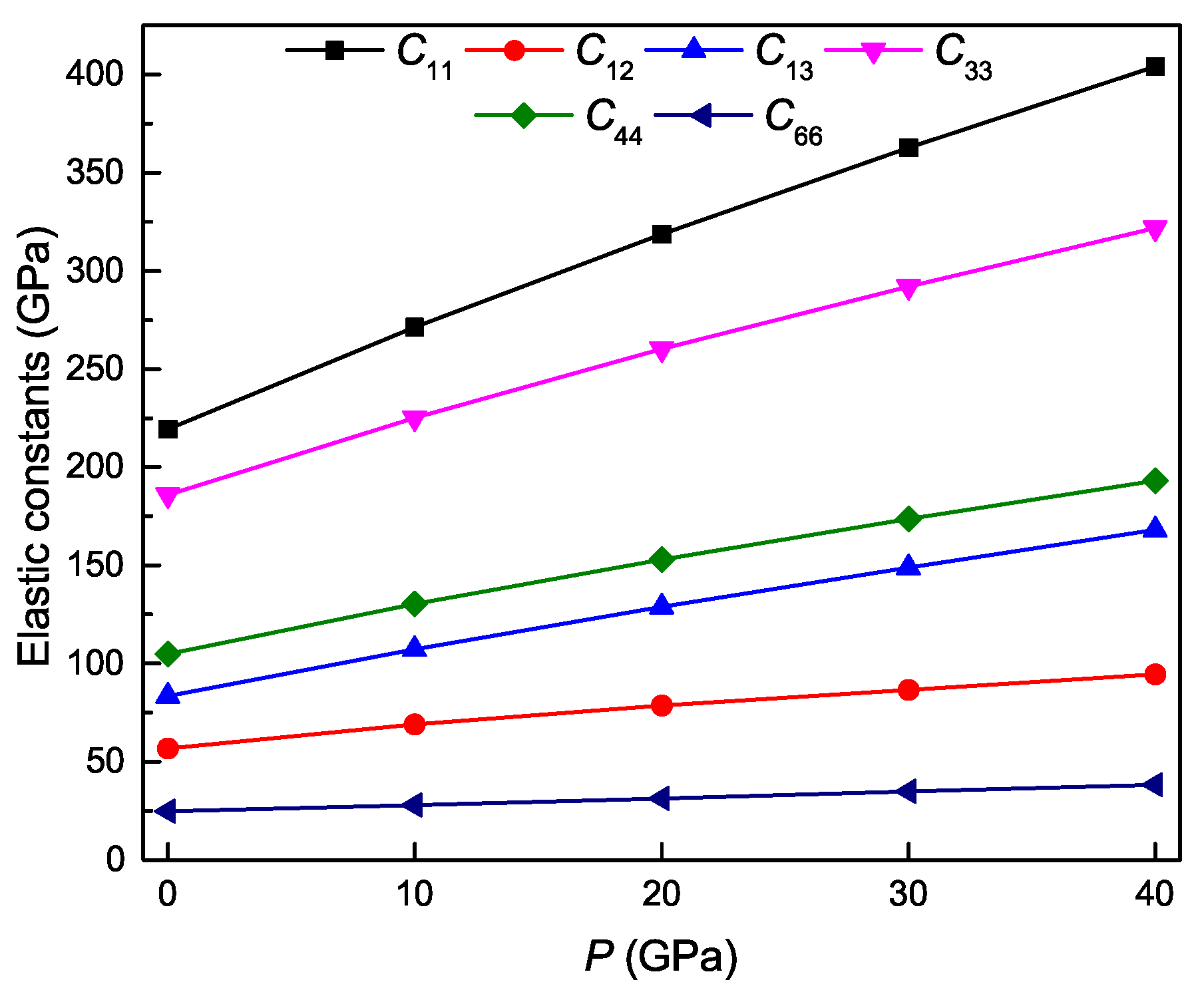
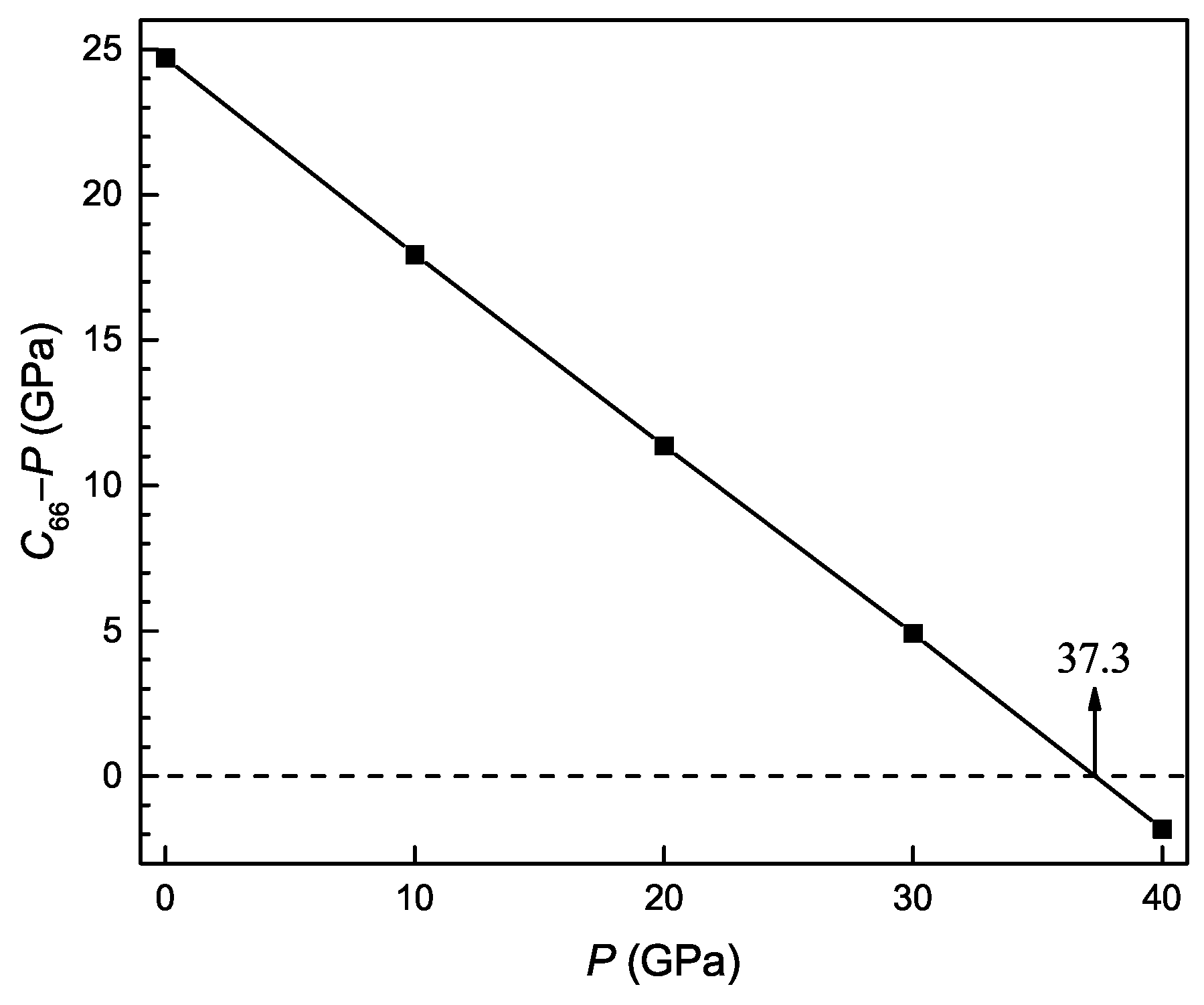
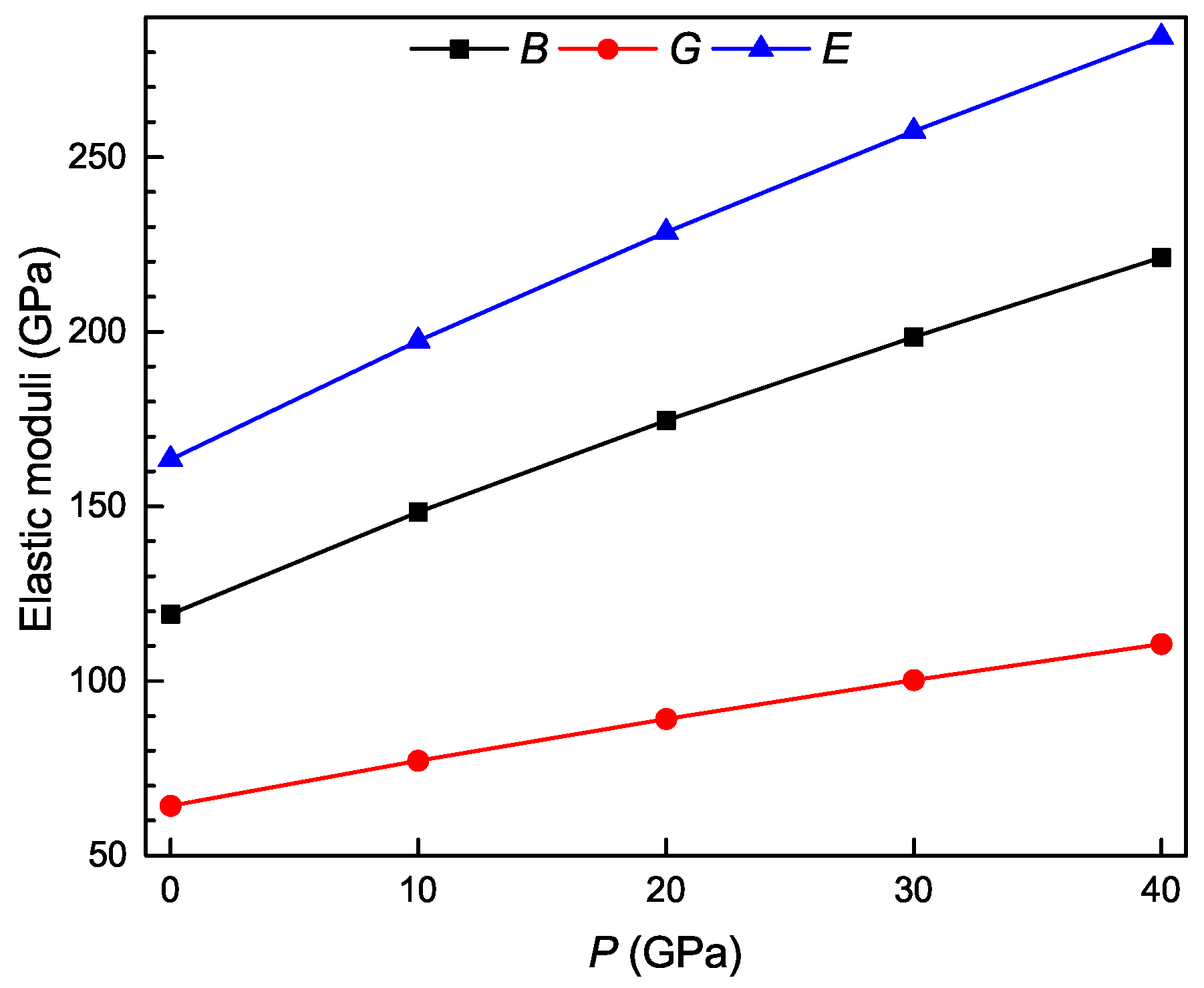
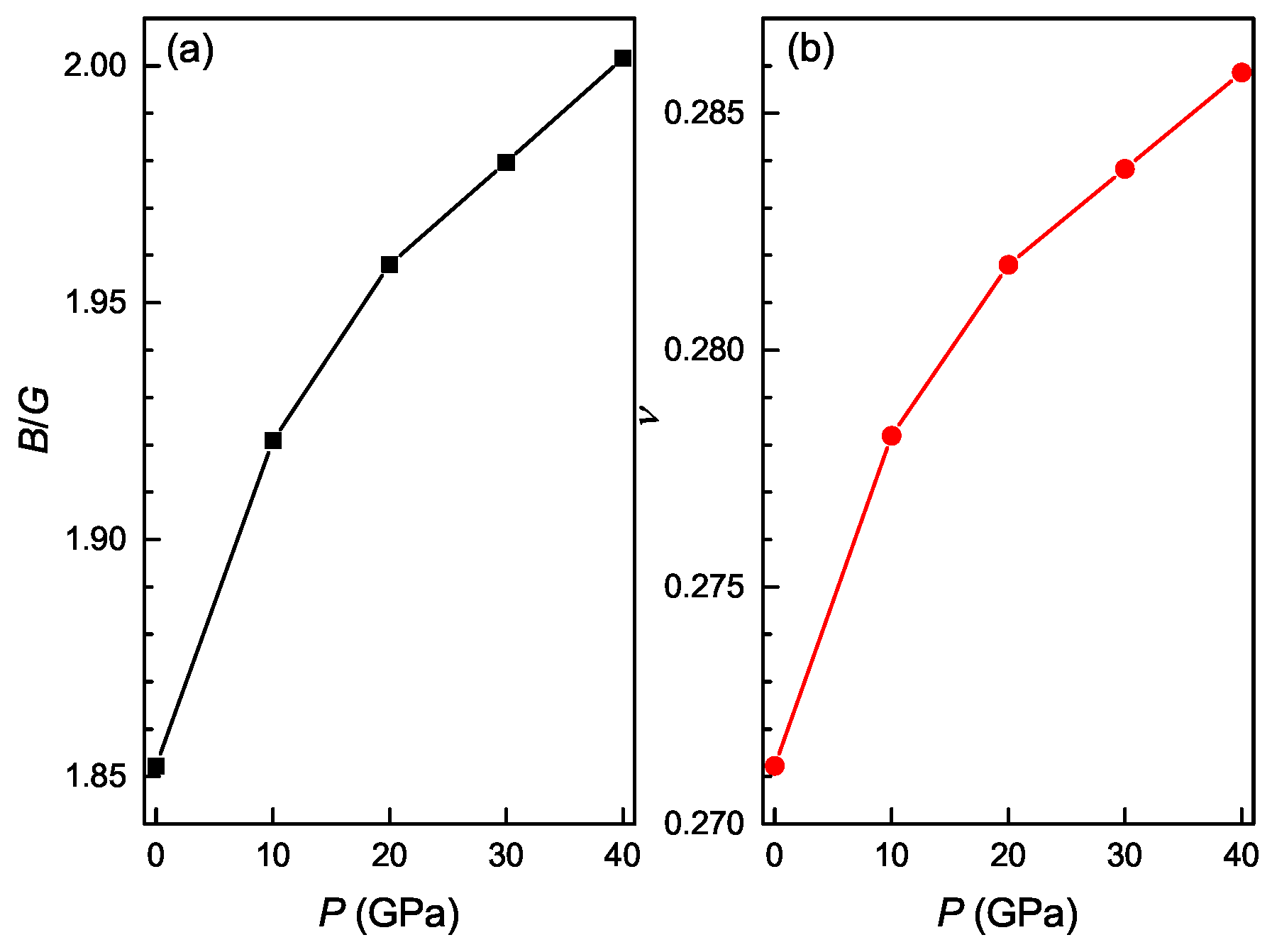
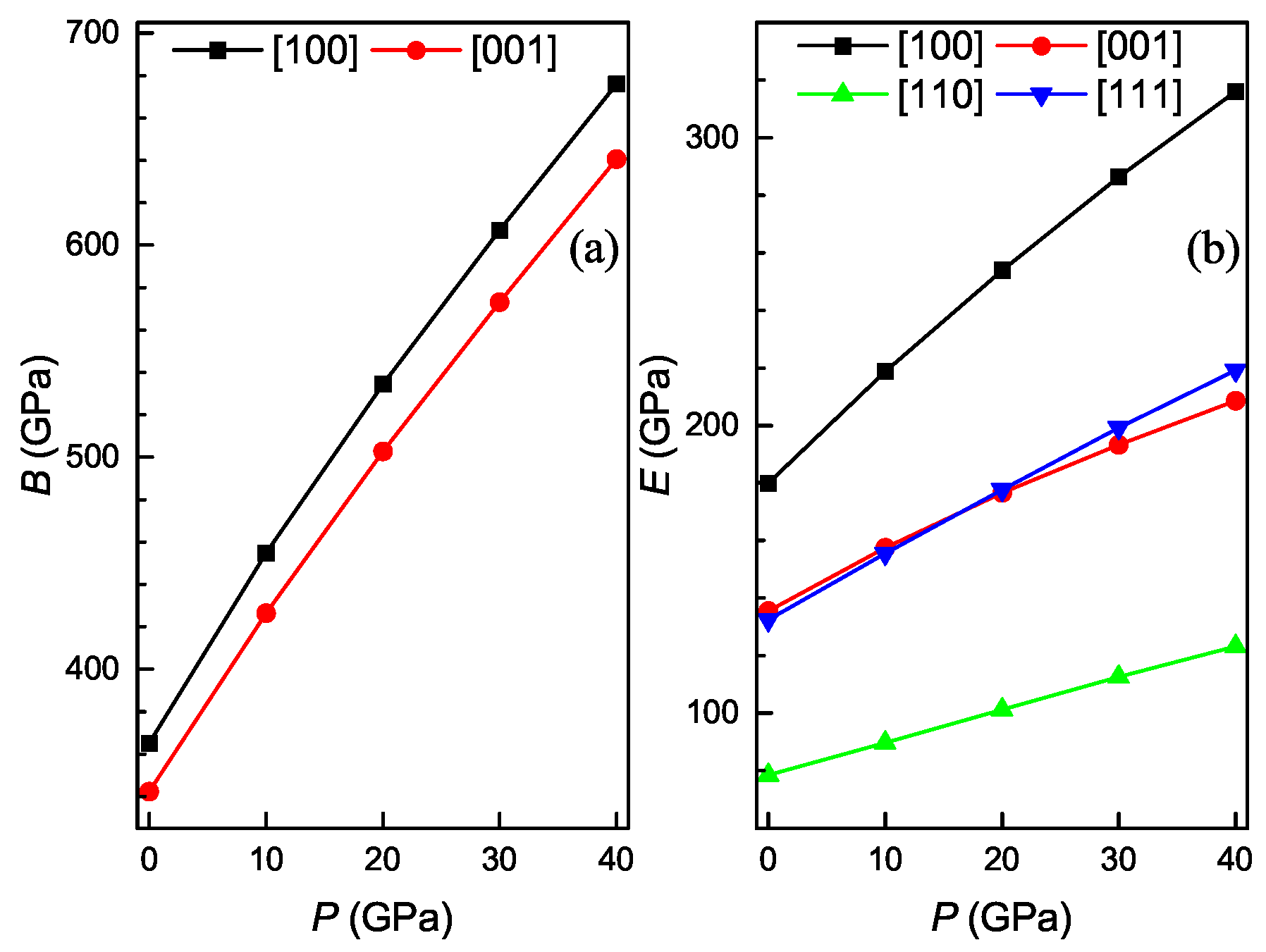
3.3. Pressure Dependence of Elastic Properties
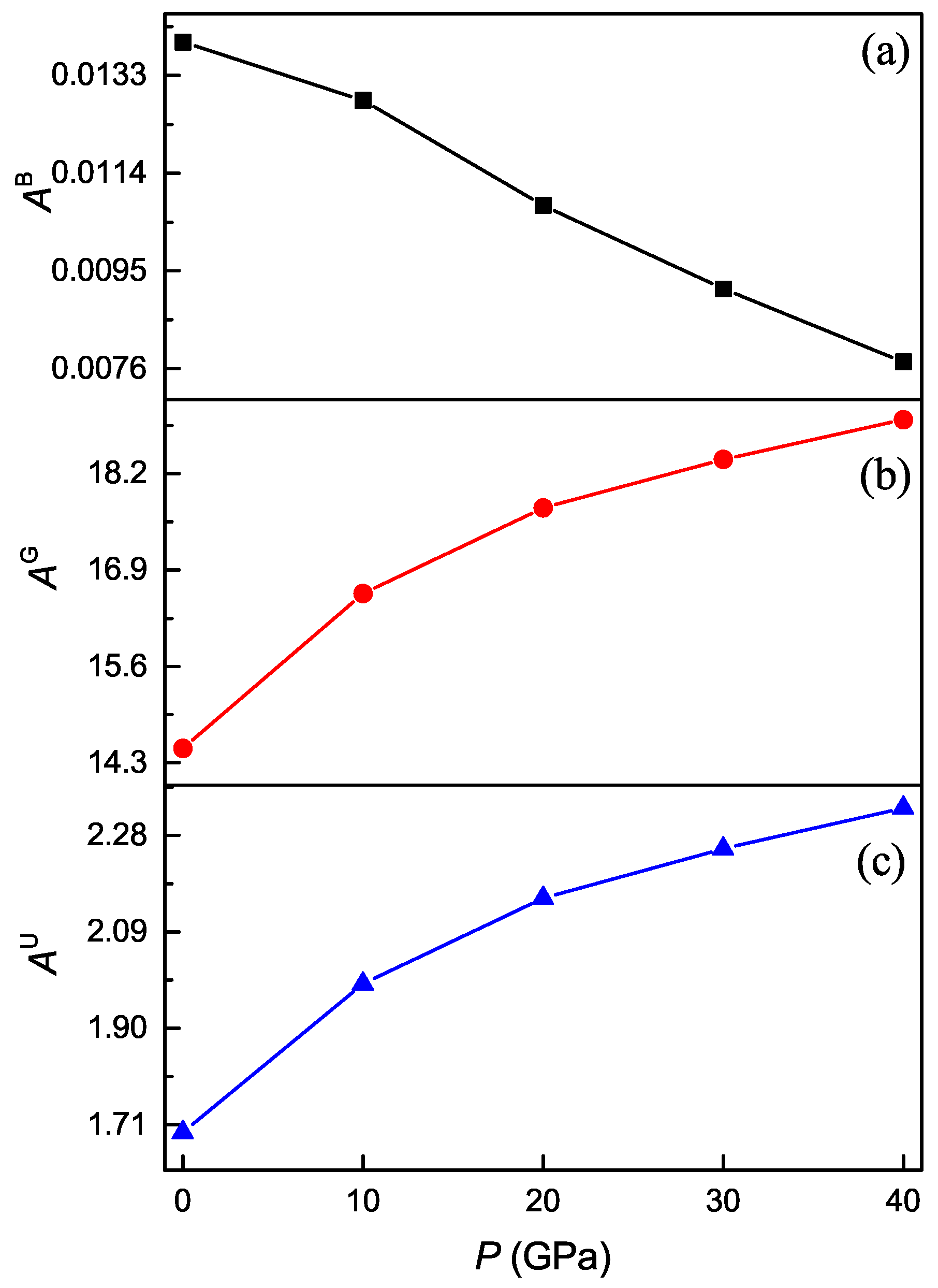
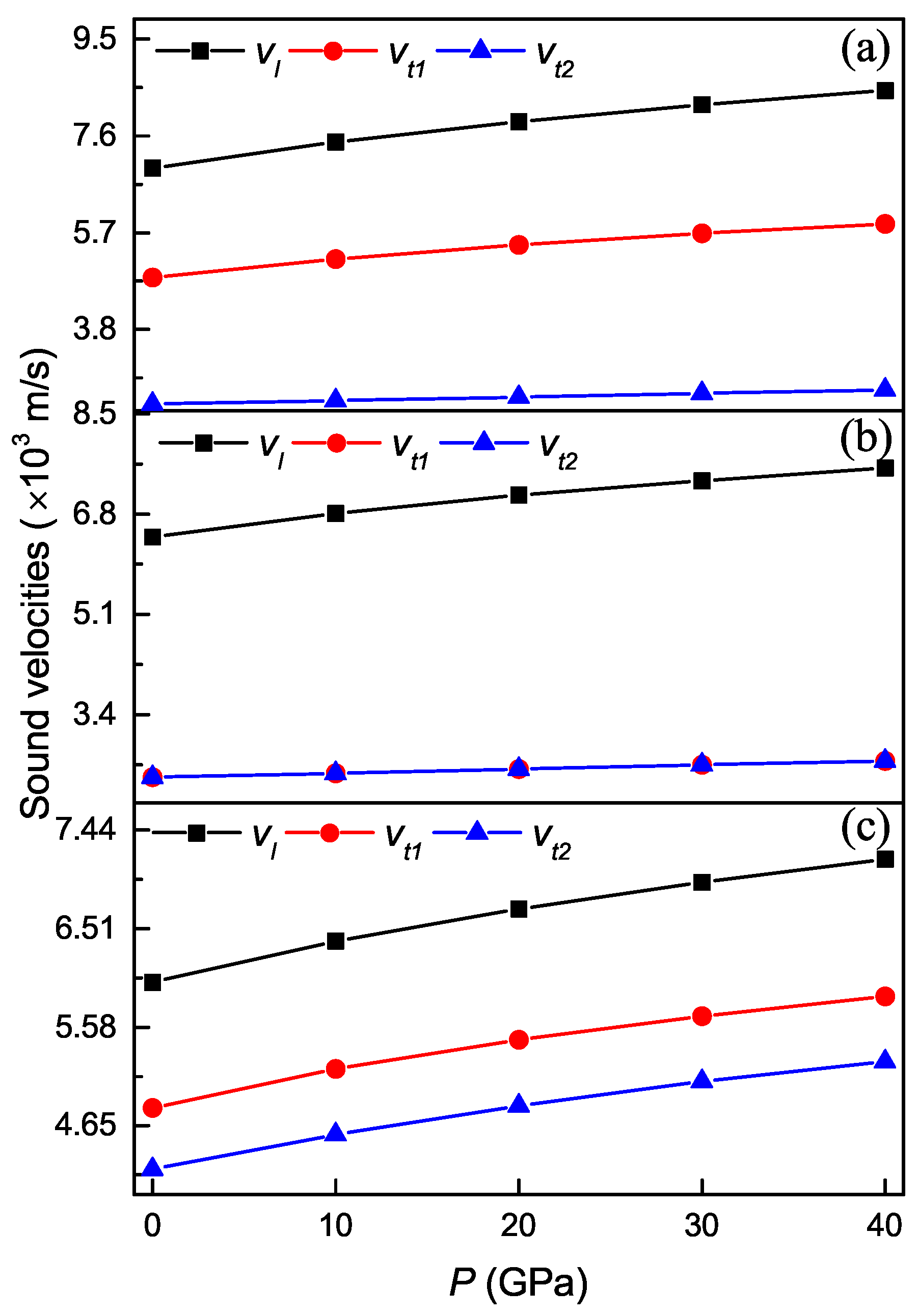
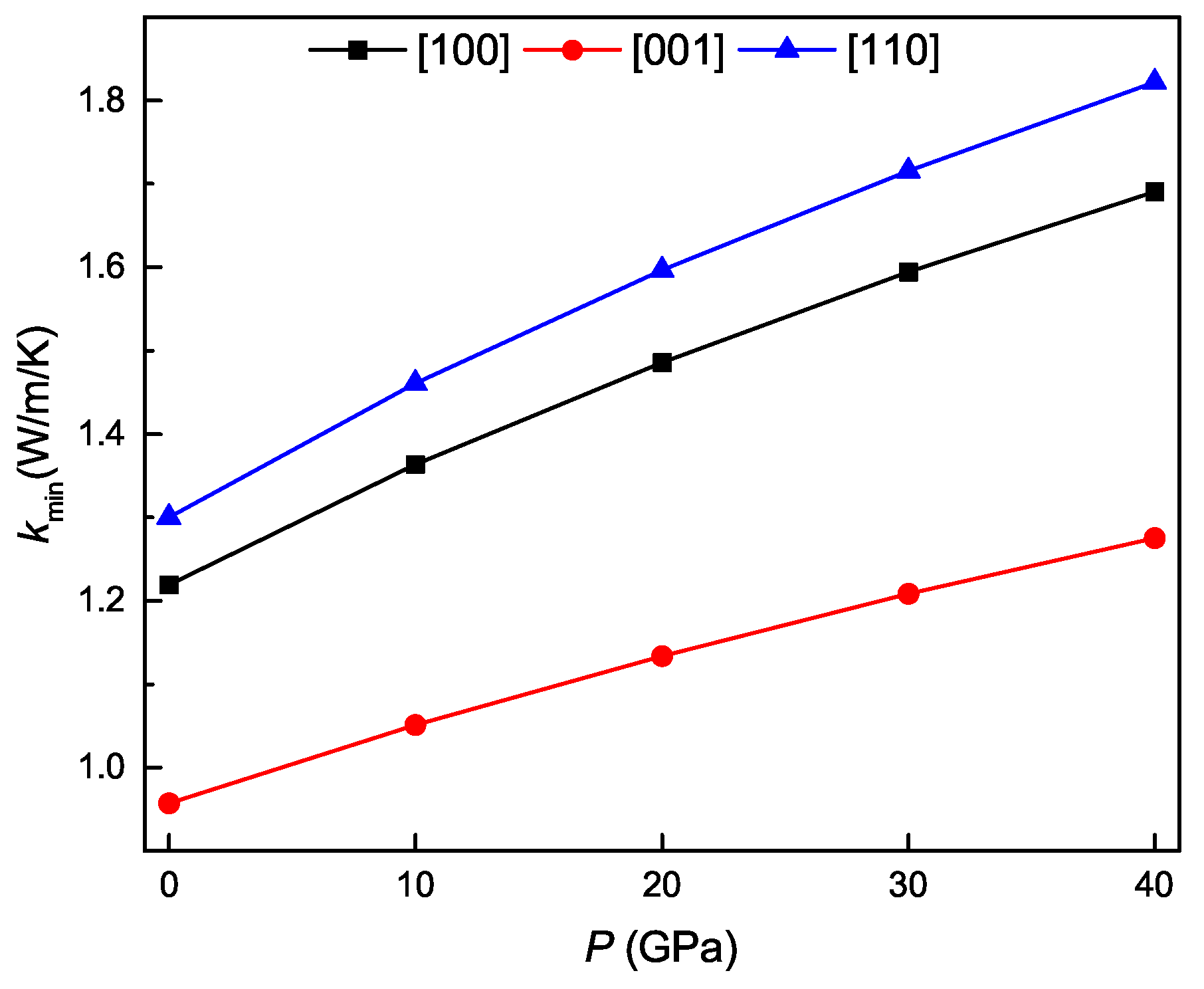
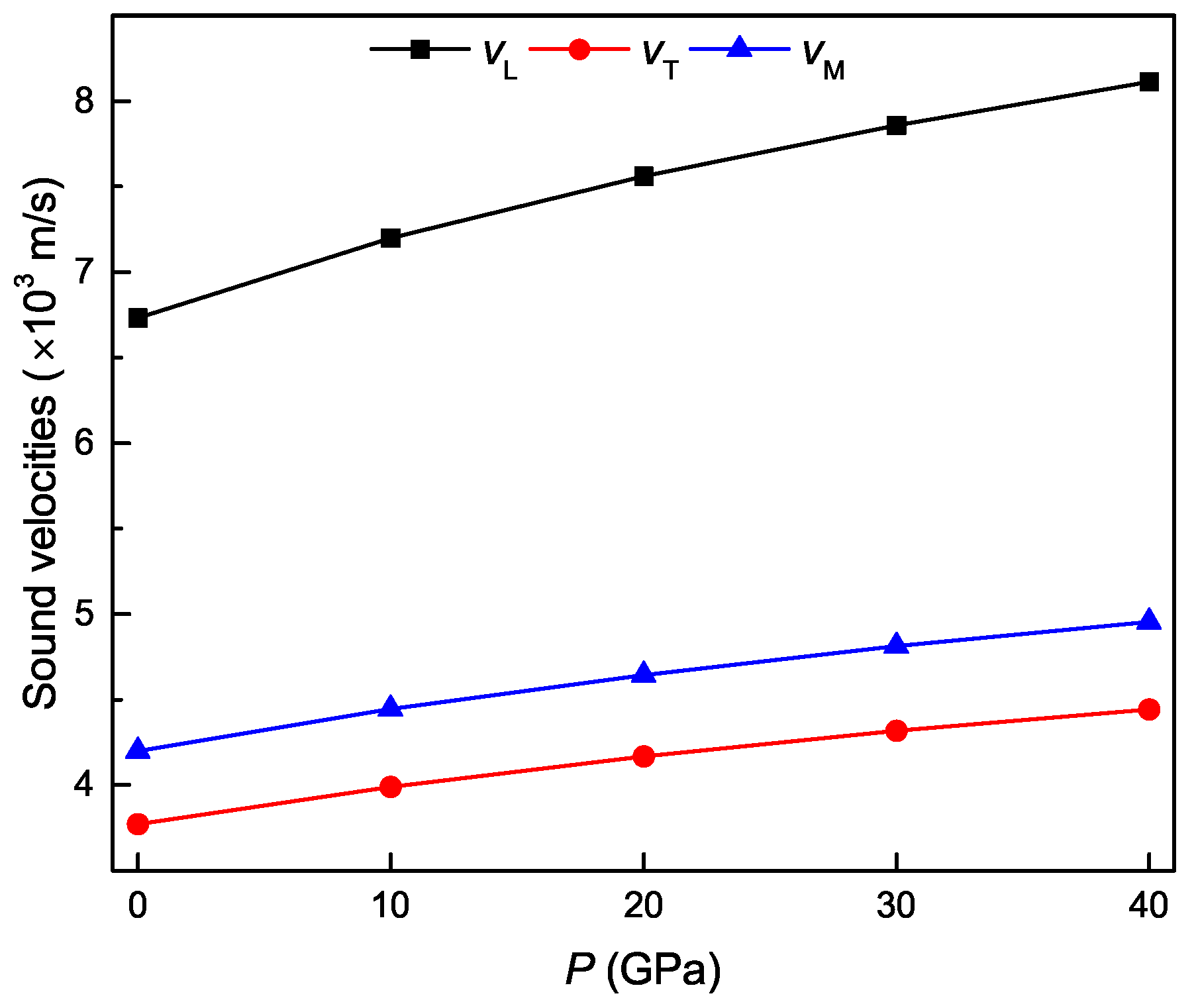
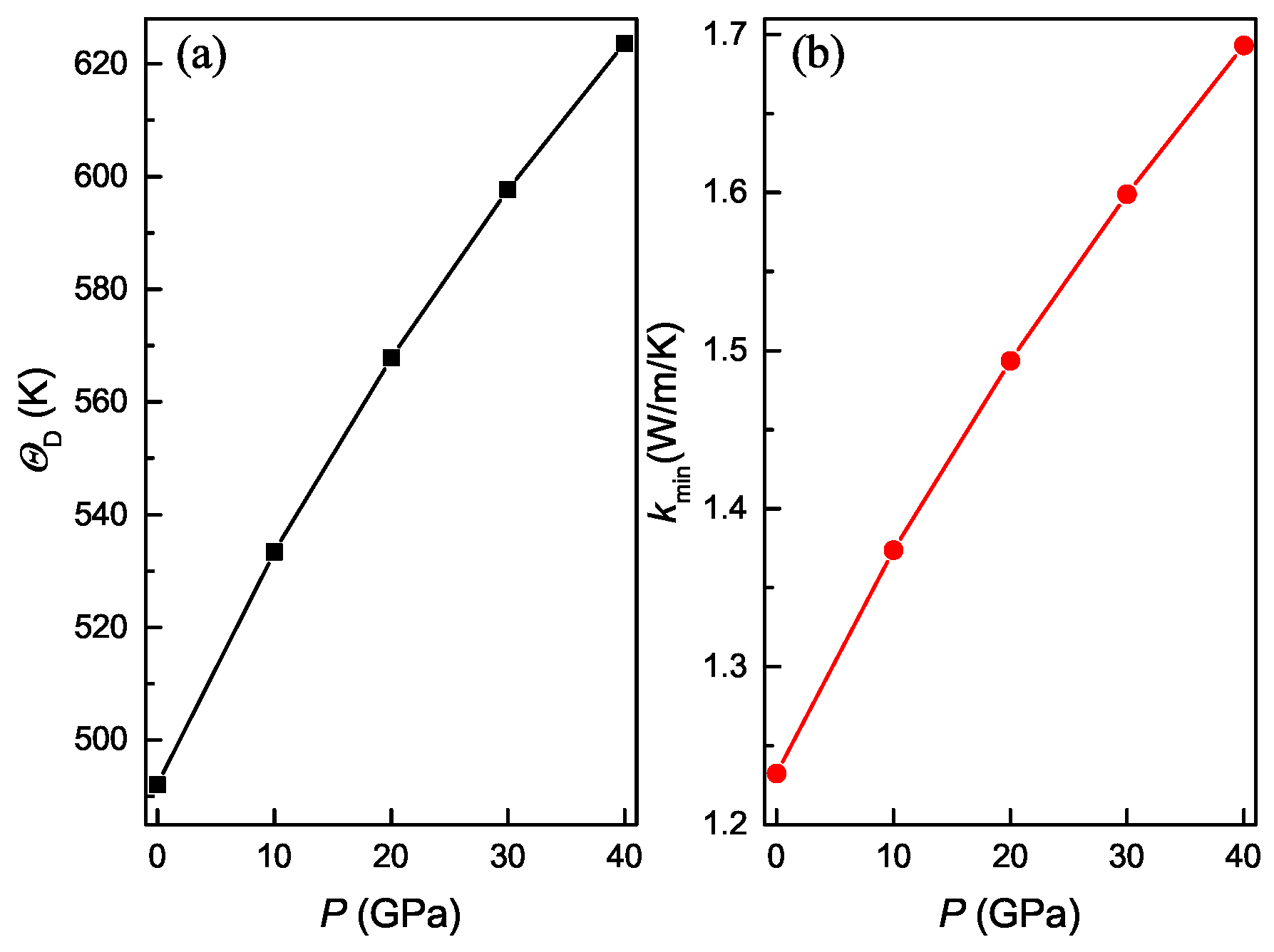
3.4. Pressure Dependence of Acoustic and Related Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liang, Y.F.; Xu, X.J.; Lin, J.P. Advances in phase relationship for high Nb-containing TiAl alloys. Rare Met. 2016, 35, 15–25. [Google Scholar] [CrossRef]
- Wesemann, J.; Falecki, W.; Frommeyer, G. Distribution of the transition metals V, Nb, Cr and their influence on the composition of the γ-phase of TiAl base alloys. Phys. Stat. Sol. (a) 2000, 177, 319–329. [Google Scholar] [CrossRef]
- Chen, G.L.; Wang, J.G.; Ni, X.D.; Ling, J.P.; Wang, Y.L. A new intermetallic compound in TiAl + Nb composition area of the Ti–Al–Nb ternary system. Intermetallics 2005, 13, 329–336. [Google Scholar] [CrossRef]
- Wang, J.G.; Chen, G.L.; Sun, Z.Q.; Ye, H.Q. Continuous ordering in the TiAl + Nb system. Intermetallics 1994, 2, 31–36. [Google Scholar]
- Chen, G.L.; Wang, X.T.; Ni, K.Q.; Hal, S.M.; Cao, J.X.; Ding, J.J.; Zhang, X. Investigation on the 1000, 1150 and 1400 °C isothermal section of the Ti-Al-Nb system. Intermetallics 1996, 4, 13–22. [Google Scholar] [CrossRef]
- Jewett, T.J. Comment on ‘Investigation on the 1000, 1150 and 1400 °C isothermal section of the Ti-Al-Nb system’. Intermetallics 1997, 5, 157–159. [Google Scholar] [CrossRef]
- Liu, H.W.; Yuan, Y.; Liu, Z.G.; Liu, J.M.; Zhao, X.N. TEM characterization of the precipitation reaction in Ti-48Al-10Nb alloys. Mater. Sci. Eng. A 2005, 412, 328–335. [Google Scholar] [CrossRef]
- Liu, H.W.; Luo, C.P.; Yuan, Y.; Liu, J.M.; Liu, Z.G. Interpretation of the morphology and crystallography of precipitate γ1-Ti4Nb3Al9 in L10-TiAl(Nb)-based intermetallics by invariant line theory. Intermetallics 2007, 15, 1497–1503. [Google Scholar]
- Zhang, X.J.; Hu, Y.F.; Zhang, L.Q.; Zheng, W.W.; Lin, J.P. The precipitatin processes of the γ1 phase in Ti–53Al–18Nb alloys. Scr. Mater. 2012, 66, 467–470. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, X.; Lin, J.; Chen, G. Infulence of heat treatment on the precipitation of γ1 phase in high Nb containing TiAl-based intermetallic alloys. Procedia Eng. 2012, 27, 1048–1053. [Google Scholar] [CrossRef]
- Chen, G.L.; Lin, J.P.; Song, X.P.; Wang, Y.L.; Ren, R.R. Development of high Nb containing high temperature TiAl alloys. In International Symposium on Niobium for High Temperature Applications; Kim, Y.-W., Carneiro, T., Eds.; Minerals, Metals & Materials Society: Warrendale, PA, USA, 2004; pp. 153–166. [Google Scholar]
- Kim, D.; Shang, S.L.; Liu, Z.K. Effects of alloying elements on elastic properties of Ni by first-principles calculations. Comput. Mater. Sci. 2010, 47, 254–260. [Google Scholar] [CrossRef]
- Music, D.; Schneider, J.M. Effect of transition metal additives on electronic structure and elastic properties of TiAl and Ti3Al. Phys. Rev. B 2006, 74, 174110–174114. [Google Scholar] [CrossRef]
- Liu, Y.L.; Liu, L.M.; Wang, S.Q.; Ye, H.Q. First-principles study of shear deformation in TiAl and Ti3Al. Intermetallics 2007, 15, 428–435. [Google Scholar] [CrossRef]
- Tang, P.; Tang, B.; Su, X. First-principles studies of typical long-period superstructures Al5Ti3, h-Al2Ti and r-Al2Ti in Al-rich alloys. Comp. Mater. Sci. 2011, 50, 1467–1476. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, L.; Liu, H.; Song, L. Ab initio study of the elastic and mechanical properties of B19 TiAl. Crystals 2017, 7, 39. [Google Scholar] [CrossRef]
- Wen, Y.; Zeng, X.; Hu, Z.; Peng, R.; Sun, J.; Song, L. A comparative first-principles study of tetragonal TiAl and Ti4Nb3Al9. Intermetallics 2018, 101, 72–80. [Google Scholar] [CrossRef]
- Pathak, A.; Singh, A.K. A first principles study of Ti2AlNb intermetallic. Solid State Commun. 2015, 204, 9–15. [Google Scholar] [CrossRef]
- Hu, K.; Huang, J.; Wei, Z.; Peng, Q.; Xie, Z.; Sa, B.; Wu, B. Elastic and thermodynamic properties of the Ti2AlNb orthorhombic phase from frist-principles calculations. Phys. Status Solidi B 2017, 254, 1600634. [Google Scholar] [CrossRef]
- He, Y.; Schwarz, R.B.; Migliori, A.; Whang, S.H. Elastic constants of single crystal γ-TiAl. J. Mater. Res. 1995, 10, 1187–1195. [Google Scholar] [CrossRef]
- Tanaka, K.; Koiwa, M. Single-crystal elastic constants of intermetallic compounds. Intermetallics 1996, 4, S29–S39. [Google Scholar] [CrossRef]
- Chu, F.; Mitchell, T.E.; Majumdar, B.; Miracle, D.; Nandy, T.K.; Banerjee, D. Elastic properties of the O phase in Ti-Al-Nb alloys. Intermetallics 1997, 5, 147–156. [Google Scholar] [CrossRef]
- Sot, R.; Kurzydłowski, K.J. Ab initio calculations of elastic properties of Ni3Al and TiAl under pressure. Mater. Sci. 2005, 23, 587–590. [Google Scholar]
- Fu, H.; Li, D.; Peng, F.; Gao, T.; Cheng, X. Structural and elastic properties of γTiAl under high pressure from electronic structure calculations. J. Alloy. Compd. 2009, 473, 255–261. [Google Scholar] [CrossRef]
- Zhang, C.; Hou, H.; Zhao, Y.; Yang, Z.; Guo, Y. First-principles study on structural, elastic and thermal properties of γ-TiAl and α2-Ti3Al phases in TiAl-based alloy under high pressure. Int. J. Mod. Phys. B 2017, 31. [Google Scholar] [CrossRef]
- Liu, L.; Wu, X.; Wang, R.; Nie, X.; He, Y.; Zou, X. First-principles investigations on structural and elastic properties of orthorhombic TiAl under pressure. Crystals 2017, 7, 111. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104–104117. [Google Scholar] [CrossRef]
- Wu, X.; Vanderbilt, D.; Hamann, D.R. Systematic treatment of displacements, and electric fields in density-functional perturbation theory. Phys. Rev. B 2005, 72, 035105–035117. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik; Taubner: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The elastic anisotropy of crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Brugger, K. Determination of third-order elastic coefficients in crystals. J. Appl. Phys. 1965, 36, 768–773. [Google Scholar] [CrossRef]
- Cahill, D.G.; Watson, S.K.; Pohl, R.O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 1992, 46, 6131–6140. [Google Scholar] [CrossRef]
- Schreiber, E.; Anderson, O.L.; Soga, N. Elastic Constants and Their Measurements; McGraw: New York, NY, USA, 1973. [Google Scholar]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104–224107. [Google Scholar] [CrossRef]
- Wen, Y.; Wu, D.; Cao, R.; Liu, L.; Song, L. The third-order elastic moduli and Debye temperature of SrFe2As2 and BaFe2As2: a first-principles study. J. Supercond. Nov. Magn. 2017, 30, 1749–1756. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Frantsevich, I.N.; Voronov, F.F.; Bokuta, S.A. Elastic Constants and Elastic Moduli of Metals and Insulators Handbook; Frantsevich, I.N., Ed.; Naukova Dumka: Kiev, Ukraine, 1983; pp. 60–180. [Google Scholar]
- Callaway, J. Model for lattice thermal conductivity at low temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
| Method | a | c | ||||||
|---|---|---|---|---|---|---|---|---|
| Present | 5.6510 | 8.2051 | 219.36 | 56.83 | 83.43 | 185.91 | 104.86 | 24.71 |
| Exp. [4,5] | 5.58–5.84 | 8.15–8.45 | ||||||
| Exp. [3] | 5.607 | 8.270 | ||||||
| Theo. [17] | 5.651 | 8.205 | 222.71 | 60.27 | 87.99 | 187.36 | 104.77 | 23.06 |
| P | a | c | V | ||
|---|---|---|---|---|---|
| 0 | 5.6510 | 8.2051 | 1.4520 | 262.02 | 4.5194 |
| 10 | 5.5224 | 8.0042 | 1.4494 | 244.10 | 4.8511 |
| 20 | 5.4209 | 7.8525 | 1.4486 | 230.75 | 5.1317 |
| 30 | 5.3379 | 7.7269 | 1.4475 | 220.16 | 5.3785 |
| 40 | 5.2685 | 7.6168 | 1.4457 | 211.42 | 5.6009 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Peng, R.; Yu, Y.; Hu, Z.; Wen, Y.; Song, L. First-Principles Calculations on Structural Property and Anisotropic Elasticity of γ1-Ti4Nb3Al9 under Pressure. Materials 2018, 11, 2025. https://doi.org/10.3390/ma11102025
Zeng X, Peng R, Yu Y, Hu Z, Wen Y, Song L. First-Principles Calculations on Structural Property and Anisotropic Elasticity of γ1-Ti4Nb3Al9 under Pressure. Materials. 2018; 11(10):2025. https://doi.org/10.3390/ma11102025
Chicago/Turabian StyleZeng, Xianshi, Rufang Peng, Yanlin Yu, Zuofu Hu, Yufeng Wen, and Lin Song. 2018. "First-Principles Calculations on Structural Property and Anisotropic Elasticity of γ1-Ti4Nb3Al9 under Pressure" Materials 11, no. 10: 2025. https://doi.org/10.3390/ma11102025
APA StyleZeng, X., Peng, R., Yu, Y., Hu, Z., Wen, Y., & Song, L. (2018). First-Principles Calculations on Structural Property and Anisotropic Elasticity of γ1-Ti4Nb3Al9 under Pressure. Materials, 11(10), 2025. https://doi.org/10.3390/ma11102025






