Properties of Novel Non-Silicon Materials for Photovoltaic Applications: A First-Principle Insight
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Structural Properties
3.2. Electronic Properties
3.3. Effective Mass Calculation
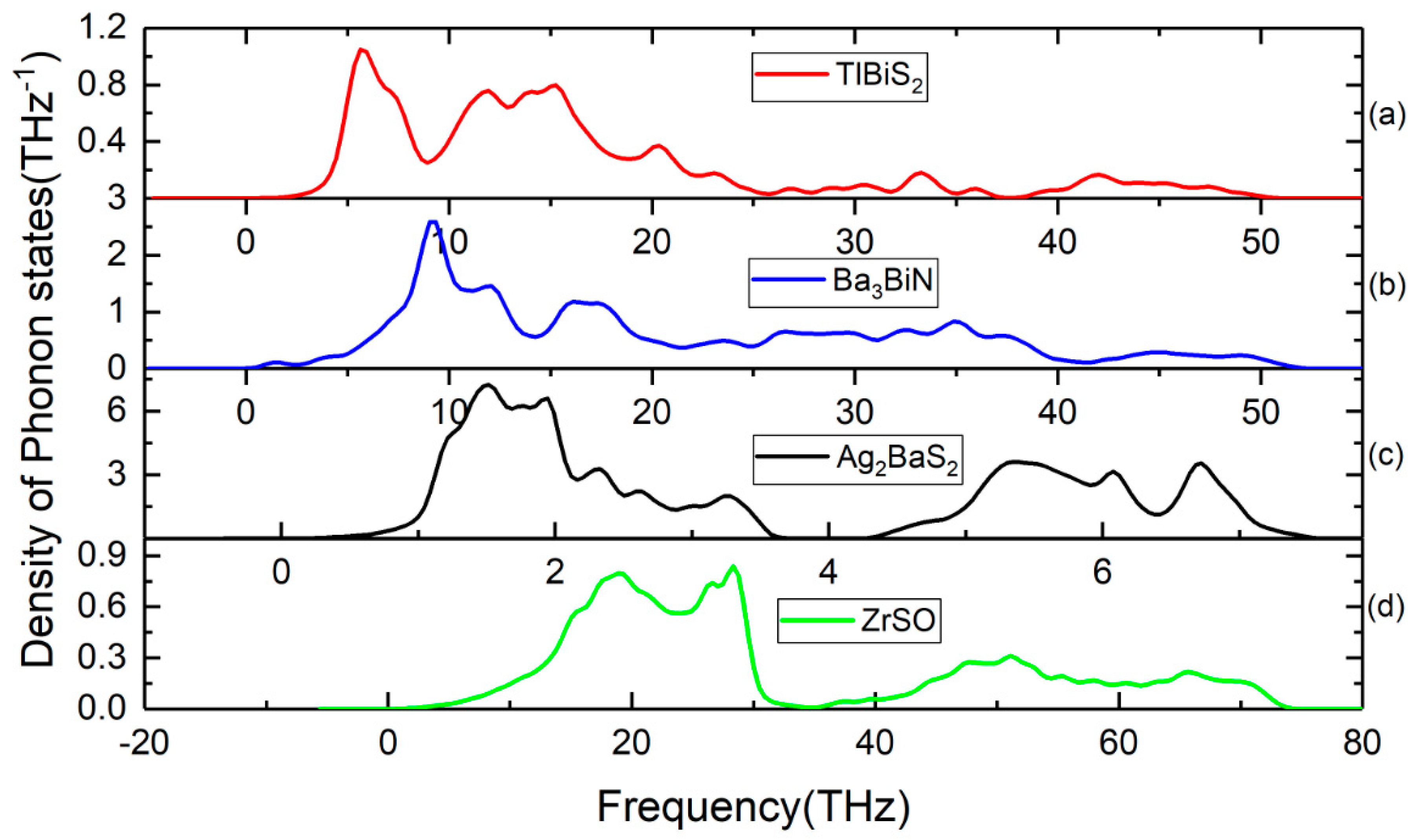
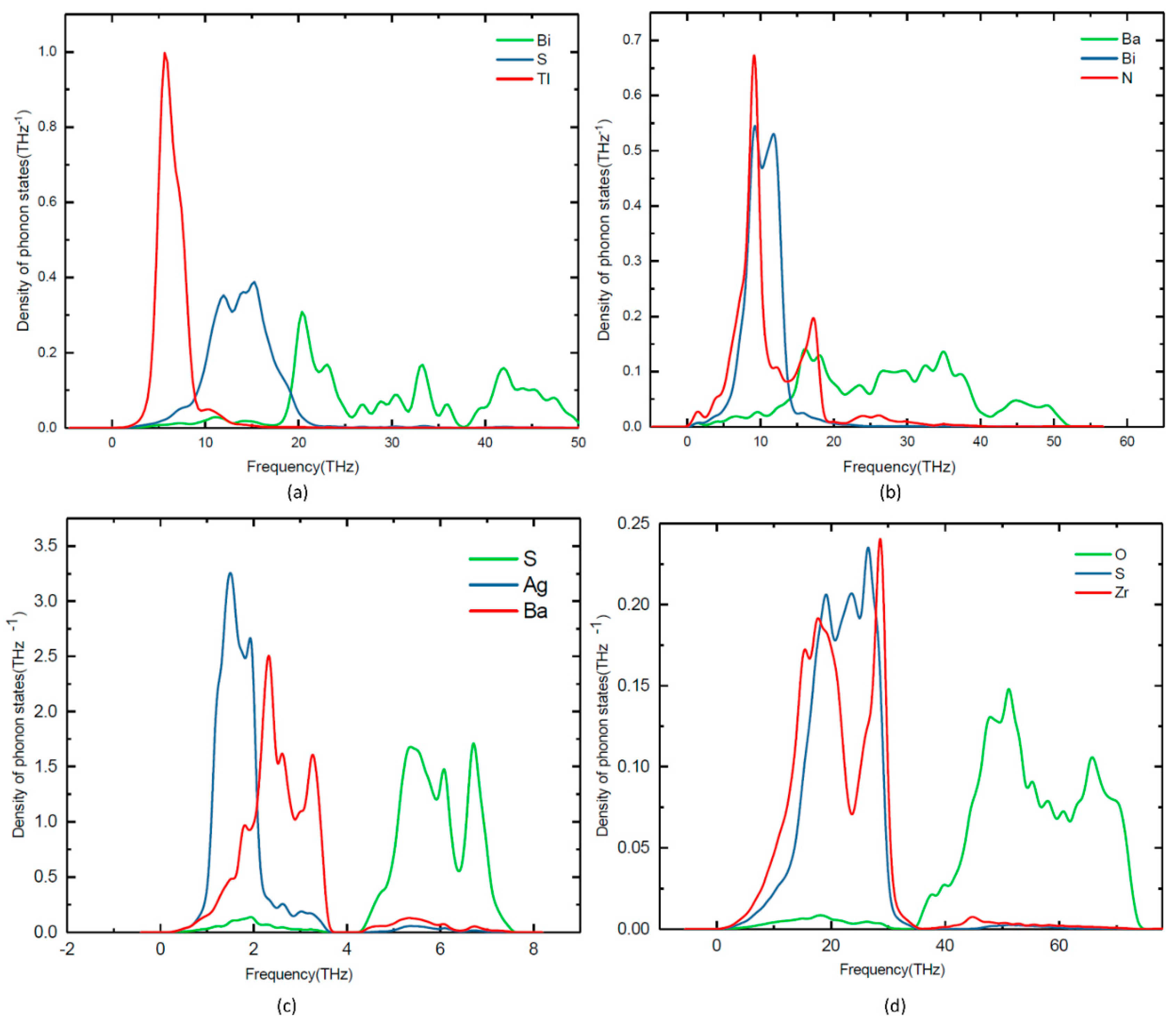
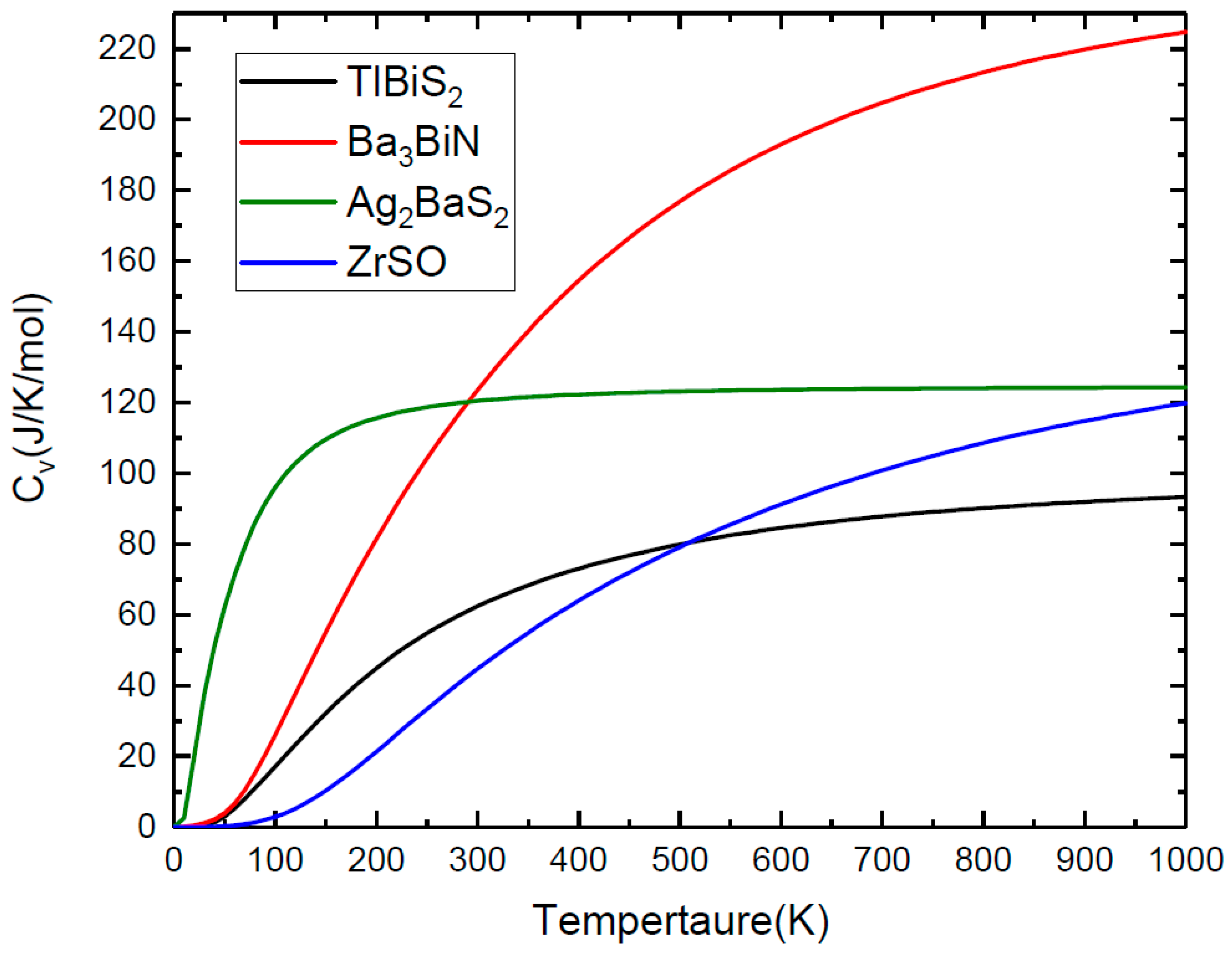
3.4. Lattice Dynamic Stability
3.5. Mechanical Stability
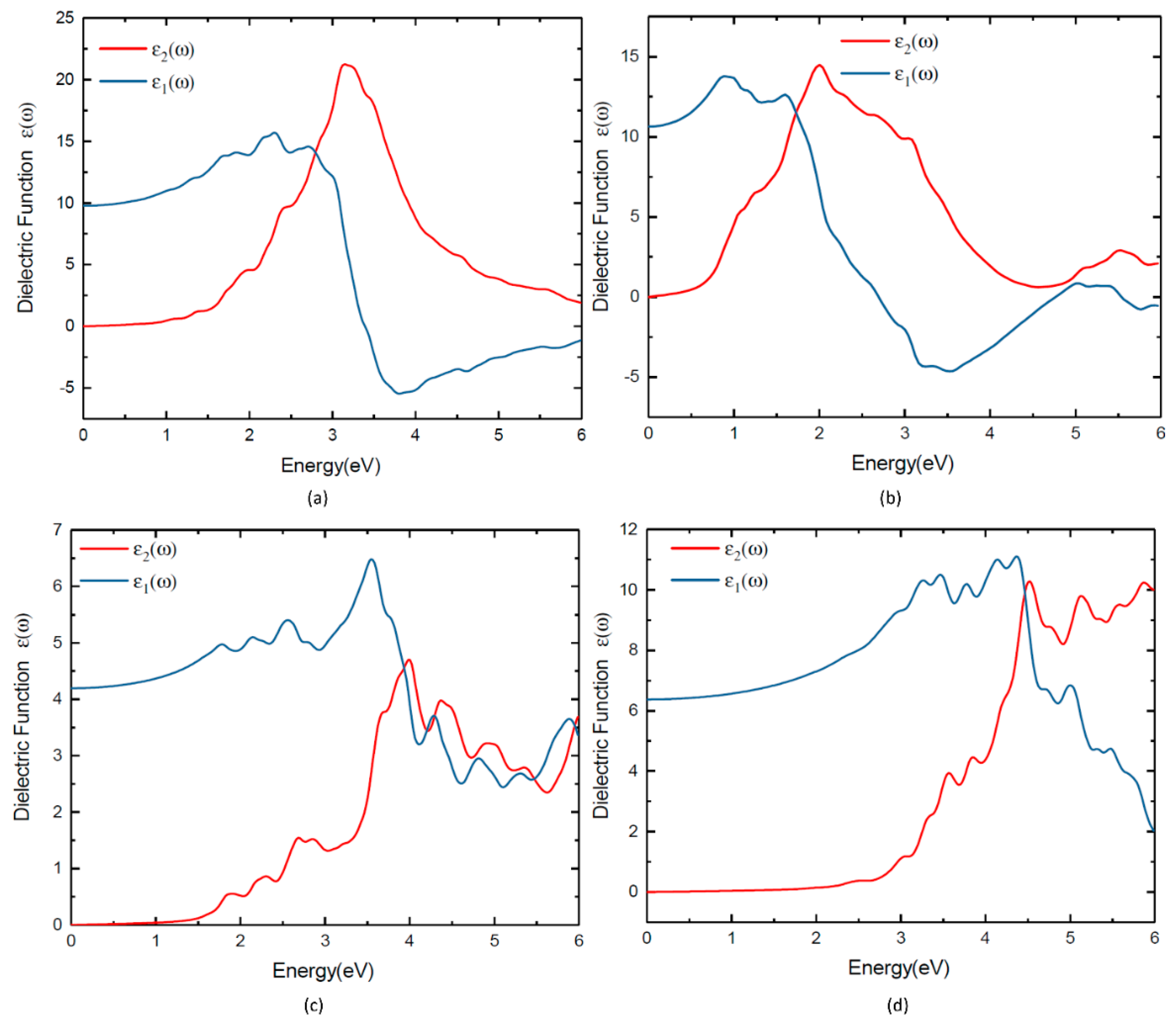
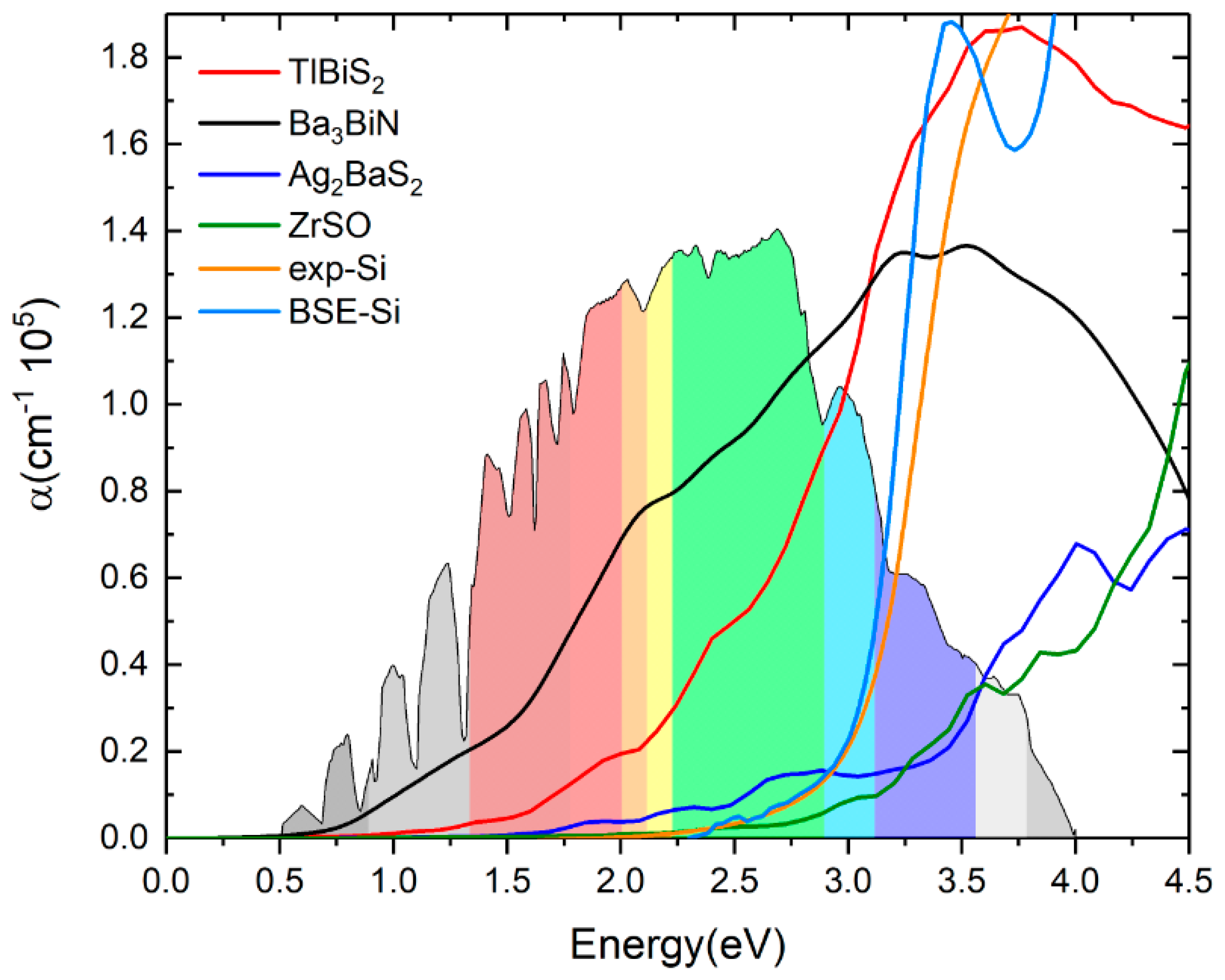
3.6. Optical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Unold, T.; Schock, H.-W. Nonconventional (non-silicon-based) photovoltaic materials. Annu. Rev. Mater. Res. 2011, 41, 297–321. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Goetzberger, A.; Hebling, C.; Schock, H.-W. Photovoltaic materials, history, status and outlook. Mater. Sci. Eng. R Rep. 2003, 40, 1–46. [Google Scholar] [CrossRef]
- Bube, R.H. Materials for photovoltaics. Annu. Rev. Mater. Sci. 1990, 20, 19–50. [Google Scholar] [CrossRef]
- Birkmire, R.W.; Eser, E. Polycrystalline thin film solar cells: Present status and future potential. Annu. Rev. Mater. Sci. 1997, 27, 625–653. [Google Scholar] [CrossRef]
- Mitchell, K.W. Status of new thin-film photovoltaic technologies. Annu. Rev. Mater. Sci. 1982, 12, 401–413. [Google Scholar] [CrossRef]
- Boer, K.; Rothwarf, A. Materials for solar photovoltaic energy conversion. Annu. Rev. Mater. Sci. 1976, 6, 303–333. [Google Scholar] [CrossRef]
- Rasukkannu, M.; Velauthapillai, D.; Vajeeston, P. Computational modeling of novel bulk materials for the intermediate-band solar cells. ACS Omega 2017, 2, 1454–1462. [Google Scholar] [CrossRef]
- Rasukkannu, M.; Velauthapillai, D.; Vajeeston, P. A first-principle study of the electronic, mechanical and optical properties of inorganic perovskite Cs2SnI6 for intermediate-band solar cells. Mater. Lett. 2018, 218, 233–236. [Google Scholar] [CrossRef]
- Hellenbrandt, M. The inorganic crystal structure database (ICSD)—Present and future. Crystallogr. Rev. 2004, 10, 17–22. [Google Scholar] [CrossRef]
- Ponniah, V. Density Functional Theory Based Database (DFTBD); University of Oslo: Oslo, Norway, 2013. [Google Scholar]
- Rasukkannu, M.; Velauthapillai, D.; Ponniah, V. A promising high-efficiency photovoltaic alternative non-silicon material: A first-principle investigation. Scr. Mater. 2018, 156, 134–137. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.; Botton, G.; Savrasov, S.Y.; Szotek, Z.; Temmerman, W.; Sutton, A. Electronic structure and elastic properties of strongly correlated metal oxides from first principles: LSDA+ U, SIC-LSDA and EELS study of UO2 and NiO. Phys. Status Solidi A 1998, 166, 429–443. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Liechtenstein, A.; Anisimov, V.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Paier, J.; Marsman, M.; Kresse, G. Dielectric properties and excitons for extended systems from hybrid functionals. Phys. Rev. B 2008, 78, 121201. [Google Scholar] [CrossRef]
- Aroyo, M.I.; Perez-Mato, J.M.; Capillas, C.; Kroumova, E.; Ivantchev, S.; Madariaga, G.; Kirov, A.; Wondratschek, H. Bilbao Crystallographic Server: I. Databases and crystallographic computing programs. Z. Krist. Cryst. Mater. 2006, 221, 15–27. [Google Scholar] [CrossRef]
- Aroyo, M.I.; Kirov, A.; Capillas, C.; Perez-Mato, J.; Wondratschek, H. Bilbao Crystallographic Server. II. Representations of crystallographic point groups and space groups. Acta Crystallogr. Sect. A Found. Crystallogr. 2006, 62, 115–128. [Google Scholar] [CrossRef] [PubMed]
- Aroyo, M.I.; Perez-Mato, J.; Orobengoa, D.; Tasci, E.; De La Flor, G.; Kirov, A. Crystallography online: Bilbao crystallographic server. Bulg. Chem. Commun. 2011, 43, 183–197. [Google Scholar]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A Cryst. Phys. Diffr. Theor. Gen. Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Gäbler, F.; Kirchner, M.; Schnelle, W.; Schwarz, U.; Schmitt, M.; Rosner, H.; Niewa, R. (Sr3N) E and (Ba3N) E (E = Sb, Bi): Synthesis, crystal structures, and physical properties. Z. Anorg. Allg. Chem. 2004, 630, 2292–2298. [Google Scholar] [CrossRef]
- Steinbrenner, U.; Simon, A. Ba3N–a new binary nitride of an alkaline earth metal. Z. Anorg. Allg. Chem. 1998, 624, 228–232. [Google Scholar] [CrossRef]
- Bronger, W.; Lenders, B.; Huster, J. BaAg2S2, ein Thioargentat im CaAl2Si2-Strukturtyp. Z. Anorg. Allg. Chem. 1997, 623, 1357–1360. [Google Scholar] [CrossRef]
- McCullough, J.D.; Brewer, L.; Bromley, L. The crystal structure of zirconium oxysulfide, ZrOS. Acta Crystallogr. 1948, 1, 287–289. [Google Scholar] [CrossRef]
- Jellinek, F.; Songstad, J.; Viljanto, J.; Seppälä, P.; Theander, O.; Flood, H. A Tetragonal Form of Zirconium Oxide Sulfide, ZrOS. Acta Chem. Scand. 1962, 16, 791–792. [Google Scholar] [CrossRef]
- Singh, B.; Lin, H.; Prasad, R.; Bansil, A. Topological phase transition and quantum spin Hall state in TlBiS2. J. Appl. Phys. 2014, 116, 033704. [Google Scholar] [CrossRef]
- Ullah, I.; Murtaza, G.; Khenata, R.; Mahmood, A.; Muzzamil, M.; Amin, N.; Saleh, M. Structural and Optoelectronic Properties of X3ZN (X = Ca, Sr, Ba; Z = As, Sb, Bi) Anti-Perovskite Compounds. J. Electron. Mater. 2016, 45, 3059–3068. [Google Scholar] [CrossRef]
- Krishnapriyan, A.; Barton, P.T.; Miao, M.; Seshadri, R. First-principles study of band alignments in the p-type hosts BaM2X2 (M = Cu, Ag; X = S, Se). J. Phys. Condens. Matter 2014, 26, 155802. [Google Scholar] [CrossRef] [PubMed]
- Fonari, A.; Sutton, C. Effective Mass Calculator for Semiconductors. 2015. Available online: https://github.com/afonari/emc (accessed on 2 July 2018).
- Van Zeghbroeck, B. Principles of Semiconductor Devices; Colarado University: Denver, CO, USA, 2004. [Google Scholar]
- Ashcroft, N. ND Mermin Solid State Physics WB Saunders Company; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef]
- Yang, L.-M.; Vajeeston, P.; Ravindran, P.; Fjellvåg, H.; Tilset, M. Revisiting isoreticular MOFs of alkaline earth metals: A comprehensive study on phase stability, electronic structure, chemical bonding, and optical properties of A–IRMOF-1 (A = Be, Mg, Ca, Sr, Ba). Phys. Chem. Chem. Phys. 2011, 13, 10191–10203. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, S.; Reining, L.; Del Sole, R.; Onida, G. Ab initio calculation of excitonic effects in the optical spectra of semiconductors. Phys. Rev. Lett. 1998, 80, 4510. [Google Scholar] [CrossRef]
- Bokdam, M.; Sander, T.; Stroppa, A.; Picozzi, S.; Sarma, D.; Franchini, C.; Kresse, G. Role of polar phonons in the photo excited state of metal halide perovskites. Sci. Rep. 2016, 6, 28618. [Google Scholar] [CrossRef] [PubMed]
- Rohlfing, M.; Louie, S.G. Electron-hole excitations in semiconductors and insulators. Phys. Rev. Lett. 1998, 81, 2312. [Google Scholar] [CrossRef]
- Aspnes, D.E.; Studna, A. Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 ev. Phys. Rev. B 1983, 27, 985. [Google Scholar] [CrossRef]


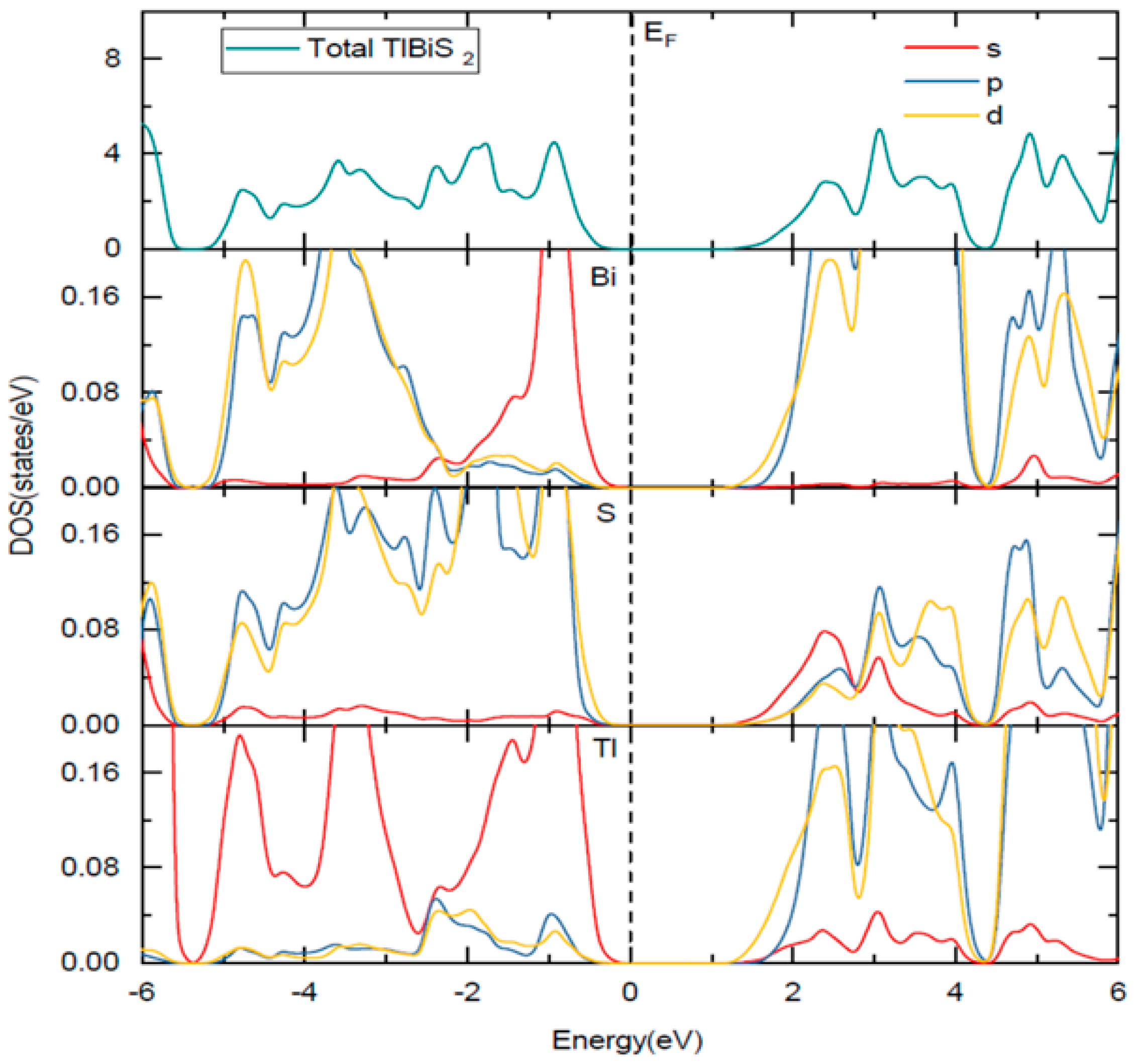
| Compounds | GGA (eV) | HSE06 (eV) | Type of Band Gap |
|---|---|---|---|
| TlBiS2 | 0.505 | 1.10 | direct |
| Ba3BiN | 0.679 | 1.29 | direct |
| Ag2BaS2 | 0.716 | 1.95 | direct |
| ZrSO | 0.891 | 2.60 | direct |
| Serial No. | Plane Directions | Compound | m*lh × me | m*hh × me | m*e × me |
|---|---|---|---|---|---|
| 1. | 110 | TlBiS2 | 0.182 | 0.224 | 0.154 |
| 2. | 110 | Ba3BiN | 0.016 | 0.165 | 0.092 |
| 3. | 110 | Ag2BaS2 | 0.150 | 0.728 | 0.149 |
| 4. | 110 | ZrSO | 0.308 | 0.482 | 0.361 |
| Compounds | Supercell Size | Number of Atoms | ZPE (eV) | Dynamical Stability |
|---|---|---|---|---|
| TlBiS2 | 2 × 2 × 2 | 32 | 0.4045 | stable |
| Ba3BiN | 2 × 2 × 2 | 80 | 1.3050 | stable |
| Ag2BaS2 | 2 × 2 × 2 | 40 | 0.1093 | stable |
| ZrSO | 2 × 2 × 2 | 48 | 1.2100 | stable |
| Properties | TlBiS2 | Ba3BiN | Ag2BaS2 | ZrSO |
|---|---|---|---|---|
| Cij | C11 = 63.47 C12 = 34.68 C13 = 27.49 C14 = 0.608 C33 = 88.90 C44 = 28.90 | C11 = 56.604 C12 = 14.1 C13 = 7.947 C33 = 75.35 C44 = 21.20 | C11 = 84.61 C12 = 31.538 C13 = 34.611 C14 = 0.0732 C33 = 89.994 C44 = 26.642 C66 = 14.590 | C11 = 293.04 C12 = 133.66 C13 = 118.96 C33 = 303.06 C44 = 100.64 C66 = 91.94 |
| BV | 44.85 | 27.762 | 51.59 | 181.407 |
| BR | 44.46 | 27.5620 | 51.28 | 181.39 |
| BVRH | 44.65 | 27.662 | 51.34 | 181.403 |
| GV | 54.99 | 47.7264 | 53.45 | 194.92 |
| GR | 21.08 | 5.70729 | 19.24 | 90.88 |
| GVRH | 38.04 | 26.716 | 36.35 | 142.90 |
| Ductility | 0.852 | 0.96 | 0.708 | 0.7877 |
| σ | 0.168 | 0.1346 | 0.213 | 0.188 |
| E | 89 | 61 | 29 | 339 |
| compressibility | 0.022 | 0.04 | 0.02 | 0.0055 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasukkannu, M.; Velauthapillai, D.; Bianchini, F.; Vajeeston, P. Properties of Novel Non-Silicon Materials for Photovoltaic Applications: A First-Principle Insight. Materials 2018, 11, 2006. https://doi.org/10.3390/ma11102006
Rasukkannu M, Velauthapillai D, Bianchini F, Vajeeston P. Properties of Novel Non-Silicon Materials for Photovoltaic Applications: A First-Principle Insight. Materials. 2018; 11(10):2006. https://doi.org/10.3390/ma11102006
Chicago/Turabian StyleRasukkannu, Murugesan, Dhayalan Velauthapillai, Federico Bianchini, and Ponniah Vajeeston. 2018. "Properties of Novel Non-Silicon Materials for Photovoltaic Applications: A First-Principle Insight" Materials 11, no. 10: 2006. https://doi.org/10.3390/ma11102006
APA StyleRasukkannu, M., Velauthapillai, D., Bianchini, F., & Vajeeston, P. (2018). Properties of Novel Non-Silicon Materials for Photovoltaic Applications: A First-Principle Insight. Materials, 11(10), 2006. https://doi.org/10.3390/ma11102006






