Abstract
Based on the genetic algorithm (GA) incorporated with density functional theory (DFT) calculations, the structural and electronic properties of neutral and charged arsenic clusters Asn (n = 2–24) are investigated. The size-dependent physical properties of neutral clusters, such as the binding energy, HOMO-LUMO gap, and second difference of cluster energies, are discussed. The supercluster structures based on the As8 unit and As2 bridge are found to be dominant for the larger cluster Asn (n ≥ 8). Furthermore, the possible geometric structures of As28, As38, and As180 are predicted based on the growth pattern.
1. Introduction
In recent years, due to the fast development of nanotechnology, people are more interested in atomic clusters, which are composed of several to thousands of atoms, molecules, or ions through a physical or chemical bonding force [1]. Clusters can also be regarded as the transitional forms between atoms and bulk, and their fundamental properties depend vitally on the cluster size. Therefore, it is quite meaningful to study the structural and electronic properties of clusters using theoretical research, identifying their potential capacities for numerous applications. Arsenic has been widely applied in many fields such as semiconductors, optoelectronics, and biopharmaceutics [2,3,4,5,6,7,8,9,10,11]. Besides, vanadium doped phosphorus clusters, and pure and doped arsenic clusters have received a large amount of attention from both experimental and theoretical fields in recent years [12,13,14,15,16,17,18,19,20,21,22,23].
Experimentally, the study of Asn clusters has focused on small-sized clusters with n ≤ 5 [12,13,14,15,16,17]. For example, Wang et al. [12] utilized high-resolution photoelectron spectroscopy to study the electronic vibration and spin orbit of As4. Bennett et al. [13] have measured the appearance potentials and ion translational energies for the As1, As2, and As3 ions formed by the dissociative resonance capture of As4. Lippa et al. [14] have probed the electron affinities of Asn (n = 1–5) using photoelectron spectra in 1998. Brumbach and Rosenblatt [15] have investigated the vibrational modes of As4 with Raman spectroscopy. Yonezo [16] designed a high-temperature nozzle assembly for gas-electron diffraction to determine the structure of As4. Jeffrey et al. [17] measured the ionization potentials (IPs) for Asn (n = 1–5) using gas-phase charge-transfer reactions. No experimental data are available for Asn with n ≥ 6 right now.
In the theoretical aspect, Zhao et al. [18] and Bai et al. [21] studied the structures, thermochemistry, and electron affinities of Asn (n = 1–16) and their anions. Their results showed that the even-numbered neutral Asn species are more stable than the odd-numbered clusters, but the even-numbered anionic Asn species are less stable than the odd-numbered species. Liang et al. [19] probed the electronic structure and property of neutral and charged arsenic clusters Asn(+1,0,−1) (n = 2–8). At the B3LYP/6-311+G(d) theoretical level, Guo [20] investigated the geometries and energies for neutral and charged Asn (n = 2–15) clusters, and reported their relative stability, ionization potential, and electron affinity. Baruah et al. [23] using a generalized gradient approximation (GGA) to explore the geometry, vibrational modes, and polarizabilities, as well as the infrared and Raman spectra of fullerene-like arsenic cages with n = 4, 8, 20, 28, 32, 36, and 60. Zhao et al. [22] investigated the structures and electronic properties of Asn clusters with even-numbered Asn (n = 6–28) using density functional theory (DFT) with the Perdew–Burke–Ernzerhof functional and a doubled numerical basis set with d-polarization functions(PBE/DND) scheme and found that the supercluster structures based on As4, As6, and As8 units, and the As2 bridge were dominant for the larger Asn with n ≥ 14.
Although many theoretical works have been performed on the Asn clusters, all the results are always most of the artificial speculation studies to investigate the structure of clusters in certain symmetries. In this work, we have performed a genetic algorithm (GA) incorporated with density functional theory (DFT) calculations to explore the structures and electronic properties of Asn (n = 2–24) neutral and charged clusters. After we have determined the growth pattern of Asn clusters, the possible geometric structures of As28, As38, and As180 are predicted based on the growth pattern. We also discussed the size-dependent physical properties of neutral clusters such as the binding energy, HOMO-LUMO gap and second difference of cluster energies.
2. Computational Methodology
In order to search the global minimum structures of Asn clusters, we combined a genetic algorithm (GA) simulation with local optimization at the Dmol3 level [24,25,26,27,28,29]. The fundamental aim in GA is to divide the potential-energy surface (PES) into a number of regions and find the locally stable isomers in each region. In the GA program, we generated 15 Asn (n = 3–12) and 20 Asn (n = 13–24) initial populations to ensure that we could find the local minimum. Any population can be chosen as parents to generate their child cluster according to a crossover operation. In addition, there was a possibility of a 30% mutation rate for a single parent to produce child alone. The child cluster was optimized with Dmol3, and then compared with its parent in energy. The child with lower energy replaced its high-energy parent. The whole process of genetic algorithm with 2000 iterations was to ensure we got the lowest energy structure.
The optimization of Asn (n = 2–24) clusters was performed using DFT with the Perdew–Burke–Ernzerhof (PBE) [24] exchange-correlation functional and an all-electron basis set of the double-numerical-plus-d-polarization (DND) type, as implemented in the Dmol3 [25] package. A self-consistent field calculation kept the accuracy with an energy convergence for 10−6 a.u., and the forces for 2 × 10−3 a.u. There was no symmetry restriction for geometry optimization.
For each Asn (n = 2–24) cluster, we saved ten energetically lower isomer structures for further electronic structure calculations, which were performed using the Vienna Ab-initio Simulation Package (VASP) codes. The Kohn–Sham equations were solved variationally in a plane wave basis set using the projector-augmented-wave (PAW) method. The exchange-correlation energy was described by the functional of Perdew, Burke, and Ernzerhof (PBE) based on the generalized gradient approximation (GGA). The energy cutoff was set to be 400 eV and the vacuum space was set to be at least 14 Å to separate the interactions between the neighboring slabs. Only the Gamma k-point was used to sample the Brillouin zone for the geometry and electronic structure calculations. All structures were fully relaxed by Gaussian smearing and electronic structure calculations by tetrahedron smearing method until the convergence criteria (with the force less than 0.02 eV/Å and the energy less than 10−5 eV). Although each structure of Asn (n = 2–24) cluster was further optimized by VASP, the energy sequencing of each cluster was basically unchanged.
3. Results and Discussions
3.1. Asn (n = 2–8) Clusters
The bond length of an As2 cluster (2a in Figure 1) is 2.103 Å through experimental measurement [30]. In our calculation the distance between the As atoms was 2.118 Å, which is closer to the experimental data compared with the 2.142 Å calculated using PBE/DND methods [22].
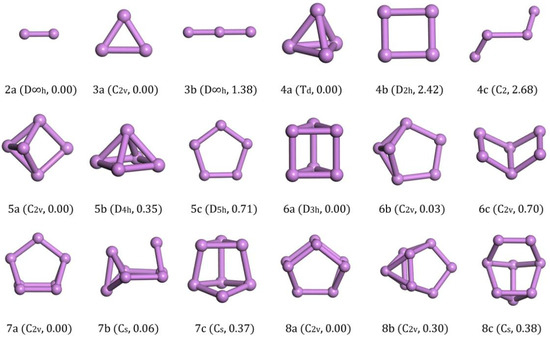
Figure 1.
Lowest-energy and isomorphic structures for Asn (n = 2–8) clusters. The relative total energies are in eV.
For the As3 cluster, the energy of the structure with C2v symmetry (3a in Figure 1) was the global minimum. It was an isosceles triangle structure with a top angle of 65.14° and side length of 2.325 Å. It was energetically lower than the linear chain structure with D∞h symmetry (3b in Figure 1), in which structure, the bond length was 2.204 Å.
The ground-state structure of As4 with Td symmetry (4a in Figure 1) was a regular tetrahedron, which was consistent with the previous reports [18,19,20]. Its energy was much lower than other isomorphic configurations. The energy of the rectangular structure with D2h symmetry (4b in Figure 1) was 0.605 eV/atom higher than that of the ground state and the chain structure with C2 symmetry (4c in Figure 1) was energetically higher than the rectangular structure.
The lowest energy structure of As5 had C2v symmetry (5a in Figure 1) and it may be considered as adding an atom in the cross section of a dihedral formed by four atoms. It had 0.07 eV/atom less energy than the rectangular pyramid structure with D4h symmetry (5b in Figure 1) and 0.142 eV/atom less than the planar structure with D5h symmetry (5c in Figure 1).
The trigonal prism with D3h symmetry (6a in Figure 1) was the ground-state structure for As6 and was only 0.005 eV/atom lower than the benzvalene type with C2v symmetry (6b in Figure 1) and 0.117 eV/atom lower than the dihedral angle structure of six atoms with C2v symmetry (6c in Figure 1). The side length was 2.522 Å and the edge length was 2.559 Å. Our ground state was consistent with the result calculated by B3LYP/6-311+G(d) [20] or PBE/DND methods [22]. However, the structure 6b in Figure 1 was found to be the lowest energy by Liang [19] using MP2(full)/g-31G(d) methods and Bai [21] using B3LYP/DZP++ methods. As the outer shell structure of As is 3s23p3, we think our results are reasonable as the completely three-coordination structure (6a in Figure 1) must be more stable than the structure with two two-coordinations (6b in Figure 1).
In the case of As7, the ground-state structure with C2v symmetry (7a in Figure 1) could be derived from the trigonal prism of As6 by edge-capping with an additional As atom. This low-energy structure is also predicted in Refs. [19,20,21]. Its energy was lower than the structure with Cs symmetry (7b in Figure 1) by 0.008 eV/atom and the structure with Cs symmetry (7c in Figure 1) by 0.053 eV/atom.
The wedge-like structure that looks like a cage with C2v symmetry was obtained as the lowest energy structure for As8, as seen from 8a in Figure 1. It was energetically lower than the structure with C2v symmetry (8b in Figure 1) by 0.038 eV/atom and the structure with Cs symmetry (8c in Figure 1) by 0.048 eV/atom. We also checked the cage structure with Oh symmetry cut from the bulk phase reported by Baruah [23], and we found that it was 0.64 eV energy higher than our ground state structure.
After analysis of the ground structures of Asn (n = 2–8) clusters, we find that As2 was a one-dimensional bridge, As3 was a two-dimensional isosceles triangle and As4 became a three-dimensional tetrahedron. When n was larger than 3, the two-dimensional cluster structure, such as 4b and 5c in Figure 1, sorts more and more backward energetically. We can conclude that the structure of small As clusters tends towards a three-dimensional cage structure and it was not stable for a 2-D planar structure.
3.2. Asn (n = 9–18) Clusters
The ground-state structure of As9 with Cs symmetry (9a in Figure 2) could be regarded as being derived from a cage-like As8 structure by attaching an As atom at one side. The isomers (C2v) with a higher symmetry (9b,c in Figure 2) were less stable based on our VASP calculations. It also hinted to us that the ground structure of As8 might be a stable cluster with a magic number. From further calculations, we found that the cage-like As8 structures unit served as the primary building unit for forming the As clusters with larger sizes.
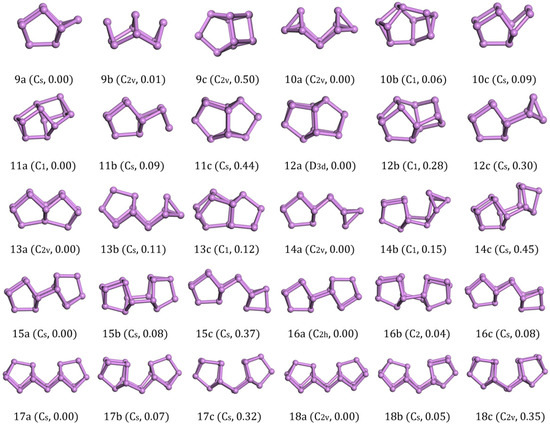
Figure 2.
Lowest-energy and isomorphic structures for Asn (n = 9–18) clusters. The relative total energies are in eV.
The lowest-energy structure (C2v) of As10 consistd of the cage structure of 8a in Figure 1 that was edge-capped by each As atom. After relaxation, the upper bond broke to form two four-atom cages and an As2 bridge. The structure 10b in Figure 2 was a new structure discovered by our GA global searching. The structure obtained by Zhao [22] is structure 10c in Figure 2, whose energy was higher than 10b in Figure 2 by 0.006 eV/atom and 10a in Figure 2 by 0.009 eV/atom.
The ground structure of As11 was 11a in Figure 2 which was formed on the base of As10 with an As atom added above the As2 dimer and linked with an As8 cage. It was more stable than the 11b in Figure 2 isomer with Cs symmetry by 0.008 eV/atom and 11c in Figure 2 isomer by 0.04 eV/atom with Cs symmetry in energy.
For As12, the structure with D3d symmetry was confirmed to be the lowest energy structure among all the structural candidates considered. The highly-symmetric structure was shaped of two As8 cages that share a four-atom plane. From another point of view, the ground-state structure of As12 was a layered structure of three layers of atoms (3 + 6 + 3). Such a nice structure was energetically lower than 12b in Figure 2 with C1 symmetry by 0.023 eV/atom and 12c in Figure 2 with Cs symmetry by 0.025 eV/atom.
Viewing the ground-state structure of As13 carefully, we also found two As8 cages. Different from As12, the two cages jointly owned a three-atom plane. It had 0.008 eV/atom less energy than the structural 13b in Figure 2 (C1) and 0.009 eV/atom less than the structure 13c in Figure 2 (Cs).
As shown in the picture, As14 with Cs symmetry could be considered to be composed of an As atom link to the three-atom plane on one side of the As13 (13a in Figure 2). The less stable isomer 14b was a distorted structure of 14a, which was energetically higher by 0.011eV/atom. The 14c was a structure without an As2 dimer bridge, it was linked by As8 cage with an As6 cage and had 0.032 eV/atom more energy than 14a in Figure 2.
The ground-state structure of As15 with Cs symmetry was composed of two connected cages (As8 and As7). The other two candidates 15b in Figure 2 with Cs symmetry and 15c in Figure 2 with Cs symmetry were less stable than the ground-state structure by 0.005 eV/atom and 0.025 eV/atom in energy, respectively.
An upward As8 cage and a downward As8 cage connected to form a new structure as the ground state of As16 (16a in Figure 2 with C2h symmetry). It was more stable than the C2-symmetry isomer 16b in Figure 2 and the Cs-symmetry isomer 16c in Figure 2 by 0.05 eV and 0.08 eV in energy. Although structural 16c in Figure 2 contained an As8 cage and an As2 bridge, the As6 cage in the structure led to the overall energy as being higher than other two isomers.
The lowest energy structure of As17 (17a in Figure 2) with Cs symmetry was built by As8 and As7 units with an As2 bridge in the middle. The two Cs-symmetry isomorphic structure 17b,c in Figure 2 were also formed by the As8 and As7 units with different orientation connections.
The ground-state of As18 (18a in Figure 2) with C2v symmetry was formed by two identical As8 units and an As2 bridge in the middle. Our structure was exactly the same as that in Ref. [22]. Two slightly higher energy isomers (18b in Figure 2) with C2h symmetry and 18c in Figure 2 with C2v symmetry were combined by the same units as 18a in Figure 2 with different orientations, and they were energetically higher than 18a in Figure 2 by 0.05 eV and 0.35 eV energy. The calculations showed that the structure with As8 unit and As2 bridge in the middle was more stable than other cage structures. We also generated one As18 structure cut from bulk phase and the energy was 3.17 eV higher than the ground state. So, we think the chain structure with As8 units and an As2 bridge is much more important for middle-sized Asn clusters.
3.3. Asn (n = 19–24) Clusters
The ground-state structure of As19 (19a in Figure 3) with Cs symmetry could be regarded as an As atom added into one side of As18. Therefore, As19 (19a in Figure 3) could be considered as the combination of As8-As2-As8-As1. The isomers of As19 (19b,c in Figure 3) with only C1 symmetry were both built up by two identical As8 units and an As3 bridge. Due to the distortion of the structures, they had 0.008 eV/atom and 0.009 eV/atom higher energy than 19a in Figure 3.
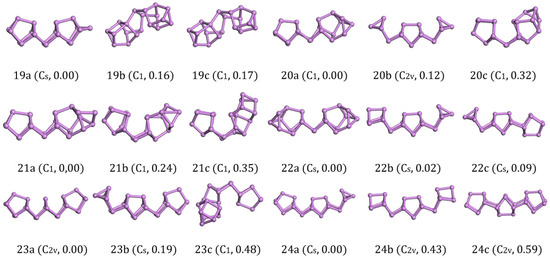
Figure 3.
Lowest-energy and isomorphic structures for Asn (n = 19–24) clusters. The relative total energies are in eV.
The ground-state structures of As20 was predicted to be C1 symmetry, as shown in 20a in Figure 3. It could be regarded as an As8 cage link with an As10 cage joined by an As2 bridge. As20 (20a in Figure 3) could be considered as the combination of As8-As2-As10. Zhao [22] predicted the optimal combinations for the As20 is super-clusters of As4-As2-As8-As2-As4. The energy of As20 (20a in Figure 3) we got based on the genetic algorithm was energetically lower than the structure 20b in Figure 3 with C2v symmetry. A distorted structure 20c in Figure 3 originated from 20a in Figure 3 also appeared in our calculations. After the calculations with VASP, two isomers showed 0.006 eV/atom and 0.053 eV/atom higher energy than 20a in Figure 3. This result shows the super-clusters of As4-As2-As8-As2-As4 did not have much of an advantage.
For As21, the most stable structure (21a in Figure 3) could be regarded as an As atom link to the As10 cage of As20 (20a in Figure 3). Two other isomers (21b,c in Figure 3) were constituted by an As8 cage and an irregular As11 structure linked with an As2 bridge. They were energetically higher than 21a in Figure 3 by 0.011 eV/atom and 0.017 eV/atom.
Rather than simply increasing the number of atoms on the edge, the ground-state structure of As22 with Cs symmetry are formed with two symmetrical As10 cages in the As20 units and an As2 bridge in the middle. The isomers were two kinds of super-clusters (22b in Figure 3, As6-As2-As8-As2-As4 and 22c in Figure 3, As4-As2-As8-As8), and they were stretched by more units compared to the ground-state structures (22a in Figure 3). Although we could find stable As8 and As4 units in isomers, they each had 0.02 eV and 0.09 eV higher energy than 22a in Figure 3. According to previous findings, it can be found that the second lower energy As10 cage 10b in Figure 2 will be favorable if the structure is composed by an As8 unit connected with an As2 bridge.
The ground-state structures of As23 (23a in Figure 3) with C2v symmetry seemed to be four As8 cages linked to each other to share the three-atom plane, and the bottom edge of the middle two cages were broken. At the same time, we could also regard 23a in Figure 3 as a super-cluster of As8-As2-As3-As2-As8. The other two candidates, 23b in Figure 3 with Cs symmetry and 23c in Figure 3 with C1 symmetry, were less stable than the structure 23a in Figure 3 by 0.008 eV/atom and 0.021 eV/atom in energy, respectively.
The lowest energy structure of As24 with Cs symmetry (24a in Figure 3) was built by three units (an As4 cage and two identical As8 cages), connecting the neighboring structure with an As2 bridge. Zhao [22] considered that the optimal combinations of the super-clusters As24 are As6-As2-As8-As2-As6 (24b in Figure 3) with C2v symmetry. DFT calculations show that the ground-state structure of As24 we get based on the genetic algorithm weare the combinations of As8-As2-As8-As2-As4, which was energetically lower than the structure 24b in Figure 3 by 0.018 eV/atom. Besides, we also gained another high symmetric structure with C2v symmetry (24c in Figure 3) that was constituted by three As8 units. However, its energy was 0.025 eV/atom higher than the ground state structure (24a in Figure 3). We could realize from this result that the lowest energy structures of larger As clusters not only have the combination of As8 units but also needed an As2 bridge in the middle of adjacent units.
3.4. Asn (n = 2–24) Charged Clusters
We also studied the ground structures of Asn (n = 2–24) charged clusters. Theoretically, it was easy to simulate a cationic or anionic cluster by adjusting the total electrons from the neutral cluster. From Figures S2 and S3, we could know the lowest energy structures of charged clusters (n = 2–4) were almost the same as with neutral cases. For As8 clusters, 8a in Figure 1 structures were quite stable even in cationic or anionic cases and it was the cluster with the magic number. For other Asn (n < 16) clusters, the isomers changed the energy sequence as the system changed the electron numbers. It was interesting to find that the structures for Asn (15 < n < 24) clusters were quite stable whatever attachment of extra electron to the neutral or losing of an electron from the neutral cluster.
3.5. Asn (n = 28, 38, 40, 180) Clusters
With the increase of cluster size, it was more and more difficult to exhaust all possible local minimum structures. We tried to study the larger clusters As28, As38, and As40 based on the above findings. The structural size evolution and electronic properties of arsenic clusters indicated that the clusters combined by an As2 bridge and an As8 cage had lower energy than their isomers and showed more stability in each local size-dependent range. Here we have to emphasize that As4 and As6 units were not dominant for the larger Asn cluster, which was different from Zhao’s result [22]. Furthermore, different sizes of fullerene cage structure isomers were also calculated to compare with our ground state structures in energy, and their energies were far more than units-linked one-dimensional structures. Given this understanding, we constructed As28 as As8-As2-As8-As2-As8 and As38 as As8-As2-As8-As2-As8-As2-As8 in all possible ways. The structures we calculated of As28 are listed along with the increase of energy in Figure 4. The lowest energy structure of As28 with C2v symmetry (Figure 4a) had 0.05 eV less energy than the structure with Cs symmetry (Figure 4b) and 0.10 eV less than the structure with C2v symmetry (Figure 4c). In addition to considering structure growth in the one-dimensional direction, we also calculated the longitudinal growth mode. Three isomers Figure 4c,e,f were all with Cs symmetry and energetically higher than the lowest energy structure a with 0.08 eV, 0.35 eV, and 0.40 eV, respectively. Besides, the other two semi-ring isomers Figure 4g,h had 0.44 eV and 0.70 eV energy higher than the ground state structure. Compared with the bulk truncated structure of As28, the lowest energy structure of As28 was 0.16 eV/atom lower.
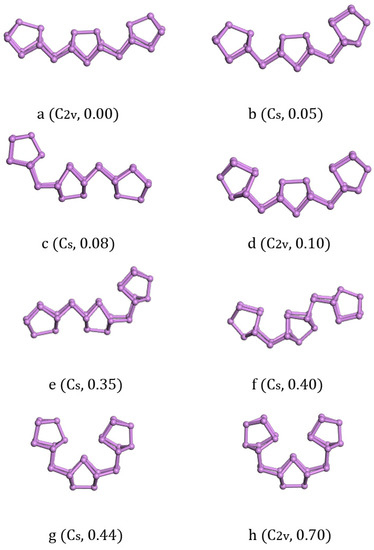
Figure 4.
Lowest-energy and isomorphic structures for As28 clusters. The relative total energies in eV.
The lowest energy structure of As38 with C2v symmetry (Figure 5a) and its isomers are listed in Figure 5. We could find that the structure of Figure 5a was a continuation of As8, As18, and As28 clusters, and all of them were constructed with As8 cages in the same direction with As2 bridges. The structural isomers Figure 5b with C2v symmetry and Figure 5c with C2h symmetry could be regarded as one-dimensional chain structures, the same as Figure 5a. Their respective energies were 0.10 eV and 0.22 eV higher than Figure 5a. The C2v isomer Figure 5d could be regarded as a two-dimensional structure that has four As8 cages held in four directions and all of them point to the center. The energy of this structure was highest in our calculation with 1.11 eV higher energy than a. Compared with the bulk truncated structure of As38, the lowest energy structure of As38 was 0.156 eV/atom lower. We could find that the structures did not change previous growth tendencies even with increasing the size of the clusters.
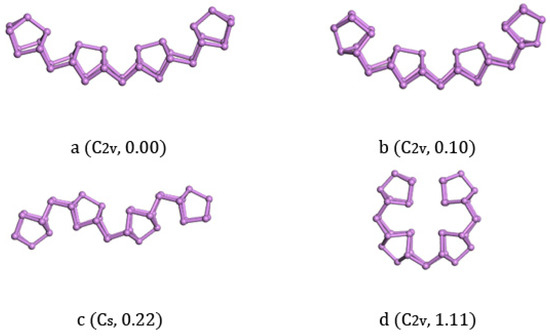
Figure 5.
Lowest-energy and isomorphic structures for As38 clusters. The relative total energies are in eV.
Considering that As40 can form ring and fullerene cage structures, we also studied the structures of As40. The structures we calculated of As40 are listed along with the increase of energy in Figure 6. We found that the lowest energy structure of As40 with C1 symmetry (Figure 6a) and its isomers Figure 6b (0.42 eV energy higher) with Cs symmetry both were one-dimensional chain structures. Three isomers Figure 6c,d,e could all be regarded as two-dimensional structures and energetically higher than the lowest energy structure a with 0.014 eV/atom, 0.044 eV/atom, and 0.09 eV/atom, respectively. Seemingly stable three-dimensional fullerene cage isomers Figure 6f with D5d symmetry and Figure 6g with D5d symmetry were 0.194 eV/atom and 0.226 eV/atom higher in energy than the lowest energy structure.
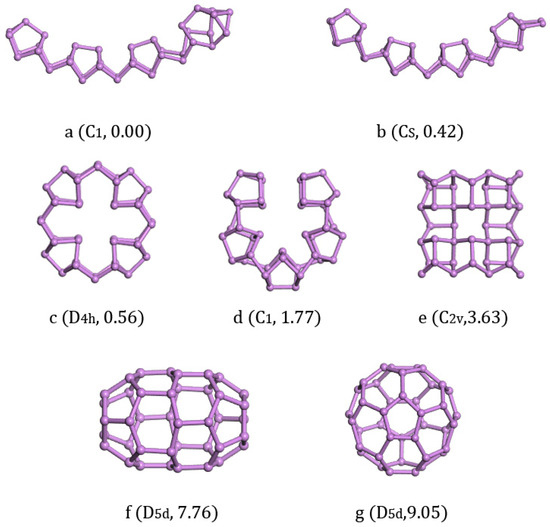
Figure 6.
Lowest-energy and isomorphic structures for As40 clusters. The relative total energies in are eV.
Based on the finding above, we could construct the ring structure of an As180 cluster based on the As8 units and As2 bridge, which is shown in Figure 7. The HOMO-LUMO gap of As180 was 1.868 eV and the binding energy per atom was −2.901 eV.

Figure 7.
Possible structure for As180 cluster.
3.6. Electronic Properties of Asn Clusters
The binding energy per atom for the ground states of Asn (n = 2–24) clusters are shown in Figure 8a. In the size range of n = 12–24, the binding energy increased smoothly with weak odd-even oscillation properties. This result can be related to the evolution of the ground-state from cage-like structure to cage-link structure at n = 12. Besides, the binding energy of As8 was a peak value in the small size of n = 3–11, and this suggests the ground structure of As8 would be a vital growth unit in larger structures. Our next calculation also proved the conjecture.
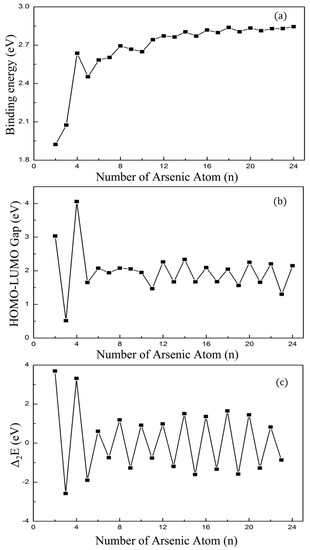
Figure 8.
(a) Average binding energies (b) HOMO-LUMO Gaps and (c) second-order difference of cluster energies of Asn clusters.
In Figure 8b, we present the energy gaps between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) for the lowest-energy state of Asn (n = 2–24) clusters. As is known, the cluster with the larger energy gap is more stable and easier to prepare. As the largest energy gap of As4 is 4.06 eV, it is the most prominent species in arsenic vapor, leading to a number of experimental and theoretical studies on As4 clusters. Although the gaps of Asn clusters from n = 5–10 change smoothly, we also observe the gap of As8 is highest locally, which points out that the stability of As8 was higher than the neighboring cluster. The HOMO-LUMO gap was higher for Asn (n = 4, 6, 8, 12, 14, 16, 18, 20, 22, and 24) than their adjacent structures. The atoms in these even-numbered sequences were all three-coordination and eight-electron structure. The odd-numbered clusters were unable to achieve this condition, so they were less stable than the odd-numbered species.
In clusters physics, the second-order difference of cluster energy is a more sensitive datum to reflect the stability of clusters. We plotted the second-order difference of cluster energies defined by Δ2E = E(n + 1) + E(n − 1) − 2E(n). Figure 8c describes how the second-order differential energy changed with the increase of atom number and it shows good odd–even oscillation properties. The second-order difference of cluster energies of even-numbered clusters were all higher than their adjacent odd-numbered clusters. Therefore, we could draw the conclusion that even-numbered clusters were more stable than their neighboring odd-numbered clusters. Above all peaks for Δ2E, three local maximum peaks were found at n = 4, 8, and 18, where Asn (n = 4, 8, and 18) clusters were chemically stable.
4. Conclusions
We have adopted the genetic algorithm and all-electron DFT calculations to systematically study the structures and electronic properties of Asn (n = 2–24). The ground-state structures of Asn clusters change from two to three dimensional after n = 3. Arsenic clusters followed a structural growth pattern starting from n = 8 and the structures of Asn (n = 9–24) clusters could all be regarded as evolving from the ground state structure of an As8 unit and an As2 bridge. The binding energy of Asn (n = 2–24) clusters had a periodic step-like behavior, and the size-dependent HOMO-LUMO gap and second-order difference of cluster energies exhibited obvious even–odd alternations with several magic numbers. Based on the growth pattern concluded from small Asn clusters, the possible superstructures of As28, As38, As40, and As180 were discussed.
Supplementary Materials
The following are available online at http://www.mdpi.com/1996-1944/11/9/1596/s1, Figure S1: Low energy isomers of Asn (n = 2–24) neutral clusters, Figure S2: Low energy isomers of As+n (n = 2–24) cationic clusters, Figure S3: Low energy isomers of As-n (n = 2–24) anionic clusters.
Author Contributions
Conceptualization, B.W. and Q.Z.; Methodology, Q.Z.; Validation, J.Y., Q.Z. and B.W.; Formal Analysis, J.Y.; Investigation, Q.Z.; Resources, J.X. and B.Z.; Data Curation, J.Y. and Q.Z.; Writing-Original Draft Preparation, B.W. and Q.Z.; Writing-Review & Editing, J.Y. and Q.Z.; Visualization, J.Y., Q.Z. and B.W; Supervision, Q.Z. and B.W.; Project Administration, J.Y. and Q.Z.; Funding Acquisition, J.Y. and Q.Z.
Funding
This work was supported by the NSFC [11474246, 11774178, 11850410442, 11750110415], the Natural Science Foundation of Jiangsu Province [BK20160061].
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Berry, R.S. Clusters of Atoms and Molecules: Theory, Experiment and Clusters of Atoms; Haberland, H., Ed.; Springer Science & Business Media: Berlin, Germany, 2013; p. 52. [Google Scholar]
- Neugebauer, J.; Zywietz, T.; Scheffler, M.; Northrup, J.E.; Van de Walle, C.G. Clean and As-covered zinc-blende GaN (001) surfaces: Novel surface structures and surfactant behavior. Phys. Rev. Lett. 1998, 80, 3097. [Google Scholar] [CrossRef]
- Bernstein, R.W.; Borg, A.; Husby, H.; Fimland, B.O.; Grepstad, J.K. Capping and decapping of MBE grown GaAs (001), Al0.5Ga0.5As (001), and AlAs (001) investigated with ASP, PES, LEED, and RHEED. Appl. Surf. Sci. 1992, 56, 74–80. [Google Scholar] [CrossRef]
- Smith, D.L. Thin-Film Deposition: Principles and Practice; McGraw-hill: New York, NJ, USA, 1995; p. 108. [Google Scholar]
- Garcia, J.C.; Neri, C.; Massies, J. A comparative study of the interaction kinetics of As2 and As4 molecules with Ga-rich GaAs (001) surfaces. J. Cryst. Growth 1989, 98, 511–518. [Google Scholar] [CrossRef]
- Shiraishi, K.; Ito, T. First principles study of arsenic incorporation on a GaAs (001) surface during MBE growth. Surf. Sci. 1996, 357, 451–454. [Google Scholar] [CrossRef]
- Wu, B.J.; Mii, Y.J.; Chen, M.; Wang, K.L.; Murray, J.J. Reduced silicon donor incorporation in MBE grown GaAs layers using cracker-generated dimer arsenic. J. Cryst. Growth 1991, 111, 252–259. [Google Scholar] [CrossRef]
- Kawanaka, M.; Iguchi, N.; Fujieda, S.; Furukawa, A.; Baba, T. GeAs as a novel arsenic dimer source for n-type doping of Ge grown by molecular beam epitaxy. J. Appl. Phys. 1993, 74, 3886–3889. [Google Scholar] [CrossRef]
- Fernandez, R.; Chow, R. Molecular Beam Epitaxy. In Workbook of the Fifth International Conference; Kaare, S., Ed.; The Norwegian Committee on Permafrost: Trondheim, Norway, 1988; p. 584. [Google Scholar]
- Duker, A.A.; Carranza, E.J.; Hale, M. Spatial dependency of Buruli ulcer prevalence on arsenic-enriched domains in Amansie West District, Ghana: Implications for arsenic mediation in Mycobacterium ulcerans infection. Int. J. Health Geogr. 2004, 3, 19. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jay, J.A.; Blute, N.K.; Hemond, H.F.; Durant, J.L. Arsenic-sulfides confound anion exchange resin speciation of aqueous arsenic. Water Res. 2004, 38, 1155–1158. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.S.; Niu, B.; Lee, Y.T.; Shirley, D.A.; Ghelichkhani, E.; Grant, E.R. Photoelectron spectroscopy and electronic structure of clusters of the group V elements. III. Tetramers: The 2T2 and 2A1 excited states of P4+, As4+, and Sb4+. J. Chem. Phys. 1990, 93, 6327–6333. [Google Scholar] [CrossRef]
- Bennett, S.L.; Margrave, J.L.; Franklin, J.L.; Hudson, J.E. High temperature negative ions: Electron impact of As4 vapor. J. Chem. Phys. 1973, 59, 5814–5819. [Google Scholar] [CrossRef]
- Lippa, T.P.; Xu, S.J.; Lyapustina, S.A.; Nilles, J.M.; Bowen, K.H. Photoelectron spectroscopy of As−, As2−, As3−, As4−, and As5−. J. Chem. Phys. 1998, 109, 10727–10731. [Google Scholar] [CrossRef]
- Brumbach, S.B.; Rosenblatt, G.M. In-Cavity Laser Raman Spectroscopy of Vapors at Elevated Temperatures. As4 and As4O6. J. Chem. Phys. 1972, 56, 3110–3117. [Google Scholar] [CrossRef]
- Morino, Y.; Ukaji, T.; Ito, T. Molecular structure determination by gas electron diffraction at high temperatures. I. Arsenic. Bull. Chem. Soc. Jpn. 1966, 39, 64–71. [Google Scholar] [CrossRef]
- Zimmerman, J.A.; Bach, S.B.; Watson, C.H.; Eyler, J.R. Ion/molecule reactions of arsenic and phosphorus cluster ions: Ionization potentials and novel reaction pathways. J. Phys. Chem. 1991, 95, 98–104. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, W.; Li, Q.; Xie, Y.; Schaefer, H.F. The arsenic clusters Asn (n = 1–5) and their anions: Structures, thermochemistry, and electron affinities. J. Comp. Chem. 2004, 25, 907–920. [Google Scholar] [CrossRef] [PubMed]
- Liang, G.; Wu, Q.; Yang, J. Probing the electronic structure and property of neutral and charged arsenic clusters (Asn (+ 1, 0,–1), n ≤ 8) using Gaussian-3 theory. J. Phys. Chem. A 2011, 115, 8302–8309. [Google Scholar] [CrossRef] [PubMed]
- Guo, L. Evolution of the electronic structure and properties of neutral and charged arsenic clusters. J. Mater. Sci. 2007, 42, 9154–9162. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, Q.; Gao, A.; Yang, J. Arsenic clusters Asn (n = 6–16) and their anions: Structures, thermochemistry, and electron affinities. Comput. Theor. Chem. 2013, 1009, 94–102. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, X.; Chen, X.; Wang, J.; Jellinek, J. Density-functional study of small and medium-sized Asn clusters up to n = 28. Phys. Rev. B. 2006, 73, 115418. [Google Scholar] [CrossRef]
- Baruah, T.; Pederson, M.R.; Zope, R.R.; Beltran, M.R. Stability of Asn [n = 4, 8, 20, 28, 32, 36, 60] cage structures. Chem. Phys. Lett. 2004, 387, 476–480. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Delley, B. DMOL is a density functional theory (DFT) program distributed by Accelrys, Inc. J. Chem. Phys. 1990, 92, 508. [Google Scholar] [CrossRef]
- Zhao, J.; Luo, Y.; Wang, G. Tight-binding study of structural and electronic properties of silver clusters. Eur. Phys. J. D 2001, 14, 309–316. [Google Scholar] [CrossRef]
- Zhao, J. Density-functional study of structures and electronic properties of Cd clusters. Phys. Rev. A 2001, 64, 043204. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, R.H. Genetic algorithms for the geometry optimization of atomic and molecular clusters. J. Comput. Theor. Nanosci. 2004, 1, 117–131. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, R.; Sai, L.; Huang, X.; Su, Y. Comprehensive genetic algorithm for ab initio global optimisation of clusters. Mol. Simul. 2016, 42, 809–819. [Google Scholar] [CrossRef]
- Huber, K.-P. Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
Sample Availability: Samples of the compounds are available from the authors. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).