1. Introduction
In the past decade, spin-gapless semiconductors (SGS) have attracted increasing interest because of their unique physical properties, leading to their potential application in electronic devices, such as field-effect transistors, optoelectronics, electronic sensors, and supercapacitors, amongst others [
1,
2,
3,
4,
5,
6]. Among them, the PbPdO
2-based spin gapless semiconductor is considered as a promising candidate because of its non-toxicity, compatibility to the oxide semiconductor devices, and sensitivity to the doping metal elements, electric field, and operation current. Based on local density approximation calculations, the oxide-based PbPdO
2 gapless semiconductor was firstly discovered by Wang [
4]. Following this, extensive investigations on the electric and magnetic properties of PbPdO
2-based semiconductors were carried out theoretically and experimentally. Wang et al. studied the roles of both electrical current and magnetic field on the resistivity of PbPd
0.75Co
0.25O
2 thin films, and unusual colossal electroresistance and magnetoresistance were observed [
5]. Moreover, the distinct different magnetoresistance effects were observed in PbPd
0.9Cu
0.1O
2 and PbPd
0.9Zn
0.1O
2, which would be attributed to local structure deformation due to Pd/O deficiencies [
7]. Based on the bound magnetic polaron (BMP) theory, the potential mechanism behind the observed ferromagnetic, paramagnetic, and antiferromagnetic properties coexisting in Co–doped PbPdO
2 film were suggested [
8]. It was suggested that Pd–O hybridization in Co–doped PbPdO
2 thin films were responsible for the transition from weak localization and weak anti-localization [
9]. Simultaneously, many studies on valence states and band structures have been carried out to understand the mechanism on the observed physical behaviors. For example, Chen et al. revealed that a small band gap of PbPdO
2 would be induced by Pd deficiency in composites, resulting in increased hybridization of O(2p)–Pb(6p) and decreased O(2p)–Pd(4d) hybridizations [
10]. It was found that Pd–O hybridization would efficiently mediate the magnetic coupling among Co atoms [
11]. The ferromagnetism and paramagnetism were found to coexist in the Fe–doped PbPdO
2, and the bound magnetic polaron model was used to account for the ferromagnetism origin [
12]. Based on the measured electronic structures, Pb(Pd
0.9T
0.1)O
2 (T = Mn, Co) oxides were found to be the small-gap semiconductors [
13]. In our previous study, it was observed that the external electric field in PbPdO
2 slab with (002)-preferred orientation influences sensitively the band gap and carrier concentration, which explains the extraordinary electrical behaviors [
14].
Recently, the strain effects on the physical properties of two-dimensional materials were investigated [
15,
16,
17,
18]. The direct-indirect band gap transition induced by strain was also found in two-dimensional phosphorene, which is explained by the near-band-edge electronic orbital theory [
15]. It has been established that the strain induces modulation of the band gap resulting in a piezoresistive effect in silicon [
16]. Recently, the piezoresistive effect was also found in single-atomic-layer and atomically thin MoS
2 films [
17,
18]. Strain dependent carrier concentration is generally characterized with piezoresistive gauge factor. The gauge factor (GF) of piezoresistance can be calculated as follows [
18],
where
is the resistance without strain and
is change of resistance with strain
ε. The resistivity (
) is in inverse proportion to carrier concentration (
n). As
= 0, let
n =
n0;
≠ 0, let
n =
. The gauge factor can be re-expressed as follows,
In PbPdO
2-based composites, different preparation and processing methods result unavoidably in different microstructure and strain states, which consequently influences the band gap, carrier concentration, and corresponding electrical properties. Specifically, being similar to the layered MoS
2, (002) preferred orientation layered PbPdO
2 has a small band gap [
14], and the piezoresistive effect is expected.
In this work, based on the first-principle calculation method, a plane strain model was set up to obtain a deformed lattice with in-plane arbitrary uniaxial strain. In-plane anisotropy strain dependence of band-gap and carrier concentration were systematically investigated in the PbPdO2 and PbPd0.75Co0.25O2 slabs with preferred (002) orientation. These results can be well explained according to the p-d exchange interaction. Moreover, it is strongly suggested that the element-doping PbPdO2 should become an important piezoresistance candidate material.
3. Results and Discussion
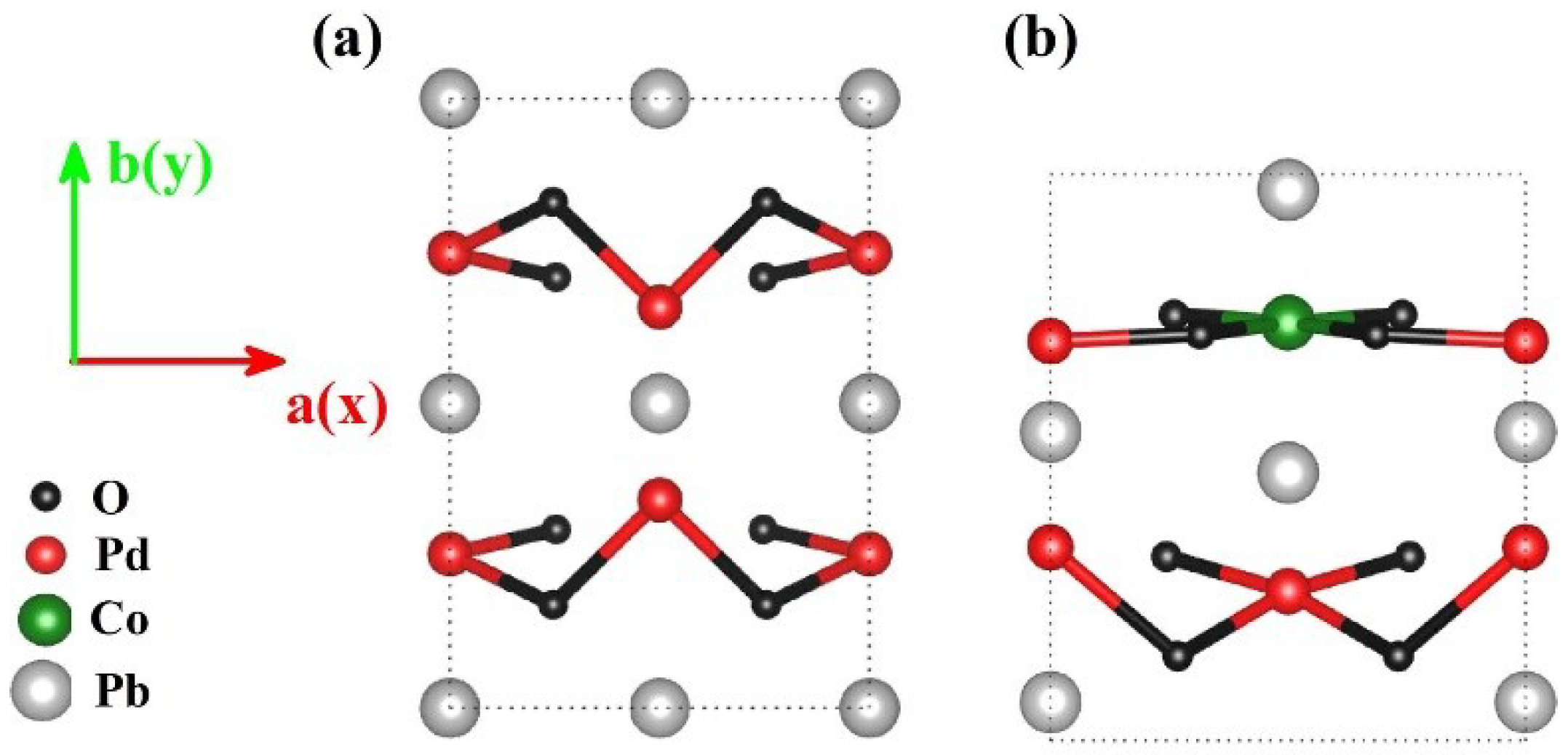
Figure 1 shows the relaxed crystal structures of PbPdO
2 and PbPd
0.75Co
0.25O
2 ultrathin slabs with (002) preferred orientation. As shown in
Figure 1, the unstrained PbPdO
2 and ultrathin slab revealed an in-plane symmetric configuration, maintaining the important properties of PbPdO
2. After Co-doping, the symmetric configuration of PbPd
0.75Co
0.25O
2 was broken. In comparison to the pristine PbPdO
2, the broken-symmetry in PbPd
0.75Co
0.25O
2 was expected to bring different physical properties. It should be noted that the anisotropy of PbPd
0.75Co
0.25O
2 was greatly affected by the state of the Co-substitution. Moreover, its configurations were fairly complicated. Here, the configuration with the least number of atoms and only one Co doping atom was considered, as seen in
Figure 1b. Specifically, this Co atom forms square planar bonding with the nearest-neighbor four O atoms, which plays an important role on the electrical properties of PbPd
0.75Co
0.25O
2.
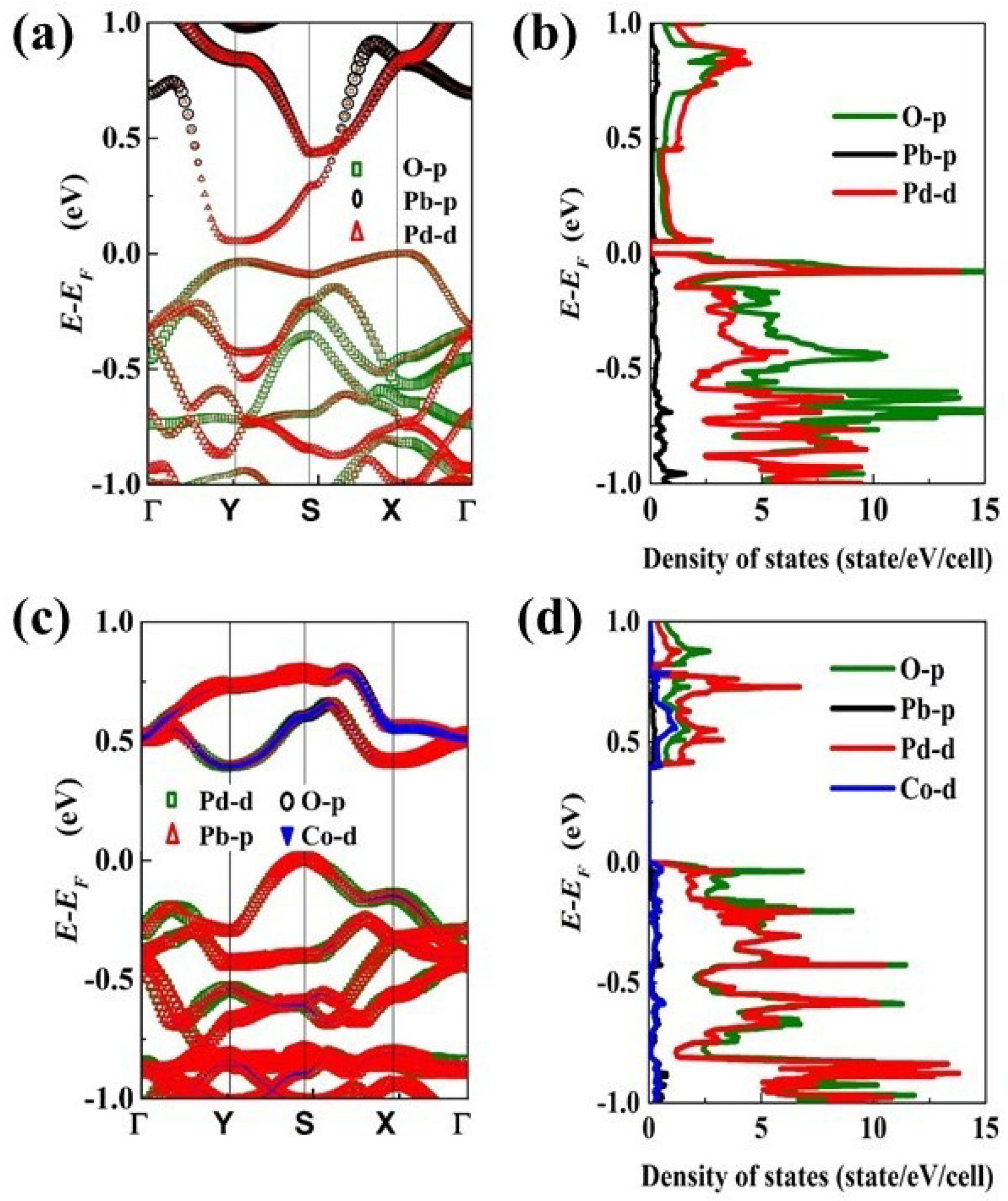
Figure 2a–d shows the calculated electronic structures and the partial densities of states of Pb, Pd, O, and Co in PbPdO
2 and PbPd
0.75Co
0.25O
2 slabs, respectively. It was found that PbPdO
2 exhibits intrinsic characteristics of narrow band gap (0.051 eV), which was much smaller than that (0.4 eV) of the PbPd
0.75Co
0.25O
2 slab. In our previous experimental work, PbPdO
2 with (002) preferred orientation was prepared, and its band gap was found to be close to zero [
22]. It is suggested that the localized Co would be responsible for the large band gap of 0.35 eV for the PbPd
0.75Co
0.25O
2 bulk material. Interestingly, our calculated results were consistent with the reported results [
23]. The band gap of PbPdO
2 slab was slightly larger than that reported in our previous calculated work because of the different full in-plane structure relaxation [
14]. From the density of electronic states in
Figure 2b,d, it is found that DOSs of the pristine and Co-doped PbPdO
2 slabs at minimum of the conduction band and maximum of the valence band were mainly composed of 4d(Pd) and 2p(O) states. These results were similar to those found by many research groups [
6,
10]. In contrast, the PbPd
0.75Co
0.25O
2 slab had more distinct contribution of hybridization of 2p(O)–4d(Pd) states, where a Co 3d state added modified energy to the DOS at the Fermi energy level.
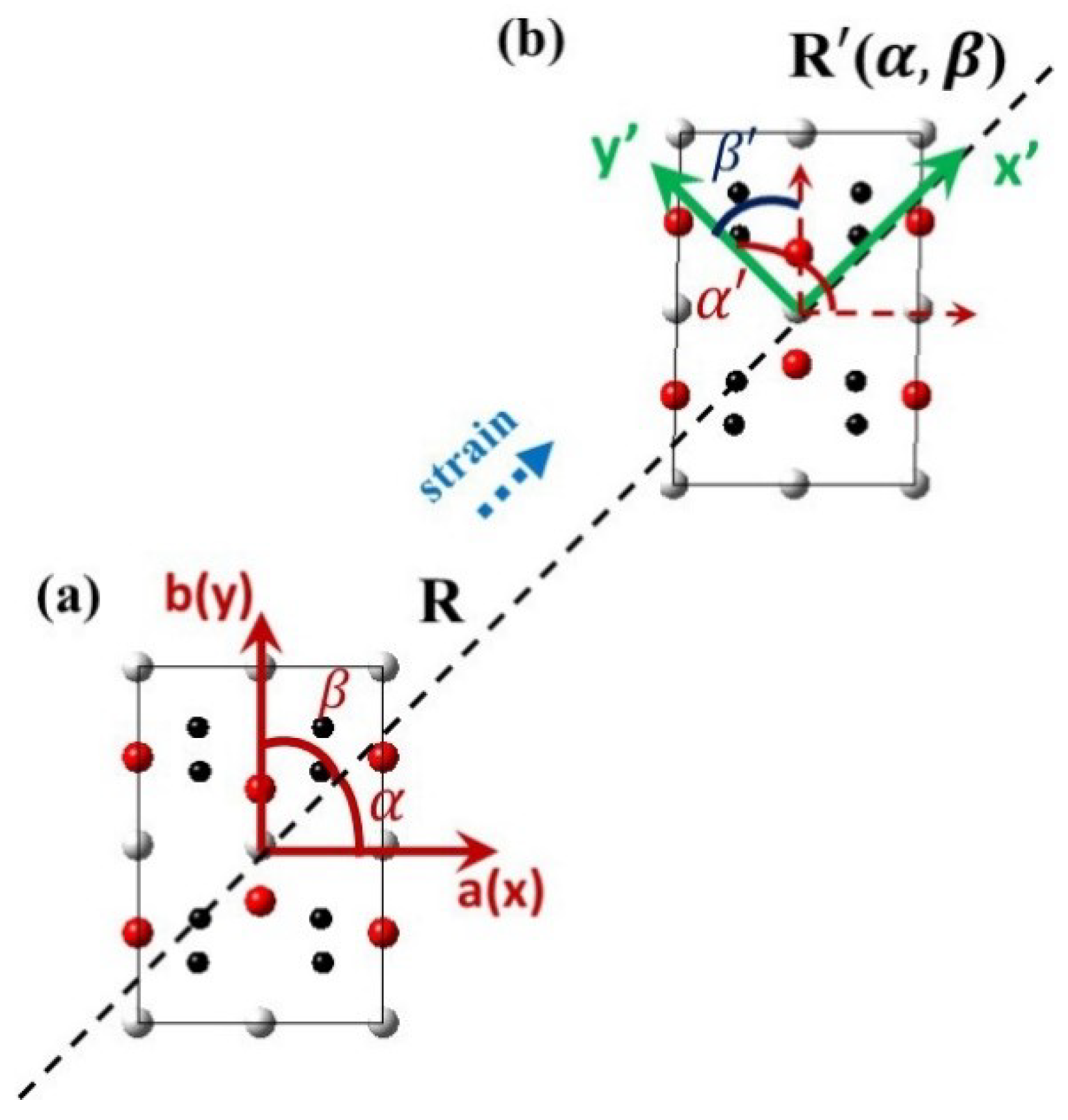
To gain insight into the potential mechanism of strain-induced electronic properties in PbPdO
2-base composites, a plane-stress-strain model was set up.
Figure 3a,b present the undeformed lattice and a deformed lattice with in-plane arbitrary uniaxial tensile strain (directional cosines
), respectively. The strain-related components could be obtained based on the coordinate transformation method. Assuming uniaxial strain
is along the x′ direction in an unprimed coordinate system x-y, the strain tensor elements in the primed coordinate system are given as follows,
where
(
) and
are normal (tensile or compressive) and shear strains, respectively [
24]. The directional cosines are
where
,
,
,
are arbitrary directions in the x-y and x′-y′ coordinate system, as seen in
Figure 3.
A deformation of the unit cell is created by changing the Bravais lattice vectors
R of the undeformed unit cell to
R′ using a strain matrix as follows:
where
R is the Bravais lattice vectors with strain, and
R′ is the Bravais lattice vectors without strain,
(
) and
(
) are the normal (tensile or compressive) and shear strain-related components, respectively.
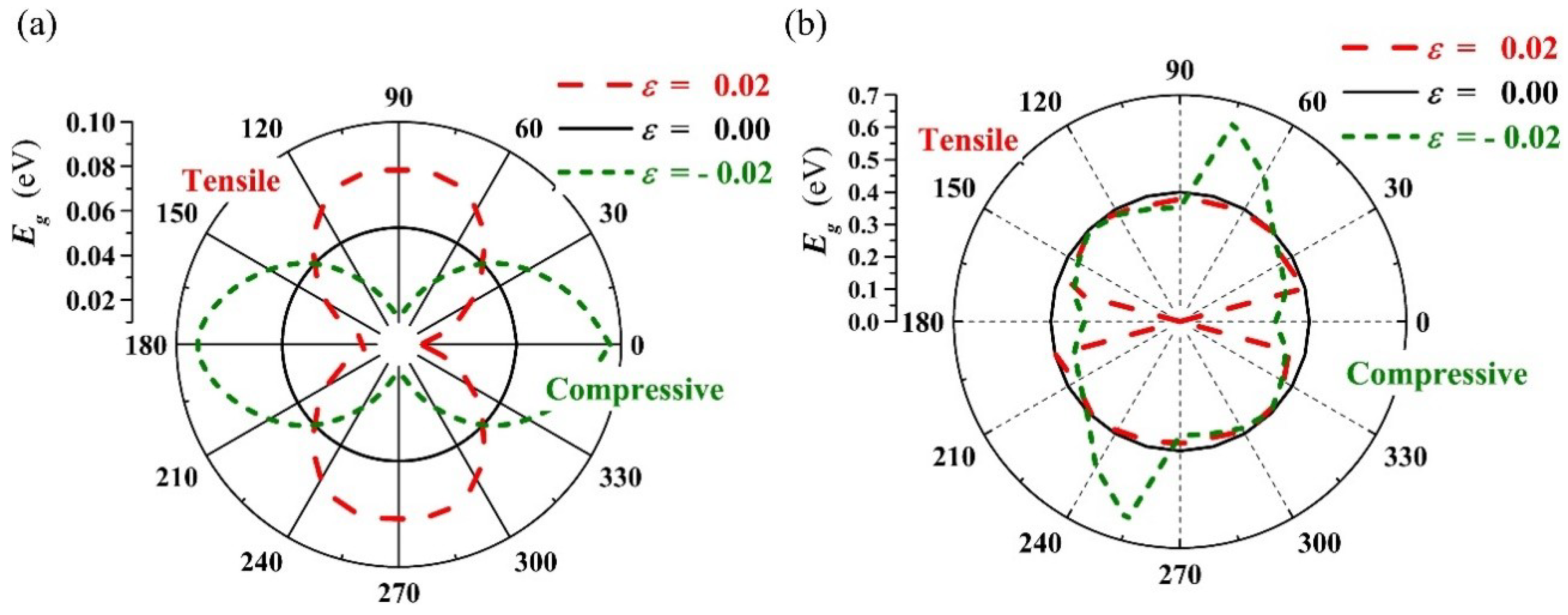
Figure 4a,b shows the orientation distribution curves of band gap
with
= −0.02, 0.00, 0.02 for the PbPdO
2 and PbPd
0.75Co
0.25O
2 slabs, respectively. It is clear that both slabs show a distinct anisotropy of gap with different strain. In
Figure 4a, the PbPdO
2 slab shows the symmetrical and peanut-like
curves, and having the largest and smallest band-gap values along the x axis (
) or y axis (
), respectively. In contrast, as shown in
Figure 4b, the PbPd
0.75Co
0.25O
2 slab has a maximum gap for the strain
= −0.02 at about
and a minimum gap for the strain
= 0.02 at about
.
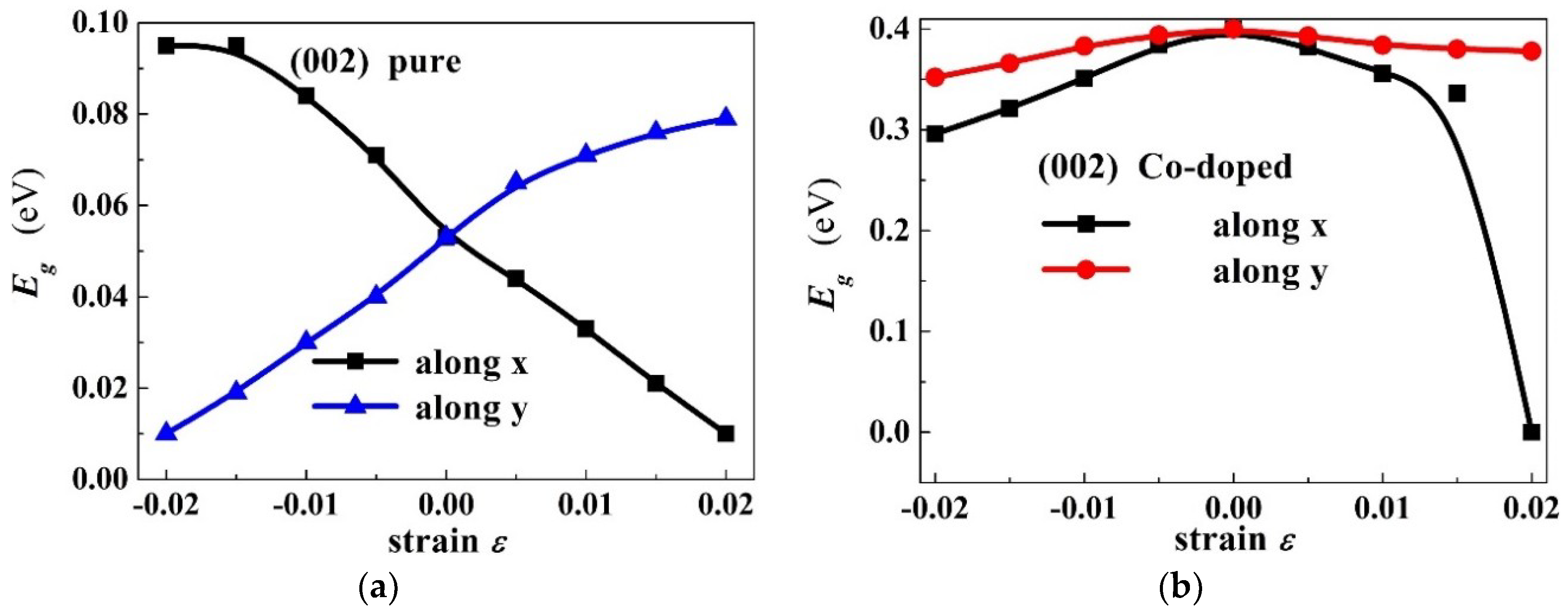
Figure 5a,b shows the band gap as a function of the strain for PbPdO
2 and PbPd
0.75Co
0.25O
2 along x axis (
) and y axis (
), respectively. As shown in
Figure 5a, it is found that the band-gap value increases with increasing strain along the y-axis, whilst the band-gap value decreases with increasing strain along the x-axis. It is interesting that the band gap of the PbPdO
2 slab would widen when a compressive stress is applied closely to the x-axis or a tensile stress is applied closely to the y-axis, as seen in
Figure 4a. These calculated results can be explained according to the interaction of Pd–O bonding. It is expected that a compressive stress along the x-axis or tensile stress along the y-axis pulls O atoms apart from Pd atoms, which weakens the interaction of Pd and O. On the other hand, a tensile stress along the x-axis or compressive stress along the y-axis would push O atoms closely to Pd atoms and strengthen the interaction of Pd and O. As a result, the band gap is decreased. A similar result has also been reported in MoS
2 and black phosphorus [
25,
26].
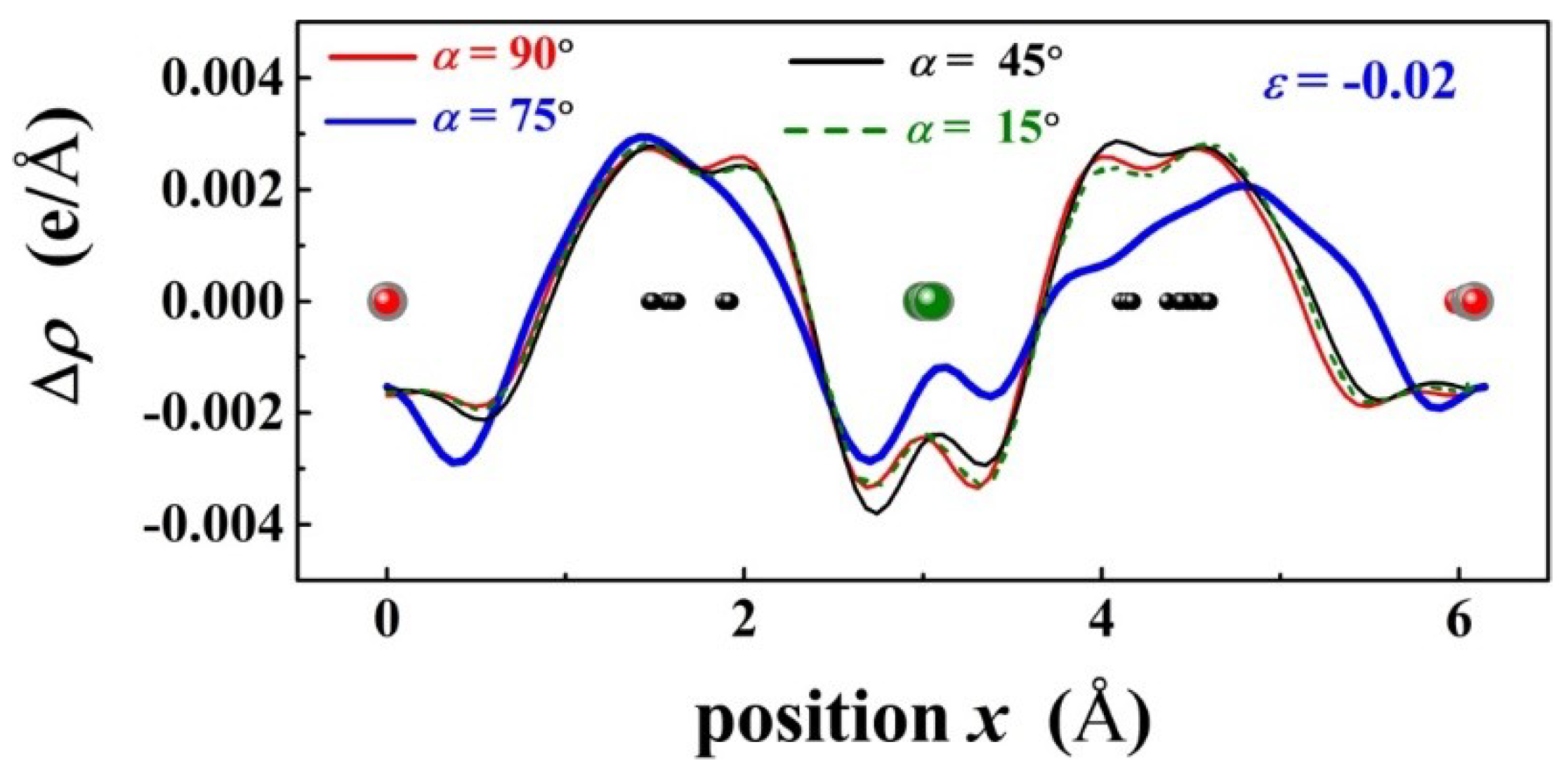
Figure 6 shows the plane averaged electron density difference Δ
ρ of PbPd
0.75Co
0.25O
2 projected along the x axis and under
= −0.02, with
α = 15°, 45°, 75°, and 90°, respectively. In comparison, it is found that p-d charge transfer Δ
ρ between Co and O exhibits an evident change for
α = 75°. Therefore, the band gap of PbPd
0.75Co
0.25O
2 is expected to be changed significantly as the compressive stress direction is along a particular direction with
α = 75°.
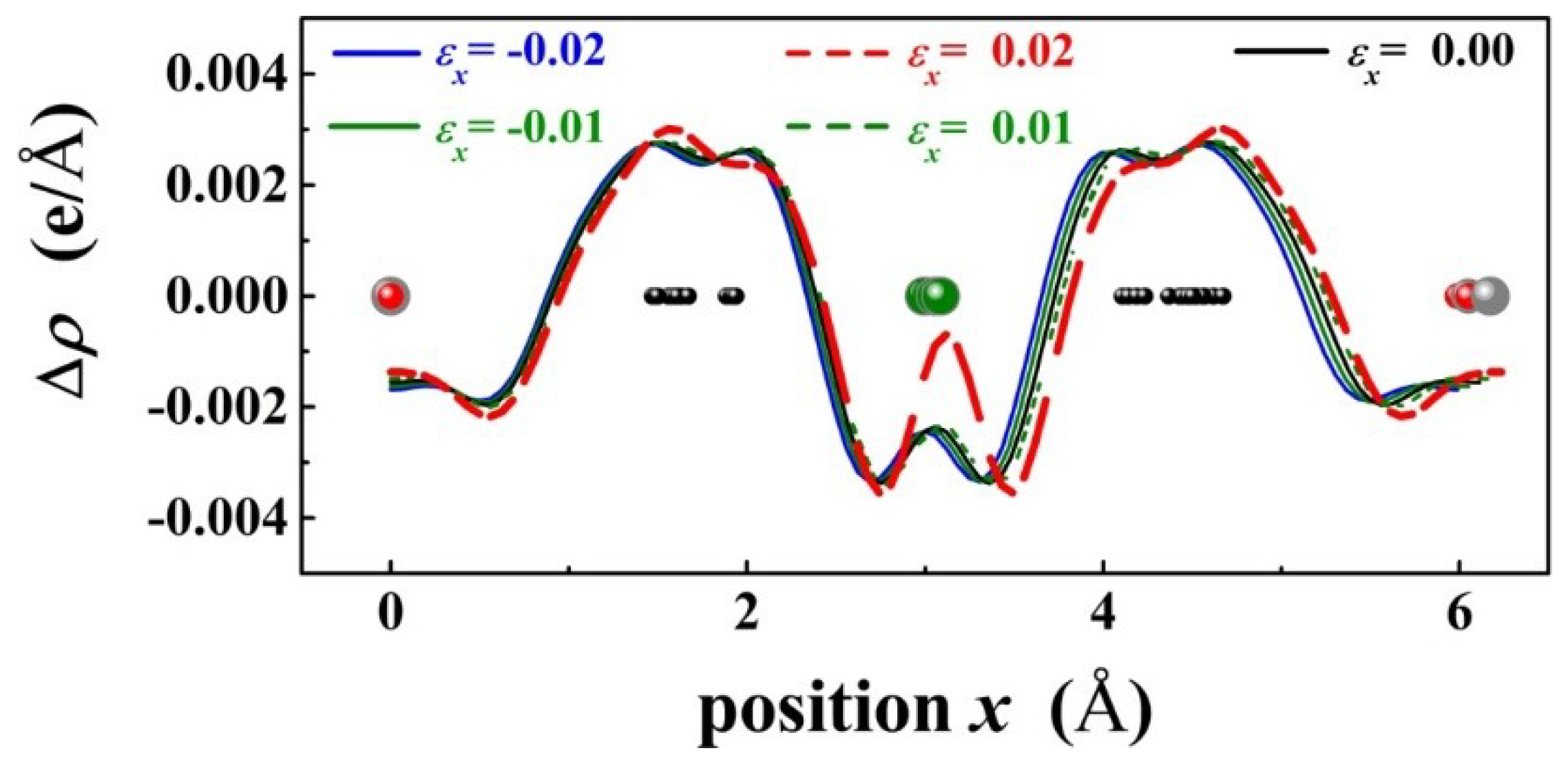
Figure 7 shows the plane averaged electron density difference
of PbPd
0.75Co
0.25O
2 projected along the x axis under
= −0.02, −0.01, 0.00, 0.01, 0.02, respectively. Based on spin-splitting theory, the minimum gap of the PbPd
0.75Co
0.25O
2 slab with the strain
= 0.02 is strongly related to the variation of
. From
Figure 7, it is concluded that Co atom should act as the source of the localized magnetic moment, and the coupling between the p-state from O and d-state from Co could induce a strong exchange interaction (named as p-d exchange interaction) in PbPd
0.75Co
0.25O
2. Moreover, the p-d exchange interaction was found to be nearly inversely proportional to the unit cell volume [
27]. Therefore, p-d exchange interaction mediated by strain should be responsible for variation of the plane averaged electron density difference, leading to a clear change of the band gap.
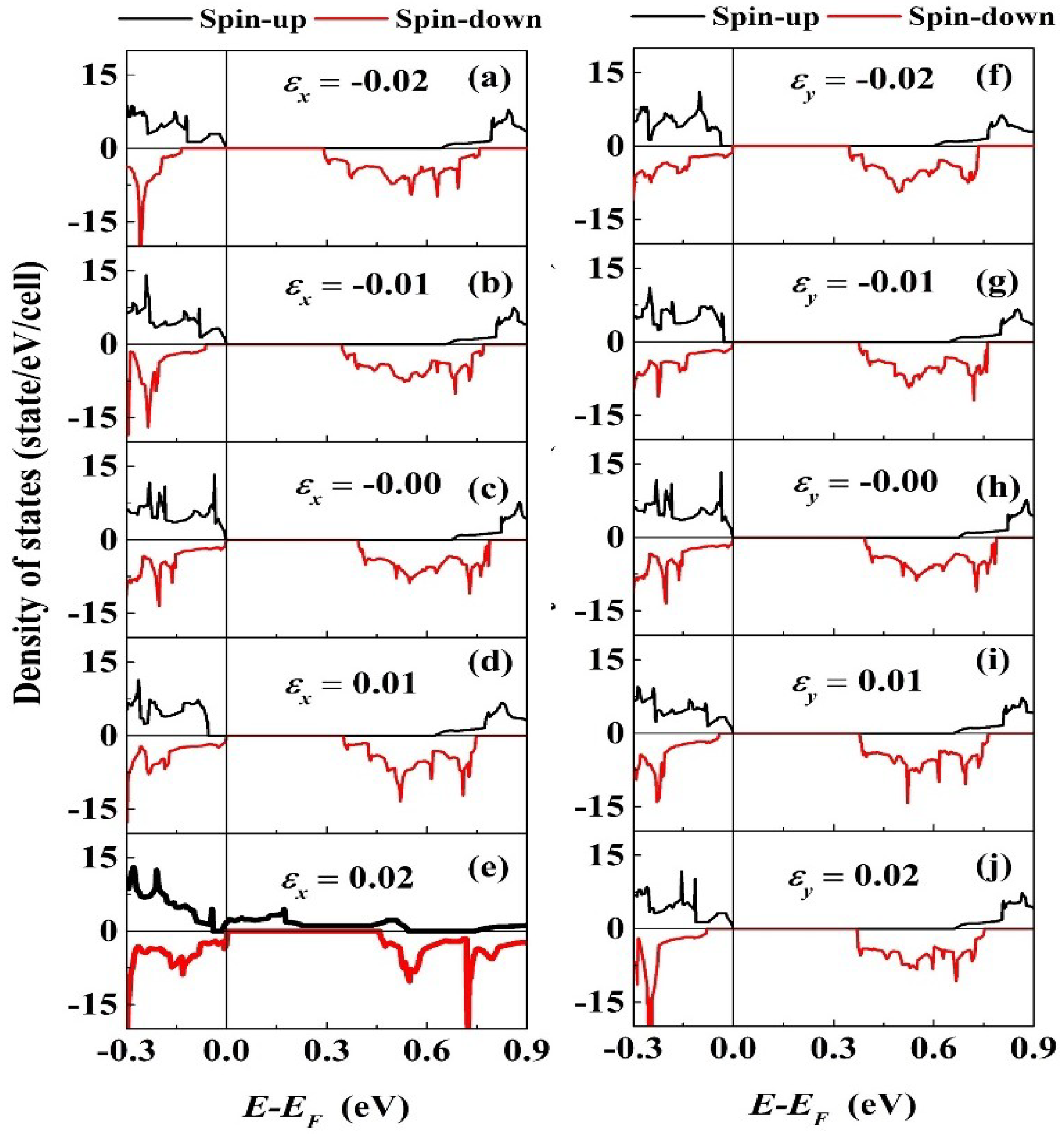
Figure 8 shows the spin polarized total density states of the PbPd
0.75Co
0.25O
2 slab with different strain along the x and y-axes external uniaxial strain directions. From the figure, it is found that the spin-up and spin-down DOSs are asymmetric, which means the existence of magnetic moment. The magnetic properties in element doped PbPdO
2 will be studied in subsequent research work. Interestingly, as shown in
Figure 8e, the tensile strain with
= 0.02 leads to the zero-band gap structure. The strain gives rise to the evident left shift of the bottom of the conduction band in spin-down DOSs, which effectively modulates the band gap. When the strain is large enough, the top of the valence band and the bottom of the conduction band in spin-up and spin-down DOSs all shift with changing strain, which leads to clear modulation of the band gap. This interesting phenomenon is similar to the fact that the slight tensile strain results in the zero-band gap structure [
4].
Unique electrical properties are highly desirable for practical application, and charge carrier concentration is a key parameter for the intrinsic semiconductor. For the intrinsic semiconductor, the charge charier concentration can be estimated as follows [
28],
where
KB,
Eg are the Boltzmann constant and band gap, respectively. In this paper, all the temperatures in carrier concentration were calculated at
T = 100 K. As
= 0, let
n =
n0;
≠ 0, let
n =
.
Combined with the results presented in
Figure 4a,b, the external strain dependence of charge carrier concentration ratio (
) for PbPdO
2 and PbPd
0.75Co
0.25O
2 slabs were evaluated, respectively.
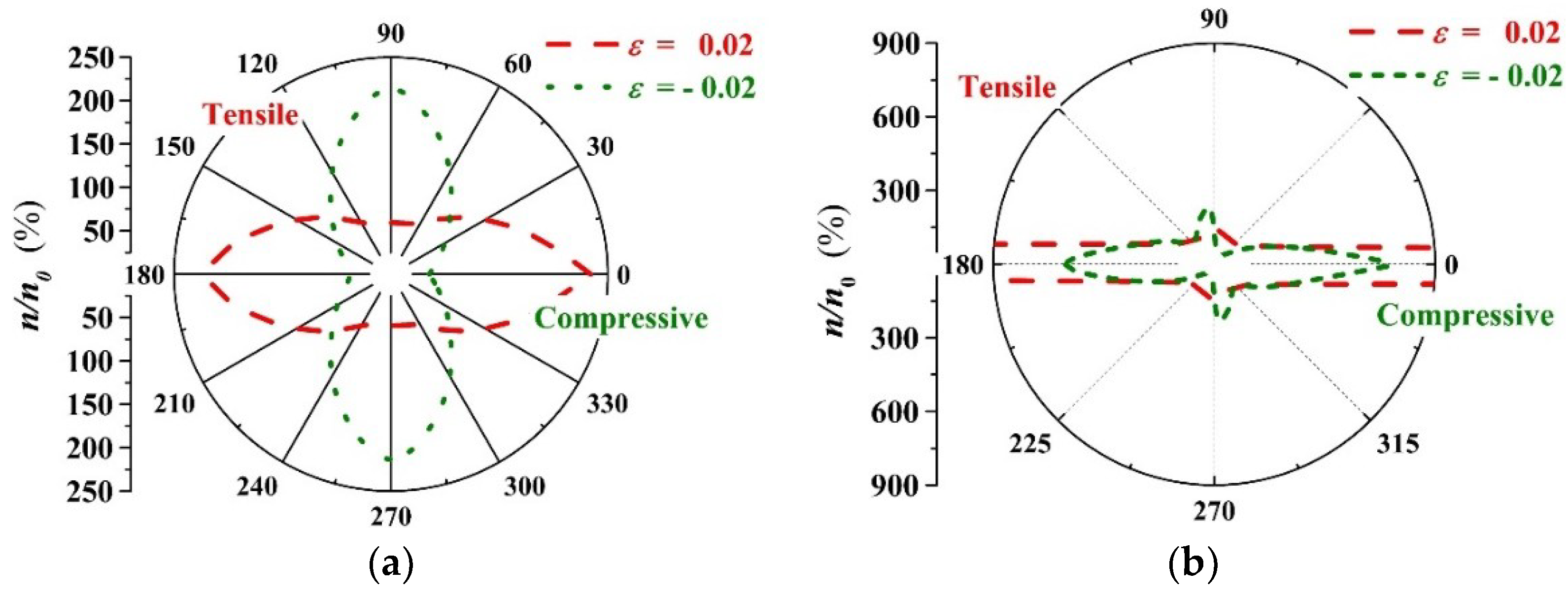
Figure 9a,b shows the orientation distribution curves of the intrinsic charge carrier concentration ratio
for PbPdO
2 and PbPd
0.75Co
0.25O
2 slabs with
= −0.02, −0.01, 0.00, 0.01, 0.02, respectively. Similar to the dependence of band gap
on strain orientation, PbPd
0.75Co
0.25O
2 exhibits more distinct anisotropy in carrier concentration with strain direction, especially along the x-axis. As shown in
Figure 9a, the pristine PbPdO
2 slab demonstrates the symmetrical and olive-like
curves, and having its largest and smallest band-gap values along the x-axis or y-axis, respectively. For the PbPd
0.75Co
0.25O
2 slab, the carrier concentration is sensitive to the application direction of strain. When the compressive stress applies along a direction of 75° (
) and x-axis, the remarkable variety in carrier concentration appears, as shown in
Figure 9b.
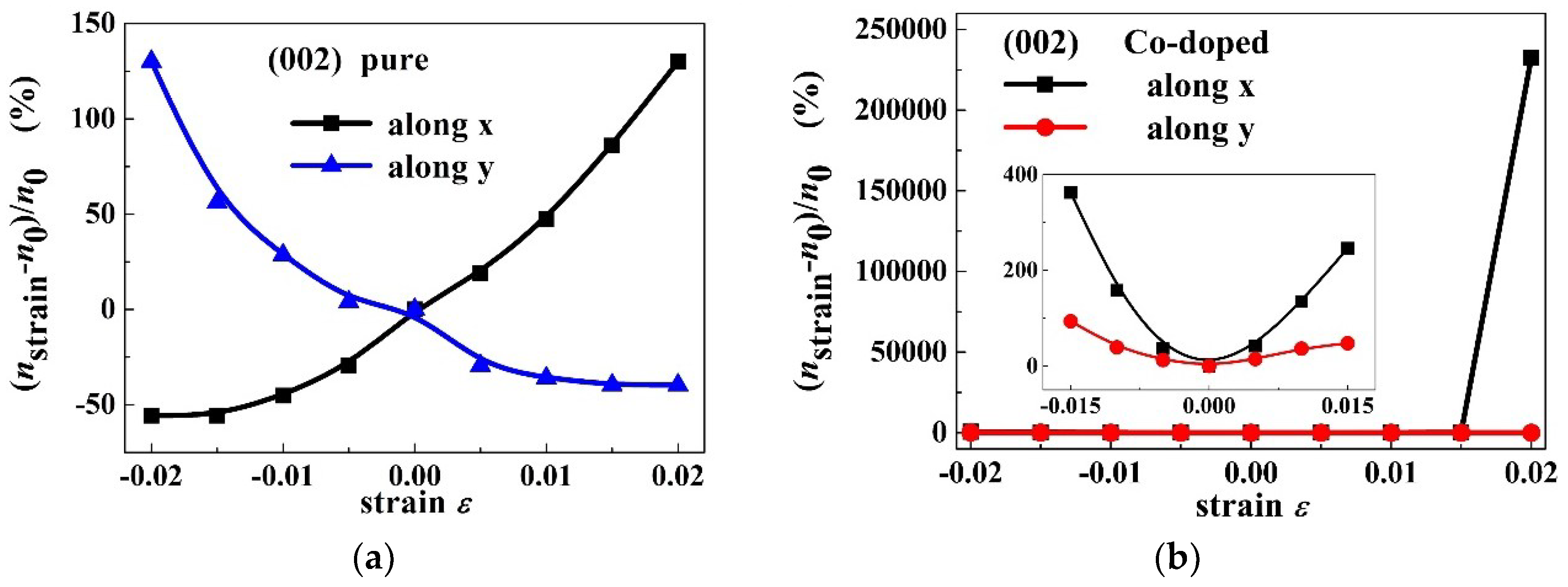
Figure 10c,d shows the intrinsic charge carrier concentration ratio
as a function of strain for PbPdO
2 and PbPd
0.75Co
0.25O
2 slabs along the x and y-axes, respectively. For the PbPdO
2 slab, the carrier concentration increases monotonically with increasing compressive stress, but decreasing with increasing tensile stress along the x-axis. On the contrary, the carrier concentration decreases with increasing compressive stress, while increasing with increasing tensile stress along the y-axis. In contrast, the carrier concentration of PbPd
0.75Co
0.25O
2 slab increases with increasing compressive and tensile stresses along both the x and y-axes. As the compressive stress increases beyond 0.015 along the x-axis, carrier concentration of the PbPd
0.75Co
0.25O
2 slab increases rapidly. It was found that the carrier concentration of PbPd
0.75Co
0.25O
2 could sharply increase up to 5–6 orders of magnitude with the help of external strain with
= 0.02. The calculated results suggest strongly that the element-doping PbPdO
2 should become an important piezoresistance candidate material.
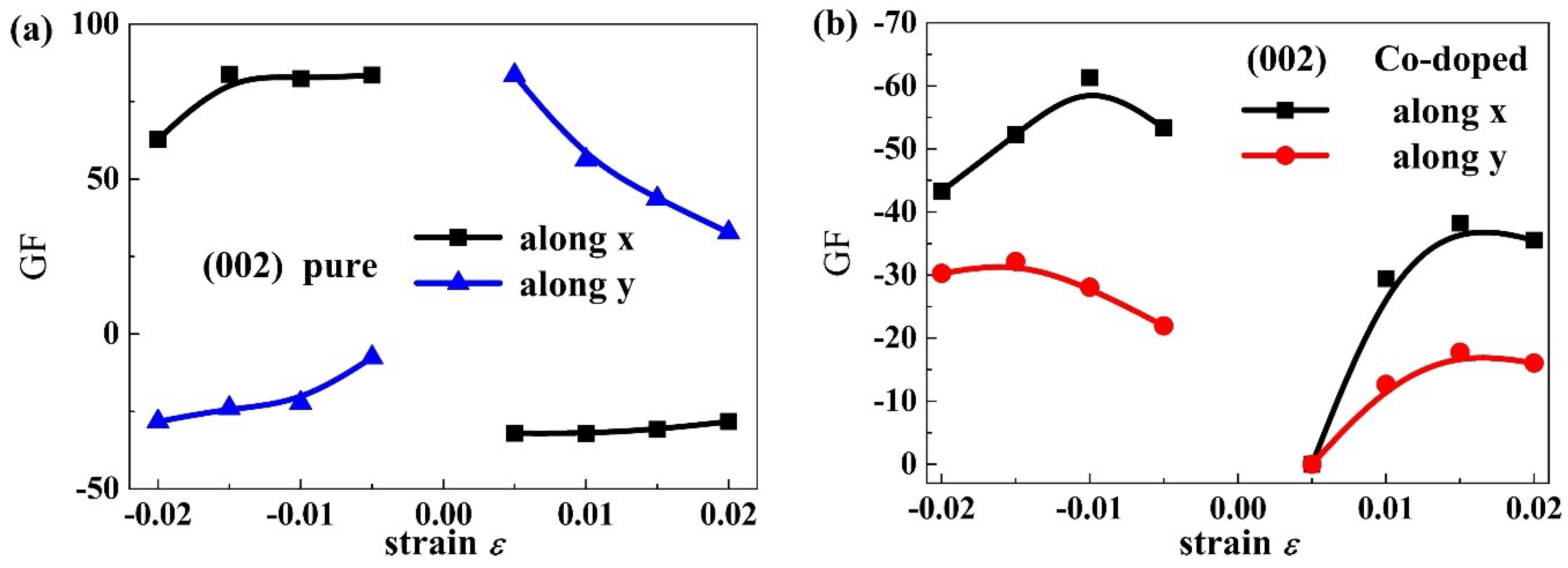
Figure 11 presents the strain dependence of gauge factor for the PbPdO
2 and PbPd
0.75Co
0.25O
2 slab along the x and y axes.
Table 1 gives some typical gauge factor values. When the tensile strain is 0.02, the piezoresistive gauge factors for the PbPdO
2 and PbPd
0.75Co
0.25O
2 slab along the x-axis are calculated to be respectively 62.8 and −43.3, which is comparable to trilayer MoS
2 and much higher than suspended-graphene-based strain sensor [
29]. As Pd–O (Co–O) polar covalent bond is different from C–C bond, PbPdO
2-based semiconductors can exhibit a higher piezoresistive gauge factor than graphene-based strain sensors. The predicted large gauge factors in our work implies that the element-doping PbPdO
2 may have promising opportunities to be used as strain sensors.