Miniature Spectroscopes with Two-Dimensional Guided-Mode Resonant Metal Grating Filters Integrated on a Photodiode Array
Abstract
:1. Introduction
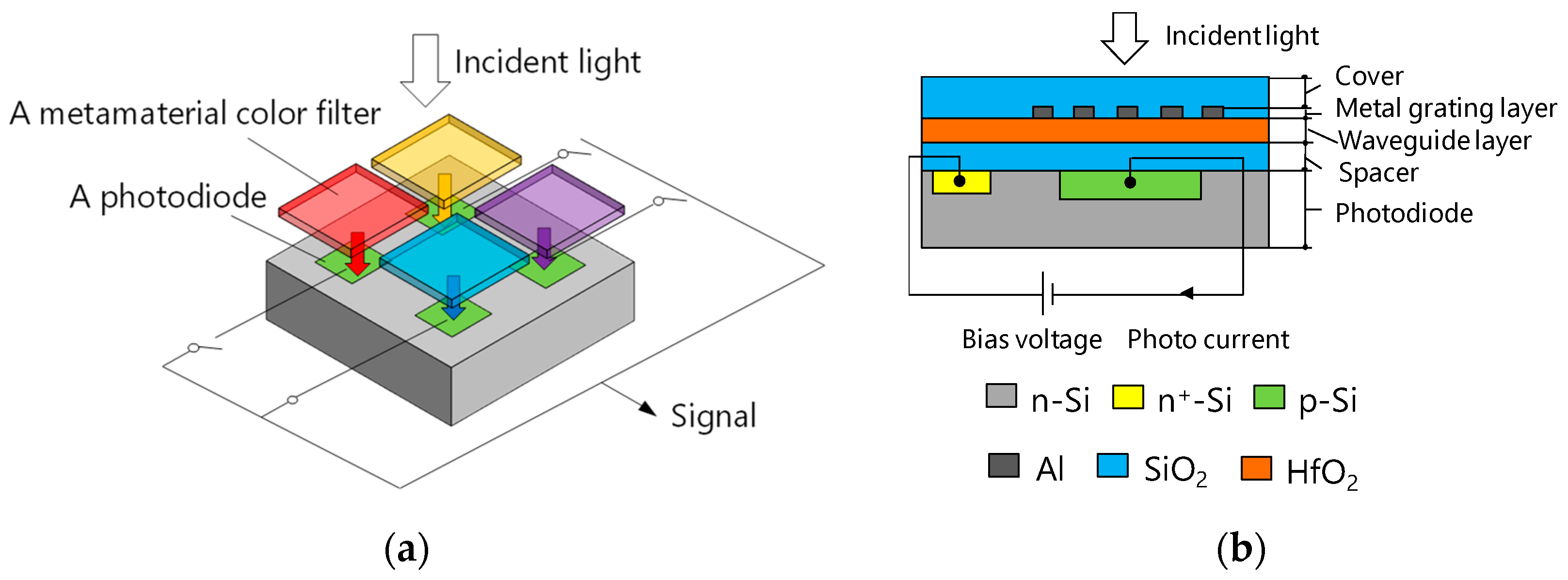
2. Device Configuration
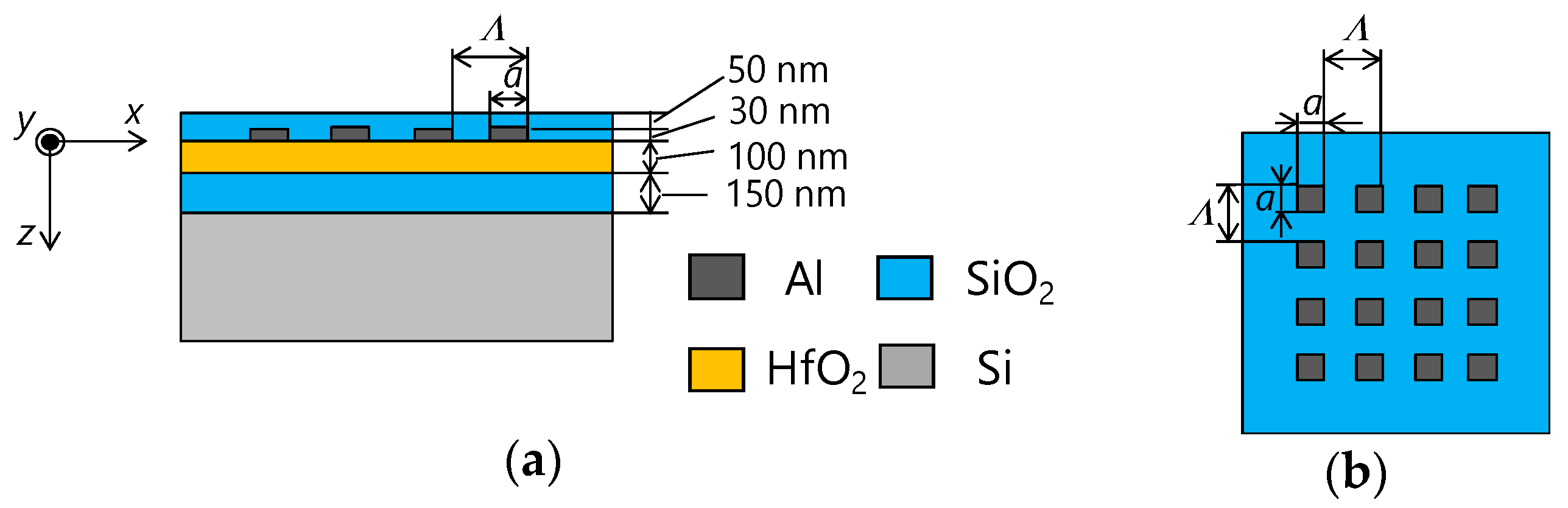
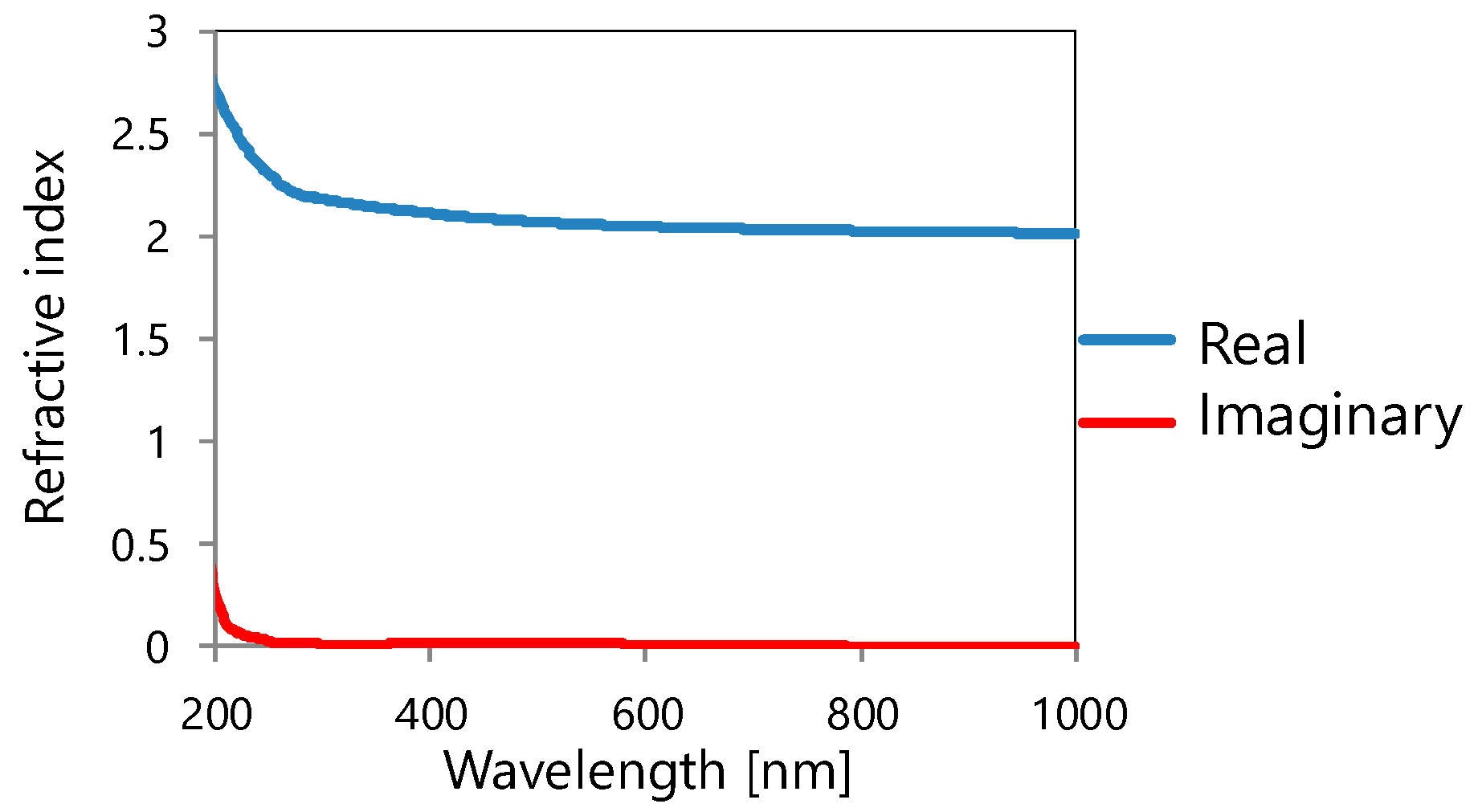
3. Design and Numerical Analysis
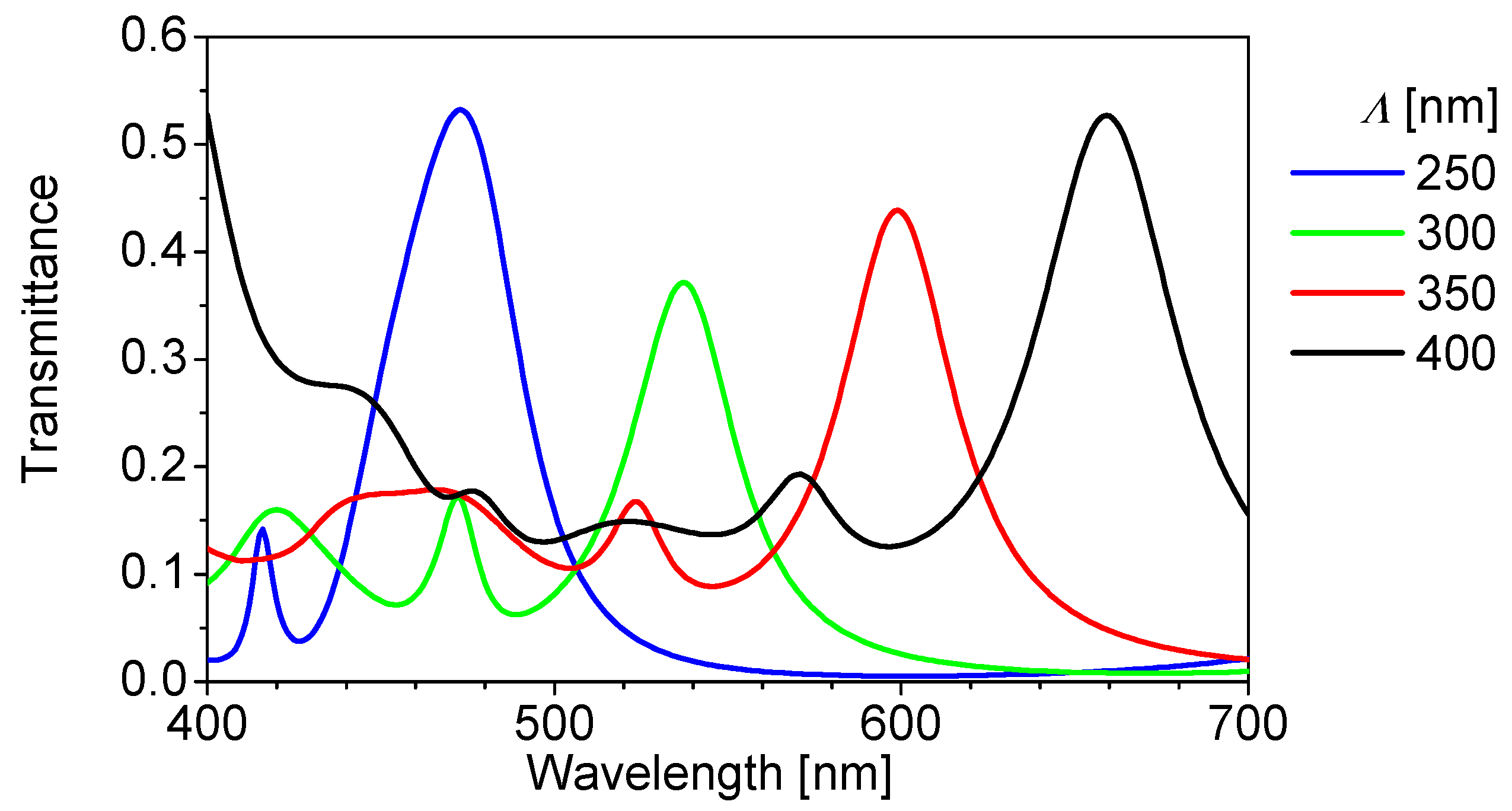
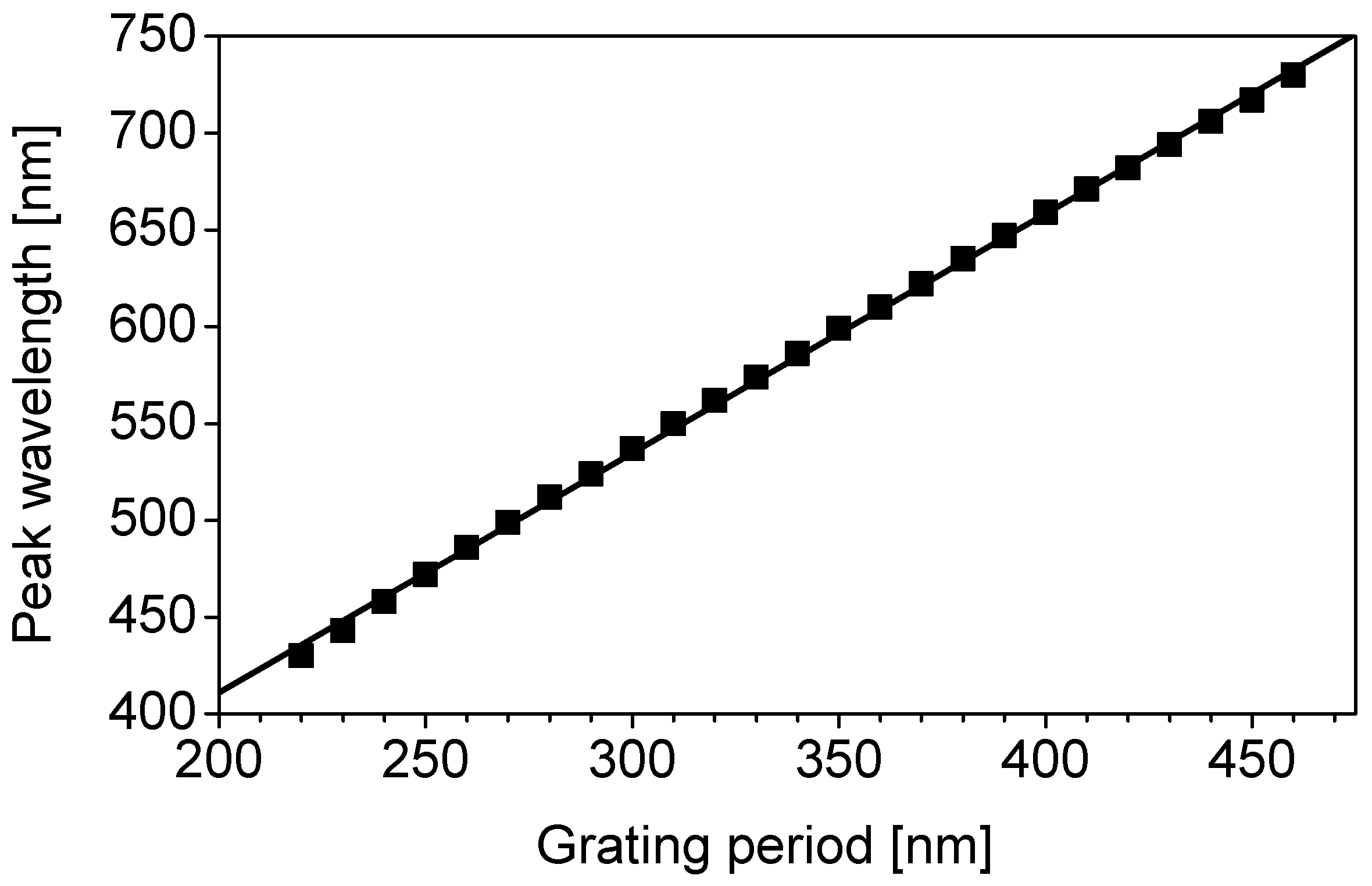
3.1. Design of Color Filters
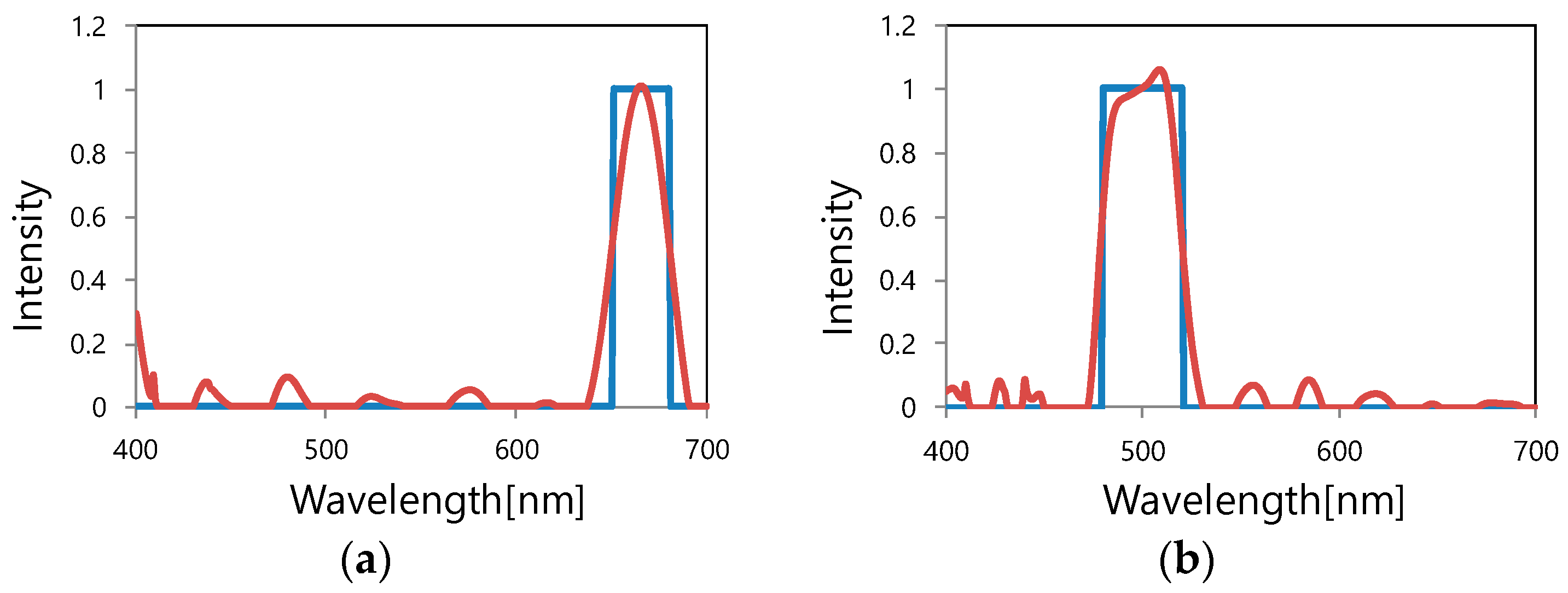
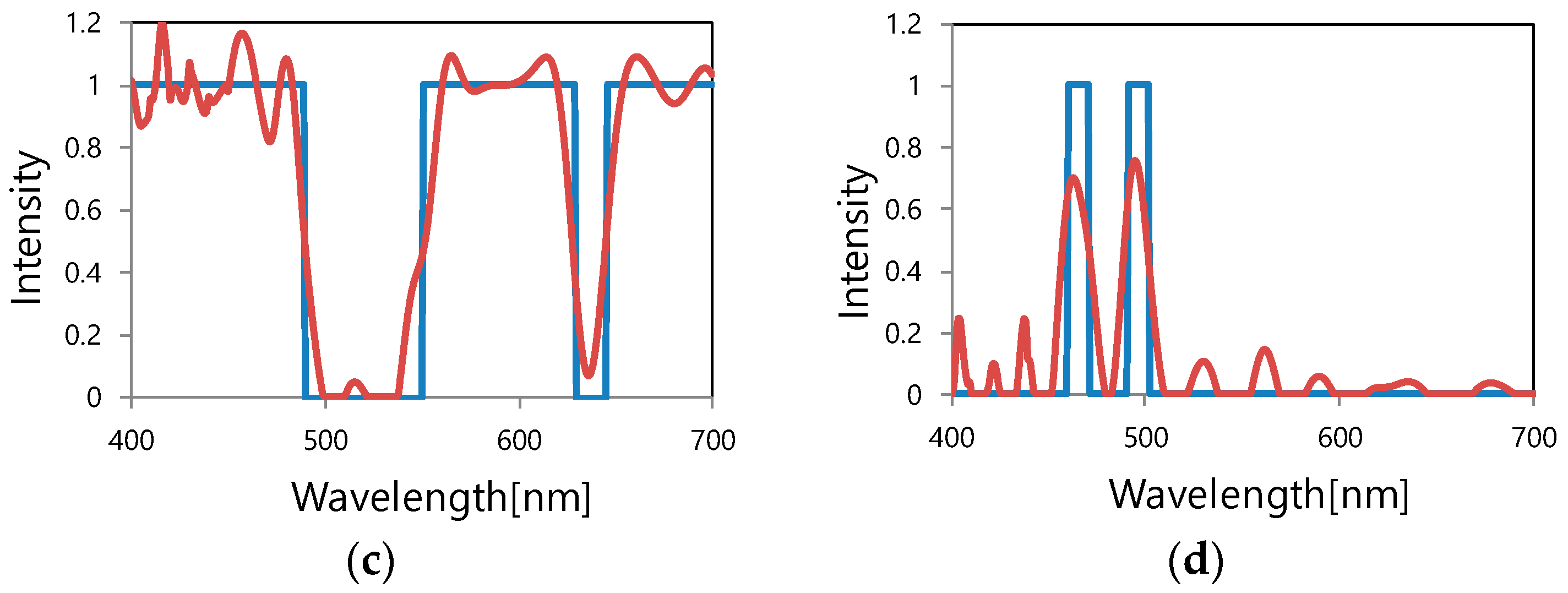
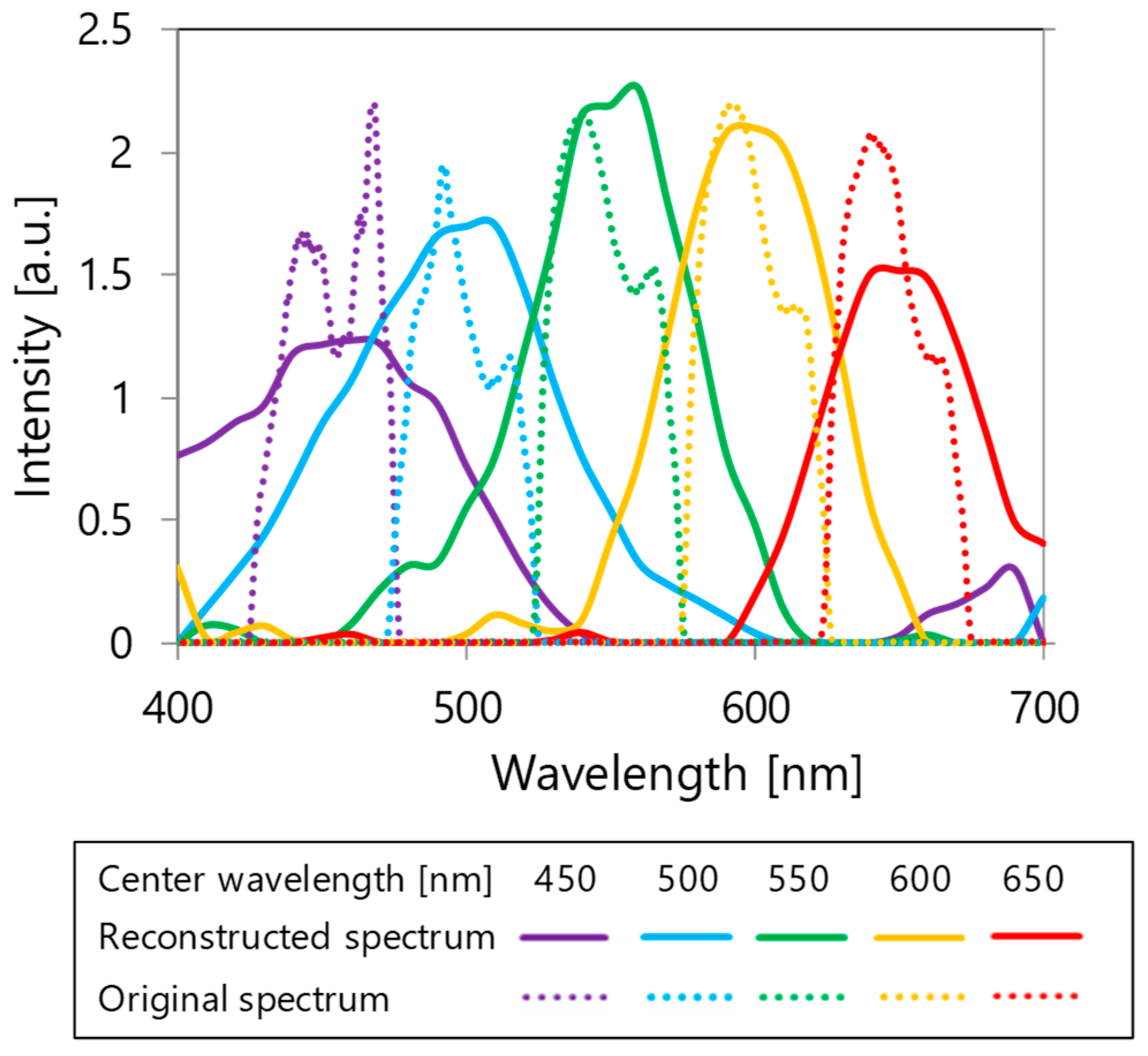
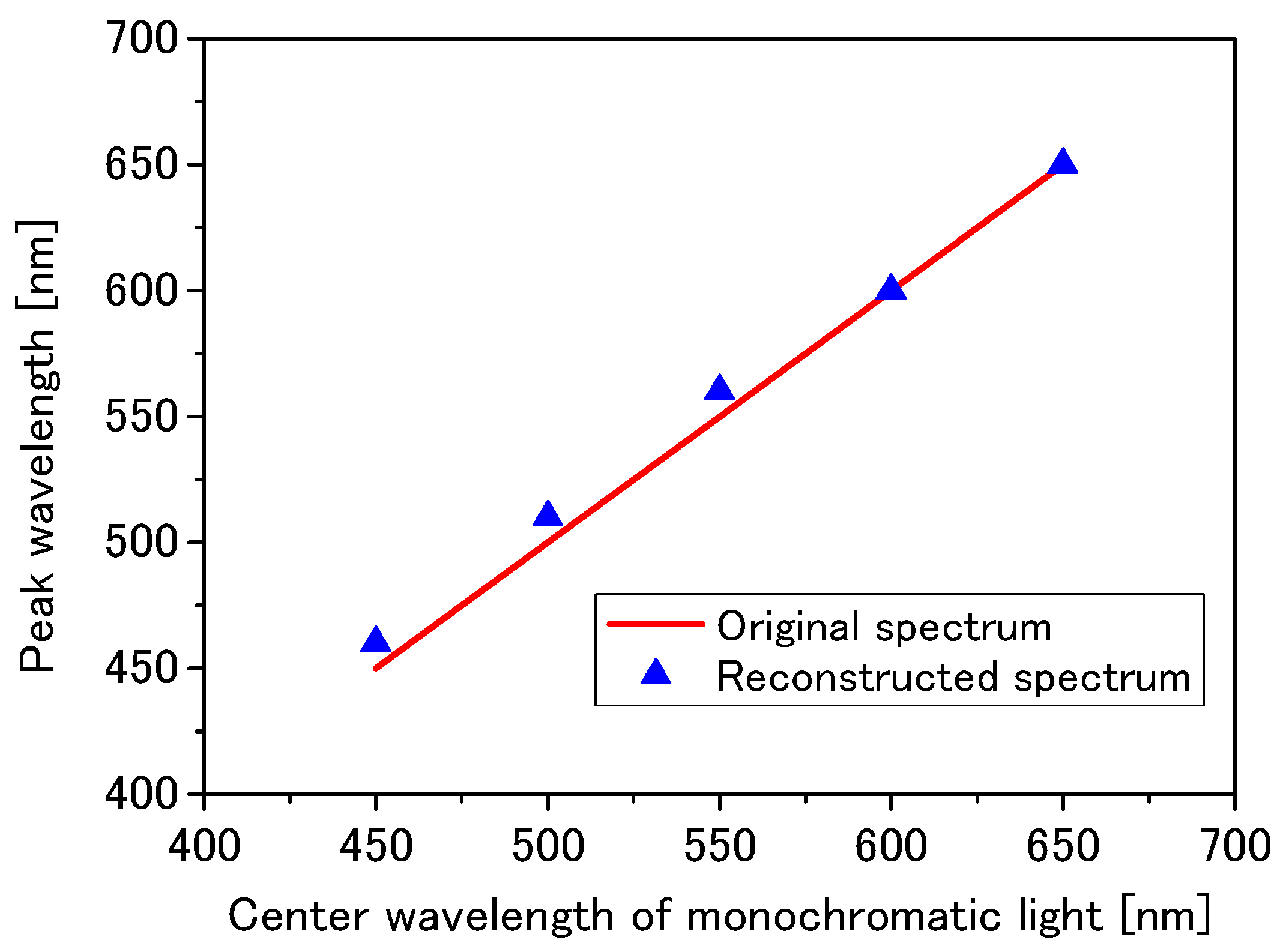
3.2. Spectrum Reconstruction: Principle and Calculation Examples
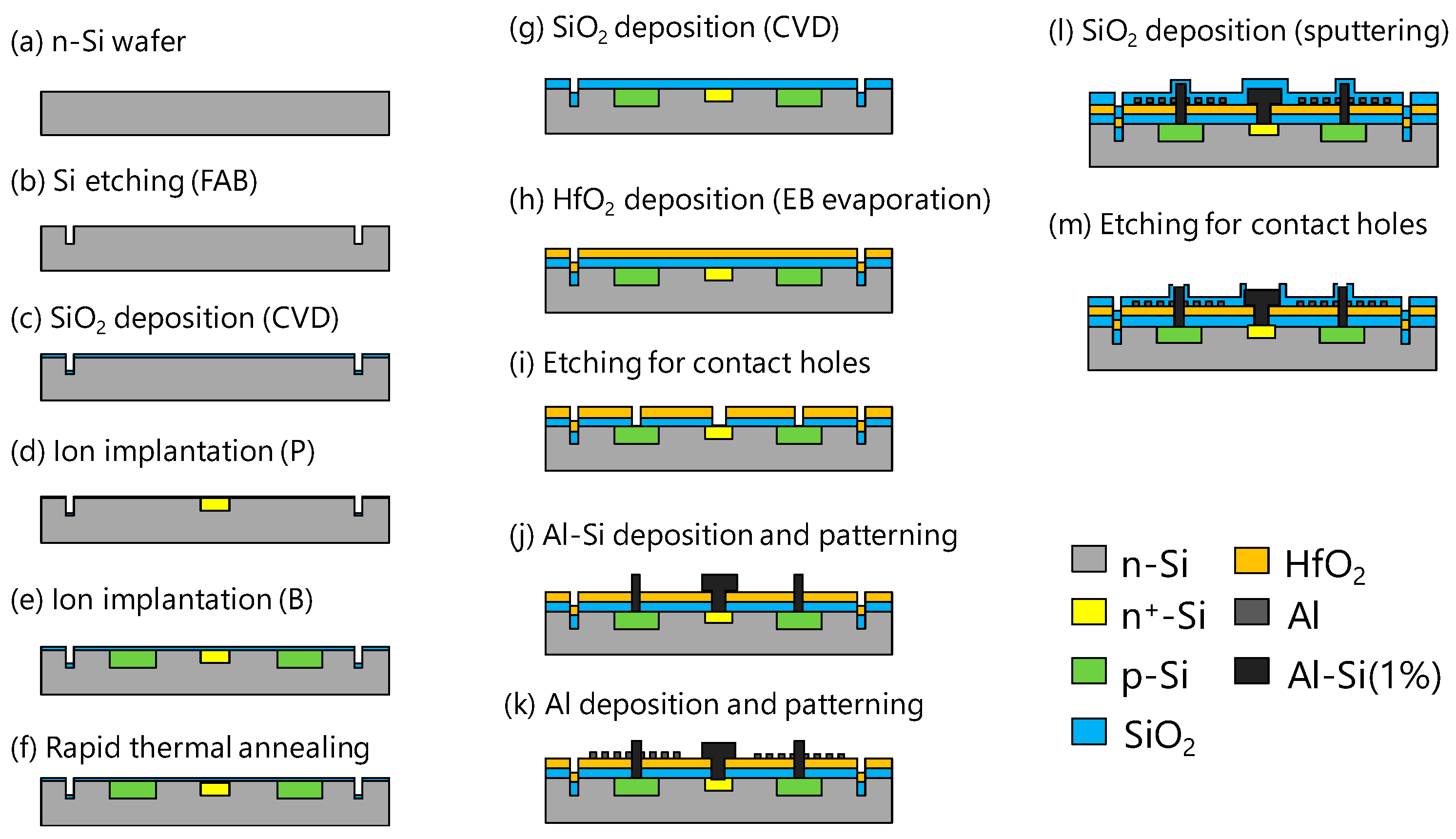
4. Fabrication
5. Measured Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ebbesen, T.W.; Lezec, H.J.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Genet, C.; Ebbesen, T.W. Light in tiny holes. Nature 2007, 445, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, A.F.; Xu, T.; Guo, L.J. High efficiency resonance-based spectrum filters with tunable transmission bandwidth fabricated using nanoimprint lithography. Appl. Phys. Lett. 2011, 99, 143111. [Google Scholar] [CrossRef]
- Xu, T.; Wu, Y.K.; Luo, X.; Guo, L.J. Plasmonic nanoresonators for high-resolution colour filtering and spectral imaging. Nat. Commun. 2010, 1, 59. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.S.; Yoon, Y.T.; Lee, S.S.; Kim, S.H.; Lee, K.D. Color filter based on a subwavelength patterned metal grating. Opt. Express 2007, 15, 15457–15463. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Cumming, D.R.S. High transmission and low color cross-talk plasmonic color filters using triangular-lattice hole arrays in aluminum films. Opt. Express 2010, 18, 14056–14062. [Google Scholar] [CrossRef] [PubMed]
- Chou, S.Y.; Krauss, P.R.; Renstrom, P.J. Nanoimprint lithography. J. Vac. Sci. Technol. B 1996, 14, 4129–4133. [Google Scholar] [CrossRef]
- Chou, S.Y.; Krauss, P.R.; Zhang, W.; Guo, L.; Zhuang, L. Sub-10 nm imprint lithography and applications. J. Vac. Sci. Technol. B 1997, 15, 2897–2904. [Google Scholar] [CrossRef]
- Bao, L.R.; Cheng, X.; Huang, X.D.; Guo, L.J.; Pang, S.W.; Yee, A.F. Nanoimprinting over topography and multilayer three-dimensional printing. J. Vac. Sci. Technol. B 2002, 20, 2881–2886. [Google Scholar] [CrossRef]
- Zhang, W.; Chou, S.Y. Fabrication of 60-nm transistors on 4-in. wafer using nanoimprint at all lithography levels. Appl. Phys. Lett. 2003, 83, 1632–1634. [Google Scholar] [CrossRef]
- Alkaisi, M.M.; Jayatissa, W.; Konijn, M. Multilevel nanoimprint lithography. Curr. Appl. Phys. 2004, 4, 111–114. [Google Scholar] [CrossRef]
- Roy, E.; Kanamori, Y.; Belotti, M.; Chen, Y. Enhanced UV imprint ability with a tri-layer stamp configuration. Microelectron. Eng. 2005, 78–79, 689–694. [Google Scholar] [CrossRef]
- Kanamori, Y.; Okochi, M.; Hane, K. Fabrication of antireflection subwavelength gratings at the tips of optical fibers using UV nanoimprint lithography. Opt. Express 2013, 21, 322–328. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Kikuchi, E.; Watanabe, M.; Sugiyama, Y.; Kanamori, Y.; Nakagawa, M. Silica imprint templates with concave patterns from single-digit nanometers fabricated by electron beam lithography involving argon ion beam milling. Jpn. J. Appl. Phys. 2017, 56, 06GL01. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, K.S.; Ahn, J.; Lee, J.J.; Kim, M.G.; Shin, Y.B. Highly sensitive biosensing using arrays of plasmonic Au nanodisks realized by nanoimprint lithography. ACS Nano 2011, 5, 897–904. [Google Scholar] [CrossRef] [PubMed]
- Peer, A.; Biswas, R. Extraordinary optical transmission in nanopatterned ultrathin metal films without holes. Nanoscale 2016, 8, 4657–4666. [Google Scholar] [CrossRef] [PubMed]
- Nishiguchi, K.; Sueyoshi, K.; Hisamoto, H.; Endo, T. Fabrication of gold-deposited plasmonic crystal based on nanoimprint lithography for label-free biosensing application. Jpn. J. Appl. Phys. 2016, 55, 08RE02. [Google Scholar] [CrossRef]
- Peer, A.; Hu, Z.; Singh, A.; Hollingsworth, J.A.; Biswas, R.; Htoon, H. Photoluminescence enhancement of CuInS2 quantum dots in solution coupled to plasmonic gold nanocup array. Small 2017, 13, 1700660. [Google Scholar] [CrossRef] [PubMed]
- Hutley, M.C. Diffraction gratings. In Diffractive Optics for Industrial and Commercial Applications; Turunen, J., Wyrowski, F., Eds.; Akademie Verlag: Berlin, Germany, 1997; pp. 59–80. ISBN 3055017331. [Google Scholar]
- Ema, D.; Kanamori, Y.; Sai, H.; Hane, K. Plasmonic color filters integrated on a photodiode array. Electron. Commun. Jpn. 2018, 101, 95–104. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, N.T.; Kurokawa, U.; Choi, B.I. Spectrum reconstruction for filter-array spectrum sensor from sparse template selection. Opt. Eng. 2011, 50, 114402. [Google Scholar] [CrossRef]
- Kurokawa, U.; Choi, B.I.; Chang, C.C. Filter-Based Miniature Spectrometers: Spectrum Reconstruction Using Adaptive Regularization. IEEE Sens. J. 2011, 11, 1556–1563. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, H.Y. Spectrum Reconstruction for On-Chip Spectrum Sensor Array Using a Novel Blind Nonuniformity Correction Method. IEEE Sens. J. 2012, 12, 2586–2592. [Google Scholar] [CrossRef]
- Chang, C.C.; Su, Y.J.; Kurokawa, U.; Choi, B.I. Interference Rejection Using Filter-Based Sensor Array in VLC Systems. IEEE Sens. J. 2012, 12, 1025–1032. [Google Scholar] [CrossRef]
- Oliver, J.; Lee, W.B.; Lee, H.N. Filters with random transmittance for improving resolution in filter-array-based spectrometers. Opt. Express 2013, 21, 3969–3989. [Google Scholar] [CrossRef] [PubMed]
- Oliver, J.; Lee, W.; Park, S.; Lee, H.N. Improving resolution of miniature spectrometers by exploiting sparse nature of signals. Opt. Express 2012, 20, 2613–2625. [Google Scholar] [CrossRef] [PubMed]
- Norton, S.M.; Erdogan, T.; Morris, G.M. Coupled-mode theory of resonant-grating filters. J. Opt. Soc. Am. A 1997, 14, 629–639. [Google Scholar] [CrossRef]
- Jacob, D.K.; Dunn, S.C.; Moharam, M.G. Design considerations for narrow-band dielectric resonant grating reflection filters of finite length. J. Opt. Soc. Am. A 2000, 17, 1241–1249. [Google Scholar] [CrossRef]
- Brundrett, D.L.; Glytsis, E.N.; Gaylord, T.K.; Bendickson, J.M. Effects of modulation strength in guided-mode resonant subwavelength gratings at normal incidence. J. Opt. Soc. Am. A 2000, 17, 1221–1230. [Google Scholar] [CrossRef]
- Peters, D.W.; Kemme, S.A.; Hadley, G.R. Effect of finite grating, waveguide width, and end-facet geometry on resonant subwavelength grating reflectivity. J. Opt. Soc. Am. A 2004, 21, 981–987. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kanamori, Y.; Hane, K. Surface laser emission from solid polymer dye in a guided mode resonant grating filter structure. Appl. Phys. Lett. 2005, 87, 151106. [Google Scholar] [CrossRef]
- Kanamori, Y.; Kitani, T.; Hane, K. Guided-Mode Resonant Grating Filter Fabricated on Silicon-on-Insulator Substrate. Jpn. J. Appl. Phys. 2006, 45, 1883–1885. [Google Scholar] [CrossRef]
- Kanamori, Y.; Kitani, T.; Hane, K. Control of guided resonance in a photonic crystal slab using microelectromechanical actuators. Appl. Phys. Lett. 2007, 90, 031911. [Google Scholar] [CrossRef]
- Kanamori, Y.; Katsube, H.; Furuta, T.; Hasegawa, S.; Hane, K. Design and Fabrication of Structural Color Filters with Polymer-Based Guided-Mode Resonant Gratings by Nanoimprint Lithography. Jpn. J. Appl. Phys. 2009, 48, 06FH04. [Google Scholar] [CrossRef]
- Kanamori, Y.; Ozaki, T.; Hane, K. Fabrication of Ultrathin Color Filters for Three Primary Colors Using Guided-Mode Resonance in Silicon Subwavelength Gratings. Opt. Rev. 2014, 21, 723–727. [Google Scholar] [CrossRef]
- Kanamori, Y.; Ozaki, T.; Hane, K. Reflection color filters of the three primary colors with wide viewing angles using common-thickness silicon subwavelength gratings. Opt. Express 2014, 22, 25663–25672. [Google Scholar] [CrossRef] [PubMed]
- Moharam, M.G.; Grann, E.B.; Pommet, D.A.; Gaylord, T.K. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Lalanne, P.; Morris, G.M. Highly improved convergence of the coupled-wave method for TM polarization. J. Opt. Soc. Am. A 1996, 13, 779–784. [Google Scholar] [CrossRef]
- Smith, D.Y.; Shiles, E.; Inokuti, M. The Optical Properties of Metallic Aluminum. In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Orlando, FL, USA, 1985; Volume 1, pp. 369–406. ISBN 0125444206. [Google Scholar]
- Edwards, D.F. Silicon (Si). In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Orlando, FL, USA, 1985; Volume 1, pp. 547–569. ISBN 0125444206. [Google Scholar]
- Philipp, H.R. Silicon Dioxide (SiO2) (Glass). In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Orlando, FL, USA, 1985; Volume 1, pp. 749–763. ISBN 0125444206. [Google Scholar]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems, 2nd ed.; Academic Press: Waltham, MA, USA, 2012; pp. 93–127. ISBN 9780128100929. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanamori, Y.; Ema, D.; Hane, K. Miniature Spectroscopes with Two-Dimensional Guided-Mode Resonant Metal Grating Filters Integrated on a Photodiode Array. Materials 2018, 11, 1924. https://doi.org/10.3390/ma11101924
Kanamori Y, Ema D, Hane K. Miniature Spectroscopes with Two-Dimensional Guided-Mode Resonant Metal Grating Filters Integrated on a Photodiode Array. Materials. 2018; 11(10):1924. https://doi.org/10.3390/ma11101924
Chicago/Turabian StyleKanamori, Yoshiaki, Daisuke Ema, and Kazuhiro Hane. 2018. "Miniature Spectroscopes with Two-Dimensional Guided-Mode Resonant Metal Grating Filters Integrated on a Photodiode Array" Materials 11, no. 10: 1924. https://doi.org/10.3390/ma11101924
APA StyleKanamori, Y., Ema, D., & Hane, K. (2018). Miniature Spectroscopes with Two-Dimensional Guided-Mode Resonant Metal Grating Filters Integrated on a Photodiode Array. Materials, 11(10), 1924. https://doi.org/10.3390/ma11101924



