A Hybrid Finite Volume and Extended Finite Element Method for Hydraulic Fracturing with Cohesive Crack Propagation in Quasi-Brittle Materials
Abstract
1. Introduction
2. Methodology
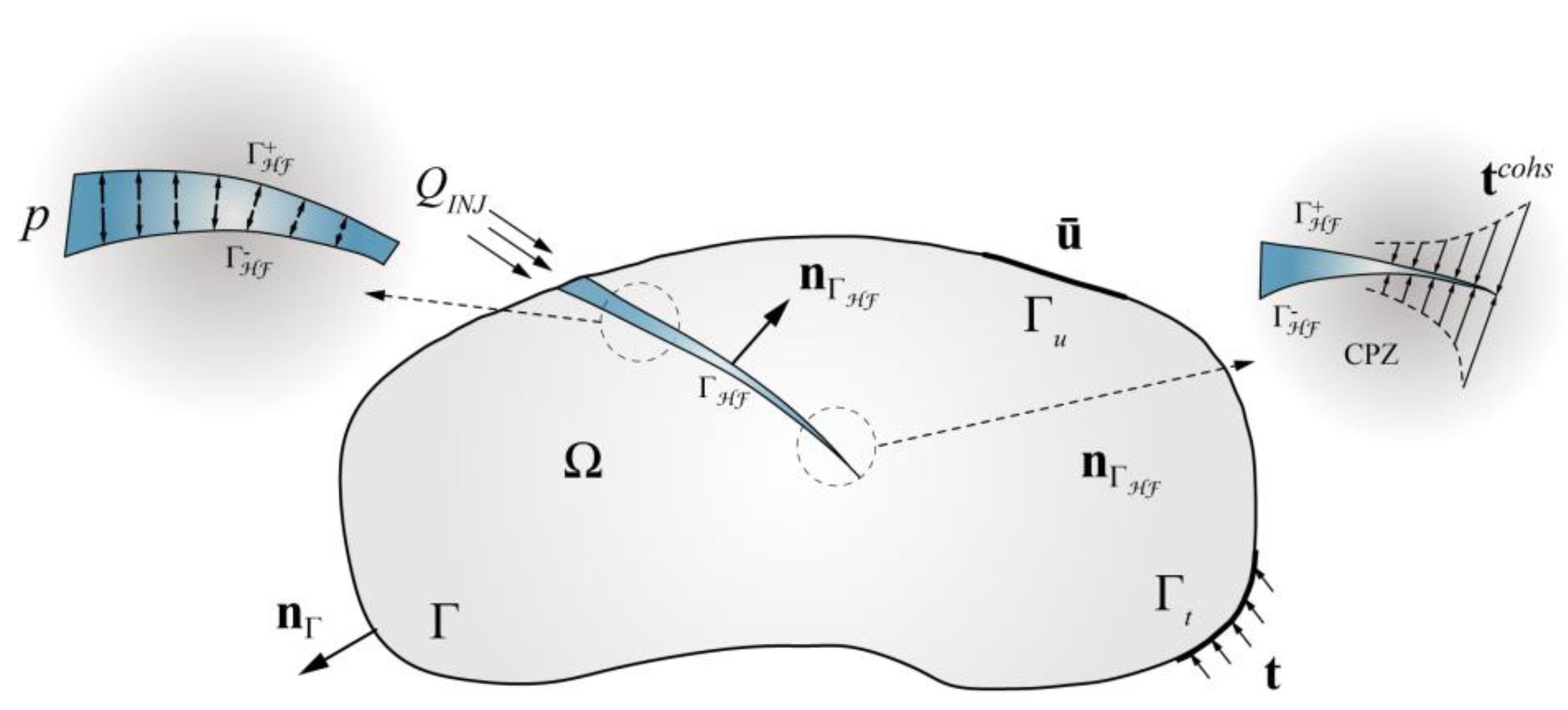
2.1. Conceptual Model
2.2. Deformation Model
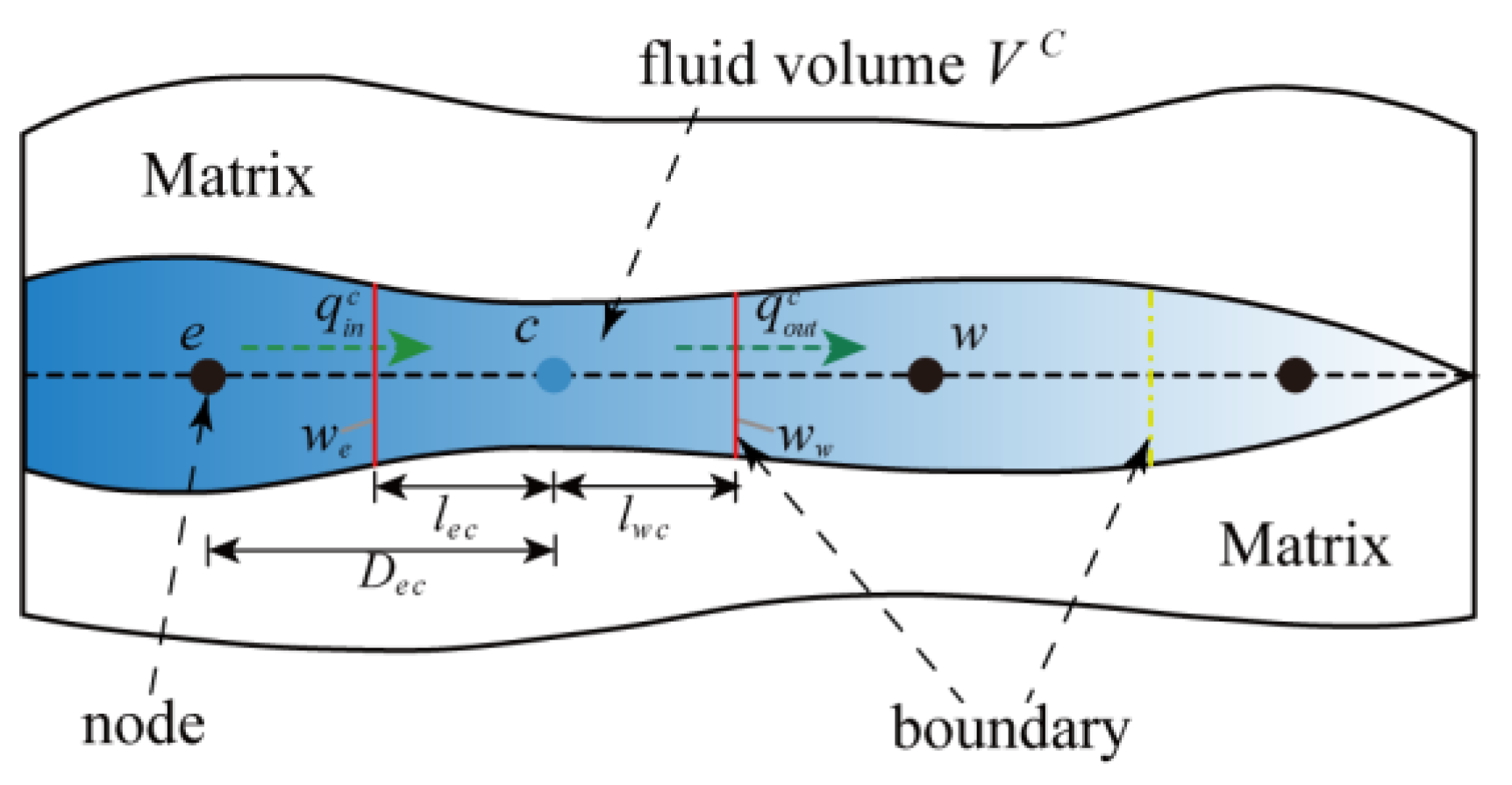
2.3. Fracture Flow Model
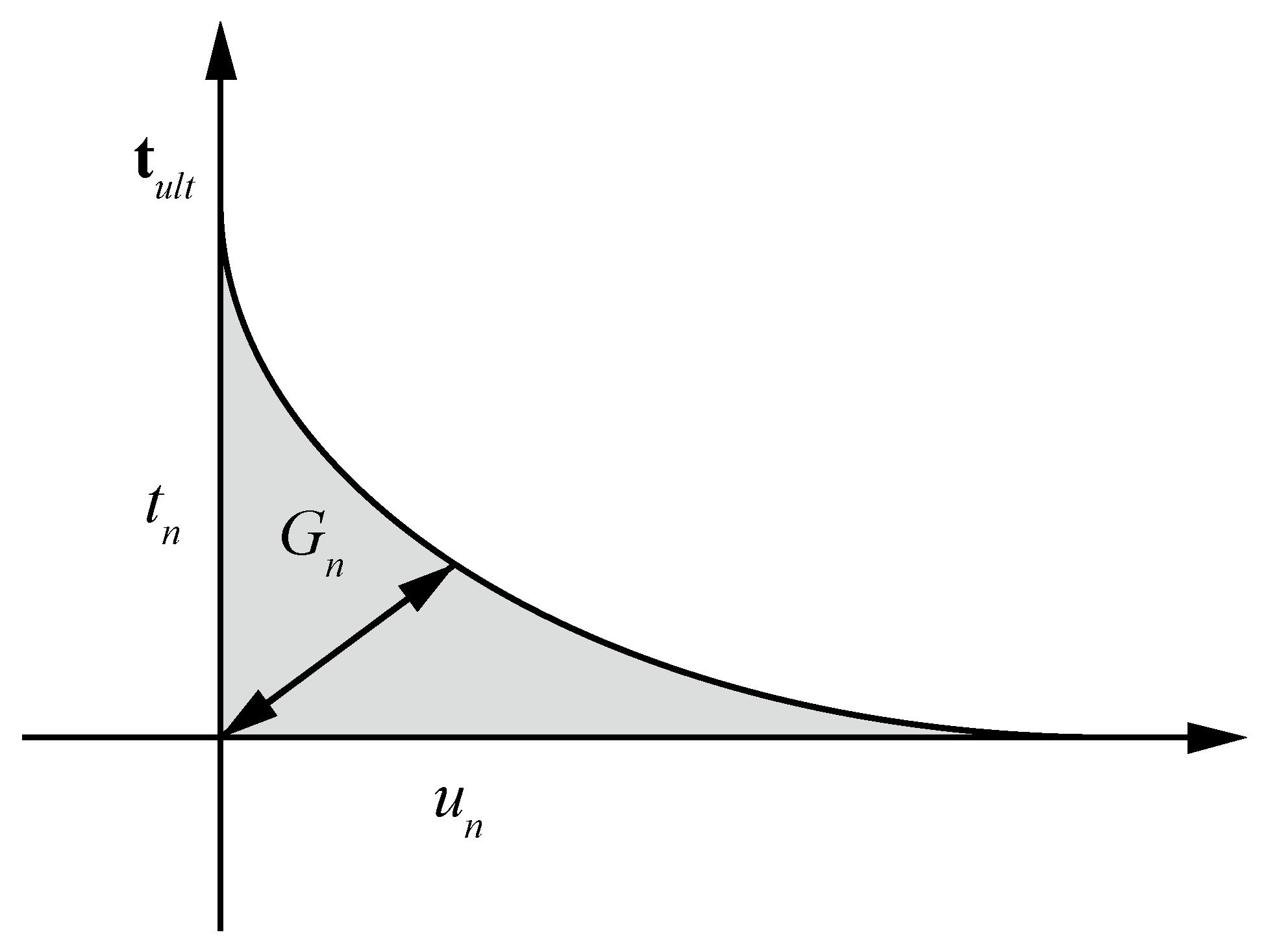
2.4. Fracture Propagation Model
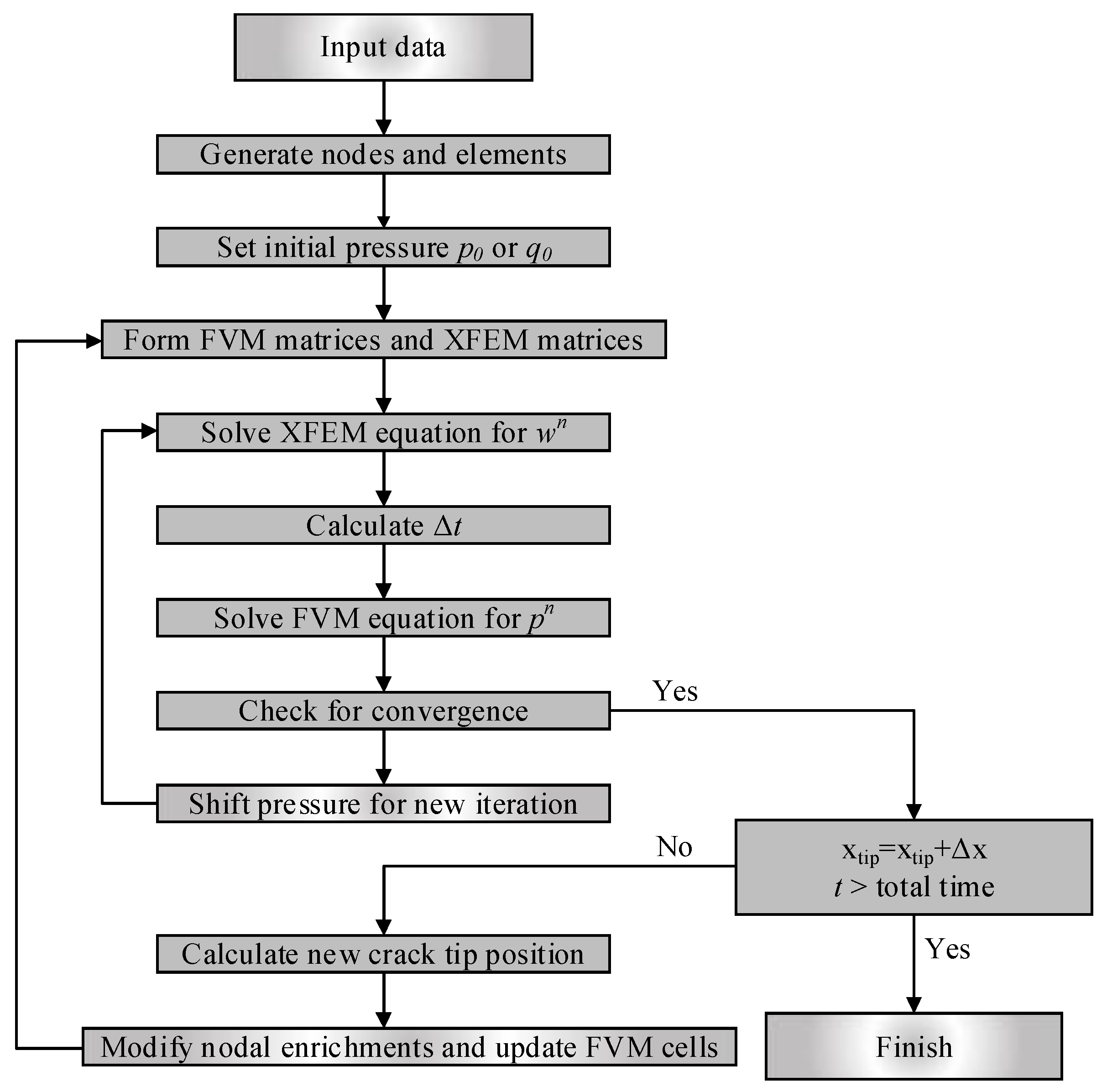
2.5. Discretization and Solution Algorithms
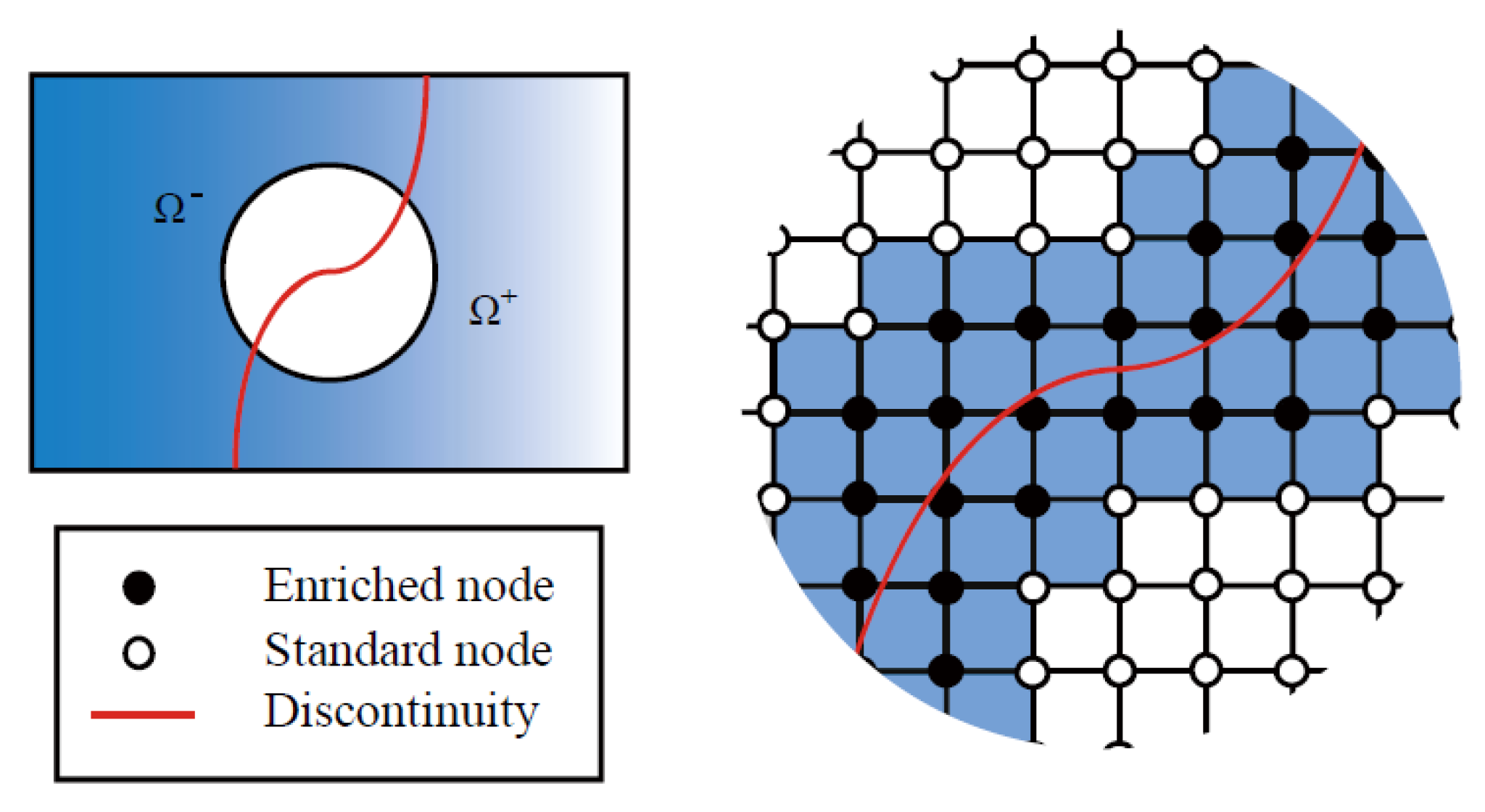
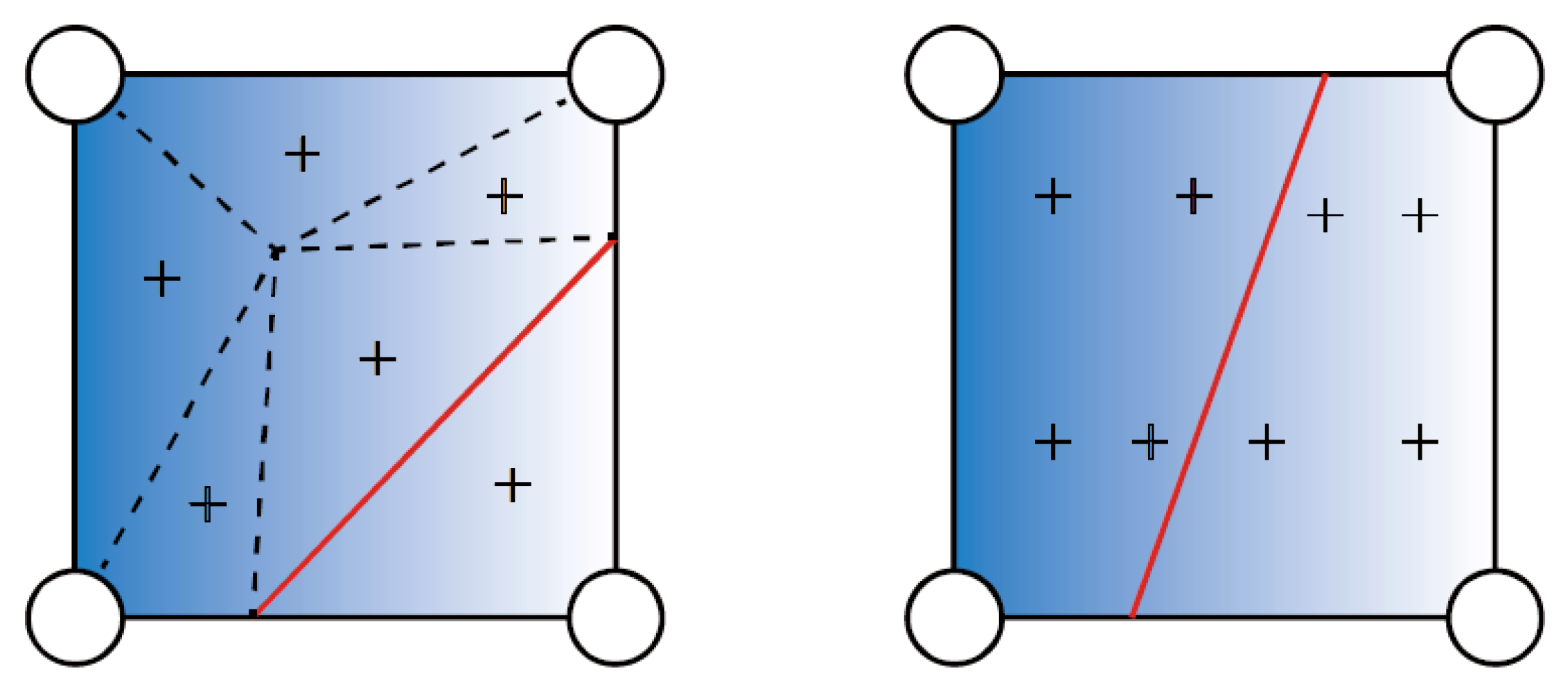
2.5.1. Discretization of Equilibrium Equation
2.5.2. Discretization of the Fracture Flow
2.6. Fluid–Solid Coupling Procedure and the Picard Iteration Approach
3. Results and Discussion
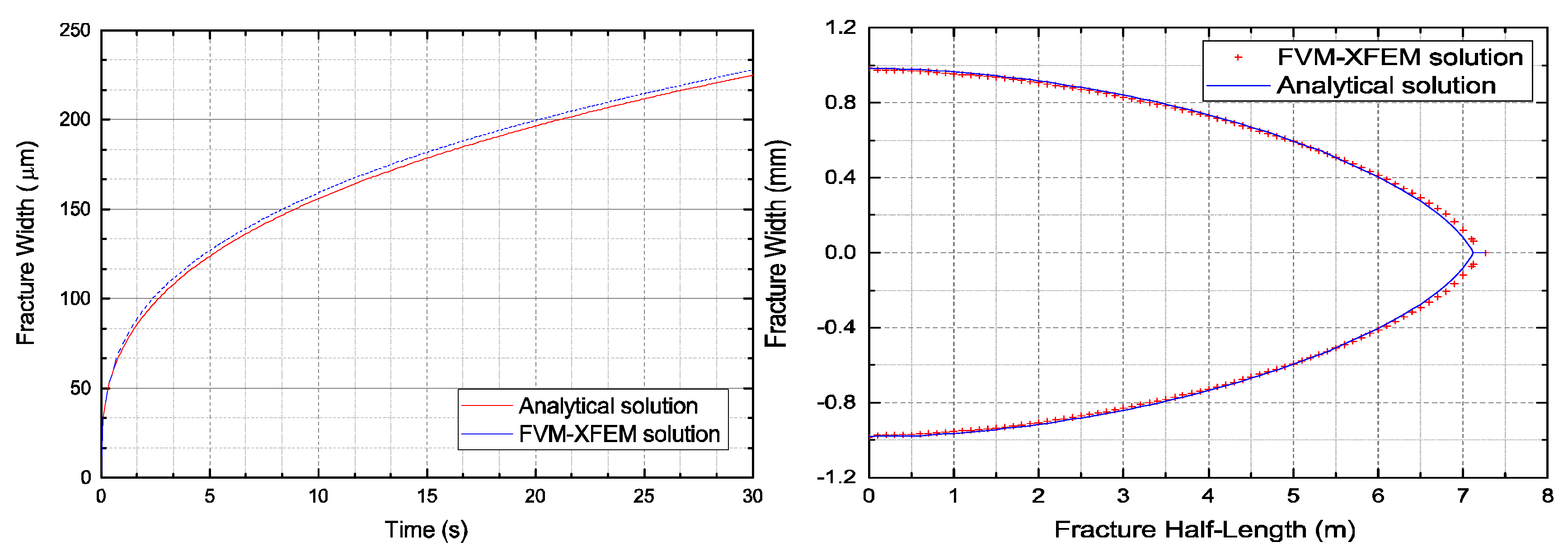
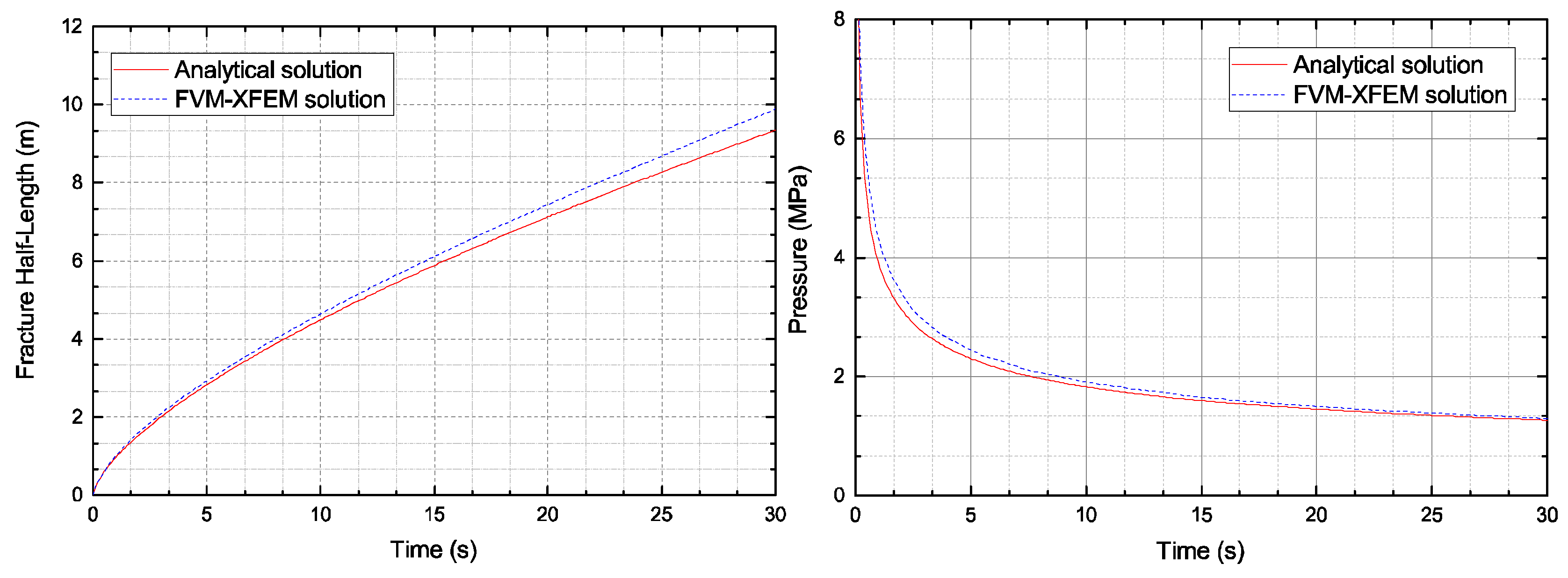
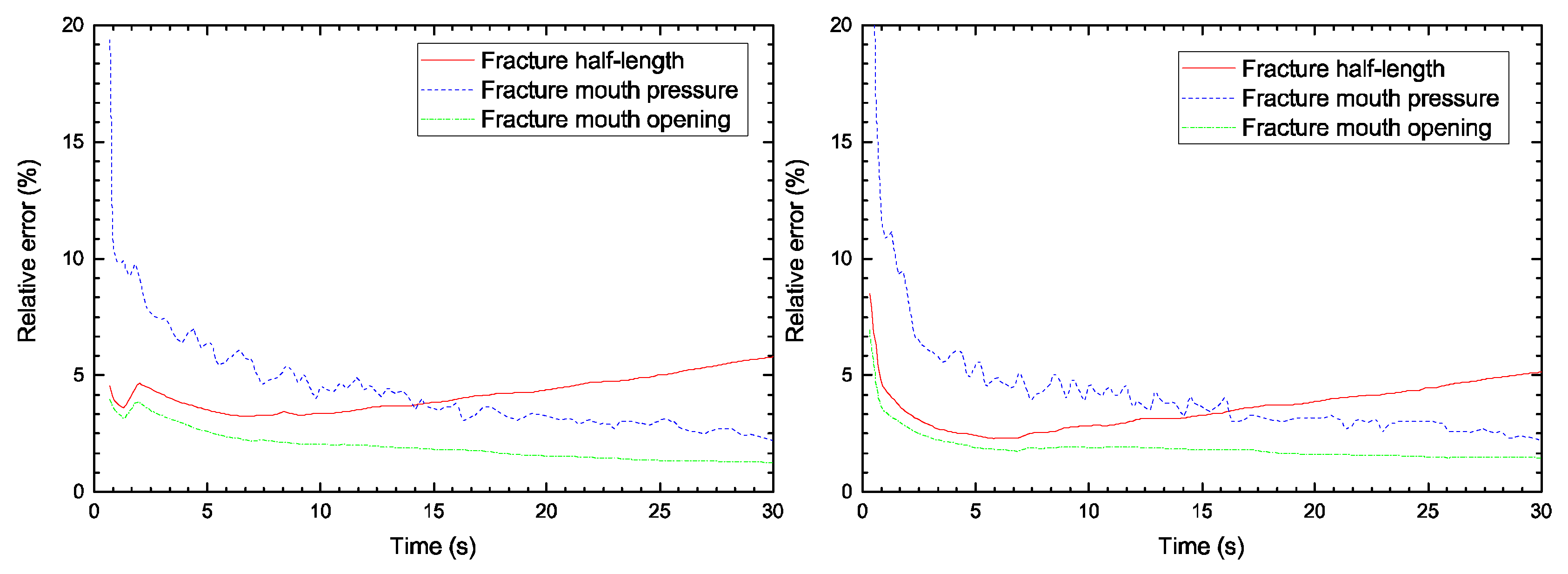
3.1. Khristianovic–Geertsma–de Klerk (KGD) Model
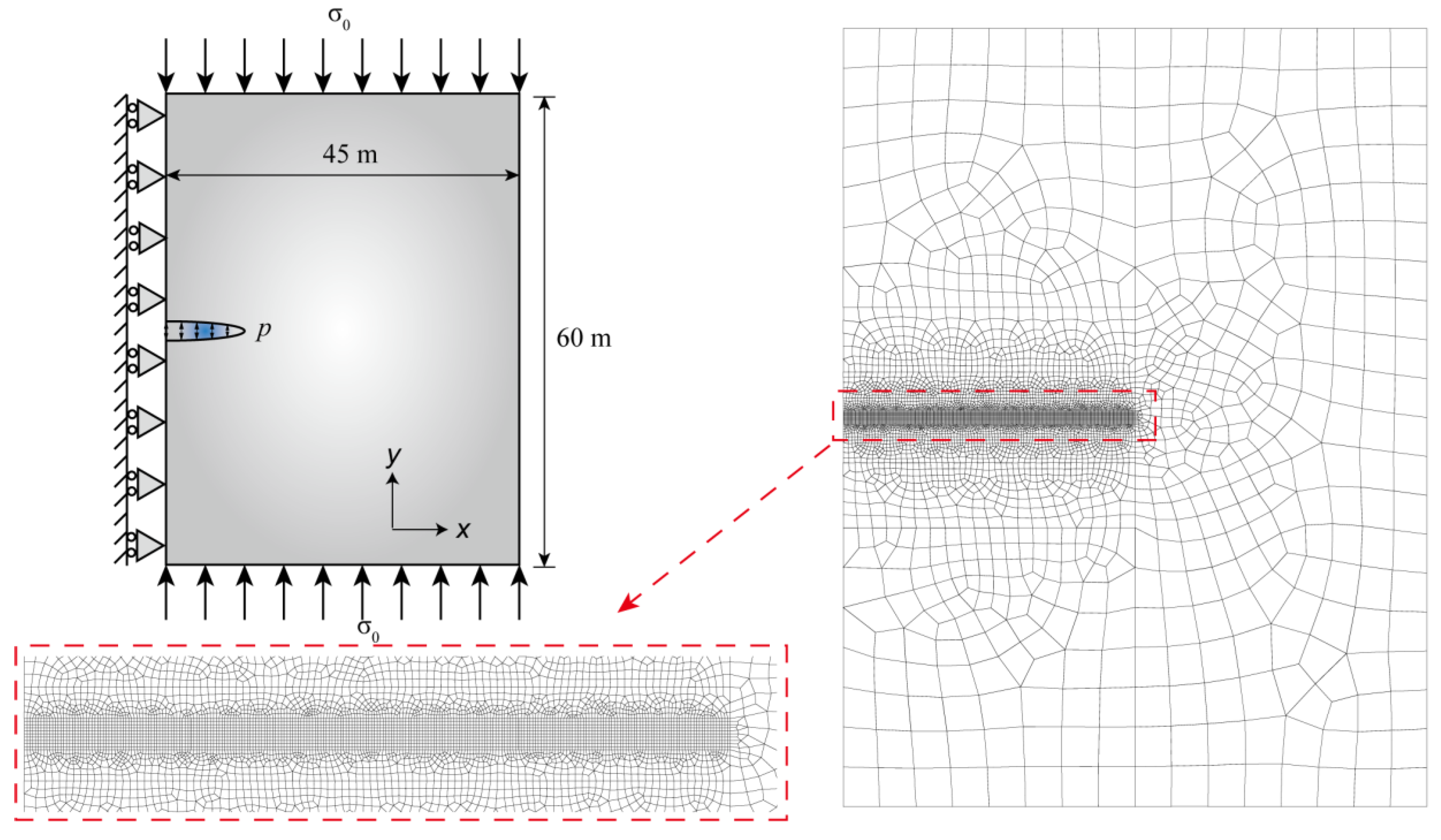
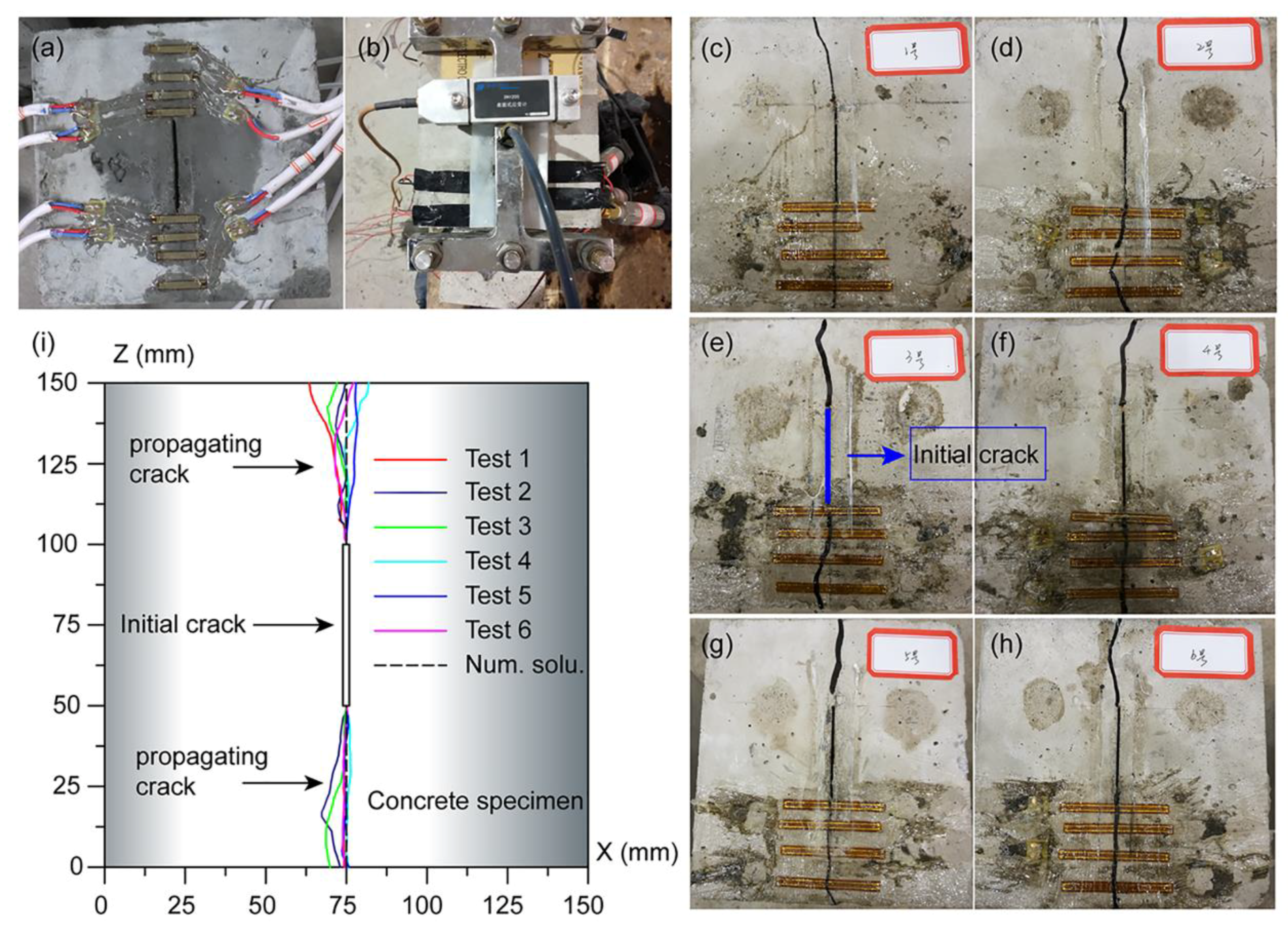
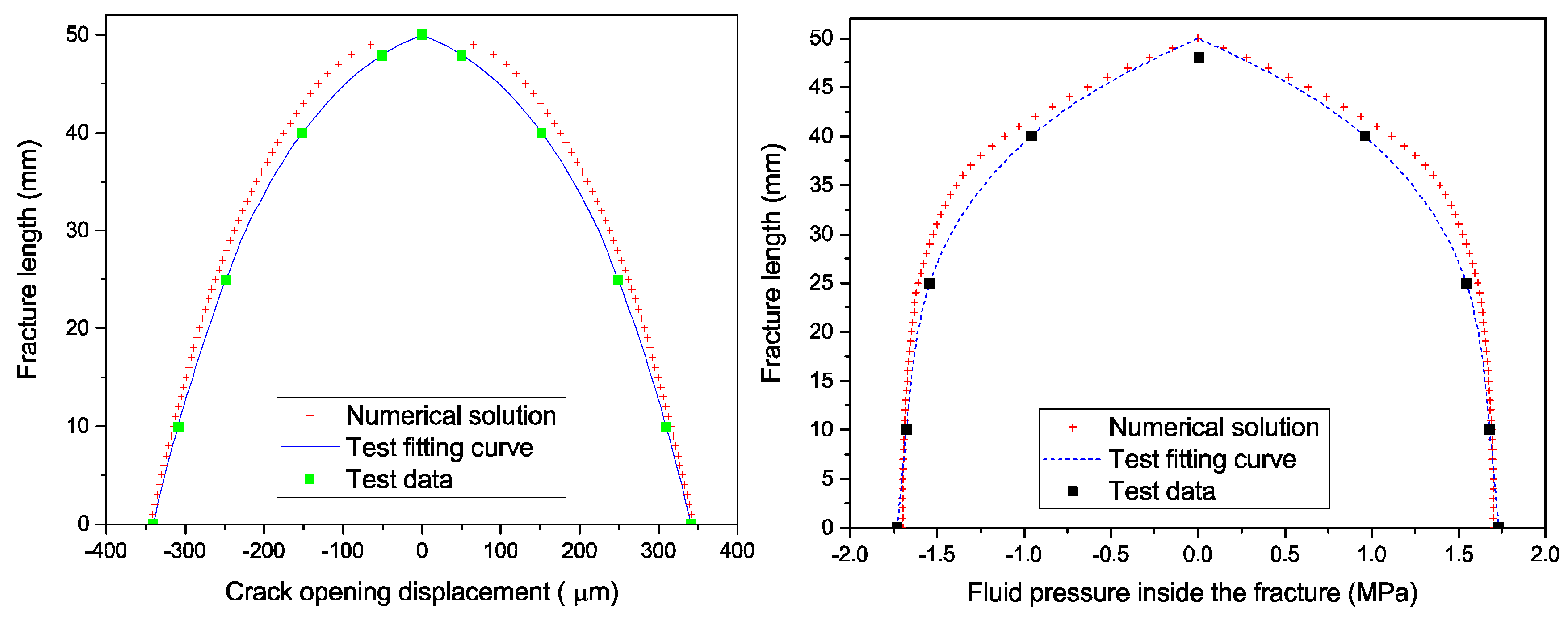
3.2. Hydraulic Fracturing Test
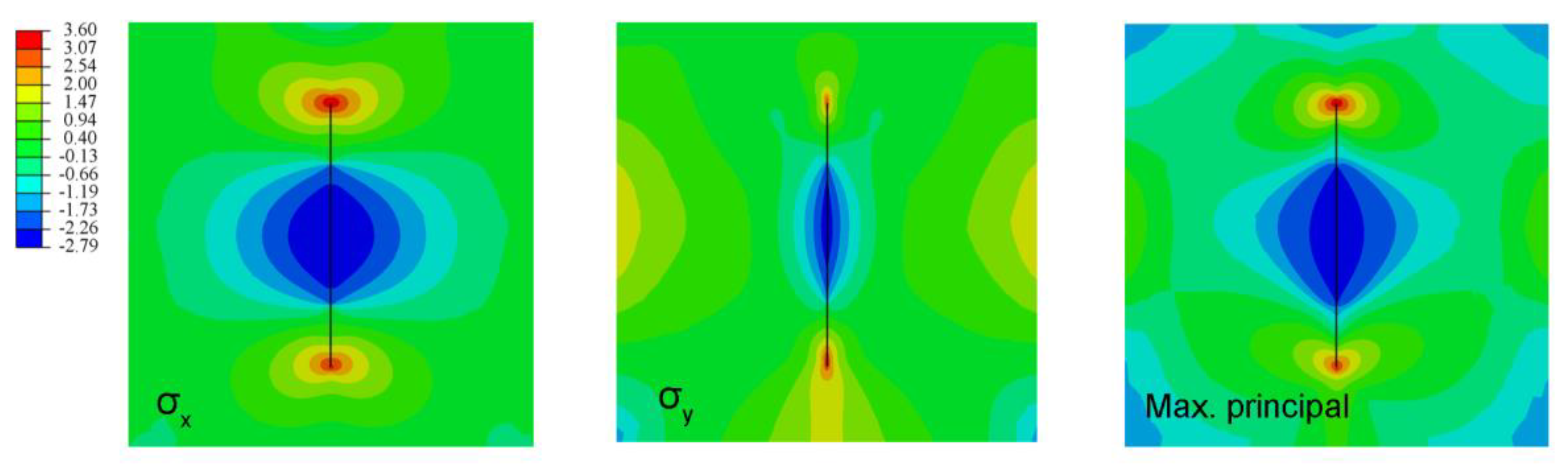
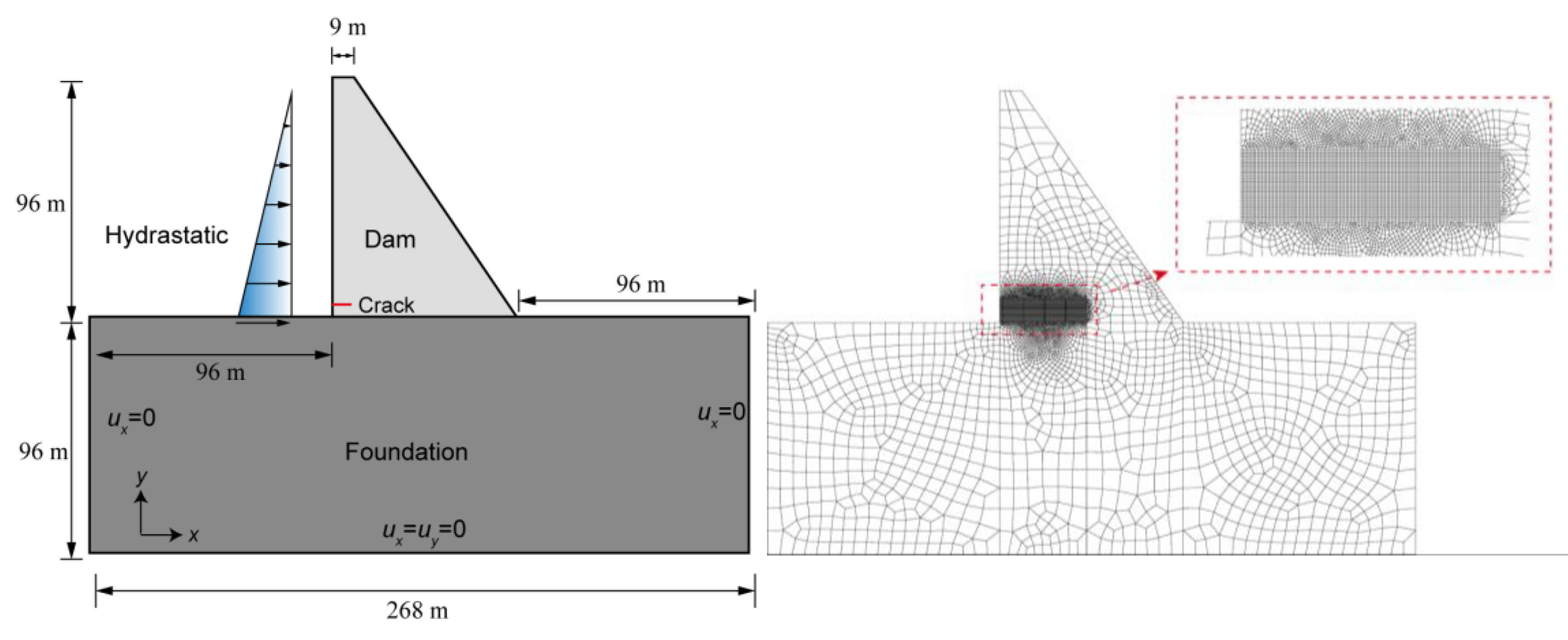
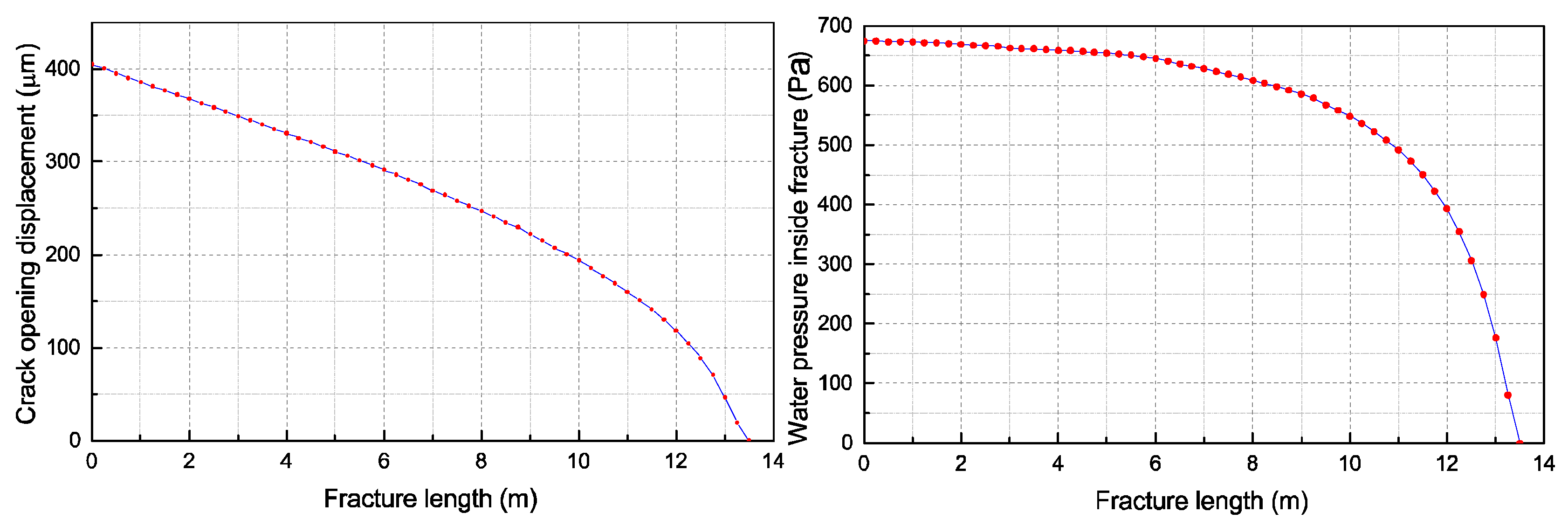
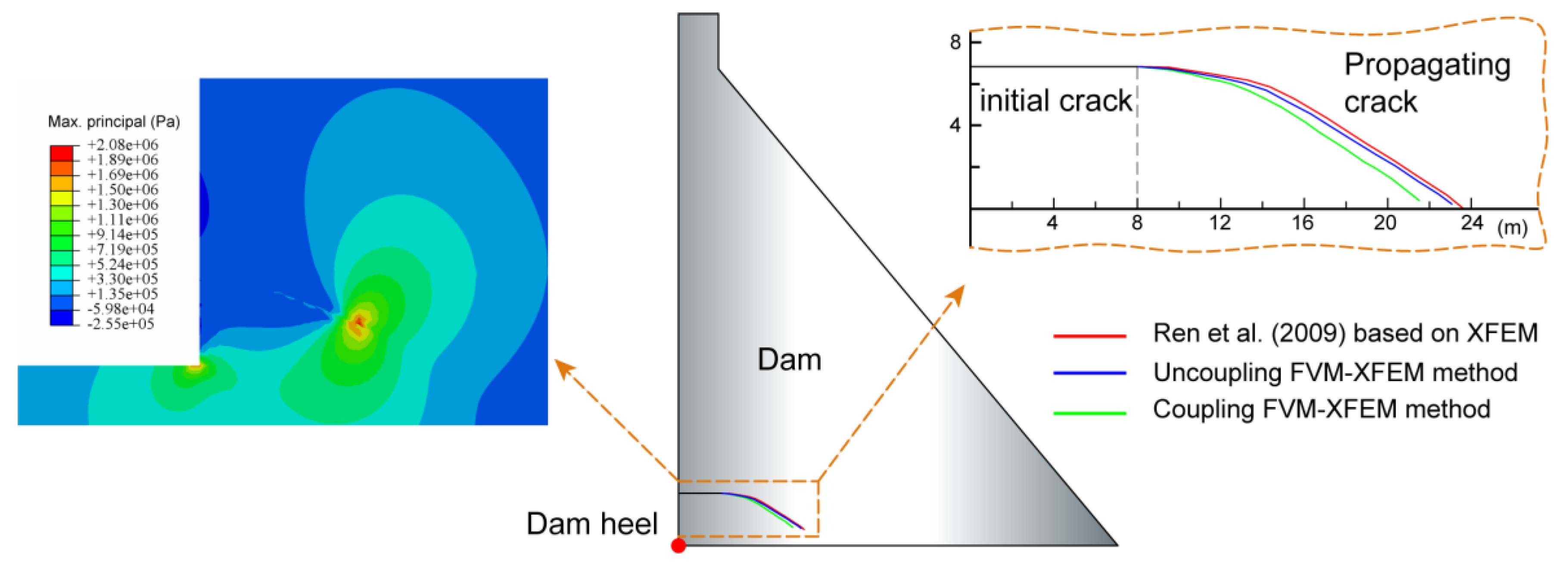
3.3. Hydraulic Fracturing in a Concrete Gravity Dam
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Detournay, E. Mechanics of Hydraulic Fractures. Annu. Rev. Fluid Mech. 2016, 48, 311–339. [Google Scholar] [CrossRef]
- Levasseur, S.; Charlier, R.; Frieg, B.; Collin, F. Hydro-mechanical modelling of the excavation damaged zone around an underground excavation at Mont Terri Rock Laboratory. Int. J. Rock Mech. Min. 2010, 47, 414–425. [Google Scholar] [CrossRef]
- Rahm, D. Regulating hydraulic fracturing in shale gas plays: The case of Texas. Energy Policy 2011, 39, 2974–2981. [Google Scholar] [CrossRef]
- Adachi, J.I.; Detournay, E. Plane strain propagation of a hydraulic fracture in a permeable rock. Eng. Fract. Mech. 2008, 75, 4666–4694. [Google Scholar] [CrossRef]
- Perkins, T.K.; Kern, L.R. Widths of hydraulic fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Nordgren, R. Propagation of a vertical hydraulic fracture. SPE J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Geertsma, J.; de Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Pet. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Khristianovic, S.; Zheltov, Y. Formation of vertical fractures by means of highly viscous liquid. In Proceedings of the Fourth World Petroleum Congress, Rome, Italy, 6–15 June 1955; pp. 579–586. [Google Scholar]
- Bazant, Z.P. Pore Pressure, uplift, and failure analysis of concrete dams. In Proceedings of the Numerical Analysis of Dams International Symposium, Swansea, UK, 8–11 September 1975. [Google Scholar]
- Bazant, Z.P. Stability and post-critical growth of a system of cooling or shrinkage cracks. Int. J. Fract. 1979, 15, 443–456. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Ohtsubo, H. Stability conditions for propagation of a system of cracks in a brittle solid. Mech. Res. Commun. 1977, 4, 353–366. [Google Scholar] [CrossRef]
- Brühwiler, E.; Saouma, V.E. Water fracture interaction in concrete—Part II: Hydrostatic pressure in cracks. ACI Mater. J. 1995, 92, 383–390. [Google Scholar]
- Gan, L.; Zhang, K.L.; Zhang, H.W.; Tian, Z.Y. Coupling analysis of hydraulic fracturing computation base on element-free method. Cluster Comput. 2017, 20, 3213–3224. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Meth. Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Paggi, M.; Corrado, M.; Reinoso, J. Fracture of solar-grade anisotropic polycrystalline Silicon: A combined phase field–cohesive zone model approach. Comput. Meth. Appl. Mech. Eng. 2018, 330, 123–148. [Google Scholar] [CrossRef]
- Nguyen, T.H.A.; Bui, T.Q.; Hirose, S. Smoothing gradient damage model with evolving anisotropic nonlocal interactions tailored to low-order finite elements. Comput. Meth. Appl. Mech. Eng. 2018, 328, 498–541. [Google Scholar] [CrossRef]
- Boone, T.; Ingraffea, A. A numerical procedure for simulation of hydraulically-driven fracture propagation in poroelastic media. Int. J. Numer. Anal. Methods Geomech. 1990, 14, 27–47. [Google Scholar] [CrossRef]
- Schrefler, B.A.; Secchi, S.; Simoni, L. On adaptive refinement techniques in multi-field problems including cohesive fracture. Comput. Meth. Appl. Mech. Eng. 2006, 195, 444–461. [Google Scholar] [CrossRef]
- Secchi, S.; Schrefler, B.A. A method for 3-D hydraulic fracturing simulation. Int. J. Fract. 2012, 178, 245–258. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. The influence of the cohesive process zone in hydraulic fracturing modelling. Int. J. Fract. 2011, 167, 33–45. [Google Scholar] [CrossRef]
- Segura, J.M.; Carol, I. On zero-thickness interface elements for diffusion problems. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 947–962. [Google Scholar] [CrossRef]
- Carrier, B.; Granet, S. Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model. Eng. Fract. Mech. 2012, 79, 312–328. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Meth. Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron J. 1977, 12, 1013–1024. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuska, I. The partition of unity finite element method: Basic theory and applications. Comput. Meth. Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Aliabadi, M.H.; Brebbia, C.A. Advanced Formulations in Boundary Element Methods; Computational Mechanics Publications: Southampton, UK; Elserier Applied Science: London, UK, 1993. [Google Scholar]
- Ganis, B.; Mear, M.E.; Sakhaee-Pour, A.; Wheeler, M.F.; Wick, T. Modeling fluid injection in fractures with a reservoir simulator coupled to a boundary element method. Comput. Geosci. 2014, 18, 613–624. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Zi, G.; Belytschko, T. New crack-tip elements for XFEM and applications to cohesive cracks. Int. J. Numer. Methods Eng. 2003, 57, 2221–2240. [Google Scholar] [CrossRef]
- Liu, F.S.; Gordon, P.; Meier, H.; Valiveti, D. A stabilized extended finite element framework for hydraulic fracturing simulations. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 654–681. [Google Scholar] [CrossRef]
- Jiang, S.Y.; Du, C.B. Coupled Finite Volume Methods and Extended Finite Element Methods for the Dynamic Crack Propagation Modelling with the Pressurized Crack Surfaces. Shock Vib. 2017. [Google Scholar] [CrossRef]
- Song, J.H.; Areias, P.M.A.; Belytschko, T. A method for dynamic crack and shear band propagation with phantom nodes. Int. J. Numer. Methods Eng. 2006, 67, 868–893. [Google Scholar] [CrossRef]
- Zamani, A.; Eslami, M.R. Implementation of the extended finite element method for dynamic thermoelastic fracture initiation. Int. J. Solids Struct. 2010, 47, 1392–1404. [Google Scholar] [CrossRef]
- De Borst, R.; Réthoré, J.; Abellan, M.A. A numerical approach for arbitrary cracks in a fluid-saturated medium. Arch. Appl. Mech. 2006, 75, 595–606. [Google Scholar] [CrossRef]
- Réthoré, J.; de Borst, R.; Abellan, M.A. A two-scale approach for fluid flow in fractured porous media. Int. J. Numer. Methods Eng. 2007, 71, 780–800. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A.R. Hydro-mechanical modeling of cohesive crack propagation in multiphase porous media using the extended finite element method. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1247–1279. [Google Scholar] [CrossRef]
- Shi, L.; Yu, T.; Bui, T.Q. Numerical Modelling of Hydraulic Fracturing in Rock Mass by Xfem. Soil Mech. Found. Eng. 2015, 52, 74–83. [Google Scholar] [CrossRef]
- Zhang, X.; Bui, T.Q. A fictitious crack XFEM with two new solution algorithms for cohesive crack growth modeling in concrete structures. Eng. Comput. 2015, 32, 473–497. [Google Scholar] [CrossRef]
- Wang, K.F.; Zhang, Q.; Xia, X.Z.; Wang, L.; Liu, X.C. Analysis of hydraulic fracturing in concrete dam considering fluid-structure interaction using XFEM-FVM model. Eng. Fail. Anal. 2015, 57, 399–412. [Google Scholar] [CrossRef]
- Zhou, L.; Gou, Y.; Hou, Z.M.; Were, P. Numerical modeling and investigation of fracture propagation with arbitrary orientation through fluid injection in tight gas reservoirs with combined XFEM and FVM. Environ. Earth Sci. 2015, 73, 5801–5813. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Longman Scientific and Technica: London, UK, 1995. [Google Scholar]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef]
- Wells, G.N.; Sluys, L.J. A new method for modelling cohesive cracks using finite elements. Int. J. Numer. Methods Eng. 2001, 50, 2667–2682. [Google Scholar] [CrossRef]
- Hillerborg, A.; Mod’eer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Dias-da-Costa, D.; Alfaiate, J.; Sluys, L.J.; Julio, E. A comparative study on the modelling of discontinuous fracture by means of enriched nodal and element techniques and interface elements. Int. J. Fract. 2010, 161, 97–119. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Q.D.; Mohammadizadeh, S.; Su, X.Y. An efficient augmented finite element method for arbitrary cracking and crack interaction in solids. Int. J. Numer. Methods Eng. 2014, 99, 438–468. [Google Scholar] [CrossRef]
- Fries, T.P.; Baydoun, M. Crack propagation with the extended finite element method and a hybrid explicit-implicit crack description. Int. J. Numer. Methods Eng. 2012, 89, 1527–1558. [Google Scholar] [CrossRef]
- Rabczuk, T.; Zi, G.; Gerstenberger, A.; Wall, W.A. A new crack tip element for the phantom-node method with arbitrary cohesive cracks. Int. J. Numer. Methods Eng. 2008, 75, 577–599. [Google Scholar] [CrossRef]
- Khoei, A.R.; Vahab, M.; Haghighat, E.; Moallemi, S. A mesh-independent finite element formulation for modeling crack growth in saturated porous media based on an enriched-FEM technique. Int. J. Fract. 2014, 188, 79–108. [Google Scholar] [CrossRef]
- Ren, Q.W.; Dong, Y.W.; Yu, T.T. Numerical modeling of concrete hydraulic fracturing with extended finite element method. Sci. China-Technol. Sci. 2009, 52, 559–565. [Google Scholar] [CrossRef]

| Young’s modulus | E = 17.0 GPa |
| Poisson’s ratio | ν = 0.2 |
| Tensile strength | ft = 1.25 MPa |
| Cohesive fracture energy | Gc = 120 N/m |
| Water density | ρw = 1000 kg/m3 |
| Water dynamic viscosity | μ = 1.00 × 10−4 Pa s |
| Fluid injection rate | Q0 = 5.00 × 10−4 m2/s |
| Young’s modulus | E = 27.25 GPa |
| Poisson’s ratio | ν = 0.173 |
| Tensile strength | ft = 2.01 MPa |
| Cohesive fracture energy | Gc = 140 N/m |
| Water density | ρw = 1000 kg/m3 |
| Water dynamic viscosity | μ = 1.00 × 10−6 kPa s |
| Young’s modulus | E = 25.0 GPa |
| Poisson’s ratio | ν = 0.167 |
| Tensile strength | ft = 2.05 MPa |
| Cohesive fracture energy | Gc = 150 N/m |
| Water density | ρw = 1000 kg/m3 |
| Water dynamic viscosity | μ = 1.00 × 10−6 kPa∙s |
| Solid density | ρw = 2400 kg/m3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Shen, Z.; Gan, L.; Jin, T.; Zhang, H.; Liu, D. A Hybrid Finite Volume and Extended Finite Element Method for Hydraulic Fracturing with Cohesive Crack Propagation in Quasi-Brittle Materials. Materials 2018, 11, 1921. https://doi.org/10.3390/ma11101921
Liu C, Shen Z, Gan L, Jin T, Zhang H, Liu D. A Hybrid Finite Volume and Extended Finite Element Method for Hydraulic Fracturing with Cohesive Crack Propagation in Quasi-Brittle Materials. Materials. 2018; 11(10):1921. https://doi.org/10.3390/ma11101921
Chicago/Turabian StyleLiu, Chong, Zhenzhong Shen, Lei Gan, Tian Jin, Hongwei Zhang, and Detan Liu. 2018. "A Hybrid Finite Volume and Extended Finite Element Method for Hydraulic Fracturing with Cohesive Crack Propagation in Quasi-Brittle Materials" Materials 11, no. 10: 1921. https://doi.org/10.3390/ma11101921
APA StyleLiu, C., Shen, Z., Gan, L., Jin, T., Zhang, H., & Liu, D. (2018). A Hybrid Finite Volume and Extended Finite Element Method for Hydraulic Fracturing with Cohesive Crack Propagation in Quasi-Brittle Materials. Materials, 11(10), 1921. https://doi.org/10.3390/ma11101921






