Forming Quality Analysis on the Cold Roll Forming C-channel Steel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment and Simulation Model Set Up
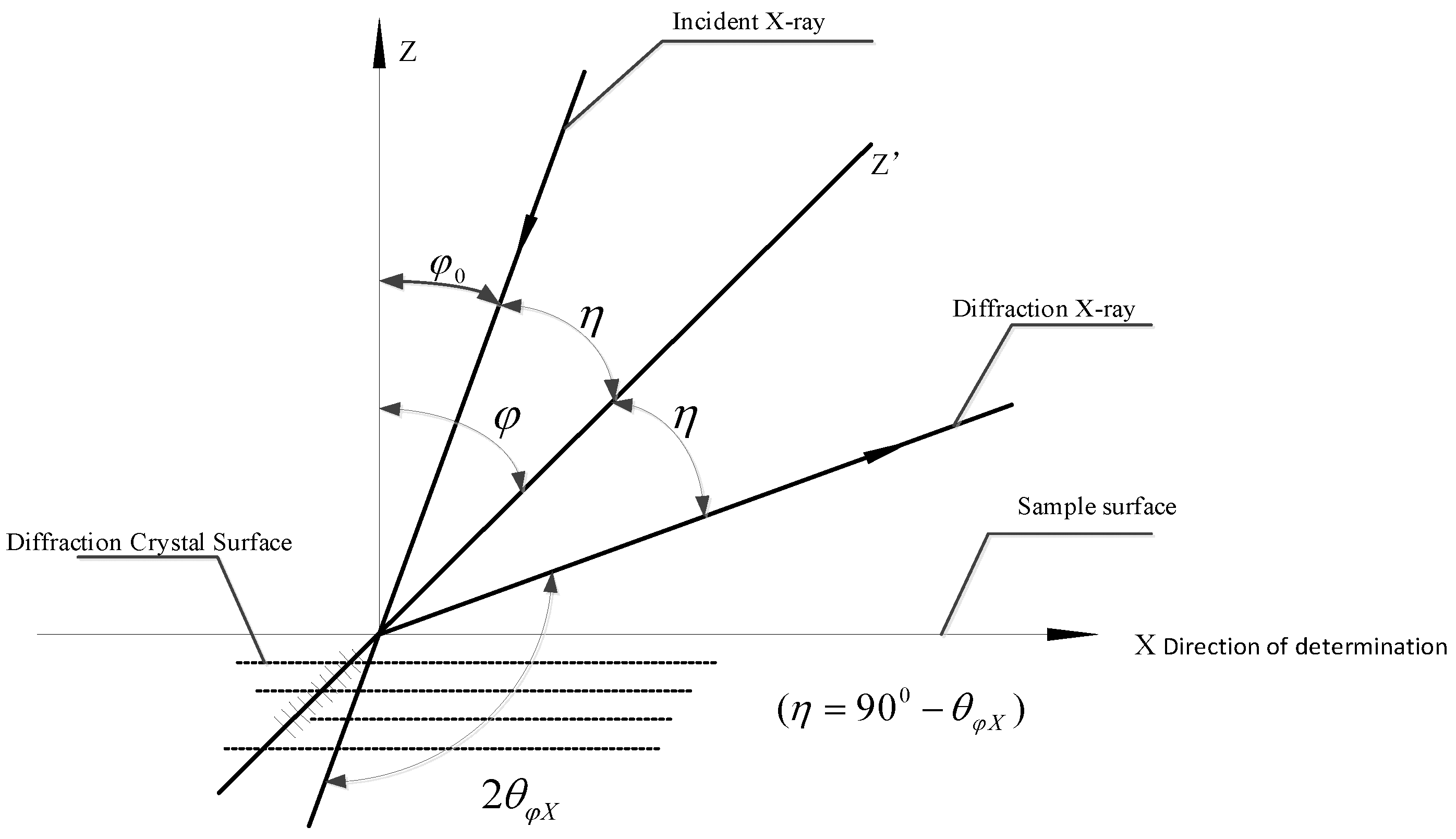
2.2. Residual Stress Measurement
3. Forming Passes Design and Analysis
4. Results and Discussion
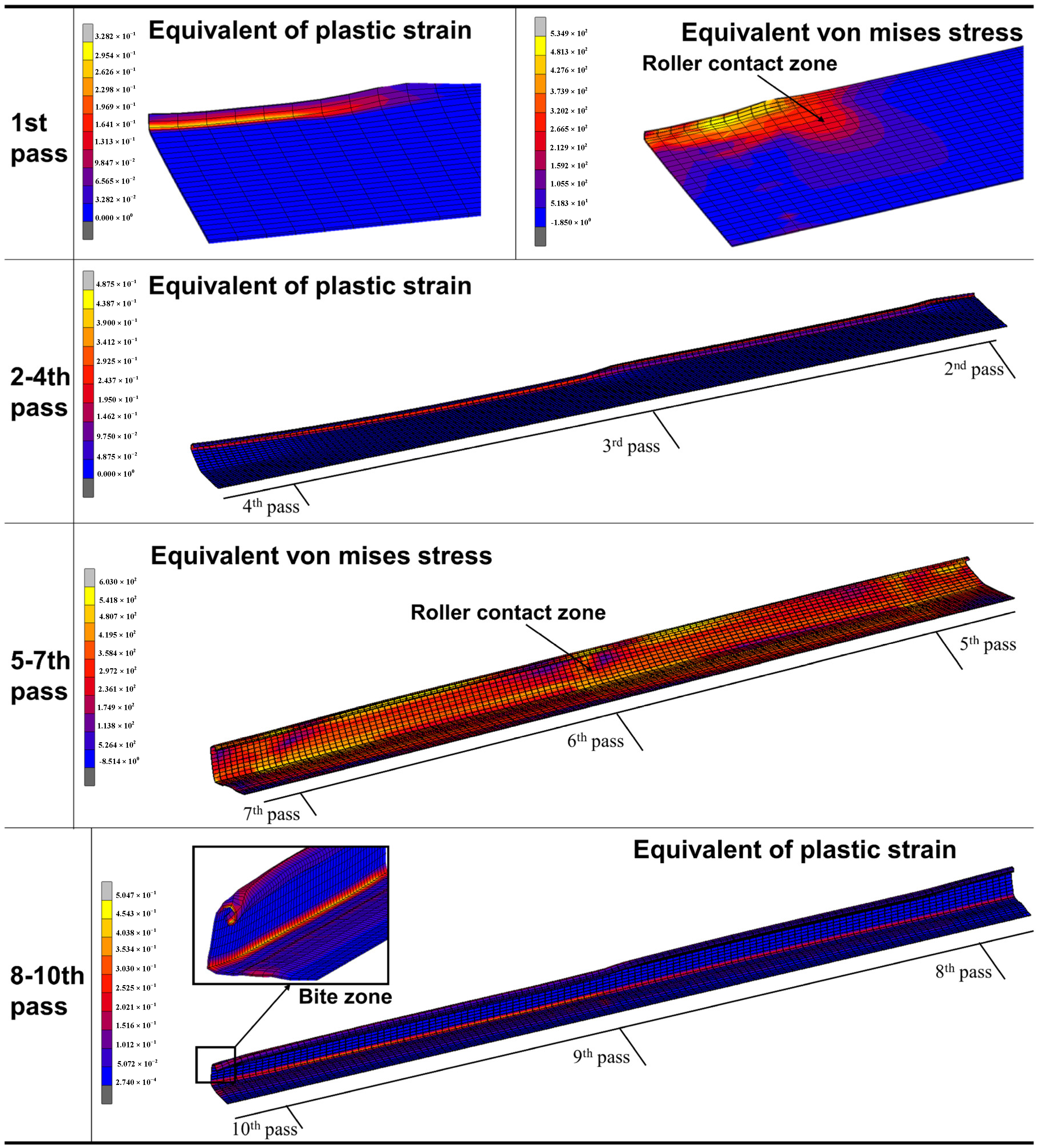
4.1. Simulation Analysis of the Forming Process on the C-Channel Steel
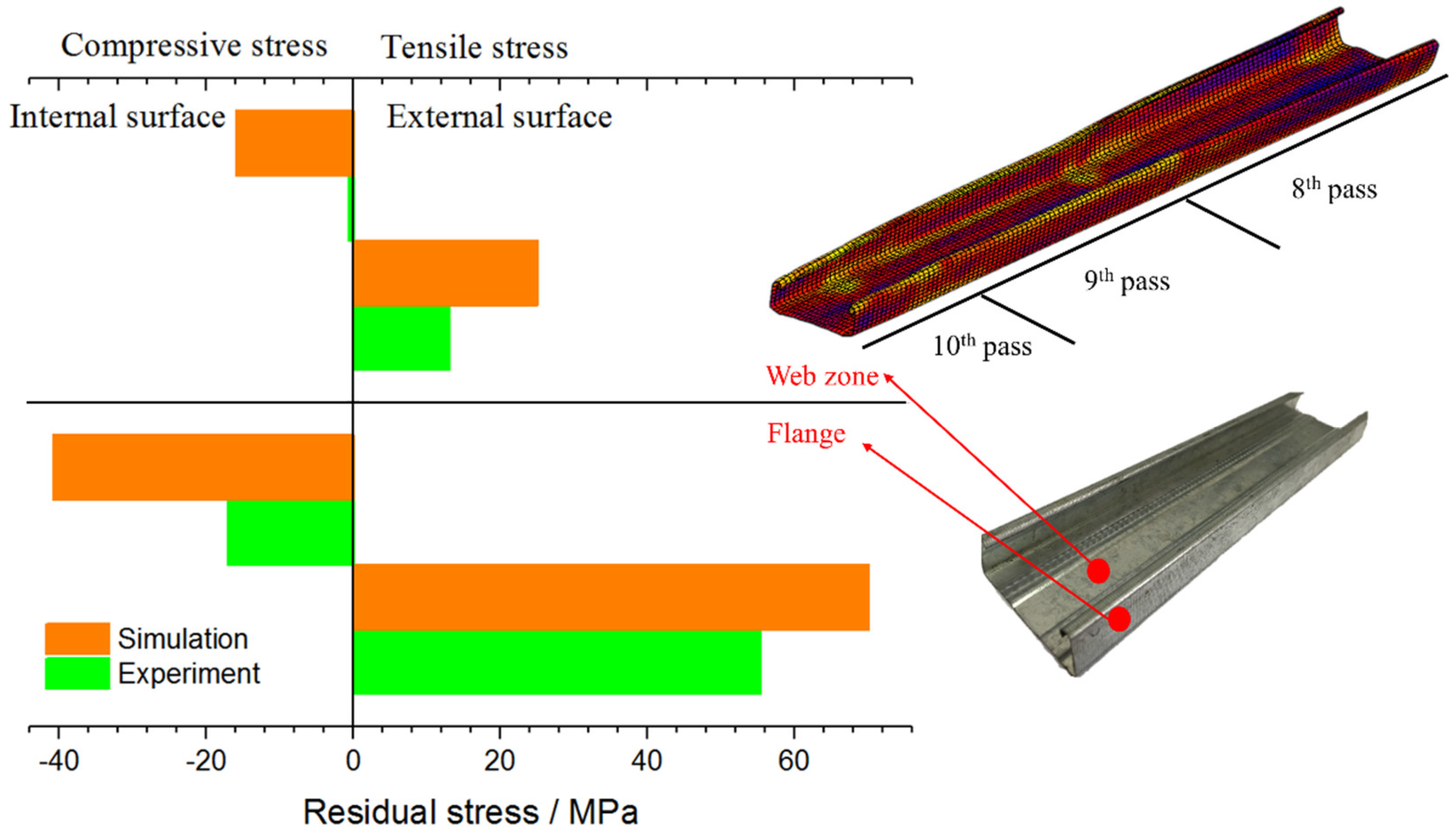
4.2. Residual Stress Analysis on the C-Channel Steel
5. Conclusions
- (1)
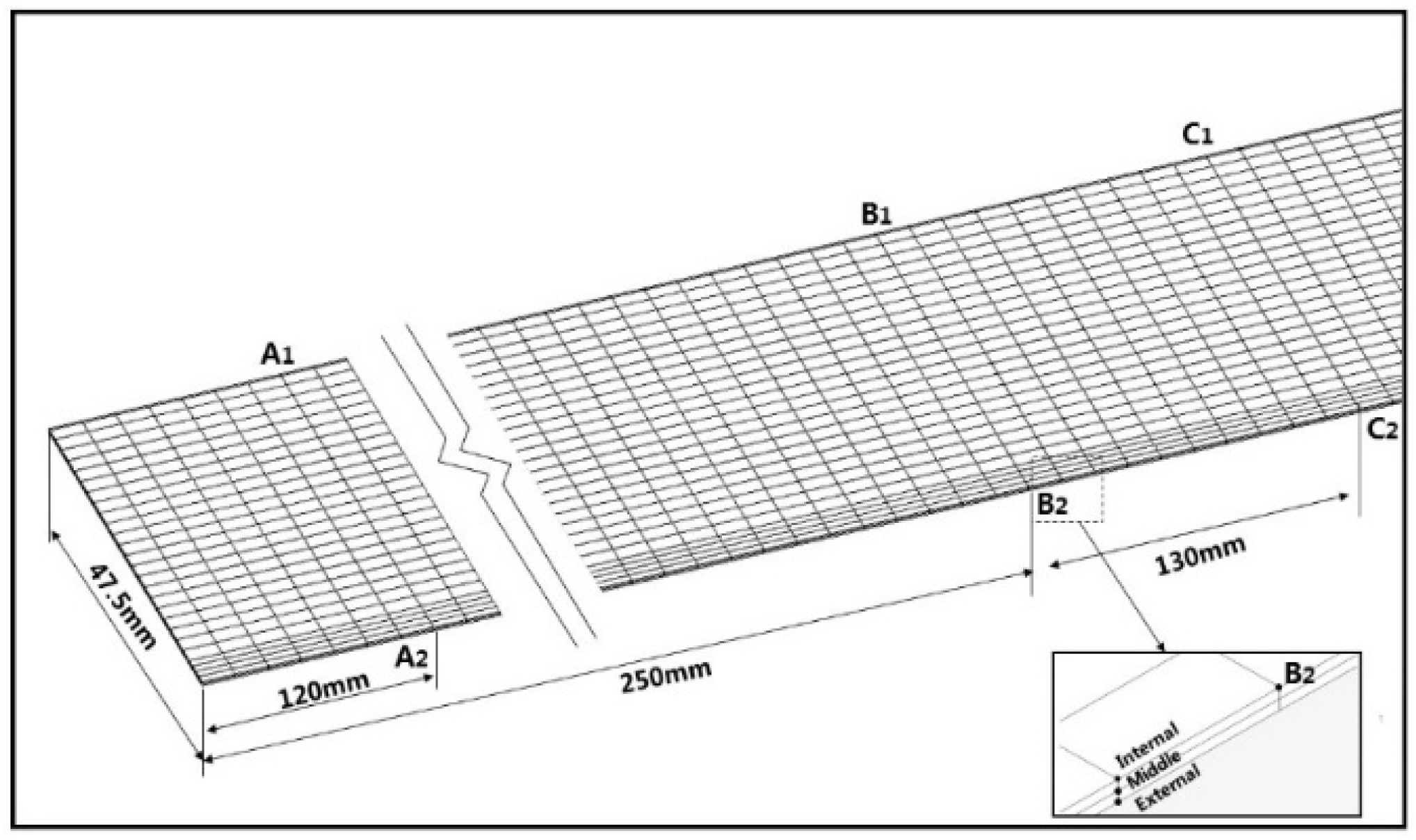
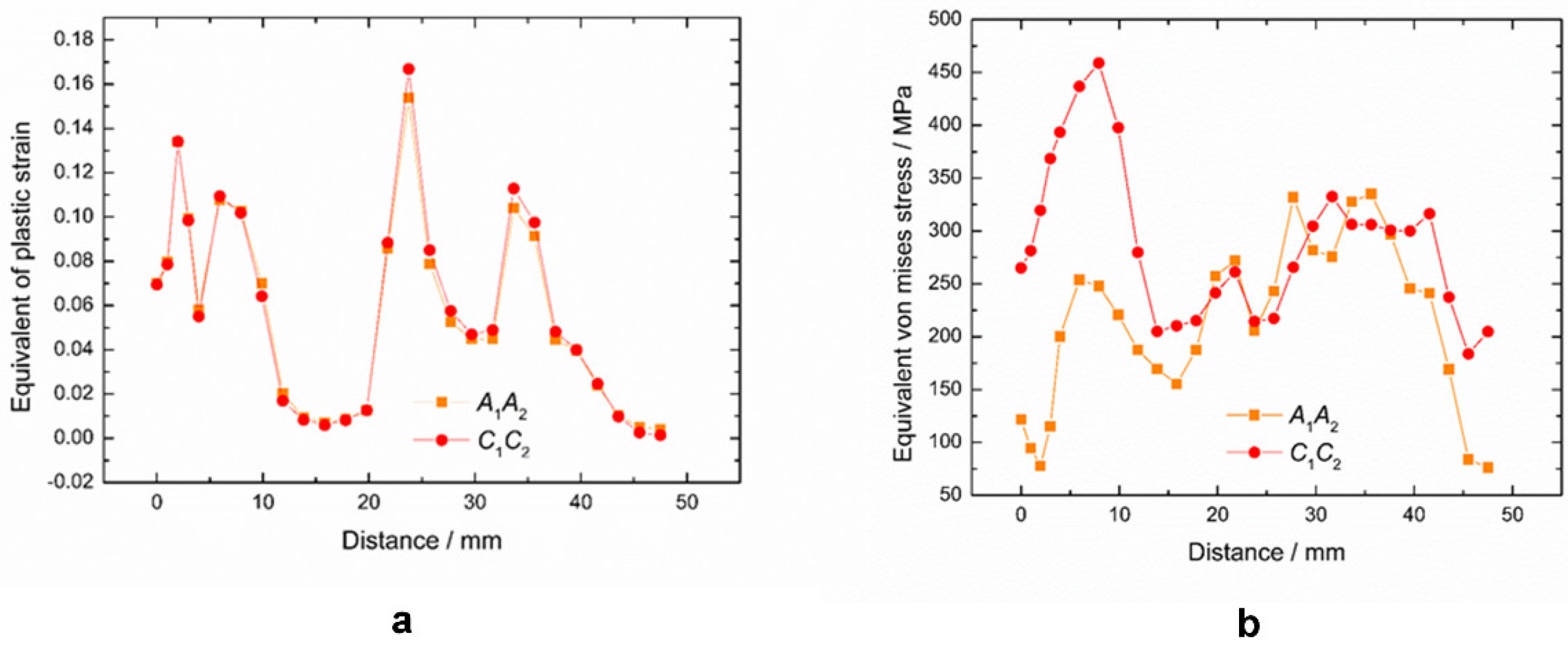
- The forming quality of the bite zone is the worst in the whole cold roll forming process. The analysis of the layered distribution of sheet shows that the external layer is mainly subject to tensile stress, while the internal layer is mainly subject to compressive stress, and the internal layer residual stress is slightly larger than the external layer. It offers a reference for the forming of anisotropy material and the material with different coatings at internal and external surfaces.
- (2)
- The equations for calculating forming passes that are proposed by many scholars are based on the materials and shapes of the products they studied and lack of universality. They can only predict the number of forming passes roughly and verified by experience.
- (3)
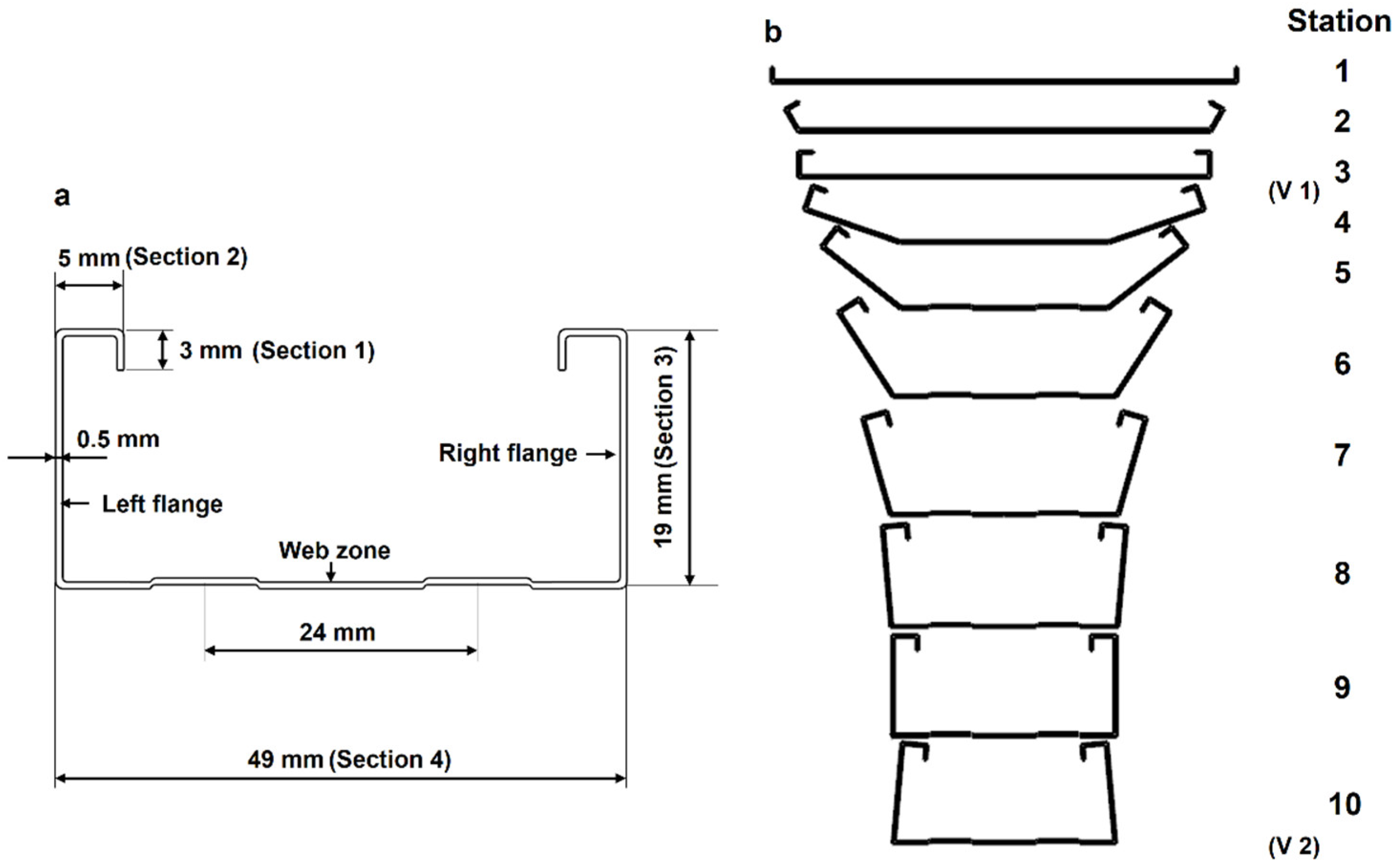
- In order to save costs, one forming pass can be used to shaping the short edge of the target product (such as Section 1 in Figure 2a 3 mm short edge in this paper). However, the forming shape and dimension accuracy are not very good. This design method is suitable for those products that do not require high quality at the short edges. For the high quality and accuracy dimension products, more forming passes are needed for the short edge forming.
- (4)
- For long edge forming of the target product (such as Section 3 in Figure 2a 19 mm long edge), several forming passes (seven passes are used in this paper) are needed to avoid the dangerous area and keep the dimension accuracy. An over bending pass is needed to compensate the material springback, especially in the long edge forming.
- (5)
- The forming process in this paper offers a reference for the forming pass design of U-channel and V-channel steel.
- (6)
- Residual stress measurement of C-channel steel shows that the external surface of C-channel steel is mainly tensile stress, the internal surface is mainly compressive stress, and the residual stress of flange is far greater than that of web zone, which hardly deforms during cold roll forming and residual stress is very small.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hiroshi, O.; Liu, J.Y. Cold Forming Technology, 1st ed.; Chemical Industry Press: Beijing, China, 2008; pp. 1–14. ISBN 9787122010667. (In Chinese) [Google Scholar]
- Halmos, G.T. Roll Forming Handbook, 1st ed.; Chemical Industry Press: Beijing, China, 2009; pp. 1–190. ISBN 9787122029522. [Google Scholar]
- Zeng, G.; Li, S.H.; Yu, Z.Q.; Lai, X.M. Optimization design of roll profiles for cold roll forming based on response surface method. Mater. Des. 2009, 30, 1930–1938. [Google Scholar] [CrossRef]
- Zeng, G.; Lai, X.M.; Yu, Z.Q.; Guo, Y.J. The simulation of roll forming with multiple passes. J. Shanghai Jiaotong Univ. 2007, 41, 1598–1602. [Google Scholar]
- Li, D.Y.; Jiang, J.M.; Peng, Y.H.; Yin, J.L. Study on roll forming process simulation and roll diameters optimization. J. Syst. Simul. 2007, 19, 893–896. [Google Scholar]
- Li, B.; Zhang, S.H.; Hu, L. Numerical simulation on cold roll forming process of profiled strip. Iron Steel 2004, 39, 82–85. [Google Scholar]
- Xu, S.C.; Wang, X.J. Analysis of displacement and velocity field in channel steel roll forming process using elastic-plastic large-deformations finite element method. J. Plast. Eng. 1999, 6, 71–75. [Google Scholar]
- Zheng, J.X. Finite Element Method Simulation and Springback Research on Cold Roll Forming. Master’s Thesis, Kunming University of Science & Technology, Kunming, China, November 2006. [Google Scholar]
- Heislitz, F.; Livatyali, H.; Ahmetoglu, M.A.; Kinzel, G.L.; Altan, T. Simulation of roll forming process with the 3-D FEM code PAM-STAMP. J. Mater. Process. Technol. 1996, 59, 59–67. [Google Scholar] [CrossRef]
- Sukmoo, H.; Seungyoon, L.; Naksoo, K. A parametric study on forming length in roll forming. J. Mater. Process. Technol. 2001, 113, 774–778. [Google Scholar]
- Park, J.C.; Yang, D.Y.; Cha, M.H.; Kim, D.G.; Nam, J.B. Investigation of a new incremental counter forming in flexible roll forming to manufacture accurate profiles with variable cross-sections. Int. J. Mach. Tool. Manuf. 2014, 86, 68–80. [Google Scholar] [CrossRef]
- Liu, C.F.; Zhou, W.L.; Fu, X.S.; Chen, G.Q. A new mathematical model for determining the longitudinal strain in cold roll forming process. Int. J. Adv. Manuf. Technol. 2015, 79, 1055–1061. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Tieu, A.K. A simulation of three-dimensional metal rolling processes by rigid-plastic finite element method. J. Mater. Process. Technol. 2011, 112, 144–151. [Google Scholar] [CrossRef]
- Jeong, S.H.; Lee, S.H.; Kim, G.H.; Seo, H.J.; Kim, T.H. Computer simulation of U-channel for under-rail roll forming using rigid-plastic finite element methods. J. Mater. Process. Technol. 2008, 201, 118–122. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Li, L.L.; Wang, M.; Li, M.Z. Process design and longitudinal deformation prediction in continuous sheet metal roll forming for three-dimensional surface. Int. J. Precis. Eng. Manuf. 2014, 15, 1889–1895. [Google Scholar] [CrossRef]
- Luo, X.L.; Yu, Z.Q.; Li, S.H.; Zeng, G. Finite element analysis of the springback in high strength steel roll forming. J. Plast. Eng. 2008, 15, 83–86. [Google Scholar]
- Chen, Z.Y.; Wang, H.B.; Yan, Y.; Jia, F.H. Design and analysis of roll-forming machine based on ABAQUS equivalent simplified model. Forg. Stam. Technol. 2014, 39, 82–86. [Google Scholar]
- Bui, Q.V.; Ponthot, J.P. Numerical simulation of cold roll-forming processes. J. Mater. Process. Technol. 2008, 202, 275–282. [Google Scholar] [CrossRef]
- Bidabadi, B.S.; Naeini, H.M.; Tafti, R.A.; Mazdak, S. Experimental investigation of the ovality of holes on pre-notched channel products in the cold roll forming process. J. Mater. Process. Technol. 2015, 225, 213–220. [Google Scholar] [CrossRef]
- Weng, C.C.; Pekoz, T. Residual stress in cold-formed steel members. J. Struct. Eng. 1990, 116, 1611–1625. [Google Scholar] [CrossRef]
- Li, S.H.; Zeng, G.; Ma, Y.F.; Guo, Y.J.; Lai, X.M. Residual stresses in roll-formed square hollow sections. Thin Wall Struct. 2009, 47, 505–513. [Google Scholar] [CrossRef]
- Zeng, G. Simulation and Experimental Study on Residual Stresses for Multi-Stand Roll-Formed Sections. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, June 2009. [Google Scholar]
- Sánchez Egea, A.J.; González Rojas, H.A.; Celentano, D.J.; Peiró, J.J. Mechanical and metallurgical changes on 308L wires drawn by electropulses. Mater. Des. 2016, 90, 1159–1169. [Google Scholar] [CrossRef]
- Sánchez Egea, A.J.; González Rojas, H.A.; Celentano, D.J.; Peiró, J.J.; Cao, J. Thermomechanical analysis of an electrically-assisted wire drawing process. J. Manuf. Sci. Eng. 2017. [Google Scholar] [CrossRef]
- Non-Destructive Testing-Practice for Residual Stress Measurement by X-Ray; GB/T 7704-2008; Standardization Administration of the People’s Republic of China: Beijing, China, 2008. (In Chinese)
- Zhao, Y.H. Design way to the forming roller of cold-forming profiled bar. Shanxi Mach. 2003, 2, 30–32. [Google Scholar]


| C | S | Si | Mn | P |
|---|---|---|---|---|
| 0.150 | 0.035 | 0.300 | 0.350 | 0.035 |
| Yield Strength (MPa) | Tensile Strength (MPa) | Elongation (%) |
|---|---|---|
| 235 | 423 | 26 |
| Parameter | Value |
|---|---|
| Bragg crystal angle | 82.33° |
| Crystal surface | 211 |
| Wavelength | 1.54 angstrom |
| Light seams | 1 mm |
| Calculation Method | Number of Forming Passes |
|---|---|
| Equation (4) | 10 |
| Equation (5) | 14 |
| Equation (6) | 9 |
| Equation (7) | 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hui, X.; Wang, X. Forming Quality Analysis on the Cold Roll Forming C-channel Steel. Materials 2018, 11, 1911. https://doi.org/10.3390/ma11101911
Hui X, Wang X. Forming Quality Analysis on the Cold Roll Forming C-channel Steel. Materials. 2018; 11(10):1911. https://doi.org/10.3390/ma11101911
Chicago/Turabian StyleHui, Xiangjun, and Xianming Wang. 2018. "Forming Quality Analysis on the Cold Roll Forming C-channel Steel" Materials 11, no. 10: 1911. https://doi.org/10.3390/ma11101911
APA StyleHui, X., & Wang, X. (2018). Forming Quality Analysis on the Cold Roll Forming C-channel Steel. Materials, 11(10), 1911. https://doi.org/10.3390/ma11101911




