Unexpected Ground-State Structure and Mechanical Properties of Ir2Zr Intermetallic Compound
Abstract
1. Introduction
2. Computational Methods
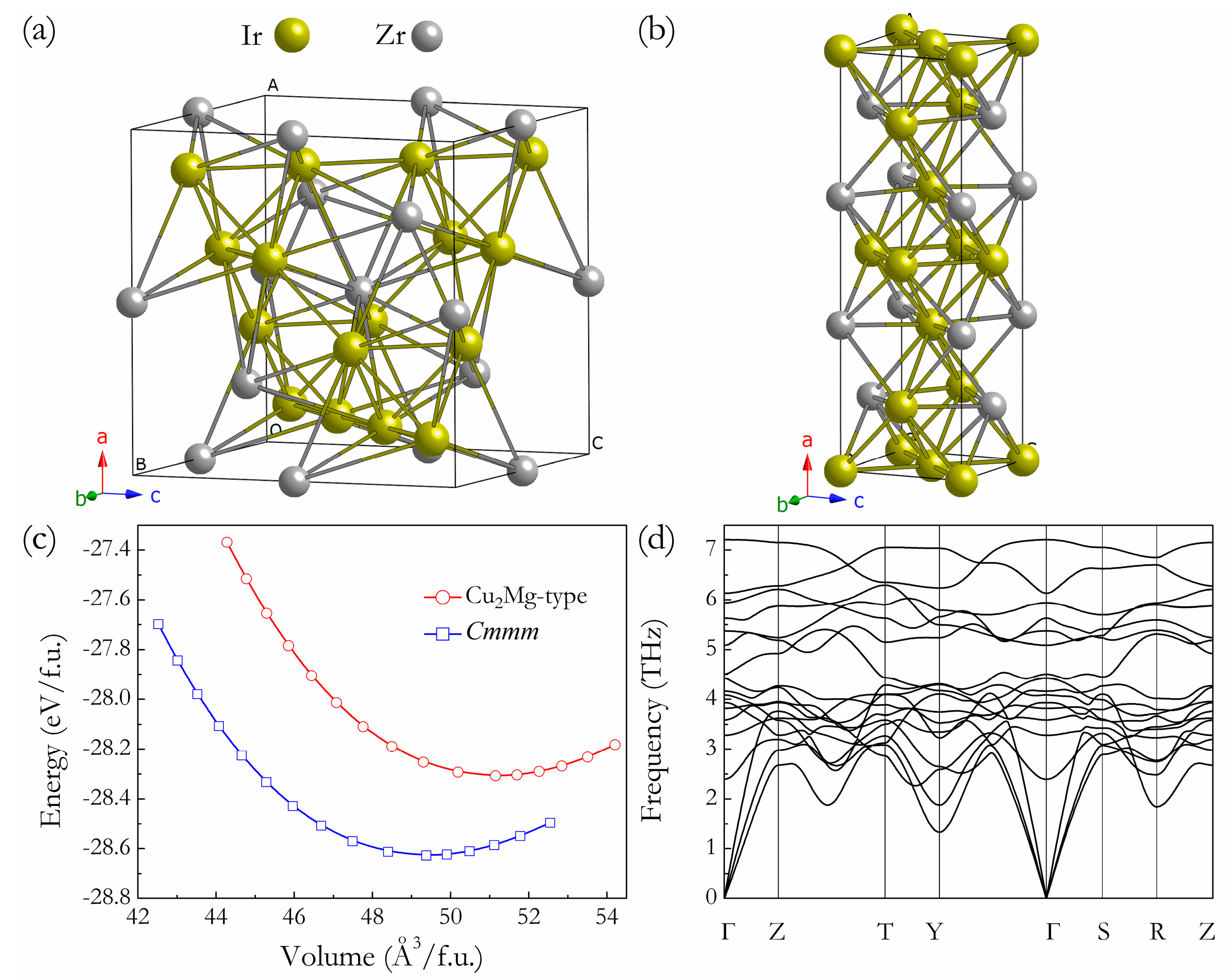
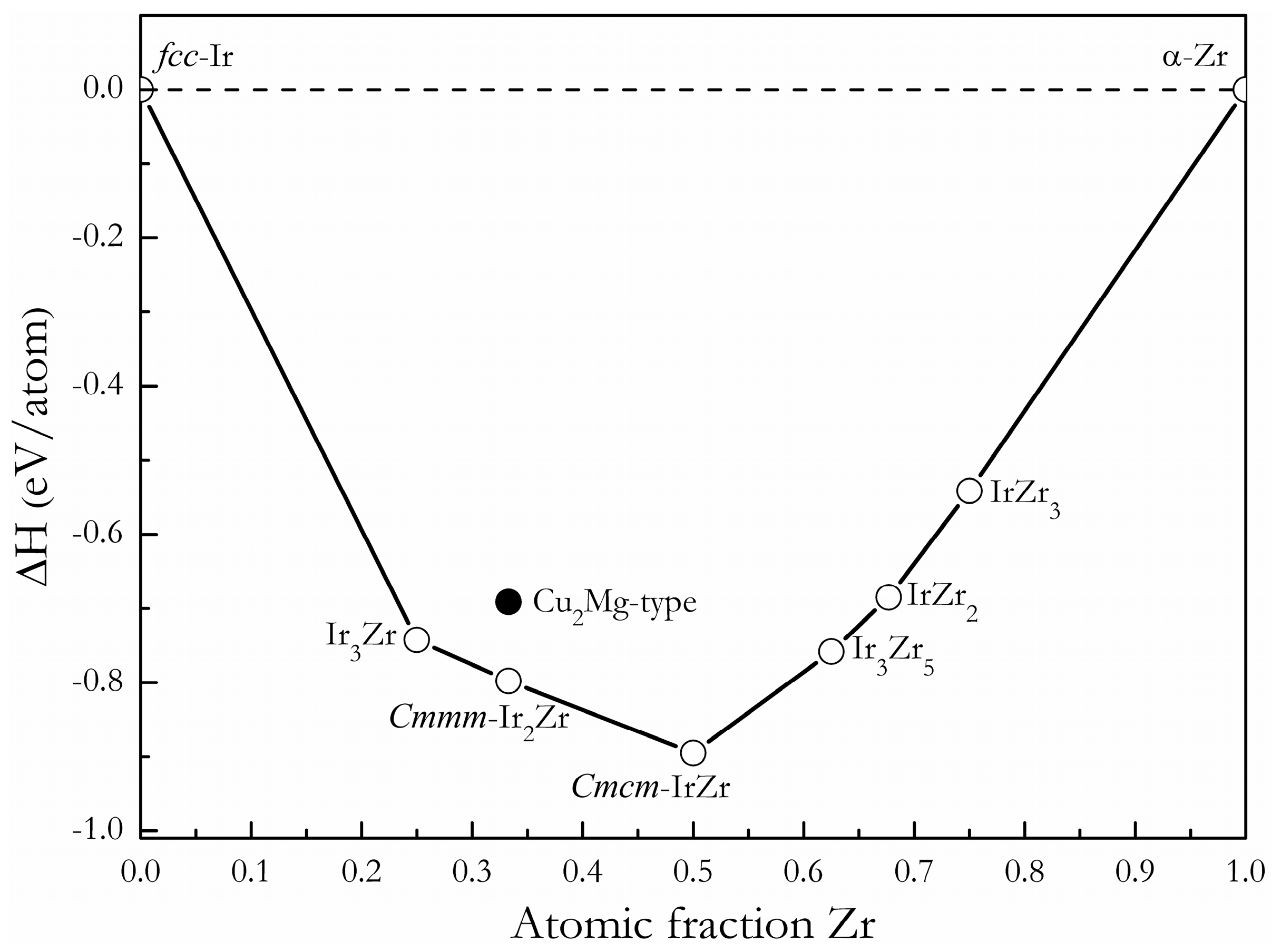
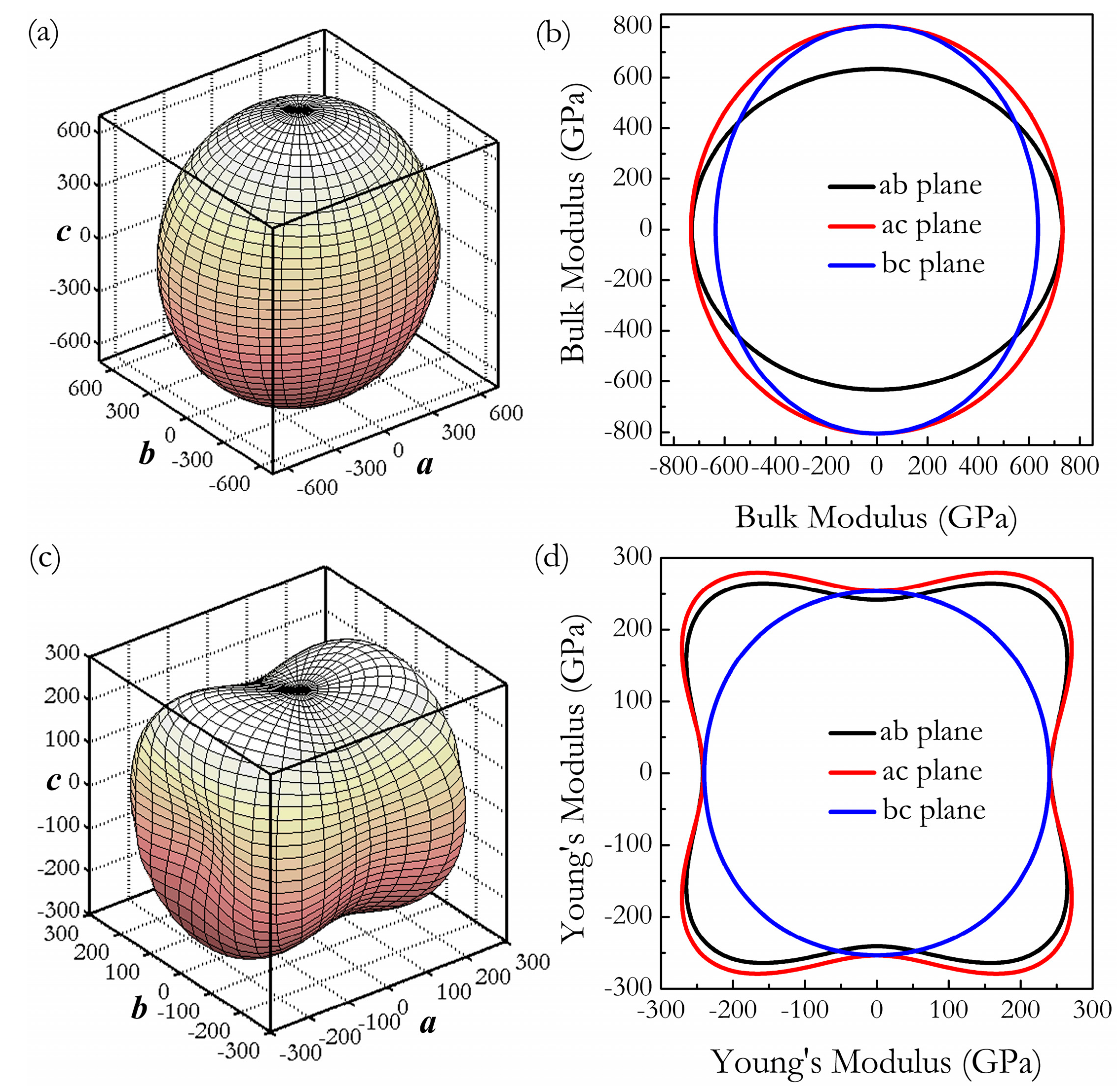
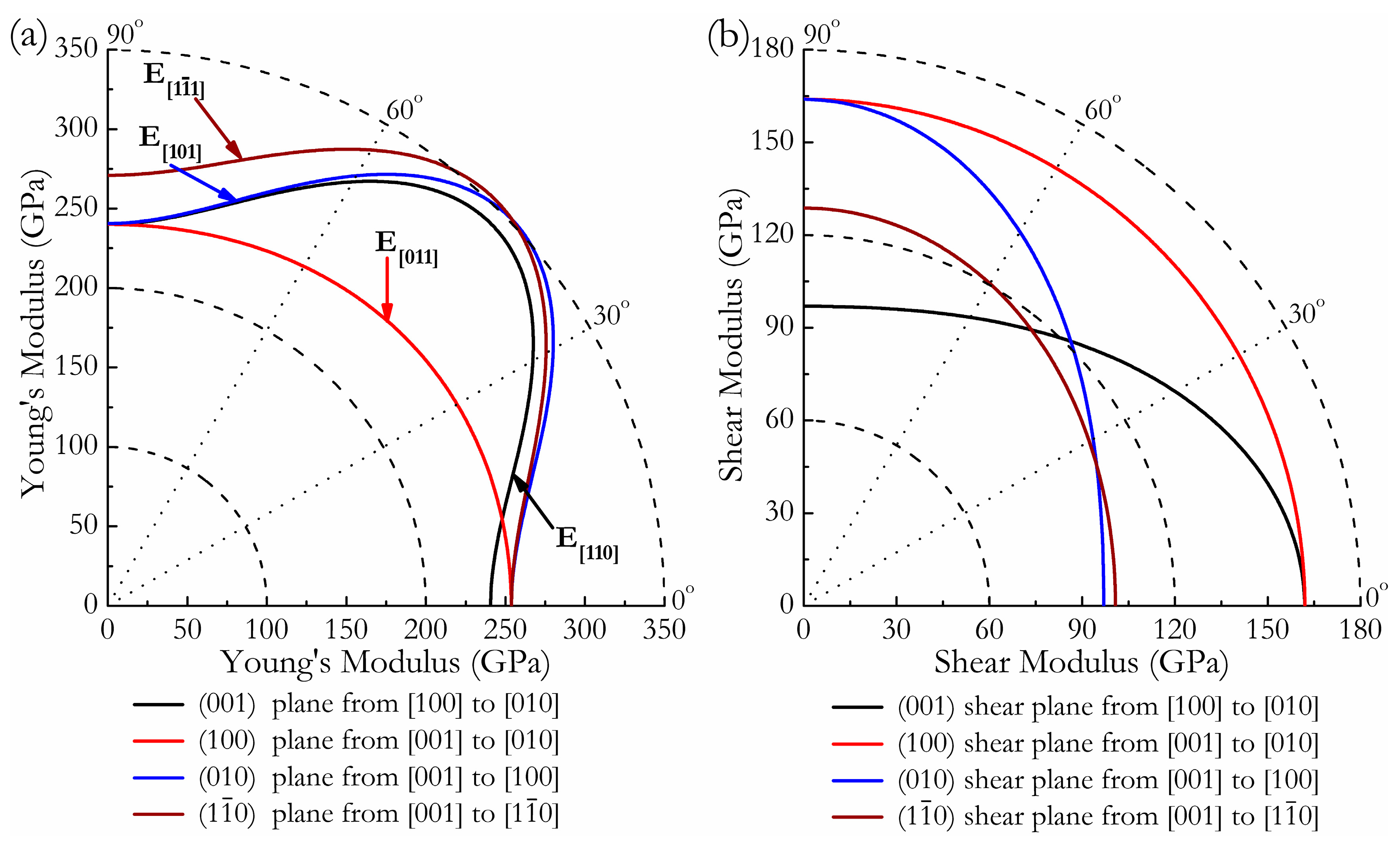
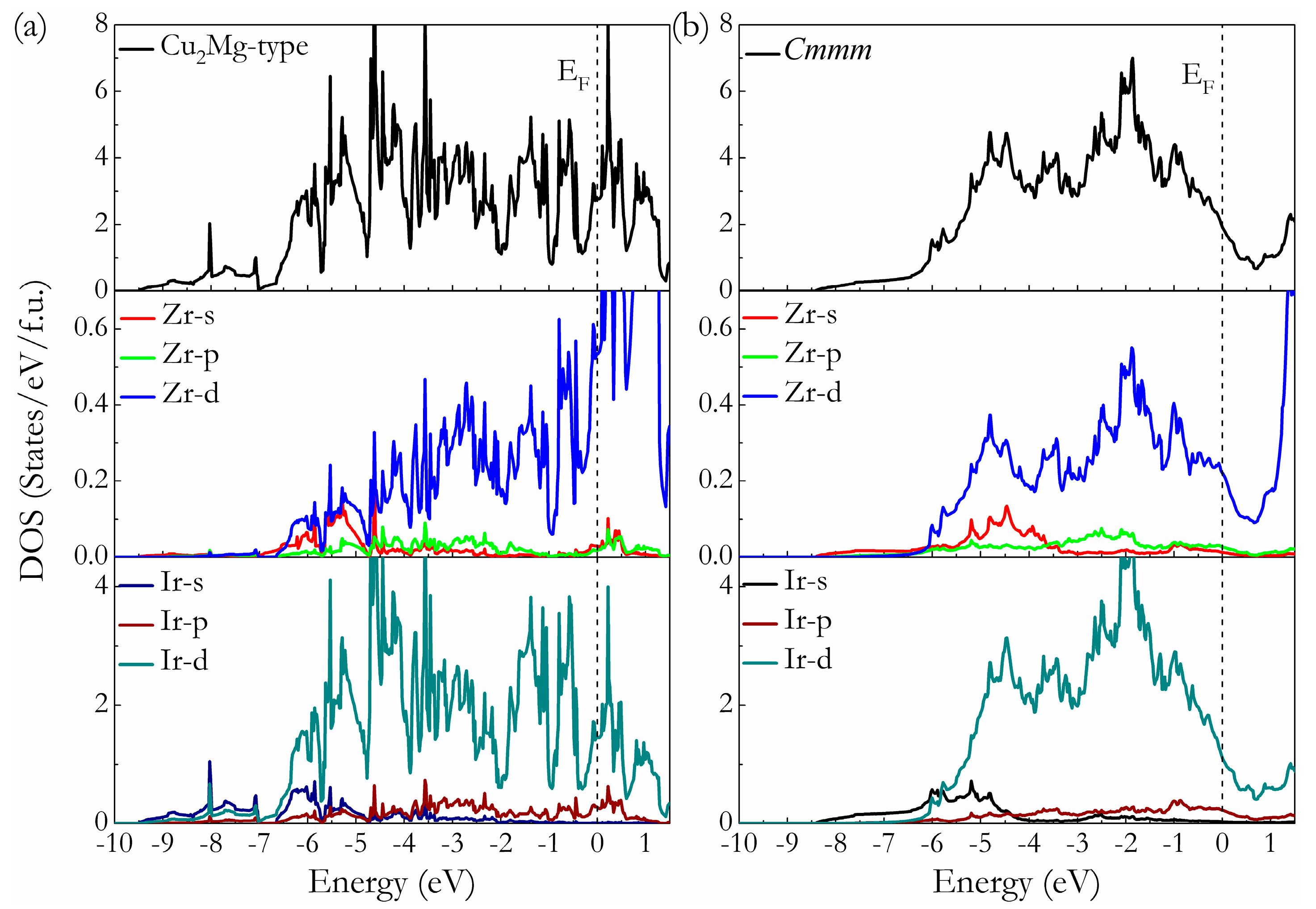
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kuznetsova, T.; Zubar, T.; Chizhik, S.; Gilewicz, A.; Lupicka, O.; Warcholinski, B. Surface microstructure of Mo(C)N coatings investigated by AFM. J. Mater. Eng. Perform. 2016, 25, 5450–5459. [Google Scholar] [CrossRef]
- Warcholinski, B.; Gilewicz, A.; Lupicka, O.; Kuprin, A.S.; Tolmachova, G.N.; Ovcharenko, V.D.; Kolodiy, I.V.; Sawczak, M.; Kochmanska, A.E.; Kochmanski, P.; et al. Structure of CrON coatings formed in vacuum arc plasma fluxes. Surf. Coat. Technol. 2017, 309, 920–930. [Google Scholar] [CrossRef]
- Warcholinski, B.; Gilewicz, A.; Kuznetsova, T.A.; Zubar, T.I.; Chizhik, S.A.; Abetkovskaia, S.O.; Lapitskaya, V.A. Mechanical properties of Mo(C)N coatings deposited using cathodic arc evaporation. Surf. Coat. Technol. 2017, 319, 117–128. [Google Scholar] [CrossRef]
- Yamabe-Mitarai, Y.; Ro, Y.; Maruko, T.; Harada, H. Microstructure dependence of strength of Ir-base refractory superalloys. Intermetallics 1999, 7, 49–58. [Google Scholar] [CrossRef]
- Ran, H.T.; Du, Z.M. Thermodynamic assessment of the Ir-Zr system. J. Alloys Compd. 2006, 413, 101–105. [Google Scholar] [CrossRef]
- Sha, J.B.; Yamabe-Mitarai, Y.; Harada, H. Microstructural evaluation and mechanical properties of Ir-Hf-Zr ternary alloys at room and high temperatures. Intermetallics 2006, 14, 1364–1369. [Google Scholar] [CrossRef]
- Yamabe-Mitarai, Y.; Gu, Y.; Harada, H.; Huang, C. Compressive creep properties of Ir-base refractory superalloys. Metall. Mater. Trans. A 2005, 36, 547–557. [Google Scholar] [CrossRef]
- Yamabe-Mitarai, Y.; Harada, H. Face centered cubic and L12 two-phase structure of Ir-Nb-Zr alloys. J. Alloys Compd. 2003, 361, 169–179. [Google Scholar] [CrossRef]
- Kim, W.Y.; Tanaka, H.; Kasama, A.; Hanada, S. Microstructure and room temperature fracture toughness of Nbss/Nb5Si3 in situ composites. Intermetallics 2001, 9, 827–834. [Google Scholar] [CrossRef]
- Chen, B.S.; Li, Y.Z.; Guan, X.Y.; Wang, C.; Wang, C.X.; Gao, Z.Y. First-principles study of structural, elastic and electronic properties of ZrIr alloy. Comput. Mater. Sci. 2015, 105, 66–70. [Google Scholar] [CrossRef]
- Kudryavtsev, Y.V.; Semenova, O.L. Shape memory effect in ZrIr and Zr-Ir-Co alloys. Powder Metall. Met. Ceram. 2011, 50, 471–478. [Google Scholar] [CrossRef]
- Okamoto, H. The Ir-Zr (iridium-zirconium) system. J. Phase Equilib. 1992, 13, 653–656. [Google Scholar] [CrossRef]
- Eremenko, V.N.; Semenova, E.L.; Shtepa, T.D. State diagram of the Zr-Ir system. Russ. Metall. 1980, 5, 210–213. [Google Scholar]
- Semenova, E.L.; Kudryavtsev, Y.V. Structural phase transformation and shape memory effect in ZrRh and ZrIr. J. Alloys Compd. 1994, 203, 165–168. [Google Scholar] [CrossRef]
- Stalick, J.K.; Waterstrat, R.M. The crystal structure of martensitic ZrIr and ZrRh. J. Alloys Compd. 2009, 477, 123–126. [Google Scholar] [CrossRef]
- Xing, W.; Chen, X.Q.; Li, D.Z.; Li, Y.Y.; Fu, C.L.; Meschel, S.V.; Ding, X. First-principles studies of structural stabilities and enthalpies of formation of refractory intermetallics: TM and TM3 (T = Ti, Zr, Hf; M = Ru, Rh, Pd, Os, Ir, Pt). Intermetallics 2012, 28, 16–24. [Google Scholar] [CrossRef]
- Hart, G.L.; Curtarolo, S.; Massalski, T.B.; Levy, O. Comprehensive search for new phases and compounds in binary alloy systems based on platinum-group metals, using a computational first-principles approach. Phys. Rev. X 2013, 3, 041035. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, B.; Zhan, Y. Ab initio investigation into the structure and properties of Ir-Zr intermetallics for high-temperature structural applications. Comput. Mater. Sci. 2017, 131, 146–159. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lv, J.; Zhu, L.; Ma, Y.M. Crystal structure prediction via particle swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lv, J.; Zhu, L.; Ma, Y.M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Lv, J.; Wang, Y.C.; Zhu, L.; Ma, Y.M. Predicted novel high-pressure phases of lithium. Phys. Rev. Lett. 2011, 106, 015503. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Wang, H.; Wang, Y.C.; Lv, J.; Ma, Y.M.; Cui, Q.L.; Ma, Y.M.; Zou, G.T. Substitutionally alloy of Bi and Te at high pressure. Phys. Rev. Lett. 2011, 106, 145501. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.W.; Hao, J.; Liu, H.Y.; Li, Y.L.; Ma, Y.M. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 2014, 140, 174712. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef]
- Milman, V.; Warren, M.C. Elasticity of hexagonal BeO. J. Phys. Condens. Matter 2001, 13, 241. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Ghosh, G.; Van de Walle, A.; Asta, M. First-principles calculations of the structural and thermodynamic properties of bcc, fcc and hcp solid solutions in the Al-TM (TM = Ti, Zr and Hf) systems: A comparison of cluster expansion and supercell methods. Acta Mater. 2008, 56, 3202–3221. [Google Scholar] [CrossRef]
- Chen, X.Q.; Niu, H.Y.; Li, D.Z.; Li, Y.Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Born, M. On the stability of crystal lattices. Math. Proc. Camb. Philos. Soc. 1940, 36, 160–172. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Panda, K.B.; Ravi Chandran, K.S. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory. Comput. Mater. Sci. 2006, 35, 134–150. [Google Scholar] [CrossRef]
- He, Y.; Schwarz, R.B.; Migliori, A. Elastic constants of single crystal γ-TiAl. J. Mater. Res. 1995, 10, 1187–1195. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Vajeeston, P.; Ravindran, P.; Ravi, C.; Asokamani, R. Electronic structure, bonding, and ground-state properties of AlB2-type transition-metal diborides. Phys. Rev. B 2001, 63, 045115. [Google Scholar] [CrossRef]
| Ir2Zr | Source | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 |
|---|---|---|---|---|---|---|---|---|---|---|
| Cu2Mg-type | This work | 379 | - | - | 152 | - | - | 181 | - | - |
| - | Theory [18] | 379 | - | - | 151 | - | - | 180 | - | - |
| Cmmm | This work | 362 | 348 | 378 | 97 | 162 | 164 | 173 | 188 | 174 |
| Ir2Zr | Source | B | G | E | v | B/G | H |
|---|---|---|---|---|---|---|---|
| Cu2Mg-type | This work | 248 | 129 | 323 | 0.283 | 1.972 | 18.9 |
| - | Theory [18] | 246 | 128 | 327 | 0.278 | 1.920 | 20.3 |
| Cmmm | This work | 239 | 117 | 302 | 0.289 | 2.038 | 18.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Cao, R.; Zhao, M.; Du, J.; Cheng, K. Unexpected Ground-State Structure and Mechanical Properties of Ir2Zr Intermetallic Compound. Materials 2018, 11, 103. https://doi.org/10.3390/ma11010103
Zhang M, Cao R, Zhao M, Du J, Cheng K. Unexpected Ground-State Structure and Mechanical Properties of Ir2Zr Intermetallic Compound. Materials. 2018; 11(1):103. https://doi.org/10.3390/ma11010103
Chicago/Turabian StyleZhang, Meiguang, Rui Cao, Meijie Zhao, Juan Du, and Ke Cheng. 2018. "Unexpected Ground-State Structure and Mechanical Properties of Ir2Zr Intermetallic Compound" Materials 11, no. 1: 103. https://doi.org/10.3390/ma11010103
APA StyleZhang, M., Cao, R., Zhao, M., Du, J., & Cheng, K. (2018). Unexpected Ground-State Structure and Mechanical Properties of Ir2Zr Intermetallic Compound. Materials, 11(1), 103. https://doi.org/10.3390/ma11010103




