Material Viscoelasticity-Induced Drift of Micro-Accelerometers
Abstract
:1. Introduction
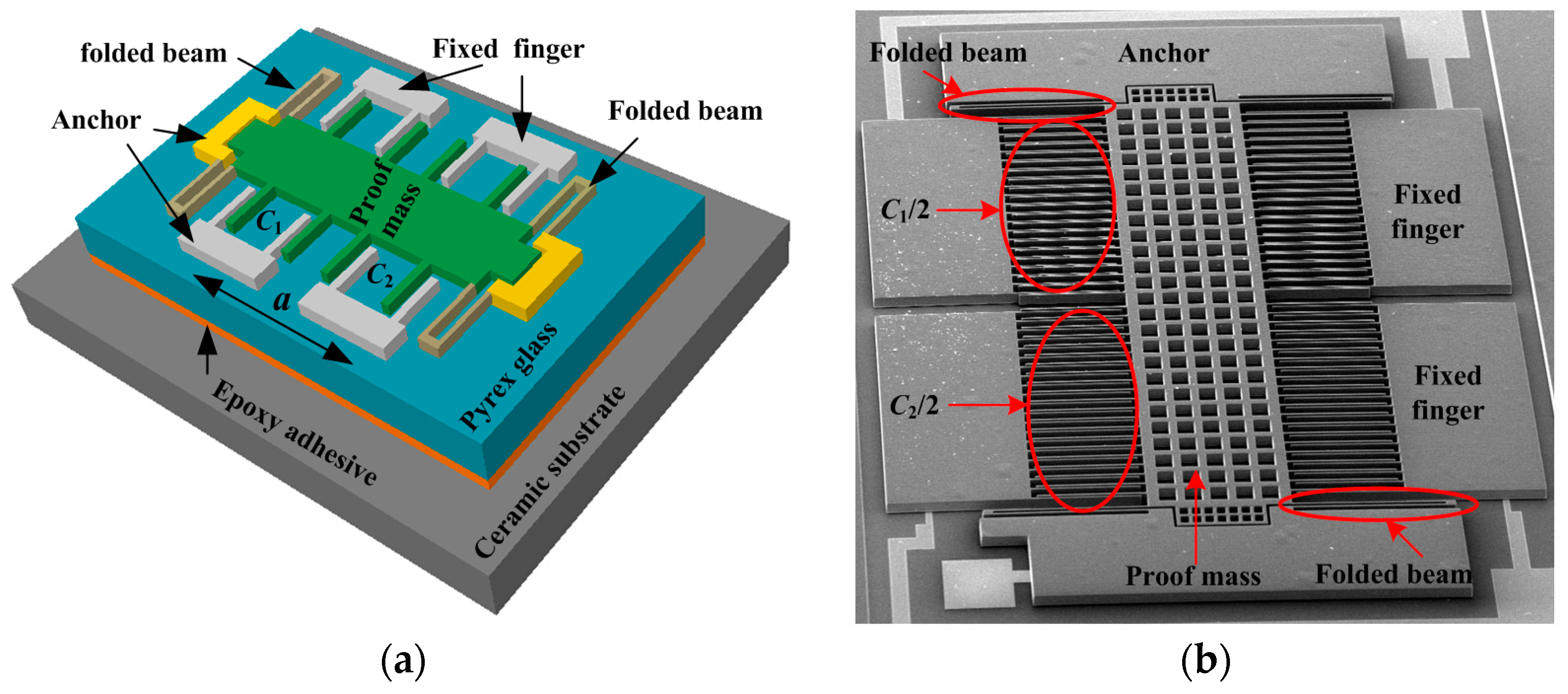
2. Structure and Principle
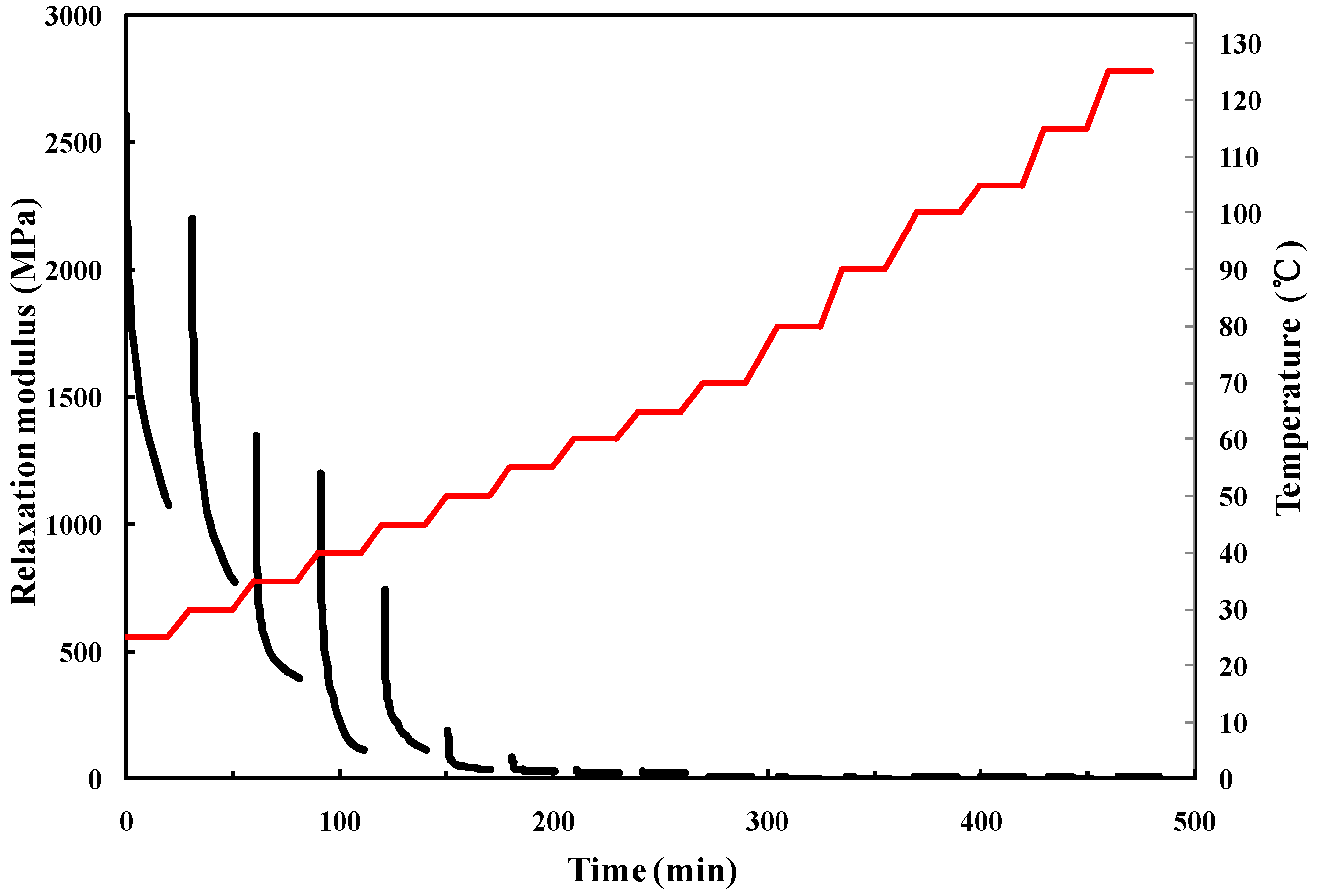
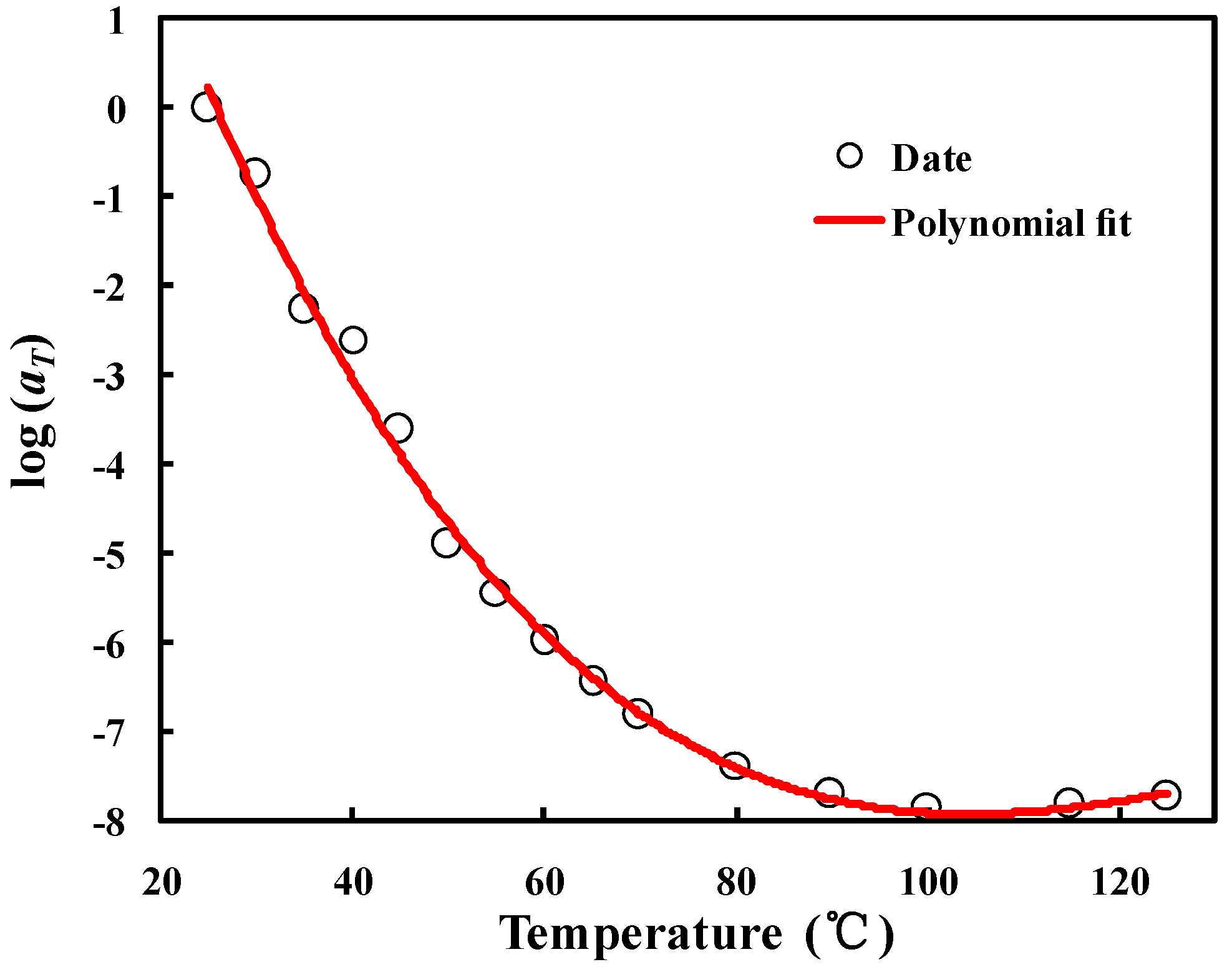
3. Material Property
4. Simulation and Experiments
5. Discussion
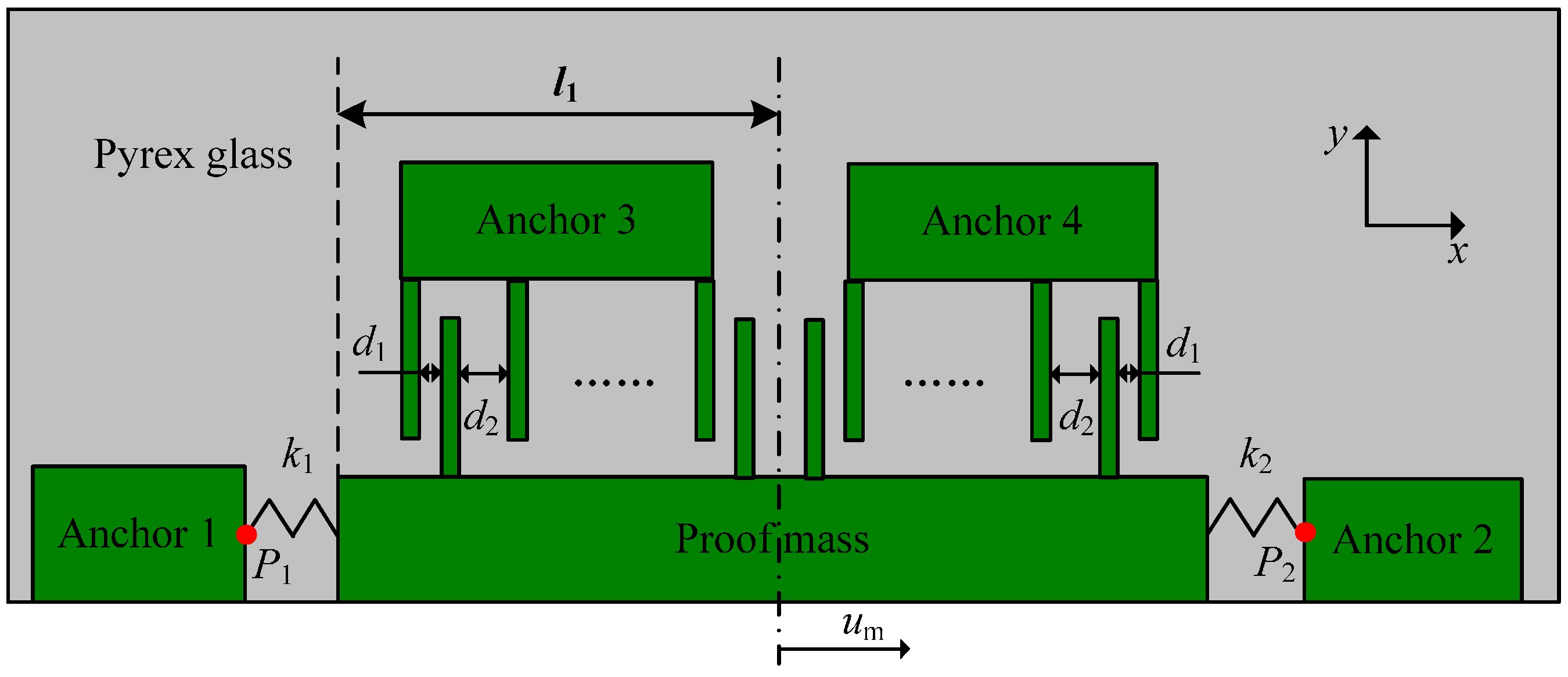
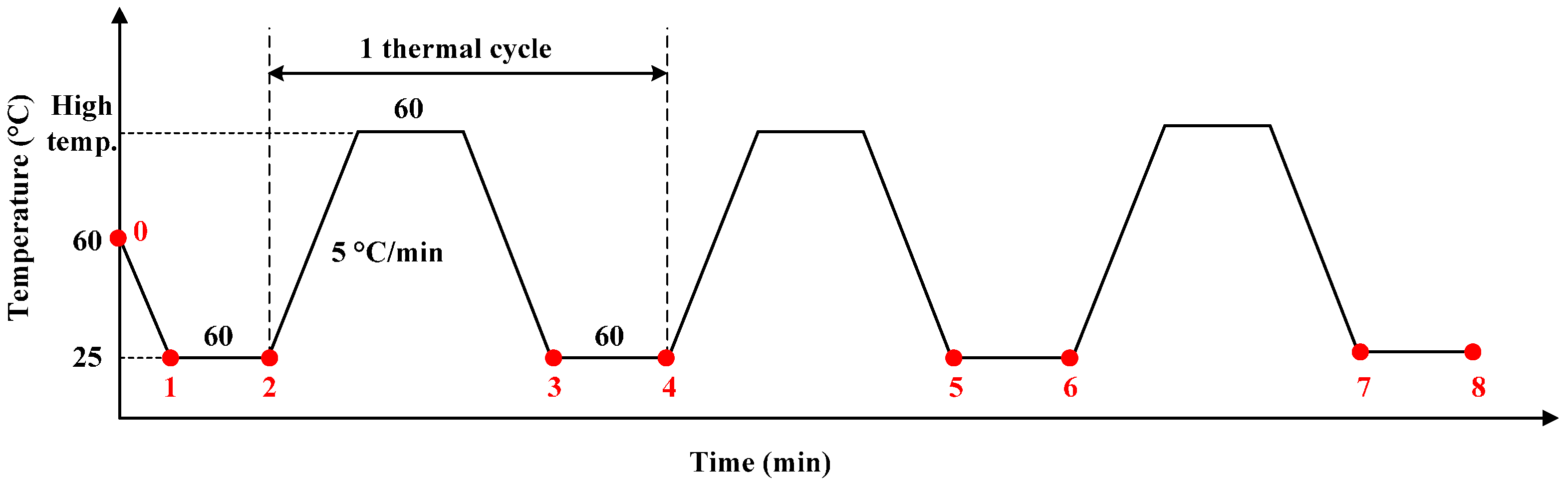
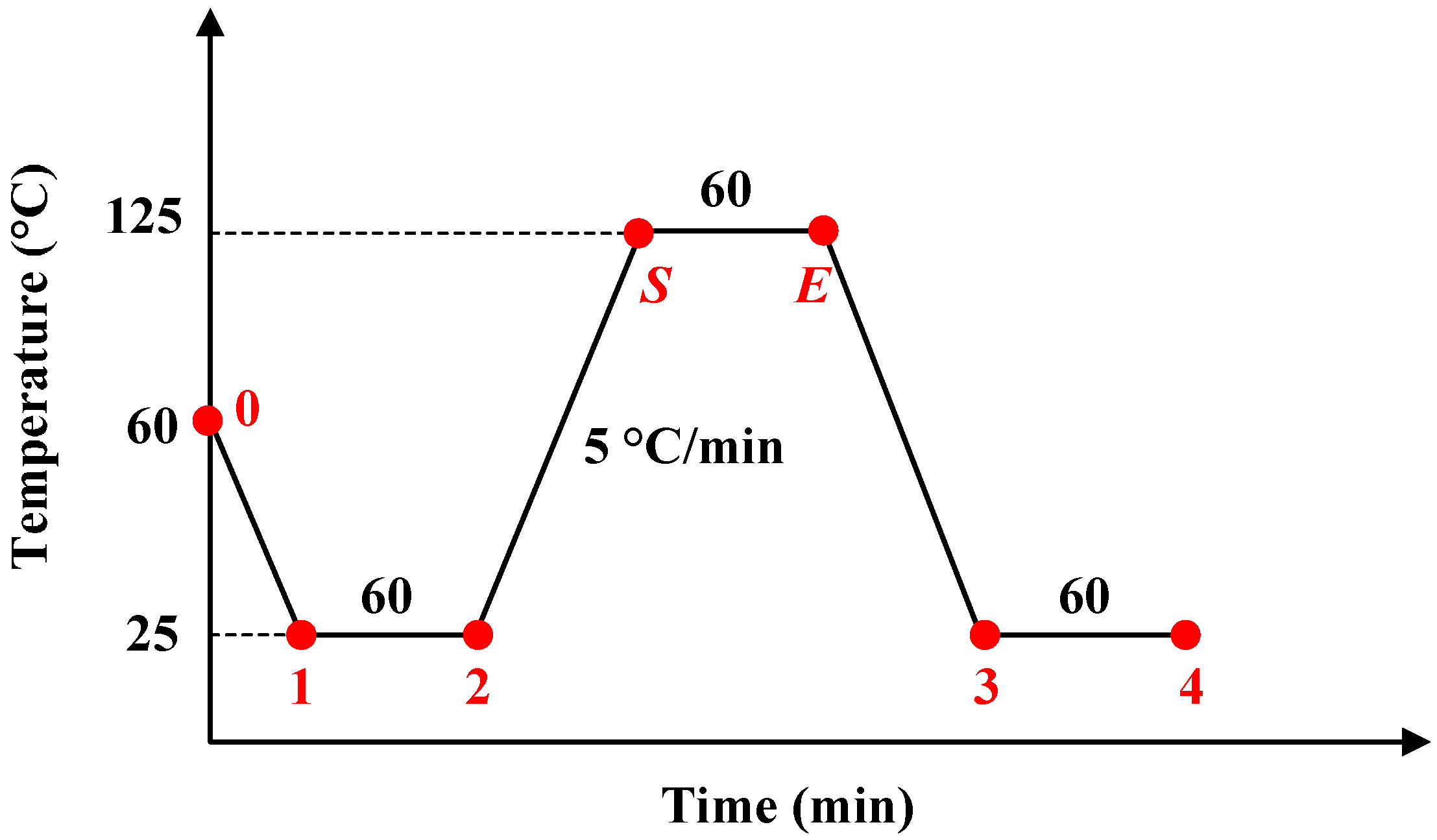
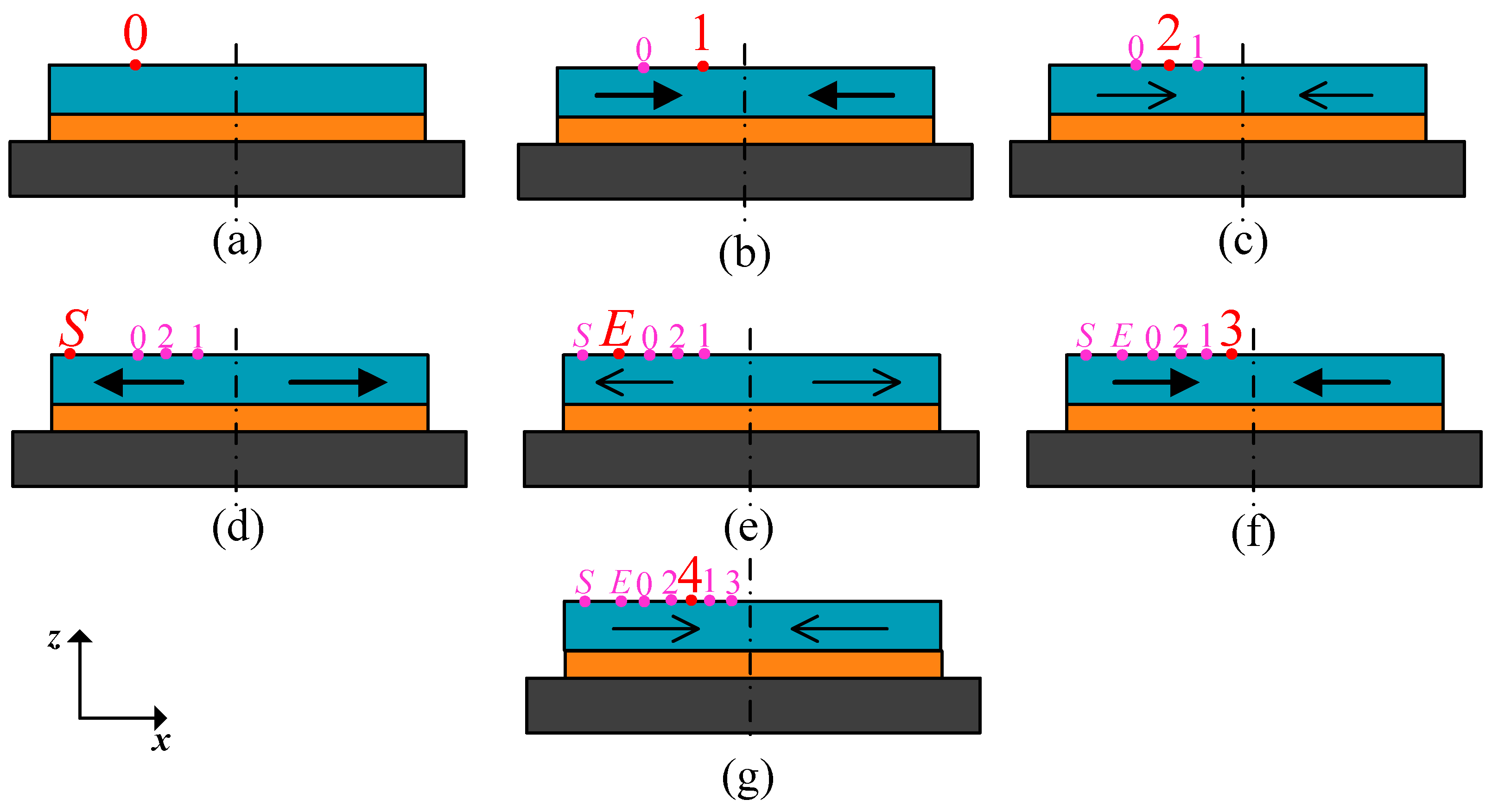
- Step 1—curing process: The initial state or stress-free state of the sensor appeared at 60 °C where the curing process started, and the P1 was located at position 0 in Figure 10a.
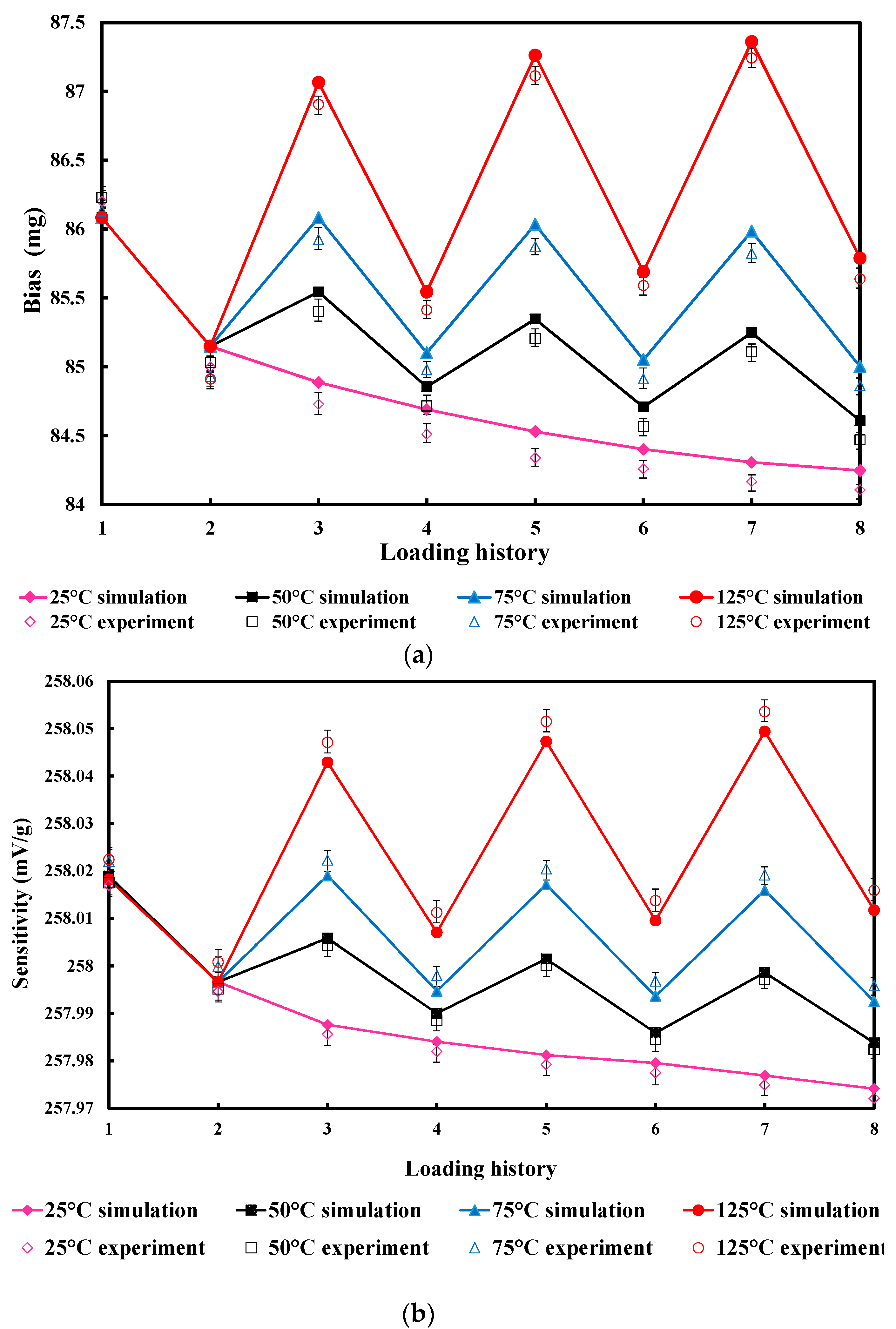
- Step 3—room temperature retention: The compression of glass decreased due to stress relaxation, and P1 slightly moved in the negative x direction, which led to the decrease of um and increase of d1 (Figure 10c). The offset and sensitivity decreased.
- Step 4—starting point of high temperature: The model expanded, and the point P1 moved in the negative x direction substantially, which caused the decrease of um and increase of d1 (Figure 10d). Therefore, the offset and sensitivity continued to decrease.
- Step 5—ending point of high temperature: During the thermal treatment process, the tension on the glass decreased due to stress relaxation, and P1 slightly moved in the positive x direction to result in a higher offset and sensitivity (Figure 10e).
- Step 6—cooling to room temperature again: The model shrank, and the shrinkage included both the thermal part in step 4 and additional shrinkage value generated by strong viscoelasticity at 125 °C. Hence, the point P1 moved to the right position 1 (Figure 10f). Consequently, the offset and sensitivity at this stage were larger than those of Figure 10b.
- Step 7—room temperature retention again: The offset and sensitivity decreased, due to stress relaxation, but they were still larger than those in Figure 10c. This indicated that the offset level is influenced by thermal treatment, so higher-temperature dwells lead to greater offset and sensitivity (Figure 10g).
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Higgins, A. Adhesive bonding of aircraft structures. Int. J. Adhes. Adhes. 2000, 20, 367–376. [Google Scholar] [CrossRef]
- Narisawa, M. Silicone resin applications for ceramic precursors and composites. Materials 2010, 3, 3518–3536. [Google Scholar] [CrossRef]
- Walwadkar, S.S.; Cho, J. Evaluation of die stress in MEMS packaging: Experimental and theoretical approaches. IEEE Trans. Compon. Packag. Technol. 2006, 29, 735–742. [Google Scholar] [CrossRef]
- Nysæ ther, J.B.; Larsen, A.; Liverød, B.; Ohlckers, P. Measurement of package-induced stress and thermal zero shift in transfer molded silicon piezoresistive pressure sensors. J. Micromech. Microeng. 1998, 8, 168. [Google Scholar] [CrossRef]
- Zarnik, M.S.; Rocak, D.; Macek, S. Residual stresses in a pressure-sensor package induced by adhesive material during curing: A case study. Sens. Actuators A Phys. 2004, 116, 442–449. [Google Scholar] [CrossRef]
- Song, J.; Huang, Q.A.; Li, M.; Tang, J.Y. Influence of environmental temperature on the dynamic properties of a die attached MEMS device. Microsyst. Technol. 2009, 15, 925–932. [Google Scholar] [CrossRef]
- Zhang, Z.; Wan, Z.; Liu, C.; Cao, G.; Lu, Y.; Liu, S. Effects of adhesive material on the output characteristics of pressure sensor. In Proceedings of the International Conference on Electronic Packaging Technology & High Density Packaging, Xi’an, China, 16–19 August 2010. [Google Scholar]
- Chuang, C.H.; Huang, Y.H.; Lee, S.L. The influence of adhesive materials on chip-on-board packing of MEMS microphone. Microsyst. Technol. 2012, 18, 1931–1940. [Google Scholar] [CrossRef]
- Joo, J.W.; Choa, S.H. Deformation behavior of MEMS gyroscope sensor package subjected to temperature change. IEEE Trans. Compon. Packag. Technol. 2007, 30, 346–354. [Google Scholar] [CrossRef]
- Peng, P.; Zhou, W.; Yu, H.; Peng, B.; Qu, H.; He, X. Investigation of the thermal drift of MEMS capacitive accelerometers induced by the overflow of die attachment adhesive. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 822–830. [Google Scholar] [CrossRef]
- Guillemenet, J.; Bistac, S.; Schultz, J. Relationship between polymer viscoelastic properties and adhesive behaviour. Int. J. Adhes. Adhes. 2002, 22, 1–5. [Google Scholar] [CrossRef]
- Obaid, N.; Kortschot, M.T.; Sain, M. Understanding the stress relaxation behavior of polymers reinforced with short elastic fibers. Materials 2017, 10, 472. [Google Scholar] [CrossRef] [PubMed]
- Srikanth, N. Warpage analysis of epoxy molded packages using viscoelastic based model. J. Mater. Sci. 2006, 41, 3773–3780. [Google Scholar] [CrossRef]
- Zhang, X.; Park, S.; Judy, M.W. Accurate assessment of packaging stress effects on MEMS sensors by measurement and sensor-package interaction simulations. J. Microelectromech. Syst. 2007, 16, 639–649. [Google Scholar] [CrossRef]
- Krondorfer, R.H.; Kim, Y.K. Packaging effect on MEMS pressure sensor performance. IEEE Trans. Compon. Packag. Technol. 2007, 30, 285–293. [Google Scholar] [CrossRef]
- Park, S.; Liu, D.; Kim, Y.; Lee, H.; Zhang, S. Stress evolution in an encapsulated MEMS package due to viscoelasticity of packaging materials. In Proceedings of the IEEE 62nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 29 May–1 June 2012. [Google Scholar]
- Kim, Y.; Lee, H.; Zhang, X.; Park, S. Optimal material properties of molding compounds for MEMS package. IEEE Trans. Compon. Packag. Manufac. Technol. 2014, 4, 1589–1597. [Google Scholar]
- Kim, Y.; Liu, D.; Lee, H.; Liu, R.; Sengupta, D.; Park, S. Investigation of stress in MEMS sensor device due to hygroscopic and viscoelastic behavior of molding compound. IEEE Trans. Compon. Packag. Manufac. Technol. 2015, 5, 945–955. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, H.; Peng, B.; Shen, H.; He, X.; Su, W. Modeling the microstructure curvature of boron-doped silicon in bulk micromachined accelerometer. Materials 2013, 6, 244–254. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Chen, L.; Yu, H.; Peng, B.; Chen, Y. Sensitivity jump of micro accelerometer induced by micro-fabrication defects of micro folded beams. Meas. Sci. Rev. 2016, 16, 228–234. [Google Scholar] [CrossRef]
- Dai, G.; Li, M.; He, X.; Du, L.; Shao, B.; Su, W. Thermal drift analysis using a multiphysics model of bulk silicon MEMS capacitive accelerometer. Sens. Actuators A Phys. 2011, 172, 369–378. [Google Scholar] [CrossRef]
- He, J.; Xie, J.; He, X.; Du, L.; Zhou, W. Analytical study and compensation for temperature drifts of a bulk silicon MEMS capacitive accelerometer. Sens. Actuators A Phys. 2016, 239, 174–184. [Google Scholar] [CrossRef]
- Suhir, E. Predictive analytical thermal stress modeling in electronics and photonics. Appl. Mech. Rev. 2009, 62, 933–944. [Google Scholar] [CrossRef]
- Chae, S.H.; Zhao, J.H.; Edwards, D.R.; Ho, P.S. Characterization of the viscoelasticity of molding compounds in the time domain. J. Electron. Mater. 2010, 39, 419–425. [Google Scholar] [CrossRef]
- Hu, M.; Xia, Y.; Daeffler, C.S.; Wang, J.; McKenna, G.B.; Kornfield, J.A.; Grubbs, R.H. The linear rheological responses of wedge-type polymers. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 899–906. [Google Scholar] [CrossRef]
- Kim, Y.K.; White, S.R. Stress relaxation behavior of 3501-6 epoxy resin during cure. Polym. Eng. Sci. 2010, 36, 2852–2862. [Google Scholar] [CrossRef]
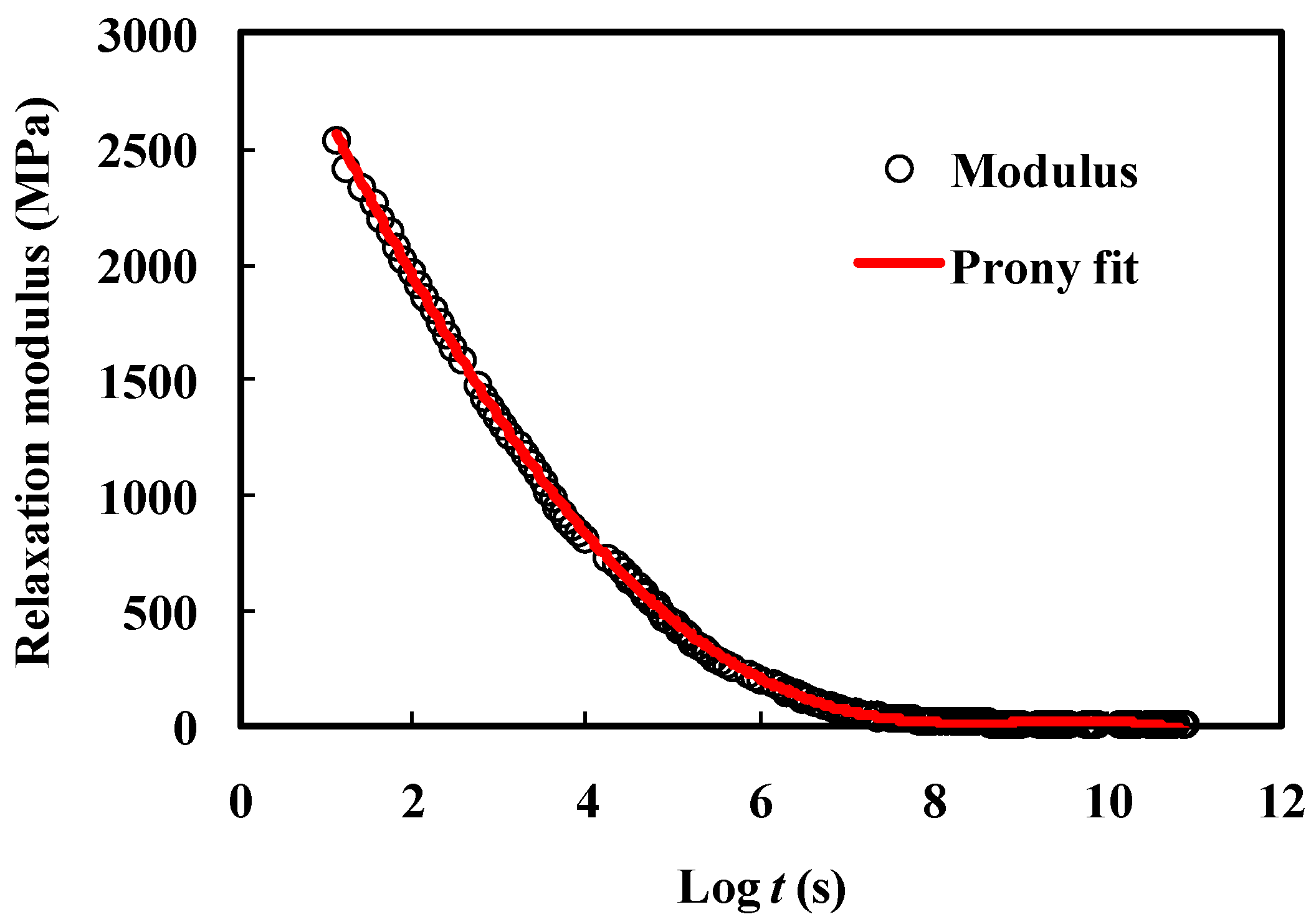

| Material | Young’s Modulus (Gpa) | Poisson Ratio | CTE (ppm/°C) |
|---|---|---|---|
| Silicon | 160 | 0.22 | 2.6 |
| Glass | 62.7 | 0.2 | 3.25 |
| Ceramic | 360 | 0.22 | 6.5 |
| Adhesive | Table 2 | 0.37 | 60 |
| i | Ei/E0 1 | |
|---|---|---|
| 1 | 0.08510 | 3041.87694 |
| 2 | 0.14589 | 981,765.85865 |
| 3 | 0.22654 | 243.32699 |
| 4 | 0.11248 | 2083.25650 |
| 5 | 0.15906 | 48,993.21024 |
| 6 | 0.21617 | 31.16988 |
| 7 | 0.03923 | 5052.23180 |
| 8 | 0.00025 | 6992.77554 |
| 9 | 0.00676 | 3321.33054 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Peng, P.; Yu, H.; Peng, B.; He, X. Material Viscoelasticity-Induced Drift of Micro-Accelerometers. Materials 2017, 10, 1077. https://doi.org/10.3390/ma10091077
Zhou W, Peng P, Yu H, Peng B, He X. Material Viscoelasticity-Induced Drift of Micro-Accelerometers. Materials. 2017; 10(9):1077. https://doi.org/10.3390/ma10091077
Chicago/Turabian StyleZhou, Wu, Peng Peng, Huijun Yu, Bei Peng, and Xiaoping He. 2017. "Material Viscoelasticity-Induced Drift of Micro-Accelerometers" Materials 10, no. 9: 1077. https://doi.org/10.3390/ma10091077
APA StyleZhou, W., Peng, P., Yu, H., Peng, B., & He, X. (2017). Material Viscoelasticity-Induced Drift of Micro-Accelerometers. Materials, 10(9), 1077. https://doi.org/10.3390/ma10091077





