Research on the Mechanism of In-Plane Vibration on Friction Reduction
Abstract
:1. Introduction
2. Experiment
2.1. Experimental Setup
2.2. Materials
2.3. Procedures
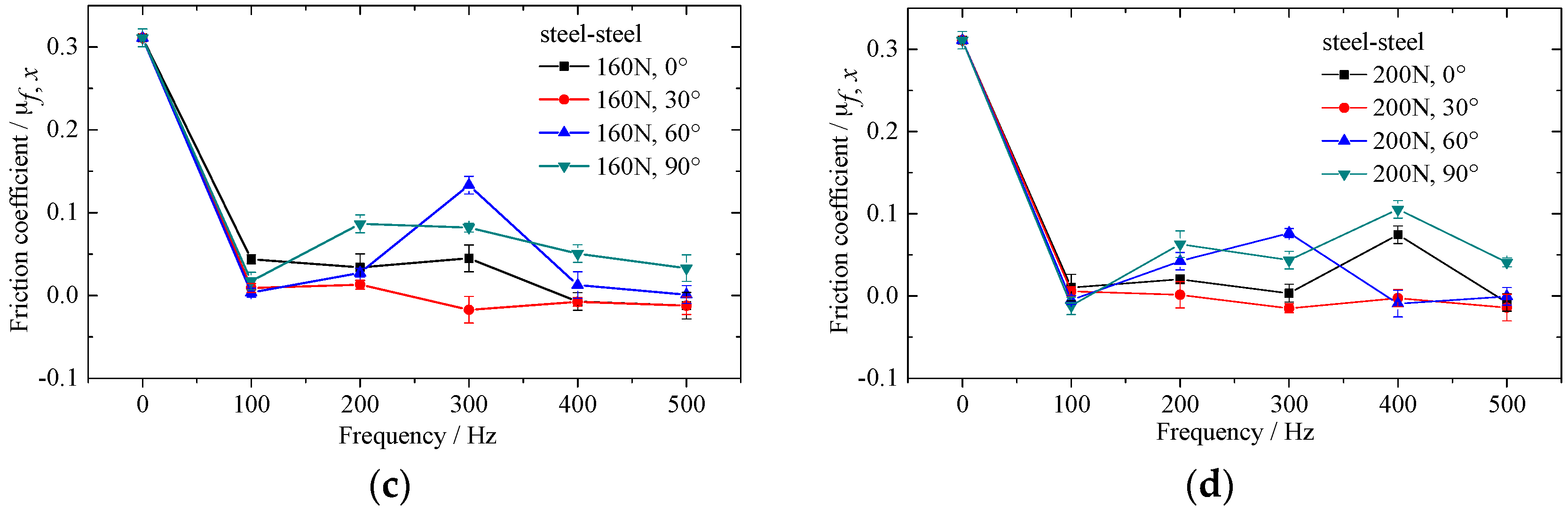
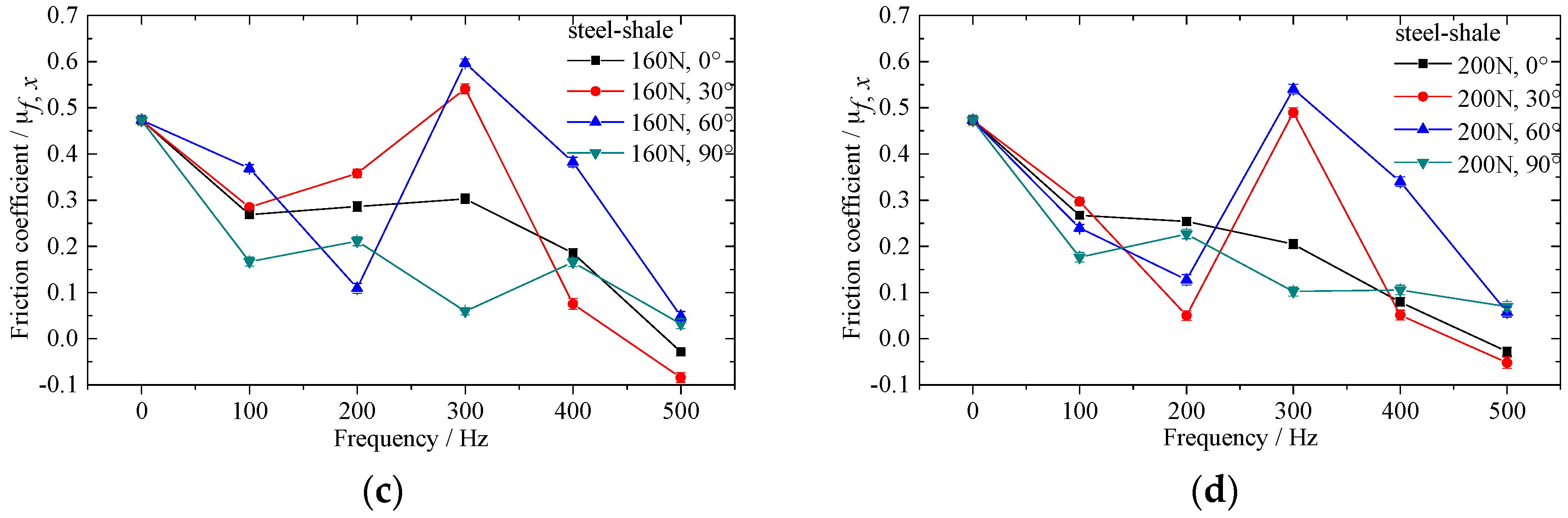
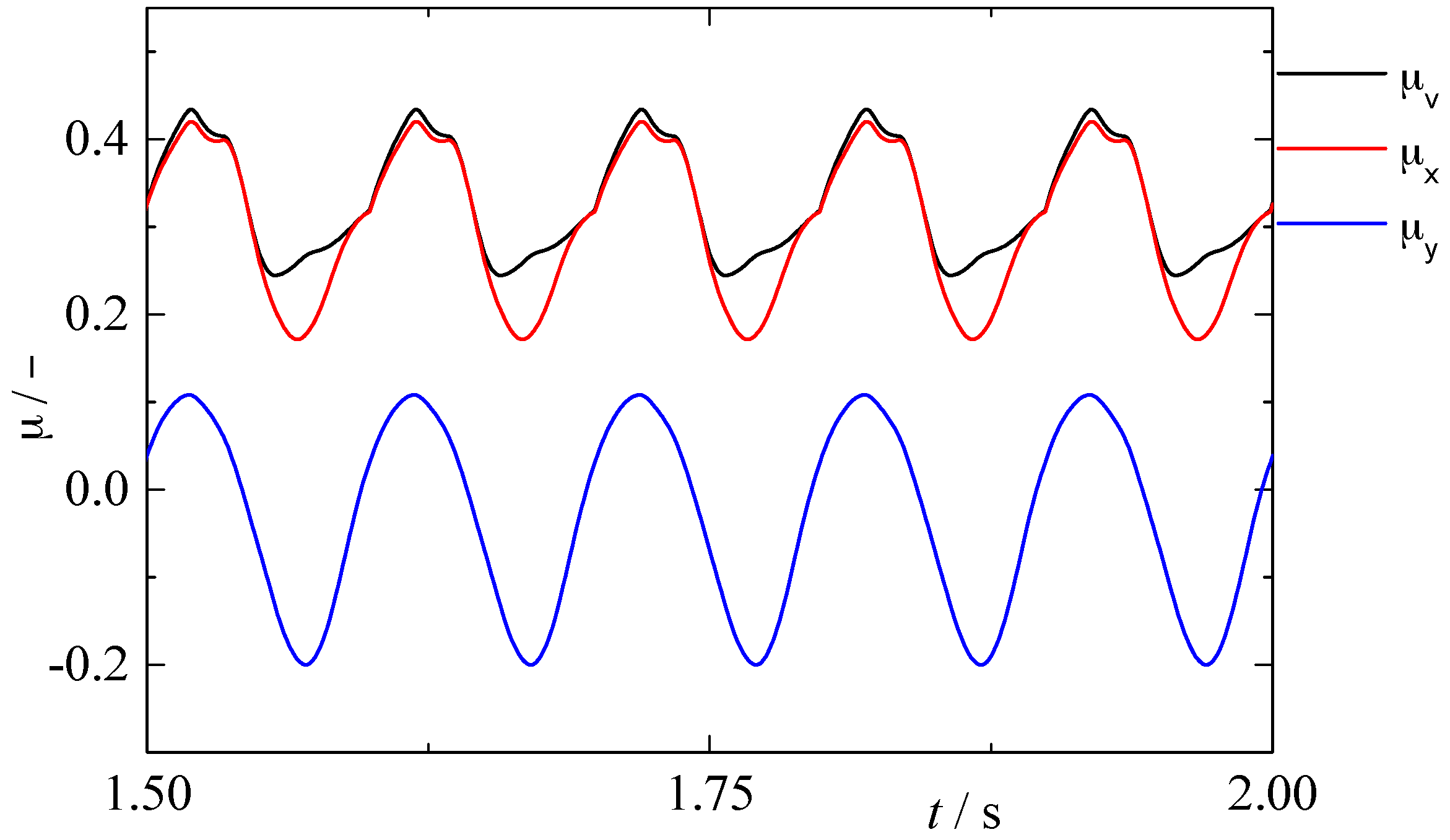
2.4. Results and Discussion
3. Theoretical Model
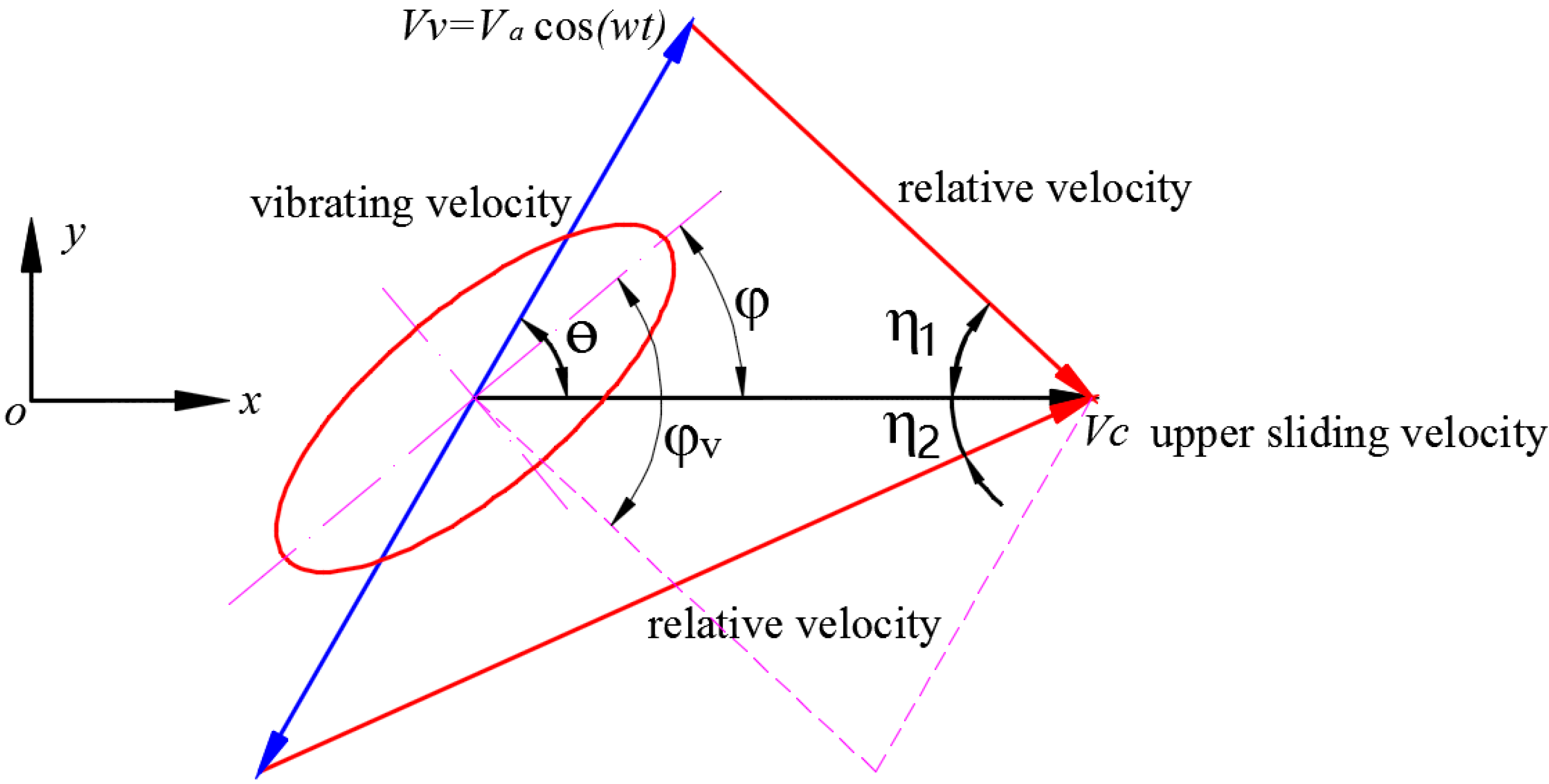
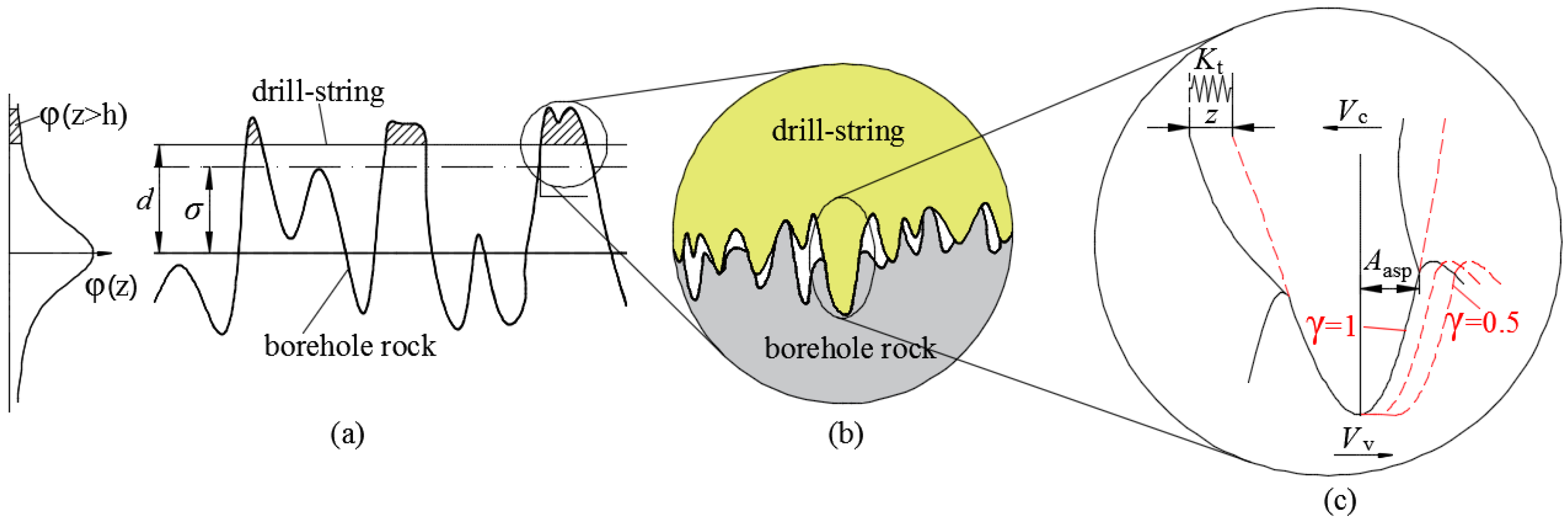
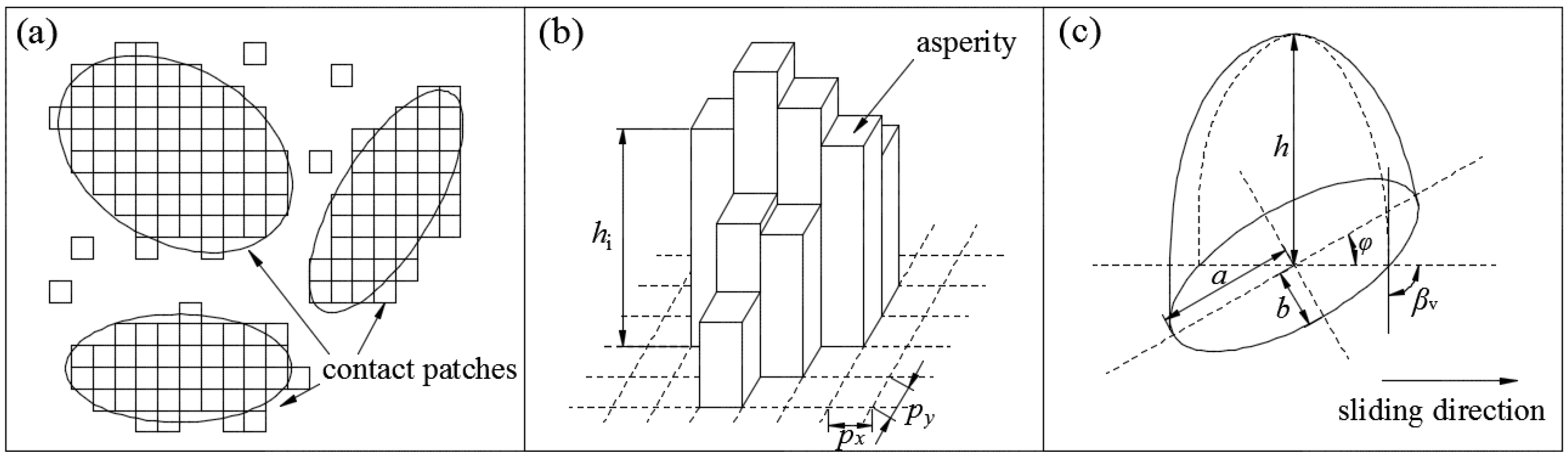
3.1. Contact Model under In-Plane Vibration
3.2. Frictional Coefficient under In-Plane Vibration
3.3. Frictional Force in Sliding Direction
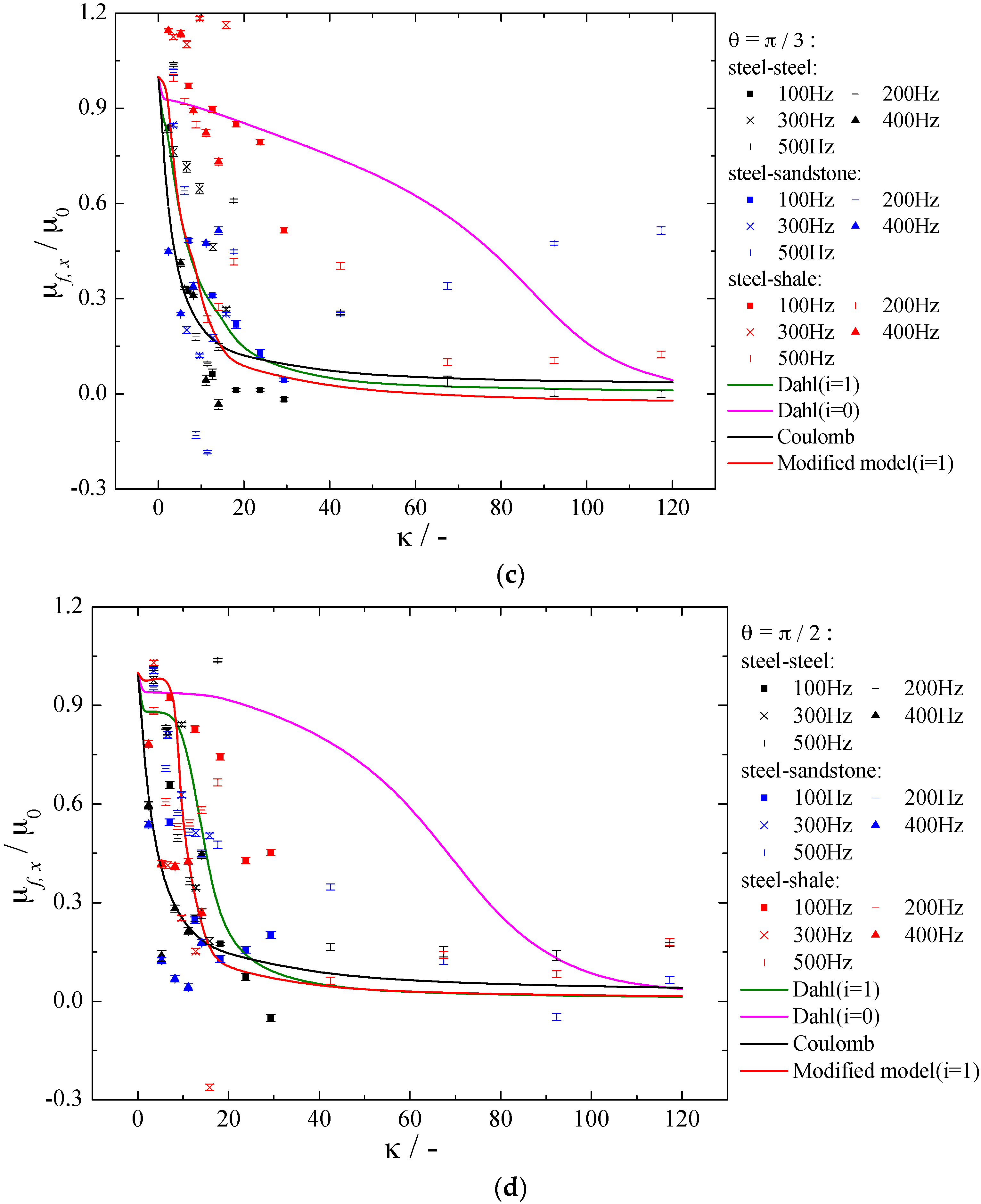
4. Experimental Verification of Numerical Result
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Roman symbols | |
| Area of base ellipse (m2) | |
| , | Major and minor semi axis of the base ellipse of paraboloid (m) |
| Constant sliding velocity (m/s) | |
| Instantaneous vibrating velocity (m/s) | |
| Amplitude of in-plane vibration velocity (m/s) | |
| The relative velocity (m/s) | |
| The deflection velocity of asperities (m/s) | |
| Velocity ratio of and | |
| Nominal normal pressure (Pa) | |
| Hardness of the softer material (Pa) | |
| d | The separation of mean planes of contacting pairs (m) |
| The tangential stiffness of surfaces (N/m) | |
| i | Shape parameter of stress-strain curve |
| z | The average deflection of asperities (m) |
| Nominal normal force (N) | |
| Tangential force (N) | |
| Position of top point of asperity at time t (m) | |
| Position of bottom point of asperity at time t (m) | |
| Deflection displacement of top point and bottom point of asperity (m) | |
| Deflection displacement magnitude of asperities (m) | |
| Volume of representative elliptical paraboloid (m3) | |
| Height of elliptical paraboloid (m) | |
| Number of contact patches in a representative area (-) | |
| Discrete surface points number of contact patch (-) | |
| Greek symbols | |
| Fraction of real contact area, i.e., degree of contact (-) | |
| Circular frequency of in-plane vibration (rad/s) | |
| Angle between vibration direction and sliding direction, (rad) | |
| , | Orientation angle between the sliding direction and the major axis of the ellipse without and with in-plane vibration,, (rad) |
| Attack angle of elliptical paraboloid under in-plane vibration (rad) | |
| Kinetic friction coefficient (-) | |
| Instantaneous frictional coefficient in relative direction, sliding direction and direction perpendicular to the sliding direction under in-plane vibration (-) | |
| Arithmetic average frictional coefficient in sliding direction (-) | |
| Arithmetic average frictional coefficient in sliding direction calculated by models (-) | |
| Arithmetic average frictional coefficient in sliding direction measured by experiment (-) | |
| Arithmetic average frictional coefficient during a in-plane vibration period (-) | |
| Standard deviation of equivalent rough surface heights (m) | |
| , | Standard deviation of surface heights of upper specimen and bottom specimen (m) |
| Elastic recovery factor, (-) | |
| The surface height probability density distribution (-) | |
Appendix A. Slip-Line Friction Model
References
- Hess, D.P.; Soom, A.; Kim, C.H. Normal vibrations and friction at a Hertzian contact under random excitation: Theory and experiments. J. Sound Vib. 1992, 153, 491–508. [Google Scholar] [CrossRef]
- Grudziński, K.; Kostek, R. Influence of normal micro-vibrations in contact on sliding motion of solid body. J. Theor. Appl. Mech. 2005, 43, 37–49. [Google Scholar]
- Godfrey, D. Vibration reduces metal to metal contact and causes an apparent reduction in friction. ASLE Trans. 1967, 10, 183–192. [Google Scholar] [CrossRef]
- Siegert, K.; Ulmer, J. Superimposing ultrasonic waves on the dies in tube and wire drawing. J. Eng. Mater. Technol. 2001, 123, 517–523. [Google Scholar] [CrossRef]
- Socoliuc, A.; Gnecco, E.; Maier, S. Atomic-scale control of friction by actuation of nanometer-sized contacts. Science 2006, 313, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Skyles, L.; Amiraslani, Y.; Wilhoit, J. Converting Static Friction to Kinetic Friction to Drill Further and Faster in Directional Holes. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, San Diego, CA, USA, 6–8 March 2012. [Google Scholar]
- Maidla, E.; Haci, M.; Jones, S.; Cluchey, M.; Alexander, M.; Warren, T. Field Proof of the New Sliding Technology for Directional Drilling. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 23–25 February 2005. [Google Scholar]
- Xciter Variable Frequency Drill String Vibrator. Available online: http://www.loganxtend.com (accessed on 22 January 2017).
- Popov, V.L.; Starcevic, J.; Filippov, A.E. Influence of Ultrasonic In-plane Oscillations on Static and Sliding Friction and Intrinsic Length Scale of Dry Friction Processes. Tribol. Lett. 2010, 39, 25–30. [Google Scholar] [CrossRef]
- Hess, D.P.; Soom, A. Normal vibrations and friction under harmonic loads: Part I-Hertzian contacts. J. Tribol. 1971, 113, 80–86. [Google Scholar] [CrossRef]
- Tolstoi, D.M.; Borisova, G.A.; Grigorova, S.R. Friction regulation by perpendicular oscillation. Sov. Phys.-Dokl. 1973, 17, 907–909. [Google Scholar]
- Mitskevich, A.M. Motion of the body over tangentially vibrating surface, taking account of friction. Sov. Phys.-Acoust. 1968, 13, 343–351. [Google Scholar]
- Skare, T.; Stahl, J.E. Static and dynamic friction processes under the influence of external vibrations. Wear 1992, 154, 177–192. [Google Scholar] [CrossRef]
- Mutuonga, S.; Onoda, J. New gravity compensation method by dither for low-g simulation. J. Spacecr. Rocket. 1995, 32, 364–369. [Google Scholar] [CrossRef]
- Littmann, W.; Stork, H.; Wallaschek, J. Sliding friction in the presence of ultrasonic oscillations: Superposition of longitudinal oscillations. Arch. Appl. Mech. 2001, 71, 549–554. [Google Scholar] [CrossRef]
- Littmann, W.; Stork, H.; Wallaschek, J. Reduction of friction using piezoelec-trically excited ultrasonic vibrations. In Proceedings of the SPIE’s 8th Annual International Symposium on Smart Structures and Material, Newport Beach, CA, USA, 2 July 2001; pp. 302–311. [Google Scholar]
- Stork, H.; Littmann, W.; Wallaschek, J.; Mracek, M. The effect of friction reduction in presence of ultrasonic vibrations and its relevance to travelling wave ultrasonic motors. Ultrasonics 2002, 40, 379–383. [Google Scholar] [CrossRef]
- Kumar, V.C.; Hutchings, I.M. Reduction of sliding friction of metals by the application of longitudinal or transverse ultrasonic vibration. Tribol. Int. 2004, 37, 833–840. [Google Scholar] [CrossRef]
- Dahl, P. A Solid Friction Model; Technical Report No. TOR-0158H3107-181-1; The Aerospace Corporation: El Segundo, CA, USA, 1968. [Google Scholar]
- Dahl, P. Solid friction damping of mechanical vibrations. AIAA J. 1976, 14, 1675–1682. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Dupont, P.; Armstrong, B.; Heyward, V. Elasto-plastic model contact compliance and stiction. In Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No.00CH36334), Chicago, IL, USA, 28–30 June 2000; IEEE: New York, NY, USA, 2000; Volume 6, pp. 1072–1077. [Google Scholar]
- Dupont, P.; Hayward, V.; Armstrong, B.; Altpeter, F. Single state elasto-plastic friction models. IEEE Trans. Autom. Control 2002, 47, 787–792. [Google Scholar] [CrossRef]
- Leus, M.; Gutowski, P. Analysis of longitudinal tangential contact vibration effect on friction force using Coulomb and Dahl models. J. Theor. Appl. Mech. 2008, 46, 171–184. [Google Scholar]
- Tsai, C.C.; Tseng, C.H. The effect of friction reduction in presence of in-plane vibrations. Arch. Appl. Mech. 2006, 75, 164–176. [Google Scholar] [CrossRef]
- Gutowski, P.; Leus, M. The effect of longitudinal tangential vibrations on friction and driving forces in sliding motion. Tribol. Int. 2012, 55, 108–118. [Google Scholar] [CrossRef]
- Gutowski, P.; Leus, M. Computational model for friction force estimation in sliding motion at transverse tangential vibrations of elastic contact support. Tribol. Int. 2015, 90, 455–462. [Google Scholar] [CrossRef]
- Wang, P.; Ni, H.; Wang, R.; Li, Z.; Wang, Y. Experimental investigation of the effect of in-plane vibrations on friction for different materials. Tribol. Int. 2016, 99, 237–247. [Google Scholar] [CrossRef]
- Valentin, L.P. Contact Mechanics and Friction: Physical Principles and Applications; Springer: Berlin, Germany, 2010. [Google Scholar]
- Pullen, J.; Williamson, J.B.P. On the plastic contact of rough surfaces. Proc. R. Soc. Lond. A 1972, 327, 159–173. [Google Scholar] [CrossRef]
- Ma, X.; De Rooij, M.; Schipper, D. A load dependent friction model for fully plastic contact conditions. Wear 2010, 269, 790–796. [Google Scholar] [CrossRef]
- Hol, J.; Meinders, V.T.; de Rooij, M.B.; van den Boogaard, A.H. Multi-scale friction modeling for sheet metal forming: The boundary lubrication regime. Tribol. Int. 2015, 81, 112–128. [Google Scholar] [CrossRef]
- Hokkirigawa, K.; Kato, K. An experimental and theoretical investigation of ploughing, cutting and wedge formation during abrasive wear. Tribol. Int. 1988, 21, 51–57. [Google Scholar] [CrossRef]
- Challen, J.M.; Oxley, P.L.B. An explanation of the different regimes of friction and wear using asperity deformation models. Wear 1979, 53, 229–243. [Google Scholar] [CrossRef]
- Hol, J. Multi-Scale Friction Modeling for Sheet Metal Forming. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]
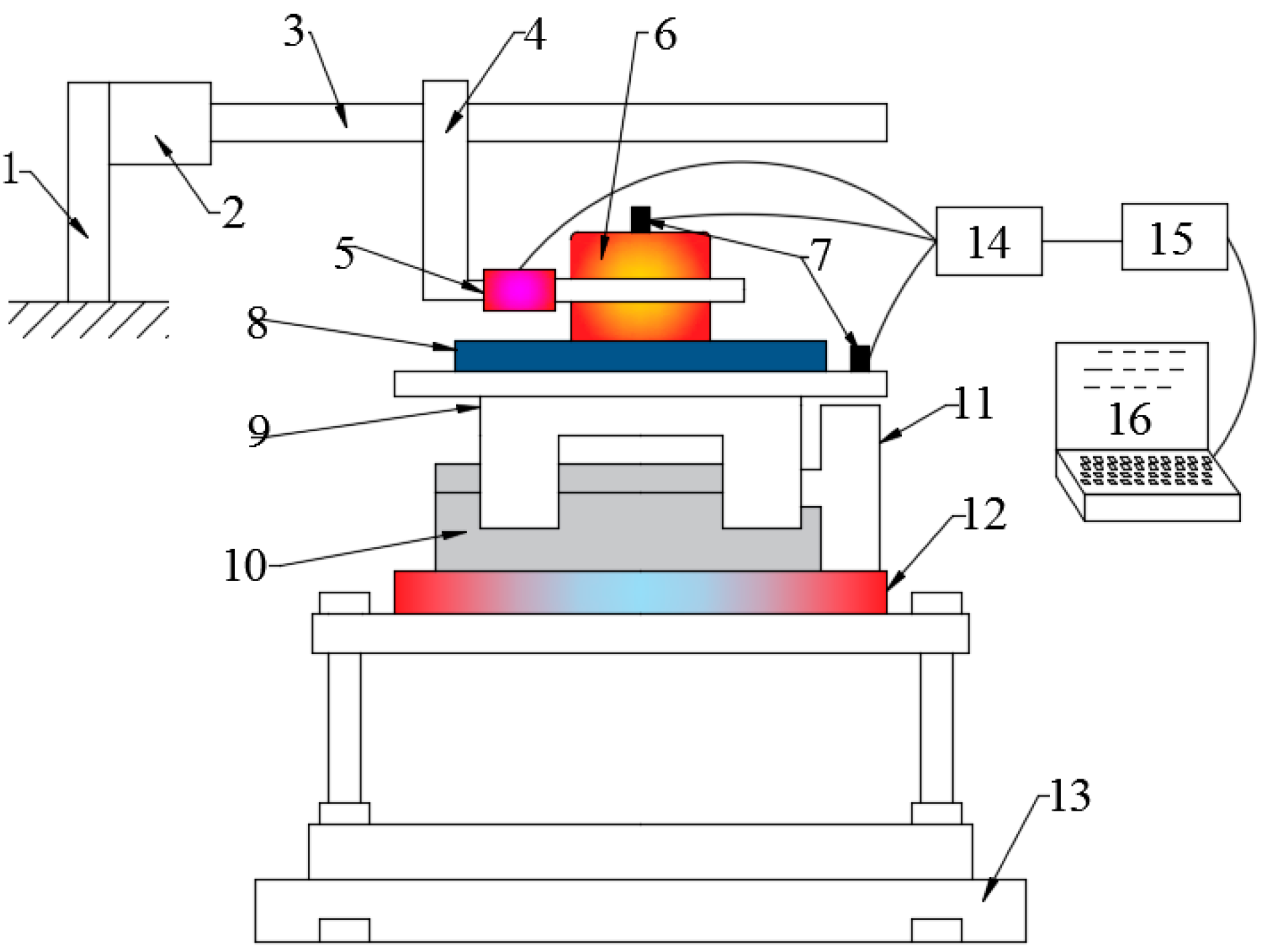

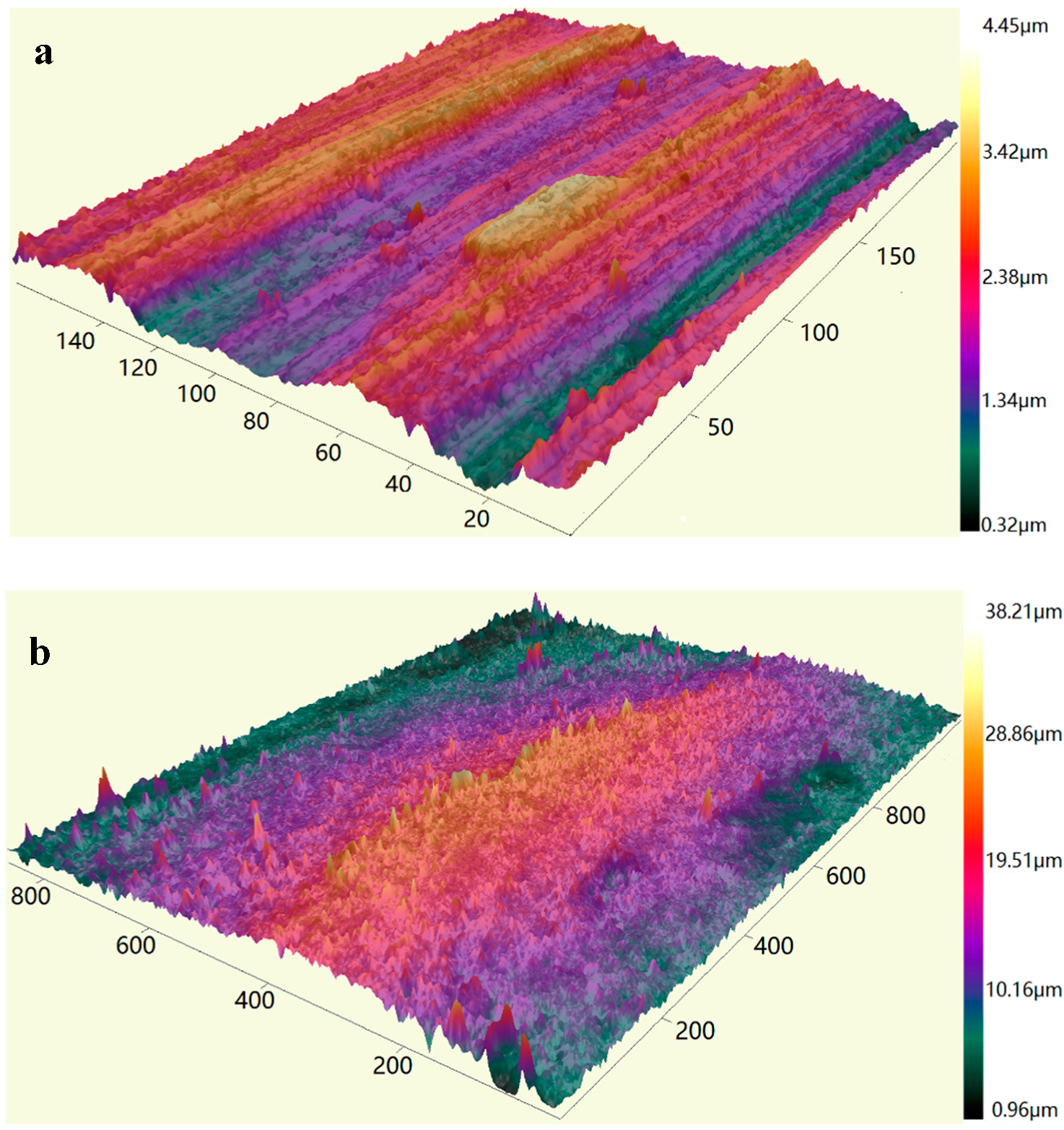

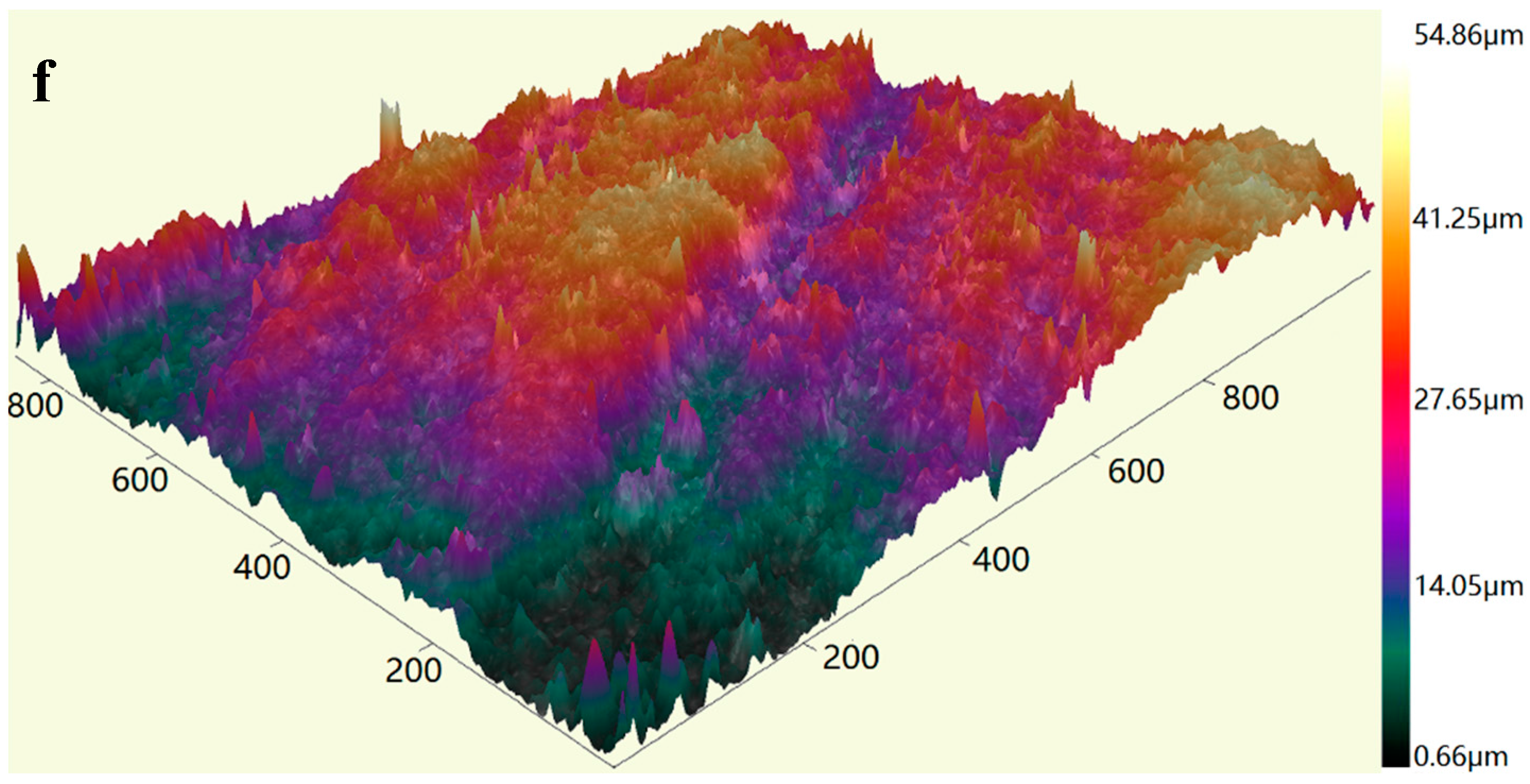







| Specimen | Measurement Area (μm) | Sampling Interval (μm) | Type of Filtering |
|---|---|---|---|
| a | 232.4 × 174.4 | 0.4 | median filter |
| b~f | 1161 × 869.4 | 1.8 |
| Material | Modulus of Elasticity (GPa) | Poisson’s Ratio | Hardness HB30 | Roughness (RMS) after Surface Finishing (Sandpaper 400) | ||
|---|---|---|---|---|---|---|
| Before Test | After Test | |||||
| Upper specimen | Alloyed steel | 206 | 0.30 | 380 | 0.83 | 2.57 |
| Bottom specimen | Alloyed steel | 1.2 | 3.42 | |||
| Sandstone | 40 | 0.25 | 226 | 5.38 | 4.28 | |
| Shale | 80 | 0.24 | 417 | 4.26 | 3.95 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Ni, H.; Wang, R.; Liu, W.; Lu, S. Research on the Mechanism of In-Plane Vibration on Friction Reduction. Materials 2017, 10, 1015. https://doi.org/10.3390/ma10091015
Wang P, Ni H, Wang R, Liu W, Lu S. Research on the Mechanism of In-Plane Vibration on Friction Reduction. Materials. 2017; 10(9):1015. https://doi.org/10.3390/ma10091015
Chicago/Turabian StyleWang, Peng, Hongjian Ni, Ruihe Wang, Weili Liu, and Shuangfang Lu. 2017. "Research on the Mechanism of In-Plane Vibration on Friction Reduction" Materials 10, no. 9: 1015. https://doi.org/10.3390/ma10091015
APA StyleWang, P., Ni, H., Wang, R., Liu, W., & Lu, S. (2017). Research on the Mechanism of In-Plane Vibration on Friction Reduction. Materials, 10(9), 1015. https://doi.org/10.3390/ma10091015




