Force Transmission Modes of Non-Cohesive and Cohesive Materials at the Critical State
Abstract
:1. Introduction
2. Discrete Element Modeling
2.1. Brief Introduction of the Discrete Element Method
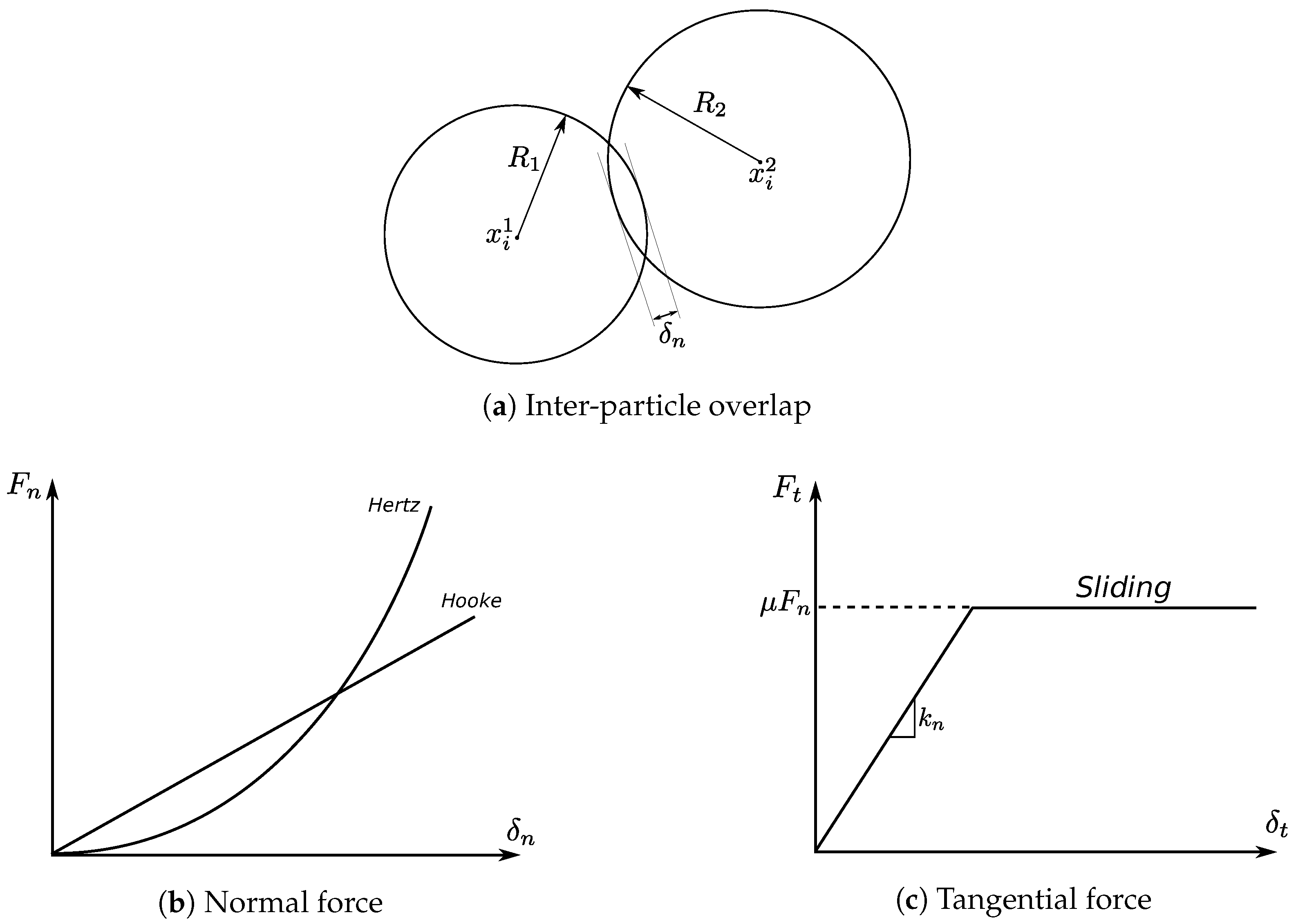
2.2. Linear Hooke’s Contact
2.3. Non-Linear Hertz Contact
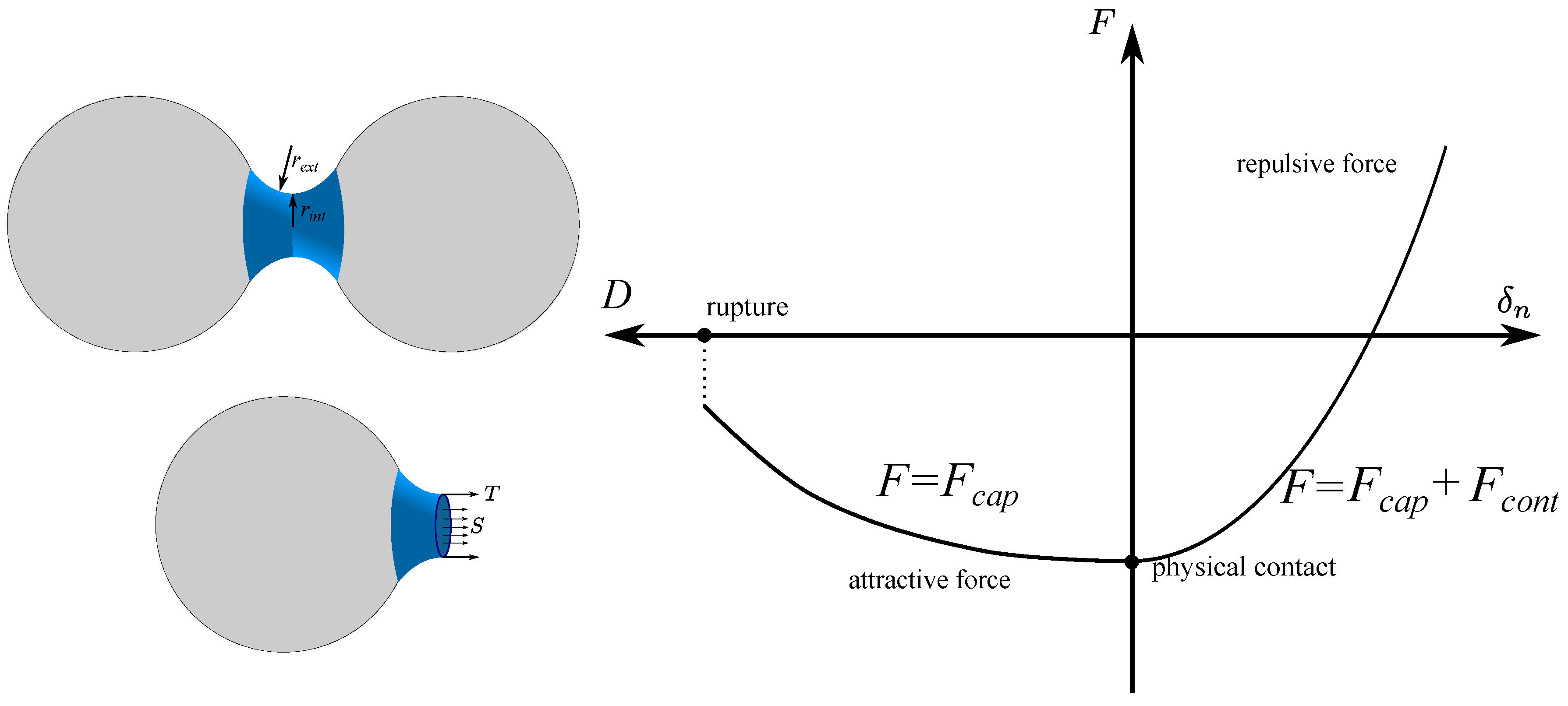
2.4. Capillary Bridge Model
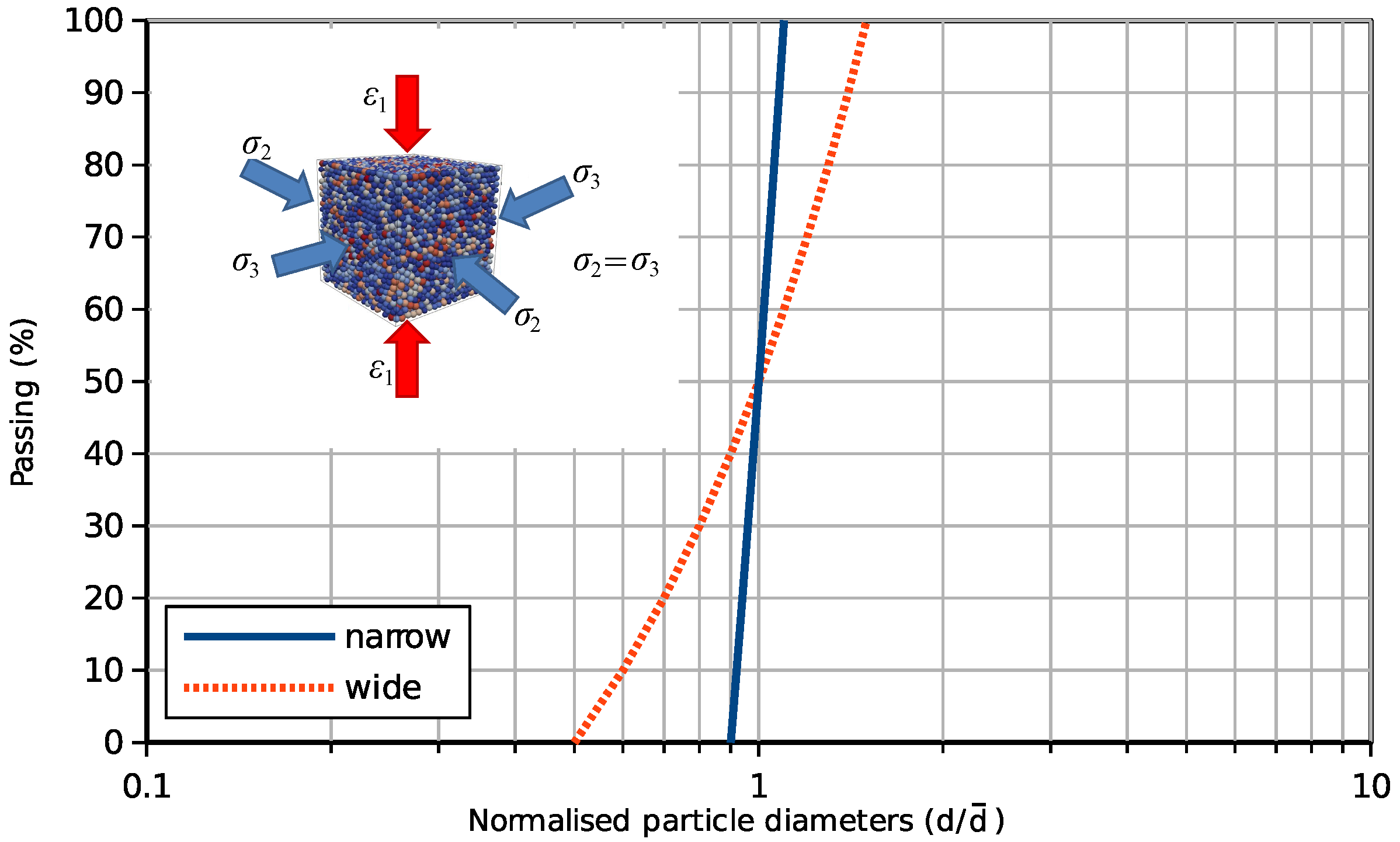
2.5. Model Parameters and Sample Preparation
3. Force Transmission of Dry Granular Materials
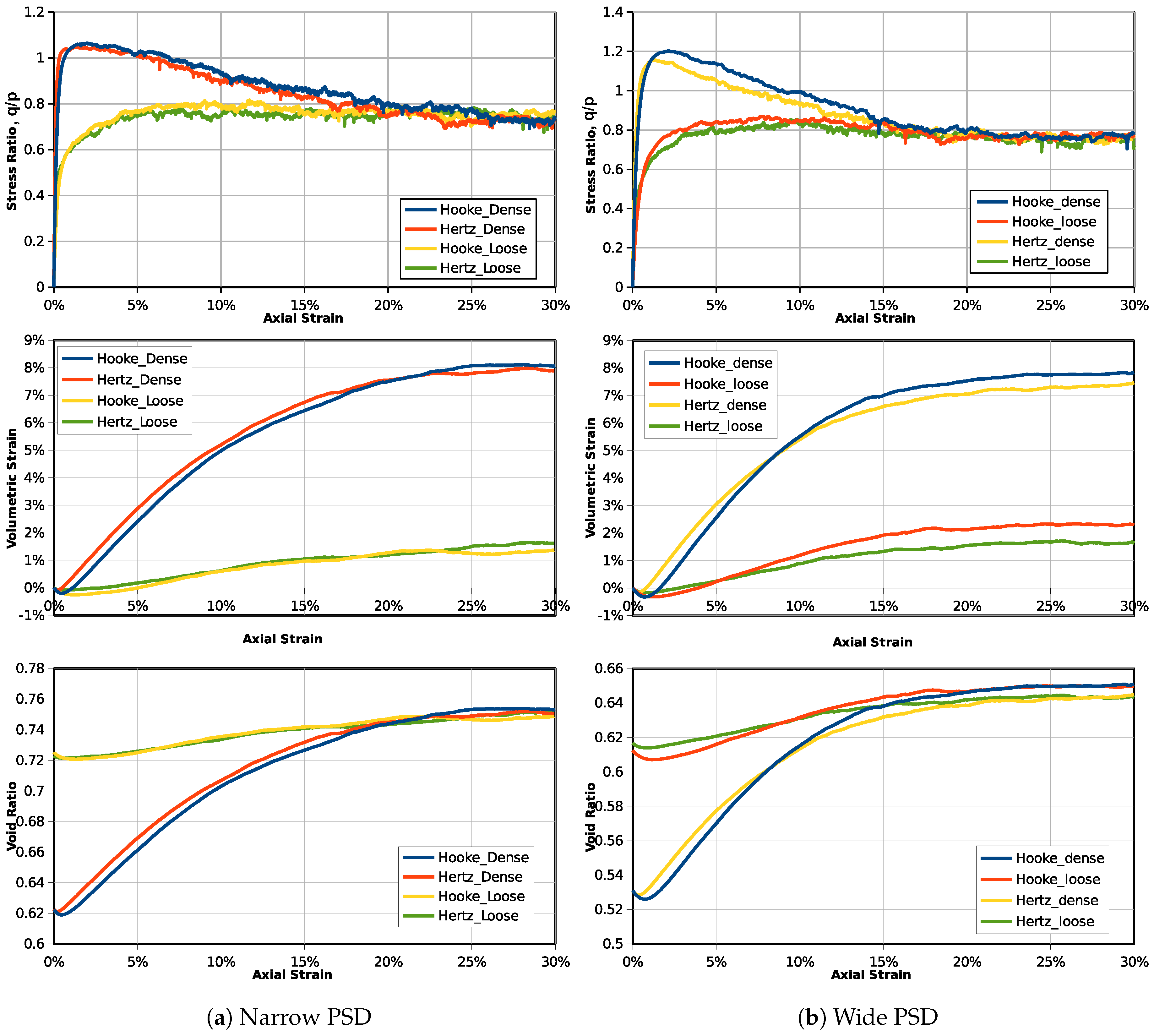
3.1. Triaxial Test from the Same Dimensionless Stress State
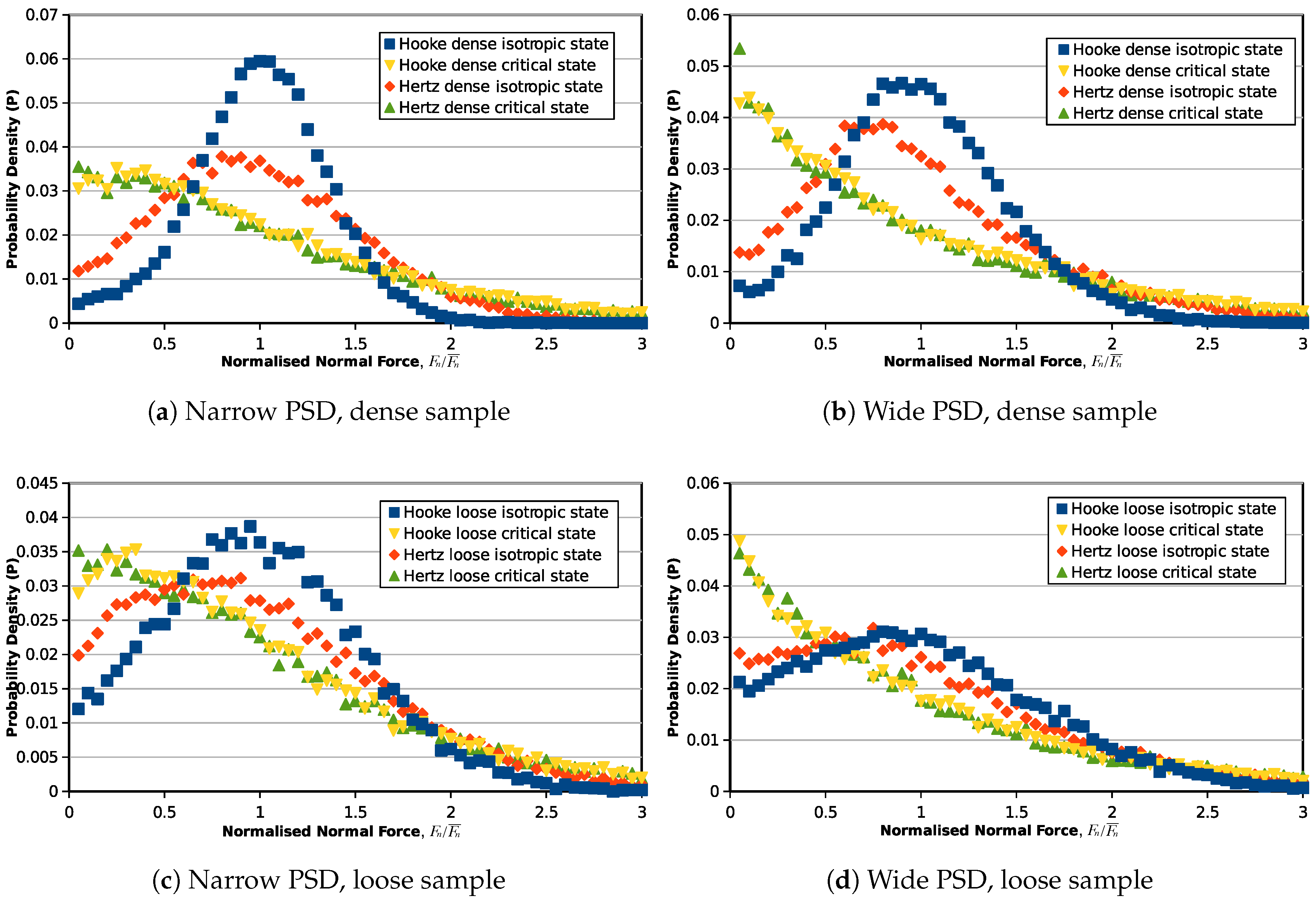
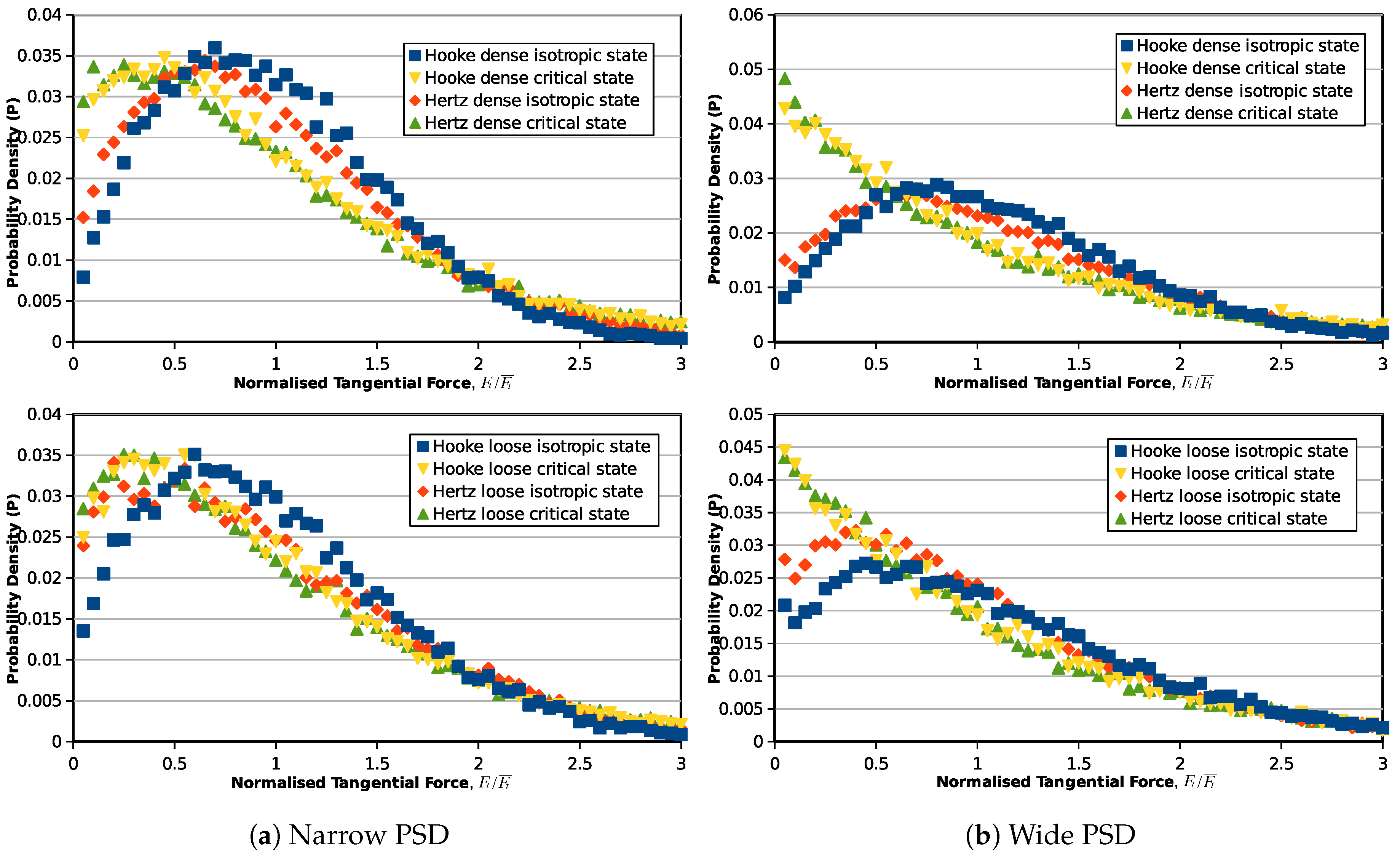
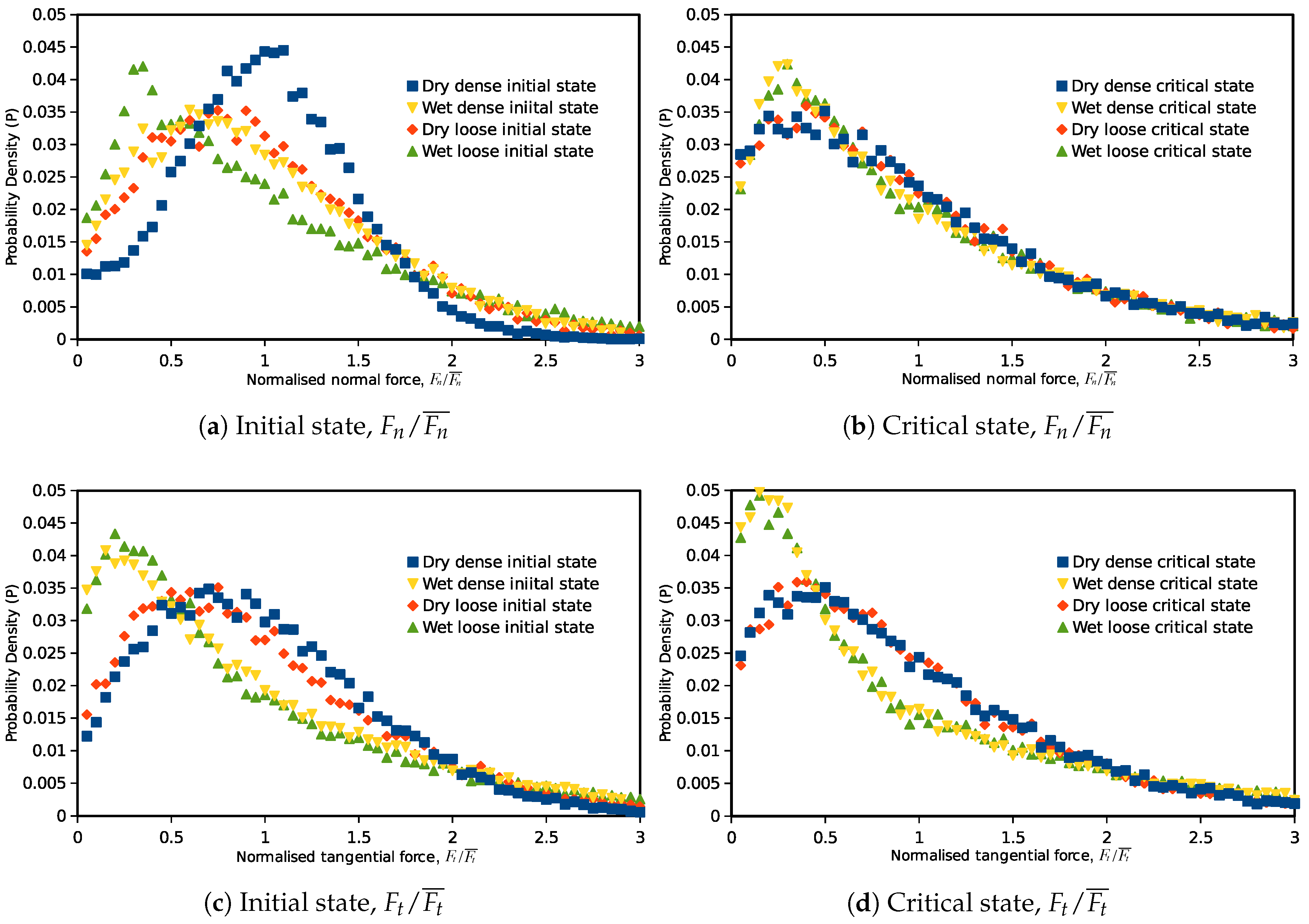
3.2. Probability Density Distribution of Overlaps and Forces
3.3. The Unique Force Transmission Pattern at the Critical State
4. Force Transmission of Wet Granular Materials
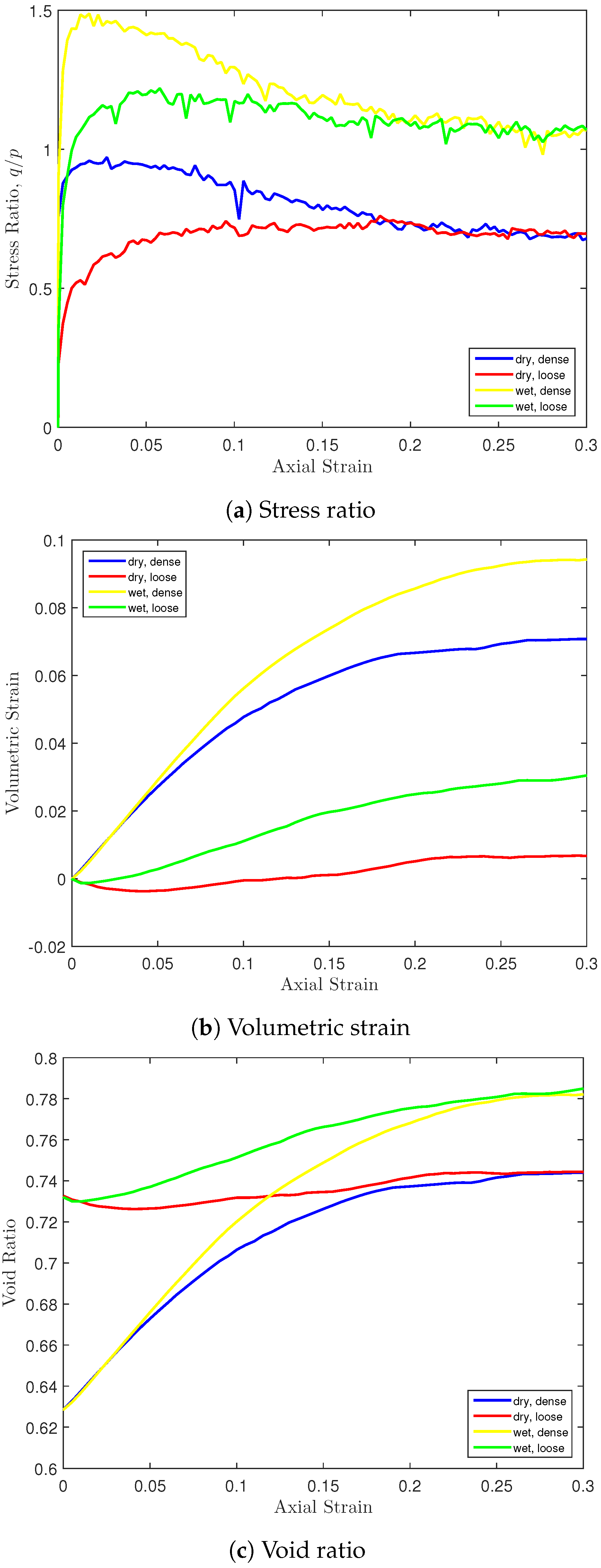
4.1. Capillary Effect on Mechanical Behaviors
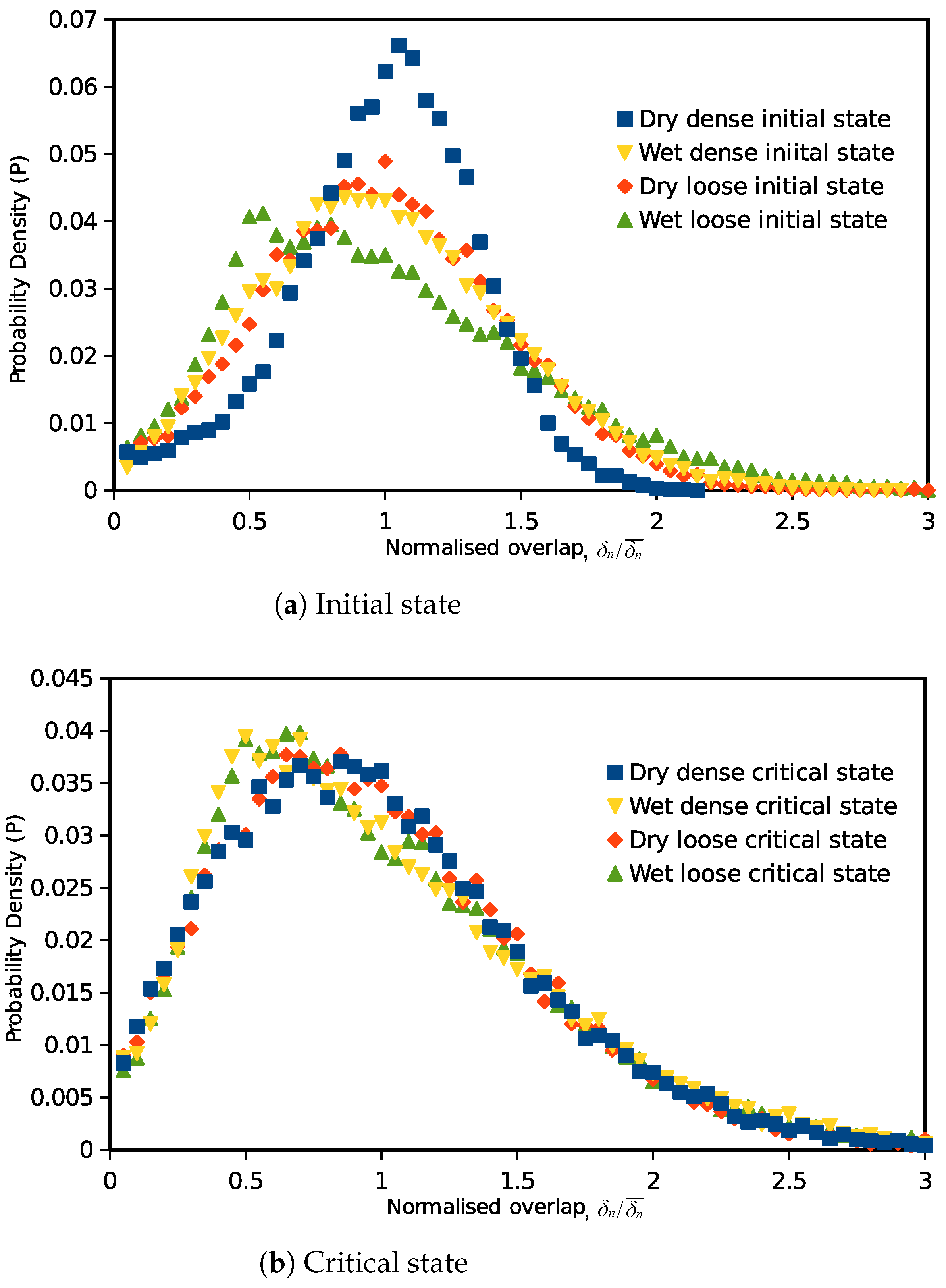
4.2. Force Transmission Pattern with Cohesive Capillary Effect
4.3. Capillary Effect on Stress Transmission
5. Conclusions
- Using either the Hooke or Hertz contact model does not alter the stress-strain behaviors of a specimen with a nearly mono-sized particle size distribution if it is sheared from the same dimensionless stress state. However, if the grain gradation becomes wider, discrepancies between these two models increase as the critical state void ratio of the Hooke model result is higher.
- At the initial state (isotropic state), both the inter-particle overlaps and inter-particle forces are in normal distributions. The void ratio and particle gradation may affect the width of the distribution. Additionally, when the material reaches the critical state, the probability of relatively weak forces (forces less than average) is increased.
- There is a unique critical state force transmission pattern for a non-cohesive granular material independent of the contact model. The normal and tangential force distributions can be formulated by a certain probability density function, which is only related to the grain size distribution.
- The material strength and dilatancy are higher than those of the non-cohesive material. The critical state also exists for a wet granular material, and the critical state stress ratio and void ratio are increased by the inter-particle attractive force.
- The cohesive force between particles alters the contact force distribution. There are more weak forces (forces less than the average force) in the cohesive materials at both the initial and ultimate states.
- Corresponding to the critical state strength and void ratio, the dense and loose materials have the same contact force distribution at the critical state. However, the distribution is different from those of non-cohesive samples, as the probability of weak forces is higher.
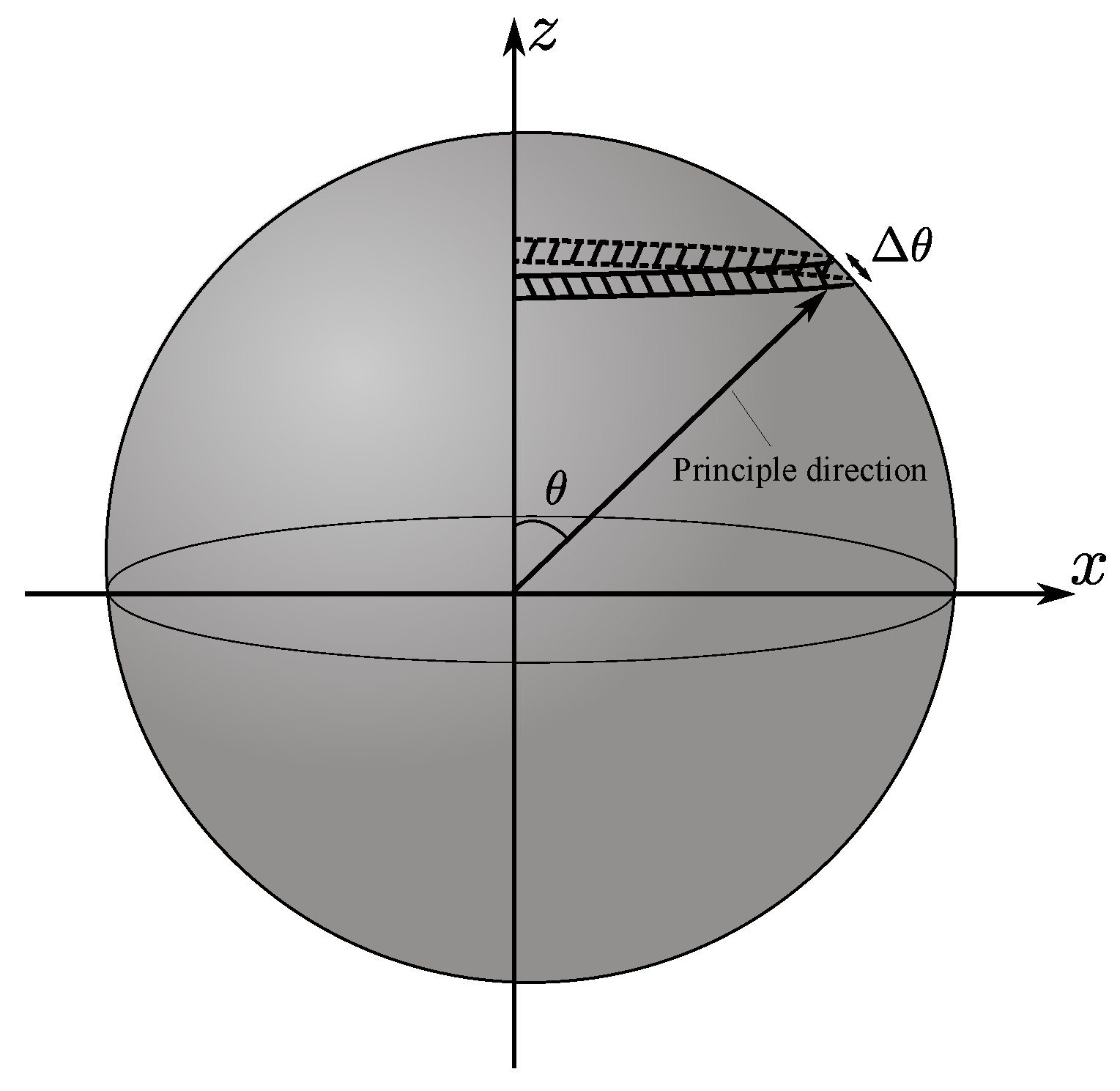
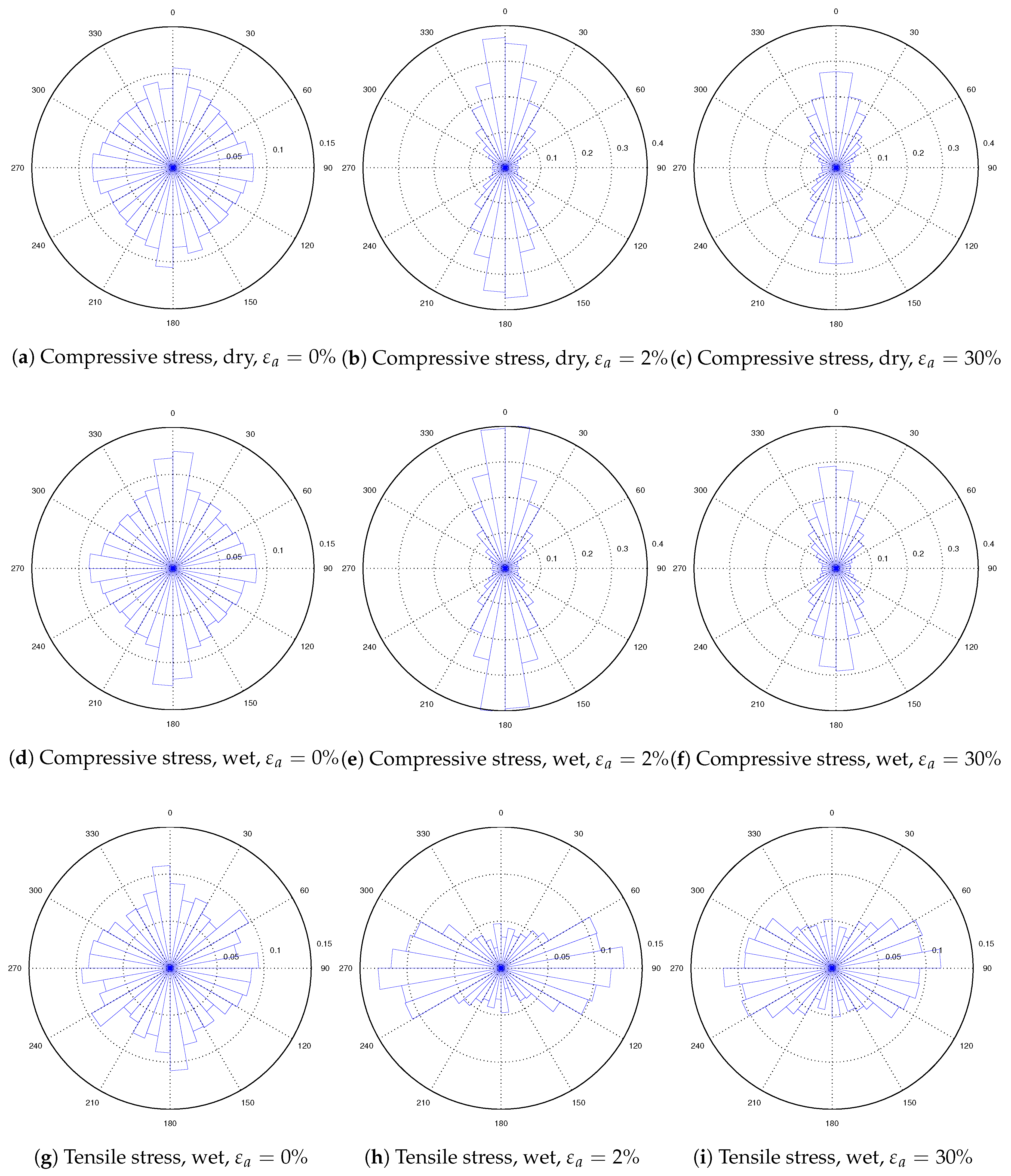
- Particles in non-cohesive materials are mainly under compressive stresses. However, in cohesive materials, some grains are in tensile stresses. Upon triaxial loading, the principal directions of compressive stresses are mainly in the axial direction, and the tensile stresses are acting in the horizontal plane. The additional confinement by the tensile stress increased the material strength and dilatancy.
Conflicts of Interest
References
- Drescher, A.; de Josselin de Jong, G. Photoelastic verification of a mechanical model for the flow of a granular material. J. Mech. Phys. Solids 1972, 20, 337–340. [Google Scholar] [CrossRef]
- Mueth, D.; Jaeger, H.; Nagel, S. Force distribution in a granular medium. Phys. Rev. E 1998, 57, 3164–3169. [Google Scholar] [CrossRef]
- Liu, C.H.; Nagel, S.R.; Schecter, D.A.; Coppersmith, S.N.; Majumdar, S.; Narayan, O.; Witten, T.A. Force Fluctuations in Bead Packs. Science 1995, 269, 513–515. [Google Scholar] [CrossRef] [PubMed]
- Ostojic, S.; Somfai, E.; Nienhuis, B. Scale invariance and universality of force networks in static granular matter. Nature 2006, 439, 828–830. [Google Scholar] [CrossRef] [PubMed]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Radjai, F.; Jean, M.; Moreau, J.; Roux, S. Force Distributions in Dense Two-Dimensional Granular Systems. Phys. Rev. Lett. 1996, 77, 274–277. [Google Scholar] [CrossRef] [PubMed]
- Thornton, C.; Antony, S. Quasi-static deformation of particulate media. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1998, 356, 2763–2782. [Google Scholar]
- Antony, S. Evolution of force distribution in three-dimensional granular media. Phys. Rev. E 2000, 63, 011302. [Google Scholar] [CrossRef] [PubMed]
- Antony, S.J. Link between single-particle properties and macroscopic properties in particulate assemblies: Role of structures within structures. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2007, 365, 2879–2891. [Google Scholar] [CrossRef] [PubMed]
- Schofield, A.; Wroth, P. Critical State Soil Mechanics; McGraw-Hill: London, UK, 1968. [Google Scholar]
- Luding, S. Cohesive, frictional powders: Contact models for tension. Granul. Matter 2008, 10, 235–246. [Google Scholar] [CrossRef]
- Richefeu, V.; El Youssoufi, M.; Radjaï, F. Shear strength properties of wet granular materials. Phys. Rev. E 2006, 73, 051304. [Google Scholar] [CrossRef] [PubMed]
- Soulié, F.; El Youssoufi, M.S.; Cherblanc, F.; Saix, C. Capillary cohesion and mechanical strength of polydisperse granular materials. Eur. Phys. J. E Soft Matter 2006, 21, 349–357. [Google Scholar] [CrossRef] [PubMed]
- Richefeu, V.; El Youssoufi, M.S.; Peyroux, R.; Radjaï, F. A model of capillary cohesion for numerical simulations of 3D polydisperse granular media. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1365–1383. [Google Scholar] [CrossRef]
- Scholtès, L.; Hicher, P.; Nicot, F.; Chareyre, B.; Darve, F. On the capillary stress tensor in wet granular materials. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 1289–1313. [Google Scholar] [CrossRef]
- Gabrieli, F.; Lambert, P.; Cola, S.; Calvetti, F. Micromechanical modeling of erosion due to evaporation in a partially wet granular slope. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 918–943. [Google Scholar] [CrossRef]
- Richefeu, V.; Radjaı, F.; El Youssoufi, M.S. Stress transmission in wet granular materials. Eur. Phys. J. E 2006, 21, 359–369. [Google Scholar] [CrossRef] [PubMed]
- Richefeu, V.; El Youssoufi, M.S.; Azéma, E.; Radjaï, F. Force transmission in dry and wet granular media. Powder Technol. 2009, 190, 258–263. [Google Scholar] [CrossRef]
- Wheeler, S.J.; Sivakumar, V. An elasto-plastic critical state framework for unsaturated soil. Géotechnique 1995, 45, 35–53. [Google Scholar] [CrossRef]
- Toll, D.G.; Ong, B.H. Critical-state parameters for an unsaturated residual sandy clay. Géotechnique 2003, 53, 93–103. [Google Scholar] [CrossRef]
- Toll, D.G.; Ali Rahman, Z. Critical state shear strength of an unsaturated artificially cemented sand. Géotechnique 2017, 67, 208–215. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A. Models, algorithms and validation for opensource DEM and CFD-DEM. Progress Comput. Fluid Dyn. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Hertz, H. Über die berührung fester elastischer körper. J. Reine Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Brilliantov, N.; Spahn, F.; Hertzsch, J.M.; Pöschel, T. Model for collisions in granular gases. Phys. Rev. E 1996, 53, 5382–5392. [Google Scholar] [CrossRef]
- Silbert, L.; Ertaş, D.; Grest, G.; Halsey, T.; Levine, D.; Plimpton, S. Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E 2001, 64, 051302. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.P.; Makse, H.A. Jamming transition in emulsions and granular materials. Phys. Rev. E 2005, 72, 011301. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.P. Discrete Element Modeling and Micromechanics of Pendular State Unsaturated Granular Materials. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2015. [Google Scholar]
- Wang, J.P.; Li, X.; Yu, H.S. A micro-macro investigation of the capillary strengthening effect in wet granular materials. Acta Geotech. 2017. submitted for publication. [Google Scholar]
- Mindlin, R. Compliance of Elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar]
- Wang, J.P.; Li, X.; Yu, H.S. Stress-Force-Fabric Relationship for Unsaturated Granular Materials in Pendular States. J. Eng. Mech. 2017, 143, 04017068. [Google Scholar] [CrossRef]
- Wang, J.P.; Gallo, E.; François, B.; Gabrieli, F.; Lambert, P. Capillary force and rupture of funicular liquid bridges between three spherical bodies. Powder Technol. 2017, 305, 89–98. [Google Scholar] [CrossRef]
- Hotta, K.; Takeda, K.; Iinoya, K. The capillary binding force of a liquid bridge. Powder Technol. 1974, 10, 231–242. [Google Scholar] [CrossRef]
- Rothenburg, L.; Bathurst, R.J. Micromechanical features of granular assemblies with planar elliptical particles. Géotechnique 1992, 42, 79–95. [Google Scholar] [CrossRef]
- Jiang, M.; Konrad, J.; Leroueil, S. An efficient technique for generating homogeneous specimens for DEM studies. Comput. Geotech. 2003, 30, 579–597. [Google Scholar] [CrossRef]
- Cates, M.; Wittmer, J.; Bouchaud, J.P.; Claudin, P. Jamming, Force Chains, and Fragile Matter. Phys. Rev. Lett. 1998, 81, 1841–1844. [Google Scholar] [CrossRef]
- Agnolin, I.; Roux, J.N. Internal states of model isotropic granular packings. I. Assembling process, geometry, and contact networks. Phys. Rev. E 2007, 76, 061302. [Google Scholar] [CrossRef] [PubMed]
- Padbidri, J.M.; Mesarovic, S.D. Acceleration of DEM algorithm for quasistatic processes. Int. J. Numer. Methods Eng. 2011, 86, 816–828. [Google Scholar] [CrossRef]
- Yousefi, A.; Ng, T.T. Dimensionless input parameters in discrete element modeling and assessment of scaling techniques. Comput. Geotech. 2017, 88, 164–173. [Google Scholar] [CrossRef]
- Coppersmith, S.N.; Liu, C.H.; Majumdar, S.; Narayan, O.; Witten, T.A. Model for force fluctuations in bead packs. Phys. Rev. E 1996, 53, 4673–4685. [Google Scholar] [CrossRef]
- Christoffersen, J.; Mehrabadi, M.M.; Nemat-Nasser, S. A Micromechanical Description of Granular Material Behavior. J. Appl. Mech. 1981, 48, 339. [Google Scholar] [CrossRef]


| RVE Length | (mm) | (kg/m) | Contact Model | Other Parameters | |||
|---|---|---|---|---|---|---|---|
| 0.02 | 0.5 | 2500 | Hertz (dry and wet) | E (GPa) | |||
| 70 | 0.25 | 0.2 | |||||
| Hooke (dry) | (N/m) | (N/m) | and | ||||
| 0.7 | |||||||
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.-P. Force Transmission Modes of Non-Cohesive and Cohesive Materials at the Critical State. Materials 2017, 10, 1014. https://doi.org/10.3390/ma10091014
Wang J-P. Force Transmission Modes of Non-Cohesive and Cohesive Materials at the Critical State. Materials. 2017; 10(9):1014. https://doi.org/10.3390/ma10091014
Chicago/Turabian StyleWang, Ji-Peng. 2017. "Force Transmission Modes of Non-Cohesive and Cohesive Materials at the Critical State" Materials 10, no. 9: 1014. https://doi.org/10.3390/ma10091014
APA StyleWang, J.-P. (2017). Force Transmission Modes of Non-Cohesive and Cohesive Materials at the Critical State. Materials, 10(9), 1014. https://doi.org/10.3390/ma10091014





