Measurement Techniques of the Magneto-Electric Coupling in Multiferroics
Abstract
1. Introduction
2. Measurement Issues
3. Magneto-Electric Coupling Coefficient
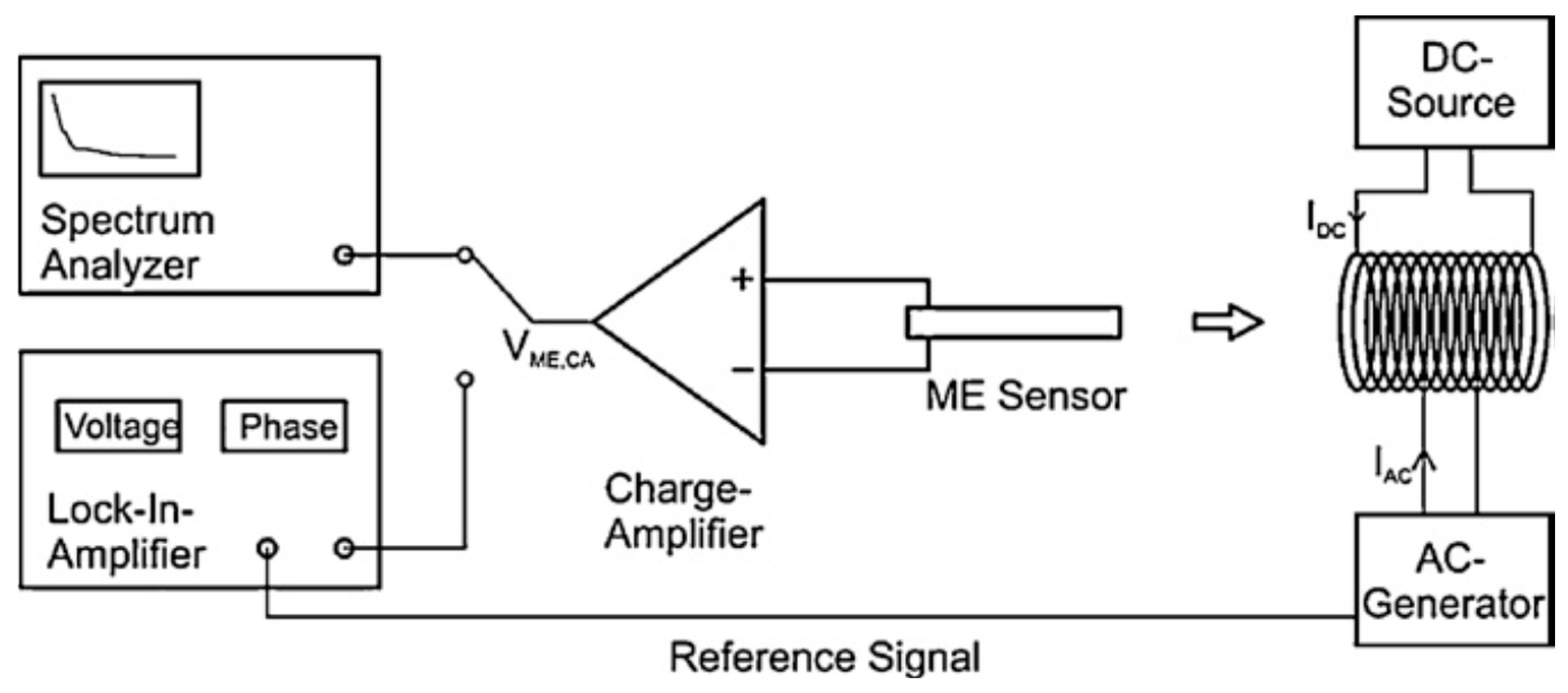
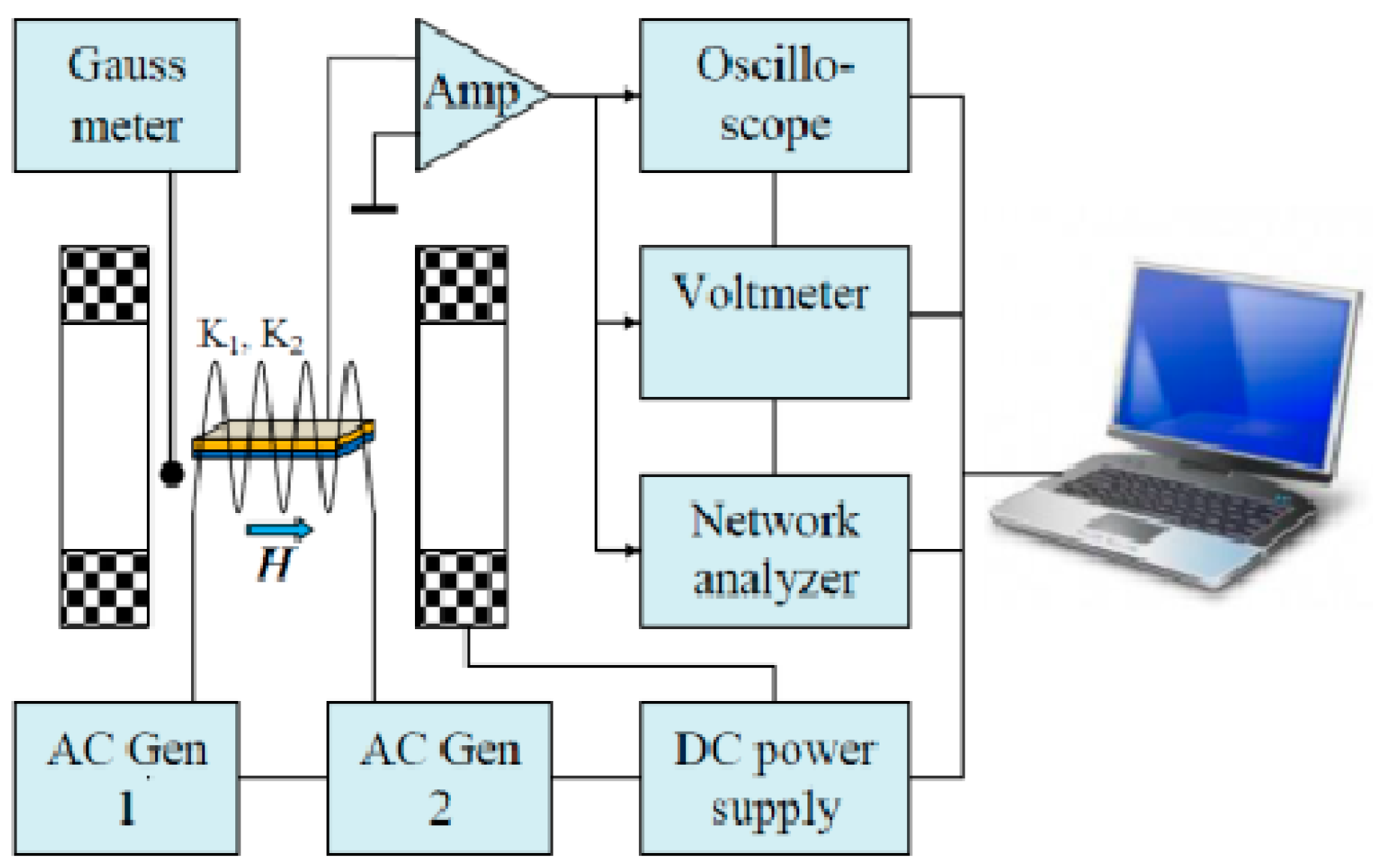
4. Measurement of Magnetically Induced Magneto-Electric Coupling
- (a)
- Bias the multiferroic sample under an optimal DC magnetic field bias;
- (b)
- Apply an AC magnetic field of fixed frequency and amplitude at 0 or π angle, or any non-transverse direction, to the DC magnetic bias field [24];
- (c)
- Measure the voltage response output of the multiferroic at various amplitudes of the applied AC magnetic field, at fixed DC magnetic bias and fixed frequency of the AC field;
- (d)
- Plot the measured voltages as a function of the amplitude of the applied AC magnetic fields;
- (e)
- From the obtained linear graph, as predicted by Equation (13), the magneto-electric coupling coefficient is determined as the slope of the graph divided by the thickness of the dielectric.
5. Measurement of Electrically Induced Magneto-Electric Coupling
- (a)
- Place the multiferroic sample in a suitable magnetometer;
- (b)
- Under zero applied magnetic field, excite the sample with an AC electric field/voltage of fixed frequency;
- (c)
- Measure the magnetization of the multiferroic sample at various amplitudes of the applied AC electric field/voltage;
- (d)
- Plot the measured M values as a function of the amplitude of the applied AC electric field/voltage;
- (e)
- From the obtained linear graph, as predicted by Equation (14), the magneto-electric coupling coefficient is determined as the slope of the graph if M = M(E), or the slope of the graph times the thickness of the dielectric if M = M(V) is measured;
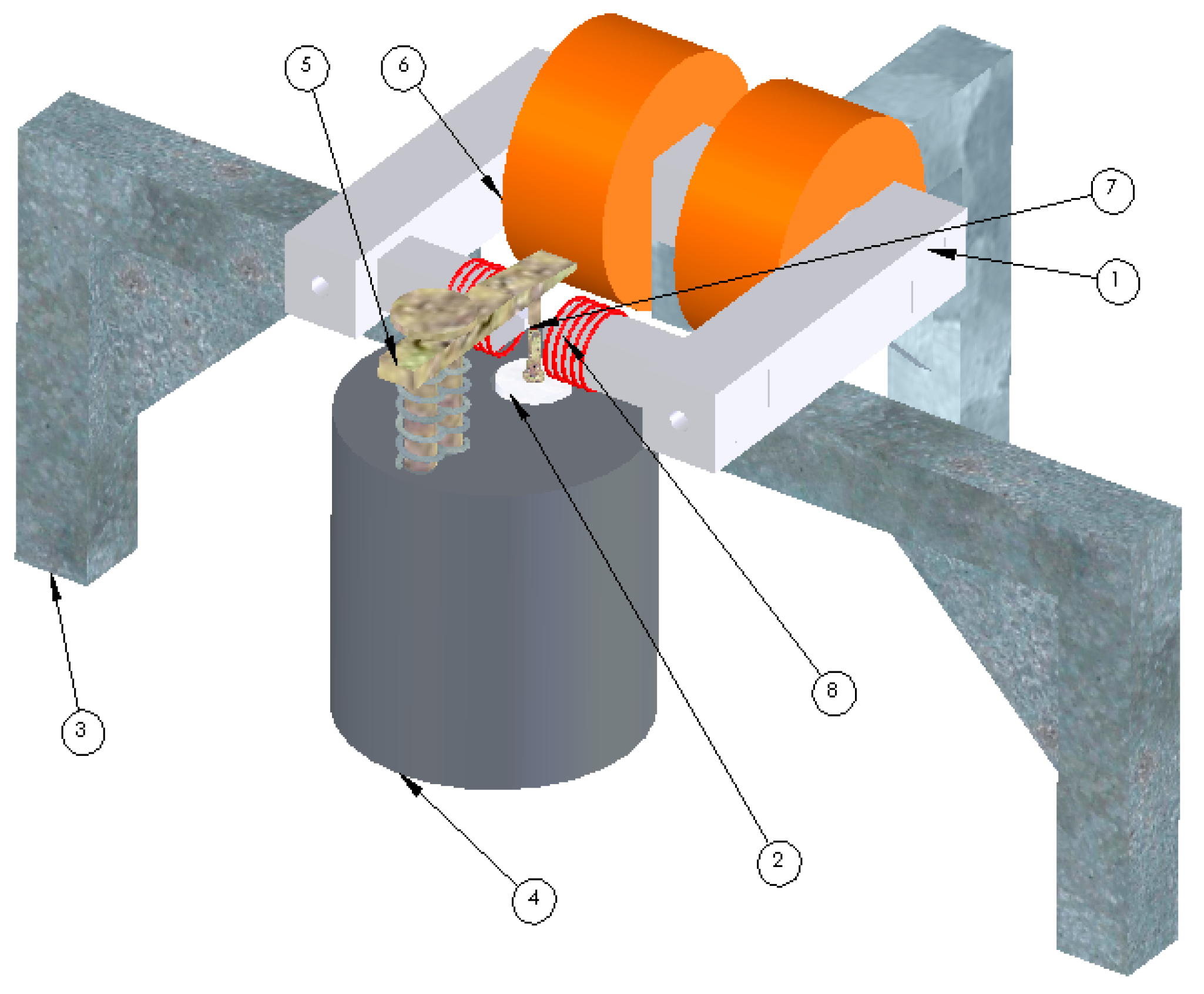
6. Measurement of Magneto-Electric Coupling from Piezo-Electric Measurements
- (a)
- Place the multiferroic sample in a suitable piezo-electric testing instrument;
- (b)
- The instrument must be modified to allow the simultaneous application of AC and DC magnetic fields to the sample;
- (c)
- Measure the piezo-electric coefficient at various amplitudes of the applied AC magnetic field at fixed DC optimum bias field;
- (d)
- Plot the piezo-electric coefficient values as a function of the amplitude of the AC magnetic field;
- (e)
- From the slope of the linear graph, determine the magneto-electric coupling coefficient using either Equation (18) or (20), depending whether the experimental conditions are short-circuit or open-circuit.
7. Measurement of Magneto-Electric Coupling via Scanning Probe Microscopy
8. Measurement of Magneto-Electric Coupling via Frequency Mixing/Conversion
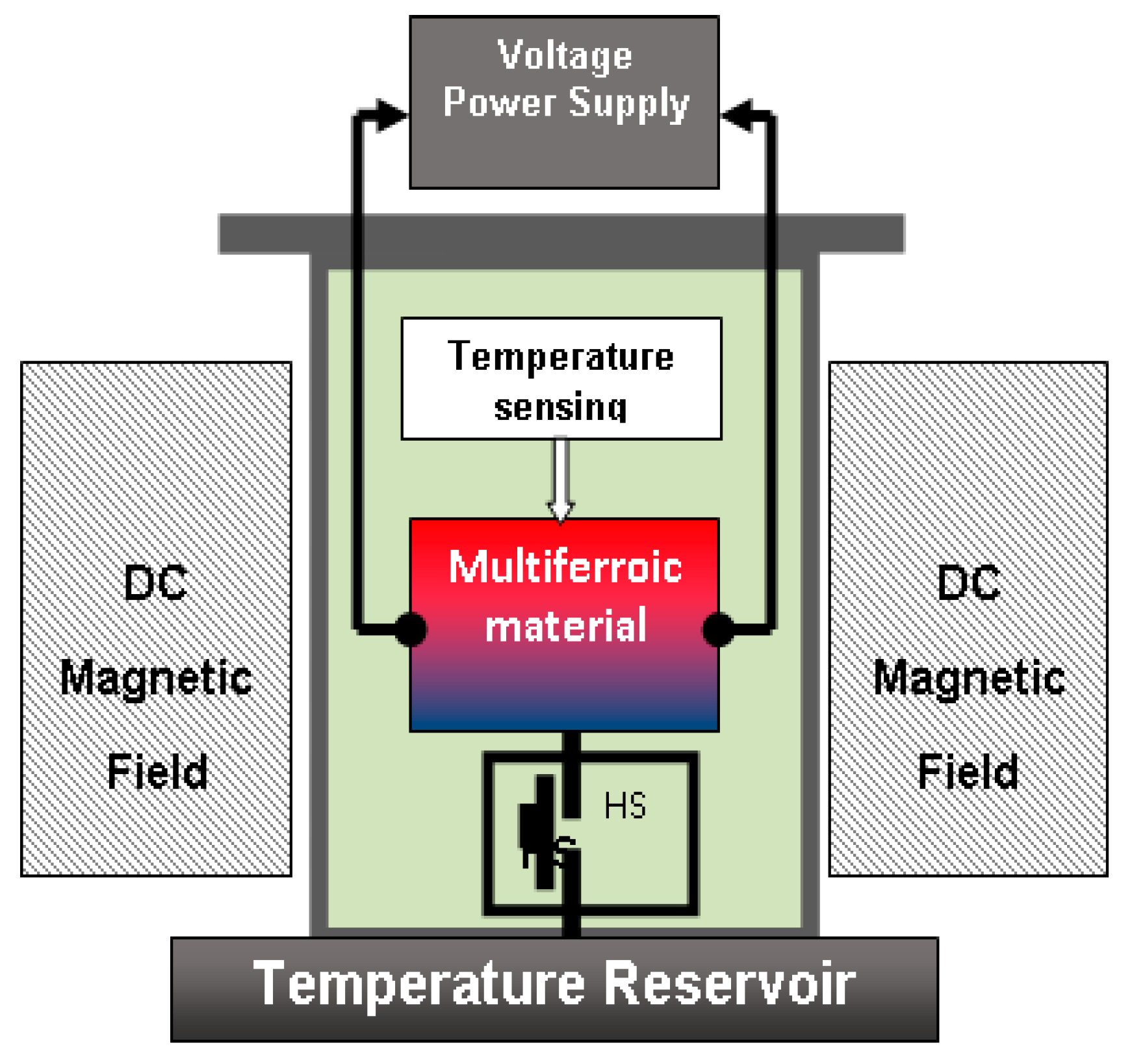
9. Measurement of Magneto-Electric Coupling from Thermal Measurements
- (a)
- Place the multiferroic sample in vacuum chamber in adiabatic conditions;
- (b)
- The instrument must be capable to apply magnetic field and electric fields to the sample, as well as to measure accurately the temperature change of the sample;
- (c)
- A temperature reservoir can be set at a desired operating temperature and then brought in contact with the multiferroic sample via a thermal switch;
- (d)
- Apply a large E field to the sample;
- (e)
- While the E field is ON, if Tcm > Tce, choose the operating temperature T = Tce and bring the sample at T = Tce via the thermal switch;
- (f)
- Cut the thermal link to the reservoir;
- (g)
- Reduce the E applied field to zero;
- (h)
- Measure the temperature change ΔTE;
- (i)
- Bring the sample back to the operating temperature T = Tce;
- (j)
- Apply a large magnetic field and then bring the sample to adiabatic conditions;
- (k)
- Reduce the applied magnetic field to zero and measure the temperature change ΔTH;
- (l)
- Use Equation (34) to derive the magnetically induced magneto-electric coupling coefficient.
- (m)
- If Tcm < Tce, choose the operating temperature T = Tcm and repeat the above procedure;
- (n)
- Extract the electrically induced magneto-electric coupling coefficient using Equation (35).
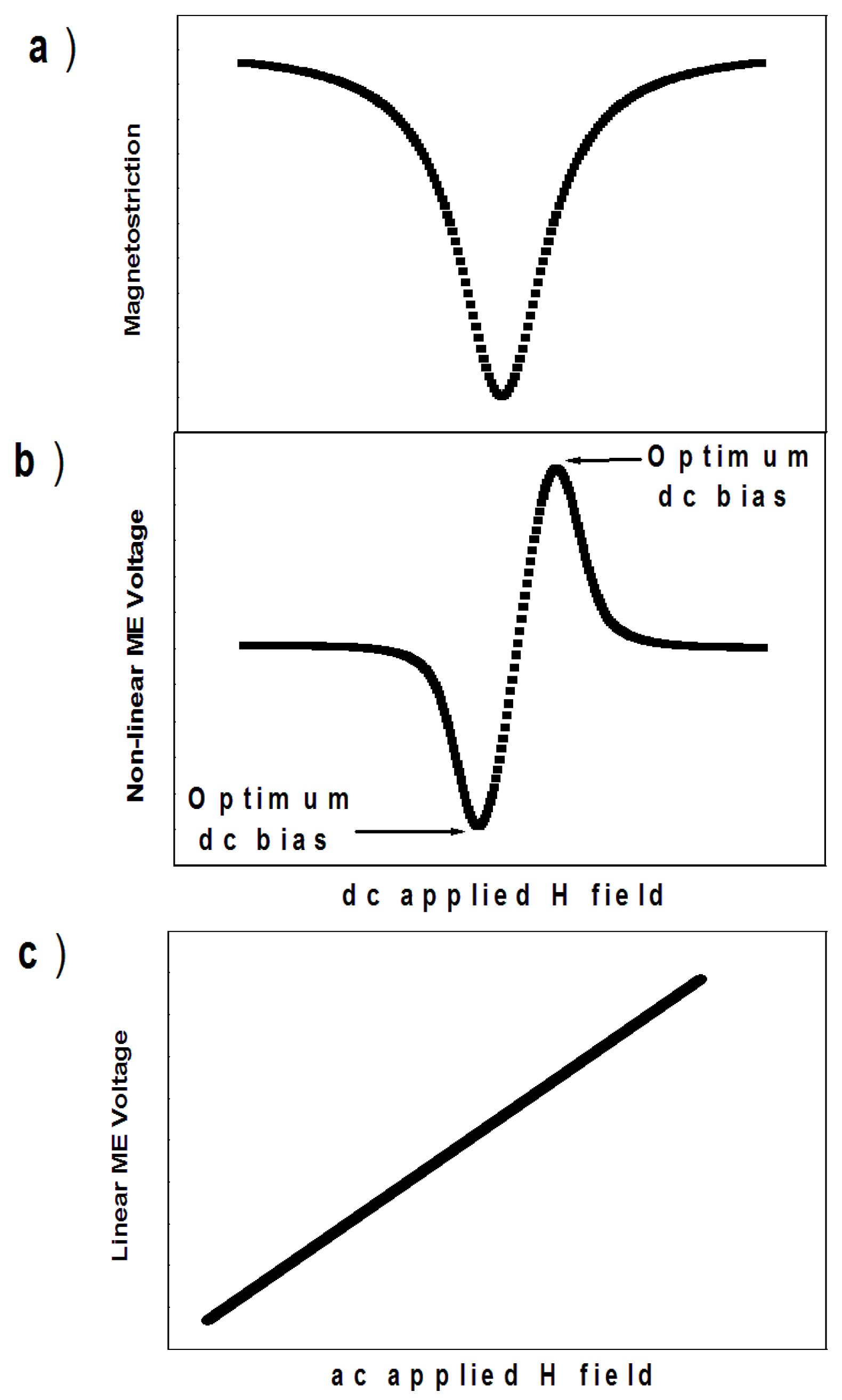
10. Measurement of Non-Linear Magneto-Electric Coupling Coefficients
- (1)
- The standard linear magneto-electric coupling coefficients (units of V/cm⋅Oe):
- (2)
- The non-linear magneto-electric coupling due to the frequency doubling voltage component (units of V/cm⋅Oe2):
- (3)
- The non-linear magneto-electric coupling due to the frequency mixing voltage component (units of V/cm⋅Oe2):
11. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Prellier, W.; Singh, M.P.; Murugavel, P. The single-phase multiferroic oxides: From bulk to thin film. J. Phys Condens. Matter 2005, 17, R803–R832. [Google Scholar] [CrossRef]
- Hill, N.A. Why Are There so Few Magnetic Ferroelectrics? J. Phys. Chem. B 2000, 104, 6694–6709. [Google Scholar] [CrossRef]
- Khomskii, D. Classifying multiferroics: Mechanisms and effects. Physics 2009, 2, 20. [Google Scholar] [CrossRef]
- Eerenstein, W.; Mathur, N.D.; Scott, J.F. Multiferroic and magnetoelectric materials. Nature 2006, 442, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Picozzi, S.; Yamauchi, K.; Sergienko, I.A.; Sen, C.; Sanyal, B.; Dagotto, E. Microscopic mechanisms for improper ferroelectricity in multiferroic perovskites: A theoretical review. J. Phys. Condens. Matter 2008, 20, 434208. [Google Scholar] [CrossRef]
- Srinivasan, G. Magnetoelectric composites. Ann. Rev. Mater. Res. 2010, 40, 153–178. [Google Scholar] [CrossRef]
- Nan, C.W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Lin, Y.; Nan, C.-W. Multiferroic magnetoelectric composite nanostructures. NPG Asia Mater. 2010, 2, 61–68. [Google Scholar] [CrossRef]
- Zhai, J.; Xing, Z.; Dong, S.; Li, J.; Viehland, D. Magnetoelectric Laminate Composites: An Overview. J. Am. Ceram. Soc. 2008, 91, 351–358. [Google Scholar] [CrossRef]
- Vopson, M.M. Fundamentals of Multiferroic Materials and Their Possible Applications. Crit. Rev. Solid State Mater. Sci. 2015, 40, 223–250. [Google Scholar] [CrossRef]
- Van Suchtelen, J. Product properties: A new application of composite materials. Philips Res. Rep. 1972, 27, 28–37. [Google Scholar]
- Boomgard, J.; Terrell, D.R.; Born, R.A.J.; Giller, H.F.J.I. An in situ grown eutectic magnetoelectric composite material. J. Mater. Sci. 1974, 9, 1710–1714. [Google Scholar]
- Boomgard, J.; Run, A.M.J.G.; Suchtelen, J. Magnetoelectricity in Piezoelectric-Magnetostrictive Composites. Ferroelectrics 1976, 10, 295–298. [Google Scholar] [CrossRef]
- Boomgard, J.; Born, R.A.J. A sintered magnetoelectric composite material BaTiO3–Ni(Co,Mn)Fe3O4. J. Mater. Sci. 1978, 13, 1538–1548. [Google Scholar] [CrossRef]
- Kimura, T.; Goto, T.; Shintani, H.; Ishizaka, K.; Arima, T.; Tokura, Y. Magnetic control of ferroelectric polarization. Nature 2003, 426, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Zurbuchen, M.A.; Wu, T.; Saha, S.; Mitchell, J.; Streiffer, S.K. Multiferroic composite ferroelectric-ferromagnetic films. Appl. Phys. Lett. 2005, 87, 232908. [Google Scholar] [CrossRef]
- Bennett, S.P.; Wong, A.T.; Glavic, A.; Herklotz, A.; Urban, C.; Valmianski, I.; Lauter, V. Giant Controllable Magnetization Changes Induced by Structural Phase Transitions in a Metamagnetic Artificial Multiferroic. Sci. Rep. 2016, 6, 22708. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.K.; Nath, T.K.; Eom, C.B.; Smoak, M.C.; Tsui, F. Strain modification of epitaxial perovskite oxide thin films using structural transitions of ferroelectric BaTiO3 substrate. Appl. Phys. Lett. 2000, 77, 3547. [Google Scholar] [CrossRef]
- Fiebeg, M.; Lottermoser, T.; Frohlich, D.; Goltsev, A.V.; Pisarev, R.V. Observation of coupled magnetic and electric domains. Lett. Nat. 2002, 419, 818–820. [Google Scholar] [CrossRef] [PubMed]
- Lottermoser, T.; Fiebig, M. Magnetoelectric behavior of domain walls in multiferroic HoMnO3. Phys. Rev. B 2004, 70, 220407. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123. [Google Scholar] [CrossRef]
- Lawes, G.; Srinivasan, G. Introduction to magnetoelectric coupling and multiferroic films. J. Phys. D Appl. Phys. 2011, 44, 243001. [Google Scholar] [CrossRef]
- Rivera, J.P. On definitions, units, measurements, tensor forms of the linear magnetoelectric effect and on a new dynamic method applied to Cr-Cl boracite. Ferroelectrics 1994, 161, 165–180. [Google Scholar] [CrossRef]
- Fetisov, Y.K.; Bush, A.A.; Kamentsev, K.E.; Ostashchenko, A.Y.; Srinivasan, G. Ferrite-Piezoelectric Multilayers for Magnetic Field Sensors. IEEE Sens. J. 2006, 6, 935–938. [Google Scholar] [CrossRef]
- Jahns, R.; Piorra, A.; Lage, E.; Kirchhof, C.; Meyners, D.; Gugat, J.L.; Krantz, M.; Gerken, M.; Knöchel, R.; Quandt, E. Giant Magnetoelectric Effect in Thin-Film Composites. J. Am. Ceram. Soc. 2013, 96, 1673–1681. [Google Scholar] [CrossRef]
- Ryu, J.; Priya, S.; Carazo, A.V.; Uchino, K.; Kim, H.E. Effect of the Magnetostrictive Layer on Magnetoelectric Properties in Lead Zirconate Titanate/Terfenol-D Laminate Composites. J. Am. Chem. Soc. 2001, 84, 2905–2908. [Google Scholar] [CrossRef]
- Dong, S.X.; Li, J.F.; Viehland, D. Ultrahigh magnetic field sensitivity in laminates of TERFENOL-D and Pb(Mg1/3Nb2/3)O3–PbTiO3 crystals. Appl. Phys. Lett. 2003, 83, 2265. [Google Scholar] [CrossRef]
- Nan, C.W.; Li, M.; Huang, J.H. Calculations of giant magnetoelectric effects in ferroic composites of rare-earth–iron alloys and ferroelectric polymers. Phys. Rev. B 2001, 63, 144415. [Google Scholar] [CrossRef]
- Ryu, J.; Carazo, A.V.; Uchino, K.; Kim, H.E. Magnetoelectric Properties in Piezoelectric and Magnetostrictive Laminate Composites. Jpn. J. Appl. Phys. 2001, 40, 4948. [Google Scholar] [CrossRef]
- Mori, K.; Wuttig, M. Magnetoelectric coupling in Terfenol-D/polyvinylidenedifluoride composites. Appl. Phys. Lett. 2002, 81, 100. [Google Scholar] [CrossRef]
- Vopsaroiu, M.; Stewart, M.; Fry, T.; Cain, M.; Srinivasan, G. Tuning the magneto-electric effect of multiferroic composites via crystallographic texture. IEEE Trans. Magn. 2008, 44, 3017–3020. [Google Scholar] [CrossRef]
- Dong, S.; Cheng, J.; Li, J.F.; Viehland, D. Enhanced magnetoelectric effects in laminate composites of Terfenol-D/Pb(Zr,Ti)O3 under resonant drive. Appl. Phys. Lett. 2003, 83, 4812. [Google Scholar] [CrossRef]
- Dong, S.; Li, J.F.; Viehland, D. Circumferentially magnetized and circumferentially polarized magnetostrictive/piezoelectric laminated rings. J. Appl. Phys. 2004, 96, 3382. [Google Scholar] [CrossRef]
- Dong, S.X.; Zhai, J.Y.; Bai, F.; Li, J.-F.; Viehland, D. Push-pull mode magnetostrictive/piezoelectric laminate composite with an enhanced magnetoelectric voltage coefficient. Appl. Phys. Lett. 2005, 87, 062502. [Google Scholar] [CrossRef]
- Vopsaroiu, M.; Cain, M.G.; Sreenivasulu, G.; Srinivasan, G.; Balbashov, A.M. Multiferroic composite for combined detection of static and alternating magnetic fields. Mater. Lett. 2012, 66, 282–284. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Xing, Z.; Dong, S.X.; Li, J.; Viehland, D. Detection of pico-Tesla magnetic fields using magneto-electric sensors at room temperature. Appl. Phys. Lett. 2006, 88, 062510. [Google Scholar] [CrossRef]
- Kirchhof, C.; Krantz, M.; Teliban, I.; Jahns, R.; Marauska, S.; Wagner, B.; Knochel, R.; Gerken, M.; Mayners, D.; Quandt, E. Giant magnetoelectric effect in vacuum. Appl. Phys. Lett. 2013, 102, 232905. [Google Scholar] [CrossRef]
- Jahns, R.; Greve, H.; Woltermann, E.; Quandt, E.; Knochel, R. Sensitivity enhancement of magnetoelectric sensors through frequency-conversion. Sens. Actuators A 2012, 183, 16–21. [Google Scholar] [CrossRef]
- Jahns, R.; Greve, H.; Woltermann, E.; Quandt, E.; Knochel, R. Noise Performance of Magnetometers with Resonant Thin-Film Magnetoelectric Sensors. IEEE Trans. Instrum. Meas. 2011, 60, 2995–3001. [Google Scholar] [CrossRef]
- Laletsin, U.; Padubnaya, N.; Srinivasan, G.; Devreugd, C.P. Frequency dependence of magnetoelectric interactions in layered structures of ferromagnetic alloys and piezoelectric oxides. Appl. Phys. A 2004, 78, 33–36. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, V.M.; Ryabkov, O.V.; Averkin, S.V.; Srinivasan, G. Theory of magnetoelectric effects at magnetoacoustic resonance in single-crystal ferromagnetic-ferroelectric heterostructures. Phys. Rev. B 2005, 72, 060408R. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, V.M.; Srinivasan, G. Theory of low-frequency magnetoelectric coupling in magnetostrictive-piezoelectric bilayers. Phys. Rev. B 2003, 68, 054402. [Google Scholar] [CrossRef]
- Blackburn, J.; Vopsaroiu, M.; Cain, M.G. Composite multiferroics as magnetic field detectors: How to optimize magneto-electric coupling. Adv. Appl. Ceram. 2010, 109, 169–174. [Google Scholar] [CrossRef]
- Kerr, J. On rotation of the plane of polarization by reflection from the pole of a magnet. Proc. R. Soc. Lond. 1876–1877, 25, 447–450. [Google Scholar] [CrossRef]
- Qui, Z.Q.; Bader, S.D. Surface magneto-optic Kerr effect. Rev. Sci. Instrum. 2000, 71, 1243. [Google Scholar] [CrossRef]
- Allwood, D.A.; Xiong, G.; Cooke, M.D.; Cowburn, R.P. Magneto-optical Kerr effect analysis of magnetic nanostructures. J. Phys. D Appl. Phys. 2003, 36, 2175–2182. [Google Scholar] [CrossRef]
- Thiele, C.; Dorr, K.; Bilani, O.; Rodel, J.; Schultz, L. Influence of strain on the magnetization and magnetoelectric effect in La0.7A0.3MnO3/PMN−PT(001) (A = Sr, Ca). Phys. Rev. B 2007, 75, 054408. [Google Scholar] [CrossRef]
- Ma, J.; Lin, Y.; Nan, C.W. Anomalous electric field-induced switching of local magnetization vector in a simple FeBSiC-on-Pb(Zr,Ti)O3 multiferroic bilayer. J. Phys. D Appl. Phys. 2010, 43, 012001. [Google Scholar] [CrossRef]
- He, X.; Wang, Y.; Wu, N.; Caruso, A.N.; Vescovo, E.; Belashchenko, K.D.; Dowben, P.A.; Binek, C. Robust Isothermal Electric Control of Exchange Bias at Room Temperature. Nat. Mater. 2010, 9, 579–585. [Google Scholar] [CrossRef] [PubMed]
- Borisov, P.; Hochstrat, A.; Chen, X.; Kleemann, W.; Binek, C. Magnetoelectric Switching of Exchange Bias. Phys. Rev. Lett. 2005, 94, 117203. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Hochstrat, A.; Borisov, P.; Kleemann, W. Magnetoelectric exchange bias systems in spintronics. Appl. Phys. Lett. 2006, 89, 202508. [Google Scholar] [CrossRef]
- Chiba, D.; Matsukura, F.; Ohno, H. Electric-field control of ferromagnetism in (Ga,Mn)As. Appl. Phys. Lett. 2006, 89, 162505. [Google Scholar] [CrossRef]
- Hu, J.M.; Li, Z.; Wang, J.; Nan, C.W. Electric-field control of strain-mediated magnetoelectric random access memory. J. Appl. Phys. 2010, 107, 093912. [Google Scholar] [CrossRef]
- Stolichnov, I.; Reister, S.W.E.; Trodahl, H.J.; Setter, N.; Rushforth, A.W.; Edmonds, K.W.; Campion, R.P.; Foxton, C.T.; Gallagher, B.L.; Jungwirth, T. Non-volatile ferroelectric control of ferromagnetism in (Ga,Mn)As. Nat. Mater. 2008, 7, 464–467. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, J.; Xiao, X.H.; Peng, T.C.; Jiang, C.Z.; Lin, Y.H.; Nan, C.W. Large reversible electric-voltage manipulation of magnetism in NiFe/BaTiO3 heterostructures at room temperature. J. Phys. D Appl. Phys. 2010, 43, 082002. [Google Scholar] [CrossRef]
- Sahoo, S.; Polisetty, S.; Duan, C.-G.; Jaswal, S.S.; Tsymbal, E.Y.; Binek, C. Ferroelectric control of magnetism in BaTiO3/Fe heterostructures via interface strain coupling. Phys. Rev. B 2007, 76, 092108. [Google Scholar] [CrossRef]
- Moutis, N.; Sandoval, D.S.; Niarchos, D. Voltage-induced modification in magnetic coercivity of patterned Co50Fe50 thin film on piezoelectric substrate. J. Magn. Magn. Mater. 2008, 320, 1050–1055. [Google Scholar] [CrossRef]
- Vopson, M.; Lepadatu, S. Solving the electrical control of magnetic coercive field paradox. Appl. Phys. Lett. 2014, 105, 122901. [Google Scholar] [CrossRef]
- Boukari, H.; Cavaco, C.; Eyckmans, W.; Lagae, L.; Borghs, G. Voltage assisted magnetic switching in Co50Fe50 interdigitated electrodes on piezoelectric substrates. J. Appl. Phys. 2007, 101, 054903. [Google Scholar] [CrossRef]
- Folen, V.J.; Rado, G.T.; Stader, E.W. Anisotropy of the Magnetoelectric Effect in Cr2O3. Phys. Rev. Lett. 1961, 6, 607–608. [Google Scholar] [CrossRef]
- Rado, G.T.; Folen, V.J. Observation of the Magnetically Induced Magnetoelectric Effect and Evidence for Antiferromagnetic Domains. Phys. Rev. Lett. 1961, 7, 310–311. [Google Scholar] [CrossRef]
- Vopsaroiu, M.; Cain, M.G.; Woolliams, P.D.; Stewart, P.M.W.M.; Wright, C.D.; Tran, Y. Voltage control of the magnetic coercive field: Multiferroic coupling or artifact? J. Appl. Phys. 2011, 109, 066101. [Google Scholar] [CrossRef]
- Matsukura, F.; Tokura, Y.; Ohno, H. Control of magnetism by electric fields. Nat. Nanotechnol. 2015, 10, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Vopsaroiu, M.; Stewart, M.; Hegarty, T.; Muniz-Piniella, A.; McCartney, N.; Cain, M.; Srinivasan, G. Experimental determination of the magnetoelectric coupling coefficient via piezoelectric measurements. Meas. Sci. Technol. 2008, 19, 045106. [Google Scholar] [CrossRef]
- Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Rep. Prog. Phys. 1998, 61, 1267–1324. [Google Scholar] [CrossRef]
- Vellekoop, S.J.L.; Abelmann, L.; Porthun, S.; Lodder, J.C.; Miles, J.J. Calculation of playback signals from MFM images using transfer functions. J. Magn. Magn. Mater. 1999, 193, 474–478. [Google Scholar] [CrossRef]
- Gruverman, A.; Auciello, O.; Tokumoto, H. Imaging and control of domain structures in ferroelectric thin films via scanning force microscopy. Ann. Rev. Mater. Sci. 1998, 28, 101–123. [Google Scholar] [CrossRef]
- Hong, J.W.; Kahng, D.S.; Shin, J.C.; Kim, H.J.; Khim, Z.G. Detection and control of ferroelectric domains by an electrostatic force microscope. J. Vac. Sci. Technol. B 1998, 16, 2942. [Google Scholar] [CrossRef]
- Caruntu, G.; Yourdkhani, A.; Vopsaroiu, M.; Srinivasan, G. Probing the local strain-mediated magnetoelectric coupling in multiferroic nanocomposites by magnetic field-assisted piezoresponse force microscopy. Nanoscale 2012, 4, 3218–3227. [Google Scholar] [CrossRef] [PubMed]
- Yourdkhani, A.; Caruntu, D.; Vopson, M.; Caruntu, G. 1D core-shell magnetoelectric nanocomposites by template-assisted liquid phase deposition. CrystEngComm 2017, 19, 2079–2088. [Google Scholar] [CrossRef]
- Jahns, R.; Knoechel, R.; Quandt, E. Verfahren zur Magnetfeldmessung mit magnoelektrischen Sensoren. Patent DPMA, DE 10 2011 008 866.0, 18 January 2011. [Google Scholar]
- Weiss, P.; Piccard, A. Le phenomene magnetocalorique. J. Phys. Theor. Appl. 1917, 7, 103–109. [Google Scholar] [CrossRef]
- Manosa, L.; Alonso, D.G.; Planes, A.; Bonnot, E.; Barrio, M.; Tamarit, J.-L.; Aksoy, S.; Acet, M. Giant solid-state barocaloric effect in the Ni–Mn–In magnetic shape-memory alloy. Nat. Mater. 2010, 9, 478–481. [Google Scholar] [CrossRef] [PubMed]
- Bonnot, E.; Romero, R.; Mañosa, L.; Vives, E.; Planes, A. Elastocaloric Effect Associated with the Martensitic Transition in Shape-Memory Alloys. Phys. Rev. Lett. 2008, 100, 125901. [Google Scholar] [CrossRef] [PubMed]
- Gschneidner, K.A.; Pecharsky, V.K.; Tsokol, A.O. Recent developments in magnetocaloric materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
- Scott, J.F. Electrocaloric Materials. Annu. Rev. Mater. Res. 2011, 41, 1–12. [Google Scholar] [CrossRef]
- Castan, T.; Planes, A.; Saxena, A. Thermodynamics of ferrotoroidic materials: Toroidocaloric effect. Phys. Rev. B 2012, 85, 144429. [Google Scholar] [CrossRef]
- Reis, M.S. Oscillating adiabatic temperature change of diamagnetic materials. Solid State Commun. 2012, 152, 921–923. [Google Scholar] [CrossRef]
- Alisultanov, Z.Z.; Meilanov, R.P.; Paixao, L.S.; Reis, M.S. Oscillating magnetocaloric effect in quantum nanoribbons. Physica E 2015, 65, 44–50. [Google Scholar] [CrossRef]
- Vopson, M.M. The multicaloric effect in multiferroic materials. Solid State Commun. 2012, 152, 2067–2070. [Google Scholar] [CrossRef]
- Vopson, M.M. Theory of giant-caloric effects in multiferroic materials. J. Phys. D Appl. Phys. 2013, 46, 345304. [Google Scholar] [CrossRef]
- Vopson, M.M. The induced magnetic and electric fields’ paradox leading to multicaloric effects in multiferroics. Solid State Commun. 2016, 231, 14–16. [Google Scholar] [CrossRef]
- Vopson, M.M.; Zhou, D.; Caruntu, G. Multicaloric effect in bi-layer multiferroic composites. Appl. Phys. Lett. 2015, 107, 182905. [Google Scholar] [CrossRef]
- Burdin, D.A.; Chashin, D.V.; Ekonomov, N.A.; Fetisov, L.Y.; Fetisov, Y.K.; Sreenivasulu, G.; Srinivasan, G. Nonlinear magneto-electric effects in ferromagnetic-piezoelectric composites. J. Magn. Magn. Mater. 2014, 358–359, 98–104. [Google Scholar] [CrossRef]
- Fetisov, L.Y.; Baraban, I.A.; Fetisov, Y.K.; Burdin, D.A.; Vopson, M.M. Nonlinear magnetoelectric effects in flexible composite ferromagnetic–piezopolymer structures. J. Magn. Magn. Mater. 2017, 441, 628–634. [Google Scholar] [CrossRef]

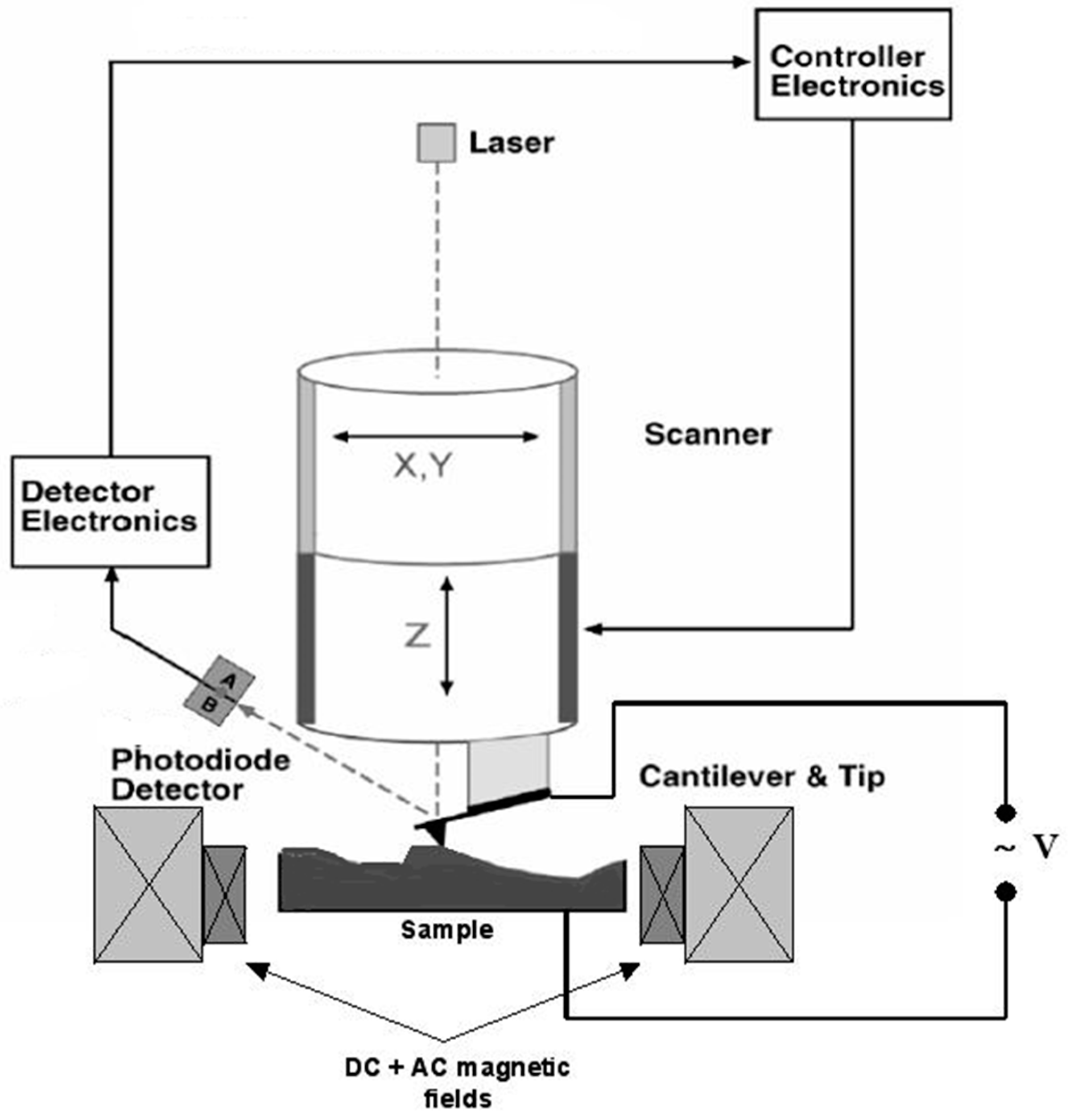
| Measurement Mode | Contact SPM | Non-Contact SPM | |
|---|---|---|---|
| Non-zero applied magnetic field and tip voltage | magnetic tip | Fa + Fe + Fpiezo + Fmag + FH | Fe + Fmag + FH |
| non-magnetic tip | Fa + Fe + Fpiezo | Fe | |
| Non-zero tip voltage, zero applied magnetic field | magnetic tip | Fa + Fe + Fpiezo + Fmag | Fe + Fmag |
| non-magnetic tip | Fa + Fe + Fpiezo | Fe | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vopson, M.M.; Fetisov, Y.K.; Caruntu, G.; Srinivasan, G. Measurement Techniques of the Magneto-Electric Coupling in Multiferroics. Materials 2017, 10, 963. https://doi.org/10.3390/ma10080963
Vopson MM, Fetisov YK, Caruntu G, Srinivasan G. Measurement Techniques of the Magneto-Electric Coupling in Multiferroics. Materials. 2017; 10(8):963. https://doi.org/10.3390/ma10080963
Chicago/Turabian StyleVopson, M. M., Y. K. Fetisov, G. Caruntu, and G. Srinivasan. 2017. "Measurement Techniques of the Magneto-Electric Coupling in Multiferroics" Materials 10, no. 8: 963. https://doi.org/10.3390/ma10080963
APA StyleVopson, M. M., Fetisov, Y. K., Caruntu, G., & Srinivasan, G. (2017). Measurement Techniques of the Magneto-Electric Coupling in Multiferroics. Materials, 10(8), 963. https://doi.org/10.3390/ma10080963







