Formation and Properties of Laser-Induced Periodic Surface Structures on Different Glasses
Abstract
:1. Introduction
2. Results and Discussion
2.1. LIPSS Formation on Different Glasses
- (1)
- (2)
- LIPSS formation on soda-lime-silicate glass is remarkably determined by melt formation in the entire investigated fluence range. Even at the lowest fluence, F = 3.3 J/cm2 (Figure 1g), HSFL are only barely visible. Although the SEM micrograph shows certain points with HSFL-like structures, their formation and appearance is difficult to verify. Moreover, due to melt formation the morphology of the homogenous LSFL pattern fabricated with F = 4.1 J/cm2 (Figure 1h) differs remarkably from LSFL on fused silica and borosilicate glass (Figure 1b,e) generated with the corresponding fluences required for LSFL formation (F > FthLSFL).
- (3)
- At the highest value F = 14.6 J/cm2, the area where melt formation occurs is strongly increased on borosilicate glass (Figure 1f) when compared to fused silica and covers the total ablation spot for soda-lime-silicate glass (Figure 1i). In both cases, the surface of this centered area is very flat without any LIPSS-like surface modulation.
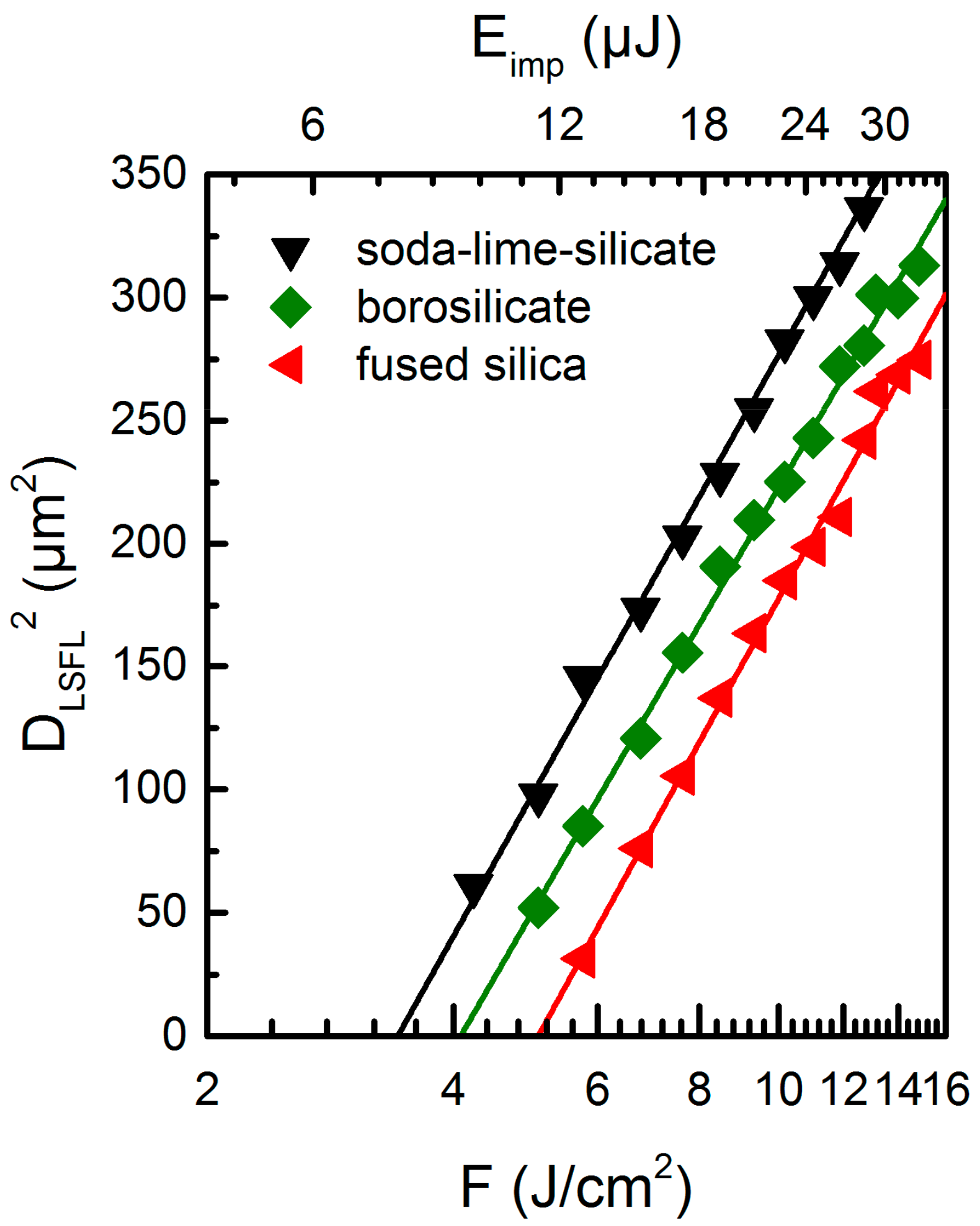
2.2. LSFL Formation Threshold
2.3. Melt Formation and Viscosity
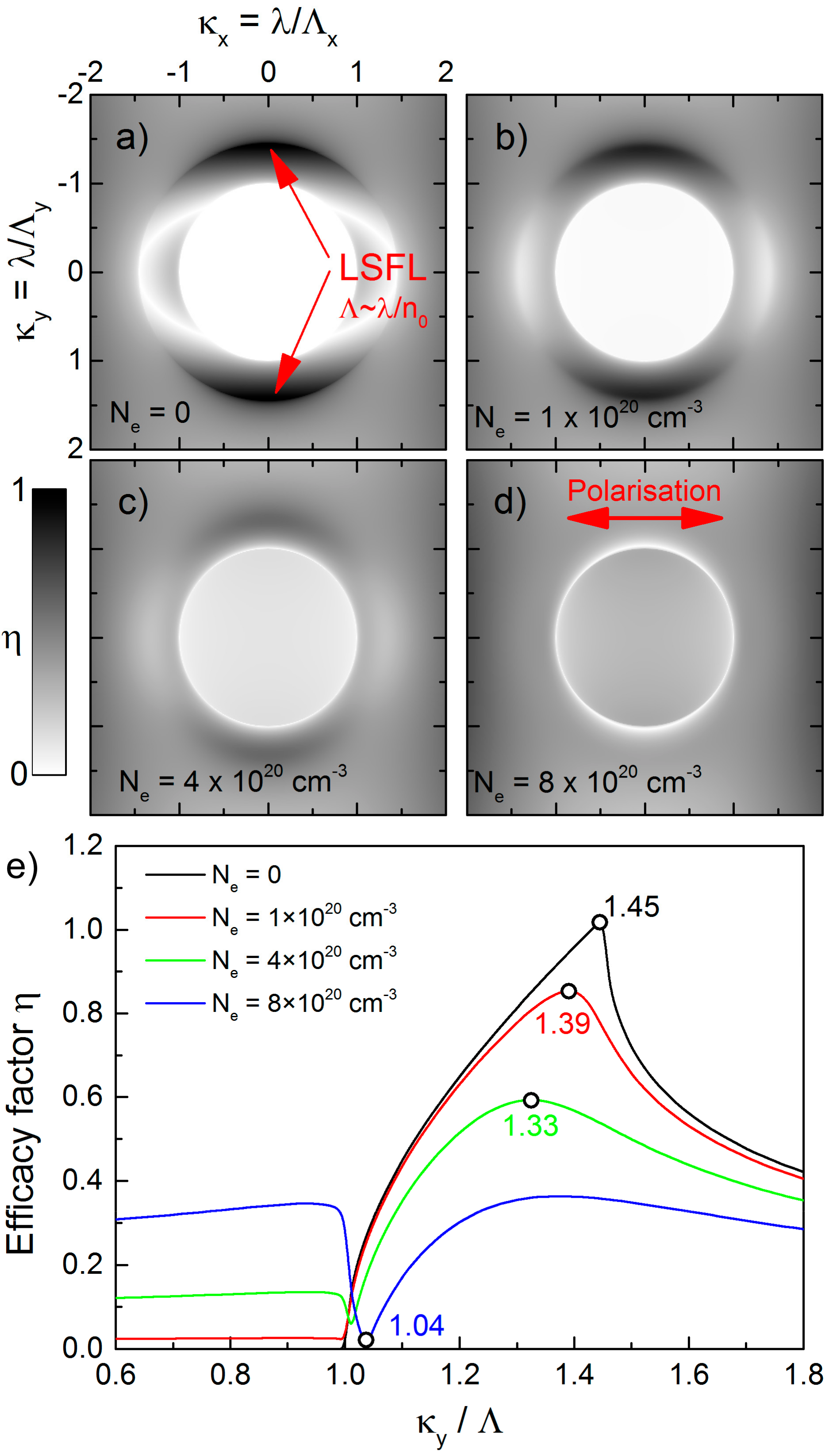
2.4. Theoretical Analysis of LIPSS Formation
3. Materials and Methods
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zimmermann, F.; Plech, A.; Richter, S.; Tunnermann, A.; Nolte, S. The onset of ultrashort pulse-induced nanogratings. Laser Photonics Rev. 2016, 10, 327–334. [Google Scholar] [CrossRef]
- Shimotsuma, Y.; Kazansky, P.G.; Qiu, J.R.; Hirao, K. Self-organized nanogratings in glass irradiated by ultrashort light pulses. Phys. Rev. Lett. 2003, 91, 247405. [Google Scholar] [CrossRef] [PubMed]
- Phillips, K.C.; Gandhi, H.H.; Mazur, E.; Sundaram, S.K. Ultrafast laser processing of materials: A review. Adv. Opt. Photonics 2015, 7, 684–712. [Google Scholar] [CrossRef]
- Bonse, J.; Hohm, S.; Kirner, S.V.; Rosenfeld, A.; Kruger, J. Laser-induced periodic surface structures-a scientific evergreen. IEEE J. Sel. Top. Quant. Electron. 2017, 23, 109–123. [Google Scholar] [CrossRef]
- Muller, F.A.; Kunz, C.; Graf, S. Bio-inspired functional surfaces based on laser-induced periodic surface structures. Materials 2016, 9, 476. [Google Scholar] [CrossRef] [PubMed]
- Birnbaum, M. Semiconductor surface damage produced by ruby lasers. J. Appl. Phys. 1965, 36, 3688–3689. [Google Scholar] [CrossRef]
- Bonse, J.; Kruger, J.; Hohm, S.; Rosenfeld, A. Femtosecond laser-induced periodic surface structures. J. Laser Appl. 2012, 24, 042006. [Google Scholar] [CrossRef]
- Sipe, J.E.; Young, J.F.; Preston, J.S.; Vandriel, H.M. Laser-induced periodic surface-structure. 1. Theory. Phys. Rev. B 1983, 27, 1141–1154. [Google Scholar] [CrossRef]
- Keilmann, F.; Bai, Y.H. Periodic surface-structures frozen into CO2 laser-melted quartz. Appl. Phys. A Mater. Sci. Process. 1982, 29, 9–18. [Google Scholar] [CrossRef]
- Guosheng, Z.; Fauchet, P.M.; Siegman, A.E. Growth of spontaneous periodic surface-structures on solids during laser illumination. Phys. Rev. B 1982, 26, 5366–5381. [Google Scholar] [CrossRef]
- Dufft, D.; Rosenfeld, A.; Das, S.K.; Grunwald, R.; Bonse, J. Femtosecond laser-induced periodic surface structures revisited: A comparative study on zno. J. Appl. Phys. 2009, 105, 034908. [Google Scholar] [CrossRef]
- Reif, J.; Costache, F.; Henyk, M.; Pandelov, S.V. Ripples revisited: Non-classical morphology at the bottom of femtosecond laser ablation craters in transparent dielectrics. Appl. Surf. Sci. 2002, 197, 891–895. [Google Scholar] [CrossRef]
- Borowiec, A.; Haugen, H.K. Subwavelength ripple formation on the surfaces of compound semiconductors irradiated with femtosecond laser pulses. Appl. Phys. Lett. 2003, 82, 4462–4464. [Google Scholar] [CrossRef]
- Li, X.F.; Zhang, C.Y.; Li, H.; Dai, Q.F.; Lan, S.; Tie, S.L. Formation of 100-nm periodic structures on a titanium surface by exploiting the oxidation and third harmonic generation induced by femtosecond laser pulses. Opt. Express 2014, 22, 28086–28099. [Google Scholar] [CrossRef] [PubMed]
- Campbell, E.E.B.; Ashkenasi, D.; Rosenfeld, A. Ultra-short-pulse laser irradiation and ablation of dielectrics. Lasers Mater. Sci. 1999, 301, 123–144. [Google Scholar] [CrossRef]
- Rohloff, M.; Das, S.K.; Hohm, S.; Grunwald, R.; Rosenfeld, A.; Kruger, J.; Bonse, J. Formation of laser-induced periodic surface structures on fused silica upon multiple cross-polarized double-femtosecond-laser-pulse irradiation sequences. J. Appl. Phys. 2011, 110, 014910. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Rohloff, M.; Hohm, S.; Kruger, J.; Bonse, J. Formation of laser-induced periodic surface structures on fused silica upon multiple parallel polarized double-femtosecond-laser-pulse irradiation sequences. Appl. Surf. Sci. 2012, 258, 9233–9236. [Google Scholar] [CrossRef]
- Hohm, S.; Rosenfeld, A.; Kruger, J.; Bonse, J. Femtosecond laser-induced periodic surface structures on silica. J. Appl. Phys. 2012, 112, 014901. [Google Scholar] [CrossRef]
- Hohm, S.; Herzlieb, M.; Rosenfeld, A.; Kruger, J.; Bonse, J. Formation of laser-induced periodic surface structures on fused silica upon two-color double-pulse irradiation. Appl. Phys. Lett. 2013, 103, 254101. [Google Scholar] [CrossRef]
- Hohm, S.; Herzlieb, M.; Rosenfeld, A.; Kruger, J.; Bonse, J. Laser-induced periodic surface structures on fused silica upon cross-polarized two-color double-fs-pulse irradiation. Appl. Surf. Sci. 2015, 336, 39–42. [Google Scholar] [CrossRef]
- Schwarz, S.; Rung, S.; Hellmann, R. Generation of laser-induced periodic surface structures on transparent material-fused silica. Appl. Phys. Lett. 2016, 108, 181607. [Google Scholar] [CrossRef]
- Fang, Z.; Zhao, Y.A.; Shao, J.D. Femtosecond laser-induced periodic surface structure on fused silica surface. Optik 2016, 127, 1171–1175. [Google Scholar] [CrossRef]
- Nieto, D.; Arines, J.; O’connor, G.M.; Flores-Arias, M.T. Single-pulse laser ablation threshold of borosilicate, fused silica, sapphire, and soda-lime glass for pulse widths of 500 fs, 10 ps, 20 ns. Appl. Opt. 2015, 54, 8596–8601. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.M. Simple technique for measurements of pulsed gaussian-beam spot sizes. Opt. Lett. 1982, 7, 196–198. [Google Scholar] [CrossRef] [PubMed]
- Grehn, M.; Seuthe, T.; Hofner, M.; Griga, N.; Theiss, C.; Mermillod-Blondin, A.; Eberstein, M.; Eichler, H.; Bonse, J. Femtosecond-laser induced ablation of silicate glasses and the intrinsic dissociation energy. Opt. Mater. Express 2014, 4, 689–700. [Google Scholar] [CrossRef]
- Sudrie, L.; Couairon, A.; Franco, M.; Lamouroux, B.; Prade, B.; Tzortzakis, S.; Mysyrowicz, A. Femtosecond laser-induced damage and filamentary propagation in fused silica. Phys. Rev. Lett. 2002, 89, 186601. [Google Scholar] [CrossRef] [PubMed]
- Little, D.J.; Ams, M.; Withford, M.J. Influence of bandgap and polarization on photo-ionization: Guidelines for ultrafast laser inscription [invited]. Opt. Mater. Express 2011, 1, 670–677. [Google Scholar] [CrossRef]
- Zaid, M.H.M.; Matori, K.A.; Aziz, S.H.A.; Zakaria, A.; Ghazali, M.S.M. Effect of zno on the physical properties and optical band gap of soda lime silicate glass. Int. J. Mol. Sci. 2012, 13, 7550–7558. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.H. Fundamental condition of glass formation. J. Am. Ceram. Soc. 1947, 30, 277–281. [Google Scholar] [CrossRef]
- Sun, K.H.; Huggins, M.L. Energy additivity in oxygen-containing crystals and glasses. J. Phys. Colloid Chem. 1947, 51, 438–443. [Google Scholar] [CrossRef] [PubMed]
- Martienssen, W.; Warlimont, H. Springer Handbook of Condensed Matter and Materials Data; Springer: Heidelberg, Germany, 2005; p. xviii. 1119p. [Google Scholar]
- Urbain, G.; Bottinga, Y.; Richet, P. Viscosity of liquid silica, silicates and alumino-silicates. Geochim. Cosmochim. Acta 1982, 46, 1061–1072. [Google Scholar] [CrossRef]
- Ben-Yakar, A.; Harkin, A.; Ashmore, J.; Byer, R.L.; Stone, H.A. Thermal and fluid processes of a thin melt zone during femtosecond laser ablation of glass: The formation of rims by single laser pulses. J. Phys. D Appl. Phys. 2007, 40, 1447–1459. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Skoulas, E.; Papadopoulos, A.; Stratakis, E. Convection roll-driven generation of supra-wavelength periodic surface structures on dielectrics upon irradiation with femtosecond pulsed lasers. Phys. Rev. B 2016, 94, 081305. [Google Scholar] [CrossRef]
- Battezzati, L.; Greer, A.L. The viscosity of liquid-metals and alloys. Acta Metall. 1989, 37, 1791–1802. [Google Scholar] [CrossRef]
- Bonse, J.; Munz, M.; Sturm, H. Structure formation on the surface of indium phosphide irradiated by femtosecond laser pulses. J. Appl. Phys. 2005, 97, 013538. [Google Scholar] [CrossRef]
- Derrien, T.J.Y.; Kruger, J.; Bonse, J. Properties of surface plasmon polaritons on lossy materials: Lifetimes, periods and excitation conditions. J. Opt. 2016, 18, 115007. [Google Scholar] [CrossRef]
- Temnov, V.V. Ultrafast Laser-Induced Phenomena in Solids Studied by Time-Resolved Interferometry; University of Duisburg-Essen: Duisburg, Germany, 2004. [Google Scholar]
- Wray, J.H.; Neu, J.T. Refractive index of several glasses as a function of wavelength and temperature. J. Opt. Soc. Am. 1969, 59, 774–776. [Google Scholar] [CrossRef]
- Huang, M.; Zhao, F.L.; Cheng, Y.; Xu, N.S.; Xu, Z.Z. Origin of laser-induced near-subwavelength ripples: Interference between surface plasmons and incident laser. ACS Nano 2009, 3, 4062–4070. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, A.; Lorenz, M.; Stoian, R.; Ashkenasi, D. Ultrashort-laser-pulse damage threshold of transparent materials and the role of incubation. Appl. Phys. A Mater. Sci. Process. 1999, 69, S373–S376. [Google Scholar] [CrossRef]
- Rubin, M. Optical-properties of soda lime silica glasses. Solar Energy Mater. 1985, 12, 275–288. [Google Scholar] [CrossRef]
- Schott. Available online: http://www.schott.com (accessed on 22 June 2017).
- Gurevich, E.L.; Levy, Y.; Gurevich, S.V.; Bulgakova, N.M. Role of the temperature dynamics in formation of nanopatterns upon single femtosecond laser pulses on gold. Phys. Rev. B 2017, 95, 054305. [Google Scholar] [CrossRef]
- Volkov, A.N.; Zhigilei, L.V. Melt dynamics and melt-through time in continuous wave laser heating of metal films: Contributions of the recoil vapor pressure and marangoni effects. Int. J. Heat Mass Transf. 2017, 112, 300–317. [Google Scholar] [CrossRef]
- Graf, S.; Staupendahl, G.; Gerling, P.; Muller, F.A. Optical constants n and kappa of various technical and optical glasses at lambda = 10.59 mu m. J. Appl. Phys. 2013, 113, 013101. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Stratakis, E.; Ranella, A.; Fotakis, C. Biomimetic micro/nanostructured functional surfaces for microfluidic and tissue engineering applications. Biomicrofluidics 2011, 5, 013411. [Google Scholar] [CrossRef] [PubMed]
- Flemming, R.G.; Murphy, C.J.; Abrams, G.A.; Goodman, S.L.; Nealey, P.F. Effects of synthetic micro- and nano-structured surfaces on cell behavior. Biomaterials 1999, 20, 573–588. [Google Scholar] [CrossRef]
- Martinez-Calderon, M.; Manso-Silvan, M.; Rodriguez, A.; Gomez-Aranzadi, M.; Garcia-Ruiz, J.P.; Olaizola, S.M.; Martin-Palma, R.J. Surface micro- and nano-texturing of stainless steel by femtosecond laser for the control of cell migration. Sci. Rep. 2016, 6, 36296. [Google Scholar] [CrossRef] [PubMed]
- Yu, E.; Kim, S.C.; Lee, H.J.; Oh, K.H.; Moon, M.W. Extreme wettability of nanostructured glass fabricated by non-lithographic, anisotropic etching. Sci. Rep. 2015, 5, 9362. [Google Scholar] [CrossRef] [PubMed]
- Skoulas, E.; Manousaki, A.; Fotakis, C.; Stratakis, E. Biomimetic surface structuring using cylindrical vector femtosecond laser beams. Sci. Rep. 2017, 7, 45114. [Google Scholar] [CrossRef] [PubMed]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gräf, S.; Kunz, C.; Müller, F.A. Formation and Properties of Laser-Induced Periodic Surface Structures on Different Glasses. Materials 2017, 10, 933. https://doi.org/10.3390/ma10080933
Gräf S, Kunz C, Müller FA. Formation and Properties of Laser-Induced Periodic Surface Structures on Different Glasses. Materials. 2017; 10(8):933. https://doi.org/10.3390/ma10080933
Chicago/Turabian StyleGräf, Stephan, Clemens Kunz, and Frank A. Müller. 2017. "Formation and Properties of Laser-Induced Periodic Surface Structures on Different Glasses" Materials 10, no. 8: 933. https://doi.org/10.3390/ma10080933
APA StyleGräf, S., Kunz, C., & Müller, F. A. (2017). Formation and Properties of Laser-Induced Periodic Surface Structures on Different Glasses. Materials, 10(8), 933. https://doi.org/10.3390/ma10080933




