Micro-Mechanical Viscoelastic Properties of Crosslinked Hydrogels Using the Nano-Epsilon Dot Method
Abstract
1. Introduction
2. Results
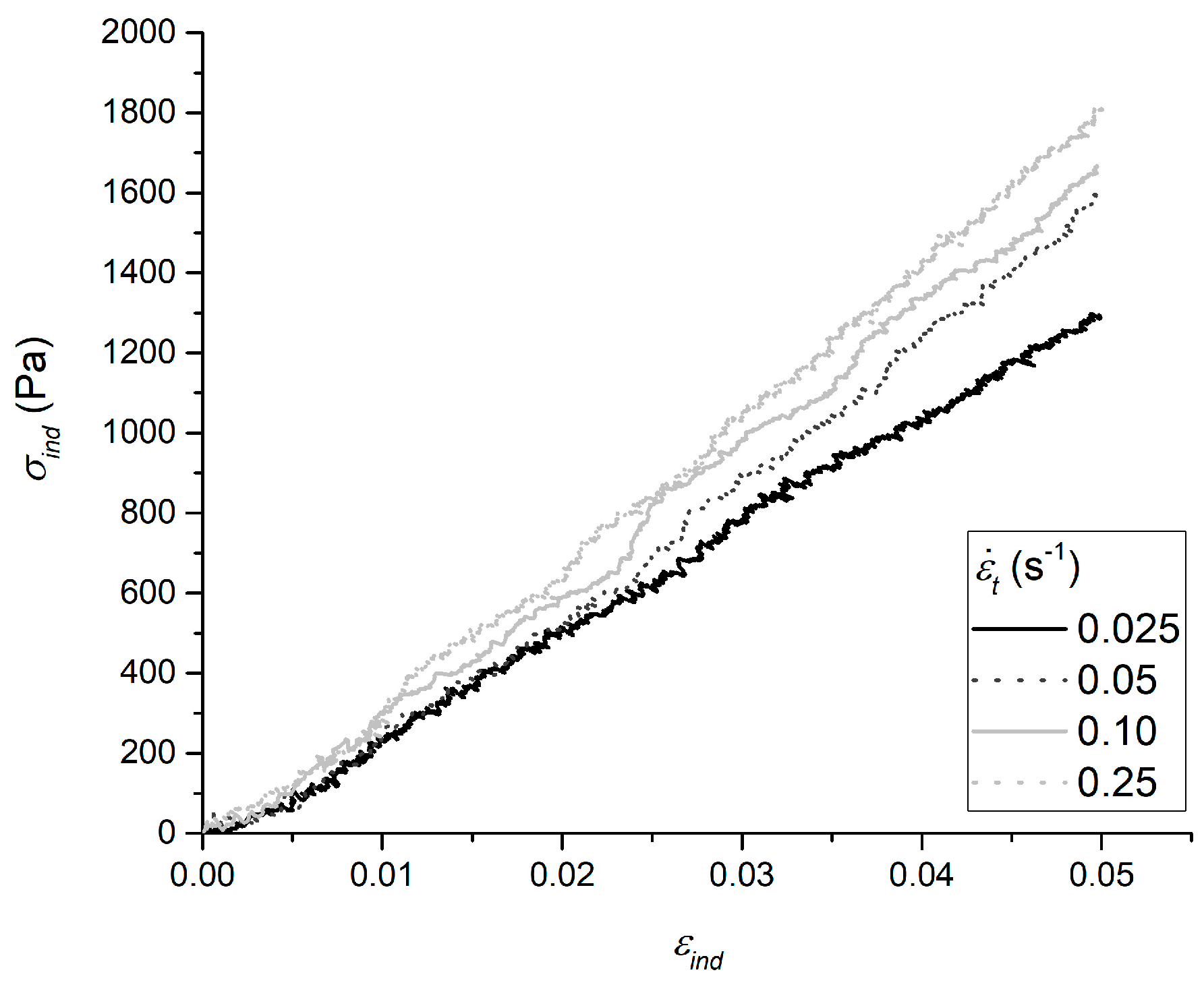
2.1. Apparent Elastic Moduli and Actual Sample Indentation Strain Rate
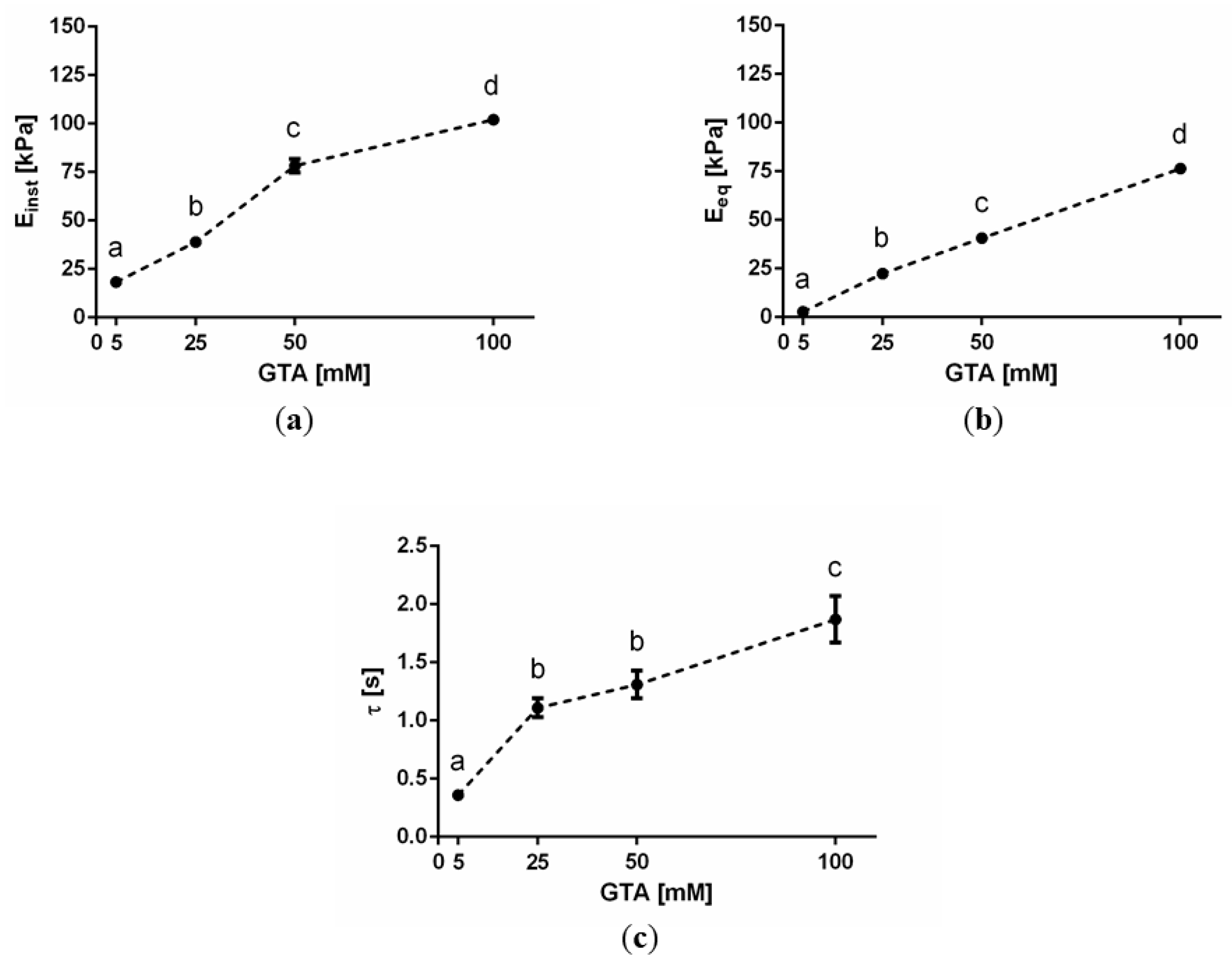
2.2. Maxwell Standard Linear Solid (SLS) Lumped Viscoelastic Constants
3. Discussion
- (i)
- the scale-dependency of a sample’s mechanical properties, i.e., surface micro-mechanical properties could be different from bulk volumetric ones [40];
- (ii)
- differences in testing and analysis methods, i.e., nano-indentation and unconfined compression techniques use different definitions of stress and strain, different models, etc., possibly affecting the mechanical properties obtained thereof [18]; and
- (iii)
- sample volumetric heterogeneity, i.e., GTA-crosslinking might be not uniform within the gelatin hydrogel volume due to the passive diffusion-reaction mechanism, which is established when submerging physically crosslinked gelatin hydrogels in GTA solution. This may lead to a highly crosslinked hydrogel shell and less crosslinked core, resulting in a lower increase of bulk mechanical properties with increasing GTA [41].
4. Materials and Methods
4.1. Sample Preparation
4.2. Nano-Indentation Measurements
4.3. Data Analyses and Viscoelastic Parameters Identification
4.4. Statistical Analyses
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Frantz, C.; Stewart, K.M.; Weaver, V.M. The extracellular matrix at a glance. J. Cell Sci. 2010, 123, 4195–4200. [Google Scholar] [CrossRef] [PubMed]
- Mammoto, T.; Mammoto, A.; Ingber, D.E. Mechanobiology and developmental control. Annu. Rev. Cell Dev. Biol. 2013, 29, 27–61. [Google Scholar] [CrossRef] [PubMed]
- Carver, W.; Goldsmith, E.C. Regulation of tissue fibrosis by the biomechanical environment. Biomed. Res. Int. 2013, 2013, 101979. [Google Scholar] [CrossRef] [PubMed]
- Mattei, G.; Ferretti, C.; Tirella, A.; Ahluwalia, A.; Mattioli-Belmonte, M. Decoupling the role of stiffness from other hydroxyapatite signalling cues in periosteal derived stem cell differentiation. Sci. Rep. 2015, 5, 10778. [Google Scholar] [CrossRef] [PubMed]
- Mattei, G.; Magliaro, C.; Giusti, S.; Ramachandran, S.D.; Heinz, S.; Braspenning, J.; Ahluwalia, A. On the adhesion-cohesion balance and oxygen consumption characteristics of liver organoids. PLoS ONE 2017, 12, e0173206. [Google Scholar] [CrossRef] [PubMed]
- Ingber, D.E. Cellular mechanotransduction: Putting all the pieces together again. FASEB J. 2006, 20, 811–827. [Google Scholar] [CrossRef] [PubMed]
- Vogel, V. Mechanotransduction involving multimodular proteins: Converting force into biochemical signals. Annu. Rev. Biophys. Biomol. Struct. 2006, 35, 459–488. [Google Scholar] [CrossRef] [PubMed]
- De Volder, R.; Kong, H. Biomaterials for studies in cellular mechanotransduction. In Mechanobiology of Cell-Cell and Cell-Matrix Interactions; Springer: Boston, MA, USA, 2011; pp. 267–277. [Google Scholar]
- Tibbitt, M.W.; Anseth, K.S. Hydrogels as extracellular matrix mimics for 3D cell culture. Biotechnol. Bioeng. 2009, 103, 655–663. [Google Scholar] [CrossRef] [PubMed]
- Geckil, H.; Xu, F.; Zhang, X.; Moon, S.; Demirci, U. Engineering hydrogels as extracellular matrix mimics. Nanomedicine 2010, 5, 469–484. [Google Scholar] [CrossRef] [PubMed]
- Chai, Q.; Jiao, Y.; Yu, X. Hydrogels for biomedical applications: Their characteristics and the mechanisms behind them. Gels 2017, 3, 6. [Google Scholar] [CrossRef]
- Ahearne, M. Introduction to cell-hydrogel mechanosensing. Interface Focus 2014, 4, 20130038. [Google Scholar] [CrossRef] [PubMed]
- Tirella, A.; La Marca, M.; Brace, L.-A.; Mattei, G.; Aylott, J.W.; Ahluwalia, A. Nano-in-Micro self-reporting hydrogel constructs. J. Biomed. Nanotechnol. 2015, 11, 1451–1460. [Google Scholar] [CrossRef] [PubMed]
- Watt, F.M.; Huck, W.T.S. Role of the extracellular matrix in regulating stem cell fate. Nat. Rev. Mol. Cell Biol. 2013, 14, 467–473. [Google Scholar] [CrossRef] [PubMed]
- Mason, B.N.; Califano, J.P.; Reinhart-King, C.A. Matrix stiffness: A regulator of cellular behavior and tissue formation. Eng. Biomater. Regen. Med. 2012, 1, 19–37. [Google Scholar]
- Engler, A.J.; Sen, S.; Sweeney, H.L.; Discher, D.E. Matrix elasticity directs stem cell lineage specification. Cell 2006, 126, 677–689. [Google Scholar] [CrossRef] [PubMed]
- Handorf, A.M.; Zhou, Y.; Halanski, M.A.; Li, W.-J. Tissue stiffness dictates development, homeostasis, and disease progression. Organogenesis 2015, 11, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Mattei, G.; Ahluwalia, A. Sample, testing and analysis variables affecting liver mechanical properties: A review. Acta Biomater. 2016, 45, 60–71. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Mattei, G.; Tirella, A.; Gallone, G.; Ahluwalia, A. Viscoleastic characterisation of pig liver in unconfined compression. J. Biomech. 2013, 47, 2641–2646. [Google Scholar] [CrossRef] [PubMed]
- Tirella, A.; Mattei, G.; Ahluwalia, A. Strain rate viscoelastic analysis of soft and highly hydrated biomaterials. J. Biomed. Mater. Res. Part A 2014, 102, 3352–3360. [Google Scholar] [CrossRef] [PubMed]
- Martucci, J.F.; Ruseckaite, R.A.; Vázquez, A. Creep of glutaraldehyde-crosslinked gelatin films. Mater. Sci. Eng. A 2006, 435–436, 681–686. [Google Scholar] [CrossRef]
- Knapp, D.M. Rheology of reconstituted type I collagen gel in confined compression. J. Rheol. 1997, 41, 971. [Google Scholar] [CrossRef]
- Janmey, P.A. Rheology of Fibrin Clots. VI. Stress relaxation, creep, and differential dynamic modulus of fine clots in large shearing deformations. J. Rheol. 1983, 27, 135. [Google Scholar] [CrossRef]
- Chaudhuri, O.; Gu, L.; Darnell, M.; Klumpers, D.; Bencherif, S.A.; Weaver, J.C.; Huebsch, N.; Mooney, D.J. Substrate stress relaxation regulates cell spreading. Nat. Commun. 2015, 6, 6364. [Google Scholar] [CrossRef] [PubMed]
- Caliari, S.R.; Burdick, J.A. A practical guide to hydrogels for cell culture. Nat. Methods 2016, 13, 405–414. [Google Scholar] [CrossRef] [PubMed]
- Oyen, M.L. Nanoindentation of biological and biomimetic materials. Exp. Tech. 2013, 37, 73–87. [Google Scholar] [CrossRef]
- Oyen, M.L.; Cook, R.F. A practical guide for analysis of nanoindentation data. J. Mech. Behav. Biomed. Mater. 2009, 2, 396–407. [Google Scholar] [CrossRef] [PubMed]
- Oyen, M.L. Mechanical characterisation of hydrogel materials. Int. Mater. Rev. 2013, 59, 44–59. [Google Scholar] [CrossRef]
- Mattei, G.; Gruca, G.; Rijnveld, N.; Ahluwalia, A. The nano-epsilon dot method for strain rate viscoelastic characterisation of soft biomaterials by spherical nano-indentation. J. Mech. Behav. Biomed. Mater. 2015, 50, 150–159. [Google Scholar] [CrossRef] [PubMed]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Li, X.; Bhushan, B. A review of nanoindentation continuous stiffness measurement technique and its applications. Mater. Charact. 2002, 48, 11–36. [Google Scholar] [CrossRef]
- Franke, O.; Göken, M.; Meyers, M.A.; Durst, K.; Hodge, A.M. Dynamic nanoindentation of articular porcine cartilage. Mater. Sci. Eng. C 2011, 31, 789–795. [Google Scholar] [CrossRef]
- Hayes, S.A.; Goruppa, A.A.; Jones, F.R. Dynamic nanoindentation as a tool for the examination of polymeric materials. J. Mater. Res. 2011, 19, 3298–3306. [Google Scholar] [CrossRef]
- Dawson, E.; Mapili, G.; Erickson, K.; Taqvi, S.; Roy, K. Biomaterials for stem cell differentiation. Adv. Drug Deliv. Rev. 2008, 60, 215–228. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.; Pacelli, S.; Haj, A.; Dua, H.; Hopkinson, A.; White, L.; Rose, F. Gelatin-Based materials in ocular tissue engineering. Materials 2014, 7, 3106–3135. [Google Scholar] [CrossRef]
- Olde Damink, L.H.H.; Dijkstra, P.J.; Van Luyn, M.J.A.; Van Wachem, P.B.; Nieuwenhuis, P.; Feijen, J. Glutaraldehyde as a crosslinking agent for collagen-based biomaterials. J. Mater. Sci. Mater. Med. 1995, 6, 460–472. [Google Scholar] [CrossRef]
- Bigi, A.; Cojazzi, G.; Panzavolta, S.; Rubini, K.; Roveri, N. Mechanical and thermal properties of gelatin films at different degrees of glutaraldehyde crosslinking. Biomaterials 2001, 22, 763–768. [Google Scholar] [CrossRef]
- Kaufman, J.D.; Miller, G.J.; Morgan, E.F.; Klapperich, C.M. Time-dependent mechanical characterization of poly(2-hydroxyethyl methacrylate) hydrogels using nanoindentation and unconfined compression. J. Mater. Res. 2008, 23, 1472–1481. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Orsi, G.; Fagnano, M.; De Maria, C.; Montemurro, F.; Vozzi, G. A new 3D concentration gradient maker and its application in building hydrogels with a 3D stiffness gradient. J. Tissue Eng. Regen. Med. 2017, 11, 256–264. [Google Scholar] [CrossRef] [PubMed]
- Chavan, D.; Van De Watering, T.C.; Gruca, G.; Rector, J.H.; Heeck, K.; Slaman, M.; Iannuzzi, D. Ferrule-top nanoindenter: An optomechanical fiber sensor for nanoindentation. Rev. Sci. Instrum. 2012, 83. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Qiang, B.; Greenleaf, J. Comparison of the surface wave method and the indentation method for measuring the elasticity of gelatin phantoms of different concentrations. Ultrasonics 2011, 51, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Czerner, M.; Fellay, L.S.; Suarez, M.P.; Frontini, P.M.; Fasce, L.A. Determination of elastic modulus of gelatin gels by indentation experiments. Procedia Mater. Sci. 2015, 8, 287–296. [Google Scholar] [CrossRef]
- Clayton, E.H.; Okamoto, R.J.; Wilson, K.S.; Namani, R.; Bayly, P.V. Comparison of dynamic mechanical testing and mr elastography of biomaterials. Appl. Imaging Tech. Mech. Mater. Struct. 2012, 4, 143–150. [Google Scholar]
- Pulieri, E.; Chiono, V.; Ciardelli, G.; Vozzi, G.; Ahluwalia, A.; Domenici, C.; Vozzi, F.; Giusti, P. Chitosan/gelatin blends for biomedical applications. J. Biomed. Mater. Res. Part A 2008, 86, 311–322. [Google Scholar] [CrossRef] [PubMed]
- Roylance, D. Engineering viscoelasticity. Dep. Mater. Sci. Eng. Inst. Technol. Camb. MA 2001, 2139, 1–37. [Google Scholar]
| GTA (mM) | (s−1) | (kPa) | (s−1) |
|---|---|---|---|
| 5 | 0.025 | 5.3 ± 0.3 | 0.021 ± 0.001 |
| 0.05 | 9.3 ± 0.8 | 0.047 ± 0.001 | |
| 0.10 | 12.4 ± 0.6 | 0.070 ± 0.001 | |
| 0.25 | 17.3 ± 1.1 | 0.150 ± 0.001 | |
| 25 | 0.025 | 27.5 ± 0.6 | 0.012 ± 0.001 |
| 0.05 | 30.9 ± 2.1 | 0.024 ± 0.001 | |
| 0.10 | 35.2 ± 0.8 | 0.044 ± 0.001 | |
| 0.25 | 37.3 ± 0.9 | 0.124 ± 0.001 | |
| 50 | 0.025 | 53.9 ± 0.8 | 0.008 ± 0.001 |
| 0.05 | 57.8 ± 0.6 | 0.016 ± 0.001 | |
| 0.10 | 62.9 ± 0.2 | 0.031 ± 0.001 | |
| 0.25 | 65.3 ± 1.9 | 0.098 ± 0.001 | |
| 100 | 0.025 | 76.7 ± 2.9 | 0.006 ± 0.001 |
| 0.05 | 79.7 ± 1.3 | 0.013 ± 0.001 | |
| 0.10 | 83.0 ± 1.3 | 0.025 ± 0.001 | |
| 0.25 | 84.8 ± 1.1 | 0.067 ± 0.001 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mattei, G.; Cacopardo, L.; Ahluwalia, A. Micro-Mechanical Viscoelastic Properties of Crosslinked Hydrogels Using the Nano-Epsilon Dot Method. Materials 2017, 10, 889. https://doi.org/10.3390/ma10080889
Mattei G, Cacopardo L, Ahluwalia A. Micro-Mechanical Viscoelastic Properties of Crosslinked Hydrogels Using the Nano-Epsilon Dot Method. Materials. 2017; 10(8):889. https://doi.org/10.3390/ma10080889
Chicago/Turabian StyleMattei, Giorgio, Ludovica Cacopardo, and Arti Ahluwalia. 2017. "Micro-Mechanical Viscoelastic Properties of Crosslinked Hydrogels Using the Nano-Epsilon Dot Method" Materials 10, no. 8: 889. https://doi.org/10.3390/ma10080889
APA StyleMattei, G., Cacopardo, L., & Ahluwalia, A. (2017). Micro-Mechanical Viscoelastic Properties of Crosslinked Hydrogels Using the Nano-Epsilon Dot Method. Materials, 10(8), 889. https://doi.org/10.3390/ma10080889






